密码学(5)
密码学入门5(棋盘密码)

制作者:0风雨中的回忆0
普莱菲尔密码
加密 ①假设密匙为crazydog 记住密匙一定要字母不重复,然后按字母表顺序排 前面有的自动跳过,一般i,L看做同一字母,但本文中例子是去掉Z
②输入明文:story ③对照密码表:54 15 12 21 41 ④得到密文:54 15 12 21 41
⑤最后,按照钥匙字字母顺序「ACGOR」依次抄下该字下整行讯息,形成新 密文。如下: FAXDF ADDDG DGFFF AFAXX AFAFX(输出密文)
注:解密只需要反向加密就不多说了
制作者:0风雨中的回忆0
ADFGVX密码
拓展介绍
在实际应用中,移位钥匙字通常有两打字符那么长,且分解钥匙和移位钥匙 都是每天更换的。 在 1918年 6月,再加入一个字 V 扩充。变成以 6 × 6 格共 36 个字符加密。 这使得所有英文字母(不再将 I 和 J 视为同一个字)以及数字 0 到 9 都可混 合使用。这次增改是因为以原来的加密法发送含有大量数字的简短信息有问 题。
他破解的方法是依靠于找到多份开头相同的讯息这表示说它们是被相同的分解钥匙和移位钥匙加密的
制作者:0风雨中的回忆0
ADFGVX密码
ADFGVX密码是德军在第一次世界大战中使用的栏块密码。事实上,它是早 先一种密码 ADFGX 的增补版。1918年3月Fritz Nebel上校发明了这种密码, 并提倡使用。它结合了改良过的Polybius方格替代密码与单行换位密码。这个 密码以使用于密文当中六个字母 A, D, F, G, V, X命名。ADFGVX 是被法国陆 军中尉 Georges Painvin 所破解的。以古典密码学的标准来说,此密码破解 的工作是属于格外困难的,在这期间,Painvin 更因此健康蒙受了严重损伤。 他破解的方法是依靠于找到多份开头相同的讯息,这表示说它们是被相同的 分解钥匙和移位钥匙加密的。
信息安全导论5密码学数学基础

2024/4/3
13
3、模运算:对于某个固定模m的同余式可以象普通的等式那 样相加相减和相乘:
a(mod m)±b(mod m)=(a±b)(mod m)
a(mod m)*b(mod m)=a*b(mod m)
例:由同余式演算证明560-1是56的倍数,223-1是47的倍数。
解:
注意53=125≡13(mod56) 于是有56≡169≡1(mod56) 对同余式的两边同时升到10次幂, 即有56∣(560-1)。 其次, 注意26=64≡-30(mod47),
2024/4/3
5
互素与最大公约数
最大公约数(最大公因子):
若a,b,c∈Z,如果c∣a,c∣b,称c是a和b的公约数。正 整数d称为a和b的最大公约数(记d=gcd(a,b)或(a,b)) ,如 果它满足:
d是a和b的公约数。 对a和b的任何一个公约数c有c∣d。
等价的定义形式是:
gcd(a,b)=max{k: k∣a,k∣b} 若gcd(a,b)=1,称a与b是互素的。
2024/4/3
4
整除基本性质 a|a; b≠0,b | 0;
If a|b,b|c,then a|c;
if a|1, then a=±1; if a|b, and b|a,then a=±b; if b|g and b|h, then b|(mg+nh),for any integers m and n 注意: if a=0 mod n, then n|a
g c d ( a ,b ) = P 1 m in ( e 1 ,f1 )P 2 m in ( e 2 ,f2 )
P m in ( e t,ft) t
lc m ( a ,b ) = P 1 m a x ( e 1 ,f 1 ) P 2 m a x ( e 2 ,f2 )
密码学5补充 S-DES解密算法细节
R1=(1 1 0 0) E/P(R1)=(0 1 1 0 1 0 0 1)
III. 将E/P(R1)与子密钥 进行异或 与子密钥k2进行异或 与子密钥 E/P(R1)=(0 1 1 0 1 0 0 1) k2=(0 1 0 0 0 0 1 1) c2=E/P(R1)⊕ c2=E/P(R1)⊕k2=(0 0 1 0 1 0 1 0) IV. 将c2左右 位分别进行 、S1盒变换 左右4位分别进行 左右 位分别进行S0、 盒变换 S0=
1 3 0 3 0 2 2 1 3 1 1 3 2 0 3 2 0 2 3 2 1 0 0 1 2 1 1 0 3 3 0 3
S1=
位输入码第1、 位的十进制数作为行标 位的十进制数作为行标i 将4位输入码第 、4位的十进制数作为行标 (0~3) 位输入码第 位输入码第2、 位的十进制数作为列标 位的十进制数作为列标j 将4位输入码第 、3位的十进制数作为列标 (0~3) 位输入码第 即得到与S 对应的2位输入码 即得到与 ij对应的 位输入码
L7=(1 1 1 0), 故 S0(L7)=S020=0=(0 0) R7=(0 1 0 1), 故 S1(R7)=S122=1=(0 1) 前后拼接后得: 前后拼接后得: L8=(0 0 0 1) V. 将L8进行 位置换 进行4位置换 进行 位置换P4 P4=
1 2 3 4 2 4 3 1
于是:L9=P4(L8)=(0 1 0 0) 于是:
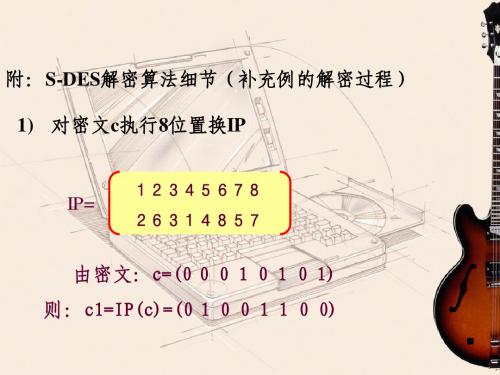
解密算法细节( 附:S-DES解密算法细节(补充例的解密过程) 解密算法细节 补充例的解密过程) 1) 对密文 执行8位置换 对密文c执行 位置换 执行 位置换IP
1 2 3 4 5 6 7 8 2 6 3 1 4 8 5 7
IP=
由密文:c=(0 0 0 1 0 1 0 1) 由密文: 则:c1=IP(c)=(0 1 0 0 1 1 0 0)
应用密码学习题5

习题五
1. 什么是篡改检测码(MDC)?MDC 是如何产生和怎样使用的?消息认证码(MAC)
是MDC 吗?(消息的)数字签名是MDC 吗?
2. 什么是随机预言机?随机预言机存在吗?随机预言机的行为是如何逼近现实世界的?
3. 设杂凑函数的输出空间大小为2160,找到该杂凑函数碰撞所的花费时间期望值是什么?
4. 为什么说杂凑函数实际上是不可逆的?
5. 对称和非对称数据完整性技术的主要区别是什么?
6. “来自Malice 的数据完整性”安全性概念?
7. RSA-OAEP 算法的密文输出是一个有效的MDC 吗?
8. 设f: {0, 1}*→{0, 1}*为一保长单向函数,证明g(x) =f(x)⊕x也是单向函数。
9. 设 f(x),g(x)都是单向函数,问f(x)+g(x),f(x)g(x), f(g(x)) 是否都是单向函数?指出哪
个是?哪个不是?并给出直观说明。
应用密码学习题答案5

《应用密码学》习题和思考题答案第5章 对称密码体制5-1 画出分组密码算法的原理框图,并解释其基本工作原理。
答:图5-1 分组密码原理框图1210-t 1210-t )分组密码处理的单位是一组明文,即将明文消息编码后的数字序列im m m m ,,,,210 划分成长为L 位的组()0121,,,,L m m m m m -=,各个长为L 的分组分别在密钥()0121,,,,t k k k k k -= (密钥长为t )的控制下变换成与明文组等长的一组密文输出数字序列()0121,,,,L c c c c c -= 。
L 通常为64或128。
解密过程是加密的逆过程。
5-2 为了保证分组密码算法的安全强度,对分组密码算法的要求有哪些? 答:(1)分组长度足够大;(2)密钥量足够大;(3)密码变换足够复杂。
5-3 什么是SP 网络?答:SP 网络就是由多重S 变换和P 变换组合成的变换网络,即迭代密码,它是乘积密码的一种,由Shannon 提出。
其基本操作是S 变换(代替)和P 变换(换位),前者称为S 盒,后者被称为P 盒。
S 盒的作用是起到混乱作用,P 盒的作用是起到扩散的作用。
5-4 什么是雪崩效应?答:雪崩效应是指输入(明文或密钥)即使只有很小的变化,也会导致输出发生巨大变化的现象。
即明文的一个比特的变化应该引起密文许多比特的改变。
5-5 什么是Feistel 密码结构?Feistel 密码结构的实现依赖的主要参数有哪些? 答:1K nK i密文明文图5-6 Feistel密码结构Feistel 密码结构如图5-6所示。
加密算法的输入是长为2w 位的明文和密钥K ,明文被均分为长度为w 位的0L 和0R 两部分。
这两部分经过n 轮迭代后交换位置组合在一起成为密文。
其运算逻辑关系为:1(1,2,,)i i L R i n -==11(,)(1,2,,)i i i i R L F R K i n --=⊕=每轮迭代都有相同的结构。
现代密码学第5章:序列密码

密钥流生成器的分解
k
k
驱动子 系统
非线性 组合子 系统
zi
25
常见的两种密钥流产生器
目前最为流行和实用的密钥流产生器如 图所示,其驱动部分是一个或多个线性反馈 移位寄存器。
LFSR
………
LFSR1
LFSR2 ……
F
zi
F
zi
LFSRn
26
KG的一般结构
通常,人们总是把KG设计得具有一定 的结构特点,从而可以分析和论证其强度, 以增加使用者的置信度。一般有以下模式:
23
同步序列密码密钥流产生器
由于具有非线性的υ的有限状态自动机理 论很不完善,相应的密钥流产生器的分析工 作受到极大的限制。相反地,当采用线性的 φ和非线性的ψ时,将能够进行深入的分析 并可以得到好的生成器。为方便讨论,可将 这类生成器分成驱动部分和非线性组合部分 (如下图)。 驱动部分控制生成器的状态转移,并为 非线性组合部分提供统计性能好的序列;而 非线性组合部分要利用这些序列组合出满足 要求的密钥流序列。
6
1.1 同步序列密码
根据加密器中记忆元件的存储状态σi是 否依赖于输入的明文字符,序列密码可进一 步分成同步和自同步两种。 σi独立于明文字符的叫做同步序列密码, 否则叫做自同步序列密码。由于自同步序列 密码的密钥流的产生与明文有关,因而较难 从理论上进行分析。目前大多数研究成果都 是关于同步序列密码的。
18
密钥序列生成器(KG)基本要求
人们就目前的想象和预见,对KG提出 了以下基本要求: 种子密钥k的变化量足够大,一般应 在2128以上; KG产生的密钥序列k具极大周期,一 般应不小于255; k具有均匀的n-元分布,即在一个周 期环上,某特定形式的n-长bit串与其求反, 两者出现的频数大抵相当(例如,均匀的游 程分布);
密码学笔记(5)——Rabin密码体制和语义安全性

密码学笔记(5)——Rabin密码体制和语义安全性⼀、Rabin密码体制 Rabin密码体制是RSA密码体制的⼀种,假定模数n=pq不能被分解,该类体制对于选择明⽂攻击是计算安全的。
因此,Rabin密码体制提供了⼀个可证明安全的密码体制的例⼦:假定分解整数问题是整数上不可⾏的,那么Rabin密码体制是安全的。
Thm1 (Rabin密码体制)设n=pq,其中p和q是素数,且p,q \equiv 3 (mod \, 4),设P=C=Z^{\star}_{n},且定义\kappa =\{(n,p,q)\}对K=(n,p,q),定义e_{K}(x)=x^{2} (mod \, n)和d_{K}=\sqrt{y} (mod \, n)n为公钥,p和q为私钥。
注:条件p,q \equiv 3 (mod \, 4)可以省去,条件P=C=Z^n_{\star}也可以弱化为P=C=Z^n,只是在使⽤更多的限制性描述的时候,简化了许多⽅⾯的计算和密码体制分析。
注意看到这个函数y=x^{2}对于加密来说不是⼀个单射,所以解密不能以⼀种明显的⽅式完成,特别的,对于y \equiv x^{2} (mod \, n),对于某⼀个x \in Z^{\star}_{n},存在y模n的是个解,除⾮有其他的冗余信息,否则⽆法确认是那⼀个值。
从Bob的观点来看解密问题,它有⼀个密⽂y,要想得到x使得x^2 \equiv y(mod \, n)这是⼀个关于Z_{n}中未知元x的⼆次⽅程,解密需要求出模n的平⽅根,等价于求解以下两个同余⽅程。
z^{2} \equiv y (mod \, p)z^{2} \equiv y (mod \, q)虽然我们可以利⽤Euler准则来判断y是否为⼀个模p或模q的⼆次剩余。
事实上,如果加密正确的执⾏,y是⼀个模p和模q的⼆次剩余,遗憾的是它并不能帮助我们找到y。
当p \equiv 3(mod \, 4)时,有⼀个简单公式来计算模p的⼆次剩余的平⽅根,假定y是⼀个模p的⼆次剩余,且y \equiv 3 (mod \, 4)那么有\begin{align} (\pm y^{\frac {p+1}{4}})^{2} \equiv & y^{\frac{p+1}{2}} (mod \, p) \\ \equiv & y^{\frac{p-1}{2}}y (mod \, p) \\ \equiv & y(mod \, p) \\ \end{align}这⾥⼜⼀次使⽤了Euler准则,即当y是⼀个模p的⼆次剩余时,有y^{\frac{p-1}{2}} \equiv 1 (mod \, p),因此,y模p的两个平⽅根为\pm y^{\frac{p+1}{4}} (mod \, p),同样的讨论可以知道,y模q的两个平⽅根为\pm y^{\frac{p+1}{4}} (mod \, q),再利⽤中国剩余定理可以得到y模n的四个平⽅根。
密码学第五章 分组密码1

➢ 事实上,并没有一个真正实用的密码被证明是计算上安 全的。一般地人们只能证明某个密码是不安全的,因为 这只要找到一种方法,其复杂度远小于 2n 和 2t 。
3. 分组密码的设计原则
➢ 一个好的分组密码应是既难破译又易于实现的。 ➢ 安全性原则
密码学
第5章 分组密码(1)
1. 概述
分组密码就是将明文消息序列
m1, m2 ,, mk ,
分成等长的消息组
(m1, m2 , , mn )(mn1, mn2 , , m2n )
在密钥控制下,按固定的算法 Ek 一组一组进行加密。 加密后输出等长密文组
( y1, y2 , , ym )( ym1, ym2 , , y2m )
➢ 计算安全性只是一个相对概念,它依赖于攻击者的计算 能力和所采用的攻击方式。一般地,计算上安全是指对该 密码的最佳攻击方法的困难性超过了攻击者的计算能 力。
➢ 人们为了定量描述这种“困难性”,通常使用“复杂度” 的概念:一种攻击的复杂度是指为了实施该攻击所需的 平均运算次数。一个密码的安全性的评估,依据已知的 关于该密码的最佳攻击方法的复杂度。
➢ 70 年代,美国数据加密标准 DES 的出台,标志着现代分组密 码学的开始。从此揭开了商用民用密码研究的序幕。
➢ 这是信息化社会发展的产物。
越来越多的敏感信息通过网络传输和存贮,迫切需要具有高强 度、高速率、便于软硬实现、易于标准化的加密体制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机预言机模型的定义
随机预言机( Oracle) 随机预言机(Random Oracle)的定义是一个确定性的公共 可访问的随机均匀分布函数( Distributed), 可访问的随机均匀分布函数(Uniformly Distributed), 对于任意长度的输入, 对于任意长度的输入,在输出域中均匀选择一个确定性长 度的值作为询问的回答。 度的值作为询问的回答。 随机预言机模型是在标准模型的基础上增加了一个公共可 访问的随机预言机,将方案中所使用的散列函数( 访问的随机预言机,将方案中所使用的散列函数(Hash Function)理想化为随机预言机,攻击者(Adversary) Function)理想化为随机预言机,攻击者(Adversary)只 能通过询问随机预言机来获得所需要的散列值( 能通过询问随机预言机来获得所需要的散列值(Hash Value)。然后仿真者(Simulator) )。然后仿真者 Value)。然后仿真者(Simulator)通过一定的步骤利用 该攻击者, 该攻击者,将攻击者的能力转化为攻破某已知困难问题的 优势(Advantage)。 优势(Advantage)。
随机预言机模型的定义
[1]M.Bellare and P.Rogaway.Random oracles are practical-a paradigm for designing efficient protocols.In Proceedings of the First ACM Conference on Computer and Communications Security,pages 62– 73,1993. [2]M.Bellare and P.Rogaway.The exact security of digital signatureshow to sign with rsa and rabin. In U.Maurer, editor,Advances in Cryptology-Proceedings of EUROCRYPT’96,volume LNCS ’ 1070,pages 399–416,1996. [3]M.Bellare and P.Rogaway.Optimal asymmetric encryption—how to encrypt with rsa.In Advances in Cryptology– EUROCRYPT’94,volume LNCS 950,pages 92–111.Springer’ Verlag,1995. [4]E.Fujisaki and T.Okamoto.Secure integration of asymmetric and symmetric en- cryption schemes.In Advances in CryptologyCrypto’99,volume LNCS 1666,pages537–554,1999. ’
随机预言机模型的定义
虽然计算复杂性安全模型下的方案已经比信息论安全 模型下的方案更加实用, 模型下的方案更加实用,但仅从标准模型下的现有绝 大部分方案来看,都无法在实际当中推广开来, 大部分方案来看,都无法在实际当中推广开来,造成 了密码学理论和实践中的一个鸿沟. 了密码学理论和实践中的一个鸿沟. 原因在于有许多广泛应用的方案虽然无法给出标准模 型下的证明,但在长期应用中抵御住了实际的攻击者, 型下的证明,但在长期应用中抵御住了实际的攻击者, 取得了大众的信任。 取得了大众的信任。同时标准模型下设计一个安全的 方案十分困难,没有形成一套方法论, 方案十分困难,没有形成一套方法论,方案的设计成 为一种科学艺术,而非工程。 为一种科学艺术,而非工程。 这种状况在1993年 Bellare和Rogaway创造性地提出 这种状况在1993年,Bellare和Rogaway创造性地提出 1993 随机预言机模型后[1] 取得了飞跃性的进步。 [1], 随机预言机模型后[1],取得了飞跃性的进步。
密码学与信息安全
可证明安全性
根据所基于的不同理论,可分为信息论安全( 根据所基于的不同理论,可分为信息论安全(Information Theory Security)和计算复杂性安全(Computational Complexity )和计算复杂性安全( Security)两大类。 )两大类。 信息论安全由C.Shannon在其开创性的文献 在其开创性的文献[12]中给出定义,一个方 中给出定义, 信息论安全由 在其开创性的文献 中给出定义 案如果满足信息论安全, 案如果满足信息论安全,那么无论攻击者具有什么样的计算能力都无 法破解,所以信息论安全又被称为无条件安全。 法破解,所以信息论安全又被称为无条件安全。虽然信息论安全在安 全上是完美的,但却有着难以实用的缺点, 全上是完美的,但却有着难以实用的缺点,因而只是用在军事和外交 等对信息保密极度敏感的领域。 等对信息保密极度敏感的领域。 计算复杂性安全是基于复杂性理论之上的一套模型, 计算复杂性安全是基于复杂性理论之上的一套模型,它将攻击者的能 力限定为多项式时间, 力限定为多项式时间,一个方案是否安全取决于攻击者成功的优势能 否规约到以不可忽略的概率解决某个已知困难问题,例如大整数分解, 否规约到以不可忽略的概率解决某个已知困难问题,例如大整数分解, 二次剩余,离散对数等。 二次剩余,离散对数等。 计算复杂性安全虽然并不能保证无条件安全( 计算复杂性安全虽然并不能保证无条件安全(例如在量子计算机中大 数分解问题不再是困难的),并且对攻击者的能力加以了限制, ),并且对攻击者的能力加以了限制 数分解问题不再是困难的),并且对攻击者的能力加以了限制,但在 理论下的攻击者的计算能力实际上已远远超过现实当中存在的攻击者, 理论下的攻击者的计算能力实际上已远远超过现实当中存在的攻击者, 因而计算复杂性安全模型下的方案在实际应用中仍然是可以信赖的。 因而计算复杂性安全模型下的方案在实际应用中仍然是可以信赖的。 因而在现实环境当中,攻击者在计算能力上并无任何特别的优势可言。 因而在现实环境当中,攻击者在计算能力上并无任何特别的优势可言。
随机预言机模型下可证明安全过程
由于事先确定的挑战包含有仿真者可用来解答方 案所基于的困难问题的知识(Knowledge) 案所基于的困难问题的知识(Knowledge),如果 仿真游戏成功的概率为不可忽略的值,那么必然 仿真游戏成功的概率为不可忽略的值, 方案所基于的困难问题在给定攻击者的环境下不 再是困难的, 再是困难的 , 这与现实环境中该已知困难问题的 不可计算性( Intractable) 不可计算性(Computational Intractable)相矛 因而该攻击者实际是不存在的, 盾 , 因而该攻击者实际是不存在的 , 方案在模型 下是安全的。 下是安全的。
标准模型
早期基于计算复杂性安全的密码方案一般是基于标准模型 (Standard Model)下,该模型首先对方案中攻击者的 ) 能力加以定义,而且必须强调攻击者一定是自适应性的。 能力加以定义,而且必须强调攻击者一定是自适应性的。 然后假设该攻击者成功的概率为某个多项式时间不可忽略 的值,然后通过一定的步骤利用该攻击者, 的值,然后通过一定的步骤利用该攻击者,将攻击者的能 力转化为攻破某已知困难问题的优势。 力转化为攻破某已知困难问题的优势。由于该困难问题在 多项式时间下无法求解, 多项式时间下无法求解,因而可以得出存在攻击者以不可 忽略概率攻破方案这一假设与事实相矛盾。 忽略概率攻破方案这一假设与事实相矛盾。幸的是,基于标准模型的密码方案往往需要大量的计算, 难以实用。如现有最高效的标准模型下安全的公钥加密方 难以实用。 案],数字签名方案 ,仍然没有广泛加以使用。如何设计 ,数字签名方案],仍然没有广泛加以使用。 一个面向具体应用的密码方案,同时平衡可证明安全性和 一个面向具体应用的密码方案, 实用性,成为了密码方案设计中首要考虑的问题。 实用性,成为了密码方案设计中首要考虑的问题。因为一 个低效率的方案与不安全的方案一样, 个低效率的方案与不安全的方案一样,都无法在实际当中 被广大用户接受并广泛使用。 被广大用户接受并广泛使用。
随机预言机模型下可证明安全过程
在随机预言机模型下, 在随机预言机模型下 , 我们将整个证明过程定义 为一个仿真游戏(Game) 为一个仿真游戏(Game)。 在模型中除了随机预言机之外, 在模型中除了随机预言机之外 , 还存在一个仿真 Simulator, 简称Simon Simon) 者 ( Simulator, 简称 Simon), 该仿真者对攻击 Adversary,简称MALICE MALICE) 者(Adversary,简称MALICE)所有定义的询问进 行回答,这一过程被称之为训练(Trainning) 行回答,这一过程被称之为训练(Trainning)。 在仿真游戏的最后,仿真者Simon Simon给出事先确定的 在仿真游戏的最后,仿真者Simon给出事先确定的 挑战(Challenge) 如果攻击者MALICE完成挑战, MALICE完成挑战 挑战(Challenge),如果攻击者MALICE完成挑战, 则仿真游戏成功。
随机预言机模型的定义
在实际应用中, 在实际应用中,一般用一个安全的散列函数来替代随机预 言机, 言机,方案的安全性便基于可证明安全的规约结果和散列 函数本身与随机预言机的可区分性之上。 可区分性之上 函数本身与随机预言机的可区分性之上。 散列函数与随机预言机相似的性质(快速,确定,单向, 散列函数与随机预言机相似的性质(快速,确定,单向, 均匀分布) 均匀分布)使其在密码方案设计中扮演了非常重要的角 实际上, 色。实际上,对某个消息进行散列运算之后再处理可以 增加该消息的冗余度, 增加该消息的冗余度,从信息论安全的角度来看是十分 有益的。 有益的。 同时与标准模型下可证明安全的方案相比较, 同时与标准模型下可证明安全的方案相比较,方案的计 算开销也会因为随机预言机模型下许多紧规约技巧而大 大降低。 大降低。
随机预言机的类型
在基于随机预言机模型下的密码方案的证明当中, 使用随 在基于随机预言机模型下的密码方案的证明当中, 机预言机的方法也有不同, 机预言机的方法也有不同,从仿真者对随机预言机加以控制 的程度不同可以分为以下三种类型: 的程度不同可以分为以下三种类型:
