奈奎斯特采样定理与相关双采样
香农奈奎斯特采样定理

香农奈奎斯特采样定理
香农-奈奎斯特采样定理(Shannon-Nyquist Sampling Theorem)是一项基本的信号处理原理,它规定了一个连续时间信号的采样频率应该至少是该信号中最高频率成分的两倍,以便在离散时间中完整地重构原始信号。
这个定理是由克劳德·香农(Claude Shannon)和哈里·奈奎斯特(Harry Nyquist)在20世纪初提出的。
具体来说,香农-奈奎斯特采样定理表述如下:
如果一个连续时间信号的最高频率成分为f_max,那么为了在离散时间中准确地重建原始信号,采样频率f_s(采样率)必须满足:
f_s ≥ 2 * f_max
这意味着采样频率应至少是信号中最高频率的两倍。
如果采样频率不满足这个条件,就会出现所谓的"混叠"或"奈奎斯特折叠",导致信号在离散时间中无法准确还原。
香农-奈奎斯特采样定理在数字信号处理、通信系统、音频处理、图像处理和各种数据采集应用中具有重要作用。
它强调了适当选择采样频率的重要性,以避免信息丢失和混叠问题,确保准确的信号重建。
因此,合理的采样频率选择是数字信号处理的基本原则之一。
奈奎斯特,香农定理,采样原理分析及ADC的选择

奈奎斯特,香农定理,采样原理分析及ADC的选择奈奎斯特,香农定理,久采样原理分析及ADC的选择欠采样或奈奎斯特(Nyquist)准则是 ADC 应用上经常使用的一种技术。
射频(RF)通信和诸如示波器等高性能测试设备就是其中的一些实例。
在这个“灰色”地带中经常出现一些困惑,如是否有必要服从 Nyquist 准则,以获取一个信号的内容。
对于 Nyquist 和 Shannon 定理的检验将证明:ADC 采样频率的选择与最大输入信号频率对输入信号带宽的比率有很强的相关性。
奈奎斯特(Nyquist)原理分析Nyquist 定理被表达成各种各样的形式,它的原意是:如果要从相等时间间隔取得的采样点中,毫无失真地重建模拟信号波形,则采样频率必须大于或等于模拟信号中最高频率成份的两倍。
因而对于一个最大信号频率为 fMAX的模拟信号fa,其最小采样频率 fs 必须大于或等于2×fMAX 。
fs ? 2 fMAX最简单的模拟信号形式是正弦波,此时所有的信号能量都集中在一个频率上。
现实中,模拟信号通常具有复杂的信号波形,并带有众多频率成份或谐波。
例如,一个方波除了它的基频之外,还包含有无穷多的奇次谐波。
因此,根据 Nyquist 定理,要从时间交叉的采样中完整地重建一个方波,采样频率必须远远高于方波的基频。
请注意:当以采样率fs对模拟信号fa进行采样时,实际上产生了两个混叠成份,一个位于fs+fa,另一个位于fs,fa。
它的频率域显示在图 1中。
较高频的混叠成份基本上不会引起问题,因为它位于Nyquist 带宽(fs/2)以外。
较低频的混叠成份则可能产生问题,因为它可能落在Nyquist 带宽之内,破坏所需要的信号。
鉴于采样系统的混叠现象,Nyquist 准则要求采样率fs > fa,以避免混叠成份覆盖到第一Nyquist 区。
为防止有害的干扰, 任何落在感兴趣的带宽之外的信号(无论是寄生信号或是随机噪声)都应该在抽样之前进行过滤。
奈奎斯特采样定理
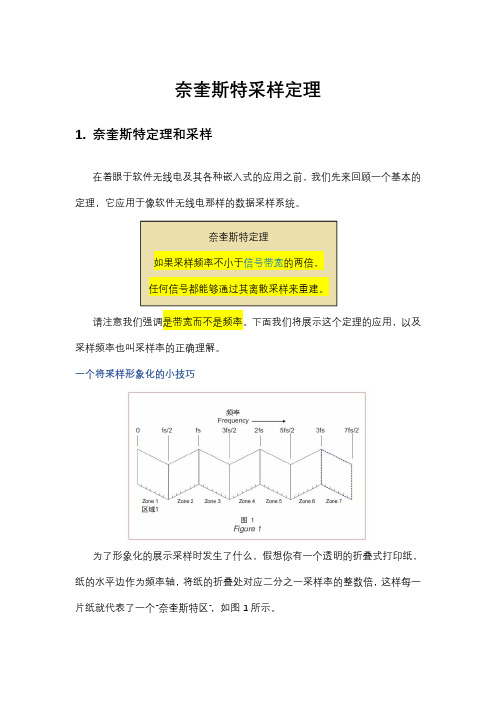
奈奎斯特采样定理1.奈奎斯特定理和采样在着眼于软件无线电及其各种嵌入式的应用之前,我们先来回顾一个基本的定理,它应用于像软件无线电那样的数据采样系统。
请注意我们强调是带宽而不是频率。
下面我们将展示这个定理的应用,以及采样频率也叫采样率的正确理解。
一个将采样形象化的小技巧为了形象化的展示采样时发生了什么,假想你有一个透明的折叠式打印纸,纸的水平边作为频率轴,将纸的折叠处对应二分之一采样率的整数倍,这样每一片纸就代表了一个“奈奎斯特区”,如图1所示。
奈奎斯特定理如果采样频率不小于信号带宽的两倍,任何信号都能够通过其离散采样来重建。
采样基础知识使用折叠纸的纵轴表示信号能量,画出待采样信号的频谱,如图2所示,将透明折叠纸合起来看一下采样带来的效果。
我们透过合起来的纸看过去,就会看到采样所导致的频谱,每一片纸上也就是每一个奈奎斯特区上的信号都合到了一起,不能再被区分开来,这个现象也称作“混叠”。
一旦采样时发生了混叠,采样结果将是损坏的不能恢复。
“混叠”这个词很恰当,高奈奎斯特区的信号采样后出现在一个不同的频率。
2.基带采样一个基带信号的频谱起始于零频,终止于其最高频率。
为了防止采样基带信号时损坏数据,需要确保所有的信号频谱只落在第一个奈奎斯特区,如图4所示,有两种方式来实现:一是使用低通滤波器来滤除高于f s /2的信号,二是提高采样率使得所有信号频谱落入f s /2以内。
注意f s /2也称作“折叠频率”。
3.带通信号采样让我们考虑一个带通信号,比如一个通信接收机的中频信号,它的中心频率为70MHz,带宽为10MHz,那么这个信号的频谱在65~75MHz。
如果我们按照基带采样的规则,必须在信号最高频率的两倍以上进行采样,也就是采样率至少为150MHz。
但是,利用一种“欠采样”的技术,我们就可以使用更低的采样率。
4.欠采样欠采样允许我们利用混叠,假设我们遵循奈奎斯特定理的严格要求。
对于上述中频信号,设想我们尝试40MHz的采样率,那么折叠纸的图像就是图5所示,可以看到60~80MHz的第4奈奎斯特区,恰好包含了整个65~75MHz的中频信号。
采样定理和奈奎斯特定理

采样定理和奈奎斯特定理1 采样定理采样定理又称为抽样定理或者采样-再构建定理,是数字信号处理和声学认知中重要的定理。
它指出,只要采样信号的频率高于Nyquist 频率,就可以从采样信号中恢复原始信号。
采样定理可以说是数字信号处理中的经典成果之一。
采样定理的发现最早属于美国科学家Harry Nyquist,他于1928年提出了采样定理,他的定理又称为Nyquist定理,他明确的指出了采样和记录信号的条件,要求采样信号的频率必须大于称之为Nyquist 频率的二倍才能精确的采样出信号描述的形状。
采样定理的核心精神是这样的,只要待采样的信号具有有限的频带,并且采样频率超过该信号的Nyquist频率,就能够通过采样频率正确得采样出信号,这样采样出来的信号就没有任何失真。
在NJQ频率(Nyquist频率)可以称为最低保真度频率,任何高于NJQ频率的采样都可以保证无失真,任何低于NJQ的采样将产生失真。
2 奈奎斯特定理奈奎斯特定理是由乔治·梅克尔·奈奎斯特于 1947年发现的,它是数字信号处理的概念,主要指出了数字信号处理系统中滤波器的特性。
它是采样定理的推广,是信号处理领域当之无愧的重要定理。
奈奎斯特定理指出,任何有限带宽的滤波器都可以通过采样和再构造技术被完全模拟,而且采样频率只需要比滤波器的有效频带宽度大一倍即可。
在实际的数字信号处理系统中,滤波器的频率和时间的信息表示在数字空间中就会消失不见,因为它们的分量频率没有被采样到,而奈奎斯特定理恰好可以解决这个问题,滤波器就可以在数字空间重新被模拟出来,这就可以恢复数字信号处理系统中分量频率的时间和频率的信息表示。
因此,奈奎斯特定理可以为数字信号处理系统提供了完美的模拟滤波器,可以实现信号的恢复。
而且,奈奎斯特定理具有无失真、精度远超传统数字信号处理的优点,因此它在数字信号处理的领域中得到了广泛的应用。
04奈奎斯特三准则

04奈奎斯特三准则奈奎斯特三准则(Nyquist's Three Criteria)也称为奈奎斯特采样准则(Nyquist Sampling Criteria),是一种理论方法,用于确定采样频率,以防止采样过程中出现不可逆的失真。
奈奎斯特三准则基于奈奎斯特频率,即信号最高频率的两倍。
根据奈奎斯特三准则,要想恢复一个连续时间信号的所有信息,采样频率必须超过信号最高频率的两倍。
这意味着,在信号的频率范围内进行等间隔采样,并且采样频率大于信号频谱的两倍。
奈奎斯特三准则的三个具体准则如下:1.采样频率至少是信号频率的两倍:根据奈奎斯特三准则,采样频率必须至少是信号频率的两倍。
这是由于,如果采样频率太低,则可能无法完整地恢复信号。
采样频率低于信号频率的两倍时,会发生混叠现象,导致结果失真。
2.防止混叠现象:混叠现象是指当采样频率低于信号频率两倍时,高于采样频率一半(或称为奈奎斯特频率)的频率信号出现在频谱中。
这些高频信号会被误认为是低频信号,从而引起失真。
为了避免混叠现象,采样频率必须高于信号最高频率的两倍。
3.低通滤波器:为了消除混叠现象,必须使用低通滤波器,以便在信号被采样之前,将超过奈奎斯特频率的高频信号滤除。
低通滤波器可以确保在采样过程中只保留信号频谱范围内的信号。
奈奎斯特三准则实际上是为了确保采样过程中不会丢失信号的任何信息。
通过满足这些准则,我们可以在采样过程中还原原始信号,从而在数字领域中对其进行处理和分析。
不满足奈奎斯特三准则可能导致信号失真或信息丢失。
奈奎斯特三准则在许多领域都有应用,特别是在数字信号处理、通信系统和数据采集领域。
在实际应用中,我们需要了解信号的频谱分布,然后根据信号的最高频率来确定合适的采样频率和滤波器。
总之,奈奎斯特三准则是一种重要的理论方法,用于确定采样频率,以防止采样过程中出现混叠现象和信号失真。
通过确保采样频率至少是信号频率的两倍,并使用合适的低通滤波器,我们可以在数字领域中准确恢复连续时间信号。
奈奎斯特采样定理和香农采样定理

奈奎斯特采样定理和香农采样定理
一、奈奎斯特采样定理
1、奈奎斯特采样定理(Nyquist Sampling Theorem)指出,对
任何一个连续的时间函数,如果它在时间轴上有频率不超过一个上限,则只要把它采样频率设计在该上限的两倍以上即可完全重建出这个
函数。
奈奎斯特采样定理是数字信号处理的基本原理之一,该定理指出如果采样频率大于两倍最高信号频率,则可以完全重建出信号的完整信息。
该定理的意义在于,在信号数字化时,我们只需要采样频率大于信号最高频率两倍即可精确无损地重建信号,因此也可称其为“无损采样定理”。
2、基于奈奎斯特采样定理,在模拟信号转换为数字信号时,需
要将模拟信号先做低通滤波,使阻带范围不超过采样频率的一半,被称为“奈奎斯特限制频率”,与此同时,将采样频率设置在奈奎斯特
限制频率的两倍以上,这样可以保证数字信号重建时无损传输。
二、香农采样定理
1、香农采样定理(Shannon Sampling Theorem)又称“总变换
定理”,由Shannon于1949年提出,表明任何一个带宽有限的连续信号都可以通过取样的方式近似表示,而且取样频率满足一定条件时,信号可以完整的重建。
2、香农采样定理的条件是采样频率为该信号的频率范围的两倍
以上,并且频率范围的宽度要大于频谱中峰值频率的两倍,此时采样
时的取样频率叫做重建阈值,即信号可以完整重建所需要的最低采样频率。
香农采样定理是分析数字信号的基础原理,它解决了模拟信号数字化的问题,指出任何一个带宽有限的连续信号都可以通过取样的方式近似表达,并且只要实现正确的采样取样频率,就可以完整重建数字信号。
nyquist抽样定理

nyquist抽样定理
纳奎斯特抽样定理,又称纳奎斯特采样定理,是信号处理学中的一个重要定理,是由瑞典电子工程师Harry Nyquist于1928年提出的。
纳奎斯特抽样定理指出,要将连续时间的信
号无损地采样成离散时间的信号,采样频率必须大于原信号最大频率的两倍,即采样频率必须大于最高频率的两倍,也就是说,采样频率必须大于信号最高频率的两倍。
简单来说,纳奎斯特抽样定理指出,要想得到完整的信号,最低的采样频率必须大于信号最高频率的两倍。
这就是所谓的“双倍频率”原理,也叫做“纳奎斯特抽样定理”。
纳奎斯特抽样定理的最重要的概念是:在采样之前,信号的频率是有限的;在采样之后,信号的频率也是有限的,其值为原信号最高频率的一半。
也就是说,如果原信号的最高频率不超过采样频率的一半,那么在采样过程中不会丢失任何有用的信息。
如果原信号的最高频率超过采样频率的一半,那么在采样过程中就会丢失一部分有用的信息。
纳奎斯特抽样定理给信号处理提供了重要的理论基础,在数字信号处理的各个领域都得到了广泛的应用。
它是必须掌握的重要定律,并且它的实践应用也十分重要。
纳奎斯特抽样定理在数字音频处理、数字图像处理、数字视频处理等方面都有重要的应用,尤其是在数字信号处理领域,它的实践应用更为重要。
空间奈奎斯特采样定理

空间奈奎斯特采样定理
空间奈奎斯特采样定理(Spatial Nyquist Sampling Theorem)是数字图像处理和计算机视觉领域中的一项重要原理,类似于时间信号处理中的奈奎斯特采样定理。
该定理指出,为了避免出现混叠(aliasing)现象,对于连续的二维空间信号(如图像),在进行离散化采样时,采样频率必须满足特定条件。
具体来说,对于一幅二维空间信号(例如图像),如果其最高频率成分为f_max,则为了能够完全恢复原始信号而没有信息丢失,采样频率(空间采样率)必须至少是f_max的两倍。
数学表达式如下:
采样频率≥ 2 * f_max
其中,f_max是原始信号中的最高频率成分。
简单解释:在对图像进行数字化处理时,我们将其分为像素,并在每个像素点上记录颜色值。
如果我们的采样频率低于信号中的最高频率成分的两倍,那么在还原图像时,会出现混叠现象,导致图像出现失真。
因此,空间奈奎斯特采样定理
要求采样频率至少为最高频率成分的两倍,以避免信息丢失。
实际应用中,为了更好地处理信号,通常会选择更高的采样频率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奈奎斯特采样定理(采样定理):采样频率必须大于被采样信号频率的两倍以上才能还原信号。
相关双采样:Correlated Double Sample, CDS 若在光电信号的积分开始时刻t1和积分结束时刻t2,分别对输出信号采样(在一个信号输出周期内,产生两个采样脉冲,分别采样输出信号的两个电平,即一次是对复位电平进行采样,另一次是对信号电平进行采样),并且使得两次采样时间之间的间隔远小于时间常数CRon(Ron为复位管的导通电阻),这样两次采样的噪声电压相差无几,两次采样的时间又是相关的
若将两次采样值相减,就基本消除了复位噪声的干扰,得到信号电平的实际有效幅值。
