2020年辽宁省铁岭市(有详细解析)
2020年辽宁省铁岭市中考地理试卷和答案解析

2020年辽宁省铁岭市中考地理试卷和答案解析一、选择题(下面每小题只有一个正确答案,请将选择的字母代号填入相对应的答题栏中,每小题2分,共60分)1.(2分)下列关于我国自然环境的叙述,正确的是()A.我国地势西高东低,导致我国大多数河流自西向东流B.我国幅员辽阔,年降水量从东南沿海向西北内陆递增C.我国幅员辽阔,地形类型多样,气候类型单一D.我国地势东高西低,利于海洋水汽深入内陆,形成降水解析:我国地势西高东低,呈三级阶梯状分布,该地势对我国气候所产生的影响是有利于海洋上的暖湿气流深入我国内陆,形成丰沛的降水;对河流的影响是使大部分河流滚滚东流,沟通了东西交通,方便了沿海与内地的联系;我国水资源的时空分布情况受我国降水的影响,我国降水空间上来说从东南沿海向西北内陆降水逐渐减少。
我国气候类型复杂多样,季风气候显著,我国主要的气候类型有温带季风气候、亚热带季风气候、热带季风气候、温带大陆性气候和高山高原气候。
参考答案:解:我国地势西高东低,呈三级阶梯状分布,有利于海洋上的暖湿气流深入我国内陆,形成丰沛的降水;使大部分河流滚滚东流,沟通了东西交通,方便了沿海与内地的联系,故A正确。
D错误。
我国幅员辽阔,年降水量从东南沿海向西北内陆递减,故B错误;我国地形和气候都复杂多样,故C错误。
故选:A。
点拨:本题考查我国的自然环境特点,熟记课本知识点解答即可,属于中等题,要牢记。
2.(2分)《晏子使楚》中“橘生淮南则为橘,生于淮北则为枳,叶徒相似,其味不同”。
这种差异形成的主要原因是()A.淮南、淮北的地形不同B.淮南、淮北的气候不同C.淮南、淮北的栽培技术不同D.淮南、淮北的耕作制度不同解析:农业的发展既受地形、气候等自然条件的影响,又受市场需求量、与城市和工矿区的距离、农民文化技术水平等社会条件的影响。
秦岭、淮河一线是我国南方地区与北方地区的分界线,确定该界线的主导因素是气候因素。
据此解答。
参考答案:解:秦岭﹣淮河是我国一条重要的地理分界线。
辽宁省铁岭市2020年中考生物真题试题(含解析)

辽宁省铁岭市2020年中考生物真题试题一、选择题1.在嫁接中,取自优良品种植物体上的芽和接受芽的枝干依次叫作()A. 接穗和砧木B. 砧木和接穗C. 接穗和接穗D. 砧木和砧木【答案】C【考点】植物的无性生殖【解析】【解答】嫁接是指把一个植物体的芽或枝,接在另一个植物体上,使结合在一起的两部分长成一个完整的植物体,嫁接时,接上去的芽或枝叫接穗,被接的植物叫砧木,嫁接时应当使接穗和砧木的形成层紧密结合,以确保成活,因为形成层具有很强的分裂能力,能不断分裂产生新细胞,使得接穗和砧木长在一起,易于成活。
故答案为:C【分析】嫁接的接穗与砧木:2.下列属于有性生殖的繁殖方式为()A. 用根繁殖B. 用茎繁殖C. 用种子繁殖D. 用叶繁殖【答案】C【考点】植物的有性生殖【解析】【解答】植物的无性生殖通常由植物体的营养器官(根、叶、茎)产生出新的个体,这种生殖方式叫做营养生殖,选项中A、B、D都是用营养器官进行的繁殖,都是无性生殖;种子的胚是由受精卵发育成的,经过了两性生殖细胞的结合,因此用种子繁殖是有性生殖的繁殖方式。
故答案为:C【分析】无性生殖指的是不需要经过两性生殖细胞的结合,由母体直接产生新个体的过程.植物用根、茎、叶等营养器官进行繁殖的方式叫做营养繁殖,营养繁殖就是最常见的一种无性生殖的方式,常见的无性生殖的方式有扦插、嫁接、压条.而有性生殖指的是两性生殖细胞精子和卵细胞结合形成受精卵的过程.3.昆虫的完全变态发育过程是指()A. 受精卵一幼虫一成虫B. 受精卵---幼虫一蛹一成虫C. 受精卵一蛹一成虫D. 受精卵一幼虫一成虫【答案】B【考点】昆虫的发育【解析】【解答】昆虫的完全变态发育过程是指经过受精卵、幼虫、蛹和成虫四个时期,而经过受精卵、若虫、成虫三个时期的是不完全变态发育故答案为:B【分析】昆虫的发育分为完全变态发育和不完全变态发育:(1)完全变态发育经过卵、幼虫、蛹和成虫四个时期.完全变态发育的昆虫幼虫与成虫在形态构造和生活习性上明显不同,差异很大.如蚊子、苍蝇、家蚕、菜粉蝶等.(2)不完全变态发育经过卵、若虫、成虫三个时期.不完全变态发育的昆虫幼体与成体的形态结构和生活习性非常相似,但各方面未发育成熟,如蟋蟀、螳螂、蝼蛄、蝗虫等.4.养鸡场中,母鸡和公鸡一般是分开饲养的,在这种情形下,下列叙述中正确的是()A. 所有母鸡下的蛋都不能孵出小鸡B. 所有母鸡下的蛋都能孵出小鸡C. 只有小部分母鸡下的蛋能孵出小鸡D. 分开饲养的母鸡不能下蛋【答案】A【考点】鸟的生殖【解析】【解答】养鸡场的母鸡和公鸡是分开饲养的,因此,母鸡下的蛋就不是受精的蛋,都不能孵出小鸡。
2020年抚顺市、铁岭市中考语文卷作文题解析及范文点评

2020年抚顺市、铁岭市中考语文卷作文题解析及范文点评三、写作(满分60分)28.请从下面两个文题中,任选其一,按要求作文。
题目一:请以“这份深情无法复制”为题目,写篇文章。
【分析】本题为全命题作文。
从题目中的“无法复制”可以看出“深情”的独特性。
生活中很多深情是无法复制的,如父母爱你的方式以及表达方式各有特点,老师对不同性格的学生关心与爱护也是不同的,找出这些“独特”性,写出深情背后不一样的表达。
文体上应选择记叙文,从生活中选取真实的材料,表达自己的真挚感情或真实感悟。
创作时,可借鉴如下思路:把命题中的“这份深情”限定为“母爱”。
首段采用类比的手法,以自然风景的可以复制,音乐的可以复制引出真情的不能复制,而这份真情就是母爱。
主体部分写人叙事,从生活中选取典型的事件,把母爱直观化,具象化。
可以选取一件事,也可以为了丰富文章内容选取多件事,如选多件事,应注意内容上详略的安排。
末段总结全文,表达对母亲的感激之情,与首段相呼应,使文章结构完整。
【例文】这份深情无法复制毕业前最后一节课。
老师说:“你们再看看书,我再看看你们。
”根据小林漫画改编的这幅漫画,虽然画面内容并不复杂难懂,却颇耐人寻味,留给人们的是深深的感动和难以复制的深情。
“你们再看看书,我再看看你们。
”折射出的是期盼。
虽然是最后一节课,老师也不忘提醒同学们“再看看书”,这正如孙中山先生“革命尚未成功,同志仍需努力”的遗训般,体现了老师对同学们在中考中取得佳绩的期盼。
毕竟,中考对很多学生而言依然是改变命运的重要途径。
老师在最后一节课上依然希望同学们能够临阵磨枪,尽力补上自己的短板。
“你们再看看书,我再看看你们。
”折射出的是关爱。
“三更灯火五更鸡,正是男儿读书时。
”这是流传许久的诗句。
如今,激烈的社会竞争让每个学子在学业上都不敢松懈,每个同学课桌上如小山般的复习资料见证了自己主人的勤奋。
身为老师,一定是看在眼里、疼在心里。
最后一节课,老师再看看同学们,就是对同学们的心疼与关爱。
辽宁省抚顺市、铁岭市2020年中考化学试题(含答案与解析)

2020年抚顺铁岭初中毕业生学业考试化学试卷可能用到的相对原子质量:H-1 C-12 N-14 O-16 S-32 Zn-65第一部分选择题(共20分)一、选择题(本题包括15个小题,共20分,每小题只有一个选项符合题意,第1小题-第10小题,每小题1分;第11小题-第15小题,每小题2分)1.把少量下列物质分别放入水中,充分搅拌,可以形成溶液的是A. 碘B. 汽油C. 高锰酸钾D. 面粉2.下列不属于化石能源的是A. 煤B. 太阳能C. 石油D. 天然气3.如果发现火险或遭遇火灾要沉着应对。
下列做法正确的是A. 油锅中的油着火用水浇灭B. 室内起火迅速打开门窗通风C. 家中燃气泄漏,立即打开排气扇通风D. 遭遇火灾时,用湿毛巾捂住口鼻远离着火区域4.下列物质的用途主要利用了其物理性质的是A. 氧气用于医疗急救B用铜作导线.C. 用熟石灰改良酸性土壤D. 用氢氧化钠去除油污5.为减少“白色污染”,下列做法不正确的是A. 焚烧废弃塑料B. 重复使用塑料袋C. 用布袋代替塑料袋D. 使用微生物降解塑料6.下列做法不会危害人类健康的是A. 用甲醛水溶液保解海产品B. 制糖工业用活性炭脱色制白糖C. 发霉的大米清洗后煮熟食用D. 为了防止缺锌大量服用含锌保健品7.下列实验操作不正确的是A. 验满氧气B. 检查装置气密性C. 点燃酒精灯D. 用滴管取液体8.下列物质属于氧化物的是A. 氯酸钾B. 臭氧C. 硫化氢D. 五氧化二磷9.在实验室和化工生产中常用到硝酸。
硝酸是一种强氧化剂,能与碳发生氧化还原反应,化学方程式为。
则X 是A. NO 2B. COC. NOD N 2O 5 10.下列有关催化剂的说法正确的是.3224HNO +C=2H O+4X +CO ↑↑A. 在化学反应后其质量减小B. 催化剂只能加快化学反应速率C. 在化学反应后其化学性质不变D. 过氧化氢分解反应中,只能用二氧化锰作催化剂11.下列有关实验现象的描述正确的是A. 镁在空气中燃烧生成氧化镁B. 固体硝酸铵溶于水,溶液的温度降低C. 打开装有浓盐酸的试剂瓶瓶盖,瓶口出现白烟D. 硫在空气中燃烧产生明亮的蓝紫色火焰,放热,生成一种有刺激性气味的气体12.下列有关微观粒子的说法正确的是A. 氯化钠是由氯化钠分子构成的B. 分子可以分成原子而原子不能再分C. 分子是保持物质性质最小粒子D. 原子是由原子核和核外电子构成的13.将20g 质量分数为98%的浓硫酸稀释为25%的稀硫酸。
铁岭市人民政府办公室关于印发2020年市《政府工作报告》主要目标任务分解方案的通知

铁岭市人民政府办公室关于印发2020年市《政府工作报告》主要目标任务分解方案的通知文章属性•【制定机关】铁岭市人民政府办公室•【公布日期】2020.02.12•【字号】铁政办发 [2020]2 号•【施行日期】2020.02.12•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】行政法总类综合规定正文铁岭市人民政府办公室关于印发2020年市《政府工作报告》主要目标任务分解方案的通知各县(市)、区人民政府,市政府各部门、各直属机构:《2020年市〈政府工作报告〉主要目标任务分解方案》已经市政府同意,现印发给你们,并就有关要求通知如下:一、统一思想,加强领导。
2020年是全面建成小康社会和“十三五”规划收官之年,也是科学谋划“十四五”规划、推动铁岭全面振兴全方位振兴的关键之年,做好今年各项工作意义重大。
各地区、各部门要高度重视,积极主动作为,切实把落实市《政府工作报告》各项目标任务摆在更加突出位置,全力以赴,狠抓落实,确保全面完成。
二、明确责任,合力推进。
各地区、各部门要紧扣目标任务,按照责任分工要求,立足自身实际,对照任务分解表中的主要工作任务,制定详细的、具有可操作性的实施方案,建立月度目标台账,以季度为时间节点,细化、量化责任目标,做到目标任务、重点要求、关键措施、时间进度、责任人员“五个明确”,逐条逐项抓好各项任务的落实。
要加强协调配合,牵头单位要主动承担牵头责任,责任单位要全力支持、主动配合,不折不扣地落实好各项工作任务。
三、强化督办,务求落实。
各地区、各部门对推进有困难的工作,应及时报请市政府分管领导协调解决,切实把各项工作抓紧、抓实、抓细、抓好,确保今年目标任务的全面完成。
市政府将把任务完成情况作为绩效评估和政府督查工作的重要内容,加强督查、严格考核、严肃问责。
市政府督查室要加强跟踪督办,定期梳理汇总各地区、各部门落实情况,对完成工作进展缓慢的,适时通报并启动专项督查。
各牵头单位要于每季度首月10日前,将截至上季度末所牵头负责的重点工作任务完成情况以书面形式(含电子文档)报市政府督查室。
辽宁省铁岭市2020年高二下地理期末考试试题含解析
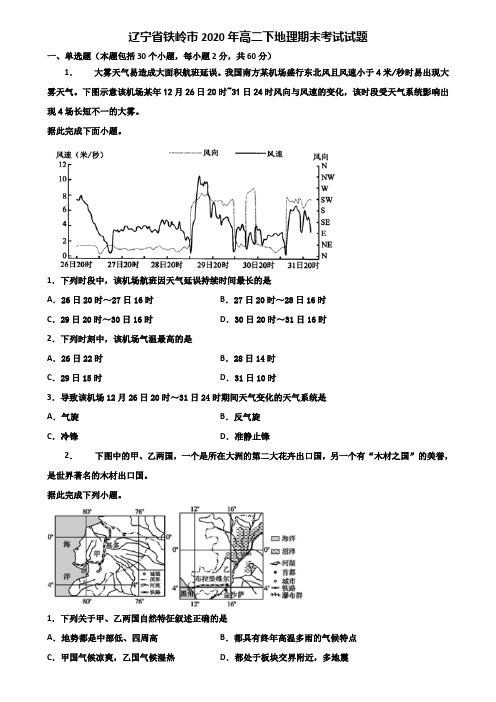
辽宁省铁岭市2020年高二下地理期末考试试题一、单选题(本题包括30个小题,每小题2分,共60分)1.大雾天气易造成大面积航班延误。
我国南方某机场盛行东北风且风速小于4米/秒时易出现大雾天气。
下图示意该机场某年12月26日20时~31日24时风向与风速的变化,该时段受天气系统影响出现4场长短不一的大雾。
据此完成下面小题。
1.下列时段中,该机场航班因天气延误持续时间最长的是A.26日20时~27日16时B.27日20时~28日16时C.29日20时~30日16时D.30日20时~31日16时2.下列时刻中,该机场气温最高的是A.26日22时B.28日14时C.29日15时D.31日10时3.导致该机场12月26日20时~31日24时期间天气变化的天气系统是A.气旋B.反气旋C.冷锋D.准静止锋2.下图中的甲、乙两国,一个是所在大洲的第二大花卉出口国,另一个有“木材之国”的美誉,是世界著名的木材出口国。
据此完成下列小题。
1.下列关于甲、乙两国自然特征叙述正确的是A.地势都是中部低、四周高B.都具有终年高温多雨的气候特点C.甲国气候凉爽,乙国气候湿热D.都处于板块交界附近,多地震2.乙国大宗货物的进出口不是通过河流而是取道从布拉柴维尔通向海洋的铁路,其主要原因是A.铁路运输速度快,方便大量花卉的快速出口B.铁路运距更短,可扩大木材的出口量C.河流下游多瀑布,不能成为出海通道D.减少货物进出口对途经国家的影响3.2015年,图中的“木材之国”作出了原木出口量不得超出原木产量15%的限制,其原因或目的是①延长木材产业链,扩大就业②国内原木短缺③提高原木的附加值,增加收入④特大洪水对原木运输造成了巨大冲击⑤保护森林资源A.①②③B.②③④C.③④⑤D.①③⑤3.2015年12月16日某媒体报道,澳大利亚天文学家发现一颗岩石球体行星,质量是地球的4 倍,距离地球仅14光年。
这颗“超级地球”行星被命名为沃尔夫1061c,天文学家表示,“那里可能有液态水甚至是生命的存在。
2020年辽宁省铁岭市中考数学试题及参考答案(word解析版)

2020年铁岭市初中毕业生学业考试数学试卷(考试时间120分钟,满分150分)一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.﹣的绝对值是()A.B.﹣C.3 D.﹣32.如图是由5个完全相同的小正方体组成的立体图形,它的俯视图是()A.B.C.D.3.下列运算正确的是()A.a2•a3=a6B.a8÷a4=a2C.5a﹣3a=2a D.(﹣ab2)2=﹣a2b44.一组数据1,4,3,1,7,5的众数是()A.1 B.2 C.2.5 D.3.55.一个不透明的口袋中有4个红球、2个白球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸到红球的概率是()A.B.C.D.6.不等式组的整数解的个数是()A.2 B.3 C.4 D.57.我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入,两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工x米,乙工程队每天施工y米.根据题意,所列方程组正确的是()A.B.C.D.8.一个零件的形状如图所示,AB∥DE,AD∥BC,∠CBD=60°,∠BDE=40°,则∠A的度数是()A.70°B.80°C.90°D.100°9.如图,矩形ABCD的顶点D在反比例函数y=(x>0)的图象上,点E(1,0)和点F(0,1)在AB边上,AE=EF,连接DF,DF∥x轴,则k的值为()A.2B.3 C.4 D.410.如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,则以下四个结论中:①abc >0,②2a+b=0,③4a+b2<4ac,④3a+c<0.正确的个数是()A.1 B.2 C.3 D.4(第9题图)(第10题图)二、填空题(本题共8小题,每小题3分,共24分)11.伴随“互联网+”时代的来临,预计到2025年,我国各类网络互助平台的实际参与人数将达到450000000,将数据450000000用科学记数法表示为.12.分解因式:ab2﹣9a=.13.甲、乙两人参加“环保知识”竞赛,经过6轮比赛,他们的平均成绩都是97分.如果甲、乙两人比赛成绩的方差分别为s甲2=6.67,s乙2=2.50,则这6次比赛成绩比较稳定的是.(填“甲”或“乙”)14.关于x的一元二次方程x2﹣2x﹣k=0有两个不相等的实数根,则k的取值范围是.15.如图,在△ABC中,AB=5,AC=8,BC=9,以A为圆心,以适当的长为半径作弧,交AB于点M,交AC于点N.分别以M,N为圆心,以大于MN的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,AF=AB,连接DF,则△CDF的周长为.16.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是.17.一张菱形纸片ABCD的边长为6cm,高AE等于边长的一半,将菱形纸片沿直线MN折叠,使点A与点B重合,直线MN交直线CD于点F,则DF的长为cm.18.如图,∠MON=45°,正方形ABB1C,正方形A1B1B2C1,正方形A2B2B3C2,正方形A3B3B4C3,…,的顶点A,A1,A2,A3,…,在射线OM上,顶点B,B1,B2,B3,B4,…,在射线ON上,连接AB2交A1B1于点D,连接A1B3交A2B2于点D1,连接A2B4交A3B3于点D2,…,连接B1D1交AB2于点E,连接B2D2交A1B3于点E1,…,按照这个规律进行下去,设△ACD与△B1DE的面积之和为S1,△A1C1D1与△B2D1E1的面积之和为S2,△A2C2D2与△B3D2E2的面积之和为S3,…,若AB=2,则S n等于.(用含有正整数n的式子表示)三、解答题(第19题10分,第20题12分,共22分)19.(10分)先化简,再求值:(x﹣1﹣)÷,其中x=3.20.(12分)某校计划组建航模、摄影、乐器、舞蹈四个课外活动小组,要求每名同学必须参加,并且只能选择其中一个小组.为了解学生对四个课外活动小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把此次调查结果整理并绘制成如图两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)本次被调查的学生有人;(2)请补全条形统计图,并求出扇形统计图中“航模”所对应的圆心角的度数;(3)通过了解,喜爱“航模”的学生中有2名男生和2名女生曾在市航模比赛中获奖,现从这4个人中随机选取2人参加省青少年航模比赛,请用列表或画树状图的方法求出所选的2人恰好是1名男生和1名女生的概率.四、解答题(第21题12分,第22题12分,共24分)21.(12分)某中学为了创设“书香校园”,准备购买A,B两种书架,用于放置图书.在购买时发现,A种书架的单价比B种书架的单价多20元,用600元购买A种书架的个数与用480元购买B种书架的个数相同.(1)求A,B两种书架的单价各是多少元?(2)学校准备购买A,B两种书架共15个,且购买的总费用不超过1400元,求最多可以购买多少个A种书架?22.(12分)如图,小明利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为60米,且AB垂直于桥面.(点A,B,C,M在同一平面内)(1)求大桥主架在桥面以上的高度AM;(结果保留根号)(2)求大桥主架在水面以上的高度AB.(结果精确到1米)(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,≈1.73)五、解答题(满分12分)23.(12分)小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量y(本)与销售单价x(元)之间满足一次函数关系,三对对应值如下表:销售单价x(元)12 14 16每周的销售量y(本)500 400 300 (1)求y与x之间的函数关系式;(2)通过与其他网店对比,小红将这款笔记本的单价定为x元(12≤x≤15,且x为整数),设每周销售该款笔记本所获利润为w元,当销售单价定为多少元时每周所获利润最大,最大利润是多少元?六、解答题(满分12分)24.(12分)如图,四边形ABCD内接于⊙O,AC是直径,AB=BC,连接BD,过点D的直线与CA的延长线相交于点E,且∠EDA=∠ACD.(1)求证:直线DE是⊙O的切线;(2)若AD=6,CD=8,求BD的长.七、解答题(满分12分)25.(12分)在等腰△ADC和等腰△BEC中,∠ADC=∠BEC=90°,BC<CD,将△BEC绕点C 逆时针旋转,连接AB,点O为线段AB的中点,连接DO,EO.(1)如图1,当点B旋转到CD边上时,请直接写出线段DO与EO的位置关系和数量关系;(2)如图2,当点B旋转到AC边上时,(1)中的结论是否成立?若成立,请写出证明过程,若不成立,请说明理由;(3)若BC=4,CD=2,在△BEC绕点C逆时针旋转的过程中,当∠ACB=60°时,请直接写出线段OD的长.八、解答题(满分14分)26.(14分)如图,抛物线y=ax2+x+c(a≠0)与x轴相交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),作直线BC.(1)求抛物线的解析式;(2)在直线BC上方的抛物线上存在点D,使∠DCB=2∠ABC,求点D的坐标;(3)在(2)的条件下,点F的坐标为(0,),点M在抛物线上,点N在直线BC上.当以D,F,M,N为顶点的四边形是平行四边形时,请直接写出点N的坐标.参考答案与解析一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.﹣的绝对值是()A.B.﹣C.3 D.﹣3【知识考点】绝对值.【思路分析】依据绝对值的性质求解即可.【解题过程】解:|﹣|=.故选:A.【总结归纳】本题主要考查的是绝对值的性质,熟练掌握绝对值的性质是解题的关键.2.如图是由5个完全相同的小正方体组成的立体图形,它的俯视图是()A.B.C.D.【知识考点】简单组合体的三视图.【思路分析】根据从上面看得到的图形是俯视图,可得答案.【解题过程】解:从上面看,底层左边是一个小正方形,上层是两个小正方形.故选:B.【总结归纳】本题考查了简单组合体的三视图,解题时注意从上面看得到的图形是俯视图.3.下列运算正确的是()A.a2•a3=a6B.a8÷a4=a2C.5a﹣3a=2a D.(﹣ab2)2=﹣a2b4【知识考点】合并同类项;同底数幂的乘法;幂的乘方与积的乘方;同底数幂的除法.【思路分析】根据整式的运算法则即可求出答案.【解题过程】解:(A)原式=a5,故A错误.(B)原式=a4,故B错误.(D)原式=a2b4,故D错误.故选:C.【总结归纳】本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.4.一组数据1,4,3,1,7,5的众数是()A.1 B.2 C.2.5 D.3.5【知识考点】众数.【思路分析】众数是指一组数据中出现次数最多的数据;据此即可求得正确答案.【解题过程】解:本题中数据1出现了2次,出现的次数最多,所以本组数据的众数是1.故选:A.【总结归纳】主要考查了众数的概念.注意众数是指一组数据中出现次数最多的数据,它反映了一组数据的多数水平,一组数据的众数可能不是唯一的.5.一个不透明的口袋中有4个红球、2个白球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸到红球的概率是()A.B.C.D.【知识考点】概率公式.【思路分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率,即可求出答案.【解题过程】解:根据题意可得:袋中有4个红球、2个白球,共6个,从袋子中随机摸出1个球,则摸到红球的概率是=.故选:D.【总结归纳】此题考查了概率公式的应用.注意概率=所求情况数与总情况数之比.6.不等式组的整数解的个数是()A.2 B.3 C.4 D.5【知识考点】一元一次不等式组的整数解.【思路分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出答案.【解题过程】解:解不等式3+x>1,得:x>﹣2,解不等式2x﹣3≤1,得:x≤2,则不等式组的解集为﹣2<x≤2,所以不等式组的整数解有﹣1、0、1、2这4个,故选:C.【总结归纳】本题考查的是一元一次不等式组的整数解,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.7.我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入,两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工x米,乙工程队每天施工y米.根据题意,所列方程组正确的是()A.B.C.D.【知识考点】由实际问题抽象出二元一次方程组.【思路分析】根据甲工程队独立施工2天后,乙工程队加入,两工程队联合施工3天后,还剩50米的工程和甲工程队每天比乙工程队多施工2米,可以列出相应的二元一次方程组,本题得以解决.【解题过程】解:由题意可得,,故选:D.【总结归纳】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.8.一个零件的形状如图所示,AB∥DE,AD∥BC,∠CBD=60°,∠BDE=40°,则∠A的度数是()A.70°B.80°C.90°D.100°【知识考点】平行线的性质.【思路分析】根据平行线的性质,可以得到∠ADB=60°和∠ABD的度数,再根据三角形内角和,即可得到∠A的度数.【解题过程】解:∵AB∥DE,AD∥BC,∴∠ABD=∠BDE,∠ADB=∠CBD,∵∠CBD=60°,∠BDE=40°,∴∠ADB=60°,∠ABD=40°,∴∠A=180°﹣∠ADB﹣∠ABD=80°,故选:B.【总结归纳】本题考查平行线的性质、三角形内角和,解答本题的关键是明确题意,利用数形结合的思想解答.9.如图,矩形ABCD的顶点D在反比例函数y=(x>0)的图象上,点E(1,0)和点F(0,1)在AB边上,AE=EF,连接DF,DF∥x轴,则k的值为()A.2B.3 C.4 D.4【知识考点】反比例函数图象上点的坐标特征;矩形的性质.【思路分析】过点D作DH⊥x轴于点H,设AD交x轴于点G,得矩形OFDH,根据点E(1,0)和点F(0,1)在AB边上,AE=EF,可以求出EG和DH的长,进而可得OH的长,所以得点D的坐标,即可得k的值.【解题过程】解:如图,过点D作DH⊥x轴于点H,设AD交x轴于点G,∵DF∥x轴,∴得矩形OFDH,∴DF=OH,DH=OF,∵E(1,0)和点F(0,1),∴OE=OF=1,∠OEF=45,∴AE=EF=,∵四边形ABCD是矩形,∴∠A=90°,∵∠AEG=∠OEF=45°,∴AG=AE=,∴EG=2,∵DH=OF=1,∠DHG=90°,∠DGH=∠AGE=45°,∴GH=DH=1,∴DF=OH=OE+EG+GH=1+2+1=4,∴D(4,1),∵矩形ABCD的顶点D在反比例函数y=(x>0)的图象上,∵k=4.则k的值为4.故选:C.【总结归纳】本题考查了反比例函数图象上点的坐标特征、矩形的性质,解决本题的关键是掌握反比例函数图象和性质.10.如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,则以下四个结论中:①abc >0,②2a+b=0,③4a+b2<4ac,④3a+c<0.正确的个数是()A.1 B.2 C.3 D.4【知识考点】二次函数图象与系数的关系.【思路分析】①根据抛物线开口向下可得a<0,对称轴在y轴右侧,得b>0,抛物线与y轴正半轴相交,得c>0,进而即可判断;②根据抛物线对称轴是直线x=1,即﹣=1,可得b=﹣2a,进而可以判断;③根据b=﹣2a,可得c<2,进而可以判断;④当x=﹣1时,y<0,即a﹣b+c<0,根据b=﹣2a,可得3a+c<0,即可判断.【解题过程】解:①根据抛物线开口向下可知:a<0,因为对称轴在y轴右侧,所以b>0,因为抛物线与y轴正半轴相交,所以c>0,所以abc<0,所以①错误;②因为抛物线对称轴是直线x=1,即﹣=1,所以b=﹣2a,所以b+2a=0,所以②正确;③因为b=﹣2a,由4a+b2<4ac,得4a+4a2<4ac,∵a<0,∴c<1+a,根据抛物线与y轴的交点,c<2,所以③错误;④当x=﹣1时,y<0,即a﹣b+c<0,因为b=﹣2a,所以3a+c<0,所以④正确.所以正确的是②④2个.故选:B.【总结归纳】本题考查了二次函数图象与系数的关系,解决本题的关键是掌握二次函数图象和性质.二、填空题(本题共8小题,每小题3分,共24分)11.伴随“互联网+”时代的来临,预计到2025年,我国各类网络互助平台的实际参与人数将达到450000000,将数据450000000用科学记数法表示为.【知识考点】科学记数法—表示较大的数.【思路分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.【解题过程】解:将数据450000000用科学记数法表示为4.5×108.故答案为:4.5×108.【总结归纳】此题考查科学记数法的表示方法,表示时关键要正确确定a的值以及n的值.12.分解因式:ab2﹣9a=.【知识考点】提公因式法与公式法的综合运用.【思路分析】根据提公因式,平方差公式,可得答案.【解题过程】解:原式=a(b2﹣9)=a(b+3)(b﹣3),故答案为:a(b+3)(b﹣3).【总结归纳】本题考查了因式分解,一提,二套,三检查,分解要彻底.13.甲、乙两人参加“环保知识”竞赛,经过6轮比赛,他们的平均成绩都是97分.如果甲、乙两人比赛成绩的方差分别为s甲2=6.67,s乙2=2.50,则这6次比赛成绩比较稳定的是.(填“甲”或“乙”)【知识考点】方差.【思路分析】根据方差的意义求解可得.【解题过程】解:∵s甲2=6.67,s乙2=2.50,∴s甲2>s乙2,∴这6次比赛成绩比较稳定的是乙,故答案为:乙.【总结归纳】本题主要考查方差,解题的关键是掌握方差的意义.14.关于x的一元二次方程x2﹣2x﹣k=0有两个不相等的实数根,则k的取值范围是.【知识考点】根的判别式.【思路分析】根据判别式的意义得到△=(﹣2)2+4k>0,然后解不等式即可.【解题过程】解:∵关于x的一元二次方程x2﹣2x﹣k=0有两个不相等的实数根,∴△=(﹣2)2+4k>0,解得k>﹣1.故答案为:k>﹣1.【总结归纳】此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.15.如图,在△ABC中,AB=5,AC=8,BC=9,以A为圆心,以适当的长为半径作弧,交AB 于点M,交AC于点N.分别以M,N为圆心,以大于MN的长为半径作弧,两弧在∠BAC 的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,AF=AB,连接DF,则△CDF 的周长为.【知识考点】作图—基本作图.【思路分析】直接利用基本作图方法结合全等三角形的判定与性质进而得出BD=DF,即可得出答案.【解题过程】解:∵AB=5,AC=8,AF=AB,∴FC=AC﹣AF=8﹣5=3,由作图方法可得:AD平分∠BAC,∴∠BAD=∠CAD,在△ABD和△AFD中,∴△ABD≌△AFD(SAS),∴BD=DF,∴△DFC的周长为:DF+FC+DC=BD+DC+FC=BC+FC=9+3=12.故答案为:12.【总结归纳】此题主要考查了基本作图以及全等三角形的判定与性质,正确理解基本作图方法是解题关键.16.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是.【知识考点】等边三角形的性质;多边形内角与外角;正多边形和圆.【思路分析】根据正五边形和等边三角形的性质得到∠EAF=108°﹣60°=48°,根据等腰三角形的性质即可得到结论.【解题过程】解:∵正五边形ABCDE,∴∠EAB==108°,∵△ABF是等边三角形,∴∠FAB=60°,∴∠EAF=108°﹣60°=48°,∵AE=AF,∴∠AEF=∠AFE=(180°﹣48°)=66°,故答案为:66°.【总结归纳】本题考查了正多边形与圆,正五边形和等边三角形的性质,等腰三角形的性质,正确的识别图形是解题的关键.17.一张菱形纸片ABCD的边长为6cm,高AE等于边长的一半,将菱形纸片沿直线MN折叠,使点A与点B重合,直线MN交直线CD于点F,则DF的长为cm.【知识考点】菱形的性质;翻折变换(折叠问题).【思路分析】根据题意分两种情况:①如图1:根据菱形纸片ABCD的边长为6cm,高AE等于边长的一半,可得菱形的一个内角为30°,根据折叠可得BH=AH=3,再根据特殊角三角函数即可求出CF的长,进而可得DF的长;如图2,将如图1中的点A和点B交换一下位置,同理即可求出DF的长就是如图1中的CF的长.【解题过程】解:①根据题意画出如图1:∵菱形纸片ABCD的边长为6cm,∴AB=BC=CD=AD=6,∵高AE等于边长的一半,∴AE=3,∵sin∠B==,∴∠B=30°,将菱形纸片沿直线MN折叠,使点A与点B重合,∴BH=AH=3,∴BG==2,∴CG=BC﹣BG=6﹣2,∵AB∥CD,∴∠GCF=∠B=30°,∴CF=CG•cos30°=(6﹣2)×=3﹣3,∴DF=DC+CF=6+3﹣3=(3+3)cm;②如图2,BE=AE=3,同理可得DF=3﹣3.综上所述:则DF的长为(3+3)或(3﹣3)cm.故答案为:(3+3)或(3﹣3).【总结归纳】本题考查了翻折变换、菱形的性质,解决本题的关键是分两种情况分类讨论,进行计算.18.如图,∠MON=45°,正方形ABB1C,正方形A1B1B2C1,正方形A2B2B3C2,正方形A3B3B4C3,…,的顶点A,A1,A2,A3,…,在射线OM上,顶点B,B1,B2,B3,B4,…,在射线ON上,连接AB2交A1B1于点D,连接A1B3交A2B2于点D1,连接A2B4交A3B3于点D2,…,连接B1D1交AB2于点E,连接B2D2交A1B3于点E1,…,按照这个规律进行下去,设△ACD与△B1DE的面积之和为S1,△A1C1D1与△B2D1E1的面积之和为S2,△A2C2D2与△B3D2E2的面积之和为S3,…,若AB=2,则S n等于.(用含有正整数n的式子表示)【知识考点】列代数式;规律型:图形的变化类;三角形的面积.【思路分析】设△ADC的面积为S,利用相似三角形的性质求出S1,S2,…S n与S的关系即可解决问题.【解题过程】解:设△ADC的面积为S,由题意,AC∥B1B2,AC=AB=2,B1B2=4,∴△ACD∽△B2B1D,∴=()2=,∴=4S,∵==,CB1=2,∴DB1=,同法D1B2=,∵DB1∥D1B2,∴==,∴=,∴S1=S+=,∵△A1C1D1∽△ACD,∴=()2=,∴=4S,同法可得,=,∴S2=4S+==×4,…S n=×4n﹣1,∵S=×2×=,∴S n=×4n﹣1.故答案为:.【总结归纳】本题考查正方形的性质,三角形的面积,相似三角形的判定和性质等知识,解题的关键是学会探究规律的方法,属于中考常考题型.三、解答题(第19题10分,第20题12分,共22分)19.(10分)先化简,再求值:(x﹣1﹣)÷,其中x=3.【知识考点】分式的化简求值.【思路分析】根据分式的减法和除法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.【解题过程】解:(x﹣1﹣)÷===,当x=3时,原式=.【总结归纳】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.20.(12分)某校计划组建航模、摄影、乐器、舞蹈四个课外活动小组,要求每名同学必须参加,并且只能选择其中一个小组.为了解学生对四个课外活动小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把此次调查结果整理并绘制成如图两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)本次被调查的学生有人;(2)请补全条形统计图,并求出扇形统计图中“航模”所对应的圆心角的度数;(3)通过了解,喜爱“航模”的学生中有2名男生和2名女生曾在市航模比赛中获奖,现从这4个人中随机选取2人参加省青少年航模比赛,请用列表或画树状图的方法求出所选的2人恰好是1名男生和1名女生的概率.【知识考点】扇形统计图;条形统计图;列表法与树状图法.【思路分析】(1)根据摄影的人数和所占的百分比求出抽取的总人数;(2)用总人数减去其他兴趣小组的人数求出航模的人数,从而补全统计图;用360°乘以“航模”所占的百分比即可得出扇形统计图中“航模”所对应的圆心角的度数;(3)根据题意画出图表得出所有等可能的情况数和所选的2人恰好是1名男生和1名女生的情况数,然后根据概率公式即可得出答案.【解题过程】解:(1)本次被调查的学生有:9÷15%=60(人);故答案为:60;(2)航模的人数有:60﹣9﹣15﹣12=24(人),补全条形统计图如图:“航模”所对应的圆心角的度数是:360°×=144°;(3)设两名男生分别为男1,男2,两名女生分别为女1,女2,列表如下:男1 男2 女1 女2 男1 (男2,男1)(女1,男1)(女2,男1)男2 (男1,男2)(女1,男2)(女2,男2)女1 (男1,女1)(男2,女1)(女2,女1)女2 (男1,女2)(男2,女2)(女1,女2)由表格可以看出,所有可能出现的结果有12种,并且它们出现的可能性相等,其中恰好是1名男生和1名女生的情况有8种.则所选的2人恰好是1名男生和1名女生的概率是=.【总结归纳】此题考查的是用列表法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.四、解答题(第21题12分,第22题12分,共24分)21.(12分)某中学为了创设“书香校园”,准备购买A,B两种书架,用于放置图书.在购买时发现,A种书架的单价比B种书架的单价多20元,用600元购买A种书架的个数与用480元购买B种书架的个数相同.(1)求A,B两种书架的单价各是多少元?(2)学校准备购买A,B两种书架共15个,且购买的总费用不超过1400元,求最多可以购买多少个A种书架?【知识考点】分式方程的应用;一元一次不等式的应用.【思路分析】(1)设B种书架的单价为x元,则A种书架的单价为(x+20)元,根据数量=总价÷单价结合用600元购买A种书架的个数与用480元购买B种书架的个数相同,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)设准备购买m个A种书架,则购买B种书架(15﹣m)个,根据题意列出不等式并解答.【解题过程】解:(1)设B种书架的单价为x元,根据题意,得.解得x=80.经检验:x=80是原分式方程的解.∴x+20=100.答:购买A种书架需要100元,B种书架需要80元.(2)设准备购买m个A种书架,根据题意,得100m+80(15﹣m)≤1400.解得m≤10.答:最多可购买10个A种书架.【总结归纳】本题主要考查了分式方程的应用和一元一次不等式的应用,分析题意,找到关键描述语,找到合适的数量关系是解决问题的关键.22.(12分)如图,小明利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为60米,且AB垂直于桥面.(点A,B,C,M在同一平面内)(1)求大桥主架在桥面以上的高度AM;(结果保留根号)(2)求大桥主架在水面以上的高度AB.(结果精确到1米)(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,≈1.73)【知识考点】解直角三角形的应用﹣仰角俯角问题.【思路分析】(1)根据正切的定义求出AM;(2)根据正切的定义求出BM,结合图形计算即可.【解题过程】解:(1)∵AB垂直于桥面,∴∠AMC=∠BMC=90°,在Rt△AMC中,CM=60,∠ACM=30°,tan∠ACM=,∴AM=CM•tan∠ACM=60×=20(米),答:大桥主架在桥面以上的高度AM为20米;(2)在Rt△BMC中,CM=60,∠BCM=14°,tan∠BCM=,∴MB=CM•tan∠BCM≈60×0.25=15(米),∴AB=AM+MB=15+20≈50(米)答:大桥主架在水面以上的高度AB约为50米.【总结归纳】本题考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.五、解答题(满分12分)23.(12分)小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量y(本)与销售单价x(元)之间满足一次函数关系,三对对应值如下表:销售单价x(元)12 14 16每周的销售量y(本)500 400 300 (1)求y与x之间的函数关系式;(2)通过与其他网店对比,小红将这款笔记本的单价定为x元(12≤x≤15,且x为整数),设每周销售该款笔记本所获利润为w元,当销售单价定为多少元时每周所获利润最大,最大利润是多少元?【知识考点】二次函数的应用.【思路分析】(1)根据题意和表格中的数据,可以求得y与x之间的函数关系式;(2)根据题意,可以得到w与x的函数关系式,然后根据二次函数的性质,可以解答本题.【解题过程】解:(1)设y与x之间的函数关系式是y=kx+b(k≠0),,得,即y与x之间的函数关系式为y=﹣50x+1100;(2)由题意可得,w=(x﹣10)y=(x﹣10)(﹣50x+1100)=﹣50(x﹣16)2+1800,∵a=﹣50<0∴w有最大值∴当x<16时,w随x的增大而增大,∵12≤x≤15,x为整数,∴当x=15时,w有最大值,∴w=﹣50(15﹣16)2+1800=1750,答:销售单价为15元时,每周获利最大,最大利润是1750元.【总结归纳】本题考查二次函数的应用,解答本题的关键是明确题意,利用二次函数的性质解答.六、解答题(满分12分)24.(12分)如图,四边形ABCD内接于⊙O,AC是直径,AB=BC,连接BD,过点D的直线与CA的延长线相交于点E,且∠EDA=∠ACD.(1)求证:直线DE是⊙O的切线;(2)若AD=6,CD=8,求BD的长.【知识考点】圆周角定理;圆内接四边形的性质;切线的判定与性质.【思路分析】(1)连接OD.想办法证明OD⊥DE即可.(2)解法一:过点A作AF⊥BD于点F,则∠AFB=∠AFD=90°,想办法求出BF,DF即可.解法二:过点B作BH⊥BD交DC延长线于点H.证明△BDH是等腰直角三角形,求出DH即可.【解题过程】(1)证明:连接OD,∵OC=OD,∴∠OCD=∠ODC,∵AC是直径,∴∠ADC=90°,∵∠EDA=∠ACD,∴∠ADO+∠ODC=∠EDA+∠ADO=90°,∴∠EDO=∠EDA+∠ADO=90°,∴OD⊥DE,∵OD是半径,∴直线DE是⊙O的切线.(2)解法一:过点A作AF⊥BD于点F,则∠AFB=∠AFD=90°,∵AC是直径,∴∠ABC=∠ADC=90°,∵在Rt△ACD中,AD=6,CD=8,∴AC2=AD2+CD2=62+82=100,∴AC=10,∵在Rt△ABC中,AB=BC,∴∠BAC=∠ACB=45°,∵,∴,∵∠ADB=∠ACB=45°,∵在Rt△ADF中,AD=6,∵,。
辽宁省抚顺、铁岭市2020年中考语文试题(含答案与解析)

阅读下面选文,完成下列小题。 【甲】……故天将降大任于是人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,行拂乱其所为,
所以动心忍性,曾益其所不能。 人恒过,然后能改;困于心,衡于虑,而后作;征于色,发于声,而后喻。入则无法家拂士,出则无
敌国外患者,国恒亡。然后知生于忧患而死于安乐也。
【乙】贞观十二年,太宗谓侍臣曰:“朕读书见前王善事,皆力行而不倦。其所任用公辈数人,诚以为 贤。 然致理比于三、五之代,犹为不逮,何也?”
魏徵对曰:“今四夷宾服天下无事诚旷古所未有。然自古帝王初即位者,皆欲励精为政,比迹于尧、舜; 及其安乐也,则骄奢放逸,莫能终其善。人臣初见任用者,皆欲匡主济时,追纵于稷、契;及其富贵也, 则思苟全官爵,莫能尽其忠节。若使君臣常无懈怠,各保其终,则天下无忧不理,自可超迈前古也。”
语境应用“锻造”。
第四空:“完善”,完备美好。“完备”,具备,不缺任何必要的东西的。根据语境应用“完善”。 故选 A。 3. 选出对下列病句修改有误的一项( ) A. 细心的读者能够及时修正并发现论文中的错误,这无疑对学术研究大有裨益。 修改:将“修正”和“发现”调换位置。 B. 为解决网络不稳定,我校教师提前录制了许多教学视频,以供学生下载观看。 修改:在“不稳定”后加“的问题”。 C. 在国外制作的电视动画中,有关校园生活等现实题材的作品占比大约为 20%左右。 修改:将“大约”或“左右”去掉。 D. 教育部门倡导的“传统戏曲进校园”活动,目的是为了弘扬中国的戏曲文化。 修改:将“弘扬”改为“发扬”。 【答案】D 【解析】 【详解】D.句式杂糅,删去“目的”或“为了”。故选 D。 4. 选出下列文学常识表述有误的一项是( ) A. 《渔家傲(天接云涛连晓雾)》作者李清照,号青莲居士,宋代女词人。 B. 《论语》是儒家经典著作,与《大学》《中庸》《孟子》合称为“四书”。 C. 欧阳修,北宋文学家,“唐宋八大家”之一,我们学过他的作品《醉翁亭记》。 D. 《木兰诗》是南北朝时北方的一首乐府民歌,选自北宋郭茂倩编纂的《乐府诗集》。 【答案】A 【解析】 【详解】A.错误。李清照,号易安居士;李白,号青莲居士。故选 A。 5. 选出下列对李白的《行路难(其一)》赏析有误的一项( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年辽宁省铁岭市、葫芦岛市中考数学试卷班级:___________姓名:___________得分:___________一、选择题(本大题共10小题,共30.0分)1.−13的绝对值是()A. 13B. −13C. 3D. −32.如图是由5个完全相同的小正方体组成的立体图形,它的俯视图是()A.B.C.D.3.下列运算正确的是()A. a2⋅a3=a6B. a8÷a4=a2C. 5a−3a=2aD. (−ab2)2=−a2b44.一组数据1,4,3,1,7,5的众数是()A. 1B. 2C. 2.5D. 3.55.一个不透明的口袋中有4个红球、2个白球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸到红球的概率是()A. 16B. 13C. 12D. 236.不等式组{3+x>12x−3≤1的整数解的个数是()A. 2B. 3C. 4D. 57.我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入,两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工x米,乙工程队每天施工y米.根据题意,所列方程组正确的是()A. {x =y −22x +3y =400 B. {x =y −22x +3(x +y)=400−50 C. {x =y +22x +3y =400−50D. {x =y +22x +3(x +y)=400−508. 一个零件的形状如图所示,AB//DE ,AD//BC ,∠CBD =60°,∠BDE =40°,则∠A的度数是( ) A. 70° B. 80° C. 90° D. 100° 9. 如图,矩形ABCD 的顶点D 在反比例函数y =kx (x >0)的图象上,点E(1,0)和点F(0,1)在AB 边上,AE =EF ,连接DF ,DF//x 轴,则k 的值为( )A. 2√2B. 3C. 4D. 4√210. 如图,二次函数y =ax 2+bx +c(a ≠0)的图象的对称轴是直线x =1,则以下四个结论中:①abc >0,②2a +b =0,③4a +b 2<4ac ,④3a +c <0.正确的个数是( )A. 1B. 2C. 3D. 4二、填空题(本大题共8小题,共24.0分)11. 伴随“互联网+”时代的来临,预计到2025年,我国各类网络互助平台的实际参与人数将达到450000000,将数据450000000用科学记数法表示为______. 12. 分解因式:ab 2−9a =______.13. 甲、乙两人参加“环保知识”竞赛,经过6轮比赛,他们的平均成绩都是97分.如果甲、乙两人比赛成绩的方差分别为s 甲2=6.67,s 乙2=2.50,则这6次比赛成绩比较稳定的是______.(填“甲”或“乙”)14. 关于x 的一元二次方程x 2−2x −k =0有两个不相等的实数根,则k 的取值范围是______.15. 如图,在△ABC 中,AB =5,AC =8,BC =9,以A 为圆心,以适当的长为半径作弧,交AB 于点M ,交AC 于点N.分别以M ,N 为圆心,以大于12MN 的长为半径作弧,两弧在∠BAC 的内部相交于点G ,作射线AG ,交BC 于点D ,点F 在AC 边上,AF =AB ,连接DF ,则△CDF 的周长为______.16. 如图,以AB 为边,在AB 的同侧分别作正五边形ABCDE和等边△ABF ,连接FE ,FC ,则∠EFA 的度数是______.17. 一张菱形纸片ABCD 的边长为6cm ,高AE 等于边长的一半,将菱形纸片沿直线MN 折叠,使点A 与点B 重合,直线MN 交直线CD 于点F ,则DF 的长为______cm . 18. 如图,∠MON =45°,正方形ABB 1C ,正方形A 1B 1B 2C 1,正方形A 2B 2B 3C 2,正方形A 3B 3B 4C 3,…,的顶点A ,A 1,A 2,A 3,…,在射线OM 上,顶点B ,B 1,B 2,B 3,B 4,…,在射线ON 上,连接AB 2交A 1B 1于点D ,连接A 1B 3交A 2B 2于点D 1,连接A 2B 4交A 3B 3于点D 2,…,连接B 1D 1交AB 2于点E ,连接B 2D 2交A 1B 3于点E 1,…,按照这个规律进行下去,设△ACD 与△B 1DE 的面积之和为S 1,△A 1C 1D 1与△B 2D 1E 1的面积之和为S 2,△A 2C 2D 2与△B 3D 2E 2的面积之和为S 3,…,若AB =2,则S n 等于______.(用含有正整数n 的式子表示)三、解答题(本大题共8小题,共96.0分)19. 先化简,再求值:(x −1−x 2x+1)÷xx 2+2x+1,其中x =3.20.某校计划组建航模、摄影、乐器、舞蹈四个课外活动小组,要求每名同学必须参加,并且只能选择其中一个小组.为了解学生对四个课外活动小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把此次调查结果整理并绘制成如图两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)本次被调查的学生有______人;(2)请补全条形统计图,并求出扇形统计图中“航模”所对应的圆心角的度数;(3)通过了解,喜爱“航模”的学生中有2名男生和2名女生曾在市航模比赛中获奖,现从这4个人中随机选取2人参加省青少年航模比赛,请用列表或画树状图的方法求出所选的2人恰好是1名男生和1名女生的概率.21.某中学为了创设“书香校园”,准备购买A,B两种书架,用于放置图书.在购买时发现,A种书架的单价比B种书架的单价多20元,用600元购买A种书架的个数与用480元购买B种书架的个数相同.(1)求A,B两种书架的单价各是多少元?(2)学校准备购买A,B两种书架共15个,且购买的总费用不超过1400元,求最多可以购买多少个A种书架?22.如图,小明利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为60米,且AB垂直于桥面.(点A,B,C,M 在同一平面内)(1)求大桥主架在桥面以上的高度AM;(结果保留根号)(2)求大桥主架在水面以上的高度AB.(结果精确到1米)(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,√3≈1.73)23.小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量y(本)与销售单价x(元)之间满足一次函数关系,三对对应值如下表:销售单价x(元)121416每周的销售量y(本)500400300(2)通过与其他网店对比,小红将这款笔记本的单价定为x元(12≤x≤15,且x为整数),设每周销售该款笔记本所获利润为w元,当销售单价定为多少元时每周所获利润最大,最大利润是多少元?24.如图,四边形ABCD内接于⊙O,AC是直径,AB=BC,连接BD,过点D的直线与CA的延长线相交于点E,且∠EDA=∠ACD.(1)求证:直线DE是⊙O的切线;(2)若AD=6,CD=8,求BD的长.25.在等腰△ADC和等腰△BEC中,∠ADC=∠BEC=90°,BC<CD,将△BEC绕点C逆时针旋转,连接AB,点O为线段AB的中点,连接DO,EO.(1)如图1,当点B旋转到CD边上时,请直接写出线段DO与EO的位置关系和数量关系;(2)如图2,当点B旋转到AC边上时,(1)中的结论是否成立?若成立,请写出证明过程,若不成立,请说明理由;(3)若BC=4,CD=2√6,在△BEC绕点C逆时针旋转的过程中,当∠ACB=60°时,请直接写出线段OD的长.x+c(a≠0)与x轴相交于点A(−1,0)和点B,与y轴相交26.如图,抛物线y=ax2+94于点C(0,3),作直线BC.(1)求抛物线的解析式;(2)在直线BC上方的抛物线上存在点D,使∠DCB=2∠ABC,求点D的坐标;),点M在抛物线上,点N在直线BC上.当(3)在(2)的条件下,点F的坐标为(0,72以D,F,M,N为顶点的四边形是平行四边形时,请直接写出点N的坐标.答案和解析1. A解:|−13|=13.2. B解:从上面看,底层左边是一个小正方形,上层是两个小正方形. 3. C解:(A)原式=a 5,故A 错误. (B)原式=a 4,故B 错误. (D)原式=a 4b 2,故D 错误. 4. A解:本题中数据1出现了2次,出现的次数最多,所以本组数据的众数是1. 5. D解:根据题意可得:袋中有4个红球、2个白球,共6个, 从袋子中随机摸出1个球,则摸到红球的概率是46=23.6. C解:解不等式3+x >1,得:x >−2, 解不等式2x −3≤1,得:x ≤2, 则不等式组的解集为−2<x ≤2,所以不等式组的整数解有−1、0、1、2这4个,7. D解:由题意可得,{x =y +22x +3(x +y)=400−50,8. B解:∵AB//DE ,AD//BC ,∴∠ABD =∠BDE ,∠ADB =∠CBD , ∵∠CBD =60°,∠BDE =40°, ∴∠ADB =60°,∠ABD =40°,∴∠A =180°−∠ADB −∠ABD =80°,9.C解:如图,过点D作DH⊥x轴于点H,设AD交x轴于点G,∵DF//x轴,∴得矩形OFDH,∴DF=OH,DH=OF,∵E(1,0)和点F(0,1),∴OE=OF=1,∠OEF=45,∴AE=EF=√2,∵四边形ABCD是矩形,∴∠A=90°,∵∠AEG=∠OEF=45°,∴AG=AE=√2,∴EG=2,∵DH=OF=1,∠DHG=90°,∠DGH=∠AGE=45°,∴GH=DH=1,∴DF=OH=OE+EG+GH=1+2+1=4,∴D(4,1),(x>0)的图象上,∵矩形ABCD的顶点D在反比例函数y=kx∵k=4.则k的值为4.10.B解:①根据抛物线开口向下可知:a<0,因为对称轴在y轴右侧,所以b>0,因为抛物线与y轴正半轴相交,所以c>0,所以abc<0,所以①错误;②因为抛物线对称轴是直线x=1,=1,即−b2a所以b =−2a , 所以b +2a =0, 所以②正确;③因为抛物线与x 轴有2个交点, 所以△>0,即b 2−4ac >0,所以b 2−4ac +4a >4a , 所以4a +b 2>4ac +4a , 所以③错误;④当x =−1时,y <0, 即a −b +c <0, 因为b =−2a , 所以3a +c <0, 所以④正确.所以正确的个数是②④2个.11. 4.5×108解:将数据450000000用科学记数法表示为4.5×108.12. a(b +3)(b −3)解:原式=a(b 2−9) =a(b +3)(b −3),13. 乙解:∵s 甲2=6.67,s 乙2=2.50, ∴s 甲2=>s 乙2,∴这6次比赛成绩比较稳定的是乙,14. k >−1解:∵关于x 的一元二次方程x 2−2x −k =0有两个不相等的实数根, ∴△=(−2)2+4k >0, 解得k >−1.15. 12解:∵AB =5,AC =8,AF =AB , ∴FC =AC −AF =8−5=3, 由作图方法可得:AD 平分∠BAC , ∴∠BAD =∠CAD , 在△ABD 和△AFD 中{AB=AF∠BAD=∠FAD AD=AD,∴△ABD≌△AFD(SAS),∴BD=DF,∴△DFC的周长为:DF+FC+DC=BD+DC+FC=BC+FC=9+3=12.16.66°解:∵正五边形ABCDE,∴∠EAB=(5−2)×180°5=108°,∵△ABF是等边三角形,∴∠FAB=60°,∴∠EAF=108°−60°=48°,∵AE=AF,∴∠AE=∠AFE=12×(180°−48°)=66°,17.(3√3+3)或(3√3−3)解:①根据题意画出如图1:∵菱形纸片ABCD的边长为6cm,∴AB=BC=CD=AD=6,∵高AE等于边长的一半,∴AE=3,∵sin∠B=AEAB =12,∴∠B=30°,将菱形纸片沿直线MN折叠,使点A与点B重合,∴BH=AH=3,∴BG=BHcos30∘=2√3,∴CG=BC−BG=6−2√3,∵AB//CD,∴∠GCF=∠B=30°,∴CF=CG⋅cos30°=(6−2√3)×√32=3√3−3,∴DF=DC+CF=6+3√3−3=(3√3+3)cm;②如图2,BE=AE=3,同理可得DF=3√3−3.综上所述:则DF的长为(3√3+3)或(3√3−3)cm.故答案为:(3√3+3)或(3√3−3).18.149×4n−1解:设△ADC的面积为S,由题意,AC//B1B2,AC=AB=2,B1B2=4,∴△ACD∽△B2B1D,∴S△ADCS△B1B2D =(ACB1B2)2=14,∴S△B1B2D=4S,∵CDDB1=ACB1B2=12,CB1=2,∴DB1=43,同法D1B2=83,∵DB1//D1B2,∴DEEB2=DB1D1B2=12,∴S△DB1E =4S3,∴S1=S+4S3=7S3,∵△A1C1D1∽△ACD,∴S△A1C1D1S△ACD =(A1C1AC)2=14,∴S△A1C1D1=4S,同法可得,S△D1B1E1=16S3,∴S2=4S+16S3=28S3=7S3×4,…S n=7S3×4n−1,∵S=12×2×23=23,∴S n=149×4n−1.19. 解:(x −1−x 2x+1)÷xx 2+2x+1=[(x−1)(x+1)x+1−x 2x+1]⋅(x+1)2x=x 2−1−x 2x+1⋅(x+1)2x=−x+1x,当x =3时,原式=−3+13=−43.20. 60解:(1)本次被调查的学生有:9÷15%=60(人); 故答案为:60;(2)航模的人数有:60−9−15−12=24(人), 补全条形统计图如图:“航模”所对应的圆心角的度数是:360°×2460=144°;好是1名男生和1名女生的情况有8种.则所选的2人恰好是1名男生和1名女生的概率是812=23.21. 解:(1)设B 种书架的单价为x 元,根据题意,得600x+20=480x.解得x =80.经检验:x =80是原分式方程的解.∴x +20=100.答:购买A 种书架需要100元,B 种书架需要80元.(2)设准备购买m 个A 种书架,根据题意,得100m +80(15−m)≤1400. 解得m ≤10.答:最多可购买10个A 种书架.22. 解:(1)∵AB 垂直于桥面, ∴∠AMC =∠BMC =90°,在Rt △AMC 中,CM =60,∠ACM =30°, tan∠ACM =AMCM ,∴AM =CM ⋅tan∠ACM =60×√33=20√3(米),答:大桥主架在桥面以上的高度AM 为20√3米; (2)在Rt △BMC 中,CM =60,∠BCM =14°, tan∠BCM =BM CM,∴MB =CM ⋅tan∠BCM ≈60×0.25=15, ∴AB =AM +MB =15+20√3≈50(米)答:大桥主架在水面以上的高度AB 约为50米.23. 解:(1)设y 与x 之间的函数关系式是y =kx +b(k ≠0), {12k +b =50014k +b =400,得{k =−50b =1100, 即y 与x 之间的函数关系式为y =−50x +1100; (2)由题意可得,w =(x −10)y =(x −10)(−50x +1100)=−50(x −16)2+1800, ∵a =−50<0 ∴w 有最大值∴当x <16时,w 随x 的增大而增大, ∵12≤x ≤15,x 为整数, ∴当x =15时,w 有最大值,∴w =−50(15−16)2+1800=1750,答:销售单价为15元时,每周获利最大,最大利润是1750元.24. (1)证明:连接OD , ∵OC =OD ,∴∠OCD =∠ODC , ∵AC 是直径, ∴∠ADC =90°, ∵∠EDA =∠ACD ,∴∠ADO +∠ODC =∠EDA +∠ADO , ∴∠EDO =∠EDA +∠ADO =90°, ∴OD ⊥DE , ∵OD 是半径,∴直线DE 是⊙O 的切线.(2)解法一:过点A作AF⊥BD于点F,则∠AFB=∠AFD=90°,∵AC是直径,∴∠ABC=∠ADC=90°,∵在Rt△ACD中,AD=6,CD=8,∴AC2=AD2+CD2=62+82=100,∴AC=10,∵在Rt△ABC中,AB=BC,∴∠BAC=∠ACB=45°,∵sin∠ACB=AB,AC∴AB=sin45°⋅AC=5√2,∵∠ADB=∠ACB=45°,∵在Rt△ADF中,AD=6,∵sin∠ADF=AF,AD∴AF=sin45°⋅AD=3√2,∴DF=AF=3√2,∵在Rt△ABF中,∴BF2=AB2−AF2=(5√2)2−(3√2)2=32,∴BF=4√2,∴BD=BF+DF=7√2.解法二:过点B作BH⊥BD交DC延长线于点H.∴∠DBH=90°,∵AC是直径,∴∠ABC=90°,∵∠ABD=90°−∠DBC∠CBH=90°−∠DBC,∴∠ABD=∠CBH,∵四边形ABCD内接于⊙O,∴∠BAD+∠BCD=180°,∵∠BCD+∠BCH=180°,∴∠BAD=∠BCH,∵AB=CB,∴△ABD≌△CBH(ASA),∴AD=CH,BD=BH,∵AD=6,CD=8,∴DH=CD+CH=14,在Rt△BDH中,∵BD2=DH2−BH2=98,∴BD=7√2.25.解:(1)DO⊥EO,DO=EO;理由:当点B旋转到CD边上时,点E必在边AC上,∴∠AEB=∠CEB=90°,在Rt△ABE中,点O是AB的中点,∴OE=OA=1AB,2∴∠BOE=2∠BAE,在Rt△ABD中,点O是AB的中点,∴OD=OA=1AB,2∴∠DOE=2∠BAD,∴OD=OE,∵等腰△ADC,且∠ADC=90°,∴∠DAC=45°,∴∠DOE=∠BOE+DOE=2∠BAE+2∠BAD=2(∠BAE+∠DAE)=2∠DAC=90°,∴OD⊥OE;(2)仍然成立,理由:如图1,延长ED到点M,使得OM=OE,连接AM,DM,DE,∵O是AB的中点,∴OA=OB,∵∠AOM=∠BOE,∴△AOM≌△BOE(SAS),∴∠MAO=∠EBO,MA=EB,∵△ACD和△CBE是等腰三角形,∠ADC=∠CEB=90°,∴∠CAD=∠ACD=∠EBC=∠BCE=45°,∵∠OBE=180°−∠EBC=135°,∴∠MAO=135°,∴∠MAD=∠MAO−∠DAC=90°,∵∠DCE=∠DCA+∠BCE=90°,∴∠MAD=∠DCE,∵MA=EB,EB=EC,∴MA=EC,∵AD=DC,∴△MAD≌△ECD,∴MD=ED,∠ADM=∠CDE,∵∠CDE+∠ADE=90°,∴∠ADM+∠ADE=90°,∴∠MDE=90°,∵MO=EO,MD=DE,ME,OD⊥ME,∴OD=12ME,∵OE=12∴OD=OE,OD⊥OE;(3)①当点B在AC左侧时,如图3,延长ED到点M,使得OM=OE,连接AM,DM,DE,同(2)的方法得,△OBE≌△OAM(SAS),∴∠OBE=∠OAM,OM=OE,BE=AM,∵BE=CE,∴AM=CE,在四边形ABECD中,∠ADC+∠DCE+∠BEC+∠OBE+∠BAD=540°,∵∠ADC=∠BEC=90°,∴∠DCE=540°−90°−90°−∠OBE−∠BAD=360°−∠OBE=360°−∠OAM−∠BAD,∵∠DAM+∠OAM+∠BAD=360°,∴∠DAM=360°−∠OAM−∠BAD,∴∠DAM=∠DCE,∵AD=CD,∴△DAM≌△DCE(SAS),∴DM=DE,∠ADM=∠CDE,∴∠EDM=∠ADM+∠ADE=∠CDE+∠ADE=∠ADC=90°,∵OM=OE,∴OD=OE=12ME,∠DOE=90°,在Rt△BCE中,CE=√22BC=2√2,过点E作EH⊥DC交DC的延长线于H,在Rt△CHE中,∠ECH=180°−∠ACD−∠ACB−∠BCE=180°−45°−60°−45°= 30°,∴EH=12CE=√2,根据勾股定理得,CH=√3EH=√6,∴DH=CD+CH=3√6,在Rt△DHE中,根据勾股定理得,DE=√EH2+DH2=2√14,∴OD=√22DE=2√7,②当点B在AC右侧时,如图4,同①的方法得,OD=OE,∠DOE=90°,连接DE,过点E作EH⊥CD于H,在Rt△EHC中,∠ECH=30°,∴EH=12CE=√2,根据勾股定理得,CH=√6,∴DH=CD−CH=√6,在Rt△DHE中,根据勾股定理得,DE=2√2,∴OD=√22DE=2,即:线段OD的长为2或2√7.26.解:(1)∵抛物线y=ax2+94x+c经过点A(−1,0),C(0,3),∴{a−94+c=0c=3,解得:{a=−34c=3,∴抛物线的解析式为:y=−34x2+94x+3;(2)如图1,过点C作CE//x轴交抛物线于点E,则∠ECB=∠ABC,过点D 作DH ⊥CE 于点H ,则∠DHC =90°, ∵∠DCB =∠DCH +∠ECB =2∠ABC , ∴∠DCH =∠ABC ,∵∠DHC =∠COB =90°, ∴△DCH∽△CBO , ∴DH CO=CH BO,设点D 的横坐标为t ,则D(t,−34t 2+94t +3), ∵C(0,3),∴DH =−34t 2+94t ,∵点B 是y =−34x 2+94x +3与x 轴的交点, ∴−34x 2+94x +3=0, 解得x 1=4,x 2=−1, ∴B 的坐标为(4,0), ∴OB =4, ∴−34t 2+94t3=t4, 解得t 1=0(舍去),t 2=2,∴点D 的纵坐标为:−34t 2+94t +3=92, 则点D 坐标为(2,92);(3)设直线BC 的解析式为:y =kx +b , 则{4k +b =0b =3,解得:{k =−34b =3, ∴直线BC 的解析式为:y =−34x +3, 设N(m,−34m +3),分两种情况:①如图2,以DF 为边,N 在x 轴的上方时,四边形DFNM 是平行四边形,∵D(2,92),F(0,72), ∴M(m +2,−34m +4),代入抛物线的解析式得:−34(m +2)2+94(m +2)+3=−34m +4, 解得:m =±√63,∴N(√63,3−√64)或(−√63,3+√64); ②如图3,以DF 为边,N 在x 轴的下方时,四边形DFMN 是平行四边形,同理得:M(m −2,−34m +2),代入抛物线的解析式得:−34(m −2)2+94(m −2)+3=−34m +2, 解得:m =4±√663,∴N(4+√663,−√664)或(4−√663,√664); 综上,点N 的坐标分别为:(√63,3−√64)或(−√63,3+√64)或(4+√663,−√664)或(4−√663,√664).。
