交变电场中电介质的损耗-计漏电导的损耗
合集下载
交变电场中电介质的损耗-计漏电导的损耗概要
4-131
由此可见： 在低频段，tgδ 随频率升高成反比地下降。
（3）当频率较高时
tgδ 与ω 的关系基本上服从于图 4-9(c) 所示变化规律。
图 4-9 (a)
与频率的关系;(b)
与频率的关系；(c)
与频率的关系
电导损耗所占比例逐步增加时，tgδ 弛豫最大值不显著；
当γ 值很大时，tgδ 的极大值有可能完全被淹没。 tgδ 与频率的关系分别如图 4-22(a) 和图 4-23(a) 所示。
e
B /T
温度很低或较低时，γ值小，介质损耗主要决定于弛豫。
一定额率下于某个温度出现 tgδ 的极大值。
频率增高，出现 tgδ 极大值对应的温度向高温方向移动。 在总的介质损耗中： 电导损耗所占比例逐渐增加时，tgδ 的弛豫极大值不明显。
电导率γ 很大的介质，tgδ 的极大值还可能被淹没，
tgδ～T 的关系服从于γ ～T 的指数变化关系。
（3）在总的介质损耗中
由电导引起的损耗分量所占比例逐渐增加时，
tgδ 的弛豫极大值不会那么明显。 电导率 γ 很大的介质，tgδ 的极大值还可能完全被淹没， tgδ～T 的关系服从于γ ～T 的指数变化关系。 tgδ 与温度的关系分别示于图 4-22(b) 和 4-23(b) 中。
温度不太高， 电导不太大。
因此，当主要考虑电导的影响时，
tgδ 随温度升高指数式增大。
（2）当温度很低或较低时
由于γ 值小，电导引起损耗的比例相对较小，
介质损耗主要决定于弛豫过程： 一定额率下于某个温度出现 tgδ 的极大值； 当频率增高时，出现 tgδ 极大值所对应的温度向高温方向移动。
图 4-22 计及漏导损耗时 tgδ的温频特性 (a) 频率；（b）温度
由此可见： 在低频段，tgδ 随频率升高成反比地下降。
（3）当频率较高时
tgδ 与ω 的关系基本上服从于图 4-9(c) 所示变化规律。
图 4-9 (a)
与频率的关系;(b)
与频率的关系；(c)
与频率的关系
电导损耗所占比例逐步增加时，tgδ 弛豫最大值不显著；
当γ 值很大时，tgδ 的极大值有可能完全被淹没。 tgδ 与频率的关系分别如图 4-22(a) 和图 4-23(a) 所示。
e
B /T
温度很低或较低时，γ值小，介质损耗主要决定于弛豫。
一定额率下于某个温度出现 tgδ 的极大值。
频率增高，出现 tgδ 极大值对应的温度向高温方向移动。 在总的介质损耗中： 电导损耗所占比例逐渐增加时，tgδ 的弛豫极大值不明显。
电导率γ 很大的介质，tgδ 的极大值还可能被淹没，
tgδ～T 的关系服从于γ ～T 的指数变化关系。
（3）在总的介质损耗中
由电导引起的损耗分量所占比例逐渐增加时，
tgδ 的弛豫极大值不会那么明显。 电导率 γ 很大的介质，tgδ 的极大值还可能完全被淹没， tgδ～T 的关系服从于γ ～T 的指数变化关系。 tgδ 与温度的关系分别示于图 4-22(b) 和 4-23(b) 中。
温度不太高， 电导不太大。
因此，当主要考虑电导的影响时，
tgδ 随温度升高指数式增大。
（2）当温度很低或较低时
由于γ 值小，电导引起损耗的比例相对较小，
介质损耗主要决定于弛豫过程： 一定额率下于某个温度出现 tgδ 的极大值； 当频率增高时，出现 tgδ 极大值所对应的温度向高温方向移动。
图 4-22 计及漏导损耗时 tgδ的温频特性 (a) 频率；（b）温度
交变电场中电介质的损耗计漏电导的损耗概要课件
漏电导损耗的影响因素与控制方法
影响因素
电场强度、频率、温度、湿度、电介质种类和状态等。
控制方法
优化电介质材料、降低工作温度、改善电场分布、采用复合绝缘结构等。
04
交变电场中电介质的损耗 计算
电介质损耗的计算方法
功率损耗计算
通过测量电介质在交变电场中的 功率损耗，可以计算出电介质的 损耗。功率损耗与电介质内部的
交变电场中电介质的 损耗计漏电导的损耗
概要课件
目录
• 交变电场简介 • 电介质损耗概述 • 漏电导的损耗概要 • 交变电场中电介质的损耗计算 • 电介质损耗的抑制与优化
01
交变电场简介
交变电场的定义与特性
交变电场的定义
在空间中随时间变化的电场，其 电场强度和电位移矢量随时间做 周期性变化。
交变电场的特性
具有频率、幅度和相位三个基本 参数，可以产生电磁波，对介质 产生电场作用。
交变电场中的电介质
电介质的定义
在电场作用下能够极化并产生电场作 用的物质。
电介质的特性
具有相对较低的导电率和较高的绝缘 性，能够承受较大的电场强度而不被 击穿。
电介质的分类与性质
电介质的分类
天然电介质和人造电介质，天然电介质包括气体、液体和部分固体，人造电介 质则通过人工合成或加工获得。
电介质材料的优化选择
高绝缘性能材料
耐电压强度
选择具有高绝缘性能的电介质材料， 降低电导率和介质损耗。
选择具有较高耐电压强度的电介质材 料，以减少电场对介质的破坏作用。
稳定性材料
优先选择具有优良热稳定性和化学稳 定性的电介质材料，以适应各种环境 条件。
电介质结构的优化设计
均匀分布设计
2014-第四章-5-交变电场中电介质的损耗-弛豫机制与松弛时间资料PPT课件
第四章 交变电场中电介质的损耗
复介电常数 介质损耗 弛豫现象 德拜方程 弛豫机制 介质损耗与温度的关系 考虑漏电导时的介质损耗
2020年9月28日
1
1. 电介质的弛豫机制与松弛时间 热转向极化与热离子极化是常见的两种松弛极化。 它们有着不同的弛豫机制。
介绍弛豫机制； 不同模型假设下所引出的松弛时间； 为下节讨论 εr’ 、εr’’ 与温度关系打下基础。
2020年9月28日
16
将式 (4-111) 代入式 (4-112)， 即得到随时间变化的热离子极化强度：
4-113
式中松弛时间：
4-114
此式表明： 1）温度 T 一定时，固体介质中弱离子活化能 U 越大，
松弛时间τ亦越大，即极化建立时间越长。 2）对一定结构的介质，U 不变时，
则松弛时间τ 随温度 T 升高而呈指数关系减小，反之亦然。
4-111
式中，由电场引起的位能变化 △U＝ qδE/2
加电场
2020年9月28日
15
式 ( 4-111) 说明，加上电场后，存在过剩跃迁离子，位置 2 与 1 相比离子 比较集中，这破坏了原先电荷均匀分布状态，出现了偶极矩。 其极化强度为：
4-112
式中 ( n2 - n1 ) 除 2 说明过剩跃迁离子数为 ( n2 - n1 ) 的一半，其含义是： 当从 “1” 迁移到 “2” 的离子数比从 “2” 迁移到 “1” 的离子数净多一个 时 ( 即过剩迁移离子为一个 )，“2” 处虽多了一个，而 “l” 处却少了一个， 其差 ( n2 - n1 ) 便为 2，因此，计算极化强度时，应取其一半计算。
2020年9月28日
10
因此，平均来说，处在 “1” 位置与处在 “2” 位置的离子 数保持相等。
复介电常数 介质损耗 弛豫现象 德拜方程 弛豫机制 介质损耗与温度的关系 考虑漏电导时的介质损耗
2020年9月28日
1
1. 电介质的弛豫机制与松弛时间 热转向极化与热离子极化是常见的两种松弛极化。 它们有着不同的弛豫机制。
介绍弛豫机制； 不同模型假设下所引出的松弛时间； 为下节讨论 εr’ 、εr’’ 与温度关系打下基础。
2020年9月28日
16
将式 (4-111) 代入式 (4-112)， 即得到随时间变化的热离子极化强度：
4-113
式中松弛时间：
4-114
此式表明： 1）温度 T 一定时，固体介质中弱离子活化能 U 越大，
松弛时间τ亦越大，即极化建立时间越长。 2）对一定结构的介质，U 不变时，
则松弛时间τ 随温度 T 升高而呈指数关系减小，反之亦然。
4-111
式中，由电场引起的位能变化 △U＝ qδE/2
加电场
2020年9月28日
15
式 ( 4-111) 说明，加上电场后，存在过剩跃迁离子，位置 2 与 1 相比离子 比较集中，这破坏了原先电荷均匀分布状态，出现了偶极矩。 其极化强度为：
4-112
式中 ( n2 - n1 ) 除 2 说明过剩跃迁离子数为 ( n2 - n1 ) 的一半，其含义是： 当从 “1” 迁移到 “2” 的离子数比从 “2” 迁移到 “1” 的离子数净多一个 时 ( 即过剩迁移离子为一个 )，“2” 处虽多了一个，而 “l” 处却少了一个， 其差 ( n2 - n1 ) 便为 2，因此，计算极化强度时，应取其一半计算。
2020年9月28日
10
因此，平均来说，处在 “1” 位置与处在 “2” 位置的离子 数保持相等。
第二章 交变电场中的介质极化和损耗
2
U
I a 有功电流振幅 = tgδ = I r 无功电流振幅
电介质的损耗可用损耗角正切tgδ来表征。 电介质的损耗可用损耗角正切tgδ来表征。
实际介质 实际介质
I I∞ IR 位 移 极 化 松 弛 极 化 Ir
Ira Irr
IR
介 质 漏 导
I I∞ δ ϕ U
I ra + I R ∴ tgδ = I rr + I∞
P = ε 0 (ε S − 1)E 当电场变化∆E，极化强度变化为 ∆P = ε 0 (ε S − 1) ⋅ ∆E ⋅ Q ∆P∞ = ε（ε ∞ − 1）∆E 0 ∴ ∆Pr = ∆P − ∆P∞ = ε（ε s − ε ∞）∆E ⋅ e ⋅ 0
−t τ
如E = E（t） 则：Pr t） （ =
−∞
∫ dP
t
ri
= ε（ε s − ε ∞） E（t i）e ⋅ 0 ∫
−∞
tdt i ⋅ τ
dt i ⋅ τ
P( t ) = ε 0 (ε ∞ − 1) ⋅ E( t ) + ε 0 (ε s − ε ∞ ) ∫ E( t i ) ⋅ e
−∞
−
t−ti τ
电介质的损耗和复介电常数
∞
三、Kramers-Kroning色散方程（与频率的关系） 当已知电介质的全电流关系，就可以求出复介电 常数与频率的关系。
& 如：E = E m e jωt ，并暂不考虑漏电流，由全电流公式： I（t） & & = = jωε ∞ ε 0 E（t） jω（ε s − ε ∞）ε 0 E（t） ϕ（x）e − jωx dx + J （t ） ∫ S 0
t
dU（u） ⋅ϕ（t − u）du ⋅ dt 0
U
I a 有功电流振幅 = tgδ = I r 无功电流振幅
电介质的损耗可用损耗角正切tgδ来表征。 电介质的损耗可用损耗角正切tgδ来表征。
实际介质 实际介质
I I∞ IR 位 移 极 化 松 弛 极 化 Ir
Ira Irr
IR
介 质 漏 导
I I∞ δ ϕ U
I ra + I R ∴ tgδ = I rr + I∞
P = ε 0 (ε S − 1)E 当电场变化∆E，极化强度变化为 ∆P = ε 0 (ε S − 1) ⋅ ∆E ⋅ Q ∆P∞ = ε（ε ∞ − 1）∆E 0 ∴ ∆Pr = ∆P − ∆P∞ = ε（ε s − ε ∞）∆E ⋅ e ⋅ 0
−t τ
如E = E（t） 则：Pr t） （ =
−∞
∫ dP
t
ri
= ε（ε s − ε ∞） E（t i）e ⋅ 0 ∫
−∞
tdt i ⋅ τ
dt i ⋅ τ
P( t ) = ε 0 (ε ∞ − 1) ⋅ E( t ) + ε 0 (ε s − ε ∞ ) ∫ E( t i ) ⋅ e
−∞
−
t−ti τ
电介质的损耗和复介电常数
∞
三、Kramers-Kroning色散方程（与频率的关系） 当已知电介质的全电流关系，就可以求出复介电 常数与频率的关系。
& 如：E = E m e jωt ，并暂不考虑漏电流，由全电流公式： I（t） & & = = jωε ∞ ε 0 E（t） jω（ε s − ε ∞）ε 0 E（t） ϕ（x）e − jωx dx + J （t ） ∫ S 0
t
dU（u） ⋅ϕ（t − u）du ⋅ dt 0
电介质物理(2)
v v P∞ = ε 0 (ε ∞ − 1)E
而松弛极化（慢极化，如偶极矩转向极化、 热离子极化）就可能跟不上电场的变化，其极化 就不再象在静电场那样，而是出现一与时间有关 的松弛极化强度Ｐｒ。 于是，在交变电场下电介质的极化强度可表示为：
v v v P = P∞ + Pr
•热离子极化
设：
Ｕ
缺陷区
二、复介电常数 相对介电常数的定义：
v C D ε= = v C0 ε0E
实数
r v D 在直流电场下： D与E同相，ε = ε0E
在交变电场下：
& = E e jωt 设：E m
1）.理想介质（无松弛极化）： 2）.有松弛极化：
& = D e j ωt D m
& = D e j( ωt −δ ) D m
∞ & = jωE( t )ε 0 ε ∞ + (ε s − ε ∞ ) ∫ ϕ( x ) cos ωxdx 0 ∞
无功电流部分 有功电流部分
& + ωE( t )ε 0 (ε s − ε ∞ ) ∫ ϕ( x ) sin ωxdx
0
∞
& I( t ) dE & & Q J( t ) = = ε0ε = ( jωε′ε 0 + ωε′′ε 0 ) ⋅ E( t ) S dt ∴ ε′ = ε ∞ + (ε s − ε ∞ ) ∫ ϕ( x ) cos ωxdx = ε ∞ + (ε s − ε ∞ ) ⋅ C(ω)
−t τ
如E = E（t） 则：Pr t） （ =
−∞
∫ dPtຫໍສະໝຸດ ri= ε（ε s − ε ∞） E（t i）e ⋅ 0 ∫
2014-第四章-5-交变电场中电介质的损耗-弛豫机制与松弛时间
4-106
式中，n1 + n2 = n，两个平衡位置离子浓度的变化为：
下面讨论几种情况：
4-107
电场引起的位能变化 △U
设电场较弱，△U《 kT，于是，ω12、ω21 可近似表示为：
4-108
加电场4-109 式中，ω Nhomakorabea 为无电场时，离子从 1 到 2 或由 2 到 1 跃迁的几率。
因此，式 ( 4 -107 ) 可改写为：
4-97
4-98
将式 (4 - 97) 和 (4 - 98) 代入式 (4 - 95a)，且设 μ0Ei / kT《 1，就有
4-99
其中，
4-100
如果 Ei 为正弦交变电场，且表示为 Ei ＝E io eiωt 设 n1 - n2＝A eiωt，用式 ( 4 - 99 ) 计算电场方向 ( + x ) 的平均感应偶极矩：
图 4-16 松弛时间分布
这些结果说明： 与德拜方程中单一松弛时间情况不同， 多数介质弛豫过程的松弛时间彼此分散 性很大，这样，ε’r - log ω 弥散曲线变得 比较平坦，弥散频率范围展宽，而ε’’r log ω 吸收曲线变宽，且其最大吸收值 ( ε’’r m ) 实际比由德拜方程算出的要小。 不过该曲线仍保持大体对称。
4-101
计及瞬时极化分量并假定有效场为洛仑兹场，用克-莫方程，于是有：
4-102
（注意：确定 =0 和 = ∞ 对应的εrs 和εr∞ ）
由式 (4 -72) 可知，对 εr* 可写成： 式中：
4-103
4-104
所得结果与极性液体德拜弥散方程一样。 但极性固体松弛时间分布要宽一些，且 εr’’ 最大值亦比理论值小得多。 上述理论称之为固体德拜理论。
式中，n1 + n2 = n，两个平衡位置离子浓度的变化为：
下面讨论几种情况：
4-107
电场引起的位能变化 △U
设电场较弱，△U《 kT，于是，ω12、ω21 可近似表示为：
4-108
加电场4-109 式中，ω Nhomakorabea 为无电场时，离子从 1 到 2 或由 2 到 1 跃迁的几率。
因此，式 ( 4 -107 ) 可改写为：
4-97
4-98
将式 (4 - 97) 和 (4 - 98) 代入式 (4 - 95a)，且设 μ0Ei / kT《 1，就有
4-99
其中，
4-100
如果 Ei 为正弦交变电场，且表示为 Ei ＝E io eiωt 设 n1 - n2＝A eiωt，用式 ( 4 - 99 ) 计算电场方向 ( + x ) 的平均感应偶极矩：
图 4-16 松弛时间分布
这些结果说明： 与德拜方程中单一松弛时间情况不同， 多数介质弛豫过程的松弛时间彼此分散 性很大，这样，ε’r - log ω 弥散曲线变得 比较平坦，弥散频率范围展宽，而ε’’r log ω 吸收曲线变宽，且其最大吸收值 ( ε’’r m ) 实际比由德拜方程算出的要小。 不过该曲线仍保持大体对称。
4-101
计及瞬时极化分量并假定有效场为洛仑兹场，用克-莫方程，于是有：
4-102
（注意：确定 =0 和 = ∞ 对应的εrs 和εr∞ ）
由式 (4 -72) 可知，对 εr* 可写成： 式中：
4-103
4-104
所得结果与极性液体德拜弥散方程一样。 但极性固体松弛时间分布要宽一些，且 εr’’ 最大值亦比理论值小得多。 上述理论称之为固体德拜理论。
关于介质损耗的一些基本概念
关于介质损耗的一些基本概念（泛华电子）1、介质损耗什么是介质损耗：绝缘材料在电场作用下，由于介质电导和介质极化的滞后效应，在其内部引起的能量损耗。
也叫介质损失，简称介损。
2、介质损耗角δ在交变电场作用下，电介质内流过的电流相量和电压相量之间的夹角(功率因数角Φ)的余角(δ)。
简称介损角。
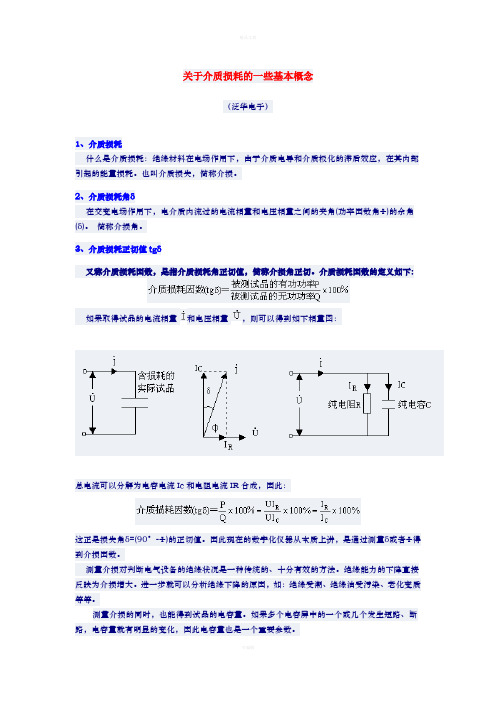
3、介质损耗正切值tgδ又称介质损耗因数，是指介质损耗角正切值，简称介损角正切。
介质损耗因数的定义如下:如果取得试品的电流相量和电压相量，则可以得到如下相量图：总电流可以分解为电容电流Ic和电阻电流IR合成，因此：这正是损失角δ=(90°-Φ)的正切值。
因此现在的数字化仪器从本质上讲，是通过测量δ或者Φ得到介损因数。
测量介损对判断电气设备的绝缘状况是一种传统的、十分有效的方法。
绝缘能力的下降直接反映为介损增大。
进一步就可以分析绝缘下降的原因，如：绝缘受潮、绝缘油受污染、老化变质等等。
测量介损的同时，也能得到试品的电容量。
如果多个电容屏中的一个或几个发生短路、断路，电容量就有明显的变化，因此电容量也是一个重要参数。
4、功率因数cosΦ功率因数是功率因数角Φ的余弦值，意义为被测试品的总视在功率S中有功功率P所占的比重。
功率因数的定义如下:有的介损测试仪习惯显示功率因数(PF:cosΦ)，而不是介质损耗因数(DF:tgδ)。
一般cosΦ<tgδ，在损耗很小时这两个数值非常接近。
5、高压电容电桥高压电容电桥的标准通道输入标准电容器的电流、试品通道输入试品电流。
通过比对电流相位差测量tgδ，通过出比电流幅值测量试品电容量。
因此用电桥测量介损还需要携带标准电容器、升压PT和调压器。
接线也十分烦琐。
国内常见高压电容电桥有：型号生产厂家性能2801Haefely 西林电桥，手动调节，介损相对误差0.5%，试验室使用。
其改进型为2809A。
QS30上海沪光厂电流比较仪电桥，手动调节，介损相对误差0.5%±0.00005，试验室使用。
交变电场中电介质的损耗弛豫现象
I (t )
（a）加脉冲电压
（b）充放电电流
（c）充放电电荷
图 4-6 线性电介质对交变电场的响应
充电过程：
在电介质上加一个脉冲电压， 电压振幅为 V0，脉冲时间间隔 为 t1 ~ tl + d t。 见图 4-6(a)。 会出现瞬时充电电流 。
充电过程：
在时刻 tl：
由于脉冲前缘作用，首先会出
特殊地，如果设式 ( 4-68 ) 中ω＝0， 可求出静态相对介电常数为：
或者写成：
4-70
上式表明： 在 εr’’ 对 logω 的关系图中，曲线下面所包括的总面积，与介电常数 的极值有关，而与色散机理无关。
关于 Kramers-Krö nig 色散公式：
给出了复介电常数与频率的相关性，但推导过程中涉及了一 个未确定的衰减函数，这个函数就是弛豫函数 φ( t )。 利用色散公式还不能计算复介电常数与频率的关系。 要解决这一问题，关键在于给出弛豫函数具体表达式。
这三部分电流特性如图 4-8 所示。
通过电介质的全电流是三者之和，大体变化如图所示。
图 4-8
2.3 Kramers-Krö nig 关系式
讨论弛豫现象后，可利用上节结果，通过电流密度与电场
强度之间的关系，推导出复介电常数的频率特性。 将式 ( 4-54 ) 关于电流强度的表达式换为电流密度的表示式， 只需代入以下几种关系：
φ( t ) 与物质成分、结构及温度等有关。
弛豫函数通用的表达式不易确定。 德拜 （Debye）： 在 “Polar Molecules” 著作中，提出并建立了复介电常数 与频率的关系式，这种关系是针对极性液体和固体介质提 出来的。解释介电弛豫和介电常数频率特性很成功。
一个令人困惑的问题！
（a）加脉冲电压
（b）充放电电流
（c）充放电电荷
图 4-6 线性电介质对交变电场的响应
充电过程：
在电介质上加一个脉冲电压， 电压振幅为 V0，脉冲时间间隔 为 t1 ~ tl + d t。 见图 4-6(a)。 会出现瞬时充电电流 。
充电过程：
在时刻 tl：
由于脉冲前缘作用，首先会出
特殊地，如果设式 ( 4-68 ) 中ω＝0， 可求出静态相对介电常数为：
或者写成：
4-70
上式表明： 在 εr’’ 对 logω 的关系图中，曲线下面所包括的总面积，与介电常数 的极值有关，而与色散机理无关。
关于 Kramers-Krö nig 色散公式：
给出了复介电常数与频率的相关性，但推导过程中涉及了一 个未确定的衰减函数，这个函数就是弛豫函数 φ( t )。 利用色散公式还不能计算复介电常数与频率的关系。 要解决这一问题，关键在于给出弛豫函数具体表达式。
这三部分电流特性如图 4-8 所示。
通过电介质的全电流是三者之和，大体变化如图所示。
图 4-8
2.3 Kramers-Krö nig 关系式
讨论弛豫现象后，可利用上节结果，通过电流密度与电场
强度之间的关系，推导出复介电常数的频率特性。 将式 ( 4-54 ) 关于电流强度的表达式换为电流密度的表示式， 只需代入以下几种关系：
φ( t ) 与物质成分、结构及温度等有关。
弛豫函数通用的表达式不易确定。 德拜 （Debye）： 在 “Polar Molecules” 著作中，提出并建立了复介电常数 与频率的关系式，这种关系是针对极性液体和固体介质提 出来的。解释介电弛豫和介电常数频率特性很成功。
一个令人困惑的问题！
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
若 tgδ 较大，则可能产生严重发热。
因为由式 (4-133) 决定的每秒钟介质每单位体积内所耗散的 能量，一般就转化为热，使介质温度升高。 如不设法使 tgδ 降低或采取有效散热措施， 有可能导致电介质的破坏。
简要总结：计及电导时的损耗情形-频率关系
tgδ 与频率的关系： 当频率很低时，损耗主要由漏导电流引起，此时：
最后应指出： 在 tgδ 的关系确定以后，只要考虑到式 (4-40)， 介质内所耗散的能量密度 w 可以计算，即：
w=
2
2 '' E0
(焦耳／米3·秒)
其中ε” 用 ε’ tgδ 代替 ( tgδ =ε”／ε’)，即有：
3-133
公式中引入了 tgδ
由式 (4-133) 可知， 在高频强电场下工作的电介质，
1) tgδ 与频率的关系 （1）对静电场 ω＝0，由 (4-130)可知， tgδ →∞。
表示静电场中，tgδ 是没有物理意义的，
tgδ 只是介质在ω ≠ 0 交变电场中的物理参数。
4-130
4-130
（2）当频率很低时
含有 ω2τ2 或 ω2τ 的项可以略去，故损耗主要由漏导电流引起，
此时有：
4-131
由此可见： 在低频段，tgδ 随频率升高成反比地下降。
（3）当频率较高时
tgδ 与ω 的关系基本上服从于图 4-9(c) 所示变化规律。
图 4-9 (a)
与频率的关系;(b)
与频率的关系；(c)
与频率的关系
电导损耗所占比例逐步增加时，tgδ 弛豫最大值不显著；
当γ 值很大时，tgδ 的极大值有可能完全被淹没。 tgδ 与频率的关系分别如图 4-22(a) 和图 4-23(a) 所示。
图 4-22 计及漏导损耗时 tgδ的温频特性 (a) 频率；（b）温度
温度比较高， 电导比较大。
图 4-23 电导率不同的介质损耗பைடு நூலகம்子温频特性 （曲线1到5对应于电导率由小到大）
直流电导率对 Cole-Cole 园图的影响 计及漏导损耗时，由式 (4-8) 可以看出， 自由电荷引起的电导率γ 对复介电常数的贡献是 ( -i γ/ω )。 通常可以把有电导的介质材料看作是：
（3）在总的介质损耗中
由电导引起的损耗分量所占比例逐渐增加时，
tgδ 的弛豫极大值不会那么明显。 电导率 γ 很大的介质，tgδ 的极大值还可能完全被淹没， tgδ～T 的关系服从于γ ～T 的指数变化关系。 tgδ 与温度的关系分别示于图 4-22(b) 和 4-23(b) 中。
温度不太高， 电导不太大。
图 4-22 计及漏导损耗
图 4-23 电导率不同的损耗
2) tgδ与 温度的关系 （1）当温度很高时
电导率 γ 变得很高，式 (4-130) 中其余各项影响相对很小， 故此时 tgδ 的表达式仍适用于式 (4-131)，即： tgδ＝
0 rg
rs
而γ 与温度的关系是：
γ＝A
e B / T
4-131
在低频段时，tgδ 随频率升高成反比地下降。
频率较高时， tgδ 与ω 的关系会出现峰值。 电导损耗逐步增加时，tgδ 弛豫最大值不显著；
当γ 值很大时，tgδ 的极大值可能完全被淹没。
简要总结：计及电导时的损耗情形–温度关系
温度很高时，电导率γ 变得很高，tgδ 的表达式：
γ＝A tgδ＝ 0 rg tgδ 随温度升高指数式增大。
由一种理想的不导电的介质与一个电阻并联而成.
所以具有电导的存在松弛机制的介质复介电常数方程是：
4-132
4-132
显然， 电导项对 Co1e-Cole 图产生影响。 并且电导率愈大，则计及直流电
导率影响的实际图形偏离 Co1eCole 半圆愈益明显。 如图 4-24 所示。
图 4-24 直流电导率对 Cole-Cole图的影响
这样，综合电介质中电流密度各种贡献.
实际电介质中电流矢量图将如图 4-21 所示。
图 4-21 实际电介质中的电流矢量
产生损耗的有功电流密度 包括如下两个分量： j lp 弛豫过程产生的有功电流密度； j lc 漏导引起的电流密度。 不产生损耗的无功电流密度 也有两个分量：
j cc
由位移极化产生的纯电容电流； j cp
图 4-21 实际电介质中的电流矢量
由弛豫过程 ( 极化 ) 产生的电容电流。
于是，在计及了漏电导时，有定义式，有： 介质损耗角正切为：
参见公式（4-11）
4-129
式中，γ 是介质的电导率。
j l p 对应弛豫贡献的电流 j l c 对应漏导贡献的电流
4-11
如果计及德拜方程 ( 式 4-73 和式 4-74 )，
并注意到式 ( 4-86 )，便有：
4-130
计及漏电导时的介质损耗 ：
4-130
比较较德拜方程：
4-75
计及漏电导的介质损耗变得复杂了。 不计漏电导的介质损耗普遍情况中的一个特例。 特殊地，介质电导率γ 很小，漏导电流可以忽略时， 式 (4-130) 转为式 (4-75)，损耗全部由弛豫过程引起。
因此，当主要考虑电导的影响时，
tgδ 随温度升高指数式增大。
（2）当温度很低或较低时
由于γ 值小，电导引起损耗的比例相对较小，
介质损耗主要决定于弛豫过程： 一定额率下于某个温度出现 tgδ 的极大值； 当频率增高时，出现 tgδ 极大值所对应的温度向高温方向移动。
图 4-22 计及漏导损耗时 tgδ的温频特性 (a) 频率；（b）温度
第四章
交变电场中电介质的损耗
复介电常数
介质损耗
弛豫现象
德拜方程
弛豫机制
介质损耗与温度的关系
考虑漏电导时的介质损耗
计及漏电导时的介质损耗
推导 Kramers-Kronig 关系式及德拜方程式时，
当时声明：暂不计及漏导电流及漏导损耗。
但是，实际电介质，受外电场作用时，除了由 弛豫导致电流密度外；也有漏电导电流密度，
e
B /T
温度很低或较低时，γ值小，介质损耗主要决定于弛豫。
一定额率下于某个温度出现 tgδ 的极大值。
频率增高，出现 tgδ 极大值对应的温度向高温方向移动。 在总的介质损耗中： 电导损耗所占比例逐渐增加时，tgδ 的弛豫极大值不明显。
电导率γ 很大的介质，tgδ 的极大值还可能被淹没，
tgδ～T 的关系服从于γ ～T 的指数变化关系。