数字逻辑电路课件第五章习题
数字电子技术黄瑞祥 第五章习题答案
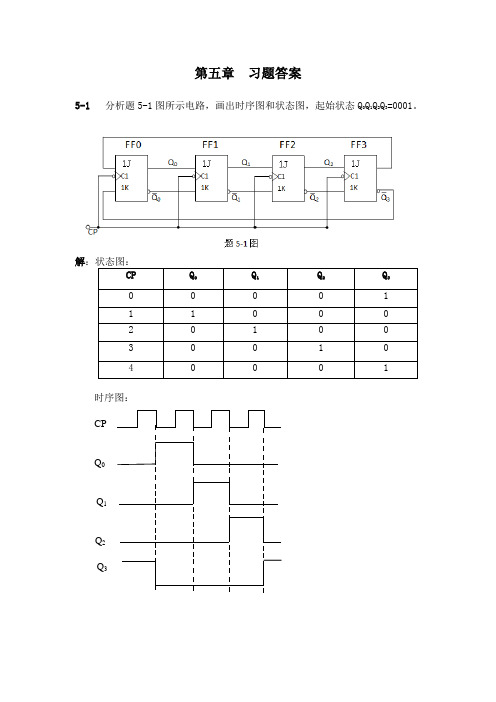
第五章习题答案5-1分析题5-1图所示电路，画出时序图和状态图，起始状态Q0Q1Q2Q3=0001。
解CP Q0 Q1Q2Q30 0 0 0 11 1 0 0 02 0 1 0 03 0 0 1 04 0 0 0 1 时序图：CPQ0Q1Q2Q35-2分析题5-2图所示电路，画出电路的状态图。
解CP Q0 Q1 Q20 0 0 01 1 0 02 0 1 03 0 0 14 0 0 05-3 JK触发器组成5-3图所示电路。
分析该电路为几进制计数器，并画出电路的状态图。
CP Q1 Q2Q30 0 0 01 1 0 02 0 1 03 1 1 04 0 0 15 0 0 0 该电路为五进制计数器5-4JK触发器促成如图5-4图所示的电路。
（1）分析该电路为几进制计数器，画出状态图。
（2）若令K3= 1，电路为几进制计数器，画出其状态图。
解：（1CP Q1 Q2Q30 1 2 3 4 5 6 7 0 0 01 0 00 1 01 1 00 0 11 0 1 0 1 1 0 0 0为7进制计数器CP Q1 Q2Q30 1 2 3 4 5 0 0 01 0 00 1 01 1 00 0 11 0 0为4进制计数器5-5 试画出题5-5图（a）所示电路中B,C端的波形。
输入端A,CP波形如题5-5图(b)所示，触发器的起始状态为零。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19CPAQ0Q1BC5-6分析题5-6图所示电路，画出电路的状态图，说明电路能否自启动。
CP Q1 Q2Q3Z0 1 2 3 4 5 6 7 0 1 0 0 0 01 0 1 0 1 1 1 00 1 1 11 0 0 0 1 1 0 00 1 0 01 0 1 00 0 1 01 0 0 0该电路能够自启动5-7 分析题5-7图所示电路，画出电路的状态图，说明电路能否自启动。
CP Q4 Q3Q2Q11234 567111111111 0 0 0 00 0 0 11 0 0 11 1 0 11 1 1 00 1 1 11 0 1 11 1 0 10 0 1 00 0 0 10 0 1 11 0 0 10 1 0 00 0 1 10 1 0 11 0 1 10 1 1 00 0 1 11 0 0 00 1 0 11 0 1 00 1 0 11 1 0 00 1 1 11 1 1 1 1 1 1 0由状态图可见，电路图能够自启动5-8画出题5-8图所示电路的状态图和时序图，简要说明电路的基本功能。
数电第五章习题答案精编版
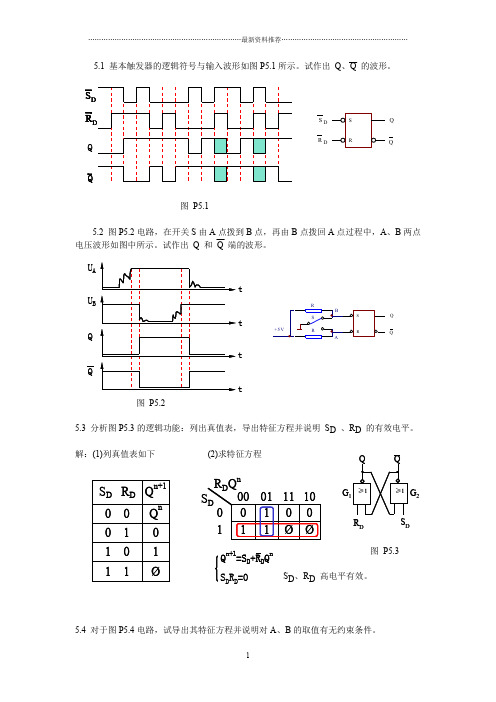
5.4 对于图P5.4电路，试导出其特征方程并说明对A、B的取值有无约束条件。
Q图P5.11P5.125.12 画出图P5.12电路中Q 1、Q 2 的波形。
解：特征方程为： ，Q 端波形如图P5.12所示。
=[D]·CP 1,Q 1n+1Q 2n+1= Q 1n[]·CP 2图P5.14 图P5.155.15 画出图P5.15电路中Q 端的波形。
解：Q 端波形如图P5.15所示。
5.16 试作出图P5.16电路中Q A 、Q B 的波形。
解：特征方程为： ， ，Q 端波形如图P5.16所示。
图P5.16 图P5.17Q A n+1= Q B n[]·A Q B n+1= Q A n []·BA R DB Q A Q BR D CP CP ⊕Q 2Q 1Q 25.17 试作出图P5.17电路中Q 1、Q 2 的波形。
解：特征方程为： ， ，Q 端波形如图P5.17所示。
5.18 试作出图P5.18电路中Q 1和Q 2的波形（设Q 1和Q 2的初态均为“0”），并说明Q 1和 Q 2对于CP 2各为多少分频。
解：特征方程为： ， ，Q 端波形如图P5.18所示。
Q 1和Q 2对于CP 2都是4分频，即图P5.18 图P5.195.19 已知电路如图P5.19，试作出Q 端的波形。
设Q 的初态为“0”。
解：特征方程为： ，Q 端波形如图P5.19所示。
5.20 已知输入u I 、输出u O 波形分别如图P5.20所示，试用两个D 触发器将该输入波形u I 转换成输出波形u O 。
解：输出u O 是对输入u I 的4分频，而采用1个DFF 可实现2分频，故实现电路如图P5.20所示。
图P5.205.21 试分别用公式法和列表图解法将主从SR 触发器转换成JK 触发器。
解1：Q 1n+1= Q 1n []·(CP ⊕Q 2)Q 2n+1= Q 2n []·Q 1?)?,(2221==CP Q CP Q f f f f Q 1n+1= Q 1n []·CP 1Q 2n+1= ·Q 2n []·CP 2Q 1n CP 2CP 1Q 1Q 241,412221==CP Q CP Q f f f f Q n+1= [ A ]·CP CP A Qu Iu OQ n+1=S+RQ n SR =0Q n+1=JQ n +KQn令新老触发器的次态方程相等，则有S=JQ n ，R=K但不满足约束条件SR =0。
数电第五版(阎石)第五章课后习题及答案pptx
03
习题三答案ຫໍສະໝຸດ 习题三第1题答案1.1 逻辑函数的表示方法 1.1答案：逻辑函数有多种表示方法， 如真值表、逻辑表达式、波形图和卡
诺图等。
1.2 逻辑函数的化简方法
1.2答案：逻辑函数的化简方法包括代 数法、公式法和卡诺图法等。
1.3 逻辑函数的运算规则
1.3答案：逻辑函数的运算规则包括与、 或、非等基本运算，以及与或、与非、 或非等复合运算。
习题一第3题答案
总结词
卡诺图化简
答案
通过卡诺图化简，我们得到最简的逻 辑表达式为(F = A'B + A'C + BC)。
02
习题二答案
习题二第1题答案
总结词
逻辑函数的表示方法
详细描述
逻辑函数的表示方法有真值表、逻辑表达式、逻辑图和波形图等。这些表示方法各有特 点，可以根据具体需求选择使用。真值表可以清晰地表示输入和输出之间的逻辑关系； 逻辑表达式简化了函数表示，便于分析和计算；逻辑图能够直观地展示逻辑函数的结构
习题三第2题答案
在此添加您的文本17字
2.1 逻辑函数的化简步骤
在此添加您的文本16字
2.1答案：逻辑函数的化简步骤包括合并项、消去项和简 化表达式等。
在此添加您的文本16字
2.2 逻辑函数的化简技巧
在此添加您的文本16字
2.2答案：逻辑函数的化简技巧包括利用运算规则、消去 项和合并项等。
在此添加您的文本16字
和功能；波形图则可以反映函数在时间序列上的动态变化。
习题二第2题答案
总结词
逻辑函数的化简方法
详细描述
逻辑函数的化简方法有多种，包括公式化简法、卡诺 图化简法和布尔代数化简法等。公式化简法基于逻辑 代数的基本公式和规则，通过简化表达式得到最简结 果；卡诺图化简法利用卡诺图的性质，通过图形直观 地找出最小项的组合，从而得到最简逻辑函数表达式 ；布尔代数化简法则通过代数运算简化逻辑函数。这 些化简方法各有优缺点，应根据具体情况选择使用。
数电第五版第五章课后习题及答案演示精品PPT课件
【题5.15】已知CMOS边沿触发方式JK触发器各输入端 的电压波形如图P5.15所示,试画出Q,Q’端对应的电压 波形。
20
解：根据JK触发器逻辑功能的定义和边沿触发方式的动作特 点，画出的Q,Q’ 端电压波形如图A5.15。
21
【题5.18】设图P5.18中各触发器的初始状态皆为Q=0，试画 出在CLK信号连续作用下各触发器输出端的电压波形
10
解：根据SR触发器逻辑功能的定义及脉冲触发方式的动作特 点，即可画出图A5.8中Q和Q’的电压波形。
11
【题5.9】 若主从结构SR触发器的CLK,S,R, 各输入端电压波 形如图P5.9所示， =1，试画出Q,Q’ 端对应的电压波形。
12
解：根据SR触发器逻辑功能的定义及脉冲触发方式的动作特 点，即可画出Q,Q’的电压波形，如图A5.9所示。
学习要点： 1、不同电路结构触发器的动作 特点； 2、不同逻辑功能触发器的特性；
1
【题5.1】 画出图P5.1由与非门组成的SR锁存器输出端Q,Q’的 电压波形，输入端 , 的电压波形如图中所示。 解：见图A5.1.
No Image
2
3
【题5.4】图P5.4所示为一个防抖动输出的开关电路。当拨动 开关S时，由于开关触点接通瞬间发生振颤 , 和 的电压波 形如图中所示，试画出Q,Q’端对应的电压波形。
从高电平跳变成低电平以后电路的工作过程与上述过 程类似。这样就得到了图A5.20的 电压波形。
25
【题5.21】 在图P5.21所示的主从JK触发器电路中，CLK 和 A 的电压波形如图中所示，试画出 Q 端对应的电压波形。设触 发器的初始状态为 Q = 0.
26
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
数字逻辑第5章习题参考解答
5.31BUT门的可能定义是：“如果A1和B1为1，但A2或B2为0，则Y1为1；Y2的定义是对称的。
”写出真值表并找出BUT门输出的最小“积之和”表达式。
画出用“与非-与非”电路实现该表达式的逻辑图，假设只有未取反的输入可用。
你可以从74x00、04、10、20、30组件中选用门电路。
解：真值表如下利用卡诺图进行化简，可以得到最小积之和表达式为Y1=A1·B1·A2’+A1·B1·B2’Y2=A1’·A2·B2+B1’·A2·B2Y2采用74x04得到各反相器采用74x10得到3输入与非采用74x00得到2输入与非5.32做出练习题5.31定义的BUT门的门级设计，要求以cmos实现时使用的晶体管数目最少，可以从74x00、04、10、20、30组件中选用门电路.写出输出表达式（不一定是二级“积之和”）并画出逻辑图。
解：cmos晶体管用量：反相器2个2输入与非门4个3输入与非门6个为了尽量减少晶体管用量，可以采用下列表达式，以便实现器件的重复使用：F1=(A1·B1)·(A2’+B2’)=(A1·B1)·(A2·B2)’=[(A1·B1)’+(A2·B2)’’]’F2=[(A2·B2)’+(A1·B1)’’]’电路图：晶体管用量：20只（原设计中晶体管用量为40只）5.34已知函数,,,(3,7,11,12,13,14)W X Y Z F =∑，说明如何利用练习题5.31定义的单个BUT 门和单个二输入或门实现F.解：BUT 门输出采用最小项和的形式表达为()∑=2,2,1,114,13,121B A B A Y ，()∑=2,2,1,111,7,32B A B A Y将两个输出相或就可以得到要求实现的函数。
5.19指出用一块或多块74x138或74x139二进制译码器以及与非门，如何构建下面每个单输出或多输出的逻辑功能（提示：每个实现等效于一个最小项之和）。
数电第五章习题答案 .doc
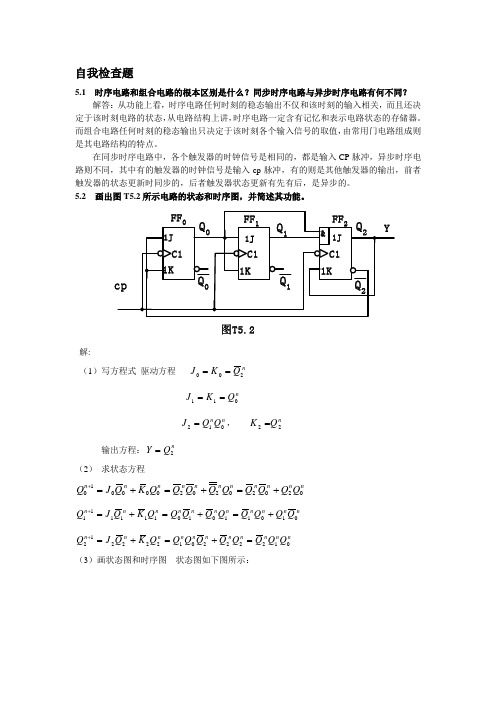
自我检查题5.1 时序电路和组合电路的根本区别是什么？同步时序电路与异步时序电路有何不同？解答：从功能上看，时序电路任何时刻的稳态输出不仅和该时刻的输入相关，而且还决定于该时刻电路的状态，从电路结构上讲，时序电路一定含有记忆和表示电路状态的存储器。
而组合电路任何时刻的稳态输出只决定于该时刻各个输入信号的取值，由常用门电路组成则是其电路结构的特点。
在同步时序电路中，各个触发器的时钟信号是相同的，都是输入CP 脉冲，异步时序电路则不同，其中有的触发器的时钟信号是输入cp 脉冲，有的则是其他触发器的输出，前者触发器的状态更新时同步的，后者触发器状态更新有先有后，是异步的。
5.2 画出图T5.2所示电路的状态和时序图，并简述其功能。
图T5.2解:（1）写方程式 驱动方程 nQ K J 200==n Q K J 011==n n Q Q J 012=， n Q K 22=输出方程：nQ Y 2= （2） 求状态方程nn n n n n n n n n n Q Q Q Q Q Q Q Q Q K Q J Q 02020202000010+=+=+=+ n n n n n n n n n n n Q Q Q Q Q Q Q Q Q K Q J Q 01011010111111+=+=+=+ n n n n n n n n n n n Q Q Q Q Q Q Q Q Q K Q J Q 01222201222212=+=+=+（3）画状态图和时序图 状态图如下图所示：101时序图如下图所示：CP Q 0Q 1Q 25.3 试用边沿JK 触发器和门电路设计一个按自然态序进行计数的七进制同步加法计数器。
解：（1）状态图如下图：（2）求状态方程、输出方程CQ Q Q n n n /101112+++的卡诺图如下图所示：输出方程为nn Q Q C 12=状态方程：n n n n n Q Q Q Q Q 120112+=+ n n n n n n Q Q Q Q Q Q 0120111+=+ n n n n n Q Q Q Q Q 120110+=+驱动方程：n n n n n n n n n n n n n n n Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q 0122120121220112)(++=++=+n n n n n n Q Q Q Q Q Q 1021011+=+n n n n n Q Q Q Q Q 0012101)(++=+与JK 触发器的特性方程 比较，可以得到驱动方程 n n Q Q J 012= 、 n Q K 12=n Q J 01= 、n n Q Q K 021=n n n n Q Q Q Q J 12120=+= 10=K（4） 无效状态转换情况 111/1000 能自启动（5） 逻辑图如下图所示：5.4 画出用时钟脉冲上升沿触发的边沿D 触发器组成的4位二进制异步加法计数器和减法计数器的逻辑电路图。
数字逻辑第五章课后习题答案
&
&
&
&
X1
X2
X3
设计的脉冲异步时序电路
5-3、解：
X1
X3 x2 >
X3
A/0
<
X1
B/0
X3 X2
D/1
X1 X3
X1
X2
X2
C/0
原始状态图
现态
y A B C D
次态 yn+1
x1
x2
x3
B
A
A
B
C
A
B
A
D
B
A
A
原始状态表
输出
Z 0 0 0 1
5-4、解：（1）写出电路的激励函数和输出函数表达式： Y2=x2+x1y2 y—1+x—1y1; Y1=x2x1+x1y2—+x2—y1;Z=x2—y1 —
x2x1=11 c/-
c/-
c/-
○c /1
○c /1
最简流程表
x2x1=10 b/○b /1 b/-
12 3 45 67 8
CP Q1 Q2 Q3
时间图
5-2、解：表所示为最小化状态表，根据状态分配原则，无“列”相
邻（行相邻在脉冲异步时序电路中不适用。），在“输出”相邻
中，应给 AD、AC 分配相邻代码。取 A 为逻辑 0，如下卡诺图所示，
状态赋值为：A=00，B=11；C=01；D=10。于是，二进制状态表如
J3 K3 CP3 010 010 110 010 011 011 111 011
次态
Q1(n+1) Q2(n+1 ) Q3(n+1)
数字逻辑电路课件第五章
0
1
与非门构成SR锁存器
0 1
SD ' 0, RD ' 1 Q 1, Q ' 0 SET
1
0
与非门构成SR锁存器
1
S D ' 1, RD ' 1
1
Q保持不变
与非门构成SR锁存器
0 1
S 0, R 0
' D ' D
0 1
Q 1, Q ' 1，矛盾
3状态转换图
状态转移方向 转移条件
触发器状态
JK触发器
1特性表
J K Q Q*
2.特性方程 : Q* JQ K Q
0 保持 置1 清0 翻转
0
0 0
0
1 1 0
0 1
0 0 0 1 1 0
1
1 1 0
3状态转移图
0 1
1
1 1 1 0
1 1
0 1
0
D触发器
1特性表
D Q Q*
2.特性方程 : Q* D
CLK输入端的 :触发器为上升沿触发方式; 若CLK端加了小圆圈:下降沿触发；
有异步置，置0端 1
二、边沿触发的动作特点 1)Q*变化发生在clk的上升沿(下降沿) 而与此前、后的状态无关
2)Q*仅取决于上升沿(下降沿)到达时输入的状态，
5.6 触发器的逻辑功能及其描述方法
SR触发器 JK触发器 T触发器
3状态转移图
0 0 1 1
0 0 1 0 0 1 1 1
T触发器
Q
0 1 0 1 0 1 0 1 0 1
Q*
0 1 0 保持 1 1 置1 1 0 清0 0 1① 不允许 1①
同步时序逻辑电路的习题 数字逻辑
* 异步二进制计数器
也用 3 个 JK 触发器实现，CR 为清零端，电路图如下所示（3 个 JK 触发器的输入端均
悬空）
Q2
Q1
Q0
•
•
IK
IJ
IK
IJ
•
CR
•
• •
IK
IJ
Cp
•
悬空
驱动方程同上（略） 输出波形如下所示（对比同步计数器，看看异同）
Cp
Q0 Q1 Q2
111
110
101
100
011
输入 x / 输出 Z
0/0 00
1/0
1/0 01
状态 y2y1
0/1 0/0
1/0 0/0
1/0
11
10
2、分析下图所示的逻辑电路，说明该电路的功能。
y3
• y2
IK
IJ
Cp
••
&
IK
IJ
• ••
。
&
。y1
y1
IK
IJ
“1”
。•
1
x
3、分析下图所示的逻辑电路，设电路初始状态为“00”，输入序列为 x=10011110110，作出 输出响应序列，并说明电路功能。
D. 触发器一定更少
4、同步时序电路设计中，状态编码采用相邻编码法的目的是（ D ）。
A. 减少电路中的触发器
B. 提高电路速度
C. 提高电路可靠性
D. 减少电路中的逻辑门
**判断题
1、同步时序逻辑电路中的存储元件可以是任意类型的触发器。
（ ×）
2、若某同步时序逻辑电路可设计成 Mealy 型或者 Moore 型，则采用 Mealy 型电路比采用 Moore
《数电》教材习题答案 第5章习题答案
思考题与习题5-1 在如图5-1所示的四位移位寄存器中，假定开始时Q3Q2Q1Q0为1101状态。
若串行输入序列101101与CP脉冲同步地加在D SR串行输入端时，请对应画出各触发器Q 3Q2Q1Q端的输出波形。
图T5-15-2 图T5-2电路中各触发器的初始状态均为0，请对应输入CP和IN的波形，画各触发器Q端的输出波形。
图T5-25-3 试用两片74LS194电路构成一个八位移位寄存器，并画出逻辑电路图。
5-4 请用上升沿触发的D触发器构成一个异步三位二进制加法计数器。
并对应CP画出Q1、Q2、Q3的波形。
图T5-45-5 请用JK 触发器构成一个脉冲反馈式异步六进制加法计数器，并画出对应于CP 脉冲的工作波形。
图T5-5用三位JK 触发器构成八进制计数器，然后在状态110时利用与非门反馈至清零端构成六进制计数器，图略。
5-6请分析如图T5-6所示的阻塞反馈式异步计数器电路的逻辑功能，指出该计数器为几进制，并画出计数状态转换图。
图T5-6解：（1）驱动方程：J I =3Q ,K 1=1; J 2=1,K 2=1;J 3=nQ n Q 21,K 3=1;代入得状态方程: （CP 脉冲下降沿时刻）（Q 1下降沿时刻） （CP 脉冲下降沿时刻）列出状态转换图（略）分析得出该计数器为5进制计数器，状态从000-100，其它的三个状态下一状态均为000，因此该电路是异步五进制计数器，具有自启动功能。
5-7 分析图T5-7同步计数器电路的逻辑功能。
图T5-7nn n n n Q K ,Q J Q K ,Q J Q K ,J 232312323111====== n Q n Q Q n 1311=+n Q Q n 221=+n Q n Q n Q Q n 31231=+nn n nn n nn n n n n n n n n n Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q 23232132123123113111=⋅+⋅=⋅+⋅=+=⋅+=+++n n n Q Q Q 123 111213+++n n n Q Q Q0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 1 0 1 0 1 1 1 1 0 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 1 0 1 1 1 1 1 1 1因为该计数器设计了清零端，因此可实现从000开始进入循环圈的2进制计数器的功能，但我们也发现，它也可以实现三进制。
(2021年整理)数字逻辑第五章
（完整）数字逻辑第五章编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）数字逻辑第五章）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）数字逻辑第五章的全部内容。
第五章触发器------—----——-—--—-——-—-——------———--—-———--———————-——-—-—-———-—————-——-—---1 ：具有：置0、置1、保持和翻转功能的触发器是（ ).A：JK触发器B:SR触发器C：D触发器D：T触发器您选择的答案: 正确答案： A知识点：JK触发器的特性为：J=0， K=0时，Q状态为保持；J=0， K=1时，Q状态为置0；J=1， K=0时，Q状态为置1;J=1, K=1时,Q状态为翻转--—--———----—----—---—---—---—-——--—-——--——--—--------——--—--———-—--—-------2 ：对于JK触发器，输入J＝0，K＝1，CLK脉冲作用后,触发器的次态应为（）。
A：0B:1C：Q'D:不确定您选择的答案: 正确答案： A知识点：JK触发器的特性为：J=1， K=1时，Q状态为翻转，即Q= Q’-————---———---————--————--—-——-————--—---—-——-—-—---——--—--------——--—--—-—-3 ：有一个或非门构成的SR锁存器，欲使该锁存器保持原态即Q*=Q,则输入信号应为（）。
A：S＝R＝0B：S＝R＝1C：S＝1，R＝0D：S＝0，R＝1您选择的答案：正确答案： A知识点：或非门构成的SR锁存器的特性为：R=1, S=0 Q＊=0, Q*'=1,即锁存器被置0（0状态）；R=0, S=1 Q＊=1， Q＊'=0，即锁存器被置 1（1状态）;R=S=0， Q*=Q，即锁存器保持原态；R= S=1 Q*=Q＊'=0，此为不允许输入。
数字逻辑(欧阳星明)第五章
4．描述电路的逻辑功能。 由状态图可知，该电路是一个2 位二进制数可逆计数器。 当输入x=0 时，可逆计数器进行加1计数，其计数序列为 00 01 10 11
当输入x=1时，可逆计数器进行减1计数，其计数序列为 00 01 10 11 在时序逻辑电路分析中，除了状态图和状态表之外，通常 还用到时间图。时间图能较形象、生动地体现时序电路的工作 过程，并可和实验观察的波形相比较，是描述时序电路工作特 性的一种常用方式。
7
第五章 同步时序逻辑电路
（2）现态与次态 同步时序电路中的现态与次态是针对某个时钟脉冲而言的。 现态----指时钟脉冲作用之前电路所处的状态。 次态----指时钟脉冲作用之后电路到达的状态。 注意：前一个脉冲的次态即后一个脉冲的现态！如 1 2 cp 次态=现态 次态=现态 （3）对时钟的要求 脉冲的宽度：必须保证触发器可靠翻转； 脉冲的频率：必须保证前一个脉冲引起的电路响应完全结 束后，后一个脉冲才能到来。 2. 异步时序逻辑电路 异步时序逻辑电路的存储电路可由触发器或延时元件组成， 电路中没有统一的时钟信号同步，电路输入信号的变化将直接导 致电路状态的变化。 8 3
19
第五章 同步时序逻辑电路
5.2.2分析举例 例1 用表格法分析下图所示同步时序逻辑电路。 解：该电路由两个J-K触 发器和一个异或门组成，电 路的输入为x，电路的状态 (即触发器状态)用y2 、y1 表示。 电路的输出即状态变量，因 此 ， 该 电 路 属 于 Moore 型 电 路的特例。
1.写出输出函数和激励函数表达式 该电路的输出即为状态，各触发器的激励函数表达式为 J1=K1=1 ；J2=K2=x⊕y1
24
第五章 同步时序逻辑电路
根据状态响应序列，可 作出时间图如下图所示。由 于前一个时钟脉冲的次态即 为后一个时钟脉冲的现态， 所以，时间图中可以将现态 和次态共用一个波形表示。
《数字逻辑》第5章作业与习题
二、习题
1）填空题
1．在数字系统中，用二进制代码表示特定对象的过程称为
；n
位二进制编码器有 个输入，有 个输出。
2．将十进制数的十个数字编成二进制代码的过程叫做
。
个。
8．输出高电平有效的 4 线-16 线译码器的输入 A3~A0=1010 时，输出 Y15～
Y0=
。
9．全加器与半加器的区别是
。
10．当输入信号改变状态时，输出端可能出现虚假过渡干扰脉冲的现象叫做
。
2）单选题
1．在二进制译码器中，若输入有 4 位代码，则输出最多有（ ）信号。
①2个
②4个
③8个
④ 16 个
5．能实现从多个输入端中选出一路作为输出的电路称为（ ）。
① 触发器
②计数器
③ 数据选择器 ④ 译码器
6．把代码所表示的特定含义翻译出来的过程称为（ ）。
① 译码
② 编码
③ 数据选择 ④ 奇偶校验
7．用输出高电平有效的译码器实现组合逻辑电路时，还需或门
8．用输出低电平有效的译码器实现组合逻辑电路时，还需要（ ）。
① 与非门 ② 或非门 ③ 与门
④ 或门
9．半导体数码管的每个显示线段都是由（ ）构成的。
① 灯丝 ② 发光二极管 ③ 发光三极管 ④ 熔丝
3）问答与设计题
1. 组合逻辑电路在功能和电路组成上各有什么特点？
4
2. 二进制编码器和优先编码器各有何特点？优先编码器适于什么场合？试 举例说明。
3. 什么是数据选择器？数据选择器有什么功能和用途？ 4. 什么是译码器？二进制译码器有哪些特点和用途？ 5. 什么是奇偶校验器？奇偶校验器有什么功能和用途？ 6. 常用的组合逻辑集成部件包括哪些类型？ 7. 分析教材 P134 图 4.64 所示电路的逻辑功能，写出 Y1、Y2 的函数表达 式，列出真值表，并指出电路完成什么功能。 8. 用 Verilog HDL 设计 1 位全减器电路，设 X、Y、BI 分别为被减数、减 数、来自低位的借位，DO、BO 分别为差、向高位的借位。 9. 采用 function 块语句设计高电平有效的 8 线-3 线编码器，然后用函数调 用的方法实现此编码器电路。假设输入信号为 din[7:0]，输出信号为 dout[2:0]。 10. 用 Verilog HDL 设计输出为低电平有效的 2 线-4 线译码器电路，使能信 号为低电平有效。 11. 分别用 assign 语句和 always 块中的赋值语句设计一个 4 位二进制数的加 /减运算电路。当控制信号 M=0 时进行加法运算，而 M=1 时进行减法运算。注 意加法运算时要考虑来自低位的进位输入和向高位的进位输出，减法运算时要考 虑来自低位的借位和向高位的借位。采用这两种语句赋值时，对变量的类型各有 什么要求？ 12. 用 Verilog HDL 设计将余 3BCD 码转换成 8421BCD 码的码转换电路。 13. 分析下面 Verilog HDL 源程序，说明程序描述电路的功能。
数字逻辑电路教程PPT第5章时序逻辑电路
示意图、功能表
74161功能表
74161符号
波形图
012 34 56 7
VCC QCC Q0 Q1 Q2 Q3 T LD 16 15 14 13 12 11 10 9
74LS161
1 2 34 56 7 8
Cr CP D0 D1 D2 D3 P GND
T4161(74LS161)的外引脚图
例5-5 试用74161构成八位二进制加法计数 器。
状态表 状态图
驱动方程 特性方程
状态方程
CP触发沿 时序图
概括逻辑功能
[例5-1]试分析图5-2所示时序电路的逻 辑功能。
⑴根据图5-2所示逻辑图写出的驱动方程为： 写出的输出方程为：
⑵将上式代入JK触发器的特性方程 ⑶求得状态方程：
求状态转换表和状态转换图，画波形图。 设电路的初始状态
代入状态方程和输出方程得
若无效状态在CP作用下不能进入有效循环，则表明电路 不能自启动。
[例5-2]试分析图5-5所示时序电路的逻辑功能。
图5-5
解：⑴根据图5-5写出的驱动方程如下：
图5-5
状态方程、输出方程如下：
⑵列状态转换表(表5-2)，画出状态转换图(图5-6)
3、确定逻辑功能：X=0，回 到00状态，且F=0；只有连续 输入四个或四个以上个1时， 才使F=1否则F=0。故该电路 称作1111序列检测器。
预置数与CP同步，清零与CP异步。
Q1
Q2
Q3
Q4
Qcc
T Q Cr LD CP
寄存器
➢ 在数字系统和计算机中，经常要把一些数据信 息暂时存放起来，等待处理。
➢ 寄存器就是能暂时寄存数码的逻辑器件。 ➢ 寄存器内部的记忆单元是触发器。 ➢ 一个触发器可以存储一位二进制数，N个触发
数电第5章习题解答张克农版
5章课后习题解答一同步时序电路如图题所示，设各触发器的起始状态均为0态。
(1) 作出电路的状态转换表； (2) 画出电路的状态图；(3) 画出CP 作用下各Q 的波形图； (4) 说明电路的逻辑功能。
[解] (1) 状态转换表见表解 。
(2) 状态转换图如图解(1)。
(3) 波形图见图解(2)。
(4) 由状态转换图可看出该电路为同步8进制加法计数器。
由JK FF 构成的电路如图题所示。
(1) 若Q 2Q 1Q 0作为码组输出，该电路实现何种功能? (2) 若仅由Q 2输出，它又为何种功能?[解] (1) 由图可见，电路由三个主从JK 触发器构成。
各触发器的J ，K 均固定接1，且为异步连接，故均实现T ＇触发器功能，即二进制计数，故三个触发器一起构成8进制计数。
当Q 2Q 1Q 0作为码组输出时，该电路实现异步8进制计数功能。
(2) 若仅由Q 2端输出，则它实现8分频功能。
图题图题CP Q 0Q 1Q 2(1) (2)图解试分析图题所示电路的逻辑功能。
[解] (1) 驱动程式和时钟方程02n J Q =，01K =；0CP CP =111J K ==；01CP Q =210n nJ Q Q =，21K =；2CP CP = (2) 将驱动方程代入特性方程得状态方程0+1000020 ()n n n n nQ J Q K Q Q Q CP =+=+1111 ()n n Q Q CP =+12210 ()n n n n Q Q Q Q CP =(3) 根据状态方程列出状态转换真值表5进制计数器。
X = 0及X = 1时[解] (1) 写驱动方程和输出方程 0J X =， n 01K X Q = n 10J XQ =， n 10K Q = n 1Y Q = (2) 求状态方程100000010n n n n n n Q J Q K Q X Q X Q Q +=+=+ 1111111010n n n n n n n Q J Q K Q X Q Q Q Q +=+=+图题图解图题(3) 画次态卡诺图求状态转换真值表(4) 作状态转换图如图解(2)所示。
《数字逻辑设计》第5章 多级门电路
Design of Multiple-Output Circuits
利用与非门设计二级电路: F1 =C＋AB, F2 =BC＋ABC
A
B
B C
C
F1
A
F2
B
C
关键：寻找共享项，追求整体最简
F1 = C + AB
B C
f = c'd(a' + b) + cd' (a + b)
5个门,16 个输入端
5个门,12 个输入端
Multi-Level Gate Circuits
二级电路的8种基本形式
二级电路的8种基本形式
Unit 5 Multi-Level Gate Circuits
多级门电路 两级门电路的设计 多输出电路的设计 Some Examples
Unit 5 Multi-Level Gate Circuits
多级门电路（Multi-Level Circuits） 两级门电路的设计 多输出电路的设计 Some Examples
Multi-Level Gate Circuits
1. 二级电路
AND-OR 电路（积之和） f = a'c'd + bc'd + bcd' + acd'
Design of Two-Level Circuits
使用单一逻辑门设计最简二级电路
利用与非门设计 利用或非门设计
——（MOOC自学：5.2节） 利用与或非门设计
——（MOOC自学：5.2节）
Design of Two-Level Circuits
数电第五版(阎石)第五章课后习题与答案
【题5.9】 若主从结构SR触发器的CLK,S,R, 各输入端电压波 形如图P5.9所示， =1，试画出Q,Q’ 端对应的电压波形。
解：根据SR触发器逻辑功能的定义及脉冲触发方式的动作特 点，即可画出Q,Q’的电压波形，如图A5.9所示。
【题5.11】已知脉冲触发JK触发器输入端J,K和CLK的电压波 形如图P5.11所示，试画出Q,Q’端对应的电压波形。设触发器 的初始状态为Q=0.
解：根据SR触发器逻辑功能的定义和脉冲触发方式的动作特 点（主从结构触发器属于脉冲触发方式），即可画出如图 A5.7所示的输出电压波形图。
【题5.8】 在脉冲触发SR触发器电路中，若S,R,CLK 端的电压 波形如图P5.8所示，试画出Q,Q’端对应的电压波形。假定触 发器的初始状态为Q=0.
解：根据SR触发器逻辑功能的定义及脉冲触发方式的动作特 点，即可画出图A5.8中Q和Q’的电压波形。
【题5.14】已知维持阻塞结构D触发器各输入端的电 压波形如图P5.14所示，试画出Q,Q’端对应的电压波形。
解：根据D触发器逻辑功能的定义及维持阻塞结构所具有的 边沿触发方式，即可画出Q和Q’的电压波形如图A5.14。
【题5.15】已知CMOS边沿触发方式JK触发器各输入端 的电压波形如图P5.15所示,试画出Q,Q式的动作特 点，画出的Q,Q’ 端电压波形如图A5.15。
【题5.18】设图P5.18中各触发器的初始状态皆为Q=0，试画 出在CLK信号连续作用下各触发器输出端的电压波形
解：根据每个触发器的逻辑功能和触发方式，画出输出端Q 的电压波形，如图A5.18。
解：见图A5.4.
【题5.5】 在图P5.5电路中，若CLK,S,R的电压波形如图中所 示，试画出Q和Q’端与之对应的电压波形。假定触发器的初 始状态为Q=0.
数电课件第五章锁存器和触发器
不同类型的触发器具有不同的工 作特性和应用场景，可以根据实 际需求选择合适的触发器类型。
03 锁存器和触发器的应用
在时序逻辑电路中的应用
存储数据
锁存器和触发器可以用于存储数 据，在时序逻辑电路中作为寄存 器使用，保存数据以便后续处理。
控制信号
锁存器和触发器可以用于控制信号 的传递，在时序逻辑电路中作为控 制门使用，根据输入信号的变化来 控制输出信号的输出。
数电课件第五章锁存器和触发器
目录
• 锁存器概述 • 触发器概述 • 锁存器和触发器的应用 • 锁存器和触发器的实例分析 • 总结与展望
01 锁存器概述
定义与特点
01
02
定义：锁存器是一种具 特点 有存储功能的电路，能 在特定条件下保存数据， 即使在电源关闭或电路 其他部分出现故障的情 况下也能保持数据的完 整性。
分析
通过仿真验证了74HC74的触发器功能，并对其工作原理有了更深入的理解。
05 总结与展望
锁存器和触发器的重要性和应用价值
锁存器和触发器是数字电路中的基本元件，在时序逻辑电路和组合逻辑 电路中有着广泛的应用。
锁存器能够存储二进制数据，在数字系统中起到数据存储和传输的作用； 触发器则能够记忆二进制数据的状态，常用于实现时序逻辑电路如计数 器和寄存器等。
03
04
05
具有记忆功能，能够保 存前一个状态；
在时钟信号的驱动下， 通常由逻辑门电路构成， 完成数据的存储和读取； 如与门、或门和非门等。
工作原理
在时钟信号的控制下，锁存器在数据输入端接收数据，并在数据输出端输出数据。
当时钟信号处于低电平状态时，锁存器处于关闭状态，无法接收新的数据输入。
数字电子技术基础第五章、第六章习题参考答案
第五章锁存器和触发器1、Q n 1二S RQ n, SR = O2、Q n, 03、324、TCP J I I I I I I I7、4-13题解图8、D= A 二BCP_ I~I I~I I~I I~I I~LI Iz卄I TH 1D i - I i i1 . I | , __ L,I ■ I ______第六章时序逻辑电路1、 输入信号，原来的状态2、 异3、 n 5、反馈清零、反馈置数扌-6、N乂—LJ UU 仑厂 II ~ 7、状态方程和输出方程：㈣ =A®Q'tZ^AQ&激励方程A =Kq = A &/. =e 0=i 状态方程0：戚；忧"无©土死输出方程Z=AQ1Q0根据状态方程组和输出方程可列出状态表，如表题解6 . 2 . 4所示，状态图如图题解2. 4 所示。
Q - M?； + M V ；* Q ； = + “：14、图题解6.2.4Q；・枫"烟00保持，01右移10左移11并行输入当启动信号端输人一低电平时，使S仁1 ,这时有So= Sl= 1 ,移位寄存器74HC194执行并行输人功能，Q3Q2Q1Q0 = D3D2D1D0 = 1110。
启动信号撤消后，由于Q°= 0,经两级与非门后，使S仁0 ,这时有S1S0= 01 ,寄存器开始执行右移操作。
在移位过程中，因为Q3Q2、Q1、Q0中总有一个为0,因而能够维持S1S0=01状态，使右移操作持续进行下去°其移位情况如图题解6, 5, 1所示。
该电路能按固定的时序输出低电平脉冲，是一个四相时序脉冲产生电路。
-JT AAA TL幺I15、状态方程为儿⑷儿個)X(O24、解：74HC194功能由S1S0控制。
第5章课后习题参考答案
第五章组合逻辑电路1．写出如下图电路的输出信号逻辑表达式，并说明其功能。
〔a〕〔b〕解：〔a〕Y1ABC〔判奇功能：1的个数为奇数时输出为1〕Y2AB(AB)CABACBC〔多数通过功能：输出与输入多数一致〕〔b〕Y1(AB)A(AB)BABAB〔同或功能：一样为1，否那么为0〕2．分析如下图电路的逻辑功能〔a〕〔b〕〔c〕解：〔a〕Y1ABAB〔判奇电路：1的个数为奇数时输出为1〕0011〔b〕Y2(((AA)A)A)〔判奇电路：1的个数为奇数时输出为1〕0123YAM00〔c〕Y1AM1〔M=0时，源码输出；M=1时，反码输出〕YAM233．用与非门设计实现以下功能的组合逻辑电路。
〔1〕实现4变量一致电路。
〔2〕四变量的多数表决电路解：〔1〕1〕定变量列真值表：ABCDYABCDY0000110000000101001000100101000011010110010*******010*******011001110001110111112〕列函数表达式：YABCDABC D ABCDABCD3〕用与非门组电路〔2〕输入变量A、B、C、D，有3个或3个以上为1时输出为1，输人为其他状态时输出为0。
1〕列真值表2〕些表达式3〕用与非门组电路4．有一水箱由大、小两台水泵ML和Ms供水，如下图。
水箱中设置了3个水位检测元件A、B、C，如图〔a〕所示。
水面低于检测元件时，检测元件给出高电平；水面高于检测元件时，检测元件给出低电平。
现要求当水位超过C点时水泵停顿工作；水位低于C点而高于B点时Ms单独工作；水位低于B点而高于A点时ML单独工作；水位低于A点时M L和Ms同时工作。
试用门电路设计一个控制两台水泵的逻辑电路，要求电路尽量简单。
解：〔1〕根据要求列真值表〔b〕〔b〕〔a〕〔2〕真值表中×对应的输入项为约束项，利用卡诺图化简〔c〕〔d〕〔c〕〔d〕〔e〕得：MABCsMBL〔M L、M S的1状态表示工作，0状态表示停顿〕〔3〕画逻辑图〔e〕5．某医院有—、二、三、四号病室4间，每室设有呼叫按钮，同时在护士值班室内对应地装有一号、二号、三号、四号4个指示灯。