新人教版高中数学必修第一册课时跟踪检测(三十九) 正切函数的性质与图象
高中数学课时跟踪检测正切函数的性质与图象

第一章 1.4 1.4.3 正切函数的性质与图象课时跟踪检测一、选择题1.下列各点中,可作为函数y =tan x 的对称中心的是( ) A.⎝⎛⎭⎫π4,0 B.⎝⎛⎭⎫π4,1 C.⎝⎛⎭⎫-π4,0 D.⎝⎛⎭⎫π2,0答案:D2.函数y =sin x +tan x ⎝⎛⎭⎫x ∈⎣⎡⎦⎤-π4,π4的值域是( ) A.⎣⎡⎦⎤-22,22 B .[-1,1] C.⎣⎢⎡⎦⎥⎤0,2+22 D.⎣⎢⎡⎦⎥⎤-2+22,2+22 解析:∵y =sin x 在⎣⎡⎦⎤-π4,π4上是增函数, y =tan x 在⎣⎡⎦⎤-π4,π4上是增函数, ∴y =sin x +tan x 在⎣⎡⎦⎤-π4,π4上是增函数. ∴当x =-π4时,y min =-22-1=-2+22,当x =π4时,y max =22+1=2+22.∴函数的值域为⎣⎢⎡⎦⎥⎤-2+22,2+22. 答案:D3.下列不等式正确的是( ) A .tan 47π>tan 37πB .tan 25π<tan 35πC .tan ⎝⎛⎭⎫-137π<tan ⎝⎛⎭⎫-158πD .tan ⎝⎛⎭⎫-134π>tan ⎝⎛⎭⎫-125π 解析:tan ⎝⎛⎭⎫-134π=tan ⎝⎛⎭⎫-3π-π4=tan ⎝⎛⎭⎫-π4=-tan π4=-1. tan ⎝⎛⎭⎫-125π=tan ⎝⎛⎭⎫-2π-2π5 =tan ⎝⎛⎭⎫-2π5=-tan 25π<-1. ∴tan ⎝⎛⎭⎫-125π<tan ⎝⎛⎭⎫-134π. 故选D. 答案:D4.下列函数中,同时满足①在⎝⎛⎭⎫0,π2上是增函数;②为奇函数;③以π为最小正周期的函数是( ) A .y =tan x B .y =cos x C .y =tan x2D .y =|sin x |答案:A5.函数y =tan ⎝⎛⎭⎫12x -π3在一个周期内的图象是下图中的( )解析:y =tan ⎝⎛⎭⎫x 2-π3的图象与x 轴交点为⎝⎛⎭⎫23π,0,故C 、D 不正确,又x 2-π3≠±π2,得x ≠53π,且x ≠-π3,故A 正确. 答案:A6.已知函数y =tan ωx 在⎝⎛⎭⎫-π2,π2内是减函数,则( ) A .0<ω≤1 B .-1≤ω<0 C .ω≥1D .ω≤-1解析:∵函数在⎝⎛⎭⎫-π2,π2上递减,则ω必小于0,而当|ω|>1时,图象将缩小周期,故-1≤ω<0. 答案:B 二、填空题7.函数f (x )=tan ⎝⎛⎭⎫π2x +π3的单调增区间为________. 解析:由k π-π2<π2x +π3<k π+π2(k ∈Z ),得-53+2k <x <13+2k (k ∈Z ).答案:⎝⎛⎭⎫2k -53,2k +13(k ∈Z ) 8.已知函数f (x )=A tan(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的部分图象如图所示,则f ⎝⎛⎭⎫π24等于________.解析:由图象知周期T =π2=πω,∴ω=2.又图象过点⎝⎛⎭⎫3π8,0,A tan ⎝⎛⎭⎫2×3π8+φ=0,∴tan ⎝⎛⎭⎫3π4+φ=0.而|φ|<π2,∴3π4+φ=π,∴φ=π4,∴f (x )=A tan2x +π4.又过(0,1)点,∴A tan π4=1,∴A =1,即f (x )=tan ⎝⎛⎭⎫2x +π4,∴f ⎝⎛⎭⎫π24=tan π3= 3. 答案: 39.若-1<tan x ≤3,则x 的取值范围是________. 解析:∵tan ⎝⎛⎭⎫-π4=-1,tan π3= 3. 又y =tan x 在⎝⎛⎭⎫-π2,π2上是增函数, ∴当-π2<x <π2时,满足-1<tan x ≤3的x 的取值范围是-π4<x ≤π3.∵y =tan x 的周期为π, ∴-π4+k π<x ≤π3+k π(k ∈Z ).答案:⎝⎛⎦⎤-π4+k π,π3+k π(k ∈Z ) 三、解答题10.求函数y =3-tan 2x 的定义域. 解:由题意得⎩⎪⎨⎪⎧3-tan 2x ≥0,x ≠k π+π2,k ∈Z , 得k π-π3≤x ≤k π+π3,k ∈Z .∴原函数的定义域为⎣⎡⎦⎤k π-π3,k π+π3,k ∈Z . 11.设函数f (x )=tan ⎝⎛⎭⎫x 2-π3.(1)求函数f (x )的定义域、周期和单调区间; (2)求不等式-1≤f (x )≤ 3的解集; (3)作出函数y =f (x )在一个周期内的简图. 解:(1)由x 2-π3≠π2+k π,k ∈Z ,解得x ≠5π3+2k π,k ∈Z ,∴函数f (x )的定义域是⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠5π3+2k π,k ∈Z .∵ω=12,∴周期T =πω=2π.由-π2+k π<x 2-π3<π2+k π,k ∈Z ,解得-π3+2k π<x <5π3+2k π,k ∈Z ,∴函数f (x )的单调递增区间是⎝⎛⎭⎫-π3+2k π,5π3+2k π,k ∈Z ,无单调减区间.(2)由-1≤tan ⎝⎛⎭⎫x 2-π3≤ 3, 得-π4+k π≤x 2-π3≤π3+k π,k ∈Z ,解得π6+2k π≤x ≤4π3+2k π,k ∈Z .∴不等式-1≤f (x )≤3的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪π6+2k π≤x ≤4π3+2k π,k ∈Z .(3)令x 2-π3=0,则x =2π3,令x 2-π3=π2,则x =5π3, 令x 2-π3=-π2,则x =-π3, ∴函数y =tan ⎝⎛⎭⎫x 2-π3的图象与x 轴的一个交点的坐标是⎝⎛⎭⎫2π3,0,在这个交点左、右两侧相邻的两条渐近线的方程分别是x =-π3,x =5π3,从而得到函数y =f (x )在区间⎝⎛⎭⎫-π3,5π3内的简图(如图所示).12.若x ∈⎣⎡⎦⎤-π3,π4,求函数y =1cos 2x +2tan x +1的最大值和最小值及相应的x 的值. 解:∵-π3≤x ≤π4,又y =tan x 在⎝⎛⎭⎫-π2,π2上是增函数, ∴-3≤tan x ≤1.∵y =sin 2x +cos 2xcos 2x +2tan x +1=tan 2x +2tan x +2 =(tan x +1)2+1,∴当tan x =-1时,y min =1, 此时x =-π4,当tan x =1时,y max =5, 此时x =π4.考题过关13.(2017·河北省衡水中学测试)已知函数y =tan(2x +φ)的图象过点⎝⎛⎭⎫π12,0,则φ可以是( ) A .-π6B.π6 C .-π12D.π12解析:由2×π12+φ=k π,k ∈Z ,得φ=-π6+k π,k ∈Z .当k =0时,φ=-π6.答案:A。
新教材高中数学基础练49正切函数的性质与图象含解析新人教A版必修第一册

正切函数的性质与图象(30分钟 60分)一、选择题(每小题5分,共30分)1.(多选题)在下列给出的函数中,以π为周期且在⎝⎛⎭⎪⎫0,π2 内单调递减的是( )A .y =sin x2B .y =cos 2xC .y =sin ⎝⎛⎭⎪⎫2x +π4 D .y =tan ⎝⎛⎭⎪⎫π4-x【解析】选B 、D.由函数周期为π可排除A.D 选项中y =tan ⎝⎛⎭⎪⎫π4-x 可变形为y =-tan⎝ ⎛⎭⎪⎫x -π4 ,当x ∈⎝ ⎛⎭⎪⎫0,π2 时,2x ∈(0,π),x -π4 ∈⎝ ⎛⎭⎪⎫-π4,π4 ,此时B ,D 中函数均是减函数.2.已知函数y =tan (2x +φ)的图象过点⎝⎛⎭⎪⎫π12,0 ,则φ可以是( )A .-π6B .π6C .-π12D .π12【解析】选A.因为函数的图象过点⎝ ⎛⎭⎪⎫π12,0 ,所以tan ⎝ ⎛⎭⎪⎫π6+φ =0,所以π6 +φ=k π,k ∈Z , 所以φ=k π-π6 ,k ∈Z ,令k =0,则φ=-π6 .3.函数f (x )=tan 2xtan x 的定义域为( )A .{x |x ∈R 且x ≠k π4,k ∈Z }B .{x |x ∈R 且x ≠k π+π2 ,k ∈Z }C .{x |x ∈R 且x ≠k π+π4 ,k ∈Z }D .{x |x ∈R 且x ≠k π-π4,k ∈Z }【解析】选A.⎩⎪⎨⎪⎧x ≠k π,x ≠k π+π2,2x ≠k π+π2 (k ∈Z )得⎩⎪⎨⎪⎧x ≠k π2,x ≠k π2+π4, 所以x ≠2k 4 π且x ≠2k +14 π,x ≠k π4,k ∈Z .4.函数y =-2+tan ⎝ ⎛⎭⎪⎫12x +π3 的单调递增区间为( )A .⎝ ⎛⎭⎪⎫2k π-53π,2k π+π3 ,k ∈ZB .⎝ ⎛⎭⎪⎫2k π-π3,2k π+53π ,k ∈ZC .⎝ ⎛⎭⎪⎫k π-53π,k π+π3 ,k ∈ZD .⎝⎛⎭⎪⎫k π-π3,k π+53π ,k ∈Z 【解析】选A.由-π2 +k π<12 x +π3 <π2 +k π,k ∈Z ,解得-53 π+2k π<x <π3+2k π,k ∈Z .5.在区间⎝ ⎛⎭⎪⎫-3π2,3π2 内,函数y =tan x 与函数y =sin x 的图象交点的个数为( ) A .1 B .2 C .3 D .4【解析】选 C.在同一坐标系中画出正弦函数与正切函数的图象(如图所示),可以看到在区间⎝ ⎛⎭⎪⎫-3π2,3π2 内二者有三个交点.6.函数f (x )=tan ωx (ω>0)的图象上的相邻两支曲线截直线y =1所得的线段长为π4 ,则ω的值是( )A .1B .2C .4D .8【解析】选C.由题意可得f (x )的周期为π4 ,则πω =π4,所以ω=4.【补偿训练】函数f (x )=tan ⎝ ⎛⎭⎪⎫ωx -π4 与函数g (x )=sin ⎝ ⎛⎭⎪⎫π4-2x 的最小正周期相同,则ω=( )A .±1B .1C .±2D .2 【解析】选A.π|ω| =2π|-2|,ω=±1. 二、填空题(每小题5分,共10分)7.f (x )=a sin x +b tan x +1,满足f (5)=7,则f (-5)=________.【解析】因为f (5)=a sin 5+b tan 5+1=7,所以a sin 5+b tan 5=6,所以f (-5)=a sin (-5)+b tan (-5)+1=-(a sin 5+b tan 5)+1=-6+1=-5. 答案:-58.-tan 6π5 与tan ⎝⎛⎭⎪⎫-13π5 的大小关系是________.【解析】-tan 6π5 =-tan π5 ,tan ⎝ ⎛⎭⎪⎫-13π5 =-tan 13π5 =-tan 3π5 .因为0<π5 <π2 <3π5<π, 所以tan π5 >0,tan 3π5 <0,所以-tan π5 <-tan 3π5 ,即-tan 6π5<tan ⎝⎛⎭⎪⎫-13π5 .答案:-tan 6π5 <tan ⎝ ⎛⎭⎪⎫-13π5 三、解答题(每小题10分,共20分)9.求函数y =tan 2x 的定义域、值域和周期,并作出它在区间[-π,π]内的图象.【解析】定义域为⎩⎨⎧⎭⎬⎫x ∈R 且x ≠π4+k π2,k ∈Z ;值域为(-∞,+∞);周期为π2;对应图象如图所示:10.若函数f (x )=2tan (ωx -π3)(ω<0)的最小正周期为2π,求f (x )的单调区间.【解析】因为f (x )=2tan ⎝ ⎛⎭⎪⎫ωx -π3 (ω<0)的最小正周期为2π,所以π|ω| =2π,所以|ω|=12 .又因为ω<0,所以ω=-12 .即f (x )=2tan ⎝ ⎛⎭⎪⎫-12x -π3 =-2tan ⎝ ⎛⎭⎪⎫12x +π3 .由k π-π2 <12 x +π3 <k π+π2(k ∈Z ),得2k π-53 π<x <2k π+π3 (k ∈Z ),所以函数f (x )的单调减区间为(2k π-53 π,2k π+π3)(k ∈Z ). 【补偿训练】求函数y =tan ⎝ ⎛⎭⎪⎫-12x +π4 的单调区间及最小正周期.【解析】y =tan ⎝ ⎛⎭⎪⎫-12x +π4 =-tan ⎝ ⎛⎭⎪⎫12x -π4 ,由k π-π2 <12 x -π4 <k π+π2 (k ∈Z ),得2k π-π2 <x <2k π+32π(k ∈Z ),所以函数y =tan ⎝ ⎛⎭⎪⎫-12x +π4 的单调递减区间是⎝ ⎛⎭⎪⎫2k π-π2,2k π+32π ,k ∈Z ,周期T =π⎪⎪⎪⎪⎪⎪-12 =2π. (35分钟 70分)一、选择题(每小题5分,共20分) 1.函数f (x )=|tan 2x |是( ) A .周期为π的奇函数 B .周期为π的偶函数 C .周期为π2 的奇函数D .周期为π2的偶函数【解析】选D.f (-x )=|tan (-2x )|=|tan 2x |=f (x )为偶函数,T =π2 .2.函数f (x )=lg tan x 的定义域是( )A .⎣⎢⎡⎭⎪⎫k π+π4,k π+π2 (k ∈Z )B .⎝ ⎛⎭⎪⎫k π-π2,k π+π2 (k ∈Z )C .⎝ ⎛⎭⎪⎫k π,k π+π4 (k ∈Z )D .⎣⎢⎡⎭⎪⎫k π-π4,k π+π2 (k ∈Z ) 【解析】选A.f (x )有意义时,⎩⎪⎨⎪⎧lg tan x ≥0tan x >0 ,所以tan x ≥1,解得k π+π4 ≤x <k π+π2(k ∈Z ),所以f (x )的定义域为⎣⎢⎡⎭⎪⎫k π+π4,k π+π2 (k ∈Z ).3.已知函数y =tan ωx 在⎝ ⎛⎭⎪⎫-π2,π2 内单调递减,则( )A .0<ω≤1B .-1≤ω<0C .ω≥1D .ω≤-1【解析】选B.因为y =tan ωx 在⎝ ⎛⎭⎪⎫-π2,π2 内是减函数,所以ω<0且T =π|ω| ≥π,所以|ω|≤1,即-1≤ω<0.【补偿训练】函数y =|tan (x +π4 )|的单调增区间为( )A .(k π-π2 ,k π+π2 )(k ∈Z )B .(k π-3π4 ,k π+π4 )(k ∈Z )C .(k π,k π+π2 )(k ∈Z )D .[k π-π4 ,k π+π4 )(k ∈Z )【解析】选 D.令t =x +π4 ,则y =|tan t |的单调增区间为⎣⎢⎡⎭⎪⎫k π,k π+π2 (k ∈Z ).由k π≤x +π4<k π+π2,得k π-π4≤x <k π+π4(k ∈Z ).K4.已知函数f (x )=A tan (ωx +φ)⎝ ⎛⎭⎪⎫ω>0,|φ|<π2 ,y =f (x )的部分图象如图,则f ⎝ ⎛⎭⎪⎫π24 =( )A .2+3B .3C .33D .2-3 【解析】选B. 由图象可知:T =2⎝⎛⎭⎪⎫3π8-π8 =π2 ,所以ω=2,所以2×π8 +φ=k π+π2 (k ∈Z ).又|φ|<π2 ,所以φ=π4 .又f (0)=1,所以A tan π4 =1,得A =1,所以f (x )=tan ⎝ ⎛⎭⎪⎫2x +π4 ,所以f ⎝ ⎛⎭⎪⎫π24 =tan ⎝ ⎛⎭⎪⎫π12+π4 =tan π3 =3 .二、填空题(每小题5分,共20分)5.y =tan x2满足下列哪些条件________(填序号). ①在⎝⎛⎭⎪⎫0,π2 上单调递增;②为奇函数;③以π为最小正周期;④定义域为{x |x ≠π4 +k π2,k ∈Z }.【解析】令x ∈(0,π2 ),则x 2 ∈(0,π4 ),所以y =tan x 2 在(0,π2)上单调递增,①正确;tan (-x 2 )=-tan x 2 ,故y =tan x 2 为奇函数,②正确;T =πω =2π,所以③不正确;由x 2 ≠π2+k π,k ∈Z ,得{x |x ≠π+2k π,k ∈Z },所以④不正确.答案:①②6.使函数y =2tan x 与y =cos x 同时单调递增的区间是________.【解析】由y =2tan x 与y =cos x 的图象(图略)知,同时单调递增的区间为⎝ ⎛⎭⎪⎫2k π-π2,2k π (k ∈Z )和⎝ ⎛⎭⎪⎫2k π+π,2k π+3π2 (k ∈Z ). 答案:⎝ ⎛⎭⎪⎫2k π-π2,2k π (k ∈Z )和⎝⎛⎭⎪⎫2k π+π,2k π+3π2 (k ∈Z )7.若函数y =tan ωx 在⎝ ⎛⎭⎪⎫-π2,π2 内是减函数,则ω的取值范围为________.【解析】由题意知其周期T ≥π,即π|ω| ≥π.所以|ω|≤1,又函数为减函数,所以ω<0. 故-1≤ω<0. 答案:[-1,0)8.若tan ⎝⎛⎭⎪⎫2x -π6 ≤1,则x 的取值范围是________. 【解析】令z =2x -π6 ,在⎝ ⎛⎭⎪⎫-π2,π2 上满足tan z ≤1的z 的值是-π2 <z ≤π4 ,在整个定义域上有-π2 +k π<z ≤π4 +k π,解不等式-π2 +k π<2x -π6 ≤π4 +k π,得-π6+k π2<x ≤5π24 +k π2,k ∈Z . 答案:-π6 +k π2 <x ≤5π24 +k π2 ,k ∈Z三、解答题(共30分)9.(10分)若x ∈⎣⎢⎡⎦⎥⎤-π3,π4 ,求函数y =1cos 2x +2tan x +1的最值及相应的x 的值.【解析】y =1cos 2x +2tan x +1=cos 2x +sin 2xcos 2x +2tan x +1=tan 2x +2tan x +2= (tan x +1)2+1.因为x ∈⎣⎢⎡⎦⎥⎤-π3,π4 ,所以tan x ∈[]-3,1 . 所以当tan x =-1时,即x =-π4 时,y 取最小值1;当tan x =1时,即x =π4 时,y 取最大值5.10.(10分)已知函数f (x )=3tan ⎝ ⎛⎭⎪⎫12x -π3 .(1)求f (x )的定义域、值域.(2)讨论f (x )的周期性,奇偶性和单调性.【解析】(1)由12 x -π3 ≠π2 +k π,k ∈Z ,解得x ≠5π3 +2k π,k ∈Z .所以定义域为{x |x ≠5π3+2k π,k ∈Z },值域为R .(2)f (x )为周期函数,周期T =π12 =2π.f (x )为非奇非偶函数.由-π2 +k π<12 x -π3 <π2+k π,k ∈Z ,解得-π3 +2k π<x <5π3 +2k π,k ∈Z .所以函数的单调递增区间为⎝ ⎛⎭⎪⎫-π3+2k π,5π3+2k π (k ∈Z ).11.(10分)已知f (x )=x 2+2x ·tan θ-1,x ∈[]-1,3 ,其中θ∈(-π2 ,π2 ).(1)当θ=-π6时,求函数f (x )的最大值与最小值.(2)求θ的取值范围,且使y =f (x )在区间[-1,3 ]上是单调函数.【解析】(1)当θ=-π6 时f (x )=x 2-233 x -1=(x -33 )2-43 ,x ∈[-1,3 ],所以当x =33 时f (x )的最小值为-43 ,当x =-1时,f (x )的最大值为233. (2)因为f (x )=x 2+2x ·tan θ-1=(x +tan θ)2-1-tan 2θ,所以原函数的图象的对称轴方程为x =-tan θ.因为y =f (x )在[-1,3 ]上是单调函数,所以-tan θ≤-1或-tanθ≥3 ,即tan θ≥1或tan θ≤-3 ,所以π4 +k π≤θ<π2 +k π或-π2+k π<θ≤-π3 +k π,k ∈Z .又θ∈(-π2 ,π2 ),所以θ的取值范围是⎝ ⎛⎦⎥⎤-π2,-π3 ∪⎣⎢⎡⎭⎪⎫π4,π2 .。
5.4.3正切函数的性质与图象 课时训练- 高一上学期数学人教A版( )必修第一册(含答案)

5.4.3 正切函数的性质与图象基础巩固1.函数y=2tan (2x +π3)的定义域为( ) A.{x |x ≠π12}B.{x |x ≠-π12} C.{x |x ≠π12+kπ,k ∈Z}D.{x |x ≠π12+kπ2,k ∈Z}2.函数y=tan (12x -π3)在一个周期内的图象是( )3.函数y=lg tan x 的单调递增区间是( ) A.(kπ-π2,kπ+π2)(k ∈Z ) B.(kπ,kπ+π2)(k ∈Z ) C.(2kπ-π2,2kπ+π2)(k ∈Z ) D.(k π,k π+π)(k ∈Z )4.如图所示,函数y=√3tan (2x +π6)的部分图象与坐标轴分别交于点D ,E ,F ,则△DEF 的面积为( )A.π4B.π2C.πD.2π5.已知函数f(x)=tan ωx(ω>0)的图象的相邻两支截直线y=π4所得的线段长为π4,则f(π4)的值是()A.0B.1C.-1D.π46.函数y=3tan(x+π3)的图象的对称中心的坐标为.7.已知函数f(x)=tan(ωx+π6)(ω>0)的最小正周期为2π,则f(π6)=.8.比较大小:tan(-2π7)tan(-π5).9.求函数y=-tan2x+4tan x+1,x∈[-π4,π4]的值域.能力提升1.已知函数y=tan ωx在区间(-π2,π2)内单调递减,则()A.0<ω≤1B.-1≤ω<0C.ω≥1D.ω≤-12.函数y=tan x+sin x-|tan x-sin x|在区间(π2,3π2)内的图象是()3.(多选题)下列关于函数y=tan(x+π3)的说法错误的是()A.在区间(-π6,5π6)内单调递增B.最小正周期是πC.图象关于点(π4,0)成中心对称D.图象关于直线x=π6成轴对称4.若tan(2x-π6)≤1,则x的取值范围是.5.已知函数f(x),任意x1,x2∈(-π2,π2)(x1≠x2),给出下列结论:①f(x+π)=f(x);②f(-x)=f(x);③f(0)=1;④f(x1)-f(x2)x1-x2>0;⑤f(x1+x22)>f(x1)+f(x2)2.当f(x)=tan x时,正确的结论为(填序号).6.已知函数f(x)=3tan(π6-x 4 ).(1)求它的最小正周期和单调递减区间;(2)试比较f(π)与f(3π2)的大小.7.已知函数f(x)=a sin(ωx+π3)(ω>0),g(x)=b tanωx-π3(ω>0),它们的周期之和为3π2,且f(π2)=g(π2),f(π4)=-√3g(π4)+1.求这两个函数的解析式,并求出g(x)的单调递增区间.参考答案基础巩固1. D2. A3. B4. A5. A6.(kπ2-π3,0)(k∈Z)7. 18. <9-π4≤x ≤π4,∴-1≤tan x ≤1. 令tan x=t ,则t ∈[-1,1].∴y=-t 2+4t+1=-(t-2)2+5.∴当t=-1,即x=-π4时,y min =-4,当t=1,即x=π4时,y max =4.故所求函数的值域为[-4,4].能力提升1. B2. D3. ACD4. {x |-π6+kπ2<x ≤5π24+kπ2,k ∈Z}5.①④6.解(1)因为f (x )=3tan (π6-x 4)=-3tan x4−π6, 所以最小正周期T=π14=4π.由k π-π2<x 4−π6<k π+π2(k ∈Z ),得4k π-4π3<x<4k π+8π3(k ∈Z ).因为y=3tan (x 4-π6)在区间4k π-4π3,4k π+8π3(k ∈Z )内单调递增, 所以f (x )=3tan (π6-x4)在区间(4k π-4π3,4k π+8π3)(k ∈Z )内单调递减. 故函数f (x )的最小正周期为4π,单调递减区间为(4k π-4π3,4k π+8π3)(k ∈Z ). (2)f (π)=3tan (π6-π4)=3tan (-π12)=-3tan π12,f (3π2)=3tan (π6-3π8)=3tan (-5π24)=-3tan 5π24, 因为0<π12<5π24<π2,且y=tan x 在区间(0,π2)内单调递增,所以tan π12<tan 5π24,所以f (π)>f (3π2).7,可得{2πω+πω=3π2,asin (ωπ2+π3)=btan (ωπ2-π3),asin (ωπ4+π3)=-√3btan (ωπ4-π3)+1,解得{ω=2,a =1,b =12,故f(x)=sin(2x+π3),g(x)=12tan(2x-π3).当kπ-π2<2x-π3<kπ+π2(k∈Z),即kπ2−π12<x<kπ2+5π12(k∈Z)时,g(x)单调递增.所以g(x)的单调递增区间为(kπ2-π12,kπ2+5π12)(k∈Z).。
新教材高中数学课时跟踪检测(三十九)正弦函数、余弦函数的性质(二)新人教A版必修第一册

新教材高中数学课时跟踪检测(三十九)正弦函数、余弦函数的性质(二)新人教A 版必修第一册课时跟踪检测(三十九) 正弦函数、余弦函数的性质(二)A 级——学考水平达标练1.函数y =1-2cos π2x 的最小值、最大值分别是( )A .-1,3B .-1,1C .0,3D .0,1解析:选A ∵cos π2x ∈[-1,1],∴-2cos π2x ∈[-2,2],∴y =1-2cos π2x ∈[-1,3],∴y min =-1,y max =3.2.下列不等式中成立的是( )A .sin ⎝ ⎛⎭⎪⎫-π8>sin ⎝ ⎛⎭⎪⎫-π10B .sin 3>sin 2C .sin 75π>sin ⎝ ⎛⎭⎪⎫-25π D .sin 2>cos 1解析:选D ∵sin 2=cos ⎝ ⎛⎭⎪⎫π2-2=cos ⎝ ⎛⎭⎪⎫2-π2,且0<2-π2<1<π,∴cos ⎝ ⎛⎭⎪⎫2-π2>cos 1,即sin 2>cos 1.故选D.3.函数y =|cos x |的一个单调减区间是( )A.⎣⎢⎡⎦⎥⎤-π4,π4B.⎣⎢⎡⎦⎥⎤π4,34πC.⎣⎢⎡⎦⎥⎤π,32π D.⎣⎢⎡⎦⎥⎤32π,2π 解析:选C 函数y =|cos x |=⎩⎪⎨⎪⎧cos x ,cos x ≥0,-cos x ,cos x <0,图象如下图所示:单调减区间有⎣⎢⎡⎦⎥⎤0,π2,⎣⎢⎡⎦⎥⎤π,32π,…,故选C.4.若函数f (x )=2sin ⎝ ⎛⎭⎪⎫ωx +π3(ω>0),且f (α)=-2,f (β)=0,|α-β|的最小值是π2,则f (x )的单调递增区间是( )A.⎣⎢⎡⎦⎥⎤2k π-5π6,2k π+π6(k ∈Z) B.⎣⎢⎡⎦⎥⎤k π-π3,kπ+π6(k ∈Z) C.⎣⎢⎡⎦⎥⎤2k π-2π3,2k π+π3(k ∈Z) D.⎣⎢⎡⎦⎥⎤k π-5π12,k π+π12(k ∈Z) 解析:选A 由题意可知14T =π2,所以T =2π,所以ω=1,所以f (x )=2sin ⎝ ⎛⎭⎪⎫x +π3.由2k π-π2≤x +π3≤2k π+π2(k ∈Z),得2k π-5π6≤x ≤2k π+π6(k ∈Z),所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤2k π-5π6,2k π+π6(k ∈Z).故选A.5.设函数f (x )=2sin ⎝ ⎛⎭⎪⎫π2x +π5.若对任意x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为( )A .4B .2C .1D .12解析:选B 依题意得f (x 1)是f (x )的最小值,f (x 2)是f (x )的最大值.因此|x 1-x 2|=⎝ ⎛⎭⎪⎫k +12T (k ∈Z).∴当k =0时,|x 1-x 2|min =12T =12×2ππ2=2.故选B.6.函数y =sin x ⎝ ⎛⎭⎪⎫π6≤x ≤4π3的值域为________.解析:画出函数y =sin x ⎝ ⎛⎭⎪⎫π6≤x ≤4π3的图象,如图.由图象可知,当x =π2时,y max =1,当x =4π3时,y min =-32,所以函数y =sin x ⎝ ⎛⎭⎪⎫π6≤x ≤4π3的值域为⎣⎢⎡⎦⎥⎤-32,1.答案:⎣⎢⎡⎦⎥⎤-32,1 7.函数y =sin 2x -cos x +1的最大值为________.解析:y =sin 2x -cos x +1=-cos 2x -cos x +2=-⎝ ⎛⎭⎪⎫cos x +122+94,∵-1≤cos x ≤1,∴当cos x =-12时,y 取最大值94.答案:948.已知函数f (x )=-sin 2ωx (ω>0)的图象关于点M ⎝ ⎛⎭⎪⎫5π4,0对称,且在区间⎣⎢⎡⎦⎥⎤0,π2上是单调函数,则ω的值为________.解析:依题意得T 4≥π2,即T ≥2π,从而0<ω≤12.又sin ⎝ ⎛⎭⎪⎫2ω×5π4=0,即sin 5ωπ2=0, ∴5ωπ2=k π(k ∈Z),解得ω=25k (k ∈Z). 由0<ω≤12知,ω=25.答案:259.求函数y =3-4cos ⎝ ⎛⎭⎪⎫2x +π3,x ∈⎣⎢⎡⎦⎥⎤-π3,π6的最大值、最小值及相应的x 值. 解:因为x ∈⎣⎢⎡⎦⎥⎤-π3,π6,所以2x +π3∈⎣⎢⎡⎦⎥⎤-π3,2π3,从而-12≤cos ⎝ ⎛⎭⎪⎫2x +π3≤1.所以当cos ⎝ ⎛⎭⎪⎫2x +π3=1,即2x +π3=0,x =-π6时,y min =3-4=-1.当cos ⎝ ⎛⎭⎪⎫2x +π3=-12,即2x +π3=2π3,x =π6时,y max =3-4×⎝ ⎛⎭⎪⎫-12=5. 综上所述,当x =-π6时,y min =-1;当x =π6时,y max =5.10.已知函数f (x )=2cos ⎝ ⎛⎭⎪⎫3x +π4. (1)求f (x )的单调递增区间;(2)求f (x )的最小值及取得最小值时相应的x 值. 解:(1)令2k π-π≤3x +π4≤2k π(k ∈Z),解得2k π3-5π12≤x ≤2k π3-π12(k ∈Z).所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤2k π3-5π12,2k π3-π12(k ∈Z).(2)当3x +π4=2k π-π(k ∈Z)时,f (x )取最小值-2.即x =2k π3-5π12(k ∈Z)时,f (x )取最小值-2.B 级——高考水平高分练1.函数f (x )=sin ⎝ ⎛⎭⎪⎫π6+x +cos ⎝ ⎛⎭⎪⎫π3-x 的最大值为( )A .1B .32C . 3D .2解析:选D 由π6+x 与π3-x 互余,得f (x )=2sin ⎝ ⎛⎭⎪⎫x +π6,故f (x )的最大值为2,故选D.2.已知ω>0,函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π3在⎝ ⎛⎭⎪⎫π2,π上单调递减,则ω的取值范围是________.解析:依题意得T 2≥π2⇒T ≥π,又ω>0,所以2πω≥π⇒0<ω≤2.由π2<x <π得ωπ2+π3<ωx +π3<ωπ+π3, 由f (x )在⎝ ⎛⎭⎪⎫π2,π上单调递减得⎩⎪⎨⎪⎧ωπ2+π3≥π2,ωπ+π3≤3π2⇒13≤ω≤76. 答案:⎣⎢⎡⎦⎥⎤13,763.若函数y =a -b sin x 的最大值为32,最小值为-12.(1)求a ,b 的值;(2)求函数y =-a sin x 取得最大值时x 的值.解:(1)当b >0时,⎩⎪⎨⎪⎧a +b =32,a -b =-12⇒⎩⎪⎨⎪⎧a =12,b =1.当b <0时,⎩⎪⎨⎪⎧a -b =32,a +b =-12⇒⎩⎪⎨⎪⎧a =12,b =-1.(2)由(1)知a =12,所以函数y =-a sin x =-12sin x ,所以当x =2k π-π2(k ∈Z)时,函数y =-a sin x 取得最大值.4.设函数f (x )=sin(2x +φ)(-π<φ<0),y =f (x )图象的一条对称轴是直线x =π8.(1)求φ;(2)求函数y =f (x )的单调增区间.解:(1)因为x =π8是函数y =f (x )图象的对称轴.所以sin ⎝ ⎛⎭⎪⎫2×π8+φ=±1,所以π4+φ=k π+π2(k ∈Z),得φ=k π+π4(k ∈Z).又因为-π<φ<0,所以φ=-3π4.(2)由(1)知φ=-3π4,则f (x )=sin ⎝ ⎛⎭⎪⎫2x -3π4. 由2k π-π2≤2x -3π4≤2k π+π2(k ∈Z),得k π+π8≤x ≤k π+5π8(k ∈Z),所以函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -3π4的单调增区间为⎣⎢⎡⎦⎥⎤k π+π8,k π+5π8(k ∈Z).5.定义在R 上的偶函数f (x )满足f (x +1)=-f (x ),且在[-4,-3]上是增函数,α,β是锐角三角形的两个内角,则f (sin α)与f (cos β)的大小关系是________.解析:由f (x +1)=-f (x ), 得f (x +2)=-f (x +1)=f (x ),所以函数f (x )是周期函数,且2是它的一个周期.因为函数f (x )是偶函数且在[-4,-3]上是增函数, 所以函数f (x )在[0,1]上是增函数.又α,β是锐角三角形的两个内角,则有α+β>π2,即π2>α>π2-β>0, 因为y =sin x 在⎣⎢⎡⎦⎥⎤0,π2上为增函数,所以sin α>sin ⎝ ⎛⎭⎪⎫π2-β=cos β, 且sin α∈[0,1],cos β∈[0,1], 所以f (sin α)>f (cos β). 答案:f (sin α)>f (cos β)。
正切函数的性质与图象 高一上学期数学人教A版(2019)必修第一册

观察正切曲线可知,正切函数在区间
,
上单调递增.由正切函数的周期性
可得,正切函数在每一个区间
k,
k
(k
Z)
上都单调递增.
当
x
,
时,
tan
x
在
(,
)
内可取到任意实数值,但没有最大值、最小值.
①定义域:把“
x
”作为一个整体,令
x
k
(k
Z)
,可得
x
的取值
范围,即得函数的定义域.
②值域: (, ) .
③单调区间:(a)把“x ( 0) ”作为一个整体;(b) A 0(A 0) 时,函数的
单调性与
y
tan
x
x
k
,
k
Z
的单调性相同(反);
(c)解不等式
k
x
k
(k
Z)
,得出
x
我们可以证 明一下吗?
正切函数周期证明:
(1)当
k
是偶函数时,
tan
x
kπ
sin x cos x
kπ kπ
sin cos
x x
tan
x
;
(2)当
k
是奇函数时,
tan
x
kπ
sin x cos x
kπ kπ
sin cos
x x
tan
x
;
综上,有 tan x kπ tan x ,其中 x R ,且 x π mπ,m Z, k Z
tan
9 4
tan
新教材高中数学第五章三角函数 正切函数的性质与图象学案含解析新人教A版必修第一册
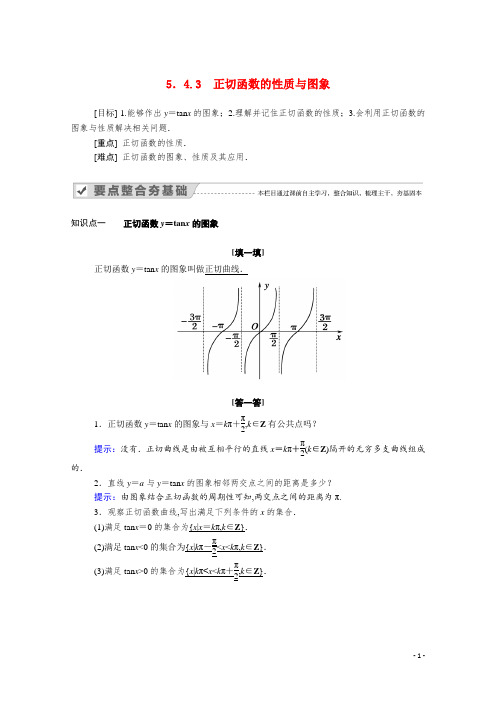
5.4.3 正切函数的性质与图象[目标] 1.能够作出y =tan x 的图象;2.理解并记住正切函数的性质;3.会利用正切函数的图象与性质解决相关问题.[重点] 正切函数的性质.[难点] 正切函数的图象、性质及其应用.知识点一 正切函数y =tan x 的图象[填一填]正切函数y =tan x 的图象叫做正切曲线.[答一答]1.正切函数y =tan x 的图象与x =k π+π2,k ∈Z 有公共点吗?提示:没有.正切曲线是由被互相平行的直线x =k π+π2(k ∈Z )隔开的无穷多支曲线组成的.2.直线y =a 与y =tan x 的图象相邻两交点之间的距离是多少? 提示:由图象结合正切函数的周期性可知,两交点之间的距离为π. 3.观察正切函数曲线,写出满足下列条件的x 的集合. (1)满足tan x =0的集合为{x |x =k π,k ∈Z }. (2)满足tan x <0的集合为{x |k π-π2<x <k π,k ∈Z }.(3)满足tan x >0的集合为{x |k π<x <k π+π2,k ∈Z }.知识点二 正切函数y =tan x 的性质[填一填](1)定义域是{x |x ≠k π+π2,k ∈Z }.(2)值域是R ,即正切函数既无最大值,也无最小值. (3)周期性:正切函数是周期函数,最小正周期是π. (4)奇偶性:正切函数是奇函数.(5)单调性:正切函数在开区间(k π-π2,k π+π2),k ∈Z 内是增函数.(6)对称性:正切函数的图象关于原点对称,正切曲线都是中心对称图形,其对称中心坐标是(k π2,0)(k ∈Z ),正切函数无对称轴.[答一答]4.y =tan x 在定义域上是增函数吗?提示:y =tan x 在每个开区间(-π2+k π,π2+k π),k ∈Z 内都是增函数,但在整个定义域上不具有单调性.5.正切函数图象与x 轴有无数个交点,交点的坐标为(k π,0)(k ∈Z ),因此有人说正切函数图象的对称中心为(k π,0)(k ∈Z ),这种说法对吗?提示:不对.正切函数的图象不仅仅关于点(k π,0)对称,还关于点(π2+k π,0)(k ∈Z )对称,因此正切函数y =tan x 的对称中心为(k π2,0)(k ∈Z ).类型一 利用正切函数图象求定义域及值域[例1] 求下列函数的定义域和值域: (1)y =tan ⎝⎛⎭⎫x +π4;(2)y =3-tan x .[解] (1)由x +π4≠k π+π2,k ∈Z 得,x ≠k π+π4,k ∈Z .所以函数y =tan ⎝⎛⎭⎫x +π4的定义域为{x ⎪⎪⎭⎬⎫x ≠k π+π4,k ∈Z ,其值域为(-∞,+∞). (2)由3-tan x ≥0得,tan x ≤ 3.结合y =tan x 的图象可知,在⎝⎛⎭⎫-π2,π2上,满足tan x ≤3的角x 应满足-π2<x ≤π3,所以函数y =3-tan x 的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪k π-π2<x ≤k π+π3,k ∈Z ,其值域为[0,+∞).(1)求与正切函数有关的函数定义域要列出使各部分都有意义的不等式(组),然后求出x 的范围.(2)求值域要用换元的思想,把tan x 看作可取任意实数的自变量.[变式训练1] (1)求函数y =tan x +1+lg(1-tan x )的定义域. (2)求函数y =sin x +tan x ,x ∈⎣⎡⎦⎤-π4,π4的值域. 解:(1)由题意得⎩⎪⎨⎪⎧tan x +1≥0,1-tan x >0,即-1≤tan x <1.∵在⎝⎛⎭⎫-π2,π2内,满足上述不等式的x 的取值范围是⎣⎡⎭⎫-π4,π4.又y =tan x 的周期为π,∴所求x 的取值范围是⎣⎡⎭⎫k π-π4,k π+π4,k ∈Z ,即为此函数的定义域. (2)y 1=sin x ,y 2=tan x 均满足在区间⎣⎡⎦⎤-π4,π4上单调递增,∴函数y =sin x +tan x 也满足在区间⎣⎡⎦⎤-π4,π4上单调递增, ∴此函数在⎣⎡⎦⎤-π4,π4上的值域为⎣⎡⎦⎤-22-1,22+1. 类型二 正切函数的周期性[例2] 求函数y =3tan ⎝⎛⎭⎫4x +π4与函数f (x )=tan x +|tan x |的最小正周期. [解] 函数y =3tan ⎝⎛⎭⎫4x +π4的最小正周期为T =π4; f (x )=tan x +|tan x |=⎩⎨⎧0,x ∈⎝⎛⎭⎫k π-π2,k π,2tan x ,x ∈⎣⎡⎭⎫k π,k π+π2,k ∈Z ,作出f (x )=tan x +|tan x |的简图,如图所示,易得函数f (x )=tan x +|tan x |的最小正周期T =π.一般地,函数y =A tan (ωx +φ)+B (A ≠0,ω>0)的最小正周期为T =πω,常常使用此公式来求周期,也可以借助函数图象求周期.[变式训练2] 若函数y =tan ⎝⎛⎭⎫3ax -π3(a ≠0)的最小正周期为π2,则a =±23. 解析:T =π|3a |=π2,所以a =±23.类型三 正切函数的单调性及应用[例3] (1)求函数y =tan ⎝⎛⎭⎫12x -π4的单调区间; (2)比较tan ⎝⎛⎭⎫-13π4与tan ⎝⎛⎭⎫-12π5的大小. [解] (1)由k π-π2<12x -π4<k π+π2,k ∈Z 得,2k π-π2<x <2k π+3π2,k ∈Z .所以函数y =tan ⎝⎛⎭⎫12x -π4的单调递增区间是⎝⎛⎭⎫2k π-π2,2k π+3π2,k ∈Z ,无单调递减区间. (2)由于tan ⎝⎛⎭⎫-13π4=tan ⎝⎛⎭⎫-3π-π4=tan ⎝⎛⎭⎫-π4=-tan π4, tan ⎝⎛⎭⎫-12π5=-tan ⎝⎛⎭⎫2π+2π5=-tan 2π5, 又0<π4<2π5<π2,而y =tan x 在⎝⎛⎭⎫0,π2上单调递增, 所以tan π4<tan 2π5,所以-tan π4>-tan 2π5,即tan ⎝⎛⎭⎫-13π4>tan ⎝⎛⎭⎫-12π5.(1)求函数y =A tan (ωx +φ)的单调性时可将ωx +φ看成一个整体,利用y =tan x 的单调性求解,但需注意A 、ω的正负性对函数单调性的影响.(2)比较正切值的大小时可利用诱导公式将角转化到区间⎝⎛⎭⎫-π2,π2内,再利用正切函数的单调性比较.[变式训练3] (1)函数y =3tan ⎝⎛⎭⎫π6-x 4的单调递减区间是⎝⎛⎭⎫4k π-4π3,4k π+8π3,k ∈Z . (2)比较大小:tan ⎝⎛⎭⎫-7π4>tan ⎝⎛⎭⎫-95π.解析:(1)y =3tan ⎝⎛⎭⎫π6-x 4=-3tan ⎝⎛⎭⎫x 4-π6,由k π-π2<x 4-π6<k π+π2,k ∈Z ,得4k π-4π3<x <4k π+8π3,k ∈Z . 所以y =3tan ⎝⎛⎭⎫π6-x 4的单调递减区间为⎝⎛⎭⎫4k π-4π3,4k π+8π3,k ∈Z . (2)∵tan ⎝⎛⎭⎫-74π=-tan ⎝⎛⎭⎫2π-π4=tan π4, tan ⎝⎛⎭⎫-95π=-tan ⎝⎛⎭⎫2π-π5=tan π5, 又0<π5<π4<π2,y =tan x 在⎝⎛⎭⎫0,π2内单调递增, ∴tan π5<tan π4,∴tan ⎝⎛⎭⎫-74π>tan ⎝⎛⎭⎫-95π. 类型四 正切函数图象与性质的综合应用[例4] 设函数f (x )=tan(ωx +φ)⎝⎛⎭⎫ω>0,0<φ<π2,已知函数y =f (x )的图象与x 轴相邻两个交点的距离为π2,且图象关于点M ⎝⎛⎭⎫-π8,0对称. (1)求f (x )的解析式; (2)求f (x )的单调区间;(3)求不等式-1≤f (x )≤3的解集.[解] (1)由题意,知函数f (x )的最小正周期T =π2,即π|ω|=π2.因为ω>0,所以ω=2. 从而f (x )=tan(2x +φ).因为函数y =f (x )的图象关于点M ⎝⎛⎭⎫-π8,0对称,所以2×⎝⎛⎭⎫-π8+φ=k π2,k ∈Z , 即φ=k π2+π4,k ∈Z .因为0<φ<π2,所以φ=π4.故f (x )=tan ⎝⎛⎭⎫2x +π4. (2)令-π2+k π<2x +π4<π2+k π,k ∈Z ,得-3π4+k π<2x <k π+π4,k ∈Z .即-3π8+k π2<x <π8+k π2,k ∈Z .所以函数的单调递增区间为⎝⎛-3π8+k π2,⎭⎫π8+k π2,k ∈Z ,无单调递减区间.(3)由(1),知f (x )=tan ⎝⎛⎭⎫2x +π4. 由-1≤tan ⎝⎛⎭⎫2x +π4≤3, 得-π4+k π≤2x +π4≤π3+k π,k ∈Z .即-π4+k π2≤x ≤π24+k π2,k ∈Z .所以不等式-1≤f (x )≤3的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪-π4+k π2≤x ≤π24+k π2,k ∈Z .(1)正切函数y =tan x 与x 轴相邻交点间的距离为一个周期;(2)y =tan x 的对称中心为⎝⎛⎭⎫k π2,0,不但包含y =tan x 的零点,而且包括直线x =π2+k π(k ∈Z )与x 轴的交点. [变式训练4] 已知函数y =tan(2x +θ)图象的一个对称中心为点⎝⎛⎭⎫π3,0,若-π2<θ<π2,求θ的值.解:因为函数y =tan x 图象的对称中心为点⎝⎛⎭⎫k π2,0,其中k ∈Z ,所以2x +θ=k π2,令x =π3,得θ=k π2-2π3,k ∈Z .又-π2<θ<π2,当k =1时,θ=-π6,当k =2时,θ=π3.所以θ=-π6或π3.1.若tan x ≥0,则( D ) A .2k π-π2<x <2k π(k ∈Z )B .x ≤(2k +1)π(k ∈Z )C .2k π-π2<x ≤k π(k ∈Z )D .k π≤x <k π+π2(k ∈Z )2.函数y =2tan ⎝⎛⎭⎫3x -π4的一个对称中心是( C ) A .⎝⎛⎭⎫π3,0 B .⎝⎛⎭⎫π6,0 C .⎝⎛⎭⎫-π4,0 D .⎝⎛⎭⎫-π2,0 解析:由3x -π4=k π2,得x =k π6+π12,令k =-2得x =-π4.故选C .3.函数y =1tan (π-x )是( A )A .奇函数B .偶函数C .既是奇函数也是偶函数D .非奇非偶函数4.使函数y =2tan x 与y =cos x 同时为单调增的区间是⎣⎡⎭⎫-π+2k π,-π2+2k π(k ∈Z )和⎝⎛⎦⎤-π2+2k π,2k π(k ∈Z ).解析:由y =2tan x 与y =cos x 的图象知,同时为单调增的区间为⎣⎡⎭⎫-π+2k π,-π2+2k π(k ∈Z )和⎝⎛⎦⎤-π2+2k π,2k π(k ∈Z ). 5.求函数y =tan(π-x ),x ∈⎝⎛⎭⎫-π4,π3的值域. 解:y =tan(π-x )=-tan x ,在⎝⎛⎭⎫-π4,π3上为减函数,所以值域为(-3,1).——本课须掌握的两大问题1.正切函数的图象正切函数有无数多条渐近线,渐近线方程为x =k π+π2,k ∈Z ,相邻两条渐近线之间都有一支正切曲线,且单调递增.2.正切函数的性质(1)正切函数y =tan x 的定义域是{x |x ≠k π+π2,k ∈Z },值域是R .(2)正切函数y =tan x 的最小正周期是π,函数y =A tan(ωx +φ)(Aω≠0)的周期为T =π|ω|. (3)正切函数在⎝⎛⎭⎫-π2+k π,π2+k π(k ∈Z )上单调递增,不能写成闭区间.正切函数无单调递减区间.。
(新教材)高中数学人教A必修第一册同步练习:5.4.3正切函数的性质与图象

由函数 f (x)= tan x 的图象可知 ,
函数在区间 确. 答案 AC
-
π
2,0
上有 f
??1+??2 2
>
??( ??1)
+??(??2) 2
,在区间
π
0,2
上有
f
??1+??2 2
<
??( ?1?
)+??(??2 2
),故
D
不正
2.在区间
(
-
3π,
2
3π
2)
范围内
,函数
y= tan x 与函数
√3
∴{
2
??=
-√3??,
1 ??=
2
-
√3
×(
√3 3
??)+
1.
??= 2??, 化简得 { 1
??= -??+ 1 ,
2
??= 1, 解得 { 1
??= 2 .
∴f(x)= sin
2x+ π
3
1
,φ(x) =2tan
π
2x- 3 .
k= 1,2 知 ②,③正确 ,④显然正确
.
答案 ①
π
6.是否存在实数 a,且 a∈ Z ,使得函数 y= tan 4-ax 在区间 值; 若不存在 ,请说明理由 .
π 5π
8, 8
上单调递增
?若存在 ,求出 a 的一个
解 y= tan
π
4 -ax
= tan
π
-ax+ 4 ,
∵y= tan x 在区间
解析 对
A, 令2x+π Nhomakorabea4≠
新人教版高中数学必修第一册 课时跟踪检测(三十九) 正切函数的性质与图象

课时跟踪检测(三十九) 正切函数的性质与图象A 级——学考合格性考试达标练1.当x ∈⎝⎛⎭⎫-π2,π2时,函数y =tan |x |的图象( )A .关于原点对称B .关于y 轴对称C .关于x 轴对称D .无法确定解析:选B 函数y =tan |x |,x ∈⎝⎛⎭⎫-π2,π2是偶函数.其图象关于y 轴对称.故 选B.2.函数y = tan x +1的定义域为( )A.⎣⎡⎭⎫k π-π4,k π+π4(k ∈Z ) B.⎣⎡⎭⎫k π-π4,k π+π2(k ∈Z ) C.⎣⎡⎭⎫k π-π3,k π+π2(k ∈Z ) D .⎣⎡⎭⎫k π-π4,+∞(k ∈Z ) 解析:选B 由题可得tan x +1≥0,即tan x ≥-1,解得x ∈⎣⎡⎭⎫k π-π4,k π+π2(k ∈Z ).3.已知函数f (x )=3tan ⎝⎛⎭⎫ωx -π4的最小正周期为π2,则正数ω=( ) A .4B .3C .2D .1解析:选C ∵ω>0,∴T =πω=π2,∴ω=2,故选C. 4.函数y =tan ⎝⎛⎭⎫12x -π3在一个周期内的图象是下图中的( )解析:选A 由函数周期T =π12=2π,排除选项B 、D . 将x =2π3代入函数式中,得tan ⎝⎛⎭⎫12×2π3-π3=tan 0=0.故函数图象与x 轴的一个交点为⎝⎛⎭⎫2π3,0.故选A. 5.与函数y =tan ⎝⎛⎭⎫2x +π4的图象不相交的一条直线是( ) A .x =π2B .y =π2C .x =π8D .y =π8 解析:选C 令2x +π4=k π+π2(k ∈Z ),得x =k π2+π8(k ∈Z ).令k =0,得x =π8. 6.函数y =tan ⎝⎛⎭⎫π4+6x 的定义域为________. 解析:由π4+6x ≠k π+π2(k ∈Z ),得x ≠k π6+π24(k ∈Z ). 答案:⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π6+π24,k ∈Z 7.函数y =tan ⎝⎛⎭⎫2x +π4的单调递增区间是___________________________________. 解析:令k π-π2<2x +π4<k π+π2,k ∈Z , 解得k π2-3π8<x <k π2+π8,k ∈Z . 答案:⎝⎛⎭⎫k π2-3π8,k π2+π8,k ∈Z 8.函数y =tan ⎝⎛⎭⎫x 2+π4,x ∈⎝⎛⎦⎤0,π6的值域是________. 解析:由0<x ≤π6得0<x 2≤π12,从而π4<x 2+π4≤π3. ∴tan π4<tan ⎝⎛⎭⎫x 2+π4≤tan π3, 即1<tan ⎝⎛⎭⎫x 2+π4≤ 3. 故填(1, 3 ].答案:(1, 3 ]9.判断下列函数的奇偶性.(1)f (x )=tan 2x -tan x 1-tan x; (2)f (x )=x tan 2x +x 4.解:(1)由⎩⎪⎨⎪⎧x ≠k π+π2(k ∈Z ),tan x ≠1得 x ≠k π+π2且x ≠k π+π4(k ∈Z ). 即定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π+π2且x ≠k π+π4,k ∈Z , 不关于原点对称,所以函数既不是奇函数,也不是偶函数.(2)函数定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π4,k ∈Z ,关于原点对称. 又f (-x )=(-x )tan[2(-x )]+(-x )4=x tan 2x +x 4=f (x ),所以函数是偶函数.10.比较下列两个正切值的大小:(1)tan 167°,tan 173°;(2)tan ⎝⎛⎭⎫-11π4,tan ⎝⎛⎭⎫-13π5. 解:(1)因为90°<167°<173°<180°,y =tan x 在(90°,180°)上为增函数.所以tan 167°<tan 173°.(2)因为tan ⎝⎛⎭⎫-11π4=tan π4, tan ⎝⎛⎭⎫-13π5=tan 2π5, 且0<π4<2π5<π2,y =tan x 在⎝⎛⎭⎫0,π2上为增函数, 所以tanπ4<tan 2π5, 即tan ⎝⎛⎭⎫-11π4<tan ⎝⎛⎭⎫-13π5. B 级——面向全国卷高考高分练1.函数y =3tan ⎝⎛⎭⎫12x +π3的图象的一个对称中心是( ) A.⎝⎛⎭⎫π6,0 B .⎝⎛⎭⎫2π3,-33 C.⎝⎛⎭⎫-2π3,0 D .(0,0)解析:选C 因为y =tan x 的图象的对称中心为⎝⎛⎭⎫k π2,0,k ∈Z .由12x +π3=k π2,k ∈Z ,得x =k π-2π3,k ∈Z ,所以函数y =3tan ⎝⎛⎭⎫12x +π3的图象的对称中心是⎝⎛⎭⎫k π-2π3,0,k ∈Z .令k =0,得⎝⎛⎭⎫-2π3,0.2.函数y =tan(cos x )的值域是( )A .⎣⎡⎦⎤-π4,π4 B .⎣⎡⎦⎤-22,22 C .[-tan 1,tan 1] D .以上均不对解析:选C ∵-1≤cos x ≤1,且函数y =tan x 在[-1,1]上为增函数,∴tan(-1)≤tan x ≤tan 1.即-tan 1≤tan x ≤tan 1.3.已知函数f (x )=x +tan x +1,若f (a )=2,则f (-a )=( )A .0B .-1C .-2D .3解析:选A 设g (x )=x +tan x ,显然g (x )为奇函数.∵f (a )=g (a )+1=2,∴g (a )=1,∴f (-a )=g (-a )+1=-g (a )+1=0.故选A.4.已知函数f (x )=tan ωx (ω>0)的图象的相邻两支截直线y =π4所得线段长为π4,则f ⎝⎛⎭⎫π4的值是( ) A .0B .-33C .-1D . 3解析:选A 由题意,可知T =π4,所以ω=ππ4=4,即f (x )=tan 4x ,所以f ⎝⎛⎭⎫π4=tan π=0.5.函数y =tan x 2满足下列哪些条件________(填序号). ①在⎝⎛⎭⎫0,π2上单调递增; ②为奇函数;③以π为最小正周期;④定义域为⎩⎨⎧x ⎪⎪⎭⎬⎫x ≠π4+k π2,k ∈Z . 解析:令x ∈⎝⎛⎭⎫0,π2,则x 2∈⎝⎛⎭⎫0,π4,所以y =tan x 2在⎝⎛⎭⎫0,π2上单调递增正确; tan ⎝⎛⎭⎫-x 2=-tan x 2,故y =tan x 2为奇函数; T =πω=2π,所以③不正确;由x 2≠π2+k π,k ∈Z ,得{x |x ≠π+2k π,k ∈Z },所以④不正确. 答案:①②6.若tan x >tan π5且x 在第三象限,则x 的取值范围是________. 解析:∵tan x >tan π5=tan 6π5,又x 为第三象限角, ∴2k π+6π5<x <2k π+3π2(k ∈Z ). 答案:⎝⎛⎭⎫2k π+6π5,2k π+3π2(k ∈Z ) 7.设函数f (x )=tan ⎝⎛⎭⎫x 2-π3. (1)求函数的定义域;(2)求不等式f (x )≤ 3的解集.解:(1)根据函数f (x )=tan ⎝⎛⎭⎫x 2-π3,可得x 2-π3≠k π+π2,k ∈Z ,得x ≠2k π+5π3, k ∈Z .故函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠2k π+5π3,k ∈Z . (2)求不等式f (x )≤ 3,即tan ⎝⎛⎭⎫x 2-π3≤ 3, 所以k π-π2<x 2-π3≤k π+π3,k ∈Z , 求得2k π-π3<x ≤2k π+4π3,k ∈Z , 故不等式的解集为⎝⎛⎦⎤2k π-π3,2k π+4π3,k ∈Z . 8.设函数f (x )=tan ⎝⎛⎭⎫x 2-π3. (1)求函数f (x )的最小正周期,图象的对称中心;(2)作出函数f (x )在一个周期内的简图.解:(1)∵ω=12,∴最小正周期T =πω=π12=2π. 令x 2-π3=k π2(k ∈Z ),得x =k π+2π3(k ∈Z ), ∴f (x )的图象的对称中心是⎝⎛⎭⎫k π+2π3,0(k ∈Z ). (2)令x 2-π3=0,得x =2π3;令x 2-π3=π2,得x =5π3;令x 2-π3=-π2,得x =-π3. ∴函数f (x )=tan ⎝⎛⎭⎫x 2-π3的图象与x 轴的一个交点坐标是⎝⎛⎭⎫2π3,0,在这个交点左、右两侧相邻的两条渐近线方程分别是x =-π3,x =5π3,从而得到函数y =f (x )在一个周期⎝⎛⎭⎫-π3,5π3内的简图,如图所示. C 级——拓展探索性题目应用练已知f (x )=tan ⎝⎛⎭⎫2x +π3, (1)求f (x )的最小正周期;(2)若f (x +φ)是奇函数,则φ应满足什么条件?并求出满足|φ|<π2的φ值. 解:(1)法一:∵y =tan x 的最小正周期是π.∴y =tan ⎝⎛⎭⎫2x +π3的最小正周期是π2. 法二:由诱导公式知:tan ⎣⎡⎦⎤⎝⎛⎭⎫2x +π3+π =tan ⎣⎡⎦⎤2⎝⎛⎭⎫x +π2+π3=tan ⎝⎛⎭⎫2x +π3, 即f ⎝⎛⎭⎫x +π2=f (x ). ∴f (x )的最小正周期是π2. (2)∵f (x +φ)=tan ⎝⎛⎭⎫2x +π3+2φ是奇函数, ∴图象关于原点中心对称,∴π3+2φ=k π2(k ∈Z ),∴φ=k π4-π6(k ∈Z ). 令⎪⎪⎪⎪k π4-π6<π2(k ∈Z ), 解得-43<k <83,k ∈Z . ∴k =-1,0,1,2.从而得φ=-5π12,-π6,π12,π3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时跟踪检测(三十九) 正切函数的性质与图象A 级——学考合格性考试达标练1.当x ∈⎝⎛⎭⎫-π2,π2时,函数y =tan |x |的图象( )A .关于原点对称B .关于y 轴对称C .关于x 轴对称D .无法确定解析:选B 函数y =tan |x |,x ∈⎝⎛⎭⎫-π2,π2是偶函数.其图象关于y 轴对称.故 选B.2.函数y = tan x +1的定义域为( )A.⎣⎡⎭⎫k π-π4,k π+π4(k ∈Z ) B.⎣⎡⎭⎫k π-π4,k π+π2(k ∈Z ) C.⎣⎡⎭⎫k π-π3,k π+π2(k ∈Z ) D .⎣⎡⎭⎫k π-π4,+∞(k ∈Z ) 解析:选B 由题可得tan x +1≥0,即tan x ≥-1,解得x ∈⎣⎡⎭⎫k π-π4,k π+π2(k ∈Z ).3.已知函数f (x )=3tan ⎝⎛⎭⎫ωx -π4的最小正周期为π2,则正数ω=( ) A .4B .3C .2D .1解析:选C ∵ω>0,∴T =πω=π2,∴ω=2,故选C. 4.函数y =tan ⎝⎛⎭⎫12x -π3在一个周期内的图象是下图中的( )解析:选A 由函数周期T =π12=2π,排除选项B 、D . 将x =2π3代入函数式中,得tan ⎝⎛⎭⎫12×2π3-π3=tan 0=0.故函数图象与x 轴的一个交点为⎝⎛⎭⎫2π3,0.故选A. 5.与函数y =tan ⎝⎛⎭⎫2x +π4的图象不相交的一条直线是( ) A .x =π2B .y =π2C .x =π8D .y =π8 解析:选C 令2x +π4=k π+π2(k ∈Z ),得x =k π2+π8(k ∈Z ).令k =0,得x =π8. 6.函数y =tan ⎝⎛⎭⎫π4+6x 的定义域为________. 解析:由π4+6x ≠k π+π2(k ∈Z ),得x ≠k π6+π24(k ∈Z ). 答案:⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π6+π24,k ∈Z 7.函数y =tan ⎝⎛⎭⎫2x +π4的单调递增区间是___________________________________. 解析:令k π-π2<2x +π4<k π+π2,k ∈Z , 解得k π2-3π8<x <k π2+π8,k ∈Z . 答案:⎝⎛⎭⎫k π2-3π8,k π2+π8,k ∈Z 8.函数y =tan ⎝⎛⎭⎫x 2+π4,x ∈⎝⎛⎦⎤0,π6的值域是________. 解析:由0<x ≤π6得0<x 2≤π12,从而π4<x 2+π4≤π3. ∴tan π4<tan ⎝⎛⎭⎫x 2+π4≤tan π3, 即1<tan ⎝⎛⎭⎫x 2+π4≤ 3. 故填(1, 3 ].答案:(1, 3 ]9.判断下列函数的奇偶性.(1)f (x )=tan 2x -tan x 1-tan x; (2)f (x )=x tan 2x +x 4.解:(1)由⎩⎪⎨⎪⎧x ≠k π+π2(k ∈Z ),tan x ≠1得 x ≠k π+π2且x ≠k π+π4(k ∈Z ). 即定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π+π2且x ≠k π+π4,k ∈Z , 不关于原点对称,所以函数既不是奇函数,也不是偶函数.(2)函数定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π4,k ∈Z ,关于原点对称. 又f (-x )=(-x )tan[2(-x )]+(-x )4=x tan 2x +x 4=f (x ),所以函数是偶函数.10.比较下列两个正切值的大小:(1)tan 167°,tan 173°;(2)tan ⎝⎛⎭⎫-11π4,tan ⎝⎛⎭⎫-13π5. 解:(1)因为90°<167°<173°<180°,y =tan x 在(90°,180°)上为增函数.所以tan 167°<tan 173°.(2)因为tan ⎝⎛⎭⎫-11π4=tan π4, tan ⎝⎛⎭⎫-13π5=tan 2π5, 且0<π4<2π5<π2,y =tan x 在⎝⎛⎭⎫0,π2上为增函数, 所以tanπ4<tan 2π5, 即tan ⎝⎛⎭⎫-11π4<tan ⎝⎛⎭⎫-13π5. B 级——面向全国卷高考高分练1.函数y =3tan ⎝⎛⎭⎫12x +π3的图象的一个对称中心是( ) A.⎝⎛⎭⎫π6,0 B .⎝⎛⎭⎫2π3,-33 C.⎝⎛⎭⎫-2π3,0 D .(0,0)解析:选C 因为y =tan x 的图象的对称中心为⎝⎛⎭⎫k π2,0,k ∈Z .由12x +π3=k π2,k ∈Z ,得x =k π-2π3,k ∈Z ,所以函数y =3tan ⎝⎛⎭⎫12x +π3的图象的对称中心是⎝⎛⎭⎫k π-2π3,0,k ∈Z .令k =0,得⎝⎛⎭⎫-2π3,0. 2.函数y =tan(cos x )的值域是( )A .⎣⎡⎦⎤-π4,π4 B .⎣⎡⎦⎤-22,22 C .[-tan 1,tan 1] D .以上均不对解析:选C ∵-1≤cos x ≤1,且函数y =tan x 在[-1,1]上为增函数,∴tan(-1)≤tan x ≤tan 1.即-tan 1≤tan x ≤tan 1.3.已知函数f (x )=x +tan x +1,若f (a )=2,则f (-a )=( )A .0B .-1C .-2D .3解析:选A 设g (x )=x +tan x ,显然g (x )为奇函数.∵f (a )=g (a )+1=2,∴g (a )=1,∴f (-a )=g (-a )+1=-g (a )+1=0.故选A.4.已知函数f (x )=tan ωx (ω>0)的图象的相邻两支截直线y =π4所得线段长为π4,则f ⎝⎛⎭⎫π4的值是( ) A .0B .-33C .-1D . 3解析:选A 由题意,可知T =π4,所以ω=ππ4=4,即f (x )=tan 4x ,所以f ⎝⎛⎭⎫π4=tan π=0.5.函数y =tan x 2满足下列哪些条件________(填序号). ①在⎝⎛⎭⎫0,π2上单调递增; ②为奇函数;③以π为最小正周期;④定义域为⎩⎨⎧x ⎪⎪⎭⎬⎫x ≠π4+k π2,k ∈Z . 解析:令x ∈⎝⎛⎭⎫0,π2,则x 2∈⎝⎛⎭⎫0,π4, 所以y =tan x 2在⎝⎛⎭⎫0,π2上单调递增正确;tan ⎝⎛⎭⎫-x 2=-tan x 2,故y =tan x 2为奇函数; T =πω=2π,所以③不正确;由x 2≠π2+k π,k ∈Z ,得{x |x ≠π+2k π,k ∈Z },所以④不正确. 答案:①②6.若tan x >tan π5且x 在第三象限,则x 的取值范围是________. 解析:∵tan x >tan π5=tan 6π5,又x 为第三象限角, ∴2k π+6π5<x <2k π+3π2(k ∈Z ). 答案:⎝⎛⎭⎫2k π+6π5,2k π+3π2(k ∈Z ) 7.设函数f (x )=tan ⎝⎛⎭⎫x 2-π3. (1)求函数的定义域;(2)求不等式f (x )≤ 3的解集.解:(1)根据函数f (x )=tan ⎝⎛⎭⎫x 2-π3,可得x 2-π3≠k π+π2,k ∈Z ,得x ≠2k π+5π3, k ∈Z .故函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠2k π+5π3,k ∈Z . (2)求不等式f (x )≤ 3,即tan ⎝⎛⎭⎫x 2-π3≤ 3, 所以k π-π2<x 2-π3≤k π+π3,k ∈Z , 求得2k π-π3<x ≤2k π+4π3,k ∈Z , 故不等式的解集为⎝⎛⎦⎤2k π-π3,2k π+4π3,k ∈Z . 8.设函数f (x )=tan ⎝⎛⎭⎫x 2-π3. (1)求函数f (x )的最小正周期,图象的对称中心;(2)作出函数f (x )在一个周期内的简图.解:(1)∵ω=12,∴最小正周期T =πω=π12=2π.令x 2-π3=k π2(k ∈Z ),得x =k π+2π3(k ∈Z ), ∴f (x )的图象的对称中心是⎝⎛⎭⎫k π+2π3,0(k ∈Z ). (2)令x 2-π3=0,得x =2π3;令x 2-π3=π2,得x =5π3;令x 2-π3=-π2,得x =-π3. ∴函数f (x )=tan ⎝⎛⎭⎫x 2-π3的图象与x 轴的一个交点坐标是⎝⎛⎭⎫2π3,0,在这个交点左、右两侧相邻的两条渐近线方程分别是x =-π3,x =5π3,从而得到函数y =f (x )在一个周期⎝⎛⎭⎫-π3,5π3内的简图,如图所示.C 级——拓展探索性题目应用练已知f (x )=tan ⎝⎛⎭⎫2x +π3, (1)求f (x )的最小正周期;(2)若f (x +φ)是奇函数,则φ应满足什么条件?并求出满足|φ|<π2的φ值. 解:(1)法一:∵y =tan x 的最小正周期是π.∴y =tan ⎝⎛⎭⎫2x +π3的最小正周期是π2. 法二:由诱导公式知:tan ⎣⎡⎦⎤⎝⎛⎭⎫2x +π3+π =tan ⎣⎡⎦⎤2⎝⎛⎭⎫x +π2+π3=tan ⎝⎛⎭⎫2x +π3, 即f ⎝⎛⎭⎫x +π2=f (x ). ∴f (x )的最小正周期是π2. (2)∵f (x +φ)=tan ⎝⎛⎭⎫2x +π3+2φ是奇函数, ∴图象关于原点中心对称,∴π3+2φ=k π2(k ∈Z ), ∴φ=k π4-π6(k ∈Z ).令⎪⎪⎪⎪k π4-π6<π2(k ∈Z ), 解得-43<k <83,k ∈Z . ∴k =-1,0,1,2.从而得φ=-5π12,-π6,π12,π3.。
