初中数学几何复习专题1
专题01 最短路径问题1 (原卷版)-初中数学几何专题之冲刺2022年满分突破大全
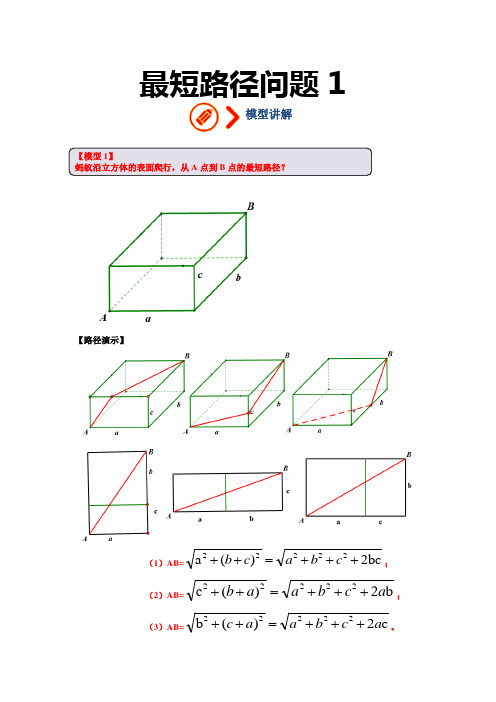
【模型1】蚂蚁沿立方体的表面爬行,从A点到B点的最短路径?【路径演示】(1)AB=bc2)(a22222+++=++cbacb;(2)AB=b2)(c22222acbaab+++=++;(3)AB=c2)(b22222acbaac+++=++。
模型讲解1由此可见,ab 、bc 、ac 谁小,则路径就最小。
【结论】 最短路径=22)(次长边最短边最长边++【模型2】 蚂蚁沿圆柱体的表面爬行,从A 点到C 点的最短路径?【路径演示】由图可知蚂蚁爬行的最短路径AC=22h )(+r π方法点拨一、解决方法:①确定水平方向移动路程②确定竖直方向移动路程③利用勾股定理求解二、方法解析:如图:点从点A出发到C点,可以看成先从A到D(水平移动),再由D到C(竖直移动)两个步骤完成例题演练1.如图,一个长方体的长宽高分别是6米、3米、2米,一只蚂蚁沿长方体的表面从点A 到点C'所经过的最短路线长为()A .B .C .D.以上都不对【解答】解:如图所示,路径一:AC ′==;路径二:AC ′==;路径三:AC ′==;∵61<73<85,∴为最短路径.故选:C.2.如图,圆柱体盒子放在水平地面上,该圆柱体的高为9cm,点M离盒底的距离为3cm,底面半径为cm,一只蚂蚁沿着该圆柱体盒子的表面从点M爬行到点N,则该蚂蚁爬行的最短路程为()cm.A.6B.10C.D.【解答】解:把圆柱侧面展开,展开图如右图所示,点M,N的最短距离为线段MN的长,∵AM=9﹣3=6(cm),AN为底面半圆弧长,AN=•π=8(cm),在Rt△AMN中,MN===10(cm).故选:B.3.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.则这只蚂蚁沿着台阶面爬行的最短路程是()A.18B.15C.12D.8【解答】解:将台阶展开,如图,因为AC=3×3+1×3=12,BC=9,所以AB2=AC2+BC2=225,所以AB=15,所以蚂蚁爬行的最短线路为15.故选:B.强化训练1.如图,长方体的高为9cm,底边是边长为6cm的正方形,一只美丽的蝴蝶从顶点A开始,爬向顶点B,那么它爬行的最短路程为()A.10cm B.12cm C.15cm D.20cm2.如图,有一长方体容器,AB=3,BC=2,AA'=4,一只蚂蚁沿长方体的表面,从点C 爬到点A'的最短爬行距离是()A .B .C.7D .3.如图所示是一个长方体纸盒,纸盒的长为12cm,宽为9cm,高为5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点G,蚂蚁爬行的最短路程是cm.4.有一长、宽、高分别是5cm,4cm,4cm的长方体木块,一只蚂蚁沿如图所示路径从顶点A处在长方体的表面爬到长方体上和A相对的棱的中点B处,则需要爬行的最短路径长为()A.cm B.cm C.cm D.cm5.如图,长方体的长EF为3cm,宽AE为2cm,高CE为4cm,B是GF的中点,一只蚂蚁如果要沿着长方体的表面从点D爬到点B,那么它需要爬行的最短距离是()A.5cm B.cm C.(2+3)cm D.(2+)cm6.如图,桌面上的长方体长为8,宽为6,高为4,B为CD的中点.一只蚂蚁从A点出发沿长方体的表面到达B点,则它运动的最短路程为()A.B.C.10 D.7.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为()A.20cm B.2cm C.(12+2)cm D.18cm8.如图,圆柱的底面周长为16,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC 的中点S,则移动的最短距离为()A.10B.12C.14D.209.如图,有一圆柱形油罐,要以A点环绕油罐建梯子,正好到A点的正上方B点,则梯子最短需m(油罐底面圆的周长为15m,高AB=8m).10.如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是()A.10B.50C.120D.13011.如图是一个三级台阶,它的每一级的长、宽、高分别等于55dm、10dm和6dm,A和B 是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁从A点出发沿着台阶爬到B点的最短距离是dm.12.如图是一个三级台阶,每级台阶都是长、宽和高分别等于90cm,25cm和15cm的长方体,A和B是这个台阶的两个相对的端点.在A点处有一只蚂蚁,想到B点去吃可口的食物,请你算一算,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短路程是多少?13.(2018•黄冈)如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为cm(杯壁厚度不计).。
初中数学几何图形初步知识点总复习含解析(1)

初中数学几何图形初步知识点总复习含解析(1)一、选择题1.如图将两块三角板的直角顶点重叠在一起,DOB ∠与DOA ∠的比是2:11,则BOC ∠的度数为( )A .45︒B .60︒C .70︒D .40︒【答案】C【解析】【分析】 设∠DOB=2x ,则∠DOA=11x ,可推导得到∠AOB=9x=90°,从而得到角度大小【详解】∵∠DOB 与∠DOA 的比是2:11∴设∠DOB=2x ,则∠DOA=11x∴∠AOB=9x∵∠AOB=90°∴x=10°∴∠BOD=20°∴∠COB=70°故选:C【点睛】本题考查角度的推导,解题关键是引入方程思想,将角度推导转化为计算的过程,以便简化推导2.∠1与∠2互余,∠1与∠3互补,若∠3=125°,则∠2=( )A .35°B .45°C .55°D .65°【答案】A【解析】【分析】【详解】解:根据题意得:∠1+∠3=180°,∠3=125°,则∠1=55°,∵∠1+∠2=90°,则∠2=35° 故选:A .【点睛】本题考查余角、补角的计算.3.将一副三角板如下图放置,使点A 落在DE 上,若BC DE P ,则AFC ∠的度数为( )A .90°B .75°C .105°D .120°【答案】B【解析】【分析】 根据平行线的性质可得30E BCE ==︒∠∠,再根据三角形外角的性质即可求解AFC ∠的度数.【详解】∵//BC DE∴30E BCE ==︒∠∠∴453075AFC B BCE =+=︒+︒=︒∠∠∠故答案为:B .【点睛】本题考查了三角板的角度问题,掌握平行线的性质、三角形外角的性质是解题的关键.4.下列立体图形中,侧面展开图是扇形的是()A .B .C .D.【答案】B【解析】根据圆锥的特征可知,侧面展开图是扇形的是圆锥.故选B.5.如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是()A.B.C.D.【答案】C【解析】【分析】分三种情况讨论,即可得到直角三角形绕一条边所在直线旋转一周后形成的几何体.【详解】解:将直角三角形绕较长直角边所在直线旋转一周后形成的几何体为:将直角三角形绕较短直角边所在直线旋转一周后形成的几何体为:将直角三角形绕斜边所在直线旋转一周后形成的几何体为:故选C .【点睛】本题考查了面动成体,点、线、面、体组成几何图形,点、线、面、体的运动组成了多姿多彩的图形世界.6.一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是()A .中B .考C .顺D .利【答案】C【解析】试题解析:正方体的表面展开图,相对的面之间一定相隔一个正方形,“祝”与“考”是相对面,“你”与“顺”是相对面,“中”与“立”是相对面.故选C .考点:正方体展开图.7.如果圆柱的母线长为5cm ,底面半径为2cm ,那么这个圆柱的侧面积是( )A .10cm 2B .10πcm 2C .20cm 2D .20πcm 2【答案】D【解析】【分析】根据圆柱的侧面积=底面周长×高.【详解】根据圆柱的侧面积计算公式可得π×2×2×5=20πcm 2,故选D .【点睛】本题考查了圆柱的计算,解题的关键是熟练掌握圆柱侧面积公式.8.下列图形中1∠与2∠不相等的是( )A.B.C.D.【答案】B【解析】【分析】根据对顶角,平行线,等角的余角相等等知识一一判断即可.【详解】解:A、根据对顶角相等可知,∠1=∠2,本选项不符合题意.B、∵∠1+∠2=90°,∠1与∠2不一定相等,本选项符合题意.C.根据平行线的性质可知:∠1=∠2,本选项不符合题意.D、根据等角的余角相等,可知∠1=∠2,本选项不符合题意.故选:B.【点睛】本题考查平行线的性质对顶角的性质,等角的余角相等等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.9.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为()A.1 B.2 C.3 D.4【答案】C【解析】试题分析:作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.∴EP+FP=EP+F′P.由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.∵四边形ABCD为菱形,周长为12,∴AB=BC=CD=DA=3,AB∥CD,∵AF=2,AE=1,∴DF=AE=1,∴四边形AEF′D 是平行四边形,∴EF ′=AD=3.∴EP+FP 的最小值为3.故选C .考点:菱形的性质;轴对称-最短路线问题10.如图,在ABC V 中,90C ∠=︒,AD 是BAC ∠的平分线,O 是AB 上一点,以OA 为半径的O e 经过点D .若5BD =,3DC =,则AC 的长为( )A .6B .43C .532-D .8【答案】A【解析】【分析】 过点D 作DE AB ⊥于E ,可证ADE ADC △△≌,所以AE AC =,3DE DC ==.又5BD =,利用勾股定理可求得4BE =.设AC AE x ==.因为90C ∠=︒,再利用勾股定理列式求解即可.【详解】解:过点D 作DE AB ⊥于E ,∵90C ∠=︒,AD 是BAC ∠的平分线,∴ADE ADC △△≌,∴AE AC =,3DE DC ==.∵5BD =,∴4BE =,设AC AE x ==.因为90C ∠=︒,∴由勾股定理可得222BC AC AB +=,即2228(4)x x +=+,解得6x =,即6AC =.故选:A .【点睛】本题主要考查圆的相关知识.掌握角平分线的性质以及熟练应用勾股定理是解此题的关键.11.如图,小慧从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20°方向行走至C 处,此时需要将方向调整到与出发时一致,则方向的调整应为( )A .左转80°B .右转80°C .左转100°D .右转100°【答案】B【解析】【分析】 如图,延长AB 到D ,过C 作CE//AD ,由题意可得∠A=60°,∠1=20°,根据平行线的性质可得∠A=∠2,∠3=∠1+∠2,进而可得答案.【详解】如图,延长AB 到D ,过C 作CE//AD ,∵此时需要将方向调整到与出发时一致,∴此时沿CE 方向行走,∵从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20°方向行走至C 处, ∴∠A=60°,∠1=20°,AM ∥BN ,CE ∥AB ,∴∠A=∠2=60°,∠1+∠2=∠3∴∠3=∠1+∠2=20°+60°=80°,∴应右转80°.故选B.【点睛】本题考查了方向角有关的知识及平行线的性质,解答时要注意以北方为参照方向,进行角度调整.12.已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数是()A.20°B.22°C.28°D.38°【答案】B【解析】【分析】过C作CD∥直线m,根据平行线的性质即可求出∠2的度数.【详解】解:过C作CD∥直线m,∵∠ABC=30°,∠BAC=90°,∴∠ACB=60°,∵直线m∥n,∴CD∥直线m∥直线n,∴∠1=∠ACD,∠2=∠BCD,∵∠1=38°,∴∠ACD=38°,∴∠2=∠BCD=60°﹣38°=22°,故选:B.【点睛】本题考查了平行线的计算问题,掌握平行线的性质是解题的关键.13.如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离()cm.A.14 B.15 C.16 D.17【答案】B【解析】【分析】在侧面展开图中,过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则AP+PC就是蚂蚁到达蜂蜜的最短距离,求出A′Q,CQ,根据勾股定理求出A′C 即可.【详解】解:沿过A的圆柱的高剪开,得出矩形EFGH,过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则AP+PC就是蚂蚁到达蜂蜜的最短距离,∵AE=A′E,A′P=AP,∴AP+PC=A′P+PC=A′C,∵CQ=12×18cm=9cm,A′Q=12cm﹣4cm+4cm=12cm,在Rt△A′QC中,由勾股定理得:A′C22129=15cm,故选:B.【点睛】本题考查了圆柱的最短路径问题,掌握圆柱的侧面展开图、勾股定理是解题的关键.14.如图:点 C 是线段 AB 上的中点,点 D 在线段 CB 上,若AD=8,DB=3AD 4,则CD 的长为( )A .4B .3C .2D .1 【答案】D【解析】【分析】根据线段成比例求出DB 的长度,即可得到AB 的长度,再根据中点平分线段的长度可得AC 的长度,根据CD AD AC =-即可求出CD 的长度.【详解】∵38,4AD DB AD ==∴6DB =∴14AB AD DB =+=∵点 C 是线段 AB 上的中点∴172AC AB == ∴1CD AD AC =-=故答案为:D .【点睛】本题考查了线段的长度问题,掌握成比例线段的性质、中点平分线段的长度是解题的关键.15.如图,在ABC V 中,90C ∠=︒,30B ∠=︒,如图:(1)以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ;(2)分别以M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ;(3)连结AP 并延长交BC 于点D .根据以上作图过程,下列结论中错误的是( )A .AD 是BAC ∠的平分线B .60ADC ∠=︒ C .点D 在AB 的中垂线上D .:1:3DAC ABD S S =△△【答案】D【解析】【分析】 根据作图的过程可以判定AD 是∠BAC 的角平分线;利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC 的度数;利用等角对等边可以证得△ADB 的等腰三角形,由等腰三角形的“三线合一”的性质可以证明点D 在AB 的中垂线上;利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.【详解】解:A 、根据作图方法可得AD 是∠BAC 的平分线,正确;B 、∵∠C=90°,∠B=30°,∴∠CAB=60°,∵AD 是∠BAC 的平分线,∴∠DAC=∠DAB=30°,∴∠ADC=60°,正确;C 、∵∠B=30°,∠DAB=30°,∴AD=DB ,∴点D 在AB 的中垂线上,正确;D 、∵∠CAD=30°,∴CD=12AD , ∵AD=DB , ∴CD=12DB , ∴CD=13CB , S △ACD =12CD•AC ,S △ACB =12CB•AC , ∴S △ACD :S △ACB =1:3,∴S △DAC :S △ABD ≠1:3,错误,故选:D .【点睛】本题考查了角平分线的性质、线段垂直平分线的性质以及作图—基本作图.解题时,需要熟悉等腰三角形的判定与性质.16.一个角的补角比这个角的余角3倍还多10°,则这个角的度数为()A.140° B.130° C.50° D.40°【答案】C【解析】【分析】根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°,列出方程,然后解方程即可.【详解】设这个角为α,则它的余角为90°-α,补角为180°-α,根据题意得,180°-α=3(90°-α)+10°,180°-α=270°-3α+10°,解得α=50°.故选C.【点睛】本题考查了互为余角与补角的性质,表示出这个角的余角与补角然后列出方程是解题的关键.17.用一副三角板(两块)画角,能画出的角的度数是()A.145C o B.95C o C.115C o D.105C o【答案】D【解析】【分析】一副三角板由两个三角板组成,其中一个三角板的度数有45°、45°、90°,另一个三角板的度数有30°、60°、90°,将两个三角板各取一个角度相加,和等于选项中的角度即可拼成.【详解】选项的角度数中个位是5°,故用45°角与另一个三角板的三个角分别相加,结果分别为:45°+30°=75°,45°+60°=105°,45°+90°=135°,故选:D.【点睛】此题主要考查学生对角的计算这一知识点的理解和掌握,解答此题的关键是分清两块三角板的锐角的度数分别是多少,比较简单,属于基础题.18.如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为()A.圆锥,正方体,三棱锥,圆柱B.圆锥,正方体,四棱锥,圆柱C.圆锥,正方体,四棱柱,圆柱D.正方体,圆锥,圆柱,三棱柱【答案】D【解析】【分析】根据常见的几何体的展开图进行判断,即可得出结果.【详解】根据几何体的平面展开图,则从左到右,其对应的几何体名称分别为:正方体,圆锥,圆柱,三棱柱.故选D.【点睛】本题考查了常见几何体的展开图;熟记常见几何体的平面展开图的特征,是解题的关键.19.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=12∠CGE.其中正确的结论是( )A.②③B.①②④C.①③④D.①②③④【答案】B【解析】【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案.【详解】①∵EG∥BC,∴∠CEG=∠ACB,又∵CD是△ABC的角平分线,∴∠CEG=∠ACB=2∠DCB,故正确;②∵∠A=90°,∴∠ADC+∠ACD=90°,∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠ADC+∠BCD=90°.∵EG∥BC,且CG⊥EG,∴∠GCB=90°,即∠GCD+∠BCD=90°,∴∠ADC=∠GCD,故正确;③条件不足,无法证明CA平分∠BCG,故错误;④∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,∴∠AEB+∠ADC=90°+12(∠ABC+∠ACB)=135°,∴∠DFE=360°-135°-90°=135°,∴∠DFB=45°=12∠CGE,,正确.故选B.【点睛】本题主要考查了角平分线的定义,平行线的性质,三角形内角和定理及多边形内角和,三角形外角的性质,熟知直角三角形的两锐角互余是解答此题的关键.20.下列说法,正确的是( )A.经过一点有且只有一条直线B.两条射线组成的图形叫做角C.两条直线相交至少有两个交点D.两点确定一条直线【答案】D【解析】【分析】根据直线的性质、角的定义、相交线的概念一一判断即可.【详解】A、经过两点有且只有一条直线,故错误;B、有公共顶点的两条射线组成的图形叫做角,故错误;C、两条直线相交有一个交点,故错误;D、两点确定一条直线,故正确,故选D.【点睛】本题考查直线的性质、角的定义、相交线的概念,熟练掌握相关知识是解题的关键.。
初中数学几何知识点和题型归纳总复习

图 形
平
线段,射线,直线
面
角的度量
两点之间 线段最短
图 形角
角
角的大小比较
平
余角补角
分
线
按柱、锥、球划分 (1) (2) 是一类,是柱体 (3)(4)是锥体 (5) 是球体
圆柱
柱体
三棱柱
四棱柱 棱柱
五棱柱
六棱柱
圆锥
锥体
三棱锥
棱锥
四棱锥 五棱锥
六棱锥
认识多面体
若围成立体图形的面是平的面,这样的立体图形又称为多面体
l
l
AB
直线AB、直
线BA、直线l
延伸性 端点个数 作图叙述
无
2 连接AB
沿OC方向 向两方无限
延伸
延伸
1
0
以点O为端 过A、B两点 点作射线OC 作直线AB
下面的知识点你掌握了吗?
知识点1:线段 (1)线段的概念:它是直线的一部分,它的
长度是有限的,它有两个端点. (2)线段的表示方法:可用它的两个端点
▪ (2)直线的表示方法:可用这条直线上 的两个点表示,也可以用一个小写字母 表示.
▪ (3)直线的基本性质:经过两点有一条 直线,并且只有一条直线.
▪ (4)直线的特点:没有端点,向两方无限 延伸,不可度量,不能比较大小.
你能解决下列问题吗?
1、图中共有几条线段?几条射线?几 条直线?能用字母表示出来的分别用 字母表示出来。
知识点2:射线
(1)射线的概念:把线段向一方无限延伸 所形成的图形叫做射线.
(2)射线的表示方法:可用两个大写字母 表示,第一个大写字母表示它的端点; 也可用一个小写字母表示.
(3)射线的特点:只有一个端点,向一方无 限延伸,无法度量,不能比较长短.
2021年中考复习讲义初中几何典型模型一:一线三垂直模型

初中数学典型模型之一: “三垂直模型”介绍总体解题思路:只要出现此典型图形,一般都要证三角形全等或相似,再根据全等或相似性质解题.(一)基本图形: 1.“三垂”例1.如图,矩形ABCD 中,E 在AD 上,且EF ⊥EC ,EF=EC ,DE=2,矩形的周长为16,则AE=__ 解析:如图1,典型的“三垂直模型”,由于有等边(EF=EC )先证△AEF ≌△DCE , ∴AE=DC ,∴AD-DC=2,∵AD+DC=8,∴AD=5,DC=3,∴AE=3例2.一块矩形木板ABCD ,长AD=3cm,宽AB=2cm,小虎将一块等腰直角三角板的一条直角边靠在顶点C 上,另一条直角边与AB 边交于点E ,三角板的直角顶点P 在AD 边上移动(不含端点A,D ),当线段BE 最短时,AP=_______解析:如图1,典型的“三垂直模型”,由于没有等边,先证△AEP ∽△DPC , ∴AP CD=AE PD。
当题目出现线段最值时,初三的数学中有两种解题方法:①几何论证方法;②代数论证方法-----通过设未知数,把几何中的线段关系转化成二次函数形式,运用二次函数求最值的方法解题;(详见“动态问题下求线段长”),此题可采用代数论证方法,设BE =y,AP =x ,∴x2=2−y3−x , ∴y =x 2−3x +4=(x −32)2+74 , ∴a =1>0 , ∴x =32 时,y 最小值=742.两种变化图形(1)“交叉型”三垂直模型 (2)“L 型”三垂直模型A BC DEF 图1PA BCD E 证明:∵∠1+∠2=90°,∠2+∠A=90°,∴∠1=∠A 又∵∠B=∠C ,若其中有一组边相等,则证ABE ≅ECD;若没有边相等,则证ABE ~ECD;21AB CED证明:∵∠1+∠2=90°,∠2+∠A=90°,∴∠1=∠A 又∵∠B=∠C ,若其中有一组边相等,则证ABE ≅FCD;若没有边相等,则证ABE ~FCD;21A BF E DC(1)若有等边,则△ABE≌△BDC(AAS )(2)若无等边,则△ABE∽△BDC(AA )EDCBA例3.如图,已知正方形ABCD 的边长为4,点E 、F 分别在边AB 、BC 上,且AE=BF=1,则OC= .解析:求线段长,要么用勾股定理,要么用相似,不管走勾股定理,还是相似,都绕不过先求出∠DOC=90°,当把这个90°标在图形时,就出现“三垂直模型的变化图形—交叉型三垂直模型”,如图1,由于有等边(BC=CD ),先证△BCE ≌△CDF ,∴∠BCE =∠CDF ,∵∠BCE +∠OCD =90°,∴∠CDF +∠OCD =90°,∴∠DOC =90°;这时图形又出现了第二个典型图形:“双垂型图形”,如图2,便易得这个典型图形的一个典型的用途----两直角边的乘积会等于斜边乘以斜边上的高。
几何复习专题卷(含答案)初中数学浙教版八年级上册

几何复习专题卷题号一二三总分得分一、选择题(每题3分,共30分)1.[母题·教材P41目标与评定T1 2024·温州期末]用三根木棒首尾相接围成△ABC,其中AC=6 cm,BC=9 cm,则AB的长可能是( )A.2 cm B.3 cm C.14 cm D.15 cm2.[新考向知识情境化]如图,在平分角的仪器中,AB=AD,BC=DC,将点A放在一个角的顶点,AB和AD分别与这个角的两边重合,能说明AC就是这个角的平分线的数学依据是( )(第2题)A.SSS B.ASA C.SAS D.AAS3.如图,已知O是△ABC中∠ABC,∠ACB的平分线的交点,OD∥AB交BC于点D,OE∥AC交BC于点E.若BC=10 cm,则△ODE 的周长为( )(第3题)A.10 cm B.8 cmC.12 cm D.20 cm4.[2024·宁波奉化区期末]下列命题的逆命题是假命题的是( ) A.直角三角形的两个锐角互余B.两直线平行,内错角相等C.三条边对应相等的两个三角形是全等三角形D.同角的余角相等5.过直线l外一点P作直线l的垂线PQ,下列尺规作图错误的是( )A B C D 6.[2024·杭州西湖区期末]如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=9,且AC+BC=10,则AB的长为( )(第6题)A.6B.7C.8D.627.如图,AB=AD,AC=AE,∠DAB=∠CAE=50°,以下结论:①△ADC≌△ABE;②CD=BE;③∠DOB=50°;④CD平分∠ACB.其中正确的有( )(第7题)A.1个B.2个C.3个D.4个8.如图,在△ABC中,∠BAC=90°,点D在边BC上,AD=AB,则有( )(第8题)A.若AC=2AB,则∠C=30°B.若3AC=4AB,则7BD=18CDC.若∠B=2∠C,则AC=2ABD.若∠B=2∠C,则S△ABD=2S△ACD9.[2024·宁波奉化区期末]如图,在△ABC中,AB=23,∠B=60°,∠A=45°,D为BC上一点,点P,Q分别是点D关于AB,AC的对称点,则PQ的最小值是( )(第9题)A.6B.8C.32D.310.[2023·金华]如图,在Rt△ABC中,∠ACB=90°,以其三边为边在AB的同侧作三个正方形,点F在GH上,CG与EF交于点P,CM与BE交于点Q.若HF=FG,则S四边形PCQE的值是( )S正方形ABEF(第10题)A.14B.15C.312D.625二、填空题(每题4分,共24分)11.如图,在△ABC中,∠ACB=90°,D为AB的中点,AC=6,BC =8,则CD= .(第11题)12.如图,在△ABC的边AB上取点D,以D为圆心,DA长为半径画圆弧,交AC于点E;以E为圆心,ED长为半径画圆弧,交AB 于点F.若∠CEF=∠BFE,则∠A= °.(第12题)13.[2024·温州期末]如图,在等腰三角形ABC中,AD是底边BC 上的高线,CE⊥AB于点E,交AD于点F.若∠BAC=45°,AF =6,则BD的长为 .(第13题)14.如图,D为等边三角形ABC的AB边的中点,P是BC上的一个动点,连结DP,将△DBP沿DP翻折,得到△DEP,连结AE,若∠BAE=40°,则∠BDP的度数为 .(第14题)15.如图,在长方形ABCD中,AB=4,AD=3,长方形内有一个点P,连结AP,BP,CP,已知∠APB=90°,CP=CB,延长CP交AD于点E,则AE等于 .(第15题)16.[新考法分类讨论法]如图①是一副直角三角板,已知在△ABC和△DEF中,∠BAC=∠EDF=90°,∠B=45°,∠F=30°,点B,D,C,F在同一直线上,点A在DE上.如图②,△ABC固定不动,将△EDF绕点D逆时针旋转α(0°<α<135°),得到△E'DF',当直线E'F'与直线AC,BC所围成的三角形为等腰三角形时,α的大小为 .(第16题)三、解答题(共66分)17.(6分) [新视角·动手操作题2024·金华月考]如图,在正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,请按要求完成下列问题(仅用无刻度的直尺作图,且保留必要的作图痕迹):(1)在AB上找一点D,使CD⊥AB;(2)在AC上找一点E,使BE平分∠ABC.18.(6分)如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.(1)求证:∠EBD=∠EDB;(2)当AB=AC时,请判断CD与ED的大小关系,并说明理由.19.(6分)“儿童散学归来早,忙趁东风放纸鸢”.又到了放风筝的最佳时节,某实践探究小组在放风筝时想测量风筝离地面的垂直高度,通过勘测,得到如下记录表:测量示意图的全部数据就可以计算出风筝离地面的垂直高度AD.请完成以下任务.(1)如图,在Rt△ABC中,∠ACB=90°,BC=15 m,AB=17 m,求线段AD的长.(2)如果小明想要风筝沿DA方向再上升12 m,BC长度不变,则他应该再放出多少米线?20.(8分) [新考法构造全等三角形法]如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,且AE=AF,CE=CF.(1)求证:CB=CD;(2)若AE=CE=5,AB=AD=8,求线段EF的长.21.(8分)[2024·杭州西湖区期中]如图,在△ABC中,点D,E分别在边AB,AC上,连结CD,BE,BD=BC=BE.(1)若∠A=30°,∠ACB=70°,求∠BDC,∠ACD的度数;(2)设∠ACD=α,∠ABE=β,求α与β之间的数量关系,并说明理由.22.(10分)[2023·宁波七中期中]如图,在△ABC中,AB=AC=2,∠A=90°.D为BC边的中点,E,F分别在边AB,AC上,DE⊥DF.(1)求证:△DEF是等腰三角形;(2)求EF的最小值.23.(10分)[2024·衢州月考]如图①,在等腰三角形ABC中,AD是BC边上的中线,延长BC至点E,使AD=DE,连结AE.(1)求证:△ADE是等腰直角三角形;(2)如图②,过点B作AC的垂线交AE于点P,试判断△ABP的形状,并说明理由;(3)如图③,在(2)的条件下,AD=4,连结CP,若△CPE是直角三角形,求CE的长.24.(12分)如果两个顶角相等的等腰三角形具有公共的顶角顶点,并将它们的底角顶点分别对应连结起来得到两个全等三角形,那么我们把这样的图形称为“手拉手”图形.如图①,在“手拉手”图形中,AB=AC,AD=AE,∠BAC=∠DAE,连结BD,CE,则△ABD ≌△ACE.(1)请证明图①的结论成立;(2)如图②,△ABC和△ADE是等边三角形,连结BD,EC交于点O,求∠BOC的度数;(3)如图③,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠BCD的数量关系.答案一、1.C 2.A 3.A 4.D 5.C 6.C7.C 【点拨】∵∠DAB =∠CAE ,∴∠DAB +∠BAC =∠CAE +∠BAC .∴∠DAC =∠BAE .在△ADC 和△ABE 中,{AD =AB ,∠DAC =∠BAE ,AC =AE ,∴△ADC ≌△ABE (SAS ).∴CD =BE ,∠ADC =∠ABE .又∵∠AFD =∠BFO ,∴∠DOB =∠DAB =50°,故①②③正确.现有条件无法得到CD 平分∠ACB .8.B 【点拨】A .若AC =2AB ,则BC =AB 2+AC 2=5AB ,若∠C =30°,则易得BC =2AB ,故A 选项错误.B .若3AC =4AB ,则AC =43AB ,∴BC =AB 2+AC 2=53AB .作AE ⊥BC ,则S △ABC =12AB ·AC =12BC ·AE ,可得AE =AB ·AC BC =45AB .∵AD =AB ,∴BE =DE =AB 2-AE 2=35AB .∴BD =65AB .∴DC =BC -BD =715AB .∴7BD =18CD ,故B 选项正确.C .若∠B =2∠C ,∵∠BAC =90°,∴∠B +∠C =90°.∴∠C =30°,∠B =60°.∴易得BC =2AB .∴AC <2AB ,故C 选项错误.D .若∠B =2∠C ,由选项C 可得∠C =30°,∠B =60°.∵AD =AB ,∴△ABD 为等边三角形.∴∠ADB=60°.∴∠DAC=∠ADB-∠C=30°=∠C.∴AD=DC=BD,即AD为△ABC的中线.∴S△ABD=S△ACD,故D选项错误.9.C 【点拨】连结AD,AP,AQ.∵点P,Q分别是点D关于AB,AC的对称点,∴AD=AP,AD=AQ,∠PAD=2∠DAB,∠QAD=2∠DAC.∴AD=AP=AQ,∠PAQ=2(∠BAD+∠CAD)=2∠BAC=90°.∴△PAQ是等腰直角三角形.∴易知PQ=2AP=2AD.∵D为BC上一点,∴当AD⊥BC时,AD取得最小值,此时PQ取得最小值.当AD⊥BC时,∠ADB=90°.∵∠ABD=60°,∴∠BAD=180°-∠ABD-∠ADB=30°.AB=3.∴AD=AB2-BD2=3.∴易得BD=12∴PQ=2AD=32.∴PQ的最小值为32.10.B 【点拨】设AC=b,AB=c,BC=a,HF=FG=x,则a2+b2=c2.∵四边形ACGH,四边形BCMN,四边形ABEF都是正方形,∴AC=AH=HG=b,AB=AF,∠H=∠G=∠EBA=∠AFE=∠BCM=90°.∴b=2x.在Rt△AHF与Rt△ACB中,∵AH=AC,AF=AB,∴Rt△AHF≌Rt△ACB(HL).∴HF=BC=FG=a=x,∠HFA=∠ABC,S△AHF=S△ACB.∵∠HFA+∠GFP=180°-90°=90°=∠ABC+∠CBQ,∴∠GFP =∠CBQ.在△GFP与△CBQ中,∵∠G=∠BCQ=90°,FG=BC,∠GFP=∠CBQ,∴△GFP≌△CBQ(ASA).∴S△GFP=S△CBQ.∵S正方形ACGH=S△AHF+S△PFG+S四边形ACPF=b2,∴S正方形ACGH=S△ABC+S△BCQ+S四边形ACPF=b2.∴S四边形PCQE=S正方形ABEF-(S△ABC+S△BCQ+S四边形ACPF)=S正方形ABEF-S正方形ACGH=c2-b2=a2.在Rt△ABC中,由勾股定理得c2=b2+a2=(2x)2+x2=5x2.∴S四边形PCQE S正方形ABEF =a2c2=x25x2=15.二、11.5 12.3613.3 【点拨】在等腰三角形ABC中,AD是底边BC上的高线,∴AD⊥BC,BD=CD.∴∠ADC=90°.∵CE⊥AB,∴∠AEF=∠CEB=90°.又∵∠BAC=45°,∴∠ACE=45°=∠BAC.∴AE=CE.∵∠ADC=∠AEF=90°,∠AFE=∠CFD,∴∠BAD=∠BCE.∴△AEF≌△CEB(ASA).∴AF=BC=6.∴BD=3.14.40° 【点拨】∵D为等边三角形ABC的AB边的中点,∴AD=BD,将△DBP沿DP翻折,得到△DEP,∴BD=DE=AD,∠BDP=∠PDE.∴∠BAE=∠AED=40°.∴∠BDE=40°+40°=80°.∠BDE=40°.∴∠BDP=12 【点拨】延长AP交CD于点F.15.43∵∠APB=90°,∴∠FPB=90°,∠OAB+∠ABP=90°.∴∠CPF+∠CPB=90°.∵四边形ABCD是长方形,∴∠D=∠DAB=∠ABC=90°,CD=AB=4,BC=AD=3.∴∠EAP+∠BAP=∠ABP+∠BAP=∠ABP+∠CBP=90°.∴∠EAP=∠ABP.∵CP=CB=3,∴∠CPB=∠CBP.∴∠CPF=∠ABP=∠EAP.又∵∠EPA=∠CPF,∴∠EAP=∠APE.∴AE=PE.在Rt△CDE中,CD2+DE2=CE2,.∴42+(3-AE)2=(3+AE)2,解得AE=4316.7.5°或75°或97.5°或120°【点拨】设直线E'F'与直线AC,BC分别交于点P,Q,∵△CPQ为等腰三角形,∴∠PCQ为顶角或∠CPQ为顶角或∠CQP为顶角.①当∠PCQ为顶角时,∠CPQ=∠CQP,若∠PCQ为钝角,如图①,∵∠BAC=90°,∠B=45°,∴∠ACB=45°.∴∠CPQ+∠CQP=∠ACB=45°.∴∠CQP=22.5°.∵∠E'F'D=30°,∴∠F'DQ=∠E'F'D-∠CQP=30°-22.5°=7.5°,即α=7.5°.若∠PCQ为锐角,如图②,则∠CPQ=∠CQP=67.5°.∵∠E'DF'=90°,∠F'=30°,∴∠E'=60°.∴∠E'DQ=∠CQP-∠E'=67.5°-60°=7.5°.∴α=90°+7.5°=97.5°.②当∠CPQ为顶角时,∠CQP=∠PCQ=45°,如图③.∵∠DE'F'=∠CQP+∠QDE',∴∠QDE'=∠DE'F'-∠CQP=60°-45°=15°.∴α=90°-15°=75°.③当∠CQP为顶角时,∠CPQ=∠PCQ=45°,如图④,∴∠CQP=90°.∴∠QDF'=90°-∠DF'E'=60°.∴∠QDE'=∠E'DF'-∠QDF'=30°,∴α=90°+30°=120°.综上所述,α的大小为7.5°或75°或97.5°或120°.三、17.【解】(1)如图,点D即为所求.(2)如图,点E即为所求.18.(1)【证明】∵BD是△ABC的角平分线,∴∠CBD=∠EBD.∵DE∥BC,∴∠CBD=∠EDB.∴∠EBD=∠EDB.(2)【解】CD=ED,理由如下:∵AB=AC,∴∠C=∠ABC.∵DE∥BC,∴∠ADE=∠C,∠AED=∠ABC.∴∠ADE=∠AED.∴AD=AE.∴CD=BE.由(1)得∠EBD=∠EDB,∴BE=DE.∴CD=ED.19.【解】(1)由题易知CD=1.7 m.∵在△ABC中,∠ACB=90°,BC=15 m,AB=17 m,∴AC=AB2-BC2=172-152=8(m).∴AD=AC+CD=8+1.7=9.7(m).(2)∵风筝沿DA方向再上升12 m后,AC=8+12=20(m),∴此时风筝线的长为202+152=25(m).25-17=8(m).答:他应该再放出8 m线.20.(1)【证明】如图,连结AC.在△AEC与△AFC中,{AC=AC,CE=CF,AE=AF,∴△AEC≌△AFC(SSS).∴∠CAE=∠CAF.又∵∠B=∠D=90°,∴CB=CD.(2)【解】如图,过F作FG⊥AB,垂足为G.∵AE=CE=5,AB=8,∴EB=3,AF=5,∠ACE=∠CAE.由勾股定理得BC=4.由(1)知△AEC≌△AFC,∴∠ECA=∠FCA.∴∠FCA=∠CAE.∴AE∥CF.∴FG=BC=4.易知AG=3,∴EG=2.在Rt△EFG中,易知EF=20.21.【解】(1)∵∠A+∠ACB+∠ABC=180°,∠A=30°,∠ACB=70°,∴∠ABC=80°.=50°.在△BDC中,BD=BC,∴∠BDC=∠BCD=180°-80°2∴∠ACD=∠BDC-∠A=20°.(2)2α=β.理由:设∠BCD=x,则∠BDC=x,∴∠DBC=180°-2x.∵BE=BC,∴∠BEC=∠BCE=α+x.∴∠EBC=180°-2(α+x).∴∠DBC-∠EBC=180°-2x°-[180°-2(α+x)]=2α.又∵∠DBC-∠EBC=∠ABE=β,∴2α=β.22.(1)【证明】如图,连结AD.∵AB=AC,∠BAC=90°,∴∠B=45°.∵D 为BC 边的中点,∴AD ⊥BC ,∠BAD =∠CAD =12∠BAC =45°=∠B .∴AD =BD =12BC ,∠ADB =90°.∵DE ⊥DF ,∴∠EDF =90°.∴∠ADF =90°-∠ADE =∠BDE .在△ADF 和△BDE 中,{∠DAF =∠B ,AD =BD ,∠ADF =∠BDE ,∴△ADF ≌△BDE (ASA ).∴DF =DE .∴△DEF 是等腰三角形.(2)【解】∵AB =AC =2,∠BAC =90°,∴BC =AB 2+AC 2=22+22=8.∴AD =12BC =12×8=82.如图,取EF 的中点G ,连结AG ,DG .∵∠EAF =∠EDF =90°,∴AG =DG =12EF .∴EF =2AG =AG +DG .又∵AG +DG ≥AD ,∴EF ≥82.∴EF 的最小值为82.23.(1)【证明】∵AB =AC ,AD 是BC 边上的中线,∴AD ⊥BC .∴∠ADC =90°.又∵AD =DE ,∴△ADE 是等腰直角三角形.(2)【解】△ABP 是等腰三角形.理由如下:∵∠ADC =90°,∴∠CAD +∠DCA =90°.∵BP ⊥AC ,∴易得∠PBE +∠DCA =90°.∴∠CAD=∠PBE.∵AB=AC,AD是BC边上的中线,∴∠BAD=∠CAD.∴∠BAD=∠PBE.∵△ADE是等腰直角三角形∴∠DAE=∠E.∴∠BAD+∠DAE=∠PBE+∠E,即∠BAP=∠BPA.∴BA=BP.∴△ABP是等腰三角形.(3)【解】①如图①,若∠PCE=90°.在△ABD和△BPC中,{∠BDA=∠BCP=90°,∠BAD=∠PBC,AB=BP,∴△ABD≌△BPC(AAS)(证△ACD≌△BPC亦可).∴BC=AD=DE =4.∵AD是BC边上的中线,∴BD=CD.设CE=x,则CD=4-x,∴BD=4-x.∴BC=8-2x.∴8-2x=4,解得x=2,即CE=2.②如图②,若∠CPE=90°.作PF⊥CE于点F,同理可证△ABD≌△BPF,∴BF=AD=4.设EF=x,易知∠E=45°,∴易得CF=EF=x.∴CD=4-2x.∴BD=4-2x.∴BC=8-4x.∴BF=8-3x.∴8-3x =4,解得x =43.∴CE =2x =83.综上,CE 的长为2或83.24.(1)【证明】∵∠BAC =∠DAE ,∴∠BAC +∠CAD =∠DAE +∠CAD ,即∠BAD =∠CAE .在△ABD 和△ACE 中,{AB =AC ,∠BAD =∠CAE ,AD =AE ,∴△ABD ≌△ACE (SAS ).(2)【解】由题意可知△ABD ≌△ACE .∴∠ADB =∠AEC .在等边三角形ADE 中,∠DAE =60°.记AD 与CE 的交点为G .∵∠AGE =∠DGO ,∴∠DOE =∠DAE =60°.∴∠BOC =∠DOE =60°.(3)【解】如图,延长DC 至点P ,使DP =DB .∵∠BDC =60°,∴△BDP 是等边三角形.∴BD =BP ,∠DBP =60°.∵∠ABC =60°=∠DBP ,∴∠ABD =∠CBP .∵AB =CB ,∴△ABD ≌△CBP (SAS ).∴∠BCP =∠A .又∵∠BCD+∠BCP=180°,∴∠A+∠BCD=180°.21。
中考复习初中数学几何证明 试题(含答案)
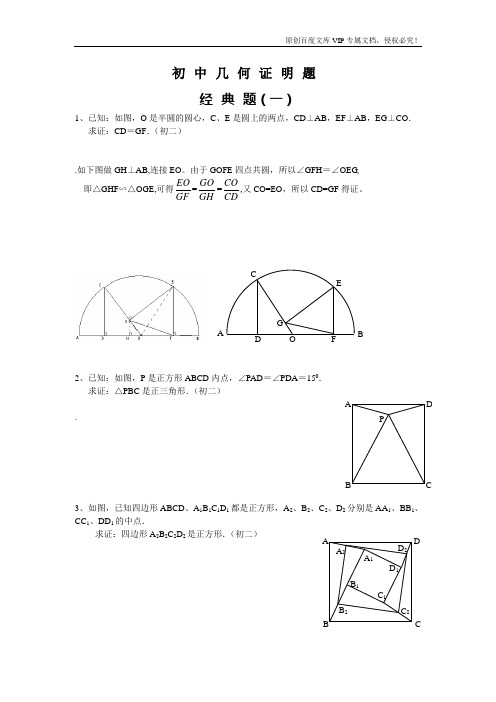
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.BF求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值. A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学复习专题 —几何隐圆模型之定边对定角

初中数学复习专题—几何隐圆模型之定边对定角班级姓名有些数学问题,将圆隐藏在已知条件里,隐晦地考查点和圆、直线和圆的位置关系.解题时,需要我们通过分析探索,发现这些隐藏的圆(简称隐圆),再利用和圆有关的一些知识进行求解. 常见的隐圆模型有以下三种:①定弦对定角;②动点到定点的距离为定长;③四点共圆等. 我们今天要讲的是定弦对定角问题,如右图:∠P 保持不变,∠P 所对的边长为d 保持不变,则∠P 的顶点P 的轨迹为圆弧.(简称:定边对定角)例1.在正方形ABCD 中,AD=2,E,F 分别为边DC,CB 上的点,且始终保持DE=CF,连接AE 和DF 交于点P,则线段CP 的最小值为.例 2.如图,在边长为2 的等边△ABC中,点 E 为AC 上一点,AE=CD,连接 BE、AD 相交于点 P,则CP 的最小值为。
例3.如图,△ABC 中,AC=3,BC=4 ,∠ACB=45°,D 为△ABC 内一动点,⊙O 为△ACD 的外接圆,直线BD 交⊙O 于P 点,交BC 于E 点,弧AE=CP,则AD 的最小值为()A.1 B.2 C.D. 4322 【巩固训练】1. 如图 1,O 的半径为 2,弦 AB =2,点 P 为优弧 AB 上一动点,AC ⊥AP 交直线 PB 于点 C ,则△ABC的最大面积是.图1图2图32. 如图 2,半径为 2cm ,圆心角为 90°的扇形 OAB 的弧 AB 上有一运动的点 P 从点 P 向半径 OA 引垂线 PH 交 OA 于点 H ,设△OPH 的内心为 I ,当点 P 在弧 AB 上从点 A 运动到点 B 时,内心 I 所经过的路径长为.3. 如图 3,以 G (0,1)为圆心,半径为 2 的圆与 x 轴交于 A 、B 两点,与 y 轴交于 C 、D 两点,点 E 为 OG 上一动点,CF ⊥AE 于 F ,当点 E 从点 B 出发顺时针运动到点 D 时,点 F 所经过的路径长为 .4. 如图 4,以正方形 ABCD 的边 BC 为一边向内部做一等腰△BCE ,CE =CB ,过 E 做 EH ⊥BC ,点 P是△BEC 的内心,连接 AP ,若 AB =2,则 AP 的最小值为.图 4 图 5 图 6 5. 如图 5,Rt △ABC 中,AB ⊥BC ,AB =6,BC =4,P 是△ABC 内部的一个动点,且满足∠PAB =∠PBC ,则线段 CP 长的最小值为 .6. 如图 6,在 Rt △ABC 中,∠C =90°,AC =10,BC =12,点 D 为线段 BC 上一动点.以 CD 为⊙O 直径,作 AD 交⊙O 于点 E ,连 BE ,则 BE 的最小值为 .7. 如图 7,在等腰 Rt △ABC 中,∠BAC =90°,AB =AC ,BC = 4 ,点 D 是 AC 边上一动点,连接 BD ,以 AD为直径的圆交 BD 于点 E ,则线段 CE 长度的最小值为 .图 78.等腰直角△ABC 中,∠C=90°,AC=BC=4,D 为线段AC 上一动点,连接BD,过点C 作CH⊥BD 于H,连接AH,则AH 的最小值为.图8 图9 图109.如图9,直线y=x+4 分别与x 轴、y 轴相交与点M、N,边长为2 的正方形OABC 一个顶点O,在坐标系的原点,直线AN 与MC 相交与点P,若正方形绕着点O 旋转一周,则点P 到点(0,2)长度的最小值是.10.如图10,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(7,3),点E在边AB 上,且AE=1,已知点P 为y 轴上一动点,连接EP,过点O 作直线EP 的垂线段,垂足为点H,在点P 从点F(0, 25)运动到原点O 的过程中,点H 的运动路径长为. 411.如图11,AB 是⊙O 的直径,AB=2,∠ABC=60°,P 是上一动点,D 是AP 的中点,连接CD,则CD 的最小值为图11 图 1212.如图12,已知△ABC是边长为4 的等边三角形,取AC 的中点E,△ABC绕E 点旋转任意角度得到△GMN,直线BN、GC 相交于点H.求△GMN绕点E 旋转时过程中,线段AH 的最大值是.13.如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.(1)使∠APB=30°的点P有个.(2)若点P在y轴上,且∠APB=30°,求满足条件的点P的坐标.(3)当点P在y轴上移动时,∠APB何时有最大值?请说明理由.14.[2019衢州]如图F10-10,在Rt△ABC中,∠C=90°,AC=6,∠BAC=60°,AD平分∠BAC交BC于点D,过点D作DE∥AC交AB于点E,点M是线段AD上的动点,连结BM并延长分别交DE,AC于点F,G.(1)求CD的长.的值.(2)若点M是线段AD的中点,求EFDF(3)请问当DM的长满足什么条件时,在线段DE上恰好只有一点P,使得∠CPG=60°?15.如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E,F 运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF,BE相交于点P,则线段DP的最小值为.8.如图,矩形ABCD中,AB=2,AD=3,点E,F分别为ADDC边上的点,且EF=2,点G为EF的中点,点P为BC边上一动点,则PA+PG的最小值为.5 ⎨ ⎩参考答案例 1【解析】解:如图,在△ADE 和△DCF 中,⎧ AD = DC ⎪∠ADE = ∠DCF ⎪DE = CF ∴△ADE 2△DCF (SAS ) ∴∠DAE =∠CDF∵∠DAE +∠AED =90°∴∠CDF +∠AED =90°,∴∠DPE =∠APD =90° .∠APD =90°保持不变∴点 P 的轨迹为以 AD 为直径的一段弧上∴取 AD 中点 Q ,连接 CQ ,与该圆弧交点即为点 P ,此时 CP 值最小在 Rt △CQD 中,CQ =∴CP =CQ -PQ = -1例 2.解析:可证△AEB ≅△CDA ∴∠ABE=∠CAD ∵∠CAD+∠BAD=60° ∴∠ABE+∠BAD=60°即∠BPB=60° ∵ AB 为定边,∠APB=120°为定角∴P 在以 AB 为弦且圆心角为 120°的圆弧上运动。
中考复习初中数学几何证明经典试题(含答案)
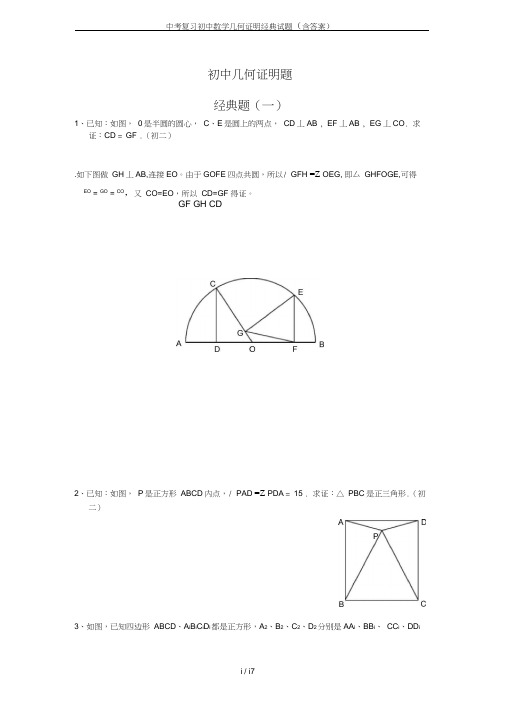
初中几何证明题经典题(一)1、已知:如图,0是半圆的圆心,C、E是圆上的两点,CD丄AB , EF丄AB , EG丄CO. 求证:CD = GF .(初二).如下图做GH丄AB,连接EO。
由于GOFE四点共圆,所以/ GFH =Z OEG, 即厶GHFOGE,可得EO = GO = CO,又CO=EO,所以CD=GF 得证。
GF GH CD2、已知:如图,P是正方形ABCD内点,/ PAD =Z PDA = 15°. 求证:△ PBC是正三角形.(初二)3、如图,已知四边形ABCD、A i B i C i D i都是正方形,A2、B2、C2、D2分别是AA i、BB i、CC i、DD i的中点.及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP = AQ .(初二)3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN P 、Q .4、 1、求证:四边形 A 2B 2C 2D 2是正方形.(初二)已知: 求证: 如图,在四边形 的延长线交 / DEN = Z△ ABC 中, MN F .ABCD 中,AD = BC , M 、N 分别是 AB 、CD 的中点,AD 、BC 于E 、F .经典题(二)已知: (1) 求证:AH = 20M ;(2) 若/ BAC = 60°,求证:H 为垂心 (各边高线的交点),0为外心,且 0M 丄BC 于M . AH = A0 .(初二)2、设MN 是圆O 外一直线,过O 作OA 丄MN 于A ,自A 引圆的两条直线,交圆于DCGN求证:AP = AQ .(初二)ECAM NP4、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于 AB 的一半.(初二)经典题(二)1、如图,四边形 ABCD 为正方形, 求证:CE = CF .(初二)2、如图,四边形 ABCD 为正方形,DE // AC ,且CE = CA ,直线EC 交DA 延长线于F . 求证:AE = AF .(初二)DE // AC , AE = AC , AE 与 CD 相交于 F .FEAD1、设P 是边长为1的正△ ABC 内任一点,4、如图,PC 切圆0于C , AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于3、设ABCD 为圆内接凸四边形,求证: AB • CD + AD • BC = AC • BD .(初三)B 、D .求证: AB = DC , BC = AD .(初三)1、已知:△ ABC 是正三角形,P 是三角形内一点 求:/ APB 的度数.(初二)2、设P 是平行四边形 ABCD 内部的一点,且/求证:/ PAB = Z PCB .(初二)4、平行四边形 ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证:/ DPA =Z DPC .(初二)AO DB EFC求证:4、如图,△ ABC 中,/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点,/ DCA = 30°, / EBA = 20°,求/ BED 的度数. LiB C经典题(一)1•如下图做GH丄AB,连接E0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
图7 O C B A 初中数学几何复习专题
【典型例题】
一、填空题
1、(08)如图1,在ΔABC 中,M 、N 分别是AB 、AC 的中点,且∠A +∠B=120°,则∠AN M= °;
2、(07)如图2,AD 是⊙O 的直径,AB ∥CD ,∠AOC=60°,则∠BAD=______度.
3、(08)如图3,已知AB 是⊙O 的直径,BC 为弦,∠A BC=30°过圆心O 作OD ⊥BC 交弧
BC 于点D ,连接DC ,则∠DCB= °.
4、(08佛山市)如图4,已知P 是正方形ABCD 对角线BD 上一点,
且BP = BC ,则∠ACP 度数是 .
5、(07广州市)如图5,点D 是AC 的中点,将周长为4㎝的菱形
ABCD 沿对角线AC 方向平移AD 长度得到菱形OB ’C ’D ’,则四边
形OECF 的周长是 ㎝
6、(08茂名市)如图6,点A 、B 、C 在⊙O 上,AO ∥BC ,∠AOB = 50°,
则∠OAC 的度数是 .
(1) (08梅州市) 如图7,要测量A 、B 两点间距离,在O 点打桩,取OA 的中点 C ,OB 的中点D ,测得CD=30米,则AB=______米.
(2) (08梅州市) 如图8, 点 P 到∠AOB 两边的距离相等,若∠POB=30°,则 ∠AOB=_____度.
(3) (09广东省) 已知⊙O 的直径AB=8cm ,C 为⊙O 上的一点,∠BAC=30°,则BC=_________cm.
图2O D C B A A M N B C 图1 O B D C A 图3 图4 B C D A P O C B
A 图6 图8 图9 图5
2 C OBB 1C C B A 111二、解答题
2、(08广东省)如图,在△ABC 中,BC>AC , 点D 在BC 上,且DC =AC,∠ACB 的平分线CF 交AD 于F ,点E 是AB 的中点,连结EF.
(1)求证:EF ∥BC.
(2)若四边形BDFE 的面积为6,求△ABD 的面积.
4、(09广东省) 在菱形ABCD 中,对角线AC 与BD 相交于点O ,A
B=5,AC=6.过D点作DE ∥AC 交BC的延长线于点E.
(1)求△BDE 的周长;
(2)点P为线段BC 上的点,
连接PO 并延长交AD 于点Q.求证:BP=DQ.
5、(09广东省) 如图所示,在矩形ABCD 中,AB=12,AC=20,两条对角线相交于点O.以OB 、OC 为邻边作第1个平行四边形C OBB 1,对角线相交于点1A ;再以C A B A 111、为邻边作第2个平行四边形C C B A 111,对角线相交于点1O ;再以1111C O B O 、为
邻边作第3个平行四边形1211C B B O ……依此类推.
(1)求矩形ABCD 的面积;
(2)求第1个平行四边形 、第2个
平行四边形
和第6个平行四边形的面积.
6、(09广东省)(1)如图1,圆内接△ABC 中,AB=BC=CA ,
OD 、OE 为⊙O 的半径,OD ⊥BC 于点F ,OE ⊥AC 于点G ,
求证:阴影部分四边形OFCG 的面积是△ABC 的面积的31. (2)如图2,若∠DOE 保持120°角度不变,求证:当∠DOE 绕着O 点旋转时,由两条半径和△ABC 的两条边围成的图形(图中阴影部分)面积始终是△ABC 的面积的
31.
7、(10广东省)如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4。
(1)求∠POA的度数;
(2)计算弦AB的长。
9、(10广东省)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G。
∠C=∠EFB=90º,∠E=∠ABC=30º,AB=DE=4。
(1)求证:△EGB是等腰三角形;
(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小_____度时,四边形ACDE成为以ED为底的梯形(如图(2)),求此梯形的高。
第9题图(1)
A B
C E
F
F
B(D)
G
G
A
C
E
D
第9题图(2)
3。
