高中数学竞赛 平面几何的几个重要定理——梅涅劳斯定理
四个重要定理(梅涅劳斯-塞瓦-托勒密-西姆松)(1)

B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理(梅氏线)△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ,则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理(塞瓦点)△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题:1、设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。
求证:FBAF 2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CB 于D 。
求证:1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ,则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅(梅氏定理) DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅(梅氏定理)∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上,λ===EACEFB AF DC BD ,AD 、BE 、CF 交成△LMN 。
求S △【分析】B【评注】梅氏定理4、以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。
求证:AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中,∠B=2∠C 。
数学奥赛平面几何

《竞赛数学解题研究》之平面几何专题一、平面几何中的一些重要定理:1、梅涅劳斯定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则D 、E 、F 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
2、塞瓦定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则AF 、BE 、CD 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
3、托勒密定理:四边形ABCD 内接于圆的充要条件是CD BC CD AB BD AC ⋅+⋅=⋅4、西摩松定理:设P 是ABC ∆外接圆上任一点,过P 向ABC ∆的三边分别作垂线,设垂足为D 、E 、F ,则D 、E 、F 三点共线。
5、斯德瓦特定理:设P 是ABC ∆的边BC 边上的任一点,则BC PC BP AP BC AB PC AC BP ⋅⋅+⋅=⋅+⋅2226、共角定理:设ABC ∆和C B A '''∆中有一个角相等或互补(不妨设A=A ')则 C A B A ACAB S S C B A ABC ''⋅''⋅='''∆∆7、共边定理:设ABC ∆和C B A '''∆中有一个边相等,则CA B A ACAB S S C B A ABC ''⋅''⋅='''∆∆举例说明:1、设M 、N 分别是正六边形ABCDEF 的对角线AC 、CE 上的点,且AM:AC=CN:CE=k,如果BMN 三点共线,试求k 。
(IMO23,1982)2、在四边形ABCD 中,ABD ∆、BCD ∆、ABC ∆的面积之比为3:4:1,点M 、N 分别 是AC 、CD 上的点,且AM:AC=CN:CD, 并且BMN 三点共线,求证:M 、N 分别是AC 、 CD 的中点。
平面几何四大定理
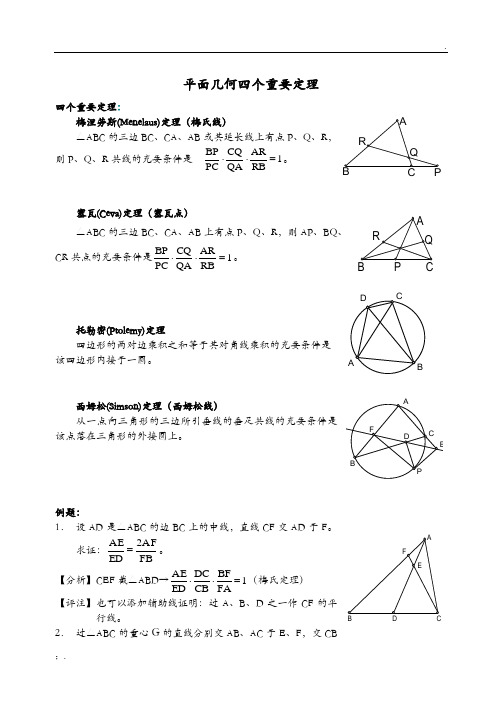
.平面几何四个重要定理四个重要定理:梅涅劳斯(Menelaus)定理(梅氏线)△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ,则P 、Q 、R 共线的充要条件是 1RB ARQA CQ PC BP =⋅⋅。
塞瓦(Ceva)定理(塞瓦点)△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是1RBAR QA CQ PC BP =⋅⋅。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)定理(西姆松线)该点落在三角形的外接圆上。
例题:1. 设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。
求证:FBAF2ED AE =。
【分析】CEF 截△ABD →1FABFCB DC ED AE =⋅⋅(梅氏定理)【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
2. 过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CBDEG 截△ABM →1DB MDGM AGEA BE =⋅⋅(梅氏定理)DGF 截△ACM →1DCMDGM AG FA CF =⋅⋅(梅氏定理)∴FACF EA BE +=MD AG )DC DB (GM ⋅+⋅=MDGM 2MD 2GM ⋅⋅=1 【评注】梅氏定理3. D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上,λ===EA CEFB AF DC BD ,AD 、BE 、CF 交成△LMN。
求S △LMN 。
【分析】【评注】梅氏定理4. 以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。
求证:AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理B5. 已知△ABC 中,∠B=2∠C 。
求证:AC 2=AB 2+AB ·BC 。
【分析】过A 作BC 的平行线交△ABC 的外接圆于D ,连结BD 。
平面几何的几个重要的定理--梅涅劳斯定理

平面几何的几个重要的定理(一)梅涅劳斯定理一、基础知识梅涅劳斯定理 若直线l 不经过△ABC 的顶点,并且与△ABC 的三边BC 、CA 、AB 或它们的延长线分别交于P 、Q 、R ,则1BP CQ AR PC QA RB ⋅⋅= 梅涅劳斯定理的逆定理 设P 、Q 、R 分别是△ABC 的三边BC 、CA 、AB 或它们的延长线上的三点(并且P 、Q 、R 三点中,位于△ABC 边上的点的个数为0或2),若1BP CQ AR PC QA RB ⋅⋅=,则P 、Q 、R 三点共线.由和分比定理可得R R '∴与重合 ∴P 、Q 、R 三点共线二、典型例题与基本方法1. 恰当地选择三角形及其截线(或作出截线),是应用梅涅劳斯定理的关键例1 如图,在四边形ABCD 中,△ABD 、△BCD 、△ABC 的面积之比是3∶4∶1,点M 、N 分别在AC 、CD 上,满足AM ∶AC =CN ∶CD ,且B 、M 、N 三点共线.求证:M 与N 分别是AC 和CD 的中点.A BC DM N1A B C C B A C A Bh h h A B C l h h h BP CQ AR PC QA RB h h h ⋅⋅=⋅⋅=证:设、、分别是、、到直线的垂线的长度,则:BP 1PC CQ AR PQ AB R QA R B ''⋅⋅='证:设直线与直线交于,于是由梅氏定理得:BP 1PC CQ AR AR AR QA RB R B RB '⋅⋅='又,则:=AR AR AB AB'=2. 梅涅劳斯定理的逆用(逆定理的应用)与迭用,是灵活应用梅氏定理的一种方法 例2 点P 位于△ABC 的外接圆上,111A B C 、、是从点P 向BC 、CA 、AB 引的垂线的垂足,证明点111A B C 、、共线.三、解题思维策略分析1. 寻求线段倍分的一座桥梁例3 △ABC 是等腰三角形,AB=AC ,M 是BC 的中点;O 是AM 延长线上的一点,使得OB ⊥AB ; Q 为线段BC 上不同于B 和C 的任意一点,E 、F 分别在直线AB 、AC 上使得E 、Q 、F 是不同的和共线的.求证:(1)若OQ EF ⊥,则QE QF =;(2)若QE QF =,则OQ EF ⊥.111111*********|cos |,|cos ||cos ||cos ||cos ||cos |,,1801BA BP PBC CA CP PCB CB CP PCA AB AP PAC AC AP PAB BC PB PBA PAC PBC PAB PCB PCA PBA BA CB AC CA AB BC A B C ⋅∠=⋅∠⋅∠=⋅∠⋅∠=⋅∠∠=∠∠=∠∠+∠=︒⋅⋅证:易得:将上面三个式子相乘,且可得=依梅涅劳斯定理可知、、三点共线.2. 导出线段比例式的重要途径例4 直角△ABC 中,CK 是斜边上的高,CE 是∠ACK 的平分线,E 点在AK 上,D 是AC的中点,F 是DE 与CK 的交点. 求证://BF CE .3. 论证点共线的重要方法例5 设不等腰△ABC 的内切圆在三边BC CA AB 、、上的切点分别为D E F 、、,证明:EF 与CB ,FD 与AC ,ED 与AB 的交点X Y Z 、、在同一条直线上.X Y Z ABC X Y Z ∆又、、都不在的边上,由梅氏定理的逆定理可得、、三点共线 例6 如图,△ABC 的内切圆分别切三边BC 、CA 、AB 于点D 、E 、F ,点X 是△ABC 的一个内点,△XBC 的内切圆也在点D 处与BC 边相切,并与CX 、XB 分别相切于点Y 、 Z. 证明:EFZY 是圆内接四边形.11BX CE AF ABC XFE XC EA FB ∆⋅⋅=证:被直线所截,由定理可得:BX FB AE AF XC CE=又代人上式可得:=CY DC AZ EA YA AF ZB BD同理可得:==1BX CY AZ XC YA ZB⋅⋅=将上面三条式子相乘可得:。
2011全国高中数学竞赛讲义-平面几何名定理

§21平面几何名定理四个重要定理:梅涅劳斯(Menelaus)定理(梅氏线)△ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线的充要条件是。
塞瓦(Ceva)定理(塞瓦点)△ABC的三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点的充要条件是。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题讲解1.设AD是△ABC的边BC上的中线,直线CF交AD于F。
求证:。
2.过△ABC的重心G的直线分别交AB、AC于E、F,交CB于D。
求证:。
3.D、E、F分别在△ABC的BC、CA、AB边上,,AD、BE、CF交成△LMN。
求S△LMN。
4.以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。
求证:AE、BF、CG相交于一点。
5.已知△ABC中,∠B=2∠C。
求证:AC2=AB2+AB·BC。
6.已知正七边形A1A2A3A4A5A6A7。
求证:。
7.△ABC的BC边上的高AD的延长线交外接圆于P,作PE⊥AB于E,延长ED交AC延长线于F。
求证:BC·EF=BF·CE+BE·CF。
8.正六边形ABCDEF的对角线AC、CE分别被内分点M、N分成的比为AM:AC=CN:CE=k,且B、M、N共线。
求k。
(23-IMO-5)9.O为△ABC内一点,分别以d a、d b、d c表示O到BC、CA、AB的距离,以R a、R b、R c表示O 到A、B、C的距离。
求证:(1)a·R a≥b·d b+c·d c;(2) a·R a≥c·d b+b·d c;(3) R a+R b+R c≥2(d a+d b+d c)。
全国高中数学联赛竞赛大纲

全国高中数学联赛竞赛大纲—试全国高中数学联赛的一试竞赛大纲,完全按照全日制中学《数学教学大纲》中所规定的教学要求和内容,即高考所规定的知识范围和方法,在方法的要求上略有提高,其中概率和微积分初步不考。
二试1.平面几何基本要求:掌握初中竞赛大纲所确定的所有内容。
补充要求:面积和面积方法。
几个重要定理:梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理。
几个重要的极值:到三角形三顶点距离之和最小的点——费马点。
到三角形三顶点距离的平方和最小的点——重心。
三角形内到三边距离之积最大的点——重心。
几何不等式。
简单的等周问题。
了解下述定理:在周长一定的n边形的集合中,正n边形的面积最大。
在周长一定的筒单闭曲线的集合中,圆的面积最大。
在面积一定的n边形的集合中,正n边形的周长最小。
在面积一定的简单闭曲线的集合中,圆的周长最小。
几何中的运动:反射、平移、旋转。
复数方法、向量方法*。
平面凸集、凸包及应用。
2.代数在一试大纲的基础上另外要求的内容:周期函数与周期,带绝对值的函数的图像。
三倍角公式,三角形的一些简单的恒等式,三角不等式。
第二数学归纳法。
递归,一阶、二阶递归,特征方程法。
函数迭代,求n次迭代*,简单的函数方程*。
n个变元的平均不等式,柯西不等式,排序不等式及应用。
复数的指数形式,欧拉公式,棣美弗定理,单位根,单位根的应用。
圆排列,有重复的排列与组合。
简单的组合恒等式。
一元n次方程(多项式)根的个数,根与系数的关系,实系数方程虚根成对定理。
简单的初等数论问题,除初中大纲中斯包括的内容外,还应包括无穷递降法,同余,欧几里得除法,非负最小完全剩余类,高斯函数[x],费马小定理,欧拉函数*,孙子定理*,格点及其质。
3.立体几何多面角,多面角的性质。
三面角、直三面角的基本性质。
正多面体,欧拉定理。
体积证法。
截面,会作截面、表面展开图。
4.平面解析几何直线的法线式,直线的极坐标方程,直线束及其应用。
二元一次不等式表示的区域。
四个重要定理(梅涅劳斯_塞瓦_托勒密_西姆松)
B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理(梅氏线)△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ,则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理(塞瓦点)△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题:1、设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。
求证:FBAF 2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CB 于D 。
求证:1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ,则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅(梅氏定理)DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅(梅氏定理)∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上,λ===EACEFB AF DC BD ,AD 、BE 、CF 交成△LMN 。
求S △【分析】【评注】梅氏定理4、以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。
求证:AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中,∠B=2∠C 。
高中数学竞赛-平面几何讲义(很详细)
HBC
(5)H 关于三边的对称点在△ABC 的外接圆上,关于三边中
点的对称点在△ABC 的外接圆上
(6)三角形任一顶点到垂心的距离
A
等于外心到对边的距离的 2 倍。 (7)设△ABC 的垂心为 H,外接圆
F
B'
半径为 R,
OH E
则 HA HB HC 2R B | cos A | | cos B | | cosC |
A
M
N
B
EF
C
D
证明:设∠BAE=∠CAF= ,∠EAF=
则
S AMDN
1 2
AM
AD sin
1 2
AD
AN sin(
)
= 1 AD[AF cos( )sin AF cos sin( )
2
= 1 AD AF sin(2 ) AF AD BC
从而 AB A' F = AC A' E ,又∠AFE=∠AEF
故
S△ABA’=
1 2
sin
AFE
AB
A'
F
=
1 2
s
in
A
EF
A
C
A'
E
=S△ACA’
由此式可知直线 AA’必平分 BC 边,即 AA’必过△
ABC 的重心
同理 BB’,CC‘必过△ABC 的重心,故结论成立。
例 3.设△ABC 的三条高线为 AD,BE,CF,自 A, B,C 分别作 AK EF 于 K,BL DF 于 L, CN ED 于 N,证明:直线 AK,BL,CN 相 交于一点。
数学竞赛平面几何定理
EDCB A平面几何一、知识点金1.梅涅劳斯定理:若直线l 不经过ABC ∆的顶点,并且与ABC ∆的三边,,BC CA AB 或它们的延长线分别交于,,P Q R ,则1BP CQ AR PC QA RB⋅⋅=注:梅涅劳斯定理的逆定理也成立(用同一法证明)2.塞瓦定理:设,,P Q R 分别是ABC ∆的三边,,BC CA AB 或它们的延长线上的点,若,,AP BQ CR 三线共点,则1BP CQ AR PC QA RB⋅⋅=注:塞瓦定理的逆定理也成立3.托勒密定理:在四边形ABCD 中,有AB CD BC AD AC BD ⋅+⋅≥⋅,并且当且仅当四边形ABCD ()ABCD E BAE CAD ABE ACDAB BE ABE ACD AB CD AC BE AC CD AB AE BAC EAD ABC AED AC AD BC ED AD BC AC ED AC ADAB CD AD BC AC BE ED AB CD AD BC AC BDE BD A B C D ∠=∠∠=∠∆∆∴=⇒⋅=⋅=∠=∠∴∆∆∴=⇒⋅=⋅∴⋅+⋅=⋅+∴⋅+⋅≥⋅ 证:在四边形内取点,使,则:和相似又且和相似且等号当且仅当在上时成立,即当且仅当、、、四点共圆时成立;注:托勒密定理的逆定理也成立4.西姆松定理:若从ABC ∆外接圆上一点P 作,,BC AB CA 的垂线,垂足分别为,,D E F ,则,,D E F 三点共线。
西姆松定理的逆定理:从一点P 作,,BC AB CA 的垂线,垂足分别为,,D E F 。
若,,D E F 三点共线,则点P 在ABC ∆的外接圆上。
5.蝴蝶定理:圆O 中的弦PQ 的中点M ,过点M 任作两弦AB ,CD ,弦AD 与BC 分别交PQ 于X ,Y ,则M 为XY 之中点。
证明:过圆心O 作AD 与BC 的垂线,垂足为S 、T ,连接OX ,OY ,OM ,SM ,MT 。
全国高中数学联赛竞赛大纲
全国高中数学联赛竞赛大纲—试全国高中数学联赛的一试竞赛大纲,完全按照全日制中学《数学教学大纲》中所规定的教学要求和内容,即高考所规定的知识范围和方法,在方法的要求上略有提高,其中概率和微积分初步不考。
二试1.平面几何基本要求:掌握初中竞赛大纲所确定的所有内容。
补充要求:面积和面积方法。
几个重要定理:梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理。
几个重要的极值:到三角形三顶点距离之和最小的点——费马点。
到三角形三顶点距离的平方和最小的点——重心。
三角形内到三边距离之积最大的点——重心。
几何不等式。
简单的等周问题。
了解下述定理:在周长一定的n边形的集合中,正n边形的面积最大。
在周长一定的筒单闭曲线的集合中,圆的面积最大。
在面积一定的n边形的集合中,正n边形的周长最小。
在面积一定的简单闭曲线的集合中,圆的周长最小。
几何中的运动:反射、平移、旋转。
复数方法、向量方法*。
平面凸集、凸包及应用。
2.代数在一试大纲的基础上另外要求的内容:周期函数与周期,带绝对值的函数的图像。
三倍角公式,三角形的一些简单的恒等式,三角不等式。
第二数学归纳法。
递归,一阶、二阶递归,特征方程法。
函数迭代,求n次迭代*,简单的函数方程*。
n个变元的平均不等式,柯西不等式,排序不等式及应用。
复数的指数形式,欧拉公式,棣美弗定理,单位根,单位根的应用。
圆排列,有重复的排列与组合。
简单的组合恒等式。
一元n次方程(多项式)根的个数,根与系数的关系,实系数方程虚根成对定理。
简单的初等数论问题,除初中大纲中斯包括的内容外,还应包括无穷递降法,同余,欧几里得除法,非负最小完全剩余类,高斯函数[x],费马小定理,欧拉函数*,孙子定理*,格点及其质。
3.立体几何多面角,多面角的性质。
三面角、直三面角的基本性质。
正多面体,欧拉定理。
体积证法。
截面,会作截面、表面展开图。
4.平面解析几何直线的法线式,直线的极坐标方程,直线束及其应用。
二元一次不等式表示的区域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梅涅劳斯定理:
1l ABC ABC BC CA AB BP P Q R 1
PC CQ AR
QA RB
∆∆⋅⋅=定理:若直线不经过的顶点,并且与的三边、、或它们的延长
线分别交于、、,则
1A B C C B A
C A B
h h h A B C l h h h BP CQ AR PC QA RB h h h ⋅⋅=⋅⋅=证:设、、分别是、、到直线的垂线的长度,则:
注:此定理常运用求证三角形相似的过程中的线段成比例的条件;
1//ABC CK CE ACK E AK D AC F DE CK BF CE ∆∠例:若直角中,是斜边上的高,是的平分线,点在上,是的中点,是与的交点,证明:。
,901EBC B BH EBC ACK HBC ACE HBC HCB ACE HCB BH CE EBC BC EP CK EP
CD AE KF
ACK D E F DA EK FC
KF EK CK EP BP BK KF BK FC AE AC AC BC BE FC BE
KF BK
FKB KC KE
∆∠∠=∠∠=∠∠+∠=∠+∠=︒
⊥∴∆=∆⋅⋅=====∴∆≅证:在中,作的平分线则:即:为等腰三角形作上的高,则:对于和三点、、依梅涅劳斯定理有:于是=即:=
依分比定理有:=//CKE BF CE
∆∴ 2P Q R ABC BC CA AB P Q R ABC BP 021PC P Q R CQ AR QA RB
∆∆⋅⋅=定理:设、、分别是的三边、、上或它们的延长线上的三点,并且
、、三点中,位于边上的点的个数为或,这时若
,求证:、、三点共线;
''
''''''''1BP BP 11PC PC 02,
PQ AB R CQ AR CQ AR AR AR QA R B
QA RB R B RB
P Q R ABC R R AB AB R R AB R R AR AR ⋅⋅=⋅⋅=∆>证:设直线与直线交于,于是由定理得:又,则:=由于在同一直线上的、、三点中,位于边上的点的个数也为或,因此与或者同在线段上,或者同在的延长线上;
若与同在线段上,则与必定重合,不然的话,设''''
'
',,AR AR AR AR AB AR AB AR BR BR BR BR BR BR
-<-<>这时即于是可得这与=矛盾''R R AB R R P Q R 类似地可证得当与同在的延长线上时,与也重合综上可得:、、三点共线;
注:此定理常用于证明三点共线的问题,且常需要多次使用 再相乘;
1111112.P ABC A B C P BC CA AB A B C ∆例点位于的外接圆上;、、是从点向、、引的垂线的垂足,证明点、、共线;
111111111
111111
cos ,
cos cos cos ,cos cos ,,1BA BP PBC
CA CP PCB CB AC CP PCA AP PAB
AB AP PAC BC PB PBA
PAC PBC PAB PCB PCA PBA BA CB AC A B C CA AB BC ⋅∠=-⋅∠⋅∠⋅∠=-=-⋅∠⋅∠∠=∠∠=∠∠+∠=⋅⋅证:易得:将上面三条式子相乘,且
可得=,依梅涅劳斯定理可知、、三点共线;
1111
11111111
1::K A B C D
AC
A D AC AD A
B
C
D BC BD B C B D =【练习】从点引四条直线,另两条直线分别交这四条直线于、、、和、、、,试证:2ABC BC CA AB D
E
F EF BC FD CA DE AB X Y Z ∆【练习】设不等腰的内切圆在三边、、上的切点分别为、、,则与,与,与的交点、、在同一条直线上;
1111121121122223AA BB CC O AB A B C BC B C A AC A C B A B C 【练习】已知直线,,相交于,直线和
的交点为,直线与的交点是,直
线与的交点是,试证:、、三点共线;
4E C A B F D AB ED CD AF CD AF EF BC L M N L M N 【练习】在一条直线上取点、、,在另一条上取点、、,记直线和,和,和,和的交点依次为、、,证明:、、共线
11111111111111111111
11
1111
111111//11111
:AD A D AD A D L A AL B BL LD A K A C LC B K
AD LC AK BC LD A D AK AC A K LC LC B C BK B D LD BK BD B K LD A C B D AD BC AC BD A D B C A AC AD BC BD ∆∆⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅⋅==练习的证明
证:若,结论显然成立;
若与相交与点,则把梅涅劳斯定理分别用于和可得:将上面四条式子相乘可得:即:1111111
:
C A
D B C B D
211
1
2BX CE AF
ABC XFE XC EA FB
BX FB
AE AF XC CE CY DC AZ EA
YA AF ZB BD
BX CY AZ
XC YA ZB
X Y Z ABC X Y Z ∆⋅⋅==⋅⋅=∆练习的证明
证:被直线所截,由定理可得:又代人上式可得:=
同理可得:==
将上面三条式子相乘可得:又、、都不在的边上,由定理可得、、三点共线
222111111112112112112112112
1121121123(,),(,),(,)111A B C BC B C AC A C AB A B OAB A B C OBC B C A OAC A C B AA OB BC OC BB CA OA CC AB OA BB AC CC OB BA AA OC CB BC ⋅⋅=⋅⋅=⋅⋅=练习的证明
证:设、、分别是直线和,和,和的交点,对所得的三角形和在它们边上的点:和,和,和,应用梅涅劳斯定理有:将上面的三条式子相乘可得:2222222221
,,AB CA AC CB BA A B C ⋅⋅=由梅涅劳斯定理可知共线
4(,,),(,,),(,,),(,,),(,,)11111EF CD EF AB AB CD U V W UVW L D E A M F B C N A C E B D F UE VL WD VA UF WM UN WC VB
VE WL UD WA VF YM VN UC WB WA UC VE WB UD VF
VA WC UE VB WD UF
VL W WL ∆⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅练习的证明
证:记直线和,和,和的交点分别为、、,对,应用梅涅劳斯定理于五组三元点,则有将上面五条式子相乘可得:1,,,M UN
L M N UM VN
⋅=∴点共线。
