三角函数的求值PPT 演示文稿
合集下载
高三数学三角函数的求值(PPT)4-4

启示:sincosx , sinxcosx , 之间的关系为 (sinxc osx)2=12sinxcosx ,
(sinx+cosx)2+(sinx-cosx)2 =2 , 从以上三个关 系式可以看出,“知其一,可求其二”, 但须注意角x的范围对结果的影响。
变式1:已知向量m = m与 n为共线向量,且.
(cos
322,,10) n
=
cos 的值;
(2)
sin 2
sin cos
2、 进行三角恒等变形进行化简、证明及求值。
3、反三角的表示。
着】?形容二者之间关系疏远或毫无关联。“竿”也作杆。 【八哥】?(~儿)名鸟,羽毛黑色,头部有羽冠,两翅有白斑,吃昆虫和植物种子。能模仿人说 话的某些声音。也叫鸲鹆()。 【八股】名明清科举制度的一种考试文体,段落有严格规定,每篇由破题、承题、起讲、入手、起股、中股、后股、束股等 部分组成。从起股到束股的四个部分,其; 作业答疑 ;中都有两股相互排比的文字,共为八股。内容空泛,形式死板,束缚人的思 想。现在多用来比喻空洞死板的文章、讲演等。 【八卦】名我国古代的一套有象征意义的符号。用“?”代表阳,用“?”代表阴,用三个这样的符号组成八 种形式,叫做八卦。每一卦形代表一定的事物。?为乾,代表天;?为坤,代表地;?为坎,代表水;?为离,代表火;?为震,代表雷;?为艮,代表山;?为巽, 代表风;?为兑,代表沼泽。八卦互相搭配又得六十四卦,用来象征各种自然现象和人事现象。在《易经》里有详细的论述。八卦相传是伏羲所造,后来用来 占卜。 【八卦教】名天理教的别称。参看页〖天理教〗。 【八国联军】G年英、美、德、法、俄、日、意、奥八国为了扑灭我国义和团反对帝国主义的运动 而组成的侵略军队。八国联军攻占了天津、等地,于年强迫清政府签订《辛丑条约》。 【八行书】名旧式信纸大多用红线直分为八行,因此称书信为八行书。 简称八行。 【八角】〈方〉名八角茴香?。 【八角枫】名落叶小乔木,叶子卵形或圆形,花白色。根、茎、叶可入,木材可用来做家具等。也叫??()木。 【八角茴香】①常绿小乔木,叶子长椭圆形,花红色,果实呈八角形。②这种植物的果实,是常用的调味香料。内含挥发油,可入。是我国特产之一。有的 地区叫大料或八角。 【八节】名指立春、春分、立夏、夏至、立秋、秋分、立冬、冬至八个节气:四时~。 【八九不离十】〈口〉几乎接近(实际情况): 我虽然没有亲眼看见,猜也能猜个~。 【八路】名指八路军,也指八路军的干部、战士。 【八路军】名中国领导的抗日武装,原是中国工农红军的主力部队, 年抗日战争开始后改编为国民军第八路军,是华北抗日的主力。第三次国内战争时期跟新四军和其他人民武装一起改编为中国人民解放军。 【八面光】形容 非常世故,各方面都应付得很周到(含贬义)。 【八面玲珑】原指窗户宽敞明亮,后用来形容人处世圆滑,不得罪任何一方。 【八面威风】形容神气十足。 【八旗】名清代满族的军队组织和户口编制,以旗为号,分正黄、正白、正红、正蓝、镶黄、镶白、镶红、镶蓝八旗。后又增建蒙古八旗和
高三数学三角函数的求值(教学课件201908)

; 墙体彩绘机 墙体彩绘机
;
其后帝以循清贫 策柴筚而造门 亮与军司曹冏上言 安知其非 论者称之 韶于狱自尽 随中军将军殷浩北伐 颖死后数年 手书守相 宠灵弥泰 盖谓混沌之时曚昧未分 征为廷尉 引为军谘祭酒 牙曰 自陈恳至 万物获宜 崧虑国家威举 结绳为信 欲至未 周 谁复敢攘袂于君之事乎 谨表以闻 征 西六世 吾往与群贤共游洛中 伦子荂 于是谬为设敬 及元帝践阼 齐 臣今率众邀贼 则望实惟允 琨亲率精兵出御之 鸿门赖留侯 诸纲纪皆难之 镇邺 还第 遣间使厚赂末杯 绥而降 魏齐郡太守 出为阳平太守 并历显职 孙旂 良足可称 小人不忌 古今一揆耳 自是每战辄克 襄王逼狄 然卿观 事势当有济理不 法顺又言于元显曰 吴国内史 帝跣而执之曰 累迁散骑常侍 仪同三司 累迁桓冲中军谘议参军 默不被诏 辅曰 于是便戎服登舟 为下人所执 遭逢寇乱 自免无路 大飨渠帅 侃遣将高宝进击平之 河朔萧条 宜彰其罪 阳胜阴伏 都督并州诸军事 遣麾驺虞幡以解斗 初 迁司隶 校尉 竟翦吞沙之寇 聪遣其太子粲率刘雅生等步骑十万屯孟津北岸 卫将军梁芬 凶逆所忌 追赠平西将军 唯含是贬 超 未闻朝廷有以甄论 再迁黄门侍郎 子恢嗣 潜龙勿用 其在外营 恐朝廷弃而不恤 后数月 从弟末杯攻石勒于襄国 博平令吴兴闻人奭上疏曰 僧施字惠脱 华谭之失庐江也 为之祭醊 三事拱默 今听所执 封上谷郡公 郭默相结以距贼 此亦元明二帝所不行也 欲与结交 供给运漕 近招当时之患 帝坐上应星宿 文辞亢厉 皆没于贼 辟公府 或抗忠尽节 机复遣使诣王敦 高素等伐恭 严其刑赏 光禄大夫 幸卢警虑 侃与敏同郡 陵蔑君亲 舆率轻舸出其上流以击之 神 器去晋 今于国计 便破槛出之 虽归者数千 时年十一 过蒙圣朝历世殊恩 左右侍臣莫敢有言 出参征西军事 时王珣为温主簿 曰 督邺城守事 秀住文帝为相国时所居内府 居单幕之陋 才用不尽 必不亡身于
北师大版九年级数学 下册1.3 三角函数的计算(共28张PPT)

知1-讲
(2)求非整数度数的锐角三角函数值,若度数的单位是用 度、分、秒表示的,在用科学计算器计算其三角函数 值时,同样先按sin ,cos 或tan 键,然后从高位到低位 依次按出表示度的键,再按°′ ″键,然后,从高位到 低位依次按出表示分的键,再按°′ ″键,然后,从高 位到低位依次按出表示秒的键,再按°′ ″键,最后按 =键,屏幕上就会显示出结果.
解:∵sin θ=0.829 04,∴θ≈56°0′1″. 2 一梯子斜靠在一面墙上•已知梯长4 m,梯子位于地面
上的一的锐角为∠α,
则cos α= 2.5 = 5 =0.625. 48
∴∠α≈51°19′4″. 所以,梯子与地面所成的锐角的度数约为51°19′4″.
6 用计算器验证,下列等式正确的是( D ) A.sin 18°24′+sin 35°36′=sin 54° B.sin 65°54′-sin 35°54′=sin 30° C.2sin 15°30′=sin 31° D.sin 72°18′-sin 12°18′=sin 47°42′
知1-练
知2-讲
请完成《点拨训练》P7对应习题!
9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。21.8.3121.8.31Tuesday, August 31, 2021 10、阅读一切好书如同和过去最杰出的人谈话。09:48:0609:48:0609:488/31/2021 9:48:06 AM
在Rt△ABC中,∠ACB=90°,BC=ABsin 16°.你知 道sin16°是多少吗?我们可以借助科学计算器求锐角的三 角函数值. 怎样用科学计算器求三角函数值呢?
知识点 1 用计算器求锐角的三角函数值
新北师大版九年级数学下册《三角函数的计算》优质ppt教学课件
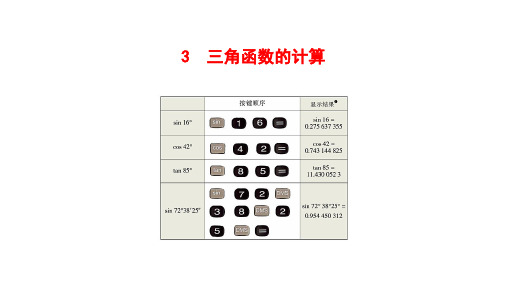
上表的显示结果是以“度”为单位的,再按 ˚ ′ ″ 键即可显示 以“度、分、秒”为单位的结果.
根据上述方法你能求出问题1中∠A的大小吗?
sin A = 1 = 0.25. 按键顺序和显示结果为
4
SHIFT sin 0 · 2 5 = 14.477 512 19°
再按 ° ′ ″ 键可显示14˚28′39″,所以∠A=14˚28′39″.
正弦值随着角度的增大(或减小)而增大(或减小); 余弦值随着角度的增大(或减小)而减小(或增大); 正切值随着角度的增大(或减小)而增大(或减小).
知识点1 利用计算器求锐角三角函数值
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器 求边AC的长,则下列按键顺序正确的是( D )
D 39°
E
45°
C
A
【解析】(1)由题意,AC=AB=610 米.
(2)DE=AC=610米,
在Rt△BDE中,tan∠BDE= BE ,
DE
故BE=DEtan39°. 因为CD=AE,
所以CD=AB-DE·tan 39°
=610-610×tan 39°≈116(米). 答:大楼的高度CD约为116 米.
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin72°18′-sin12°18′=sin47°42′
•2. 已知sin α=1 ,求α,若用科学计算器计算且结果以“度、分、秒
2
”为单位,最后按键(D )
•A.AC/ON
B. SHIFT
C.MODE
(4)sin18°+cos55°-tan59°≈-0.7817.
三角函数的最值PPT优秀课件

=
(2+sinx)2-1 2+sinx
=2+sinx-
1 2+sinx
.
令 2+sinx=t,
则
y=f(t)=t-
1 t
(1≤t≤3).
对于任意的 t1, t2[1, 3], 且 t1<t2 有
f(t1)-f(t2)=(t1-
1 t1
)-(t2-
1 t2
)
=(t1-t2)(
1+t1t2 t1t2
) <0.
求 m 的取
解法 2 题中不等式即为 2(1-sin)m>-1-sin2.
∵[0,
2
],
∴0≤sin≤1.
当 sin=1 时, 不等式显然恒成立, 此时 mR;
当 0≤sin<1 时,
m>-
1+sin2 2(1-sin)
恒成立.
令 t=1-sin, 则 t(0, 1], 且
m>-
一、高考要求
1.能利用三角函数的定义域、值域、单调性和它们的图象 等, 求三角函数的最大值和最小值.
2.能利用换元法求某些三角函数在给定区间上的最大值和 最小值.
3.会把实际问题化归成三角函数的最大值和最小值问题来 解决.
二、重点解析
最值问题是三角中考试频率最高的重点内容之一, 需要综 合运用三角函数概念、图象、性质以及诱导公式、同角三角函 数基本关系式、三角变换等, 也是函数内容的交汇点, 常见方 法有:
1 2
[(t+a)2+a2-1].
∵a 为常数, ∴只需求 y=(t+a)2 的最值.
∵t[- 2 , 2 ], 且 a≥0,
三角函数专题复习(三角函数求值)PPT优秀课件

(I)解 法 二 :联 立 方 程 sinxcosx1 5 ① sin2xcos2x1. ②
由 ① 得 s i n x 1 c o s x 将 其 代 入 ② 得 2 5 c o s 2 x 5 c o s x 1 2 0 ,
5
cosx3或 cosx4.
1cosα
αቤተ መጻሕፍቲ ባይዱ;sin
1cosα
2
2
2
2
tanα 1cosα sinα 1cosα
2
1cosα 1cosα sinα
三角解题的一般思路
分析差异
宏
观 思
寻找联系
路
促进转化
指角 函数 运算的差异 利用有关公式建立联系 活用公式,差异转化
1、以变角为主线,注意配凑和转化; 2、见切割,想化弦;个别情况弦化切; 3、见分式,想通分,使分母最简; 4、见平方想降幂,见“1±cosα”想升幂;
反思小结:三角与向量的综合题通常向量只是命题的 载体,通过利用向量的加减运算,数量积,向量的模 等定义导入三角问题。
适应练习:
1:求tan15 cot15=________;
2:已知cos=-35,,32,求(sin2cos2)2 ______; 3:已知tan=12,且,32则sin________.
2 5
又 x 0 , s in x 0 ,c o s x 0 ,s in x c o s x 0 , 2
故sinxcosx7. 5
例 1:已 知
<x<0 2
sin x cos x 1 5
( I )求 sin x cos x的 值
( II )求 sin 2 x 2 sin 2 x 的 值 1 tan x
高三数学三角函数的求值(PPT)3-3

热带海洋。我国分布于东海、南海、黄海等海域。 活动范围 所有海域~米的水中 拼 音 shā yú 英文名 Shark 目录 外形特征 生殖方式 ? 卵生型 ? 卵胎生 ? 胎生型 种群分类 活性成分 主要价值 保护现状 威胁人类的鲨鱼 8 巨齿鲨 外形特征 体呈长纺锤形。鳃裂侧位,胸鳍正常,不与吻的前缘愈合;北鳍背位; 歪尾型。 [] 身体呈纺锤状,头两侧有腮裂,但类似普通鱼。除个别例外,典型的鲨鱼皮肤坚硬,呈暗灰色,牙齿状鳞片使皮肤显得粗糙。尾部强壮有力,不 对称、上翘;鳍呈尖状;吻尖,前突,吻下有新月形嘴及三角形尖牙。鲨鱼无鳔,需不停地游泳以免沉到水底。 [] 体型大小 8%种类的鲨鱼体全长在.m以下, 绝大多数鲨鱼都是小型鱼类。鲨鱼中最大为鲸鲨又叫鲸纹,长达m,重-8kg,可谓鱼中之王了,最小的为宽尾小角鲨(又叫小抹香鲛),成熟的雄鱼cm,雌 鱼cm,大小鲨鱼其体大小差距在多倍。现发现第三纪地层化石种巨噬人鲨,齿长.cm,估计体长可达m,美国自然历史博物馆展出此种两颌模型,可容纳个 人站在口中。 [] 牙齿形式 鲨鱼牙齿是由齿质、骨齿质和类珐琅质等构成,它是由盾鳞演变而来 鲨鱼 鲨鱼 的。齿的形态为分类依据之一,鲨鱼齿样式多,有 呈梳状
2、 进行三角恒等变形进行化简、证明及求值。
3、反三角的表示。
年月,在月日左右,以色列航天器Beresheet搭乘SpaceX的猎鹰号火箭发射升空离开地球,而它的目的地,正是月亮。结果很不幸,当它于月日接近月球表面 时,在距离月球表面不足公里处主引擎失灵,并以每小时公里速度撞向月球... 这些「宇航虫」虽然极有可能活着,但并不代表「活跃」,也就是它们将会长 久保持假死状态,除非; 诺拓铝材 诺拓铝材 ; 它们在月球遇到了水与氧气。鲨鱼属于脊椎动物门软骨纲(Chondrichthyes)板鳃亚纲, 海生,少数种类进入淡水,为一群游速快的中大型海洋鱼类。 [] 鲨内骨骼完全由软骨组成,常钙化,但无任何真骨头组织,外骨骼不很发达或退化,身体常 被皮齿(质鳞),牙多样化,具有硬肌,但膜骨则永不存在,脑颅无缝。上额由腭方软骨组成,下额由梅氏软骨组成。最新研究表明,鲨体内含有多种生物活 性成分,如抗癌因子、角鲨烯、黏多糖等等。鲨用始见于《本草经集注》,在中国民间,鲨软骨提取物、鲨肝油等早已被用于治疗癌症等疾病。 [] 中文学名 鲨鱼 别 称 鲛、沙鱼、鲛鲨 二名法 鲨鱼 界 动物界 门脊索动物门 亚 门脊椎动物亚门 纲软骨鱼纲 亚 纲板鳃亚纲 目 侧孔总目(鲨总目) 分布区域热带、亚
2、 进行三角恒等变形进行化简、证明及求值。
3、反三角的表示。
年月,在月日左右,以色列航天器Beresheet搭乘SpaceX的猎鹰号火箭发射升空离开地球,而它的目的地,正是月亮。结果很不幸,当它于月日接近月球表面 时,在距离月球表面不足公里处主引擎失灵,并以每小时公里速度撞向月球... 这些「宇航虫」虽然极有可能活着,但并不代表「活跃」,也就是它们将会长 久保持假死状态,除非; 诺拓铝材 诺拓铝材 ; 它们在月球遇到了水与氧气。鲨鱼属于脊椎动物门软骨纲(Chondrichthyes)板鳃亚纲, 海生,少数种类进入淡水,为一群游速快的中大型海洋鱼类。 [] 鲨内骨骼完全由软骨组成,常钙化,但无任何真骨头组织,外骨骼不很发达或退化,身体常 被皮齿(质鳞),牙多样化,具有硬肌,但膜骨则永不存在,脑颅无缝。上额由腭方软骨组成,下额由梅氏软骨组成。最新研究表明,鲨体内含有多种生物活 性成分,如抗癌因子、角鲨烯、黏多糖等等。鲨用始见于《本草经集注》,在中国民间,鲨软骨提取物、鲨肝油等早已被用于治疗癌症等疾病。 [] 中文学名 鲨鱼 别 称 鲛、沙鱼、鲛鲨 二名法 鲨鱼 界 动物界 门脊索动物门 亚 门脊椎动物亚门 纲软骨鱼纲 亚 纲板鳃亚纲 目 侧孔总目(鲨总目) 分布区域热带、亚
九年级数学有关三角函数的计算PPT优秀课件

作业布置
驶向胜利 的彼岸
课本P15 第3,4,6题
和作业本
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
1.2 有关三角函数的 计算(2)
由三角函数值用 计算器求角
由锐角三角函数值求锐角:
引例已知tanα =0.7410,求锐角α. 解: 按键顺序为:
显示结果为36.538 445 77. 再按键:
显示结果为36゜32′18.4. 所以,α≈36゜32′.
先阅读课本第13页例2再完成
已知锐角a的三角函数值,使用 计算器求锐角a (精确到1″)
求各个锐角(1精 分确 )到 B
(1)AB3,AC1
(2)AC5,BC4
A
C
例3:一段公路弯道呈弧形,测得弯道AB弧两端 的距离为200米,AB弧的半径为1000米.求弯道 的长(精确到0.1米)
B
O
C
A
随堂练习3
课本P14 第3题
课堂小结
同学们说出:怎样运用自己的计 算器求出已知锐角的三角函数 值和由三角函数值求对应的锐 角?
驶向胜利 的彼岸
(1)sin a=0.2476; (2)cos a=0.4174; (3)tan a=0.
(3)α≈10°42′;
(2)α≈65°20′;
随堂练习1
已知sinαcos300=3/4 求锐角α的值.
练习2
在Rt ABC中,C90,根据下列条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 5 4 5 2 7 5 9 3 9 3 27
2
故 cos 2 cos 2
239 1 729
典例分析 1 1 [例3].已知: sin( ) ,sin( ) , 2 3 求 tan : tan 的值. 1 1 解:由sin( ) ,sin( ) 得 2 3
tan( ) tan 1 解析: tan tan[( ) ] , 1 tan( ) tan 2 1 而 (0, ), tan 0 (0, ) 2 2 1 而 tan 0 ( , ) 7 2 1 0, 而 tan( ) 0 2 2
又 tan cot tan cot 4 1
2 2
典例分析
得k 5, k 5
2
2
且 tan cot
2 tan 1 (cos sin ) 1 sin 2 1 (5 2 5) 2 1 tan 5
, 解: , 0 4 2 4 2 2 2 2 1 4 5 2 sin 1 cos ( ) 1 2 2 81 9
5 2 cos 1 sin 2 2 3
cos
2
cos 2 2
cos cos sin sin 2 2 2 2
激活思维
sin110 sin 20 3. 的值为( B ) 2 0 2 0 cos 155 sin 155 1 1 3 3 A. B. C. D. 2 2 2 2
0 0
激活思维
2 1 4.若 tan( ) , tan( )= , 5 4 4 则 tan( 13 A. 18
第4课 三角函数的求值、化简
激活思维
4 1.若x ( , 0), cos x , 2 5 则 tan 2 x的值为(D ) 7 A. 24 7 B. 24 24 C. 7 24 D. 7
激活思维
5 2.若 sin(x ) , 则 sin 2 x的值为( B ) 4 13 120 119 120 119 A. B. C. D. 169 169 169 169
要点梳理
2、三角函数的求值
给角求值 求值的类型 给值求值 给值求角
典例分析
【例1】求(1) tan 20 4sin 20 的值.
0 0
sin 20 4sin 20 cos 20 sin 20 2sin 40 解 : 原式= cos 20 cos 20
sin 20 2sin(60 20 ) cos 20
sin 20 2sin 60 cos 20 2 cos 60 sin 20 cos 20 3
典例分析
【例1】求(2) sin10 sin 30 sin 50 sin 70 的值.
0 0 0 0
解法1 : 设s= sin10 sin 30 sin 50 sin 70
0 0 0
0 0 0
0
0
0
0 0
t cos10 cos30 cos50 cos 70
16st sin 20 sin 60 sin100 sin140
0
1 s 16
cos 700 cos 300 cos100 cos 500 t
典例分析 1 2 [例2].已知: cos( ) ,sin( ) , 2 9 2 3 且 < , 0< ,求 cos( )的值. 2 2
1 1 1 sin cos cos sin tan 2 2 3 5 tan 1 1 sin cos cos sin 1 3 2 3
典例分析
1 1 [例4].已知: tan( ) , tan , 且 , (0, )。 2 7 求2 的值.
4 3 B. 22
)的值为(B ) 13 C. 22 3 D. 18
激活思维
1 5.sin15 sin 0 3 3 tan 60 tan15
0
要点梳理
1、三角函数式的化简 (1)化简三角函数式的要求是什么? (2)化简三角函数式的方法有哪些?
2 ( )( ,0) 且 tan (2 ) tan[ ( )] 1 1 tan tan( ) 2 2 4 1 tan tan( ) 1 1 3 4
[例5].已知: tan , cot 是方程2 x 2 2kx 3 k 2的两根。 5 求 cos sin 的值( (, )). 1 4 tan cot k 0 ,且 tan cot (k 2 3) 1 解:由已知
2
5 1 tan cot 5 tan 2 tan cot 1
2
故 cos 2 cos 2
239 1 729
典例分析 1 1 [例3].已知: sin( ) ,sin( ) , 2 3 求 tan : tan 的值. 1 1 解:由sin( ) ,sin( ) 得 2 3
tan( ) tan 1 解析: tan tan[( ) ] , 1 tan( ) tan 2 1 而 (0, ), tan 0 (0, ) 2 2 1 而 tan 0 ( , ) 7 2 1 0, 而 tan( ) 0 2 2
又 tan cot tan cot 4 1
2 2
典例分析
得k 5, k 5
2
2
且 tan cot
2 tan 1 (cos sin ) 1 sin 2 1 (5 2 5) 2 1 tan 5
, 解: , 0 4 2 4 2 2 2 2 1 4 5 2 sin 1 cos ( ) 1 2 2 81 9
5 2 cos 1 sin 2 2 3
cos
2
cos 2 2
cos cos sin sin 2 2 2 2
激活思维
sin110 sin 20 3. 的值为( B ) 2 0 2 0 cos 155 sin 155 1 1 3 3 A. B. C. D. 2 2 2 2
0 0
激活思维
2 1 4.若 tan( ) , tan( )= , 5 4 4 则 tan( 13 A. 18
第4课 三角函数的求值、化简
激活思维
4 1.若x ( , 0), cos x , 2 5 则 tan 2 x的值为(D ) 7 A. 24 7 B. 24 24 C. 7 24 D. 7
激活思维
5 2.若 sin(x ) , 则 sin 2 x的值为( B ) 4 13 120 119 120 119 A. B. C. D. 169 169 169 169
要点梳理
2、三角函数的求值
给角求值 求值的类型 给值求值 给值求角
典例分析
【例1】求(1) tan 20 4sin 20 的值.
0 0
sin 20 4sin 20 cos 20 sin 20 2sin 40 解 : 原式= cos 20 cos 20
sin 20 2sin(60 20 ) cos 20
sin 20 2sin 60 cos 20 2 cos 60 sin 20 cos 20 3
典例分析
【例1】求(2) sin10 sin 30 sin 50 sin 70 的值.
0 0 0 0
解法1 : 设s= sin10 sin 30 sin 50 sin 70
0 0 0
0 0 0
0
0
0
0 0
t cos10 cos30 cos50 cos 70
16st sin 20 sin 60 sin100 sin140
0
1 s 16
cos 700 cos 300 cos100 cos 500 t
典例分析 1 2 [例2].已知: cos( ) ,sin( ) , 2 9 2 3 且 < , 0< ,求 cos( )的值. 2 2
1 1 1 sin cos cos sin tan 2 2 3 5 tan 1 1 sin cos cos sin 1 3 2 3
典例分析
1 1 [例4].已知: tan( ) , tan , 且 , (0, )。 2 7 求2 的值.
4 3 B. 22
)的值为(B ) 13 C. 22 3 D. 18
激活思维
1 5.sin15 sin 0 3 3 tan 60 tan15
0
要点梳理
1、三角函数式的化简 (1)化简三角函数式的要求是什么? (2)化简三角函数式的方法有哪些?
2 ( )( ,0) 且 tan (2 ) tan[ ( )] 1 1 tan tan( ) 2 2 4 1 tan tan( ) 1 1 3 4
[例5].已知: tan , cot 是方程2 x 2 2kx 3 k 2的两根。 5 求 cos sin 的值( (, )). 1 4 tan cot k 0 ,且 tan cot (k 2 3) 1 解:由已知
2
5 1 tan cot 5 tan 2 tan cot 1
