历届东南数学奥林匹克试题
2009年中国第六届东南地区数学奥林匹克竞赛试题及解答(2009年7月28日)

第一天(2009年7月28日上午8:00-12:00)江西·南昌1. 试求满足方程22-+=的所有整数对(,)21262009x xy yx y.(张鹏程供题)2. 在凸五边形ABCDE中,已知,,==≠,且,,,B C D EAB DE BC EA AB EA四点共圆.证明:,,,=.A B C D四点共圆的充分必要条件是AC AD(熊斌供题)3. 设,,x y z R+∈222=-=--;x y z y z x z x y(),(),()求证:2222()++≥++.a b c ab bc ca(唐立华供题)4. 在一个圆周上给定十二个红点;求n的最小值,使得存在以红点为顶点的n个三角形,满足:以红点为端点的每条弦,都是其中某个三角形的一条边.(陶平生供题)第二天(2009年7月29日 上午8:00-12:00) 江西·南昌 5.设1,2,,9 的所有排列129(,,,)X x x x = 的集合为A ;X A ∀∈,记1239()239f X x x x x =++++ ,{()}M f X X A =∈;求M . (其中M 表示集合M 的元素个数)(熊斌供题)6.已知O 、I 分别是ABC ∆的外接圆和内切圆;证明:过O 上的任意一点D ,都可以作一个三角形DEF ,使得O 、I 分别是DEF ∆的外接圆和内切圆.(陶平生供题)7. 设(2)(2)(2)(,,)131313x y z y z x z x y f x y z x y y z z x---=++++++++, 其中,,0x y z ≥ ,且1x y z ++=. 求(,,)f x y z 的最大值和最小值.(李胜宏供题)8.在8×8方格表中,最少需要挖去几个小方格,才能使得无法从剩余的方格表中裁剪出一片形状如下完整的T 型五方连块?(孙文先供题)第六届中国东南地区数学奥林匹克试题与解答第一天1. 试求满足方程2221262009x xy y -+=的所有整数对(,)x y . (张鹏程供题)解: 设整数对(,)x y 满足方程22212620090x xy y -+-= …(1),将其看作关于x 的一元二次方程,其判别式()2222441262009500(4)36y y y ∆=-⨯-=-+的值应为一完全平方数; 若224y >,则0∆<;若224y <,则2y 可取2220,1,2,3,相应的∆值分别为8036,7536,6036和3536 ,它们皆不为平方数;因此,仅当224y =时,()2225004366y ∆=-+=为完全平方数.若4=y ,方程(1)化为2870x x -+=, 解得1=x 或7x =;若4-=y ,方程(1)化为 2870x x ++=,解得1-=x 或7x =-.综上可知,满足原方程的全部整数对为:()()()()(),1,4,7,4,1,4,7,4x y =----. 2. 在凸五边形ABCDE 中,已知,,AB DE BC EA AB EA ==≠,且,,,B C D E 四点共圆.证明:,,,A B C D 四点共圆的充分必要条件是AC AD =. (熊斌供题)证明:必要性:若,,,A B C D 共圆,则由,AB DE BC EA ==,得BAC EDA ∠=∠,ACB DAE ∠=∠,所以ABC DEA ∠=∠,故得AC AD =;充分性:记BCDE 所共的圆为O ,若AC AD =,则圆心O 在CD 的中垂线AH 上,设点B 关于AH 的对称点为F ,则F 在O 上,且因AB EA ≠,即D E D F ≠,所以,E F不共点,且AFD ∆≌ABC ∆,又由,AB DE BC EA ==,知AED ∆≌CBA ∆,因此,AED ∆≌DFA ∆,故由AED DFA ∠=∠,得AEFD 共圆,即点A 在DEF 上,也即点A在O 上,从而,,,A B C D 共圆.3. 设,,x y z R +∈222(),(),()x y z y z x z x y =--=-;求证: 2222()a b c ab bc ca ++≥++.(唐立华供题)()()(),y z z x x y =-+--()()()z x x y y z =-+--,()()()x y y z z x =-+--.所以[]2()()()()()()0y z z x x y y z z x x y =-+++---≤, 于是 2222()()a b b c c a a b c ++-++=0≤, 故 2222()a b c a b b c c a++≥++. 4. 在一个圆周上给定十二个红点;求n 的最小值,使得存在以红点为顶点的n 个三角形,满足:以红点为端点的每条弦,都是其中某个三角形的一条边.(陶平生供题)解:设红点集为:{}1212,,,A A A A = ,过点1A 的弦有11条,而任一个含顶点1A 的三角形,恰含两条过点1A 的弦,故这11条过点1A 的弦,至少要分布于6个含顶点1A 的三角形中;同理知,过点(2,3,,12)i A i = 的弦,也各要分布于6个含顶点i A 的三角形中,这样就需要12672⨯=个三角形,而每个三角形有三个顶点,故都被重复计算了三次,因此至少需要72243=个三角形. 再说明,下界24可以被取到.不失一般性,考虑周长为12的圆周,其十二等分点为红点,以红点为端点的弦共有21266C =条.若某弦所对的劣弧长为k ,就称该弦的刻度为k ;于是红端点的弦只有6种刻度,其中,刻度为1,2,,5 的弦各12条,刻度为6的弦共6条;如果刻度为,,a b c (a b c ≤≤)的弦构成三角形的三条边,则必满足以下两条件之一:3或者a b c +=;或者12a b c ++=;于是红点三角形边长的刻度组(),,a b c 只有如下12种可能:()()()1,1,2,2,2,4,3,3,6,()()()()()()()()()2,5,5,1,2,3,1,3,4,1,4,5,1,5,6,2,3,5,2,4,6,3,4,5,4,4,4;下面是刻度组的一种搭配:取()()()1,2,3,1,5,6,2,3,5型各六个,()4,4,4型四个;这时恰好得到66条弦,且其中含刻度为1,2,,5 的弦各12条,刻度为6的弦共6条;今构造如下:先作()()()1,2,3,1,5,6,2,3,5型的三角形各六个,()4,4,4型的三角形 三个,再用三个()2,4,6型的三角形来补充.()1,2,3型六个:其顶点标号为:{}{}{}{}{}{}2,3,5,4,5,7,6,7,9,8,9,11,10,11,1,12,1,3; ()1,5,6型六个:其顶点标号为:{}{}{}{}{}{}1,2,7,3,4,9,5,6,11,7,8,1,9,10,3,11,12,5; ()2,3,5型六个:其顶点标号为:{}{}{}{}{}{}2,4,11,4,6,1,6,8,3,8,10,5,10,12,7,12,2,9;()4,4,4型三个:其顶点标号为:{}{}{}1,5,9,2,6,10,3,7,11;()2,4,6型三个:其顶点标号为:{}{}{}4,6,12,8,10,4,12,2,8.(每种情况下的其余三角形都可由其中一个三角形绕圆心适当旋转而得).这样共得到24个三角形,且满足本题条件,因此,n 的最小值为24.第六届中国东南地区数学奥林匹克试题解答第二天5.设1,2,,9 的所有排列129(,,,)X x x x = 的集合为A ;X A ∀∈,记1239()239f X x x x x =++++ ,{()}M f X X A =∈;求M .(其中M 表示集合M 的元素个数).(熊斌供题)解:我们一般地证明,若4n ≥,对于前n 个正整数1,2,,n 的所有排列12(,,,)n n X x x x = 构成的集合A ,若123()23n n f X x x x nx =++++ ,{()}n M f X X A =∈,则366n n n M -+=.下面用数学归纳法证明:n M (1)(2)(1)(2)(1)(21),1,,666n n n n n n n n n ++++++⎧⎫=+⎨⎬⎩⎭.当4n =时,由排序不等式知,集合M 中的最小元素是{}()4,3,2,120f =,最大元素是{}()1,2,3,430f=.又,{}(){}(){}()3,4,2,121,3,4,1,222,4,2,1,323f f f ===,{}(){}(){}(){}()3,2,4,124,2,4,1,325,1,4,3,226,1,4,2,327f f f f ====, {}(){}()2,1,4,328,1,2,4,329ff ==,所以,4M ={}20,21,,30 共有11=34466-+个元素.因此,4n =时命题成立.假设命题在1n -(5n ≥)时成立;考虑命题在n 时的情况.对于1,2,,1n - 的任一排列1121(,,,)n n X x x x --= ,恒取n x n =,得到1,2,,n 的一个排列121,,,,n x x x n - ,则1nkk kx=∑121n k k n kx -==+∑.由归纳假设知,此时1nk k kx =∑取遍区间222(1)(1)(1)(21)(5)(1)(21),,6666n n n n n n n n n n n n n ⎡⎤-+--+++⎡⎤++=⎢⎥⎢⎥⎣⎦⎣⎦上所有整数. 再令1n x =,则11111(1)(1)2n n n k k k k k k n n kx n kx n k x --===-=+=+-+∑∑∑11(1)(1)2n k k n n k x -=+=+-∑, 再由归纳假设知,1nkk kx=∑取遍区间2(1)(1)(1)(1)(1)(21)(1)(2)2(2),,262666n n n n n n n n n n n n n n n ⎡⎤+-++--+++⎡⎤++=⎢⎥⎢⎥⎣⎦⎣⎦上的所有整数.因为222(2)(5)66n n n n ++≥,所以,1nk k kx =∑取遍区间(1)(2)(1)(21),66n n n n n n ++++⎡⎤⎢⎥⎣⎦ 上的所有整数.即命题对n 也成立.由数学归纳法知,命题成立.由于 3(1)(21)(1)(2)6666n n n n n n n n ++++-+-=,从而,集合n M的元素个数为366n n -+.特别是,当9n =时,9121M M ==.6.已知O 、I 分别是ABC ∆的外接圆和内切圆;证明:过O上的任意一点D ,都可作一个三角形DEF ,使得O 、I 分别是DEF ∆的外接圆和内切圆.(陶平生供题)证:如图,设OI d =,,R r 分别是ABC ∆的外接圆和内切圆半径,延长AI 交O 于K ,则2s in 2AK I K B R ==,sin 2r AI A =,延长OI 交O 于,M N ;则()()2R d R d IM IN AI KI Rr +-=⨯=⨯=,即222R d Rr -=;过D 分别作I 的切线,DE DF ,,E F 在O 上,连EF ,则DI 平分EDF ∠,只要证,EF 也与I 相切;设DI O P = ,则P 是 EF的中点,连PE ,则 2sin 2DPE R =,sin2r DI D =,()()22ID IP IM IN R d R d R d ⋅=⋅=+-=-,所以2222sin 2sin 22R d R d D DPI R PE DI r --==⋅==,N F由于I 在角D 的平分线上,因此点I 是DEF ∆的内心, (这是由于,()()0011180180222D E PEI PIE P F +∠=∠=-∠=-∠=,而 2D PEF ∠=,所以2EFEI ∠=,点I 是DEF ∆的内心). 即弦EF 与I 相切. 7.设(2)(2)(2)(,,)131313x y z y z x z x y f x y z x y y z z x---=++++++++, 其中,,0x y z ≥ ,且 1x y z ++=. 求(,,)f x y z 的最大值和最小值.(李胜宏供题)解:先证1,7f ≤当且仅当13x y z ===时等号成立. 因(31)121313x x y xf x y x y+-=∑=-∑++++ … ()*由哥西不等式:2()113(13)(13)x x x y x x y x x y ∑∑≥=++∑++∑++,因为7(13)(24)2.3x x y x x y z xy ∑++=∑++=+∑≤从而 3,137x x y ∑≥++3112,77f ≤-⨯=max 1,7f =当且仅当13x y z ===时等号成立. 再证0,f ≥当1,0x y z ===时等号成立.事实上,(2)(2)(2)(,,)131313x y z y z x z x y f x y z x y y z z x---=++++++++=2121()()13131313xy xz x y y z z x x y -+-++++++++21()1313yz y z z x+-++++ 77(13)(13)(13)(13)xyz xyz x y y z z x x y =+++++++++70(13)(13)xyzy z z x +≥++++ 故min 0f =,当1,0x y z ===时等号成立.另证:设{}min ,,z x y z =,若0z =,则22(,,0)0131242xy xy xy xyf x y x y y x y x y=-=-=+++++;下设,0x y z ≥>,由()*式,要证0f ≥,只要证,1132x x y ≤++∑ …①注意到12242x yx y x y =+++,于是①等价于 8()()()132413213241313z x x y y z x yz x x y x y x y y z x y x y y z≤-+-=++++++++++++++即 248131313x y x yz x x y y z+≤+++++++ …②而由柯西不等式,可得228(2)1313(13)(13)/2x y x y x y y z x x y y y z +=+++++++++ 222(2)24(3)(3)/213x y x yx x xy y y yz z x++≥=+++++++ 即②成立,从而0f ≥,故min 0f =,当1,0x y z ===时等号成立.8.在8×8方格表中,最少需要挖去几个小方格,才能使得无法从剩余的方格表中裁剪出一片形状如下完整的T 型五方连块?(孙文先供题)答:至少要如下图挖去14个小方格.如右图,将8×8棋盘切为五个区域.中央部份的区域至少要挖去2个小方格才能使T 形的五方块放不进去。
【最新精选】2016年第3届中国东南数学奥林匹克试题及答案

第三屆中國東南地區數學奧林匹克第一天(2006年7月27日, 8:00-12:00, 南昌)一、 設0,a b >>2()2()4a b x abf x x a b++=++.證明:存在唯一的正數x ,使得11333()()2a b f x +=.二、 如圖所示,在△ABC 中,90,,A B C D G ∠=︒是邊CA 上的兩點,連接BD ,BG 。
過點A ,G 分別作BD 的垂線,垂足分別為E ,F ,連接CF 。
若BE =EF ,求證:ABG DFC ∠=∠。
三、 一副紙牌共52張,其中“方塊”、“梅花”、“紅心”、“黑桃”每種花色的牌各13張,標號依次是2,3,,10,,,,J Q K A ,其中相同花色、相鄰標號的兩張牌稱為“同花順牌”,並且A 與2也算是順牌(即A 可以當成1使用). 試確定,從這副牌中取出13張牌,使每種標號的牌都出現,並且不含“同花順牌”的取牌方法數。
四、 對任意正整數n ,設n a 是方程31xx n+=的實數根,求證: (1) 1n n a a +>; (2) 211(1)nn i ia i a =<+∑。
第二天(2006年7月28日, 8:00-12:00, 南昌)五、 如圖,在ABC ∆中,60A ∠=︒,ABC ∆的內切圓I 分別切邊AB 、AC 於點D 、E ,直線DE 分別與直線BI 、CI 相交於點F 、G ,證明:12FG BC =。
BA六、 求最小的實數m ,使得對於滿足a +b +c =1的任意正實數a ,b ,c ,都有333222(61m a b c a b c ++≥+++)()。
七、 (1)求不定方程2()mn nr mr m n r ++=++的正整數解(,,)m n r 的組數。
(2)對於給定的整數k >1,證明:不定方程()mn nr mr k m n r ++=++至少有3k +1組正整數解(,,)m n r 。
2004年首届中国东南地区数学奥林匹克竞赛考试试题

首届中国东南地区数学奥林匹克竞赛试题第一天(2004年7月10日 8:00 — 12:00 温州)一、设实数a 、b 、c 满足2223232a b c ++=,求证:39271a b c---++≥ 二、设D 是ABC ∆的边BC 上的一点,点P 在线段AD 上,过点D 作一直线分别与线段AB 、PB 交于点M 、E ,与线段AC 、PC 的延长线交于点F 、N 。
如果DE=DF , 求证:DM=DN三、(1)是否存在正整数的无穷数列{}n a ,使得对任意的正整数n 都有2122n n n a a a ++≥。
(2)是否存在正无理数的无穷数列{}n a ,使得对任意的正整数n 都有2122n n n a a a ++≥。
四、给定大于2004的正整数n ,将1、2、3、…、2n 分别填入n ×n 棋盘(由n 行n 列方格构成)的方格中,使每个方格恰有一个数。
如果一个方格中填的数大于它所在行至少2004个方格内所填的数,且大于它所在列至少2004个方格内所填的数,则称这个方格为“优格”。
求棋盘中“优格”个数的最大值。
第二天(2004年7月11日 8:00 — 12:00 温州)五、已知不等式63)cos()2sin 2364sin cos a a πθθθθ+-+-<++对于0,2πθ⎡⎤∈⎢⎥⎣⎦恒成立,求a 的取值范围。
六、设点D 为等腰ABC ∆的底边BC 上一点,F 为过A 、D 、C 三点的圆在ABC ∆内的弧上一点,过B 、D 、F 三点的圆与边AB 交于点E 。
求证:CD EF DF AE BD AF ⋅+⋅=⋅七、n 支球队要举行主客场双循环比赛(每两支球队比赛两场,各有一场主场比赛),每支球队在一周(从周日到周六的七天)内可以进行多场客场比赛。
但如果某周内该球队有主场比赛,在这一周内不能安排该球队的客场比赛。
如果4周内能够完成全部比赛,球n 的最大值。
注:A 、B 两队在A 方场地举行的比赛,称为A 的主场比赛,B 的客场比赛。
第五届中国东南地区数学奥林匹克竞赛试题(缺答案)
第五届中国东南地区数学奥林匹克
福建龙岩
1.已知集合是正整数,T是S的子集,满足:对任意的(其中可以相同)都有,求所有这种集合T的元素个数的最大值。
2.设数列的表达式。
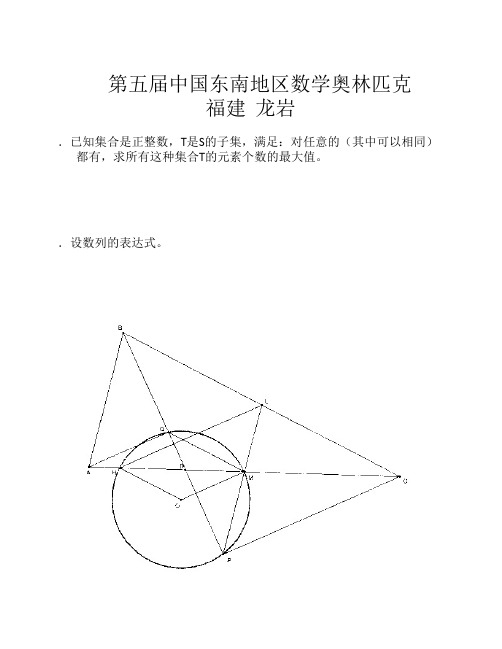
3.在△ABC中,BC>AB,BD平分∠ABC交AC于D,如图,CP垂直BD,垂足为P,AQ垂直BP,Q为垂足。
M是AC中点,E是BC中点。
若△PQM的
外接圆O与AC的另一个交点为H。
求证:O、H、E、M四点共圆。
4.设正整数,取每一对不同的数、个差按从小到大顺序排成一个数列,称为集合A的“衍生数列”,记为。
衍生数列中能被m整除的数的个数
记为(m).
证明:对于任一正整数所对应的“衍生数列” 及
5.求出最大的正实数成立不等式;
6.如下左图,△ABC的内切圆I分别切BC,AC于点M,N,点E,F分别为边AB,AC的中点,D是直线EF与BI的交点。
证明:M,N,D三点共
线。
7.杰克(Jack)船长与他的海盗们掠夺到6个珍宝箱A1,A2,A3,A4,A5,A6,其中A i内有金币a i枚,互不相等。
海盗们设计了一种箱子的布局图(如上右图),并推派一人和船长轮流拿珍宝箱。
每次可任意拿走不和两个或两个以上的箱子相连的整个箱子。
如果船长最后所取得的金币不少于海盗们所取得的金币,那么船长获胜。
问:若船长先拿,他是否有适当的取法保证获胜?
8.设n为正整数,个数;
(i)每一位数码;
(ii)当
(1)求的值;
(2)确定被13除得的余数。
2006年中国东南地区数学奥林匹克

AB, AC 于点 D, E ,直线 DE 分别与直线 BI, CI 相交于点
D F
1 F, G , 证明: FG = BC . 2 (张鹏程 供题) 证法一:分别连接 CF,,,, BG ID IE AI , 则 A、、、 D I E 四点共圆. 1 所以 ∠IDE =∠A , 2 1 从而 ∠BDF= 90° + ∠A , 2 1 1 又 ∠BIC = 180° − ()=90 ∠B + ∠C ° + ∠A , 2 2 所以 ∠BDF = ∠BIC . 又 ∠DBF = ∠CBI ,得 ∆FDB ∽∆CIB .所以 FB DB . = CB IB
第一天 (2006 年 7 月 27 日,8:00-12:00,南昌)
一、设 a > b > 0, f ( x) =
f ( x) = (
1 3 1 3
2(a + b) x + 2ab .证明:存在唯一的正数 x ,使得 4x + a + b
a +b 3 ) . 2 (李胜宏 供题)
2(a + b) x + 2ab a3 + b3 3 解法一:令 t = ( ,得 ) , 由t = 4x + a + b 2 [2(a + b) − 4t ]x = t (a + b) − 2ab , 为证○ 1 有唯一的正数解 x ,只要证, 2(a + b) − 4t > 0 及 t (a + b) − 2ab > 0 , 即
( 2)
2 1 因为 an an 1 ,所以 + = n
an = 1
2 an +
1 n
2012年第九届东南地区数学奥林匹克试题参考解答

第九届东南地区数学奥林匹克试题参考解答第一天1. 求一个正整数组(,,)(1)l m n l m n <<<,使得111,,l m n k k l k m k k k ==+=+∑∑∑依次成等比数列.(陶平生提供)解 对*N t ∈,记1(1)2t t k t t S k =+==∑.设 111,,l m n lm l n m k k l k m k S k S S k S S ==+=+==-=-∑∑∑依次成等比数列,则2()()l n m m l S S S S S -=-, ①即2()l n m l m S S S S S +-=,于是应有2|l m S S ,即 222(1)(1)l l m m ++.令1(1)m l l +=+,并取3l =,于是11m =,则3116,66l m S S S S ====, 代人①得666n S =,即(1)6662n n +=,此时36n =满足. 因此(,,)(3,11,36)l m n =是一组满足条件的解.注 满足条件的数组(,,)l m n 不是唯一的,例如还有(8,11,13),(5,9,14),(2,12,62),(3,24,171)等等,(可以证明,这种数组有无穷多).2. 如图,△ABC 的内切圆I 在边,,AB BC CA 上的切点分别是,,D E F ,直线EF 与直线,,AI BI DI 分别相交于点,,M N K .证明:DM KE DN KF ⋅=⋅.(张鹏程提供)证明 易知,,,I D E B 四点共圆.又90AID IAD ∠=-∠o ,90MED FDA IAD ∠=∠=-∠o ,所以AID MED ∠=∠,于是,,,I D E M 四点共圆.从而,,,,I D B E M 五点共圆,IMB IEB ∠=∠ 90=o,即AM BM ⊥. 同理,,,,,I D A N F 五点共圆,且BN AN ⊥.设直线,AN BM 交于点G ,则易知点I 为△GAB 的垂心.又ID AB ⊥,所以,,G I D 共线.由,,,G N D B 四点共圆,知ADN G ∠=∠.同理BDM G ∠=∠.所以DK 平分MDN ∠,从而 DM KM DN KN=. ① 又由,,,I D E M ;,,,I D N F 分别共圆,知KM KE KI KD KF KN ⋅=⋅=⋅,所以KM KF KN KE=. ② 由①,②,知DM KF DN KE=,即DM KE DN KF ⋅=⋅.3. 对正合数n ,记()f n 为其最小的三个正约数之和,()g n 为其最大的两个正约数之和.求所有的正合数n ,使得()g n 等于()f n 的某个正整数次幂.(何忆捷提供)解法一 若n 是奇数,则n 的一切约数都是奇数,故由题意知()f n 为奇数,()g n 为偶数,这样()g n 不可能等于()f n 的某个正整数次幂.因此只需考虑n 是偶数的情况,此时1,2是n 最小的两个正约数,,2n n 是n 最大的两个正约数. 设d 是n 除1,2以外的最小正约数.若存在*N k ∈使()()k g n f n =,则3(12)(3)(mod3)2k k k n d d d =++=+≡. 由于32n 显然是3的倍数,故3|k d ,即3|d ,由d 的最小性知3d =. 因此362k n =,解得146k n -=⨯,又3|n ,故其中2k ≥. 综上可知,n 的所有可能值为*46()N l n l =⨯∈.解法二 设合数n 满足*()()()N k g n f n k =∈,并设n 的最小素因子为p ,则n 的第二大正约数为n p. 若n 的第三小正约数为2p ,则2Z n p∈,此时 2()11(mod )f n p p p =++≡,2()(1)(mod )n n g n n p p p p p =+=+⋅, 从而1()()0(mod )k kf ng n p ≡=≡,矛盾.因此n 的第三小正约数不是2p ,从而必为某一素数()q q p >.易知此时Z n pq∈,故有 ()11(mod )f n p q p q =++≡+,()(1)(mod )n n g n n q p q p pq =+=+⋅. 因此 (1)()()0(mod )k kp f n g n q +≡=≡.又q 为素数,故|1q p +,从而1p q p <≤+,只有2,3p q ==.此时有 36()()2k k f n g n n ===,解得146k n -=⨯,又3|n ,故其中2k ≥. 综上可知,n 的所有可能值为*46()N l n l =⨯∈.4. 已知实数,,,a b c d 满足:对任意实数x ,均有14cos 3cos 2cos cos ≤+++x d x c x b x a ,求a b c d +-+的最大值.当a b c d +-+取最大值时,求实数,,,a b c d 的值. (李胜宏提供)解 记x d x c x b x a x f 4cos 3cos 2cos cos )(+++=. 由于(0),(),()3222a b d f a b c d f a b c d f c π=+++π=-+-+=---, 则 24(0)()()3333a b c d f f f π+-+=+π+≤, 当且仅当(0)()()13f f f π=π==,即1,1,1a b d c =+==-时取等号. 此时,令cos t x =,11t -≤≤,则()1cos cos 2cos3cos 41f x x b x x d x -=+-+-2342(1)(21)(43)(881)1t d t t t d t t =+----+-+-2(1)(1)(21)(2(1))0t t t dt d =-+---≤对任意实数[1,1]t ∈-成立.所以0d >,且2121d d -=,即21=d . 所以,a b c d +-+的最大值为3,且此时11(,,,)(1,,1,)22a b c d =-.第二天5. 如果非负整数m 及其各位数字之和均为6的倍数,则称m 为“六合数”.求小于2012的非负整数中“六合数”的个数.(陶平生提供)解法一 易知,一个非负整数为“六合数”当且仅当它末位数字是偶数且各位数字之和是6的倍数.为方便起见,将{0,1,,2011}M =L 中每个数都写成四位数abcd 的形式(当不足四位数时,在最高数位前补上若干个数字“0”,使之恰含有四个数字),并用()f k 表示M 中末位数字为k 的“六合数”的个数,其中{0,2,4,6,8}k ∈.对N n ∈,将满足x y n +=且,{0,1,,9}x y ∈L 的(,)x y 的组数记为n p ,显然1,0,1,,9;19,10,11,,18;0,19.n n n p n n n +=⎧⎪=-=⎨⎪≥⎩L L 先考虑一切小于2000的“六合数”abck .若0k =,则当0a =时,0,6,12,18b c +=;当1a =时,5,11,17b c +=,故06121851117(0)()()161632f p p p p p p p =++++++=+=.若2k =,则当0a =时,4,10,16b c +=;当1a =时,3,9,15b c +=,故410163915(2)()()171835f p p p p p p =+++++=+=.若4k =,则当0a =时,2,8,14b c +=;当1a =时,1,7,13b c +=,故28141713(4)()()171633f p p p p p p =+++++=+=.当6,8k =时,与0,2k =的情形类似,有(6)(0)32,(8)(2)35f f f f ====.因此,小于2000的“六合数”有(0)(2)(4)(6)(8)167f f f f f ++++=个.再注意到2000至2011中恰好有一个“六合数”2004,所以所求“六合数”的个数为1671168+=.解法二 对非负整数n ,令()S n 为其各位数字之和.先将小于2000的非负整数中所有6的倍数(共334个)配成如下167对:(0,1998),(6,1992),(12,1986),,(996,1002)L .对上述每对数(,)x y ,设12341234,x a a a a y bb b b ==(约定当x 或y 不足四位数时,在最高数位前补上若干个数字“0”,使之恰含有四个数字),则112233441000()100()10()()1998a b a b a b a b x y +++++++=+=.因,x y 为偶数,故44,8a b ≤,因此441618a b +≤<,只能448a b +=;又由331819a b +≤<知,只能339a b +=;类似得229a b +=;最后必有111a b +=.故11223344()()()()()()199827S x S y a b a b a b a b +=+++++++=+++=, 从而(),()S x S y 中有且仅有一个6的倍数(这是因为,x y 均被3整除,所以()S x 与()S y 均被3整除),故,x y 有且仅有一个是“六合数”.从而,小于2000的“六合数”共有167个,又2000至2011中恰好有一个“六合数”2004,所以所求“六合数”的个数为1671168+=.6. 求正整数n 的最小值,使得<.(刘桂梅 提供)解 由已知得,必有2013n ≥,此时2011(2011)2012(2012)n n ⇔-<-4023n ⇔>. ①2013(2013)2011(2011)n n ≥⇔-≥-4024n ⇔≥. ②由①,②知,当4024n ≥时,有0<≤ 当20134023n ≤≤时,有0≥> 综上可知,满足条件的正整数n 的最小值为4024.7. 如图,△ABC 中,D 为边AC 上一点且ABD C ∠=∠,点E 在边AB 上且BE DE =,设M 为CD 中点,AH DE ⊥于点H.已知2AH =,1AB =,求AME ∠的度数.(熊斌提供) 解法一 由已知,BCD ∆的外接圆O 与直线AB 切于点B .连接,,,,OB OE OG OD OM .作AN BD ⊥于点N ,//EG BD 交AC 于点G ,又显然OE BD ⊥,OM CD ⊥,所以90GEO GMO ∠==∠o,则,E G , ,M O 四点共圆,从而tan tan EG AME GOE OE ∠=∠=. 由90OBE BNA ∠=∠=o ,ABN C EOB ∠=∠=∠知:OBE ∆与BNA ∆相似.易知,,,A H N D 四点共圆,故EDG ANH ∠=∠,又180AHN ADN ∠=-∠oEGD =∠,故EGD ∆与AHN ∆相似.所以OE BE DE EG BA NA NA AH===,于是2EG AH OE AB==15AME ∠=o . 解法二 设,ABD C DBC αβ∠=∠=∠=,由已知易得 ,2BDE AED αα∠=∠=, ()ADE ADB BDE αβαβ∠=∠-∠=+-=,AB AE EB AE EH HD =+=++.因此1cos 2cot cot cot sin 2AB AE EH HD AH AH AH αβαβα++=+=+=+. ① 作,EK AC EL BD ⊥⊥,垂足为,K L ,则L 为BD 中点,结合正弦定理得sin sin sin sin EL DE EDL BD LD EK DE EDK CD MDαβ∠====∠, 所以cot LD MD MK DK EL EK EK EKα===-cot cot AME β=∠-. ②由①,②及已知条件得cot 2AB AME AH ∠===+15AME ∠=o .8. 设m 是正整数,21m n =-,{1,2,,}n P n =L 为数轴上n 个点所成的集合.一个蚱蜢在这些点上跳跃,每步从一个点跳到与之相邻的点.求m 的最大值,使对任意,n x y P ∈,从点x 跳2012步到点y 的跳法种数为偶数(允许中途经过点,x y ).(张思汇提供)解 当11m ≥时,212013m n =->,由于从点1跳2012步而到达点2013的跳法只有一种,矛盾!所以10m ≤.下证10m =满足题意.为此,我们对m 用数学归纳法证明一个更强的命题:对任意21m k n ≥=-及任意,n x y P ∈,从点x 跳k 步到点y 的跳法种数为偶数.当1m =时,跳法种数必为0,结论成立.设m l =时结论成立,对121l k n +≥=-,将从点x 跳k 步到点y 的路径分成3类,我们证明每种情况下的路径种数均为偶数即可.(1)路径从不经过点2l .此时,点x 和点y 位于点2l 的同侧,由归纳假设知,路径有偶数种.(2)路径经过点2l 恰一次.设第i 步跳到点2l ({0,1,,}i k ∈L ,0i =表示点x 就是点2l ,i k =表示点y 就是点2l),我们证明对任意i ,路径种数都是偶数.设路径为1111,,,,2,,,,l i i k x a a a a y -+-L L ,将其分为两条子路:从点x 到点1i a -,共1i -步;从点1i a +到点y ,共1k i --步(对0i =或k ,只有一条子路,共1k -步).因为121l k n +≥=-,若121l i -<-且121l k i --<-,则122l i -≤-且1k i -- 22l ≤-,相加得:122l k +≤-,矛盾!所以121l i -≥-或121l k i --≥-必有一个成立,由归纳假设,必有一条子路的路径种数为偶数,由乘法原理即知:第i 步跳到点2l的路径种数为偶数.(3)路径经过点2l不少于两次.此时将第一次与第二次到点2l之间的路径沿点2l作对称,则对(3)中的路径进行了两两配对,必为偶数种路径.由数学归纳法,命题得证.综上所述,m的最大值为10.。
2008第五届中国东南地区数学奥林匹克试题及解答

第五届中国东南地区数学奥林匹克第一天(2008年7月27日 上午8:00-12:00) 福建 龙岩1. 已知集合{}1,2,3,,3S n =,n 是正整数,T 是S 的子集,满足:对任意的,,x y z T ∈ (其中x 、y 、z 可以相同) 都有x y z T ++∉,求所有这种集合T 的元素个数的最大值。
2. 设数列{}n a 满足:111,2(12),1,2,3,n n n a a a n n +==+⋅+=。
试求通项n a 的表达式。
3. 在△ABC 中,BC >AB ,BD 平分ABC ∠交AC 于D ,如图,CP 垂直BD ,垂足为P ,AQ 垂直BP ,Q 为垂足。
M 是AC 中点,E 是BC 中点。
若△PQM 的外接圆O 与AC 的另一个交点为H ,求证: O 、H 、E 、M 四点共圆。
4. 设正整数,2m n ≥,对于任一个n 元整数集{}12,,,n A a a a =,取每一对不同的数i j a a 、()j i >,作差j ia a -,把这2n C 个差按从小到大顺序排成一个数列,称这个数列为集合A 的“衍生数列”,记为A 。
衍生数列A 中能被m 整除的数的个数记为()A m 。
证明:对于任一正整数2m ≥,n 元整数集{}12,,,n A a a a =及集合{}1,2,,B n =所对应的“衍生数列”A 及B ,满足不等式()()A m B m ≥.第二天(2008年7月28日上午8:00-12:00) 福建 龙岩5. 求出最大的正实数λ,使得对于满足2221x y z ++=的任何实数x 、y 、z 成立不等式:52xy yz λ+≤。
6. 如图,ABC ∆的内切圆I 分别切BC 、AC 于点M 、N ,点E 、F 分别为边AB 、AC 的中点,D 是直线EF 与BI 的交点。
证明:M 、N 、D 三点共线。
HOEMQD CBAIN F EDA7. 杰克(Jack)船长与他的海盗们掠夺到6个珍宝箱123456,,,,,A A A A A A ,其中i A 内有金币i a 枚,i =1、2、3、4、5、6,诸i a 互不相等。
2006年第3届中国东南数学奥林匹克试题及答案

第三屆中國東南地區數學奧林匹克第一天(2006年7月27日, 8:00-12:00, 南昌)一、 設0,a b >>2()2()4a b x abf x x a b++=++.證明:存在唯一的正數x ,使得11333()()2a b f x +=. 二、 如圖所示,在△ABC 中,90,,A B C D G ∠=︒是邊CA 上的兩點,連接BD ,BG 。
過點A ,G 分別作BD 的垂線,垂足分別為E ,F ,連接CF 。
若BE =EF ,求證:ABG DFC ∠=∠。
三、 一副紙牌共52張,其中“方塊”、“梅花”、“紅心”、“黑桃”每種花色的牌各13張,標號依次是2,3,,10,,,,J Q K A ,其中相同花色、相鄰標號的兩張牌稱為“同花順牌”,並且A 與2也算是順牌(即A 可以當成1使用). 試確定,從這副牌中取出13張牌,使每種標號的牌都出現,並且不含“同花順牌”的取牌方法數。
四、 對任意正整數n ,設n a 是方程31xx n+=的實數根,求證: (1) 1n n a a +>; (2) 211(1)nn i ia i a =<+∑。
第二天(2006年7月28日, 8:00-12:00, 南昌)五、 如圖,在ABC ∆中,60A ∠=︒,ABC ∆的內切圓I 分別切邊AB 、AC 於點D 、E ,直線DE 分別與直線BI 、CI 相交於點F 、G ,證明:12FG BC =。
BA六、 求最小的實數m ,使得對於滿足a +b +c =1的任意正實數a ,b ,c ,都有333222(61m a b c a b c ++≥+++)()。
七、 (1)求不定方程2()mn nr mr m n r ++=++的正整數解(,,)m n r 的組數。
(2)對於給定的整數k >1,證明:不定方程()mn nr mr k m n r ++=++至少有3k +1組正整數解(,,)m n r 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录2004年东南数学奥林匹克 (2)2005年东南数学奥林匹克 (4)2006年东南数学奥林匹克 (6)2007年东南数学奥林匹克 (9)2008年东南数学奥林匹克 (11)2009年东南数学奥林匹克 (14)2010年东南数学奥林匹克 (16)2011年东南数学奥林匹克 (18)2012年东南数学奥林匹克 (20)2004年东南数学奥林匹克1.设实数a、b、c满足a2+2b2+3c2=32,求证:3−a+9−b+27−c≥1.2.设D是△ABC的边BC上的一点,点P在线段AD上,过点D作一直线分别与线段AB、PB交于点M、E,与线段AC、PC的延长线交于点F、N.如果DE=DF,求证:DM=DN.3.(1)是否存在正整数的无穷数列{a n},使得对任意的正整数n都有a n+12≥2a n a n+2.(2)是否存在正无理数的无穷数列{a n},使得对任意的正整数n都有a n+12≥2a n a n+2.4.给定大于2004的正整数n,将1,2,3,⋯,n2分别填入n×n棋盘(由n行n列方格构成)的方格中,使每个方格恰有一个数.如果一个方格中填的数大于它所在行至少2004个方格内所填的数,且大于它所在列至少2004个方格内所填的数,则称这个方格为“优格”.求棋盘中“优格”个数的最大值.5.已知不等式√2(2a+3)ccc(θ−π4)+6ssnθ+ccsθ−2csn2θ<3a+ 6对于θ∈�0,π2�恒成立,求a的取值范围.6.设点D为等腰△ABC的底边BC上一点,F为过A、D、C三点的圆在△ABC内的弧上一点,过B、D、F三点的元与边AB交于点E.求证:CD⋅EE+DE⋅AE=AD⋅AE.7.N支球队要矩形主客场双循环比赛(每两支球队比赛两场,各有一场主场比赛),每支球队在一周(从周日到周六的七天)内可以进行多场客场比赛.但如果某周内该球队有主场比赛,在这一周内不能安排该球队的客场比赛.如果4周内能够完成全部比赛,球n的值.注:A、B两队在A方场地矩形的比赛,称为A的主场比赛,B的客场比赛.8.求满足x−y x+y+y−z y+z+z−u z+u>0,且1≤x、y、z、u≤10的所有四元有序整数组(x,y,z,u)的个数.2005年东南数学奥林匹克1.(1)设a∈R.求证:抛物线y=x2+(a+2)x−2a+1都经过一个顶点,且顶点都落在一条抛物线上.(2)若关于x的方程y=x2+(a+2)x−2a+1=0有两个不等实根,求其较大根的取值范围.(吴伟朝供题)2.⊙O与直线l相离,作OO⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作⊙O的两条切线QA、QB,A、B为切点,AB与OP相交于点K.过点P作OP⊥QB,ON⊥QA,M、N为垂足.求证:直线MN平分线段KP.(裘宗沪供题)3.设n(n≥3)是正整数,集合P={1,2,⋯,2n}.求最小的正整数k,使得对于M的任何一个k元子集,其中必有4个互不相同的元素之和等于4n+1.(张鹏程供题)4.试求满足a2+b2+c2=2005,且a≤b≤c的所有三元正整数数组(a,b,c).(陶平生供题)5.已知直线l与单位圆⊙O相切于点P,点A与⊙O在直线l的,且A到直线l的距离为ℎ(ℎ>2),从点A作⊙O的两条切线,分别与直线l交于B、C两点.求线段PB与线段PC的长度之乘积.(冷岗松司林供题)6.将数集A=�a1,a2,⋯,a n�中所有元素的算术平均值记为O(A)�O(A)=a1+a2+⋯+a n n�.若B是A的非空子集,且P(B)=P(A),则称B是A的一个“均衡子集”.试求数集P={1,2,3,4,5,6,7,8,9}的所有“均衡子集”的个数.(陶平生供题)7.(1) 讨论关于x的方程|x+1|+|x+2|+|x+3|=a的根的个数;(2) 设a1,a2,⋯,a n为等差数列,且|a1|+|a2|+⋯+|a n|=|a1+1|+|a2+1|+⋯+|a n+1|=|a1−2|+|a2−2|+⋯+|a n−2|=507.求项数n的最大值.(林常供题)8.设0<α、β、γ<π2,且csn3α+csn3β+csn3γ=1.求证tan2α+tan2β+tan2γ≥3√32.(李胜宏供题)2006年东南数学奥林匹克1. 设a >b >0,f (x )=2(a+b )x+2ab 4x+a+b .证明:存在唯一的正数x ,使得f (x )=�a 13+b 132�3. (李胜宏 供题)2. 如图1,在△ABC 中,∠ABC =90°,D 、G 是边CA 上的亮点,连结BD 、BG .过点A 、G 分别作BD 的垂涎,垂足分别为E 、F ,连结CF .若BE =EE ,求证:∠ABG =∠DEC .图13. 一副纸牌共52张,其中,“方块”、“梅花”、“红心”、“黑桃”每种花色的牌个13张,标号依次是2,3,⋯,10,J ,Q ,K ,A .相同花色、相邻标号的两张牌称为“同花顺”牌,并且A 与2也算同花顺牌(即A 可以当成1使用).试确定,从这副牌中取出13张牌,使每种标号的牌都出现,并且不含同花顺取牌方法数.(陶平生 供题)4. 对任意正整数n ,设a n 是方程x 3+x n =1的实数根.求证: (1) a n+1>a n ;(2) ∑1(s+1)a i n s=1<a n .(李胜宏 供题)5. 如图2,在△ABC 中,∠A =60°,△ABC 的内切圆⊙I 分别切边AB 、AC 于点D 、E ,直线DE 分别与直线BI 、CI 相交于点F 、G .证明:EG =12BC .图2 6. 求最小的实数m ,使得对于满足a +b +c =1的任意正实数a 、b 、c ,都有m (a 3+b 3+c 3)≥6(a 2+c 2+c 2)+1. (熊 斌 供题)7. (1) 求不定方程mn +nn +mn =2(m +n +n )的正整数解(m ,n ,n )的组数; (2) 对于给定的整数k (k >1),证明:不定方程mn +nn +mn =k (m +n +n )至少有3k +1组正整数解(m ,n ,n ). (吴伟朝 供题) 8. 对于周长为n (n ∈N +)的圆,称满足如下条件的最小的正整数p n 个点A 1,A 2,⋯,A p n ,对于1,2,⋯,n −1中的每一个整数m ,都存在两个点A s 、A j (1≤s 、j ≤p n ).以A s 和A j 为端点的一条弧长等于m ,圆周上每相邻两点间的弧长顺次构成的序列T n =�a 1,a 2,⋯,a p n �称为“圆剖分序列”.列入,当n =13,圆剖分数为p 13=4,图3中所标数字为相B邻两点之间的弧长,圆剖分序列为T 13=(1,3,2,7), (1,2,6,4),求p 21和p 31,并给出一个相应的圆剖分序列.图3(陶平生 供题)73112007年东南数学奥林匹克1. 试求实数a 的个数,使得对于每个a ,关于x 的三次方程x 3=ax +a +1都有满足|x |<1000的偶数根.2. 如图1所示,设C 、D 是以O 为圆心、AB 为半径的半圆上的任意两点,过点B 作⊙O 的切线交直线CD 于P ,直线PO 于直线CA ,AD 分别交于点E 、F .证明:OE =OF .图13. 设a s =msn �k +s k �k ∈N ∗�,试求S n 2=[a 1]+[a 2]+⋯+[a n 2]的值.4. 试求最小的正整数n ,使得对于满足条件∑a s n s=1=2007的任一个具有n 项的正整数数列a 1,a 2,⋯,a n ,其中必有连续若干项之和等于30. 5. 设函数f (x )满足:f (x +1)−f (x )=2x +1(x ∈R ),且当x ∈[0,1]时有|f (x )|≤1,证明:当x ∈R 时,有|f (x )|≤2+x 2.6. 如图,在直角三角形ABC 中,D 是斜边AB 的中点,PB ⊥AB ,MD 交AC 于N ;MC 的延长线交AB 于E .证明:∠DBN =∠BCE .7. 试求满足下列条件的三元数组(a ,b ,c ):E(1) a<b<c,且当a,b,c为质数;(2) a+1,b+1,c+1构成等比数列.8.设正实数a,b,c满足:abc=1,求证:对于整数k≥2,有a k a+b+b k b+c+c k c+a≥32.2008年东南数学奥林匹克1.已知集合S={1,2,⋯,3n},n是正整数,T是S的子集,满足:对任意的x、y、z∈T(x、y、z可以相同),都有x+y+z∉T.求所有这种集合T的元素个数的最大值.(李胜宏供题)2.设数列{a n}满足a1=1,a n+1=2a n+n(1+2n)(n=1,2,⋯).试求通项a n的表达式.(吴伟朝供题)3.在△ABC中,BC>AB,BD平分∠ABC交AC于点D,AQ⊥BO,垂足为Q,M是边AC的中点,E是边BC的中点.若△PQM的外接圆⊙O与AC的另一个交点为H.求证:O、H、E、M四点共圆.(郑仲义供题)4.设正整数m、n≥2,对于任一个n元整数集A=�a1,a2,⋯,a n�,取每一对不同的数a s、a j(j>s),作差a j−a s.由这C n2个差按从小到大.衍生数列顺序排成的一个数列,称为集合A的“衍生数列”,记为A生A生中能被m整除的数的个数记为A生(m).5.证明:对于任一正整数m(m≥2),n圆整数集A=�a1,a2,⋯,a n�及B={1,2,⋯,n}所对应的A生及B生,满足不等式A生(m)≥B生(m)(陶平生供题)6.求出最大的正数λ,使得对于满足x2+y2+z2=1的任何实数x、y、z成立不等式|λxy+yz|≤√52. (张正杰供题)7. 如图1,△ABC 的内切圆⊙I 分别切BC 、AC 于点M 、N ,E 、F 分别为边AB 、AC 的中点,D 是针线EF 于BI 的交点.证明:M 、N 、D 三点共线.图1(张鹏程 供题) 8. 杰克(Jack )船长与他的海盗们掠夺到6个珍宝箱A 1,A 2,A 3,A 4,A 5,A 6,其中A s (s =1,2,⋯,6)内有金币a s 枚(诸a s 互不相等).海盗们设计了一种箱子的布局图(如图2),并推派一人和船长轮流拿珍宝箱.每次可任意拿走不与两个或两个以上的箱子相连的整个箱子.如果船长最后所取得的金币不少于海盗们所取得的金币,那么船长获胜.问:若船长先拿,他是否有适当的取法保证获胜?图2 (孙文先 供题)9. 设n 为正整数,f (n )表示满足以下条件的n 位数(称为波形数)a 1a 2⋯a n �������������的个数:a 1a 2 a 3 a 4a 6 a 5i.每一位数码a s∈{1,2,3,4},且a s≠a s+1(s=1,2,⋯);ii.当n≥3时,a s−a s+1与a s+1−a s+2(s=1,2,⋯)的符号相反.(1)求f(10)的值;(2)确定f(2008)被13除得的余数.(陶平生供题)2009年东南数学奥林匹克1.试求满足方程x2−2xy+126y2=2009的所有整数对(x,y).(张鹏程供题)2.在凸五边形ABCDE中,已知AB=DE,BC=EA,AB≠EA,且B、C、D、E四点共圆.证明:A、B、C、D四点共圆的充分必要条件是AC=AD.(熊斌供题)3.设x,y,z∈R+,√a=x(y−z)2,√b=y(z−x)2,√c=z(x−y)2;求证:a2+b2+c2≥2(ab+bc+ca). (唐立华供题)4.在一个圆周上给定十二个红点;求n的最小值,使得存在以红点为顶点的n个三角形,满足:以红点为顶点的每条弦,都是其中某个三角形的一条边.(陶平生供题)5.设1,2,⋯,9的所有排列X=�x1,x2,⋯,x9�的集合为A;∀X∈A,记f(X)=x1+2x2+3x3+⋯+9x9,P={f(X)|X∈A};求|P|. (其中|P|表示集合M的元素个数).6.已知⊙O、⊙I分别是△ABC的外接圆和内切圆;证明:过⊙O上的任意一点D,都可作一个△DEF,使得⊙O、⊙I分别是△DEF的外接圆和内切圆.(陶平生供题)7.设f(x,y,z)=x(2y−z)1+x+3y+y(2z−x)1+y+3z+z(2x−y)1+z+3x,其中x,y,z≥0,且x+y+z=1.求f(x,y,z)的最大值和最小值.(李胜宏供题)8.在8×8方格表中,最少需要挖去几个小方格,才能使得无法从剩余的方格表中裁剪出一片形状如下完整的T型五方连块?(孙文先供题)2010年东南数学奥林匹克1. 设a 、b 、c ∈{0,1,⋯9}.若二次方程ax 2+bx +c =0有有理根,证明:三位数abc�����不是质数. (张鹏程 供题)2. 对于集合A ={a 1,a 2,⋯,a m },记O (A )=a 1a 2⋯a m .设A 1,A 2,⋯A n (n =C 201099)是集合{1,2,⋯,2010}的所有99元子集.求证:2011|∑O (A s )n s=1. (叶永南 供题)3. 如图1,已知△ABC 内切圆⊙I 分别与边AB 、BC 切于点F 、D ,之心啊AD 、CF 分别于⊙I 交于另一点H 、K.求证:FD⋅HK FH⋅DK =3.图1 (熊 斌 供题)4. 设正整数a 、b 满足1≤a <b ≤100.若存在正整数k ,使得ab |a k +b k ,则称数对(a ,b )是“好数对”.求所有好数对的个数.(熊 斌 供题)5. 如图2,△ABC 为直角三角形,∠ACB =90°,M 1、M 2为△ABC 内任意两点,M 为线段M 1M 2的中点,直线BM 1、BM 2、BM 与AC 分别交于点N 1、N 2、N.求证:M 1N 1BM 1M 2N 2BM 22MN BM .图2 (裘宗沪 供题)6. 设Z +为正整数集合,定义:a 1=2,a n+1=msn �λ�∑1a i n s=1+1λ<1,λ∈Z +�(n =1,2,⋯). 求证:a n+1=a n 2−a n +1. (李胜宏 供题)7. 设n 是一个正整数,实数a 1,a 2,⋯,a n 和n 1,n 2,⋯,n n 满足:a 1≤a 2≤⋯≤a n 和n 1≤r 2≤⋯≤n n .求证:∑∑==≥n i nj j i j i r r a a 110),min((朱华伟 供题)8. 在一个圆周上给定8个点A 1,A 2,⋯,A 8.求最小的正整数n ,使得以这8个点为顶点的任意n 个三角形中,必存在两个有公共边的三角形.(陶平生 供题)21B2011年东南数学奥林匹克1.已知min x∈R ax2+b√x2+1=3.(1)求b的取值范围;(2)对给定的b,求a.2.已知a、b、c为两两互质的正整数,且a2|(b3+c3),b2|(a3+ c3),c2|(a3+b3)求a、b、c的值.3.设集合P={1,2,3,⋯,50},正整数n满足:M的任意一个35元子集中至少存在两个不同的元素a,b,使a+b=n或a−b=n.求出所有这样的n.4.如图1,过△ABC的外心O任作一直线,分别与边AB,AC相交于M,N,E,F分别是BN,CM的中点.证明:∠EOE=∠A.图15. 如图2,设AA0,BB0,CC0是△ABC的三条角平分线,自A0作A0A1∥BB0,A0A2∥CC0,A1,A2分别在AC,AB上,直线A1A2∩BC=A3;类似得到点B3,C3.证明:A3,B3,C3三点共线.图26.设O 1,O 2,⋯,O n 为平面上n 个定点,M 是该平面内线段AB 上任一点,记|O s P |为点O s 与M 的距离,s =1,2,3,⋯,n ,证明:≤∑∑∑===ni i ni i n i i B P A P M P 111,max . 7.设数列{a n }满足:a 1=a 2=1,a n =7a n−1−a n−2,n >3.证明:对于每个n ∈N ∗,a n +a n+1+2皆为完全平方数.8.将时钟盘面上标有数字1,2,⋯,12的十二个点,分别用红、黄、蓝、绿四种颜色各染三个点,现以这些点为顶点构造n 个凸四边形,使其满足:(1) 每个四边形的四个顶点四色都有;(2) 任何三个四边形,都存在某一色,该色的三个顶点所标数字各不相同.求n 的最大值.32012年东南数学奥林匹克1. 求一个三元整数组(l ,m ,n )(1<l <m <n ),使得∑k l k=1,∑k m k=l+1,∑k n k=m+1依次成等比数列.2. 如图1,△ABC 的内切圆I 在边AB ,BC ,CA 上的切点分别是D ,E ,F ,直线EF 与直线AI ,BI ,DI 分别相交于点M ,N ,K .证明:DP ⋅KE =DN ⋅KE .图1 3. 对于合数n ,记f (n )为其最小的三个正约数之和,g (n )为其最大的两个正约数之和.求所有的正合数n ,使得g (n )等于f (n )的某个正整数次幂.4. 已知实数a ,b ,c ,d 满足:对任意实数x ,均有acccx +bccc 2x +cccc 3x +dccc 4x ≤1, 求a +b -c +d 的最大值.当a +b -c +d 取最大值时,求实数a ,b ,c ,d 的值.5. 如果非负整数m 及其各位数字之和均为6的倍数,则称m 为“六合数”.求小于2012的非负整数中“六合数”的个数.6. 求正整数n 的最小值,使得A东南数学奥林匹克�n−20112012−�n−20122011<�n−201320113−�n−201120133.7.如图2,△ABC中,D为边AC上一点且∠ABD=∠C,点E在边AB上且BE=DE,设M为CD重点,AA⊥DE于点H.已知AA=2−√3,AB=1,求∠APE的度数.图2设m是正整数,n=2m−1,O n={1,2,⋯,n}为数轴上n个点所成的集合.一个蚱蜢在这些点上跳跃,每步从一个点跳到与之相邻的点.求m的最大值,使对任意x,y∈O n,从点x跳2012步到点y的跳法种数为偶数(允许中途经过点x,y).。
