分数除法单元复习
合集下载
分数除法整理和复习
1 5
（32
15）15
1 5
（1150 135）15
1 5
115315
151135135
1
45 13
3163
1 5
（[ 32
15）15]
1 5
[1153115]
1
1 5
13
15113
1 65
3 5
÷
3＋
4 5
×
1 3
=
3 5
×
1 3
＋
45×
1 3
=(
3 5
＋
4 5
)×
1 3
=
7/5×
1 3
2（米） 9
1.一批煤有3 吨，5天烧完，平均每天烧多少
吨？
4
2. 10千克葵花籽可以榨油 9 千克，25千克葵
花籽可以榨油多少千克？ 5
3.一个正方形的周长是 4 米，它的边长是多少分米？
5
如果 a 是一个不等于0的自然数，
（1） ÷ 等于多少？
1
（2） a ÷33等于多少？
1 3a
a
3
a
在括号里填>、<或=
8
2 3
-4
8
3 2
-4
12-4
8朵
答：小红还剩8朵花。
1、陈爷爷每天绕操场跑6圈，2分钟可 以跑半圈。
照这个速度，陈爷爷每天跑步要用 多少时间？
小强骑车去郊游，去时平均每小时
9km，
2 3
小时到达，原路返回时只用
了 1 小时，返回时平均每小时比去时
多行2多少千米？
1 3
÷ 3×8
＝
1 3
×
分数除法整理和复习
＝1 ＋ 2 10 15
＝7 30
（5 － 2 ）× 9
63
10
＝5 × 9 － 2 × 9 6 10 3 10
＝3 － 3 45
＝3 20
应用乘法 分配律可 以使计算 简便一些
二、基础练习
2 5
3
（1）张大爷养了200只鹅，5 鹅的只数是鸭的 。养了多少只鸭？
（2）张大爷养了200只鹅，鹅的只数比鸭少 。养了多少只鸭？
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟，爷 爷走一圈需要10分钟。 （1）如果两人同时同地出发，相背而行，多少分钟后相遇？
起点 相遇
相遇 操场全长
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟，爷爷走 一圈需要10分钟。 （1）如果两人同时同地出发，相背而行，多少分钟后相遇？
请你认真读题，在题上画一画，这两道题有什么异同？
这两道题的单位“1”都是鸭的只数，题目中都没有给出，是要 求的量。要注意第二题是鹅的只数比鸭少 ，而不是鹅是鸭 的。
3
3
5
5
二、基础练习
请你用线段图来表示两道题的意思。
鸭：
“1”
？只
是鸭的 2
鹅： 5
200只
鸭： 鹅：
“1”
？只
比鸭少 3 5
200只
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟，爷爷走一圈 需要10分钟。 （2）如果两人同时同地出发，同方向而行，多少分钟后小明超出爷爷一整圈？
分析与解答
小明每分钟能超出爷爷多少呢？你有办法知道吗？
1÷8＝1
8
1÷10＝101
1÷（1
8
－101
＝7 30
（5 － 2 ）× 9
63
10
＝5 × 9 － 2 × 9 6 10 3 10
＝3 － 3 45
＝3 20
应用乘法 分配律可 以使计算 简便一些
二、基础练习
2 5
3
（1）张大爷养了200只鹅，5 鹅的只数是鸭的 。养了多少只鸭？
（2）张大爷养了200只鹅，鹅的只数比鸭少 。养了多少只鸭？
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟，爷 爷走一圈需要10分钟。 （1）如果两人同时同地出发，相背而行，多少分钟后相遇？
起点 相遇
相遇 操场全长
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟，爷爷走 一圈需要10分钟。 （1）如果两人同时同地出发，相背而行，多少分钟后相遇？
请你认真读题，在题上画一画，这两道题有什么异同？
这两道题的单位“1”都是鸭的只数，题目中都没有给出，是要 求的量。要注意第二题是鹅的只数比鸭少 ，而不是鹅是鸭 的。
3
3
5
5
二、基础练习
请你用线段图来表示两道题的意思。
鸭：
“1”
？只
是鸭的 2
鹅： 5
200只
鸭： 鹅：
“1”
？只
比鸭少 3 5
200只
三、解决问题
小明和爷爷一起去操场散步。小明走一圈需要8分钟，爷爷走一圈 需要10分钟。 （2）如果两人同时同地出发，同方向而行，多少分钟后小明超出爷爷一整圈？
分析与解答
小明每分钟能超出爷爷多少呢？你有办法知道吗？
1÷8＝1
8
1÷10＝101
1÷（1
8
－101
人教版 六上 第三单元 分数除法整理和复习(附答案)
※要点提示：（1）一个数不能称之为倒数。（2）1的倒数是1，0没有倒数。
【例题1】填空。 的倒数是（），0.45的倒数是（），最小的质数的倒数是（）。
【例题2】判断。
（1）a的数的倒数一定比这个数小。（）
（4）因为 ×0.75=1，所以 的倒数是0.75.（）
7.狮子奔跑时的最高时速可以达到60千米/时，比猎豹慢 。猎豹奔跑时的最高时速是多少？
8.武汉长江大桥全长1670米，其中引桥的长度是正桥的 。这座大桥的正桥和引桥的长度分别是多少米？
9.一批树苗共500棵，甲队单独种需要8天，乙队单独种需要10天。现在两队合种，5天能种完吗？
10.一项工程，甲、乙两队合作需要12天完成，乙丙两队合作需要15天完成，甲、丙两队合作需要20天完成。甲、乙、丙三队合作需要几天完成？
【例题9】丽丽感冒了，医生为她开了一盒感冒药。丽丽可以吃几天？
感冒药
12片
【例题10】我们平时看到的电影画面实际上是由许多连续拍摄的照片以每张 秒的速度连续播放的。请你算一算，半秒可以播放多少张照片？1分钟呢？
【例题11】李爷爷进行慢跑训练，他跑半圈大约用2分钟，照这个速度，李爷爷每天慢跑6圈要用多长时间？
法解答。
（4）工程问题。
数量关系式：工作总量=工作效率×工作时间；
工作效率=工作总量÷工作时间；
工作时间=工作总量÷工作效率。
※通常情况下，工程问题中的工作总量可以看作“1”。
【例题17】甲车从A城市到B城市要行驶2小时，乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发，几小时后相遇？
【例题4】填空。
根据 写出两道除法算式：（）和（）。
2.分数除法的计算方法：一个数除以一个不为0的数，等于乘这个数的倒数。
【例题1】填空。 的倒数是（），0.45的倒数是（），最小的质数的倒数是（）。
【例题2】判断。
（1）a的数的倒数一定比这个数小。（）
（4）因为 ×0.75=1，所以 的倒数是0.75.（）
7.狮子奔跑时的最高时速可以达到60千米/时，比猎豹慢 。猎豹奔跑时的最高时速是多少？
8.武汉长江大桥全长1670米，其中引桥的长度是正桥的 。这座大桥的正桥和引桥的长度分别是多少米？
9.一批树苗共500棵，甲队单独种需要8天，乙队单独种需要10天。现在两队合种，5天能种完吗？
10.一项工程，甲、乙两队合作需要12天完成，乙丙两队合作需要15天完成，甲、丙两队合作需要20天完成。甲、乙、丙三队合作需要几天完成？
【例题9】丽丽感冒了，医生为她开了一盒感冒药。丽丽可以吃几天？
感冒药
12片
【例题10】我们平时看到的电影画面实际上是由许多连续拍摄的照片以每张 秒的速度连续播放的。请你算一算，半秒可以播放多少张照片？1分钟呢？
【例题11】李爷爷进行慢跑训练，他跑半圈大约用2分钟，照这个速度，李爷爷每天慢跑6圈要用多长时间？
法解答。
（4）工程问题。
数量关系式：工作总量=工作效率×工作时间；
工作效率=工作总量÷工作时间；
工作时间=工作总量÷工作效率。
※通常情况下，工程问题中的工作总量可以看作“1”。
【例题17】甲车从A城市到B城市要行驶2小时，乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发，几小时后相遇？
【例题4】填空。
根据 写出两道除法算式：（）和（）。
2.分数除法的计算方法：一个数除以一个不为0的数，等于乘这个数的倒数。
分数除法整理和复习
分数除以整数：
整数除以分数：
分数除以分数：
4 4 1 8 ＝ × 5 5 8 4 5 8 ＝ 8 × 5 4 4 8 4 7 ＝ × 5 7 5 8
分数除法是转化成分数乘法来计算的。
问题3：不计算，你能很快判断这三个算式的商与被除数 的大小关系吗？
分数除以整数：
4 8 5
整数除以分数：
4 8 5 4 8 5 7
5
练习：
1.下面的说法正确吗？请说明理由。
（1）两个分数相除，商一定大于被除数。 （
1 （2）如果a÷b＝ ,b就是a的3倍。 3 3 （3）如果a÷ b＝ ,那么a＝3, b＝5。 5
）
） ）
（ （
练习：
2
（
3 ）× ＝（ 4
）
练习：
解决问题
1.冰融化成水后，水的体积变为冰的体
10 积的 11
。现有一块冰，融化成水以
后的体积是30dm3 ，这块冰的体积是多
少立方分米？
练习：
解决问题
美术小组比航模 小组多15人。
美术小组的人数是
2 航模小组的 。 5
美术小组和航模小组各多少人？
练习：
解决问题
3．甲车从A城市到B城市要行驶2小时，
乙车从B城市到A城市要行驶3小时。两 车同时分别从A城市和B城市出发，几小
当被除数不为0时，如果： 除数小于1时，商比被除数大； 除数大于1时，商比被除数小； 除数等于1时，商与被除数相等。
分数除以分数：
解决问题
养了多少只鸭？
2 1. 张大爷养了200只鹅，鹅的只数是鸭的 。 5 3 2. 张大爷养了200只鹅，鹅的只数比鸭少 5 。
养了多少只鸭？
整数除以分数：
分数除以分数：
4 4 1 8 ＝ × 5 5 8 4 5 8 ＝ 8 × 5 4 4 8 4 7 ＝ × 5 7 5 8
分数除法是转化成分数乘法来计算的。
问题3：不计算，你能很快判断这三个算式的商与被除数 的大小关系吗？
分数除以整数：
4 8 5
整数除以分数：
4 8 5 4 8 5 7
5
练习：
1.下面的说法正确吗？请说明理由。
（1）两个分数相除，商一定大于被除数。 （
1 （2）如果a÷b＝ ,b就是a的3倍。 3 3 （3）如果a÷ b＝ ,那么a＝3, b＝5。 5
）
） ）
（ （
练习：
2
（
3 ）× ＝（ 4
）
练习：
解决问题
1.冰融化成水后，水的体积变为冰的体
10 积的 11
。现有一块冰，融化成水以
后的体积是30dm3 ，这块冰的体积是多
少立方分米？
练习：
解决问题
美术小组比航模 小组多15人。
美术小组的人数是
2 航模小组的 。 5
美术小组和航模小组各多少人？
练习：
解决问题
3．甲车从A城市到B城市要行驶2小时，
乙车从B城市到A城市要行驶3小时。两 车同时分别从A城市和B城市出发，几小
当被除数不为0时，如果： 除数小于1时，商比被除数大； 除数大于1时，商比被除数小； 除数等于1时，商与被除数相等。
分数除以分数：
解决问题
养了多少只鸭？
2 1. 张大爷养了200只鹅，鹅的只数是鸭的 。 5 3 2. 张大爷养了200只鹅，鹅的只数比鸭少 5 。
养了多少只鸭？
人教版数学六上分数除法复习课件(共23张PPT)
知识要点要记牢： 1. 分数除法的计算方法：除以一个不等于0的数，等于 乘这个数的倒数。 2. 将分数除法转化为分数乘法的要点： (1)被除数不变；(2)除号变乘号；(3)除数变成它的倒数。
基础练
1. 填空。
(1)在分数除法转化为分数乘法时，要注意“一个不变， 两个变”，即(被除数)不变，( 除号 )变为(乘号)， ( 除数 )变为( 它的倒数 )。
(3)
( )和( )互为倒数。
巩固练
2. 判一判，对的画“√”，错的画“×”。
(1) 是倒数。
(2)整数a的倒数是 。
(3)得数是1的两个数互为倒数。
(4)任何一个数的倒数都小于它本身。
(5)
，所以
互为倒数。
(6)0的倒数还是0。
( ×) ( ×) ( ×) ( ×) ( ×) ( ×)
3. 求下列各数的倒数。
巩固练
2. 计算下面各题，能简算的要简算。
7
12
5
3. 下面的计算对吗？对的画“√”，错的画“×”，并 说说出错的原因。
பைடு நூலகம்
×
×
×
×
拓展练
4. 一个正方形的周长是 m，它的面积是多少平方米？
5. 小明走楼梯，他从1楼走到3楼用了 分钟，照这样的 速度，他从5楼走到10楼需要多少时间？
÷(3-1)×5=2 (分钟) 答：他从5楼走到10楼需要2分钟。
巩固练
2. 算一算。
3. 比一比，并说说你的发现。
＜
＜
＝
＝
＞
＞
我发现：两个不为0的数相除，如果除数大于1，那么商 就(小于)被除数；如果除数等于1，那么商就( 等于 )被 除数；如果除数小于1，那么商就( 小于)被除数。
基础练
1. 填空。
(1)在分数除法转化为分数乘法时，要注意“一个不变， 两个变”，即(被除数)不变，( 除号 )变为(乘号)， ( 除数 )变为( 它的倒数 )。
(3)
( )和( )互为倒数。
巩固练
2. 判一判，对的画“√”，错的画“×”。
(1) 是倒数。
(2)整数a的倒数是 。
(3)得数是1的两个数互为倒数。
(4)任何一个数的倒数都小于它本身。
(5)
，所以
互为倒数。
(6)0的倒数还是0。
( ×) ( ×) ( ×) ( ×) ( ×) ( ×)
3. 求下列各数的倒数。
巩固练
2. 计算下面各题，能简算的要简算。
7
12
5
3. 下面的计算对吗？对的画“√”，错的画“×”，并 说说出错的原因。
பைடு நூலகம்
×
×
×
×
拓展练
4. 一个正方形的周长是 m，它的面积是多少平方米？
5. 小明走楼梯，他从1楼走到3楼用了 分钟，照这样的 速度，他从5楼走到10楼需要多少时间？
÷(3-1)×5=2 (分钟) 答：他从5楼走到10楼需要2分钟。
巩固练
2. 算一算。
3. 比一比，并说说你的发现。
＜
＜
＝
＝
＞
＞
我发现：两个不为0的数相除，如果除数大于1，那么商 就(小于)被除数；如果除数等于1，那么商就( 等于 )被 除数；如果除数小于1，那么商就( 小于)被除数。
第三单元分数除法整理和复习
32
3
再如6.3:0.7的比值是9，那么6.3:0.7的最简比是 9:1，即把比值化成最简分数—9— ，看成9比1。）
1
★回忆思考：比和除法、分数有
什么联系和区别？
联 系（相 当 于） 区别
比
比的前项 ：比号 比的后项 比值
一种 关系
除法 被除数 ÷除号 除数
商
一种 运算
分数 分 子 —分数线 分母 分数值 一种数
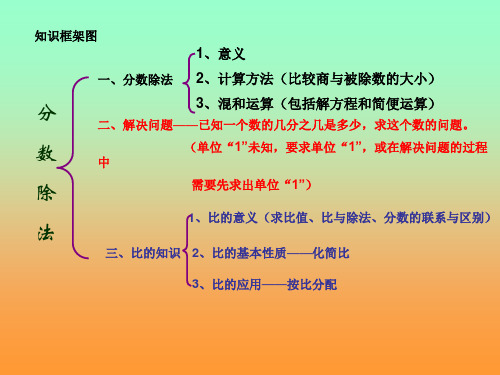
知识框架图
1、意义
一、分数除法 2、计算方法（比较商与被除数的大小）
分
3、混和运算（包括解方程和简便运算）
二、解决问题——已知一个数的几分之几是多少，求这个数的问题。
数
中
（单位“1”未知，要求单位“1”，或在解决问题的过程
除
需要先求出单位“1”）
1、比的意义（求比值、比与除法、分数的联系与区别）
法
三、比的知识 2、比的基本性质——化简比
0 .25 : 2
2) 求比值和化简比有什么联系，又有什么区别？
区别：比值是一个数，它可以是整数、小数和 分数；而最简比是一个比，前项和后项是互质的。
※联系：都可以用比的前项除以比的后项去计 算。
讨论：根据比值怎样很快说出它的最简比呢？根据 最简比你能直接说出比值吗？
如1：1 的最简比2：3， 那么它的比值是2 ，
3、比的应用——按比分配
一、分数除法的意义
• 已知两个因数的积与其中一个因数， 求另个因数的运算。
二、复习分数除法的计算法则。
除以一个数（0除外），等于（ 乘这个数的倒数）。
1、计算
2 6 5
15 26
讨论： 1） 2 6的商为什么比被除数（ 2） 小？
第三单元_分数除法复习
赵老师用60厘米长的铁丝围成一个长方形的教具， 长和宽的比是3：2。求这个长方形教具的长和宽 各是多少？
60÷2=30（厘米） 30÷（3+2） =30÷5 =6（厘米） 6×3=18（厘米） 6×2=12（厘米）
1 小明做题的数量是小华的 4 ，已知小明比小华少 做6道，小明和小华分别做多少道？ 6÷（4-1） =6÷3 =2（道） 2×4=8（道）
）
学校把栽70棵树的任务，按照六年级三个班的 人数，分配给各班。一班有46人，二班有44人， 三班有50人。三个班各应栽树多少棵？
70÷（46+44+50） =70÷140 =0.5（棵） 0.5×46=23（棵） 0.5×44=22（棵） 0.5×50=25（棵）
甲乙丙三个数的比是4：7：9。这三个数的平均数 是40，这三个数分别是多少？ 40×3=120 120÷(4+7+9) =120÷20 =6 6×4=24 6×7=42 6×9=54
1 小华体重30千克，小丽比小华重 ,小丽体重 6 多少千克？ 1 小华体重30千克，比小刚重 ,小刚体重多少 6 千克？
3 一辆汽车从甲地开往乙地，行了全程的 8 ，正 好行了81千米。两地间的公路长多少千米？ 3 一辆汽车从甲地开往乙地，行了全程的 8 ，离 乙地还有135千米。两地间的公路长多少千米？
（2）分数除法的意义是什么？ （分数除法的意义与整数除法的意义相同，都是已 知两个因数的积与其中一个因数，求另一个因数的 运算。）
说出下面各除法算式的意义。
5 5 是 3 5 表示已知两个因数的积 9 与其中一个因数是。 9 求另一个因数是多少 ？
2 40 3 1 3 2 4
2 表示已知两个因数的积 40与其中一个因数是 。 是 3 求另一个因数是多少 ？
分数除法、倒数、分数乘法知识点复习资料
分数除法、倒数、分数乘法知识点复习资料知识点复习资料1分数除法一、分数除法1、分数除法的意义：分数除法与整数除法的意义相同，表示已知两个因数的积和其中一个因数，求另一个因数的运算。
2、分数除法的计算法则：除以一个不为0的数，等于乘这个数的倒数。
3、规律(分数除法比较大小时)：(1)、当除数大于1，商小于被除数;(2)、当除数小于1(不等于0)，商大于被除数;(3)、当除数等于1，商等于被除数。
4、[]叫做中括号。
一个算式里，如果既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的。
二、分数除法解决问题(未知单位“1”的量(用除法)：已知单位“1”的几分之几是多少，求单位“1”的量。
)1、数量关系式和分数乘法解决问题中的关系式相同：(1)分率前是“的”：单位“1”的量×分率=分率对应量。
(2)分率前是“多或少”的意思：单位“1”的量×(1分率)=分率对应量。
2、解法：(建议：最好用方程解答)(1)方程：根据数量关系式设未知量为X，用方程解答。
(2)算术(用除法)：分率对应量÷对应分率=单位“1”的量。
3、求一个数是另一个数的几分之几：就一个数÷另一个数。
4、求一个数比另一个数多(少)几分之几：①求多几分之几：大数÷小数–1②求少几分之几：1-小数÷大数。
或①求多几分之几(大数-小数)÷小数②求少几分之几：(大数-小数)÷大数。
知识点复习资料2倒数1、倒数的意义：乘积是1的两个数互为倒数。
强调：互为倒数，即倒数是两个数的关系，它们互相依存，倒数不能单独存在。
(要说清谁是谁的倒数)。
2、求倒数的方法：(1)、求分数的倒数：交换分子分母的位置。
(2)、求整数的倒数：把整数看做分母是1的分数，再交换分子分母的位置。
(3)、求带分数的倒数：把带分数化为假分数，再求倒数。
(4)、求小数的倒数：把小数化为分数，再求倒数。
3、1的倒数是1;0没有倒数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（1.列方程 2.对应的量÷对应的分率=单位“1”量）
已知一个数比另一个数多或少几分之几是多少，求这个数。
（1.根据“一个数±相差数=另一个数”列方程 2.分数乘法意义列方程）
解决问题 两个未知数的和倍问题
（设单位“1”量为χ，用含有未知数的式子表示另一种量，再列方程）
工作总量用“1”表示的工程问题（假设工作总量为“1”）
1－
1 12
×
2
÷1
12
＋
1 20
一堆沙子，甲车运完要6小时，乙车运完要8小时，丙车运完 要9小时。
①甲、乙、丙三车合运1 小时，可以运走这堆 沙子的几分之几？
1 1÷（ 6
＋1 8
1 ＋9 ）
②甲、乙、丙同时合运几 小时可运完？
（1－
2
）÷（
1
1
＋
3
68
＋1 9
）
③甲、乙、丙合运几小时，
还剩这堆沙子的 2 ？ 3
5
2、张大爷养了200只鹅，鹅的只数比鸭 少 3 ，养了多少只鸭？
5 3、张大爷养的鸭和鹅共有700只，其中鹅的只 数是鸭的 2 ，鸭和鹅各有多少只？
5
一项工作，甲独做12天完成，乙独做20天
完成，
？
(只列式不计算)
11
＋
①甲乙合做1天完成全工程的几分之几？ 12 20
②甲乙合做3天完成全工程的几分之几？还剩几分之几没完
倒数的认识
什么是倒数？ （乘积是1的两个数互为倒数） 怎样求一个数的倒数？（把它的分子分母交换位置）
（1的倒数是1,0没有倒数）
计算方法：除以一个数（0除外），等于乘这个数的倒数。
分 数
分数除法计算
混合运算顺序：先算乘除，再算加减，有小括号的先算括号里的。
除
法
已知一个数的几分之几是多少，求这个数。
成？ 1
12
＋
1 20
×3
③甲乙合做工几天可完成全工程？
1－
1 12
1÷
1 12
＋
＋
1 20
×3
1
20
④甲乙合做几天完成全工程的一半？ 1
⑤甲乙合做5天后，余下的再
2 1
由乙单独完成，还需几天？ 1 － 12
＋
÷1
12
1 20
＋
1 20
×5
1
÷ 20
⑥甲先做2天后，余下的乙也 参加同做，还需几天完成？
④甲、乙同时合运3小时 后，丙也参加，还需几 小时运完？
[1－（ 1 6
＋1 8
1 ）×3]÷（ 6
＋
1 8
1
＋
9
）
1
＋
1
＋
6 89
（分钟）
如果总量没有告诉我们一个具体的数量，一般 我们都把总量看做单位“1”进行计算。
（工作效率×工作时间=工作总量 工作总量÷工作时间=工作效率 工作总量÷工作效率=工作时间 ）
倒数的复习：
乘积是1的两个数互为倒数。
3 8
和
8 3
互为倒数，就是指：
3的倒数是 8
8 ，8 的倒数是 3。
33
8
倒数是指两个数之间的关系，这两个数 相互依存，一个数不能叫倒数。
找出下列各数的倒数：
3
7
5
6
2
1
在括号里填>、<或=
3 1 （ ＞）3
42
4
20
5 4
（ ＜ ）20
3 9（＜ ） 3
5
5
当除数﹥1，商﹤被除数； 当除数﹦1，商﹦ 被除数； 当除数﹤ 1，商﹥被除数；
1、下面的说法正确吗？
（1）两个分数相除，商一定大于被除数。×
÷ 3/5
√ ×
解决问题的复习： 1、张大爷养了200只鹅，鹅的只数是 鸭的只 数的 2 ，养了多少只鸭？