8.2小波分解与重构
小波的分解与重构去噪。课件

小波变换在物联网中的应用
总结词
压缩感知、低功耗、物联网设备兼容
详细描述
物联网设备产生大量的数据,需要高效的压缩和感知技术来处理这些数据。小波变换作为一种有效的 数据压缩和感知方法,可以在保证数据完整性的同时,减少数据的存储空间和传输带宽需求。未来研 究需要进一步探索小波变换在物联网设备上的应用,降低功耗和提高设备的兼容性。
在图像处理、信号处理、数据压缩等 领域得到广泛应用。
优点
具有多尺度分析能力,能够适应不同 尺度的信号特征。
缺点
计算量较大,需要较高的计算资源和 时间。
提升小波变换
原理
应用
提升小波变换是一种基于滤波器组的小波 变换方法,通过将信号分解成低通和高通 分量,实现信号的多尺度分析。
在图像处理、信号处理、数据压缩等领域 得到广泛应用。
滤波器组
小波变换使用滤波器组来将信号分解为细节和近似成分。 滤波器组的特性决定了小波变换的性能和效果。
快速小波变换(FWT)
FWT是一种高效的小波变换算法,可以在计算机上实现。 它可以用于实时分析和处理信号。
小波变换的应用领域
图像处理
小波变换在图像处理中广泛应 用,包括图像压缩、去噪、增
强和特征提取等。
02
连续小波变换(CWT)
CWT是一种将信号分解为一系列不同尺度和频率的小波基函数的叠加
。它可以用于分析信号的时频特性。
03
离散小波变换(DWT)
DWT是一种将连续小波变换离散化,以便在计算机上实现。它可以用
于分析信号的细节和近似成分。
小波变换的基本原理
多尺度分析
多尺度分析是一种将信号分解为不同尺度和频率成分的方 法。小波变换的多尺度特性使得它可以在不同的尺度上分 析信号,从细节到整体。
用小波矩阵分析法进行函数的分解与重构

用小波矩阵分析法进行函数的分解与重构小波矩阵分析法(Wavelet Matrix Analysis)是一种用来分解和重构函数的数学方法。
它基于小波理论,将函数分解成不同频率的小波成分,并可以通过这些小波成分的线性组合来重构原始函数。
小波矩阵分析法在信号处理、图像处理、数据压缩等领域有着广泛的应用。
首先,我们需要选择合适的小波基函数。
小波基函数是用来描述小波的形状以及频率信息的,通常是一组正交函数。
常用的小波基函数有Haar小波、Daubechies小波、Symlet小波等。
选择不同的小波基函数会对分解和重构结果产生不同的影响。
在小波矩阵分析法中,我们将函数表示为小波基函数的线性组合,通过调整线性组合的系数来获得函数的分解和重构。
具体步骤如下:1.将原始函数表示为小波基函数的线性组合:f(x)=Σc(i,j)ψ(i,j)(x)其中,c(i,j)是系数矩阵,ψ(i,j)(x)是小波基函数。
2.根据小波基函数的正交性质,可以通过内积运算计算系数矩阵c(i,j)的值:c(i,j)=<f(x),ψ(i,j)(x)>3.对系数矩阵进行阈值化,去除较小的系数,得到稀疏的系数矩阵。
4.根据稀疏的系数矩阵f(x)≈Σc(i,j)ψ(i,j)(x)小波矩阵分析法的优点是可以同时分析函数在频域和时域上的信息,可以更准确地描述函数的局部特征。
同时,由于小波基函数的局部性,小波矩阵分析法对于非平稳信号的处理效果更好。
以图像处理为例,假设我们有一幅图像,我们可以将图像表示为一个二维的函数。
通过小波矩阵分析法可以将这个二维函数分解成不同频率的小波成分,每个小波成分代表图像中不同尺度和方向的特征。
通过调整系数矩阵的值,我们可以选择保留哪些小波成分,从而实现图像的降噪、压缩等操作。
最后,通过将选定的小波成分进行线性组合,可以重构原始图像。
总结来说,小波矩阵分析法是一种分析函数的有效数学方法,可以将函数表示为小波基函数的线性组合,并通过调整系数矩阵的值来实现函数的分解和重构。
小波分解与重构

小波分解与重构我理解的小波分解是将一个多频率组成的波通过小波分解将所有频率分解出来,重构就是将这些分频率加起来得到最后的重构结果,于是写了个这样的程序clcclose all;clear all;clc;fs=612;[reg,sta,data]=readmydata('beijing08.dat');data{1:end};A=ans(2:end);for i=1:609;if A(i)>50.0;A(i)=(A(i-12)+A(i+12))/2;endendfor i=609:612;if A(i)>50.0;A(i)=(A(i-12)+A(i-24))/2;endend%信号时域波形figure(1);plot(1:612,A);%使用db5小波进行尺度为7时的分解[c,l]=wavedec(A,9,'db5');%从小波分解结构[c,l]重构信号xdataa0=waverec(c,l,'db5');%检查重构效果figure(2);subplot(3,1,1);plot(A);title('原始信号')subplot(3,1,2);plot(a0);title('重构信号')subplot(3,1,3);plot(A-a0);title('误差信号')err=max(abs(A-a0))%重构第1~5层高频细节信号d9=wrcoef('d',c,l,'db5',9); d8=wrcoef('d',c,l,'db5',8); d7=wrcoef('d',c,l,'db5',7); d6=wrcoef('d',c,l,'db5',6); d5=wrcoef('d',c,l,'db5',5); d4=wrcoef('d',c,l,'db5',4); d3=wrcoef('d',c,l,'db5',3); d2=wrcoef('d',c,l,'db5',2); d1=wrcoef('d',c,l,'db5',1); %显示高频细节信号figure(3);subplot(9,1,1);plot(d9,'LineWidth',2); ylabel('d9');subplot(9,1,2);plot(d8,'LineWidth',2); ylabel('d8');subplot(9,1,3);plot(d7,'LineWidth',2);ylabel('d7');subplot(9,1,4);plot(d6,'LineWidth',2);ylabel('d6');subplot(9,1,5);plot(d5,'LineWidth',2);ylabel('d5');subplot(9,1,6);plot(d4,'LineWidth',2);ylabel('d4');subplot(9,1,7);plot(d3,'LineWidth',2);ylabel('d3');subplot(9,1,8);plot(d2,'LineWidth',2);ylabel('d2');xlabel('时间 t/s');subplot(9,1,9);plot(d1,'LineWidth',2);ylabel('d1');%第1层高频细节信号的包络谱y=hilbert(d1);ydata=abs(y);y=y-mean(y);nfft=1024;p=abs(fft(ydata,nfft));figure(4);plot((0:nfft/2-1)/nfft*fs,p(1:nfft/2));xlabel('频率 f/Hz');ylabel('功率谱 P/W');小波分解与重构程序>> clearI=imread('C:\Documents and Settings\Administrator\桌面\暑期/cidian.bmp');I=rgb2gray(I);[X,map]=gray2ind(I);subplot(2,2,1);imshow(X,map);title('原始图像');X=double(X);sX=size(X);[cA,cH,cV,cD]=dwt2(X,'db4');A0=idwt2(cA,cH,cV,cD,' db4', sX);subplot(2,2,2);imshow(A0,map);title('db4小波重构');error1=max(max(abs(X-A0)))程序很简单,也很基础。
小波分解与重构原理

小波分解与重构原理小波分解与重构是一种信号处理技术,它可以将信号分解成不同尺度和频率的成分,从而更好地理解和分析信号的特性。
在本文中,我们将介绍小波分解与重构的原理,以及它在信号处理领域的应用。
首先,让我们来看一下小波分解的原理。
小波分解是通过一组小波基函数对信号进行分解的过程。
这组小波基函数具有不同的尺度和频率特性,可以将信号分解成不同频率成分的系数。
在小波分解中,我们通常使用离散小波变换(DWT)来实现信号的分解。
DWT 是通过一系列的滤波器和下采样操作来实现信号的分解,具体过程是将信号通过低通滤波器和高通滤波器进行滤波,并对滤波后的信号进行下采样,最终得到近似系数和细节系数。
接下来,我们来谈谈小波重构的原理。
小波重构是将分解得到的近似系数和细节系数通过逆小波变换(IDWT)合成为原始信号的过程。
在小波重构中,我们需要使用逆小波变换来将近似系数和细节系数合成为原始信号。
逆小波变换的过程是通过一系列的滤波器和上采样操作来实现信号的合成,具体过程是将近似系数和细节系数通过上采样和滤波器进行滤波,并将滤波后的信号相加得到重构的信号。
小波分解与重构的原理虽然看起来比较复杂,但是它在信号处理领域有着广泛的应用。
首先,小波分解与重构可以用于信号的压缩和去噪。
通过保留重要的近似系数和细节系数,可以实现对信号的高效压缩;同时,通过去除不重要的近似系数和细节系数,可以实现对信号的去噪。
其次,小波分解与重构还可以用于信号的特征提取和模式识别。
通过分析不同尺度和频率的小波系数,可以提取信号的特征并进行模式识别。
此外,小波分解与重构还可以用于信号的分析和合成,例如音频信号的压缩和图像信号的处理等。
综上所述,小波分解与重构是一种重要的信号处理技术,它通过一组小波基函数对信号进行分解和重构,可以实现对信号的压缩、去噪、特征提取、模式识别、分析和合成等功能。
在实际应用中,我们可以根据具体的需求选择合适的小波基函数和分解层数,从而实现对不同类型信号的有效处理和分析。
小波分解与重构原理

小波分解与重构原理小波分解与重构是一种将信号分解为不同频率成分的方法,它是一种新兴的数学理论,近年来在信号处理、图像处理、压缩编码等领域得到广泛应用。
小波可以看作是一种基函数,可以用来表示任意一个非周期函数。
小波分解与重构原理便是利用小波基函数将信号进行分解和重构的过程。
首先,需要选择一个合适的小波基函数。
在小波函数中,常用的有Haar小波、Daubechies小波、Coiflet小波等,不同的小波函数适用于不同的信号特性。
接下来,通过小波基函数对原始信号进行分解。
分解的过程是逐级进行的,每一级都将信号分解为近似系数和细节系数两部分。
近似系数表示信号的低频成分,细节系数表示信号的高频成分。
通过迭代的方式,可以得到多个不同尺度的近似系数和细节系数。
分解后得到的近似系数和细节系数可以用于信号分析和处理。
近似系数表示信号的低频内容,可以用来恢复信号的平滑部分;细节系数表示信号的高频成分,可以用来提取信号的细节特征。
在重构过程中,通过逆变换操作将分解得到的近似系数和细节系数重构为原始信号。
重构的过程是逐级进行的,每一级都将近似系数和细节系数进行逆变换操作得到原始信号的一部分,并将其与上一级的逆变换结果相加得到更精确的重构结果。
小波分解与重构具有多尺度分析的特点,可以适应不同频率成分的信号处理需求。
它具有信号特征提取的能力,可以提取信号中的边缘、纹理等细节信息。
同时,小波变换还具有良好的时频局部性,可以很好地适应信号的时变特性。
小波分解与重构的应用十分广泛。
在图像处理中,可以利用小波分解与重构技术进行图像压缩、边缘提取、图像恢复等操作。
在语音信号处理中,可以提取语音的共振频率、噪声成分等信息。
此外,小波分解与重构还可以用于信号分析、数据压缩、图像处理、模式识别等领域。
总之,小波分解与重构是一种将信号分解为不同频率成分的方法,通过小波基函数的选择和分解重构过程,可以提取信号的不同尺度特征,具有良好的时频局部性和多尺度分析能力,广泛应用于各个领域。
小波的分解和重构算法

小波的分解和重构算法小波分解是将一个多频率组成的波通过小波分解将所有频率分解出来,重构就是将这些分频率加起来得到最后的重构结果。
小波变换的一级分解过程是,原始信号分别进行低通、高通滤波,再分别进行二元下采样,就得到低频、高频两部分系数;而多级分解则是对上一级分解得到的低频系数再进行小波分解,是一个递归过程。
分解过程:function [cA,cD] = mydwt(x,lpd,hpd,dim)%函数[cA,cD]=MYDWT(X,LPD,HPD,DIM) 对输入序列x进行一维离散小波分解,输出分解序列[cA,cD] ;%输入参数:x——输入序列;% lpd——低通滤波器;% hpd——高通滤波器;% dim——小波分解级数;% 输出参数:cA——平均部分的小波分解系数;% cD——细节部分的小波分解系数;cA=x; % 初始化cA,cDcD=[ ];for i=1:dimcvl=conv(cA,lpd); % 低通滤波,为了提高运行速度,调用MATLAB 提供的卷积函数conv()dnl=downspl(cvl); % 通过下采样求出平均部分的分解系数cvh=conv(cA,hpd); % 高通滤波dnh=downspl(cvh); %通过下采样求出本层分解后的细节部分系数cA=dnl; % 下采样后的平均部分系数进入下一层分解cD=[cD,dnh]; % 将本层分解所得的细节部分系数存入序列cDendfunction y=downspl(x);% 函数Y=DOWMSPL(X) 对输入序列进行下采样,输出序列Y。
% 下采样是对输入序列取其偶数位,舍弃奇数位。
N=length(x); % 读取输入序列长度M=floor(N/2); % 输出序列的长度是输入序列长度的一半i=1:M;y(i)=x(2*i);而重构则是分解的逆过程,对低频系数、高频系数分别进行上采样和低通、高通滤波处理。
重构过程:function y = myidwt(cA,cD,lpr,hpr);% 函数MYIDWT() 对输入的小波分解系数进行逆离散小波变换,重构出信号序列y% 输入参数:cA ——平均部分的小波分解系数;% cD ——细节部分的小波分解系数;% lpr、hpr ——重构所用的低通、高通滤波器。
小波变换分解与重构

小波变换是一种时频分析方法,将信号分解为不同频率的子信号。
它可以用于信号处理、数据压缩、模式识别等领域。
小波变换的分解和重构过程如下:
1. 分解(Decomposition):
a. 选择合适的小波基函数(例如哈尔小波、Daubechies小波等)。
小波基函数是具有局部性质的函数,能够反映不同频率成分的特征。
b. 将原始信号通过小波基函数与尺度函数进行卷积运算得到一组低频信号(approximation,A)和高频信号(detail,D)。
c. 将低频信号进一步分解,得到更低频的近似信号和更高频的细节信号。
这个过程可以迭代多次,形成小波分解的多个层次。
2. 重构(Reconstruction):
a. 从最低频的近似信号(A)开始,通过逆小波变换(inverse wavelet transform)将近似信号和各层的细节信号进行重构。
b. 每次重构时,使用相应的小波基函数逆向卷积
运算,将低频信号和高频信号进行合并,得到上一层的近似信号。
c. 重复上述步骤,直到最终得到重构的原始信号。
小波分解和重构的过程在频域上实现了信号的分离,将时域与频域信息结合起来,能够更好地描述信号的局部特征和瞬态特性。
小波变换的应用广泛,例如图像压缩领域中的JPEG2000标准就使用了小波变换方法。
此外,小波分析还可以用于信号降噪、信号特征提取、边缘检测、图像增强等多个领域,具有很高的实用价值。
8.2 小波分解与重构
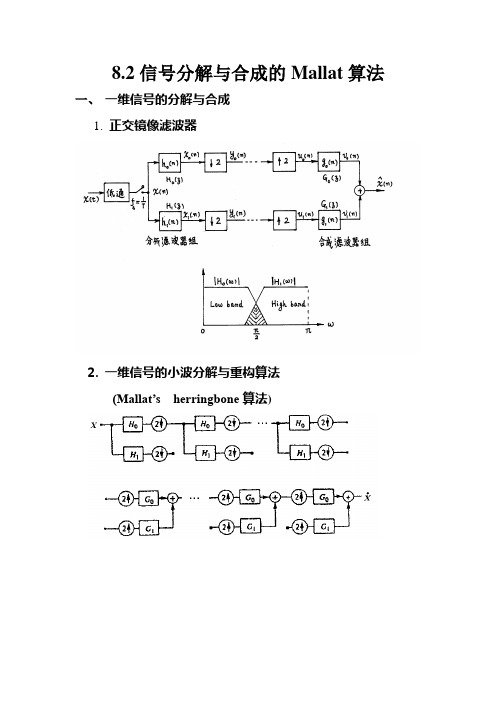
8.2信号分解与合成的Mallat算法一、一维信号的分解与合成1. 正交镜像滤波器2. 一维信号的小波分解与重构算法(Mallat’s herringbone算法)二、二维信号的分解与重构三、用Matlab实现图像的分解与合成1.dwt2与idwt2dwt2为一层二维离散小波分解函数,调用格式:[cA,cH,cV,cD]=dwt2(X,’wname’)% 用指定小波基对图像X进行一层二维离散小波变换分解。
’wname’为小波基的名称,cA为近似(低频)图像矩阵,cH, cV, cD分别为小波分解的水平方向细节系数,垂直方向细节系数,对角线方向细节系数。
[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) % 用指定的低通分解滤波器Lo_D和高通分解滤波器Hi_D对图像X进行二维离散小波分解。
Lo_D与Hi_D的长度必须一致。
idwt2为一层二维离散小波重构函数,调用格式为:X=idwt2(cA,cH,cV,cD,’wname’)% 用指定小波重构图像X,wname为小波基的名称。
X=idwt2(cA,cH,cV,cD,Lo_R,Hi_R)% 用指定低通重构滤波器Lo_R和高通重构滤波器Hi_R重构图像X,Lo_R与Hi_R的长度必须一致。
2.wavedec2与vaverec2wavedec2为多层二维离散小波分解函数,其调用格式为:[C,S]=wavedec2(X,N,’wname’)% 用指定小波基对图像X进行N层二维离散小波分解。
N为正整数,C为小波分解矢量,S为相应的标记矩阵。
C = [ A(N) | H(N) | V(N) | D(N) | ...H(N-1) | V(N-1) | D(N-1) | ... | H(1) | V(1) | D(1) ].A = approximation coefficientsH = horizontal detail coefficientsV = vertical detail coefficientsD = diagonal detail coefficients矩阵S形如S(1,:) = size of approximation coefficients(N)S(i,:) = size of detail coefficients(N-i+2) for i = 2, ...N+1 S(N+2,:) = size(X).wavwrec2为多层二维离散小波重构函数,其调用格式为:X=waverec2(C,S,’wname’) %利用指定小波基由矢量C和标记矩阵S重构图像X。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.2信号分解与合成的Mallat算法
一维信号的分解与合成
1. 正交镜像滤波器
H伽1IH㈣1
X Higk W
---
L 血b&nd
o K n
A
2. 一维信号的小波分解与重构算法
(Mallat ' herringbone 算法)
X
、二维信号的分解与重构
rl 比
horizontal
HL
LL
venic
aJ
HH
三、用Matlab实现图像的分解与合成
1. dwt2 与idwt2
dwt2为一层二维离散小波分解函数,调用格式:
[cA,cH,cV,cD]=dwt2(X, 'wname'
%用指定小波基对图像X进行一层二维离散小波变换分解。
wname'为小波基的名称,cA为近似
(低频)图像矩阵,cH, cV, cD分别为小波分解的水平方向细节系数,垂直方向细节系数,对角线方向细节系数。
[cA,cH,cV,cD]=dwt2(X丄o_D,Hi_D)
%用指定的低通分解滤波器Lo_D和高通分解滤波
器Hi_D对图像X进行二维离散小波分解。
Lo_D与
Hi_D 的长度必须一致。
idwt2 为一层二维离散小波重构函数,调用格式为:
X=idwt2(cA,cH,cV ,cD,'wname')
% 用指定小波重构图像X ,wname 为小波基的名称
X=idwt2(cA,cH,cV ,cD,Lo_R,Hi_R)
% 用指定低通重构滤波器Lo_R 和高通重构滤波器Hi_R 重构图像X,Lo_R 与Hi_R 的长度必须一致。
2. wavedec2与vaverec2
wavedec2为多层二维离散小波分解函数,其调用
格式为:
[C,S]=wavedec2(X,N,'wname')
% 用指定小波基对图像X 进行N 层二维离散小波分解。
N 为正整数,C为小波分解矢量,S为相应的标记矩阵。
C = [ A(N) | H(N) | V(N) | D(N) | ...
H(N-1) | V(N-1) | D(N-1) | ... | H(1) | V(1) | D(1) ].
A = approximation coefficients
H = horizontal detail coefficients
V = vertical detail coefficients
D = diagonal detail coefficients
矩阵S 形如
S(1,:) = size of approximation coefficients(N)
S(i,:) = size of detail coefficients(N-i+2) for i = 2,・・・
N+1
S(N+2,:) = size(X).
wavwrec2为多层二维离散小波重构函数,其调用格式为:
X=waverec2(C,S, 'wname' %利用指定小波基由矢
量C和标记矩阵S重构图像X。
X=waverec2(C,S丄o_R,Hi_R) %利用低通重构滤
波器Lo_R和高通重构滤波器Hi_R重构图像X。
3. 利用GUI (Graphical User Interface)进行小波分析
利用Matlab提供的图形用户界面GUI可使小波分析变得简单、直观。
在Command Window中键入wavemenu后回车,可进入如下图所示的小波工具箱主菜单窗口
单击Wavelet 2-D、File、load image,在Toolbox\wavelet\ wavedemo目录下调出woman图像文件就可以进行分析
Compress (压缩)、
Histograms (直方图)和De-noise (去噪)等四种
分析。
(参阅《基于 MATLA 啲系统分析与设计 一小波分析》 2.9节,西安电子科技大学出版社,2000)
了。
例如在窗口右上角选择小波种类、分解层数后,单
击Analyze,显示区域就会显示分析结果 上述工具可以对图像进行 Statistics 统
)。
