水力学(闻德荪)习题答案第四章
水力学(闻德荪)习题答案第四章
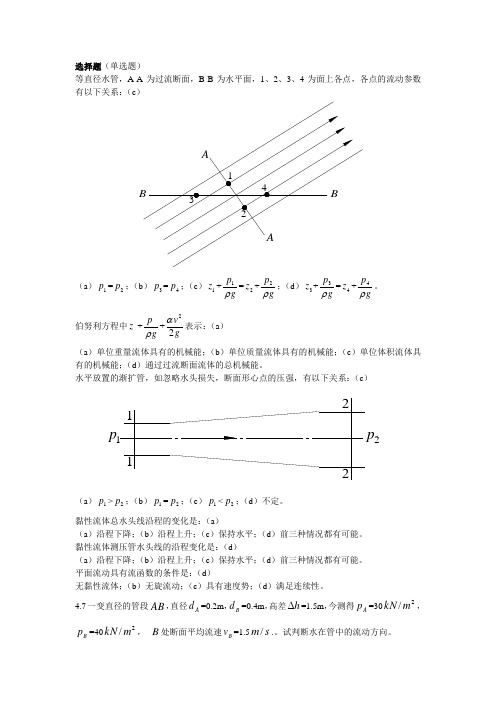
选择题（单选题）等直径水管，A-A 为过流断面，B-B 为水平面，1、2、3、4为面上各点，各点的流动参数有以下关系：（c ）（a ）1p =2p ；（b ）3p =4p ；（c ）1z +1p g ρ=2z +2p g ρ；（d ）3z +3p g ρ=4z +4pgρ。
伯努利方程中z +p g ρ+22v gα表示：（a ）（a ）单位重量流体具有的机械能；（b ）单位质量流体具有的机械能；（c ）单位体积流体具有的机械能；（d ）通过过流断面流体的总机械能。
水平放置的渐扩管，如忽略水头损失，断面形心点的压强，有以下关系：（c ）p p 2（a ）1p >2p ；（b ）1p =2p ；（c ）1p <2p ；（d ）不定。
黏性流体总水头线沿程的变化是：（a ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。
黏性流体测压管水头线的沿程变化是：（d ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。
平面流动具有流函数的条件是：（d ） 无黏性流体；（b ）无旋流动；（c ）具有速度势；（d ）满足连续性。
4.7一变直径的管段AB ，直径A d =0.2m ，B d =0.4m ，高差h ∆=1.5m ，今测得A p =302/m kN ，B p =402/m kN ， B 处断面平均流速B v =1.5s m /.。
试判断水在管中的流动方向。
解： 以过A 的水平面为基准面，则A 、B 点单位重量断面平均总机械能为：42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭（m ）2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯（m ）∴水流从B 点向A 点流动。
工程流体水力学第四章习题答案
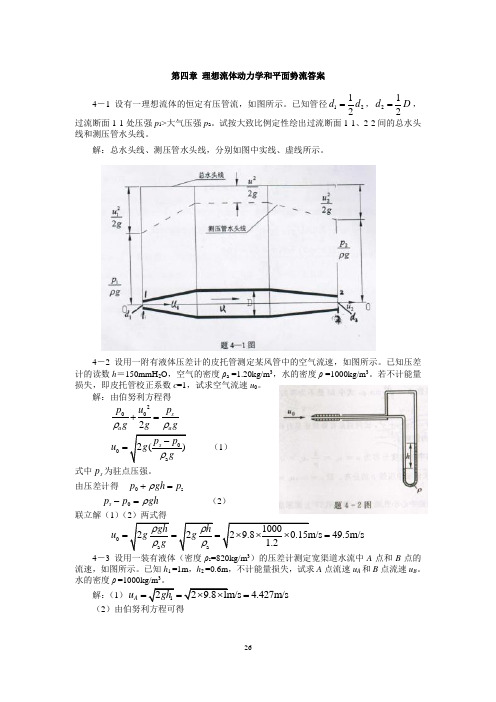
第四章 理想流体动力学和平面势流答案4－1 设有一理想流体的恒定有压管流，如图所示。
已知管径1212d d =，212d D =，过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解：总水头线、测压管水头线，分别如图中实线、虚线所示。
4－2 设用一附有液体压差计的皮托管测定某风管中的空气流速，如图所示。
已知压差计的读数h ＝150mmH 2O ，空气的密度ρa =1.20kg/m 3，水的密度ρ =1000kg/m 3。
若不计能量损失，即皮托管校正系数c =1，试求空气流速u 0。
解：由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=（1） 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= （2）联立解（1）（2）两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4－3 设用一装有液体（密度ρs =820kg/m 3）的压差计测定宽渠道水流中A 点和B 点的流速，如图所示。
已知h 1 =1m ，h 2 =0.6m ，不计能量损失，试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解：（1）1229.81m/s 4.427m/s A u gh ==⨯⨯= （2）由伯努利方程可得22A AA u p h g gρ+= （1）22B BB u p h g gρ+= （2）式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由（1）、（2）式可得2222A B A BA B p p u u h h g g gρ-=+-- （3） 由压差计得，22ρρρρ--++=A A s B B p gh gh gh gh p ，所以220.82A BA B p p h h h h gρ-=+-- (4) 由（3）式、（4）式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
水力学课后答案
答案说明以下答案是由老师自己做出来的，其中的每一题的画图都省略了，希望同学们自己在做题过程中补充上完整的图形。
在答案电子话过程中可能会有一些错误，希望同学们可多提宝贵意见。
第二章作业答案2-9 10(1.5 1.0)53.9a p p g p kpa ρ=+--=11151.9abs a p p p kpa =+= 20(1.50.5)58.8a p p g p kpa ρ=+--=22156.8abs a p p p kpa =+=1212 6.5p pZ Z m g gρρ+=+= 2-11 略2-120(2.50.9)(2.00.9)(2.00.7)(1.80.7)0Hg Hg p g g g g ρρρρ+---+---=0265p kpa =2-14 受压面为矩形平面 76.38c P gh kN ρω==34112c b a J m ⋅==289c D c c J y y y ω=+= 所以，作用点至A 点的距离 10'29D y y '=-= 根据合力矩守恒2cos 60'84.9o T P y T kN⋅=⋅=2-18 c P gh ρω=(sin 60)2146.5o ag H abkNρ=-⋅= sin 60(cos 60)o o T G G P f =⋅++⋅45.9T kN =闸门的静水压强分布图为梯形，根据梯形的压力中心距底部距离的计算公式12122()3h h a e h h +=+ 21sin h H h H a θ==-1.13e m =2-21 仅考虑左侧水：11144.1x c x P gh kN ρω== （→） 1134.6z P gV kN ρ== （↑）仅考虑右侧水22211.03x c x P gh kN ρω== （←）2217.32z P gV kN ρ== （↓）综合两侧水1233.08x x x P P P kN =-= (→)1217.32z z z P P P kN =-= （↑） 总压力37.34P kN ==tan ZxP P θ=2-23 分析上半球0x P =232[()]3ZP gVT n n g R H R R n ρρππ===+-第三章作业答案3-32max 000.0342max max 00[(1())]1/20.212/rrQ ud u d r u u r r L sωωωωπ==-=-⋅⋅=⎰⎰0.075/Qv m s ω==3-6 根据连续性方程123Q Q Q =+34/v m s =3-7根据连续性方程123Q Q Q =+234ωω= 22231482.3370.58m mωω==3-11建立能量方程22111222121222122122()2.252hg p p v p v z z g g g gz z p p v v h m g g ααρρρρρρ++=++=---===油油油油油51.1/Q L s μ==3-15在图上12d d 和断面建立能量方程2211122212122220p v p v z z g g g gz z p ααρρ++=++==联立连续性方程 1122v v ωω= 2 4.9/v m s = 在图自由液面和2d 断面建立能量方程221.232v H m g== 3-18 建立能量方程22111222121212221.8 1.680p v p v z z g g g gz m z mp p ααρρ++=++====连续性方程12211.8(1.80.30.12)1.3v v v v ⋅=--⋅=⋅13111.23/5.98/v m s Q v m sω===3-20建立的坐标系比较特别，X 轴沿着1Q 方向，Y 轴与X 轴垂直 根据能量方程可知1268.1/v v v m s ===建立动量方程，沿X 轴方向：11221212cos 600cos 60o oQ v Q v Q v Q Q Q Q Q Qρρρ--=-=+=连续性方程12(1cos 60)2(1cos 60)2o o QQ QQ =+=-313225.05/8.35/Q m s Q m s==建立动量方程，沿Y 轴方向：0(sin60)1969o y R Q v N ρ=--=3-23 在A-A ，B-B 断面间建立能量方程2.4/3.8/A b v m s v m s==221112221212222175.7p v p v z z g g g gz z p kNααρρ++=++==在A-A ，B-B 断面间建立动量方程沿X 轴方向：1cos 60(cos 60)sin 60sin 60o o A A B B x B ooB B y B p v p v R Q v v p v R Qv ρρ--=-+=-54555984y x R N R N==3-24 （1）建立能量方程2212120022v v h h g g++=++连续性方程1122h v h v =3228.9215)998(v v +⨯⨯=+ 0294107232=+-v v s m v /512.82= m h v v h 762.15512.831212=⨯==（2）以1-1断面和2-2断面之间的水体为控制体，并假设整个坝面对水体的水平反力为F '。
水力学答案——精选推荐
第四章 思考题:4-1：N-S 方程的物理意义是什么？适用条件是什么？物理意义：N-S 方程的精确解虽然不多，但能揭示实际液体流动的本质特征，同时也作为检验和校核其他近似方程的依据，探讨复杂问题和新的理论问题的参考点和出发点。
适用条件：不可压缩均质实际液体流动。
4-2 何为有势流?有势流与有旋流有何区别?答:从静止开始的理想液体的运动是有势流. 有势流无自身旋转,不存在使其运动的力矩.4—3 有势流的特点是什么？研究平面势流有何意义？有势流是无旋流，旋转角速度为零。
研究平面势流可以简化水力学模型，使问题变得简单且于实际问题相符，通过研究平面势流可以为我们分析复杂的水力学问题。
4-4.流速势函数存在的充分必要条件是流动无旋，即xu y u yx∂∂=∂∂时存在势函数，存在势函数时无旋。
流函数存在的充分必要条件是平面不可压缩液体的连续性方程，即就是0=∂∂+∂∂yu x u yx存在流函数。
4—5何为流网，其特征是什么？绘制流网的原理是什么 ？流网：等势线（流速势函数的等值线）和流线（流函数的等值线）相互正交所形成的网格 流网特征：（1）流网是正交网格（2）流网中的每一网格边长之比，等于流速势函数与流函数增值之比。
（3）流网中的每个网格均为曲线正方形 原理:自由表面是一条流线，而等势线垂直于流线。
根据入流断面何处流断面的已知条件来确定断面上 流线的位置。
4-6.利用流网可以进行哪些水力计算?如何计算？解:可以计算速度和压强。
计算如下：流场中任意相邻之间的单宽流量∆q 是一常数。
在流场中任取1、2两点，设流速为，，两端面处流线间距为∆m1，∆。
则∆q=∆m1=∆，在流网中，各点处网格的∆m 值可以直接量出来，根据上式就可以得出速度的相对变化关系。
如果流畅中某点速度已知，就可以其他各点的速度。
流畅中的压强分布，可应用能量方程求得。
z1++=++当两点位置高度z1和为已知，速度，u2已通过流亡求出时，则两点的压强差为-=-+-如果流畅中某一点压强已知，则其他个点压强均可求得4.7利用流网计算平面势流的依据是什么？（参考4.6的解释）4-8流网的形状与哪些因素有关？网格的疏密取决于什么因素？答：流网由等势线和流线构成，流网的形状与流函数φ（x,y）和流速势函数ψ(x,y)有关；由∆q=∆ψ=常数，∆q=u1∆m1=常数，得两条流线的间距愈大，则速度愈小，若间距愈小，则速度愈大。
智慧树知到《水力学(四川大学版)》章节测试答案
第1章单元测试1、水的粘性随温度升高而（）答案：减小2、水力学中单位质量力是( )。
答案：作用在单位质量液体上的质量力3、下面哪种力可以归为质量力。
答案：重力4、液体与气体的粘度，随着温度的升高，分别( )。
答案：减小，增大5、气体的粘性随温度升高而( )。
答案：增大6、理想液体的特征是( )。
答案：无粘性7、以下哪几种液体属于非牛顿流体。
答案：血液8、液体的粘滞性只有在流动时才表现出来。
答案：对9、作用于液体的质量力只有重力。
答案：错第2章单元测试1、液体某点的绝对压强是55KN/m2,若一个大气压为98KN/m2，则该点的相对压强为( )。
答案：-43KN/m22、静止液体中存在( )。
答案：压应力3、压力中心是( )。
答案：总压力的作用点4、平衡液体中的等压面必为（）答案：与质量力相正交的面5、相对压强必为正值。
答案：错6、静水压强的大小与受压面的方位无关答案：正确7、若干连通容器盛有不同的液体，则其任意水平面为等压面。
答案：错8、静水总压力的压力中心就是受力面面积的形心。
答案：错第3章单元测试1、水流的流线稀疏，说明水流的流速（）。
答案：小2、黏性流体总水头线沿程的变化是（）。
答案：沿程下降3、在恒定流中（）。
答案：同一点处不同时刻的动水压强相等4、均匀流特征不包括（）。
答案：流速缓慢5、毕托管可以用来测（）。
答案：时均流速6、均匀流的总水头线和测压管水头线的关系是（）。
答案：互相平行的直线7、液体运动总是（）。
答案：单位总机械能大处向单位总机械能小处流动8、恒定流是（）答案：流场中任意空间点的运动要素不随时间变化9、均匀流是（）答案：迁移加速度为零10、渐变流与急变流均属非均匀流。
答案：对11、恒定流一定是均匀流，非恒定流一定是非均匀流。
答案：错12、测压管水头线可高于总水头线。
答案：错13、一元流是运动参数是一个空间坐标和时间变量的函数。
答案：对第4章单元测试1、湍流的流速分布规律按（）。
水力学各章习题..
第1章绪论一、选择题1．按连续介质的概念，流体质点是指（）A .流体的分子； B. 流体内的固体颗粒；C . 无大小的几何点；D. 几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。
2．作用在流体的质量力包括（）A. 压力；B. 摩擦力；C. 重力；D. 惯性力。
3．单位质量力的国际单位是：（）A . N ；B. m/s；C. N/kg；D. m/s2。
4．与牛顿内摩擦定律直接有关系的因素是（）Ａ. 切应力和压强； B. 切应力和剪切变形速率；C. 切应力和剪切变形。
5．水的粘性随温度的升高而（）A . 增大；B. 减小；C. 不变；D，无关。
6．气体的粘性随温度的升高而（）A. 增大；Ｂ. 减小；Ｃ. 不变；D，无关。
7．流体的运动粘度υ的国际单位是（）Ａ. m2/s ；B. N/m2；C. kg/m ；D. N·s/ｍ28．理想流体的特征是（）Ａ. 粘度是常数；B. 不可压缩；C. 无粘性； D. 符合pV=RT。
9．当水的压强增加１个大气压时，水的密度增大约为（）Ａ. 200001；Ｂ. 100001；Ｃ. 40001。
10．水力学中，单位质量力是指作用在（）Ａ. 单位面积液体上的质量力；Ｂ. 单位体积液体上的质量力；Ｃ. 单位质量液体上的质量力；Ｄ. 单位重量液体上的质量力。
11．以下关于流体粘性的说法中不正确的是（）Ａ. 粘性是流体的固有属性；Ｂ. 粘性是在运动状态下流体具有抵抗剪切变形速率能力的量度Ｃ. 流体的粘性具有传递运动和阻滞运动的双重作用；Ｄ. 流体的粘性随温度的升高而增大。
12．已知液体中的流速分布µ－y Ａ.τ＝０；Ｂ.τ＝常数； Ｃ. τ＝ky 13 Ａ. 液体微团比液体质点大；Ｂ. Ｃ. 14．液体的汽化压强随温度升高而（ Ａ. 增大； Ｂ. 减小；Ｃ. 不变；15．水力学研究中，为简化分析推理， Ａ. 牛顿液体模型； Ｂ. 体模型；Ｅ. 连续介质模型。
水力学(闻德荪)习题答案第六章分析解析
选择题（单选题）1.水在垂直管内由上向下流动，测压管水头差h，两断面间沿程水头损失，则：（a）（a）hf=h；（b）h f=h+l；（c）h f=l－h；（d）h f=l。
2.圆管流动过流断面上切应力分布为：（b）（a）在过流断面上是常数；（b）管轴处是零，且与半径成正比；（c）管壁处是零，向管轴线性增大；（d）按抛物线分布。
3.圆管流的雷诺数（下临界雷诺数）：（d）（a）随管径变化；（b）随流体的密度变化；（c）随流体的黏度变化；（d）不随以上各量变化。
4.在圆管流中，紊流的断面流速分布符合：（d）（a）均匀规律；（b）直线变化规律；（c）抛物线规律；（d）对数曲线规律。
5.在圆管流中，层流的断面流速分布符合：（c）（a）均匀规律；（b）直线变化规律；（c）抛物线规律；（d）对数曲线规律。
6.半圆形明渠半径r0=4m，水力半径为：（c）（a）4m；（b）3m；（c）2m；（d）1m。
7.变直径管流，细断面直径为d1，粗断面直径d2=2d1，粗细断面雷诺数的关系是：（d）（a）Re1=0.5 Re2；（b）Re1= Re2；（c）Re1=1.5 Re2；（d）Re1=2 Re2。
8.圆管层流，实测管轴线上流速为4m/s，则断面平均流速为: （c）（a）4 m/s；（b）3 .2m/s；（c）2 m/s；（d）1 m/s。
9.圆管紊流过渡区的沿程摩阻系数λ：（c）（a）与雷诺数Re有关；（b）与管壁相对粗糙k s/d有关；（c）与Re及k s/d有关；（d）与Re和管长L有关。
10.圆管紊流粗糙区的沿程摩阻系数λ：（b）（a）与雷诺数Re有关；（b）与管壁相对粗糙k s/d有关；（c）与Re及k s/d有关；（d）与Re和管长L有关。
11.工业管道的沿程摩阻系数λ，在紊流过渡区随雷诺数的增加：（b）（a ）增加；（b ）减小；（c ）不变；（d ）不定。
计算题【6.12】水管直径d =10cm ，管中流速v =1m/s ，水温为10℃，试判别流态。
工程流体力学水力学闻德实际流体动力学基础课后答案教材
工程流体力学闻德课后习题答案第五章 实际流体动力学基础5— 1设在流场中的速度分布为 u x =2ax ， u y =- 2ay ， a 为实数，且 a ＞0。
试求切应力 τxy 、τyx 和附加压应力 p ′x 、 p ′y 以及压应力 p x 、p y 。
当 dp 0 时， u yv ，速度 ｕ为直线分布， 这种特殊情况的流动称简单柯埃梯流动或 dx h 简单剪切流动。
它只是由于平板运动，由于流体的粘滞性带动流体发生的流动。
当 dp0 时，即为一般的柯埃梯流动， 它是由简单柯埃梯流动和泊萧叶流动叠加而成， dx 速度分布为当 p ＞０时， 沿着流动方向压强减小， 速度在整个断面上的分布均为正值； 当 p ＜０时， 沿流动方向压强增加，则可能在静止壁面附近产生倒流，这主要发生 p ＜－１的情况．5－ 3 设明渠二维均匀（层流）流动，如图所示。
若忽略空气阻力，试用纳维 — 斯托克斯方程和连续性方程，证明过流断面上的速度分布为 u x = r gsinq （2zh- z 2） ，单宽流量解： xyyxuyu x xyu xuyp x2 4a ，p y 2 4a ，x yp p p p 4a p p p p 4a 5－2 设例５－ 1 中的下平板固定不动， 上平板以速度 v 沿 x 轴方向作等速运动 （如图所示） ，由于上平板运动而 引起的这种流动，称柯埃梯（ Couette ）流动。
试求在这种 流动情况下，两平板间的速度分布。
（请将 dp0 时的这 dx 一流动与在第一章中讨论流体粘性时的流动相比较） 解：将坐标系 ox 轴移至下平板，则边界条件为y ＝０， u X u 0 ； y h ， u v 。
由例５－ 1 中的（ 11）式可得 y h 2dp y vh 2 dx h (1 h y )h１）uv hy p h y (1 h y)式中2vdp)dx )２） ３）x 2mq= r gh3 sinq 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
选择题（单选题）等直径水管，A-A 为过流断面，B-B 为水平面，1、2、3、4为面上各点，各点的流动参数有以下关系：（c ）（a ）1p =2p ；（b ）3p =4p ；（c ）1z +1p g ρ=2z +2p g ρ；（d ）3z +3p g ρ=4z +4pgρ。
伯努利方程中z +p g ρ+22v gα表示：（a ）（a ）单位重量流体具有的机械能；（b ）单位质量流体具有的机械能；（c ）单位体积流体具有的机械能；（d ）通过过流断面流体的总机械能。
水平放置的渐扩管，如忽略水头损失，断面形心点的压强，有以下关系：（c ）p p 2（a ）1p >2p ；（b ）1p =2p ；（c ）1p <2p ；（d ）不定。
黏性流体总水头线沿程的变化是：（a ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。
黏性流体测压管水头线的沿程变化是：（d ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。
平面流动具有流函数的条件是：（d ） 无黏性流体；（b ）无旋流动；（c ）具有速度势；（d ）满足连续性。
4.7一变直径的管段AB ，直径A d =0.2m ，B d =0.4m ，高差h ∆=1.5m ，今测得A p =302/m kN ，B p =402/m kN ， B 处断面平均流速B v =1.5s m /.。
试判断水在管中的流动方向。
解： 以过A 的水平面为基准面，则A 、B 点单位重量断面平均总机械能为：42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭（m ）2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯（m ）∴水流从B 点向A 点流动。
答：水流从B 点向A 点流动。
4.8利用皮托管原理，测量水管中的点速度v 。
如读值h ∆=60mm ，求该点流速。
解： 10 3.85u ====（m/s ） 答：该点流速 3.85u =m/s 。
4.9水管直径50mm ，末端阀门关闭时，压力表读值为212/m kN 。
阀门打开后读值降至5.52/m kN ，如不计水头损失，求通过的流量。
解：（1）水箱水位 321100 2.1410009.807p H z g ρ⨯=+=+=⨯（m ）（2）阀门开启后，从水箱液面到仪表处列伯努利方程，可得：22p v H g gρ=+∴ 5.57v ===（m/s ） 20.055.570.0114Q vA π⨯==⨯=（m 3/s ）答：通过的流量0.011Q =m 3/s 。
4.10水在变直径竖管中流动，已知粗管直径1d =300mm ，流速1v =6s m /。
为使两断面的压力表读值相同，试求细管直径（水头损失不计）。
解： 以过下压力表处的水平面为基准面，列伯努利方程如下：22111222121222w p v p v z z h g g g gααρρ-++=+++∵120w h -=，13z =m ，20z = 取12αα=，当12p p =时，有：222211229.8073694.842v gz v =+=⨯⨯+=29.74v =（m/s ）由连续性方程 2211v A vA = ∴2300235.5d d ==（mm ） 答：细管直径为235.5mm 。
4.11为了测量石油管道的流量，安装文丘里流量计，管道直径1d =200mm ，流量计喉管直径2d =100mm ，石油密度ρ=8503/m kg ，流量计流量系数μ=0.95。
现测得水银压差计读书p h =150mm ，问此时管中流量Q 是多少。
解：Q μ=其中：0.95μ=；2210.20.0359d K ππ⨯===0.15p h =（m ）Q μμ==0.950.0359=⨯0.0511575=（m 3/s ）51.2=（l /s ）答：此时管中流量Q 51.2=l /s 。
4.12水箱中的水从一扩散短管流到大气中，直径1d =100mm ，该处绝对压强1p =0.5大气压，直径2d =150mm ，试求水头H ，水头损失忽略不计。
解：（1）以出水管轴线为基准面，列管径1d 与2d 处的伯努利方程，可得：2211122222p v p v g g g gααρρ+=+取12 1.0αα==，20p =，10.5101.32550.663p =-⨯=-kPa ∵ 221122p v v ρ-=-∴ 432221250.663101101.325d v d ρ⎡⎤⎛⎫⨯⨯⎢⎥-== ⎪⎢⎥⎝⎭⎣⎦1224101.325 4.9940.1510.1v ⎡⎤⎢⎥⎢⎥==⎢⎥⎛⎫-⎢⎥ ⎪⎝⎭⎣⎦（m/s ）（2）从液面到短管出口列能量（伯努利）方程。
222 4.994 1.27229.807v H g ===⨯（m ）答：水头H 1.27=m 。
4.13离心式通风机用集流器A 从大气中吸入空气，直径d =200mm 处接一根细玻璃管，已知管中的水上升H =150mm ，求进气流量（空气的密度ρ=1.293/m kg ）。
解： 以集流器轴线的水平面为基准面，从距进口一定距离的水平处列到测管处的伯努利方程，可得：22a H p p v g g gαρρ=+不计损失，取 1.0α= ∴v =其中 0a p =，则 H p H g ρ=-⋅水∴47.76v ===（m/s ） 247.760.2 1.54Q vA π==⨯⨯=（m 3/s ）答：进气流量 1.5Q =m 3/s 。
4.14一吹风装置，进排风口都直通大气，风扇前、后断面直径1d =2d =1m ，排风口直径3d =0.5m ，已知排风口风速3v =40s m /，空气的密度ρ=1.293/m kg ，不计压强损失，试求风扇前、后断面的压强1p 和2p 。
解： 以过轴线的水平面为基准面，以2d 及3d 截面列伯努利方程：2233322222p v p v g g g gααρρ+=+其中30p =，340v =（m/s ），23 1.0αα==，232322d v v d =⋅∴()442222332322 1.290.51401967.5222 1.0v d p v v d ρρ⎡⎤⎡⎤⎛⎫⎛⎫⎢⎥=-=-=⨯⨯-=⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦（Pa ）从大气到1d 断面，列伯努利方程：2111002a p p v g g gαρρ+=++其中 1 1.0α=，0a p =（相对压强），2312322d v v v d ==⋅∴42211 1.290.54064.522 1.0p v ρ⎛⎫=-=-⨯⨯=- ⎪⎝⎭（Pa ）答：风扇前、后断面的压强164.5p =-Pa ，2p 967.5=Pa 。
4.15两端开口的等直径U 形管，管内液柱长度为L ，使液面离开平衡位置而造成液柱振荡，水头损失忽略不计，求液柱的振荡方程z =()t f 。
解： 取0-0断面为基准面，由非恒定流的伯努利方程：221122120122Lp u p u u z z dl g g g g g tρρ∂++=+++∂⎰∵1z z =-，2z z =，120p p ==，12u u =∴012Lu L uz dl g t g t∂∂-==∂∂⎰ ∴2u gzt L∂-=∂ ∵()(),u z t u t =()dzu t dt=∴222d z gz dt L=-令 cos z ct ω=，则ω=00sin 2z z z π⎫==+⎪⎪⎭答：液柱的振荡方程00sin 2z z z π⎫==+⎪⎪⎭。
4.16水力采煤用水枪在高压下喷射强力水柱冲击煤层，喷嘴出口直径d=30mm，出口水流速度v=54sm/，求水流对煤层的冲击力。
解：取控制体如图，受力如图。
P a1F()2Q v v Fρ-=-∴22220.03100054 2.06144dF Qv vππρρ⨯==⋅=⨯⨯=（kN）水流对煤层的作用力与F构成作用力与反作用力，大小为2.061kN，方向向右。
答：水流对煤层的冲击力 2.061F=kN，方向向右。
4.17水由喷嘴射出，已知流量Q=0.4sm/3，主管直径D=0.4sm/，喷口直径d=0.1m，水头损失不计，求水流作用在喷嘴上的力。
d解：（1）取过轴线的水平面为基准面，列螺栓断面与出口断面的伯努利方程：2211122022p v v g g gααρ+=+∴()4222211212122vd p v v d ρρ⎡⎤⎛⎫⎢⎥=-=- ⎪⎢⎥⎝⎭⎣⎦()22100050.93 3.181291.8542=⨯-=（kPa ）1210.44 3.180.4Q v A π⨯===⨯（m/s ） 2220.4450.930.1Q v A π⨯===⨯（m/s ） （2）取控制体如图所示，列动量方程。
p 1p 2v 2()2111Q v v p A F ρ-=-∴()1121F p A Q v v ρ=--()20.41291.85410.450.93 3.18143.2394π⨯=⨯-⨯⨯-=（kN ）答：水流作用在喷嘴上的力为143.239kN 。
4.18闸下出流，平板闸门宽b =2m ，闸前水深1h =4m ，闸后水深2h =0.5m ，出流量Q =8s m /3，不计摩擦阻力，试求水流对闸门的作用力，并与按静水压强分布规律计算的结果相比较。
解：（1）由连续方程 1122Q h b v h b v =⋅⋅=⋅⋅∴118124Q v h b ===⨯（m/s ） 228820.5Q v h b ===⨯（m/s ） （2）由动量方程，取控制体如图。
()211122Q v v p A p A F ρ-=--∴()12122122h hF g h b g h b Q v v ρρρ=⋅-⋅-- ()22122122h h gb Q v v ρρ⎛⎫=--- ⎪⎝⎭()2240.510009.8072100088122⎛⎫=⨯⨯⨯--⨯⨯- ⎪⎝⎭98.46=（kN ）()221140.510009.807 3.52120.1422F g b ρ=-⋅⋅=⨯⨯⨯⨯=静（kN ）答：水流对闸门的作用力98.46F =kN ，按静水压强分布规律计算的结果120.14F =静kN 。
4.19矩形断面的平底渠道，其宽度B 为2.7m ，渠底在某断面处抬高0.5m ，该断面上游的水深为2m ，下游水面降低0.15m ，如忽略边壁和渠底阻力，试求：（1）渠道的流量；（2）水流对底坎的冲力。