开口和闭口圆柱壳屈曲和振动微分方程
短柱形薄壳频率计算
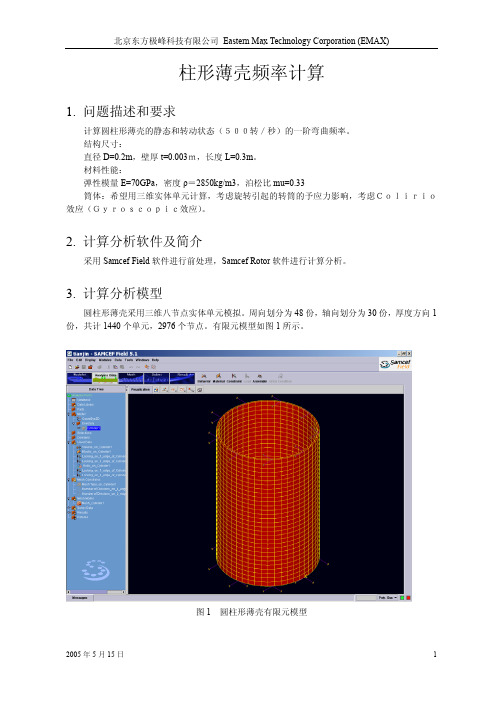
柱形薄壳频率计算1. 问题描述和要求计算圆柱形薄壳的静态和转动状态(500转/秒)的一阶弯曲频率。
结构尺寸:直径D=0.2m,壁厚t=0.003m,长度L=0.3m。
材料性能:弹性模量E=70GPa,密度ρ=2850kg/m3,泊松比mu=0.33筒体:希望用三维实体单元计算,考虑旋转引起的转筒的予应力影响,考虑Colirio效应(Gyroscopic效应)。
2. 计算分析软件及简介采用Samcef Field软件进行前处理,Samcef Rotor软件进行计算分析。
3. 计算分析模型圆柱形薄壳采用三维八节点实体单元模拟。
周向划分为48份,轴向划分为30份,厚度方向1份,共计1440个单元,2976个节点。
有限元模型如图1所示。
图1 圆柱形薄壳有限元模型4. 计算结果及分析4.1 考虑涡动效应不考虑预应力的影响静止状态(零转速)前16阶模态均为局部振动模态,第17和18阶为一阶弯曲模态,而且这两阶频率重合,均为3136Hz。
图2 第一阶弯曲模态及频率转速为30000RPM(500Hz)时,第17阶为反向涡动一阶弯曲模态,频率值为3121Hz(见图3)。
第18阶为正向涡动一阶弯曲模态,频率值为3152Hz。
图3 反向涡动一阶弯曲模态及频率图4 正向涡动一阶弯曲模态及频率频率随转速变化的曲线(坎贝尔图)见图5。
图5 频率随转速变化的曲线(坎贝尔图)4.2 考虑涡动效应和预应力的影响考虑预应力和影响,不考虑涡动效应(零转速)情况下,静止状态(零转速)前12阶模态均为局部振动模态,第13和14阶为一阶弯曲模态,而且这两阶频率重合,均为3137Hz。
图6 考虑涡动效应和考虑预应力影响的一阶弯曲模态及频率考虑预应力影响,并考虑涡动效应,即转速为30000RPM(500Hz)时,第1阶为反向涡动一阶弯曲模态,频率值为3122Hz(见图7)。
第2阶为正向涡动一阶弯曲模态,频率值为3153Hz(见图8)。
图7 反向涡动一阶弯曲模态及频率图8 正向涡动一阶弯曲模态及频率4.3 结果总结计算结果总结于下表之中。
第3章多自由度线性系统的振动

1 1 1
k1 k1 k1
k1 1 + 1 k1 k2 1 + 1 k1 k2
1
k1 m1 0 1 + 1 k1 k2 1 + 1 + 1 0 k1 k2 k3 1
0 m2 0
x &&1 x1 0 && + x = 0 x2 2 m3 &&3 x3 0 x 0 0
三自由度系统 在质量m 上施加单位力,质量m 的位移: 在质量 1上施加单位力,质量 1 、 m2和m3的位移: x1=1/k1 , x2=1/k1 , x3=1/k1 ,即h11= h21= k31= 1/k1 ; 在质量m2上施加单位力,质量 1 、 m2和m3的位移: x1=1/k1 , x2=1/k1+1/k2, 的位移: 在质量 上施加单位力,质量m x3= 1/k1+1/k2,即柔度系数 12= 1/k1 , h22= k32= 1/k1+1/k2,; 即柔度系数h 在质量m 上施加单位力,质量m 在质量 3上施加单位力,质量 1 、 m2和m3的位移: x1=1/k1, x2=1/k1+1/k2, 的位移: x3=1/k1+1/k2 +1/k3。即柔度系数 1=1/k1 , x2=1/k1+1/k2, x3= 1/k1+1/k2 +1/k3 。 即柔度系数x 振动 微分 方程
k1 + k 2 + k 6 − k2 [K ] = − k6 0 − k2
− k6 − k3 k3 + k 4 + k5 + k6 − k5
《四边固支弹性正交各向异性开口圆柱薄壳弯曲问题的辛叠加方法》范文

《四边固支弹性正交各向异性开口圆柱薄壳弯曲问题的辛叠加方法》篇一一、引言随着科技的发展,薄壳结构在众多工程领域如航空航天、机械制造等得到广泛应用。
本文关注的是四边固支的弹性正交各向异性开口圆柱薄壳的弯曲问题,针对此问题,我们将提出并运用辛叠加方法进行求解。
此方法为处理此类复杂结构力学问题提供了新的思路与手段。
二、问题描述与基本假设考虑一个四边固支的弹性正交各向异性开口圆柱薄壳,其在受到外部载荷作用时产生弯曲变形。
我们假设薄壳的材质是均匀且连续的,忽略材料的非线性效应,且仅考虑小变形的情况。
三、辛叠加方法的理论基础辛叠加方法是一种处理弹性力学问题的数值方法,其基本思想是将复杂问题分解为简单问题的叠加。
针对本问题,我们将首先对单一定义的变形问题进行求解,然后将结果进行叠加,得到整体的解。
四、正交各向异性材料的弹性常数对于正交各向异性材料,其弹性常数包括多个方向上的弹性模量和剪切模量。
在处理问题时,需要先确定这些弹性常数,这通常需要借助材料的力学性能测试或经验公式。
五、辛叠加方法的实施步骤1. 定义单个开口圆柱薄壳的变形问题,并使用适当的数学模型描述其变形行为。
2. 求解单个开口圆柱薄壳的变形问题,得到其变形解。
3. 将多个开口圆柱薄壳的变形解进行叠加,得到整体结构的变形解。
4. 结合四边固支的约束条件,对整体结构的变形解进行修正,得到最终的解。
六、计算结果与分析通过辛叠加方法,我们可以得到四边固支弹性正交各向异性开口圆柱薄壳的弯曲变形情况。
通过与实际工程案例或实验结果进行比较,可以验证本方法的准确性和有效性。
此外,我们还可以分析不同材料参数、几何尺寸以及外部载荷对结构变形的影响。
七、结论本文提出并运用了辛叠加方法来解决四边固支弹性正交各向异性开口圆柱薄壳的弯曲问题。
该方法将复杂问题分解为简单问题的叠加,为处理此类问题提供了新的思路与手段。
通过与实际工程案例或实验结果的比较,验证了本方法的准确性和有效性。
复合材料圆柱壳非轴对称动力屈曲

复合材料圆柱壳非轴对称动力屈曲孟豪;韩志军;路国运【摘要】考虑应力波效应,通过Hamilton原理得到轴向阶跃荷载下复合材料圆柱壳非轴对称动力屈曲控制方程.根据圆柱壳周向连续性设出径向位移的周向函数形式,使用分离变量法得到应力波反射前复合材料圆柱壳动力屈曲临界荷载解析解及屈曲模态,将该结果与里兹法所得结果进行了对比,结果表明两种方法所得临界荷载差值等于转动惯性的影响项.用MATLAB软件编程分析了径厚比、铺层角度等因素对临界荷载的影响.结果表明转动惯性对圆柱壳动力屈曲临界荷载的影响可以忽略,环向模态数越大,临界荷载越大且对应的屈曲模态图越复杂.%Considering effects of stress wave,the governing equation for non-axisymmetric dynamic buckling of composite cylindrical shells under an axial step load was derived using Hamilton principle.The expression of radial displacement function along the circumferential direction was assumed according to its continuity along the circumferential direction.The analytical solution to the critical load of the dynamic buckling of a composite cylindrical shell and its buckling modes were derived with the variable separation method before the reflection of stress paring the critical load with that gained with Ritz method,it was shown that the difference between the two critical loads is equal to the influence term due to rotary inertia.The influences of diameter-thickness ratio,and ply orientation,etc.on the critical load were analyzed with a self-compiled MATLAB-based code.The results showed that the effect of rotary inertia on the critical load can be neglected;thehigher the circumferential mode order,the larger the critical load and the more complex the corresponding buckling mode shape.【期刊名称】《振动与冲击》【年(卷),期】2017(036)011【总页数】5页(P27-30,78)【关键词】复合材料;应力波;动力屈曲;非轴对称;解析解【作者】孟豪;韩志军;路国运【作者单位】太原理工大学力学学院,太原030024;太原理工大学力学学院,太原030024;太原理工大学建筑与土木工程学院,太原030024【正文语种】中文【中图分类】O343;TB33复合材料圆柱壳因其优良的性能被广泛应用于军事以及航空航天等领域。
圆柱壳高频弯曲振动的能量有限元分析(2)

摘要 : 为了利用能量有限元方法得到圆柱壳体任意一点的高频振动响应 ,根据薄壳理论和能量平 衡关系 ,推导了圆柱壳弯曲振动能量密度的控制方程 ,并运用有限元方法对圆柱壳弯曲振动能量密 度的控制方程进行了求解 . 计算了 3 种不同激励下圆柱壳的能量密度分布 ,并对能量有限元方法和 统计能量方法的计算结果进行了比较 . 有限元方法的分析表明 ,使用能量有限元方法能够获得更详 细的结构振动响应信息 ,而用统计能量法只能得到整个圆柱壳体的平均能量信息 ,推导得出的能量 密度方程与梁的能量密度方程类似 ,只适用于计算圆柱壳高频轴对称弯曲的振动响应 . 关键词 : 有限元分析 ; 圆柱壳体 ; 高频振动 ; 控制方程 中图分类号 : TB123 文献标志码 : A 文章编号 : 02532987X ( 2008) 0921113204
的函数 . 假设壳体只承受法向载荷 , 则 N 1 = 0 . 运动 方程为 η ) D (1 + i
d4 w Eh 52 w h = 0 4 + 2 w +ρ dx a 5 t2
( 1)
ε ε ξ为相对 式中 : 1 、 2 分别为 x 方向和θ方向的应变 ; τ 剪切应变 ;γ 1 和γ 2 分别为 x 方向和θ方向的曲率 ; 为扭率 . 对于圆柱壳轴对称变形 , 应变和位移的关系为 μ du w ε ε ξ = 0 ( 10) =w, , 1 = 2 = dx a a d2 w γ γ τ= 0 ( 11) , 2 = 0, 1 = d x2 将式 ( 10) 和式 ( 11) 代入式 ( 9) 得 2 3 52 w 2 Eh w Eh ρ ( 12) 2 2 + 2 U = 2 a 24 ( 1 - μ ) 5 x 式中 : u 表示 x 方向的位移 ;
《四边固支弹性正交各向异性开口圆柱薄壳弯曲问题的辛叠加方法》范文

《四边固支弹性正交各向异性开口圆柱薄壳弯曲问题的辛叠加方法》篇一一、引言随着科技的发展,薄壳结构的弯曲问题一直是工程和物理领域的重要研究方向。
特别是对于四边固支的弹性正交各向异性开口圆柱薄壳的弯曲问题,其实验与理论研究均具有重要的实践价值。
这种结构由于其复杂的几何特性和材料特性,常出现于工程实践中如航天器结构、复合材料制品等。
而对其弯曲问题进行分析和研究,对设计合理结构的稳定性、承载能力及优化性能等具有重要意义。
本文将通过辛叠加方法对这一问题进行深入探讨。
二、辛叠加方法概述辛叠加方法是一种在弹性力学中广泛应用的数值分析方法,其基本思想是将复杂的物理问题分解为若干个简单的子问题,然后通过辛矩阵的叠加原理,将各个子问题的解进行叠加,从而得到整个问题的解。
该方法能够有效地处理具有复杂边界条件和材料特性的问题,对四边固支的弹性正交各向异性开口圆柱薄壳的弯曲问题具有很好的适用性。
三、问题描述与模型建立对于四边固支的弹性正交各向异性开口圆柱薄壳的弯曲问题,首先需要对问题进行准确的描述和数学建模。
考虑其几何形状、材料属性以及边界条件等因素,建立相应的物理模型和数学模型。
特别地,需要考虑到其正交各向异性的材料特性,以及四边固支的边界条件对结构弯曲的影响。
四、辛叠加方法的实施步骤1. 子问题的划分与求解:根据问题的特点和辛叠加方法的原理,将整个问题划分为若干个简单的子问题。
然后,针对每个子问题,利用弹性力学的基本原理和辛矩阵的求解方法,求解出各个子问题的解。
2. 辛矩阵的构建与叠加:根据辛矩阵的构建原理,将各个子问题的解表示为辛矩阵的形式。
然后,通过辛矩阵的叠加原理,将各个子问题的辛矩阵进行叠加,得到整个问题的辛矩阵。
3. 求解整体问题的解:通过求解得到的辛矩阵,可以得到整个问题的解。
这个解将包括位移、应力等物理量的分布情况,可以用于进一步分析和研究结构的性能。
五、结果分析与讨论通过对四边固支的弹性正交各向异性开口圆柱薄壳的弯曲问题进行辛叠加方法的求解,可以得到结构的位移、应力等物理量的分布情况。
复杂边界条件圆柱壳自由振动特性分析
复杂边界条件圆柱壳自由振动特性分析作者:李海超庞福振李玉慧缪旭弘来源:《振动工程学报》2020年第01期摘要:提出一种半解析法来分析圆柱壳结构自由振动特性。
将圆柱壳壳结构在轴向方向分解为若干壳段,用沿轴向的Jaeobi多项式和沿周向的Fourier级数来表示各个壳段的位移函数,并采用罚参数法对圆柱壳结构的边界条件和壳段问的连续性条件进行模拟;最后,基于Rayleigh-Ritz法求得圆柱壳结构的自由振动频率。
研究表明,该方法具有较好的收敛性,与公开发表文献一致性较高,研究成果可为复杂边界条件下圆柱壳结构自由振动特性分析提供数据积累和方法依据。
关键词:自由振动;圆柱壳结构;弹簧参数;半解析法中图分类号:0326;TB123 文献标志码:A 文章编号:1004-4523(2020)01-0056-08DOI:10.16385/ki.issn.1004-4523.2020.01.006引言圆柱壳结构因具有良好的结构性能,在民用机械、船舶、高铁、航空航天等各个领域应用广泛。
因此,开展圆柱壳结构自由振动特性分析研究,获取圆柱壳结构复杂边界条件下典型特征频率,对指导相应的工程应用具有重要的意义。
在此研究方面,孙述鹏通过解析分析与数值计算相结合的手段,研究了转动薄壁圆柱壳的行波振动固有特性和响应特性。
周海军通过引人波传播方法,解决了圆柱壳弹性支撑边界自由振动的求解问题。
sheng等建立了一个理论模型来研究加热功能梯度圆柱壳在热环境下的动力学稳定性和非线性振动。
Xing等提出了Donnell-Mushtari壳理论圆柱壳自由振动的精确解。
Wang等基于改进傅里叶方法,开展了中等厚度开口圆柱壳自由振动特性分析。
李文达等基于Love壳体理论,对功能梯度圆柱壳自由振动行波特性及边界约束影响进行了分析。
Lee和Kwak基于Ray-leigh-Ritz法开展了一般边界条件下圆柱壳结构自由振动特性分析,并将不同理论计算结果进行了对比,总结了各个理论方法的优缺点。
振动微分方程
2
yk ln iTr 2i yk i
2i
8.4单自由度体系的受迫振动
一、运动微分方程
体系在振动过程中有动力荷载P(t)或支座运动等外部干扰作用时,其振动称为 受迫(或强迫)振动。
P(t )
m
y(t)
S (t )
R(t )
P(t )
m
I (t )
(2)位移、加速度和惯性力同步变化,利用这一性质,可在质点振幅位置建立运动方程,所得 运动方程是代数方程而不是微分方程 (3)弹性力指向永与位移方向相反,而惯性力永与位移方向相同
例: 求图示梁频率
m1
EI=∞
m2
B
0 I2
A
a
k
a
A1
A
A2
B
2ak
2a
I10
此梁为一个自由度体系,振动达到幅值时,两质点的振幅为 A1 A2,惯性力幅值为
周期
T
2
频率
k 1 g g m mf mgf y jw
1)结构的周期、频率只与结构自身的质量、刚度(柔度)系数有关,与外 因无关,是结构自身的固有的特性,称为固有周期、固有频率; 2)结构的频率与质量的平方根成反比,与结构刚度系数的平方根成正比; 3)结构的固有周期和频率是结构动力性能的重要标志。
振幅
表示合成运动仍为简谐运动,其中A和φ 为:
初相位
v A y2 y tg 1 v
2
y
y y
v
y A t
0 -y
t
0
v
0
t -A T
第一章开口薄壁杆件的弯曲与扭转
薄壁杆件工程实例
• 薄壁杆件在实际工程应用很多,如桥梁工程 和海洋工程中的箱形、工字形和槽形梁柱, 土木工程中的各种型钢,高层建筑中的钢筋 混凝土核心墙,以及航空工业中的机翼构件, 造船工业中的船体构件。
• 薄壁杆件计算理论是20世纪40年代以后逐步 发展起来的一个力学分支。
• 掌握薄壁杆件受力(弯剪、扭)变形的主要 特点,采用的基本假定,满足工程需要的理 论体系。
断面剪力流的合力作用线位置仅由断面的几何形状所决定, 故断面的剪力中心仅决定于断面的几何形状。
剪力中心求法:合力矩定理,分力对某点力矩之和 = 合力对 某点力矩。
例题3:求图例题1(a) 所示等厚薄壁断面的剪力中心。
解: 利用合力矩定理求解 ① 求水平剪力Vx作用线位置(剪力中心纵坐标),利用例题1
3/10 4/10 -2/10 2/10
0
-2/10 2/10 4/10 3/108 91 2
q(s)图 (×d2t.Vy/Ix)
2. 剪力中心
断面剪力流的合力Vx和Vy作用线分别平行于x和y轴,两线交 点为断面的剪力中心。
不论外剪力的作用方向如何,只要通过此点,就符合只弯 无扭的平衡条件。故剪力中心也称为“弯曲中心”
狭条断面杆: 沿厚度反对称的线性分布 厚度边缘剪应力最大max
q q
2t 2t
Mt (q.b)3(q.
)b 3
厚度内,剪应力合成剪力流
q
1 2
max
t 2
相距2t/3
沿短边方向:
近似分析
相同剪力流,相距=b
max
M x.y Ix
max
Mt .t bt3 / 3
It bt3 / 3
类似定义自由 扭转的抗扭常 数(圣维南扭 转常数)I t
复杂边界条件圆柱壳自由振动特性分析
复杂边界条件圆柱壳自由振动特性分析1. 引言1.1 背景介绍圆柱壳是一种常见的结构,在工程中具有广泛的应用。
圆柱壳在多种领域中都扮演着重要的角色,比如航空航天领域的发动机壳体、海洋工程领域的钻井平台支柱等。
由于复杂的工作环境和载荷作用,圆柱壳的振动特性对结构的稳定性和安全性有着重要影响。
在实际工程中,圆柱壳往往会受到各种边界条件的限制,如固支、弹簧支座、不同形状的约束等。
这些复杂的边界条件会对圆柱壳的振动特性产生显著影响,因此需要深入研究和分析。
本文旨在通过有限元方法对具有复杂边界条件的圆柱壳进行自由振动特性分析,探讨不同边界条件对圆柱壳振动行为的影响,为工程实践提供理论支持。
通过数值模拟和参数分析,结合实验数据进行模型验证和结果讨论,揭示圆柱壳在不同工况下的振动特性。
通过对圆柱壳振动特性的研究,我们可以进一步了解结构的工作状态和性能,为优化设计和改进提供参考。
1.2 问题提出特别是在一些特殊工况下,比如边界条件不规则或者受到外部扰动等情况下,圆柱壳的振动特性会受到更大的影响,这就需要我们针对不同边界条件下的圆柱壳进行深入研究和分析。
如何解决这一问题成了当前研究的重要课题。
通过对圆柱壳的复杂边界条件进行分析,可以更好地理解结构的振动行为,为工程实践提供重要参考。
本研究旨在通过有限元方法等数值模拟手段,对复杂边界条件下圆柱壳的自由振动特性展开深入研究,为相关工程领域提供理论支持和技术指导。
1.3 研究意义研究圆柱壳的自由振动特性能够为工程设计提供重要参考。
通过深入探究圆柱壳在复杂边界条件下的振动特性,可以为工程师提供更准确的设计参数和指导,从而提高工程结构的性能和安全性。
通过对复杂边界条件下圆柱壳的自由振动特性进行深入分析,可以为工程设计和实际应用提供重要的理论基础和指导,具有重要的研究意义和应用前景。
2. 正文2.1 复杂边界条件对圆柱壳振动影响分析在研究过程中,首先需要建立合适的数学模型来描述圆柱壳的振动行为,并考虑复杂边界条件的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1 14)
Et N x x 0t ( x 0 y 0 ) 2 1 Et N y y 0t ( ) y0 x0 1 2 Et N xy xy 0t xy0 2(1 )
(1 6) (1 7)
M
y
0
M x M xy Qx 0 x y
将式(1-6)与(1-7)代入式(1-5),得
2 M xy 2 M y 2M x ( 2 )dxdy 2 2 x xy y
(1 8)
将(1-4)和(1-8)相加,并令其等于零,得:
2 2 2 用 作用于式(1-18),用 2 和 2 分别作用于式 (1 17), xy x y 得到三个方程式,由这 三个方程式,求得:
3 1 w 4u0 R x3 R xy 2
3w
(1 21)
2 2 2 2 式中: 4=( 2 2 ) ( 2 2) x y x y
(1 14)
将(1-11)、(1-12)、(1-13)代入(1-14)得:
v0 Et u0 w Nx ( ) 2 1 x y R u0 Et v0 w Ny ( ) 2 1 y R x (1 ) Et u0 v0 N xy ( ) 2 2(1 ) y x
因此圆柱壳在小变形下沿y方向的应变位移关系为:
y0
v0 w y R
(1 12)
中面剪应变不受壳曲率影响: u0 v0 xy0 (1 13) y x 中面力下薄板与圆柱壳都属于平面应力问题,因此薄板中 二维应力应变关系式也适用于圆柱壳,因此圆柱壳中面力 与位移的关系为:
板的平衡方程只有一个,是关于z方向的平衡方程,另 两个关于x方向和y方向的平衡方程,由于忽略了第二类 中面力,方程与z方向的平衡方程无关。 圆柱壳的第二类中面力不能忽略,体现在(1-19) 中保留了 Ny和1/R项,形成三个平衡方程互相依赖,必须联立求解。
将(1-17)、(1-18)和(1-20)简化成一个单一的只含位移 w的方程式。
(1 10)
沿x方向应变位移关系 对于小变形,第二项 可以略去:
x0
x0
u0 1 w 2 ( ) x 2 x u0 x
(a) (1 11)
沿y方向 对于小变形:
y0
v0 y
(b)
受曲率影响产生的应变:
A' B' AB ( R w)d Rd w AB Rd R (c )
设屈曲前出现的第一类 中面力为Px、Py 和Pxy。则总的中面 力N x、N y、N xy为
v0 Et u0 w N x N x Px ( ) Px 2 1 x y R u0 Et v0 w N y N y Py ( ) Py 2 1 y R x (1 ) Et u0 v0 N xy N xy Pxy ( ) Pxy 2 2(1 ) y x
2 2 2 4 w w w Et w D8 w 4 ( Px 2 Py 2 2Pxy ) 2 4 0 (1 23) x y xy R x
此方程称为Donnell方程,可以用来计算各种情况 下圆柱壳的临界荷载。
1轴压圆柱壳的临界应力
一 用Donnell方程计算临界应力的经典解答 研究对象:半径为R,厚度为t,长度为l两端简支轴压圆柱壳 由于只有荷载Px,并且Px=-xt,所有Donnell方程(1-23)化为
2 4 w Et w 8 4 D w xt 2 4 0 (7 24) 2 x R x
2w 简支边界条件: x 0, l 时,w 2 0 x
(7 25)
(7 26)
选取挠曲函数
mx ny w w0 sin sin l R
其中m为x方向的半波数,n为y方向的半波数,w0是最大挠 度值。为了使计算简化,令: nl R 则式(1-26)可以写成: mx y w w0 sin sin (1 27 ) l l 将式(1-27)代入(1-24),得:
u0 1 Et v0 w 2w ( ) 2 Pxy 0 (1 20) 2 1 y R x R xy 方程(1-17)、(1-18)和(1-20) 组成一组含有三个未知 量的三个方程式,称为圆柱壳屈曲微分方程。满足这组 方程的中面力为壳的临界荷载,记为Pxcr、Pycr和Pxycr。
kx
m
2
m2
2 2
m
4 2
12 2 m 2
2 2
(1 30)
2 (m 2 2) 对于临界应力,需求 k x最小值。将式 (1 30)对 m2 求导并令结果等零,得 出当
m
2
m2
2 2
12 2 1 2 4
3。材料均匀、各向同性并且符合虎克定律;
4。弯曲前垂直于中面的直线,弯曲后仍然是直线并且 保持与中面相垂直-直法线假设;
5。壳体是一个理想的圆柱壳;
6。横截面上的荷载是均匀分布并且同轴加载。
屈曲前: 薄膜力(中面力) 屈曲后: 除了薄膜力外, 还有弯曲力(弯矩、 扭矩和横向剪力) 假定Qx、Qy在x向 的平衡方程式与板 的平衡方程式相同。
2 M xy 2 M y 2M x 2w 2w 2w 1 2 N x 2 2 N xy Ny ( 2 ) 0 2 2 x xy y x xy y R (1 9) 将Mx、My和Mxy用w表示
壳体内任意 一点位移
u u0 ub
v v0 vb w w0
2w 2w 2w 1 [ N x 2 2 N xy N y ( 2 )]dxdy x xy y R
(1 4)
横向剪力在z轴方向的合力与板相同,为:
Q x Qy (1 5) x y dxdy M y M xy Qy 0 Mx 0 y x
(1 31)
时,kx有最小值。把式(1-31)代入(1-30),求得
2 2 2 用 作用于式(1-17),用 2 和 2 分别作用于式 (1 18), xy x y 也得到相应的三个方程 式,由此解得:
3 3 2 w 1 w 4 v0 2 R x y R y 3
(1 22)
再用算子4作用于方程 (1 20),有
2 2 2 w w w 8 4 D w ( Px 2 Py 2 2 Pxy ) x y xy Et 1 4 4 v0 4 u0 ( w) 0 2 R(1 ) y x R
(a)
最后,对(1 21)式作用 ,对(1 22)式作用 后代入(a)式, x y 得到一个八阶线性方程 式
(1 15)
上式中位移w是由于屈曲引起的。假 定位移u0、v0也是屈曲 引起的。那么 (1-15)给出的中面力N x、 N y 和 N xy都是屈曲引 起的中面力,所以称只 为第二类中面力。
另一类中面力是由荷载 引起的,在屈曲前就已 经产生, 称 为第一类中面力。第二 类中面力通常比第一类 中面力小。
X 0 Y 0
N x N xy 0 (1 1) x y N y N xy 0 (1 2)
y x 沿z方向平衡必须考虑曲率的影响,由 于曲率的影响,Ny在z方向分量为: 1 N y dxdy (1 3) R
Ny、Nxy及Nyx在z方向分量为零。圆柱壳微体所有的中面力 在z方向分量之和为:
(1 16)
前面(1-1)、(1-2)和(1-9)平衡方程中中面力是指总的中 面力。 用位移表示平衡微分方程。把(1-16)和(1-10)代入(1-1)、 (1-2)和方程(1-9),得:
2u0 1 2u0 1 2v0 w 0 2 2 x 2 y 2 xy R x 2v0 1 2v0 1 2u0 1 w 0 2 2 y 2 x 2 xy R y
下标“0”表示中面位移; 下标“b”表示弯曲位移
应变也分成 两部分
x x0 xb
y 0 yb xy xy0 xyb
2w 2w M x D x 2 y 2 2w 2 w M y D y 2 x 2 2 w M xy D (1 ) xy Et 3 D 12(1 2 )
2
1 2
x tl 2 kx D 2
4
可得:
其中:是Batdorf参数,是无量纲参数,代表了圆柱壳
的外形特征,用来区分长壳、短壳还是中等长度壳。 kx是壳的屈曲系数。
m
2
2 4
12m 4 2
k z m 2 (m 2 2 ) 2 0
(1 29)
由方程(1-29),解得
(1 17) (1 18)
4w 4w 4w 2w D( 4 2 2 2 4 ) ( Px N x ) 2 x x y y x 1 2w 2w ( Py N y )( 2 ) 2( Pxy N xy ) 0 R y xy (1 19)
D m2 l
8
2 4
Et R m l
4 2
x t m 2 (m 2 2 ) 2 0 l (1 28)
4
