内蒙古包头市第一中学2016-2017学年高二第一学期期末考试数学试卷文
内蒙古包头一中2016-2017学年高二上学期期中数学试卷(文科) Word版含解析

2016-2017学年内蒙古包头一中高二(上)期中数学试卷(文科)一.选择题(本大题共12题,每题5分,共60分)1.椭圆的离心率为()A.B.C.2 D.42.设a,b∈R,则“a>b”是“|a|>|b|”的()A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件3.已知||=1,||=,|﹣2|=,则向量,的夹角为()A.B.C.D.4.已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为()A.y= B.y= C.y=±x D.y=5.给出下列命题:(1)“若xy=1,则x,y互为倒数”的逆命题;(2)“面积相等的三角形全等”的否命题;(3)“若m≤1,则x2﹣2x+m=0有实根”的逆否命题;(4)“若A∩B=B,则A⊆B”的逆否命题.其中为真命题的是()A.(1)(2) B.(2)(3) C.(1)(2)(3) D.(3)(4)6.已知椭圆的长轴是8,离心率是,此椭圆的标准方程为()A.B.或C.D.或7.若向量、、两两所成的角相等,且||=1,||=1,||=3,则|++|等于()A.2 B.5 C.2或5 D.或8.设=(1,2),=(1,1)且与+λ的夹角为锐角,则实数λ的取值范围是()A.(﹣,0)∪(0,+∞)B.(﹣,+∞)C.[﹣,0)∪(0,+∞)D.(﹣,0)9.已知方程﹣=1表示双曲线,那么k的取值范围是()A.k>5 B.﹣2<k<2 C.k>2或k<﹣2 D.k>5或﹣2<k<210.设D为△ABC所在平面内一点,,则()A.B.C.D.11.已知△ABC的顶点B,C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是()A. B.6 C. D.1212.设双曲线的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则||=()A.5B.4C.3D.2二.填空题(本大题共4题,每题5分,共20分)13.命题“∃∈R,x2+2x+5=0”的否定是.14.若命题p:曲线﹣=1为双曲线,命题q:函数f(x)=(4﹣a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是.15.已知点F1(﹣4,0),F2(4,0),动点P满足|PF2|﹣|PF1|=4,则动点P的轨迹方程为.16.在直角三角形ABC中,∠C=,AB=2,AC=1,若=,则•=.三.解答题(本大题共6题,共70分)17.求符合下列条件的双曲线的标准方程(1)焦点在x轴上,顶点间的距离为6,渐近线方程为y=±(2)与椭圆+=1共焦点,它们的离心率之和为.18.已知,的夹角为60°,,,当实数k为何值时,(1)(2).19.已知点P是椭圆+=1上的一点,且以点P及焦点F1,F2为顶点的三角形面积等于1,求点P的坐标.20.在四边形ABCD中,已知∥,=(6,1),=(x,y),=(﹣2,﹣3).(1)求用x表示y的关系式;(2)若⊥,求x、y值.21.已知椭圆C: +=1(a>b>0)上的动点到焦点距离的最小值为.以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+=0相切.(Ⅰ)求椭圆C的方程;(Ⅱ)若过点M(2,0)的直线与椭圆C相交于A,B两点,P为椭圆上一点,且满足+=t(O为坐标原点).当|AB|=时,求实数t的值.22.已知椭圆E: +=1(a>b>0)过点,且离心率e为.(1)求椭圆E的方程;(2)设直线x=my﹣1(m∈R)交椭圆E于A,B两点,判断点G与以线段AB 为直径的圆的位置关系,并说明理由.2016-2017学年内蒙古包头一中高二(上)期中数学试卷(文科)参考答案与试题解析一.选择题(本大题共12题,每题5分,共60分)1.椭圆的离心率为()A.B.C.2 D.4【考点】椭圆的简单性质.【分析】根据椭圆方程和椭圆基本量的平方关系,可得a=2、b=,从而算出c=1,由此即得该椭圆离心率的值.【解答】解:∵椭圆的方程为,∴a2=4,b2=3,可得c==1,因此椭圆的离心率e=,故选:B2.设a,b∈R,则“a>b”是“|a|>|b|”的()A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据充分条件和必要条件的定义进行判断即可.【解答】解:若a=1,b=﹣2,满足a>b,但|a|>|b|不成立,若a=﹣2,b=1,满足|a|>|b|,但a>b不成立,即“a>b”是“|a|>|b|”的既不充分也不必要条件,故选:D.3.已知||=1,||=,|﹣2|=,则向量,的夹角为()A.B.C.D.【考点】平面向量数量积的运算.【分析】利用向量数量积运算性质即可得出.【解答】解:∵|﹣2|=,∴=,∴5=,解得=,∴向量,的夹角为.故选:C.4.已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为()A.y= B.y= C.y=±x D.y=【考点】双曲线的简单性质.【分析】由离心率和abc的关系可得b2=4a2,而渐近线方程为y=±x,代入可得答案.【解答】解:由双曲线C:(a>0,b>0),则离心率e===,即4b2=a2,故渐近线方程为y=±x=x,故选:D.5.给出下列命题:(1)“若xy=1,则x,y互为倒数”的逆命题;(2)“面积相等的三角形全等”的否命题;(3)“若m≤1,则x2﹣2x+m=0有实根”的逆否命题;(4)“若A∩B=B,则A⊆B”的逆否命题.其中为真命题的是()A.(1)(2) B.(2)(3) C.(1)(2)(3) D.(3)(4)【考点】命题的真假判断与应用.【分析】①写出逆命题,进行判断②写出否命题,进行判断③若m≤1,△=4﹣4m≥0,原命题为真,逆否命题也为真④若A∩B=B,则A⊆B”为假,逆否命题也为假.【解答】解:“若xy=1,则x,y互为倒数”的逆命题是“若x,y互为倒数,则xy=1”为真命题.(1)正确.“面积相等的三角形全等”是假命题,其否命题为真命题.(2)正确.当m≤1时,△=4﹣4m≥0,x2﹣2x+m=0有实根,命题为真,逆否命题也为真(3)正确.“若A∩B=B,则A⊆B”为假命题,逆否命题也为假.(4)错误综上所述,为真命题的是(1)(2)(3)故选C6.已知椭圆的长轴是8,离心率是,此椭圆的标准方程为()A.B.或C.D.或【考点】椭圆的标准方程.【分析】根据椭圆的基本概念,结合题意算出a=4且c=3,从而得到b2=a2﹣c2=7.再根据椭圆的焦点位置,即可确定此椭圆的标准方程.【解答】解:∵椭圆的长轴为8,离心率是,∴2a=8,e==,解得a=4,c=3,b2=a2﹣c2=7,因此,当椭圆的焦点在x轴上时,其方程为;椭圆的焦点在y轴上时,其方程为.故选:B7.若向量、、两两所成的角相等,且||=1,||=1,||=3,则|++|等于()A.2 B.5 C.2或5 D.或【考点】平面向量数量积的运算.【分析】设向量所成的角为α,则先求出的值即可求出,【解答】解:由向量、、两两所成的角相等,设向量所成的角为α,由题意可知α=0°或α=120°则=+++2(++)=11+2(||•||cosα+||•||cosα+||•||cosα)=11+14cosα所以当α=0°时,原式=5;当α=120°时,原式=2.故选C8.设=(1,2),=(1,1)且与+λ的夹角为锐角,则实数λ的取值范围是()A.(﹣,0)∪(0,+∞)B.(﹣,+∞)C.[﹣,0)∪(0,+∞)D.(﹣,0)【考点】平面向量数量积的运算.【分析】若设θ为与的夹角,θ为锐角⇒cosθ>0,且cosθ≠1,根据条件及两向量夹角的余弦公式即可求得λ的取值范围,并且在求时,先求它的平方.【解答】解:=(1,2)•(1+λ,2+λ)=3λ+5,=5+6λ+2λ2,;∴设与的夹角为θ且θ为锐角,则:cosθ==>0,且∴解得:λ,且λ≠0.∴实数λ的取值范围是.故选A.9.已知方程﹣=1表示双曲线,那么k的取值范围是()A.k>5 B.﹣2<k<2 C.k>2或k<﹣2 D.k>5或﹣2<k<2【考点】双曲线的简单性质.【分析】由双曲线方程的特点可得(k﹣5)(|k|﹣2)>0,解之可得.【解答】解:若方程﹣=1表示的曲线为双曲线,则(k﹣5)(|k|﹣2)>0,解得k>5或﹣2<k<2.故选D.10.设D为△ABC所在平面内一点,,则()A.B.C.D.【考点】平行向量与共线向量.【分析】将向量利用向量的三角形法则首先表示为,然后结合已知表示为的形式.【解答】解:由已知得到如图由===;故选:A.11.已知△ABC的顶点B,C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是()A. B.6 C. D.12【考点】椭圆的简单性质.【分析】由椭圆的定义:椭圆上一点到两焦点的距离之和等于长轴长2a,可得△ABC的周长.【解答】解:由椭圆的定义:椭圆上一点到两焦点的距离之和等于长轴长2a,可得△ABC的周长为4a=,故选C12.设双曲线的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则||=()A.5B.4C.3D.2【考点】双曲线的简单性质.【分析】依题意,可求得﹣=1的左焦点F1(﹣3,0),从而可求得||,利用双曲线的定义即可求得||.【解答】解:∵双曲线﹣=1中a2=3,b2=6,∴c2=a2+b2=9,∴c=3,故左焦点F1(﹣3,0).依题意,设M(﹣3,y0),则=﹣1=2,∴y0=±2,故|MF1|=2.∵M(﹣3,y0)为左支上的点,∴|MF2|﹣|MF1|=2,∴|MF2|=2+|MF1|=4,即||=4.故选B.二.填空题(本大题共4题,每题5分,共20分)13.命题“∃∈R,x2+2x+5=0”的否定是∀x∈R,x2+2x+5≠0.【考点】命题的否定.【分析】根据特称命题的否定是全称命题进行判断.【解答】解:命题的特称命题,则命题的否定是全称命题,即∀x∈R,x2+2x+5≠0,故答案为:∀x∈R,x2+2x+5≠014.若命题p:曲线﹣=1为双曲线,命题q:函数f(x)=(4﹣a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是(﹣∞,2]∪[3,6).【考点】复合命题的真假;双曲线的简单性质.【分析】通过p∨q为真命题,p∧q为假命题,判断两个命题的真假关系,分别求出命题是真命题时a的范围,即可求解结果.【解答】解:当p为真命题时,(a﹣2)(6﹣a)>0,解之得2<a<6.当q为真命题时,4﹣a>1,即a<3.由p∨q为真命题,p∧q为假命题知p、q一真一假.当p真q假时,3≤a<6.当p假q真时,a≤2.因此实数a的取值范围是(﹣∞,2]∪[3,6).故答案为:(﹣∞,2]∪[3,6).15.已知点F1(﹣4,0),F2(4,0),动点P满足|PF2|﹣|PF1|=4,则动点P的轨迹方程为.【考点】轨迹方程.【分析】由条件知,点P的轨迹是以F1、F2为焦点的双曲线左支,从而写出轨迹的方程即可.【解答】解:由|PF2|﹣|PF1|=4<|F1F2|知,点P的轨迹是以F1、F2为焦点的双曲线左支,得c=4,2a=4,∴a=2,∴b2=12,故动点P的轨迹方程是.故答案为16.在直角三角形ABC 中,∠C=,AB=2,AC=1,若=,则•=.【考点】平面向量数量积的运算.【分析】根据结合图形得出==,=0, =2××COS30°,转化得出•=()•=+求解即可.【解答】解:∵直角三角形ABC 中,∠C=,AB=2,AC=1,∴根据勾股定理得出BC=,sin ∠ABC ═=,即∠ABC=30°∵若=,∴==, =0,=2××COS30°=3∴•=()•=+=×3=故答案为:三.解答题(本大题共6题,共70分) 17.求符合下列条件的双曲线的标准方程(1)焦点在x 轴上,顶点间的距离为6,渐近线方程为y=±(2)与椭圆+=1共焦点,它们的离心率之和为.【考点】双曲线的简单性质.【分析】(1)由题意,2a=6, =,求出a ,b ,即可求出双曲线的标准方程;(2)椭圆+=1的焦点坐标为(0,±4),离心率为,可得双曲线的焦点坐标为(0,±4),离心率为2,求出a,b,即可求出双曲线的标准方程.【解答】解:(1)由题意,2a=6,=,∴a=3,b=1,∴双曲线的标准方程为=1;(2)椭圆+=1的焦点坐标为(0,±4),离心率为,∴双曲线的焦点坐标为(0,±4),离心率为2,∴,∴双曲线的标准方程为=1.18.已知,的夹角为60°,,,当实数k为何值时,(1)(2).【考点】数量积判断两个平面向量的垂直关系;平面向量共线(平行)的坐标表示.【分析】(1)由可知存在实数t,使,可得k与t的方程组,解之可得;(2)由=()•()=0可得关于k的方程,解之即可.【解答】解:(1)由可知存在实数t,使,即,解得,故k=时,可得;(2)由=()•()=0可得15+3k+(5k+9)=0,代入数据可得15×4+27k+(5k+9)×=0,解得k=﹣,故当k=﹣时,.19.已知点P是椭圆+=1上的一点,且以点P及焦点F1,F2为顶点的三角形面积等于1,求点P的坐标.【考点】椭圆的简单性质.【分析】由椭圆方程可知: +=1,c==1,由三角的面积公式可知:S=•2c•丨y丨=1,即丨y丨=1,代入椭圆方程得:=1,即可求得丨x丨=,即可求得点P的坐标.【解答】解:F1、F2是椭圆+=1的左、右焦点,c==1,则F1(﹣1,0),F2(1,0),设P(x,y)是椭圆上的一点,由三角的面积公式可知:S=•2c•丨y丨=1,即丨y丨=1,将丨y丨=1代入椭圆方程得:=1,解得:丨x丨=,∴点P的坐标为(,1))(﹣,1)()(,﹣1).20.在四边形ABCD中,已知∥,=(6,1),=(x,y),=(﹣2,﹣3).(1)求用x表示y的关系式;(2)若⊥,求x、y值.【考点】数量积判断两个平面向量的垂直关系;平面向量共线(平行)的坐标表示.【分析】(1),由,能求出y=﹣.(2)=(x+6,y+1),=(x﹣2,y﹣3),由,y=﹣,能求出x、y值.【解答】(本小题满分12分)解:(1)∵=(6,1),=(x,y),=(﹣2,﹣3),∴…∵,∴x(﹣2+y)=y(4+x)…∴y=﹣,…(2)∵=(6,1),=(x,y),=(﹣2,﹣3),∴=(x+6,y+1),=(x﹣2,y﹣3),∵,∴(x+6)(x﹣2)+(y+1)(y﹣3)=0,又∵y=﹣,解得或.21.已知椭圆C: +=1(a>b>0)上的动点到焦点距离的最小值为.以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+=0相切.(Ⅰ)求椭圆C的方程;(Ⅱ)若过点M(2,0)的直线与椭圆C相交于A,B两点,P为椭圆上一点,且满足+=t(O为坐标原点).当|AB|=时,求实数t的值.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【分析】(Ⅰ)利用椭圆C: +=1(a>b>0)上的动点到焦点距离的最小值为,可求a﹣c的值,利用直线与圆相切,可得b的值,由此可求椭圆C的方程;(Ⅱ)设直线AB的方程与椭圆方程联立,利用韦达定理及|AB|=, +=t,即可求得结论.【解答】解:(Ⅰ)由题意知a﹣c=﹣1;…又因为b==1,所以a2=2,b2=1.…故椭圆C的方程为+y2=1.…(Ⅱ)设直线AB的方程为y=k(x﹣2),A(x1,y1),B(x2,y2),P(x,y),由得(1+2k2)x2﹣8k2x+8k2﹣2=0.…△=64k4﹣4(2k2+1)(8k2﹣2)>0,∴k2.…x1+x2=,x1x2=.又由|AB|=,得|x1﹣x2|=,即=…可得…又由+=t,得(x1+x2,y1+y2)=t(x,y),则=,=…故,即16k2=t2(1+2k2).…得,t2=,即t=±.…22.已知椭圆E: +=1(a>b>0)过点,且离心率e为.(1)求椭圆E的方程;(2)设直线x=my﹣1(m∈R)交椭圆E于A,B两点,判断点G与以线段AB 为直径的圆的位置关系,并说明理由.【考点】直线与圆锥曲线的综合问题.【分析】解法一:(1)由已知得,解得即可得出椭圆E的方程.(2)设点A(x1,y1),B(x2,y2),AB中点为H(x0,y0).直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,利用根与系数的关系中点坐标公式可得:y0=.|GH|2=.=,作差|GH|2﹣即可判断出.解法二:(1)同解法一.(2)设点A(x1,y1),B(x2,y2),则=,=.直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,计算=即可得出∠AGB,进而判断出位置关系.【解答】解法一:(1)由已知得,解得,∴椭圆E的方程为.(2)设点A(x1y1),B(x2,y2),AB中点为H(x0,y0).由,化为(m2+2)y2﹣2my﹣3=0,∴y1+y2=,y1y2=,∴y0=.G,∴|GH|2==+=++.===,故|GH|2﹣=+=﹣+=>0.∴,故G在以AB为直径的圆外.解法二:(1)同解法一.(2)设点A(x1y1),B(x2,y2),则=,=.由,化为(m2+2)y2﹣2my﹣3=0,∴y1+y2=,y1y2=,从而==+y1y2=+=﹣+=>0.∴>0,又,不共线,∴∠AGB为锐角.故点G在以AB为直径的圆外.2016年12月19日。
数学---内蒙古包头一中2016-2017学年高二(下)期末试卷(文)(解析版)
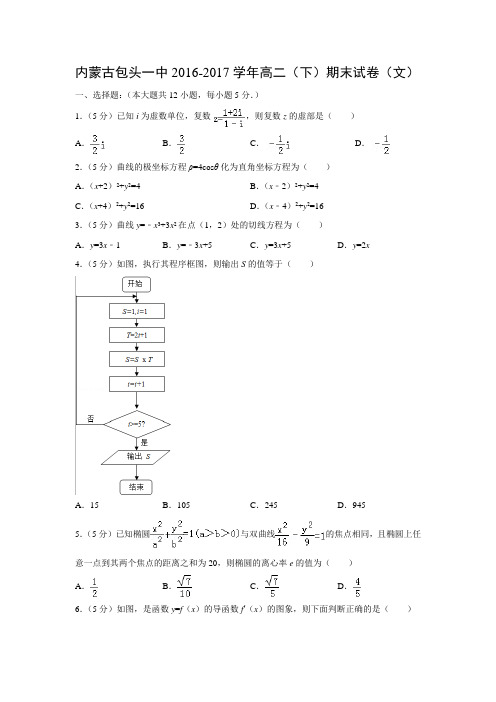
内蒙古包头一中2016-2017学年高二(下)期末试卷(文)一、选择题:(本大题共12小题,每小题5分.)1.(5分)已知i为虚数单位,复数,则复数z的虚部是()A.B.C.D.2.(5分)曲线的极坐标方程ρ=4cosθ化为直角坐标方程为()A.(x+2)2+y2=4 B.(x﹣2)2+y2=4C.(x+4)2+y2=16 D.(x﹣4)2+y2=163.(5分)曲线y=﹣x3+3x2在点(1,2)处的切线方程为()A.y=3x﹣1 B.y=﹣3x+5 C.y=3x+5 D.y=2x4.(5分)如图,执行其程序框图,则输出S的值等于()A.15 B.105 C.245 D.9455.(5分)已知椭圆与双曲线的焦点相同,且椭圆上任意一点到其两个焦点的距离之和为20,则椭圆的离心率e的值为()A.B.C.D.6.(5分)如图,是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是()A.在区间(﹣2,1)上f(x)是增函数B.在(1,3)上f(x)是减函数C.在(4,5)上f(x)是增函数D.当x=4时,f(x)取极大值7.(5分)椭圆4x2+9y2=144内有一点P(3,2)过点P的弦恰好以P为中点,那么这弦所在直线的方程为()A.3x+2y﹣12=0 B.2x+3y﹣12=0 C.4x+9y﹣144=0 D.9x+4y﹣144=0 8.(5分)O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=4,则△POF的面积为()A.2 B.2C.2D.49.(5分)设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(﹣1)=0,当x>0时,xf′(x)﹣f(x)<0,则使得f(x)>0成立的x的取值范围是()A.(﹣∞,﹣1)∪(0,1)B.(﹣1,0)∪(1,+∞)C.(﹣∞,﹣1)∪(﹣1,0)D.(0,1)∪(1,+∞)10.(5分)若曲线y=x2+ax+b在点(0,b)处的切线方程x﹣y+1=0,则()A.a=1,b=1 B.a=﹣1,b=1 C.a=1,b=﹣1 D.a=﹣1,b=﹣1 11.(5分)函数函数f(x)=(x﹣3)e x的单调递增区间是()A.(﹣∞,2)B.(0,3)C.(1,4)D.(2,+∞)12.(5分)已知三次函数f(x)=ax3﹣x2+x在(0,+∞)存在极大值点,则a的范围是()A.B.C.D.二、填空题(本大题共4小题,每小题5分.)13.(5分)函数y=x2﹣x3的单调减区间为.14.(5分)若双曲线﹣=1的离心率为,则其渐近线方程为.15.(5分)已知数列,则是该数列的第项.16.(5分)直线y=a与函数f(x)=x3﹣3x的图象有相异的三个公共点,则a的取值范围是.三、解答题(本大题共6小题,17题10分,18-22题每题12分.)17.(10分)求证:>2.18.(12分)一只口袋内有大小质量完全相同的5只球,其中2只白球(编号为b1,b2),3只黑球(编号为h1,h2,h3),从中一次摸出2只球.(1)共有多少个基本事件?列出所有基本事件;(2)求摸出两只球颜色相同的概率;(3)求至少有一只黑球的概率.19.(12分)设f(x)=x2﹣x﹣a ln x(1)当a=1时,求f(x)的单调区间;(2)若f(x)在[2,+∞)上单调递增,求a的取值范围.20.(12分)近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为.(1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;临界值表供参考:(参考公式:K2=,其中n=a+c+b+d).21.(12分)已知椭圆+=1(a>b>0)的离心率e=,焦距是函数f(x)=x2﹣8的零点.(1)求椭圆的方程;(2)若直线y=kx+2(k≠0)与椭圆交于C、D两点,|CD|=,求k的值.22.(12分)已知函数f(x)=ax﹣﹣(a+1)ln x(a>0).(Ⅰ)若曲线y=f(x)在点(2,f(2))处的切线与直线y=x平行,求实数a的值;(Ⅱ)若函数f(x)在x=1处取得极小值,且m≥﹣a2+4a,求实数m的取值范围.参考答案一、选择题1.B【解析】∵===+i,故复数z的虚部是,故选B.2.B【解析】将原极坐标方程ρ=4cosθ,化为:ρ2=4ρcosθ,化成直角坐标方程为:x2+y2﹣4x=0,即y2+(x﹣2)2=4.故选B.3.A【解析】∵y=﹣x3+3x2∴y'=﹣3x2+6x,∴y'|x=1=(﹣3x2+6x)|x=1=3,∴曲线y=﹣x3+3x2在点(1,2)处的切线方程为y﹣2=3(x﹣1),即y=3x﹣1,故选A.4.D【解析】第一次执行循环后,T=3,S=3,i=2不满足退出循环的条件,第二次执行循环后,T=5,S=15,i=3不满足退出循环的条件,第三次执行循环后,T=7,S=105,i=4不满足退出循环的条件,第四次执行循环后,T=9,S=945,i=5满足退出循环的条件,故输出的S值为945,故选:D5.A【解析】由椭圆的定义可得2a=20,即a=10,双曲线的焦点为(﹣5,0),(5,0),由题意可得椭圆的c=5,可得椭圆的离心率为e==.故选:A.6.C【解析】由于f′(x)≥0⇒函数f(x)d单调递增;f′(x)≤0⇒单调f(x)单调递减观察f′(x)的图象可知,当x∈(﹣2,1)时,函数先递减,后递增,故A错误,当x∈(1,3)时,函数先增后减,故B错误,当x∈(4,5)时函数递增,故C正确,由函数的图象可知函数在4处取得函数的极小值,故D错误,故选:C7.B【解析】设弦的端点为A(x1,y1),B(x2,y2),则x1+x2=6,y1+y2=4,把A、B坐标代入椭圆方程得,,,两式相减得,4(﹣)+9(﹣y22)=0,即4(x1+x2)(x1﹣x2)+9(y1+y2)(y1﹣y2)=0,所以=﹣=﹣=﹣,即k AB=﹣,所以这弦所在直线方程为:y﹣2=﹣(x﹣3),即2x+3y﹣12=0.故选B.8.C【解析】∵抛物线C的方程为y2=4x,∴2p=4,可得=,得焦点F(),设P(m,n),根据抛物线的定义,得|PF|=m+=4,即m+=4,解得m=3,∵点P在抛物线C上,得n2=4×3=24,∴n==,∵|OF|=,∴△POF的面积为S=|OF|×|n|==2,故选:C.9.A【解析】设g(x)=,则g(x)的导数为:g′(x)=,∵当x>0时总有xf′(x)<f(x)成立,即当x>0时,g′(x)恒小于0,∴当x>0时,函数g(x)=为减函数,又∵g(﹣x)====g(x),∴函数g(x)为定义域上的偶函数又∵g(﹣1)==0,∴函数g(x)的图象性质类似如图:数形结合可得,不等式f(x)>0⇔x•g(x)>0⇔或,⇔0<x<1或x<﹣1.故选:A.10.A【解析】y=x2+ax+b的导数为y′=2x+a,可得在点(0,b)处的切线斜率为a,由点(0,b)处的切线方程为x﹣y+1=0,可得a=1,b=1,故选:A.11.D【解析】f′(x)=(x﹣3)′e x+(x﹣3)(e x)′=(x﹣2)v x,令f′(x)>0,解得x>2.故选:D.12.D【解析】由题意知,f′(x)=3ax2﹣2x+1,∵三次函数f(x)=ax3﹣x2+x在(0,+∞)存在极大值点,∴f′(x)=3ax2﹣2x+1=0有两个不同的正实数根或一正一负根,①当a>0时,此时3ax2﹣2x+1=0有两个不同的正实数根,∴,即0<a<,②当a<0时,此时3ax2﹣2x+1=0有一正一负根,只须△>0,即4﹣12a>0,⇒a,∴a<0综上,则a的范围是故选D.二、填空题13.(﹣∞,0)和(,+∞)【解析】y′=2x﹣3x2=﹣x(3x﹣2),由y′<0,得x<0或x>,所以函数y=x2﹣x3的单调减区间为(﹣∞,0)和(,+∞).故答案为:(﹣∞,0)和(,+∞).14.y=x【解析】双曲线的离心率e==即:c=a,∴c2=a2+b2=3a2,∴b2=2a2,b=a,∴双曲线的渐近线方程为y=±x=x,故答案是15.7【解析】∵数列,∴第n项的通项是则=,∴n=7,故答案为:716.(﹣2,2)【解析】令f′(x)=3x2﹣3=0,得x=±1,可求得f(x)的极大值为f(﹣1)=2,极小值为f(1)=﹣2,如图所示,当满足﹣2<a<2时,恰有三个不同公共点.故答案为:(﹣2,2)三、解答题17.证明:(分析法)要证:>2只需:>2成立,根据不等式两边都大于0,即证:>只需证:13+2>13+2即证:42>40∵42>40显然成立,∴>2证毕.18.解:(1)共有10 个基本事件,分别为;b1h1,b1h2,b1h3,b2h1,b2h2,b2h3,b1b2,h1h2,h1h3,h23(2)即摸出两只球颜色相同的概率为事件A,则事件A中包含4 个基本事件,∴P(A)==,答:摸出两只球颜色相同的概率为,.(3)摸出两只球颜色至少有一只黑球的事件为B,则事件B中包含49个基本事件,∴P(B)=,答:摸出两只球颜色至少有一只黑球的概率为:,19.解:(1)由于f(x)=x2﹣x﹣ln x,则f'(x)=2x﹣1﹣=(x>0)令f′(x)>0,则x>1,∴x>1;令f′(x)<0,则0<x<1,∴0<x<1;∴函数的单调递增区间是(1,+∞),单调递减区间是(0,1).(2)由于f(x)=x2﹣x﹣a ln x,则f(x)=2x﹣1﹣(x>0)由于f(x)在[2,+∞)上单调递增,则2x﹣1﹣≥0在[2,+∞)上恒成立,即a≤2x2﹣x在[2,+∞)上恒成立,设g(x)=2x2﹣x,∵g(x)在[2,+∞)上单调递增,∴g(x)≥g(2)=6,∴a≤6∴实数a的取值范围(﹣∞,6].20.解:(1)列联表补充如下:(2)K2的观测值K=≈8.333>7.879,又P(K2≥7.789)=0.005=0.5%.∴我们有99.5%的把握认为是否患心肺疾病是与性别有关系.21.解:(1)∵焦距是函数f(x)=x2﹣8的零点,∴2c=2,∴c=,∵e==,∴a=,∴椭圆的方程为;(2)设C(x1,y1),D(x2,y2),则y=kx+2(k≠0)代入椭圆方程可得(1+3k2)x2+12kx+9=0,∴x1+x2=﹣,x1x2=∴|CD|=•=,∴k2=3,∴k=±.22.解:(Ⅰ),由(Ⅱ)由①当,即a>1时,函数f(x)在上单调递增,在上单调递减,在(1,+∞)上单调递增即函数f(x)在x=1处取得极小值②当,即a=1时,函数f(x)在(0,+∞)上单调递增,无极小值,所以a≠1③当,即0<a<1时,函数f(x)在(0,1)上单调递增,在上单调递减,在上单调递增,即函数f(x)在处取得极小值,与题意不符合即a>1时,函数f(x)在x=1处取得极小值,又因为m≥﹣a2+4a,所以m≥4.。
【精品】2017学年内蒙古包头一中高二上学期期中数学试卷和解析(理科)

2017学年内蒙古包头一中高二(上)期中数学试卷(理科)一.选择题(本大题共12题,每题5分,共60分)1.(5分)椭圆的离心率为()A.B.C.2D.42.(5分)设a,b∈R,则“a>b”是“|a|>|b|”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.(5分)已知||=1,||=,|﹣2|=,则向量,的夹角为()A.B.C.D.4.(5分)已知抛物线y=ax2(a>0)的焦点到准线距离为1,则a=()A.4B.2C.D.5.(5分)给出下列命题:(1)“若xy=1,则x,y互为倒数”的逆命题;(2)“面积相等的三角形全等”的否命题;(3)“若m≤1,则x2﹣2x+m=0有实根”的逆否命题;(4)“若A∩B=B,则A⊆B”的逆否命题.其中为真命题的是()A.(1)(2)B.(2)(3)C.(1)(2)(3)D.(3)(4)6.(5分)已知椭圆的长轴是8,离心率是,此椭圆的标准方程为()A.B.或C.D.或7.(5分)若向量、、两两所成的角相等,且||=1,||=1,||=3,则|++|等于()A.2B.5C.2或5D.或8.(5分)已知以F为焦点的抛物线y2=4x上的两点A、B满足=3,则弦AB的中点到准线的距离为()A.B.C.2D.19.(5分)已知方程﹣=1表示双曲线,那么k的取值范围是()A.k>5B.﹣2<k<2C.k>2或k<﹣2D.k>5或﹣2<k<210.(5分)设双曲线的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则||=()A.5B.4C.3D.211.(5分)已知点P是△ABC所在平面内的一点,边AB的中点为D,若2=(1﹣λ)+,其中λ∈R,则点P一定在()A.AB边所在的直线上B.BC边所在的直线上C.AC边所在的直线上D.△BC的内部12.(5分)F是双曲线C:﹣=1(a>0,b>0)的右焦点.过点F向C的﹣条渐近线引垂线,垂足为A,交另一条渐近线于点B,若3=,则C的心离心率是()A.B.2C.D.二.填空题(本大题共4题,每题5分,共20分)13.(5分)命题“∃∈R,x2+2x+5=0”的否定是.14.(5分)若命题p:曲线﹣=1为双曲线,命题q:函数f(x)=(4﹣a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是.15.(5分)已知双曲线的一个焦点在圆x2+y2﹣4x﹣5=0上,则双曲线的渐近线方程为.。
内蒙古包头一中2016-2017学年高一下学期期末考试数学(理)试题 Word版含答案

包头一中2017——2018学年度第一学期期末考试高一年级理科数学试题一、选择题(共12小题,每小题5分,共60分.在每小题给出的四个选项中只有一项是最符合题目要求的,请将正确答案的序号填涂到答题卡上.)1.不等式111≥-x 的解集为 A.(]2,∞- B.[)+∞,2 C. []2,1 D . (]2,12. 直线043:=-+y x l 与圆4:22=+y x C 的位置关系是A. 相交且过圆心 B . 相切C. 相交不过圆心D. 相离3. 直线04)1(2=+++y m x 与直线023=-+y mx 平行, 则=m A. 2-B. 3- C . 2或3- D. 2-或3- 4. 如果等差数列{}n a 中,34512a a a ++=,那么127...a a a +++=A. 14B.21C.28D.35 5.右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为A. 20πB. 24πC. 28πD. 32π6. 设有直线m 、n 和平面α、β,下列四个命题中,正确的是A .若m //α,m β⊂,n αβ= ,则m // n B.若m ⊂α,n ⊂α,m //β,n //β,则α//β C.若α⊥β,m ⊂α,则m ⊥β D.若α⊥β,m ⊥β,则m // α 7.已知三点(1,0),A B C ,则△ABC 外接圆的圆心到原点的距离为5A.3B.3C.34D.3 8. 设,x y 满足约束条件2+330233030x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩,则2z x y =+的最小值是A .15- B.9- C.1 D 99.在ABC △中,π4B =,BC 边上的高等于13BC ,则sin A =A.310B. C. 10. 若直线1(00)x ya b a b+=>,> 过点(1,2),则2a +b 的最小值为 A. 2 B.4 C.6 D .811. 已知{}n a 是首项为1的等比数列,n s 是{}n a 的前n 项和,且369s s =,则数列1n a ⎧⎫⎨⎬⎩⎭的前5项和为 A. 158或5 B.3116或5 C.3116 D.15812. 如图,四棱锥S —ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中错误..的是 A .AC ⊥SB B .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D .AB 与SC 所成的角等于DC 与SA 所成的角二、填空题(共4小题,每小题5分,共20分. 请将正确的答案填写到答题卡的相应位置上) 13. 已知一个正方形的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为___________.14. △ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知a =2c =,2cos 3A =,则b=______ 15.已知0x ≥,0y ≥,且x +y =1,则22x y +的取值范围是__________. 16.满足条件BC AC AB 2,2==的ABC ∆的面积的最大值为 .三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17. (本小题满分10分)已知等差数列{}n a 和等比数列{}n b 满足a 1=b 1=1,a 2+a 4=10,b 2b 4=a 5. (1)求{}n a 的通项公式; (2)求和:13521n b b b b -++++ .18. (本小题满分12分)已知圆C :012822=+-+y y x ,直线02:=++a y ax l 。
内蒙古包头市北重三中2016-2017学年高二上学期期末数学试卷(文科)(word版含答案)

2016-2017学年内蒙古包头市北重三中高二(上)期末数学试卷(文科)一.选择题:(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于()A.B.C.D.2.命题“若x2>y2则x>y”的逆否命题是()A.若x2<y2则x<y B.若x>y则x2>y2C.若x≤y则x2≤y2D.若x≥y则x2>y23.甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则甲不输的概率为()A.B.C.D.4.已知焦点在x轴上的椭圆的离心率为,且它的长轴长等于4,则椭圆的标准方程是()A.=1 B.C.D.5.设α、β为两个不同平面,若直线l在平面α内,则“α⊥β”是“l⊥β”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件6.执行如图所示的程序框图,若输入n的值为8,则输出S的值为()A.4 B.8 C.10 D.127.某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为()A.11 B.12 C.13 D.148.一个多面体的三视图如图所示,则该多面体的表面积为()A.21+B.18+C.21 D.189.已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为,底面是边长为的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为()A.120°B.60°C.45°D.30°10.已知双曲线C:的焦点为F1,F2,且C上的点P满足=0,|PF1|=3,|PF2|=4,则双曲线C的离心率为()A.B.C.D.511.过抛物线x2=4y的焦点任作一直线l交抛物线于M,N两点,O为坐标原点,则△MON的面积的最小值为()A.2 B.2 C.4 D.812.已知动点P(x,y)在椭圆C:=1上,F为椭圆C的右焦点,若点M满足||=1且=0,则||的最小值为()A.B.3 C.D.1二、填空题:(本大题共4小题,每小题5分).13.从集合{1,2,3,4,5}任取一元素a,从集合{1,2,3}任取一元素b,则b>a的概率是.14.如图,正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为.15.过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若,则|AF|=.16.双曲线(a>0,b>0)的一条渐近线的倾斜角为,离心率为e,则的最小值为.三、解答题:(共70分,解答应写出文字说明,证明过程或演算步骤.)17.(10分)给定两个命题,命题p:对任意实数x都有ax2+ax+1>0恒成立,命题q:关于x的方程x2﹣x+a=0有实数根,如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.18.(12分)某城市100户居民的月平均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240)[240,260),[260,280),[280,300]分组的频率分布直方图如图:(1)求直方图中x的值;(2)求月平均用电量的众数和中位数;(3)在月平均用电量[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则越平均用电量在[220,240)的用户中应抽取多少户?19.(12分)已知椭圆C: +=1(a>b>0)的一个长轴顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,(Ⅰ)求椭圆C的方程;(Ⅱ)当△AMN的面积为时,求k的值.20.(12分)如图,ABCD是正方形,DE⊥平面ABCD.(1)求证:AC⊥平面BDE;(2)若AF∥DE,DE=3AF,点M在线段BD上,且BM=BD,求证:AM∥平面BEF.21.(12分)如图,在四棱锥P﹣ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.(1)求证:AM⊥PD(2)求点D到平面ACM的距离.22.(12分)已知抛物线C的顶点为O(0,0),焦点F(0,1)(Ⅰ)求抛物线C的方程;(Ⅱ)过F作直线交抛物线于A、B两点.若直线OA、OB分别交直线l:y=x﹣2于M、N两点,求|MN|的最小值.2016-2017学年内蒙古包头市北重三中高二(上)期末数学试卷(文科)参考答案与试题解析一.选择题:(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于()A.B.C.D.【考点】几何概型.【分析】利用几何概型的计算概率的方法解决本题,关键要弄准所求的随机事件发生的区域的面积和事件总体的区域面积,通过相除的方法完成本题的解答.【解答】解:由几何概型的计算方法,可以得出所求事件的概率为P=.故选C.【点评】本题考查概率的计算,考查几何概型的辨别,考查学生通过比例的方法计算概率的问题,考查学生分析问题解决问题的能力,考查学生几何图形面积的计算方法,属于基本题型.2.命题“若x2>y2则x>y”的逆否命题是()A.若x2<y2则x<y B.若x>y则x2>y2C.若x≤y则x2≤y2D.若x≥y则x2>y2【考点】四种命题.【分析】根据四种命题的相互关系,将原命题的条件与结论否定,并交换位置即得答案.【解答】解:命题“若x2>y2则x>y”;条件为:“若x2>y2”,结论为:“x>y”;故其逆否命题为:若x≤y则x2≤y2故选C.【点评】本题考查逆否命题的形式,解题时要注意分清四种命题的相互关系.3.甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则甲不输的概率为()A.B.C.D.【考点】概率的基本性质.【分析】由已知结合互斥事件概率加法公式,可得答案.【解答】解:∵甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,∴甲不输的概率为+=,故选:A【点评】本题考查的知识点是互斥事件概率加法公式,难度不大,属于基础题.4.已知焦点在x轴上的椭圆的离心率为,且它的长轴长等于4,则椭圆的标准方程是()A.=1 B.C.D.【考点】椭圆的简单性质.【分析】由题意设出椭圆方程并求得a值,再由离心率求得c,结合隐含条件求得b,则椭圆方程可求.【解答】解:由题意可设椭圆方程为(a>b>0).且2a=4,∴a=2,又,∴c=1,则b2=a2﹣c2=3.∴椭圆的标准方程是.故选:A.【点评】本题考查椭圆的简单性质,考查了椭圆方程的求法,是基础题.5.设α、β为两个不同平面,若直线l在平面α内,则“α⊥β”是“l⊥β”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据充分条件和必要条件的定义结合面面垂直的判定定理进行判断即可.【解答】解:面面平行的判定定理:一个平面过另一个平面的垂线,则这两个平面垂直.因为直线l⊂α,且l⊥β所以由判断定理得α⊥β.所以直线l⊂α,且l⊥β⇒α⊥β若α⊥β,直线l⊂α则直线l⊥β,或直线l∥β,或直线l与平面β相交,或直线l在平面β内.所以“α⊥β”是“l⊥β”的必要不充分条件.故选:B.【点评】本题主要考查充分条件和必要条件的判断,利用空间面面垂直的判定定理和性质定理是解决本题的关键.6.执行如图所示的程序框图,若输入n的值为8,则输出S的值为()A.4 B.8 C.10 D.12【考点】程序框图.【分析】根据已知中的程序框图可得,该程序的功能是计算并输出变量S的值,模拟程序的运行过程,可得答案.【解答】解:当i=2时,满足进行循环的条件,故S=2,i=4,k=2;当i=4时,满足进行循环的条件,故S=4,i=6,k=3;当i=6时,满足进行循环的条件,故S=8,i=8,k=4;当i=8时,不满足进行循环的条件,故S输出的S值为8,故选:B【点评】本题考查的知识点是程序框图,当程序的运行次数不多或有规律时,可采用模拟运行的办法解答.7.某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为()A.11 B.12 C.13 D.14【考点】系统抽样方法.【分析】根据系统抽样方法,从840人中抽取42人,那么从20人抽取1人.从而得出从编号481~720共240人中抽取的人数即可.【解答】解:使用系统抽样方法,从840人中抽取42人,即从20人抽取1人.所以从编号1~480的人中,恰好抽取=24人,接着从编号481~720共240人中抽取=12人.故:B.【点评】本题主要考查系统抽样的定义和方法,属于基础题.8.一个多面体的三视图如图所示,则该多面体的表面积为()A.21+B.18+C.21 D.18【考点】由三视图求面积、体积.【分析】判断几何体的形状,结合三视图的数据,求出几何体的表面积.【解答】解:由三视图可知,几何体是正方体的棱长为2,截去两个正三棱锥,侧棱互相垂直,侧棱长为1,几何体的表面积为:S正方体﹣2S棱锥侧+2S棱锥底==21+.故选:A.【点评】本题考查三视图求解几何体的表面积,解题的关键是判断几何体的形状.9.已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为,底面是边长为的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为()A.120°B.60°C.45°D.30°【考点】直线与平面所成的角.【分析】利用三棱柱ABC﹣A1B1C1的侧棱与底面垂直和线面角的定义可知,∠APA1为PA与平面A1B1C1所成角.利用三棱锥的体积计算公式可得AA1,再利用正三角形的性质可得A1P,在Rt△AA1P中,利用tan∠APA1=,可得结论.【解答】解:如图所示,∵AA1⊥底面A1B1C1,∴∠APA1为PA与平面A1B1C1所成角,∵平面ABC∥平面A1B1C1,∴∠APA1为PA与平面ABC所成角.∵==.=AA1,解得AA1=.∴V三棱柱ABC﹣A1B1C1又P为底面正三角形A1B1C1的中心,∴A1P==1,在Rt△AA1P中,tan∠APA1=,∴∠APA1=60°.故选B.【点评】本题考查线面角,掌握正三角形的性质、线面角的定义是解题的关键.10.已知双曲线C:的焦点为F1,F2,且C上的点P满足=0,|PF1|=3,|PF2|=4,则双曲线C的离心率为()A.B.C.D.5【考点】双曲线的简单性质.【分析】根据双曲线的定义可知|PF2|﹣|PF1|=2a=1,根据勾股定理求得4c2=25,则离心率可得.【解答】解:∵C上一点P满足PF1⊥PF2,|PF1|=3,|PF2|=4,∴|PF2|﹣|PF1|=2a=1,|PF2|2+|PF1|2=4c2=25,∴e==5,故选:D.【点评】本题主要考查了双曲线的应用.考查了学生对双曲线定义和基本知识的掌握.11.过抛物线x2=4y的焦点任作一直线l交抛物线于M,N两点,O为坐标原点,则△MON的面积的最小值为()A.2 B.2 C.4 D.8【考点】抛物线的简单性质.【分析】设M(x1,y1),N(x2,y2),则S=|OF|•|x1﹣x2|,直线l方程为y=kx+1代入x2=4y得:x2﹣4kx﹣4=0,由此能求出△OAB的面积.【解答】解:抛物线焦点为(0,1),直线l方程为y=kx+1,代入x2=4y得:x2﹣4kx﹣4=0,设M(x1,y1),N(x2,y2),∴x1+x2=4k,x1x2=﹣4,∴|x1﹣x2|=≥4,∴S=|OF|•|x1﹣x2|≥2,∴△MON的面积的最小值为2.故选:A.【点评】本题主要考查了抛物线的简单性质,直线与抛物线的位置关系.在涉及焦点弦的问题时常需要把直线与抛物线方程联立利用韦达定理设而不求,进而利用弦长公式求得问题的答案.12.已知动点P(x,y)在椭圆C:=1上,F为椭圆C的右焦点,若点M满足||=1且=0,则||的最小值为()A.B.3 C.D.1【考点】椭圆的简单性质.【分析】依题意知,该椭圆的焦点F(3,0),点M在以F(3,0)为圆心,1为半径的圆上,当PF最小时,切线长PM最小,作出图形,即可得到答案.【解答】解:依题意知,点M在以F(3,0)为圆心,1为半径的圆上,PM为圆的切线,且=0,即PM⊥MF,∴|PM|2=|PF|2﹣|MF|2,而|MF|=1,∴当PF最小时,切线长PM最小.由图知,当点P为右顶点(5,0)时,|PF|最小,最小值为:5﹣3=2.此时|PM|=.故选:A.【点评】本题考查椭圆的标准方程、圆的方程,考查作图与分析问题解决问题的能力,属于中档题.二、填空题:(本大题共4小题,每小题5分).13.从集合{1,2,3,4,5}任取一元素a,从集合{1,2,3}任取一元素b,则b>a的概率是.【考点】列举法计算基本事件数及事件发生的概率.【分析】求出基本事件总数n=5×3=15,再利用列举法求出b>a包含的基本事件(a,b)的个数,由此能求出b>a的概率.【解答】解:从集合{1,2,3,4,5}任取一元素a,从集合{1,2,3}任取一元素b,基本事件总数n=5×3=15,b>a包含的基本事件(a,b)有:(1,2),(1,3),(2,3),∴b>a的概率p==.故答案:.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.14.如图,正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为.【考点】异面直线及其所成的角.【分析】先通过平移将两条异面直线平移到同一个起点B,得到的锐角∠A1BC1就是异面直线所成的角,在三角形中A1BC1用余弦定理求出此角即可得到所求.【解答】解.如图,连接BC1,A1C1,∠A1BC1是异面直线A1B与AD1所成的角,设AB=a,AA1=2a,∴A1B=C1B=a,A1C1=a,根据余弦定理可知∠A1BC1的余弦值为,故答案为:.【点评】本题主要考查了异面直线及其所成的角,考查空间想象能力、运算能力和推理论证能力,属于中档题.15.过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若,则|AF|=.【考点】抛物线的简单性质.【分析】设出点的坐标与直线的方程,利用抛物线的定义表示出|AF|、|BF|再联立直线与抛物线的方程利用根与系数的关系解决问题,即可得到答案.【解答】解:由题意可得:F(,0),设A(x1,y1),B(x2,y2).因为过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点,所以|AF|=+x1,|BF|=+x2.因为,所以x1+x2=设直线l的方程为y=k(x﹣),联立直线与抛物线的方程可得:k2x2﹣(k2+2)x+=0,所以x1+x2=.∴∴k2=24∴24x2﹣26x+6=0,∴,∴|AF|=+x1=故答案为:【点评】解决此类问题的关键是熟练掌握抛物线的定义,以及掌握直线与抛物线位置关系,并且结合准确的运算也是解决此类问题的一个重要方面16.双曲线(a>0,b>0)的一条渐近线的倾斜角为,离心率为e,则的最小值为.【考点】双曲线的简单性质;基本不等式.【分析】由双曲线渐近线的方程可知,=,离心率e=,从而利用基本不等式即可求得的最小值.【解答】解:∵双曲线﹣=1(a>0,b>0)的一条渐近线的倾斜角为,∴=,又离心率e=,∴e2=1+=4,∴===+≥2=2=.即的最小值为.故答案为:.【点评】本题考查双曲线的简单性质,考查基本不等式,属于中档题.三、解答题:(共70分,解答应写出文字说明,证明过程或演算步骤.)17.(10分)(2009•马鞍山学业考试)给定两个命题,命题p:对任意实数x 都有ax2+ax+1>0恒成立,命题q:关于x的方程x2﹣x+a=0有实数根,如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.【考点】命题的真假判断与应用;复合命题的真假;函数恒成立问题.【分析】根据二次函数恒成立的充要条件,我们可以求出命题p为真时,实数a 的取值范围,根据二次函数有实根的充要条件,我们可以求出命题q为真时,实数a的取值范围,然后根据p∨q为真命题,p∧q为假命题,则命题p,q中一个为真一个为假,分类讨论后,即可得到实数a的取值范围.【解答】解:对任意实数x都有ax2+ax+1>0恒成立⇔a=0或⇔0≤a<4;(2分)关于x的方程x2﹣x+a=0有实数根⇔△=1﹣4a≥0⇔a≤;…(4分)p∨q为真命题,p∧q为假命题,即p真q假,或p假q真,…如果p真q假,则有0≤a<4,且a>∴<a<4;…(6分)如果p假q真,则有a<0,或a≥4,且a≤∴a<0…(7分)所以实数a的取值范围为(﹣∞,0)∪(,4).…(8分)【点评】本题考查的知识点是命题的真假判断与应用,复合命题的真假,函数恒成立问题,其中判断出命题p与命题q为真时,实数a的取值范围,是解答本题的关键.18.(12分)(2016•湖南模拟)某城市100户居民的月平均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240)[240,260),[260,280),[280,300]分组的频率分布直方图如图:(1)求直方图中x的值;(2)求月平均用电量的众数和中位数;(3)在月平均用电量[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则越平均用电量在[220,240)的用户中应抽取多少户?【考点】用样本的数字特征估计总体的数字特征.【分析】(1)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1,解方程可得;(2)由直方图中众数为最高矩形上端的中点可得,可得中位数在[220,240)内,设中位数为a,解方程(0.002+0.0095++0.011)×20+0.0125×(a﹣220)=0.5可得;(3)可得各段的用户分别为25,15,10,5,可得抽取比例,可得要抽取的户数.【解答】解:(1)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1,解方程可得x=0.0075,∴直方图中x的值为0.0075;(2)月平均用电量的众数是=230,∵(0.002+0.0095+0.011)×20=0.45<0.5,∴月平均用电量的中位数在[220,240)内,设中位数为a,由(0.002+0.0095+0.011)×20+0.0125×(a﹣220)=0.5可得a=224,∴月平均用电量的中位数为224;(3)月平均用电量为[220,240)的用户有0.0125×20×100=25,月平均用电量为[240,260)的用户有0.0075×20×100=15,月平均用电量为[260,280)的用户有0.005×20×100=10,月平均用电量为[280,300)的用户有0.0025×20×100=5,∴抽取比例为=,∴月平均用电量在[220,240)的用户中应抽取25×=5户【点评】本题考查频率分布直方图,涉及众数和中位数以及分层抽样,属基础题.19.(12分)(2012•北京)已知椭圆C: +=1(a>b>0)的一个长轴顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,(Ⅰ)求椭圆C的方程;(Ⅱ)当△AMN的面积为时,求k的值.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【分析】(Ⅰ)根据椭圆一个顶点为A (2,0),离心率为,可建立方程组,从而可求椭圆C的方程;(Ⅱ)直线y=k(x﹣1)与椭圆C联立,消元可得(1+2k2)x2﹣4k2x+2k2﹣4=0,从而可求|MN|,A(2,0)到直线y=k(x﹣1)的距离,利用△AMN的面积为,可求k的值.【解答】解:(Ⅰ)∵椭圆一个顶点为A (2,0),离心率为,∴∴b=∴椭圆C的方程为;(Ⅱ)直线y=k(x﹣1)与椭圆C联立,消元可得(1+2k2)x2﹣4k2x+2k2﹣4=0设M(x1,y1),N(x2,y2),则x1+x2=,∴|MN|==∵A(2,0)到直线y=k(x﹣1)的距离为∴△AMN的面积S=∵△AMN的面积为,∴∴k=±1.【点评】本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,解题的关键是正确求出|MN|.20.(12分)(2015•烟台一模)如图,ABCD是正方形,DE⊥平面ABCD.(1)求证:AC⊥平面BDE;(2)若AF∥DE,DE=3AF,点M在线段BD上,且BM=BD,求证:AM∥平面BEF.【考点】直线与平面平行的判定;直线与平面垂直的判定.【分析】(1)证明DE⊥AC,通过直线与平面垂直的判定定理证明AC⊥平面BDE.(2)延长EF、DA交于点G,通过AF∥DE,DE=3AF,推出,证明AM ∥GB利用直线与平面平行的判定定理证明AM∥平面BEF.【解答】证明:(1)因为DE⊥平面ABCD,所以DE⊥AC.…(2分)因为ABCD是正方形,所以AC⊥BD,又BD∩DE=D,从而AC⊥平面BDE.…(2)延长EF、DA交于点G,因为AF∥DE,DE=3AF,所以,…(7分)因为,所以,所以,所以AM∥GB,…(10分)又AM⊄平面BEF,GB⊂平面BEF,所以AM∥平面BEF.…(12分)【点评】本题考查直线与平面垂直的判定定理以及直线与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.21.(12分)(2016秋•青山区校级期末)如图,在四棱锥P﹣ABCD,底面ABCD 是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.(1)求证:AM⊥PD(2)求点D到平面ACM的距离.【考点】点、线、面间的距离计算.【分析】(1)推导出AB⊥AD,AB⊥PA,从而AB⊥平面PAD,由BM⊥PD,PD ⊥平面ABM,AM⊥PD.(2)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出点D到平面ACM的距离.【解答】证明:(1)∵在四棱锥P﹣ABCD,底面ABCD是矩形,PA⊥平面ABCD,∴AB⊥AD,AB⊥PA,∵PA∩AD=A,∴AB⊥平面PAD,∵BM⊥PD于点M,AB∩BM=B,∴PD⊥平面ABM,∵AM⊂平面ABM,∴AM⊥PD.解:(2)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,则A(0,0,0),C(1,2,0),P(0,0,2),D(0,2,0),M(0,1,1),=(0,2,0),=(1,2,0),=(0,1,1),设平面ACM的法向量=(x,y,z),则,取x=2,得=(2,﹣1,1),∴点D到平面ACM的距离:d===.【点评】本题考查线线垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.22.(12分)(2013•浙江)已知抛物线C的顶点为O(0,0),焦点F(0,1)(Ⅰ)求抛物线C的方程;(Ⅱ)过F作直线交抛物线于A、B两点.若直线OA、OB分别交直线l:y=x﹣2于M、N两点,求|MN|的最小值.【考点】直线与圆锥曲线的关系;抛物线的标准方程.【分析】(I)由抛物线的几何性质及题设条件焦点F(0,1)可直接求得p,确定出抛物线的开口方向,写出它的标准方程;(II)由题意,可A(x1,y1),B(x2,y2),直线AB的方程为y=kx+1,将直线方程与(I)中所求得方程联立,再结合弦长公式用所引入的参数表示出|MN|,根据所得的形式作出判断,即可求得最小值.【解答】解:(I)由题意可设抛物线C的方程为x2=2py(p>0)则=1,解得p=2,故抛物线C的方程为x2=4y(II)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+1,由消去y,整理得x2﹣4kx﹣4=0,所以x1+x2=4k,x1x2=﹣4,从而有|x1﹣x2|==4,由解得点M的横坐标为x M===,同理可得点N的横坐标为x N=,所以|MN|=|x M﹣x N|=|﹣|=8||=,令4k﹣3=t,t≠0,则k=,当t>0时,|MN|=2>2,当t<0时,|MN|=2=2≥.综上所述,当t=﹣,即k=﹣时,|MN|的最小值是.【点评】本题主要考查抛物线的几何性质,直线与抛物线的位置关系,同时考查解析几何的基本思想方法和运算求解能力,本题考查了数形结合的思想及转化的思想,将问题恰当的化归可以大大降低题目的难度,如本题最后求最值时引入变量t,就起到了简化计算的作用.。
内蒙古包头一中2016-2017学年高二上学期期末数学试卷(

2016-2017学年内蒙古包头一中高二(上)期末数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.下列有关命题的说法正确的是()A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”B.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件C.命题“若x=y,则sinx=siny”的逆否命题为真命题D.命题“∃x0∈R,x02+x0+1<0”的否定是:“∀x∈R,x2+x+1>0”2.已知向量,满足||=||=|+|=1,则向量,夹角的余弦值为()A.B.﹣ C.D.﹣3.下列向量中与向量=(2,3)垂直的是()A.=(﹣2,3)B.=(2,﹣3)C.=(3,﹣2)D.=(﹣3,﹣2)4.已知复数z=lgm+(lgn)i,其中i是虚数单位.若复数z在复平面内对应的点在直线y=﹣x上,则mn的值等于()A.0 B.1 C.10 D.5.复数=()A.2+i B.2﹣i C.1+2i D.1﹣2i6.设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为R,四面体S﹣ABC的体积为V,则R=()A.B.C.D.7.由曲线y=,直线y=x﹣2及y轴所围成的图形的面积为()A.B.4 C.D.68.用反证法证明“如果a<b,那么”,假设的内容应是()A. B.C.且D.或9.已知双曲线﹣=1(a>b,b>0)的离心率为,则椭圆+=1的离心率为()A.B.C.D.10.在四面体P﹣ABC中,PA,PB,PC两两垂直,设PA=PB=PC=a,则点P到平面ABC的距离为()A.B.C.D.11.已知函数f(x)=,则()A.B.C.D.12.设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图象如图所示,则下列结论中一定成立的是()A.函数f(x)有极大值f(2)和极小值f(1)B.函数f(x)有极大值f(﹣2)和极小值f(1)C.函数f(x)有极大值f(2)和极小值f(﹣2)D.函数f(x)有极大值f(﹣2)和极小值f(2)二、填空题(本大题共4个小题,每小题5分,共20分)13.已知函数f(x)=2f′(1)lnx﹣x,则f′(1)的值为.14.抛物线y=4x2的准线方程为.15.函数y=(1﹣sinx)2的导数是.16.与双曲线共渐近线且过点的双曲线的标准方程是.三、解答题(共6个小题,第17题10分,其余各12分,共70分)17.用数学归纳法证明:,n∈N*.18.在边长为2的正方体ABCD﹣A′B′C′D′中,E是BC的中点,F是DD′的中点(1)求证:CF∥平面A′DE(2)求二面角E﹣A′D﹣A的平面角的余弦值.19.在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,PB与平面ABC成60°的角,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AB=BC=AD.(1)求证:平面PCD⊥平面PAC;(2)设E是棱PD上一点,且PE=PD,求异面直线AE与PB所成角的余弦值.20.椭圆C: +=1(a>b>0)的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2,|PF1|=,|PF2|=.(Ⅰ)求椭圆C的方程;(Ⅱ)若直线l过点M(﹣2,1),交椭圆C于A,B两点,且M恰是A,B中点,求直线l的方程.21.已知函数f(x)=x3﹣2ax2+bx+c.(Ⅰ)当c=0时,f(x)的图象在点(1,3)处的切线平行于直线y=x+2,求a,b的值;(Ⅱ)当时,f(x)在点A,B处有极值,O为坐标原点,若A,B,O三点共线,求c的值.22.设函数f(x)=2lnx﹣x2.(1)求函数f(x)的单调递增区间;(2)若关于x的方程f(x)+x2﹣x﹣2﹣a=0在区间[1,3]内恰有两个相异实根,求实数a的取值范围.2016-2017学年内蒙古包头一中高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.下列有关命题的说法正确的是()A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”B.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件C.命题“若x=y,则sinx=siny”的逆否命题为真命题D.命题“∃x0∈R,x02+x0+1<0”的否定是:“∀x∈R,x2+x+1>0”【考点】命题的真假判断与应用.【分析】直接写出命题的否命题判断A;利用充分必要条件的判定方法判断B;由互为逆否命题的两个命题共真假判断C;写出特称命题的否定判断D.【解答】解:命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1”,故A错误;由x=﹣1,得x2﹣5x﹣6=0,反之,由x2﹣5x﹣6=0,得x=﹣1或x=6,则“x=﹣1”是“x2﹣5x﹣6=0”的充分不必要条件,故B错误;命题“若x=y,则sinx=siny”为真命题,则其逆否命题为真命题,故C正确;命题“∃x0∈R,x02+x0+1<0”的否定是:“∀x∈R,x2+x+1≥0”,故D错误.故选:C.2.已知向量,满足||=||=|+|=1,则向量,夹角的余弦值为()A.B.﹣ C.D.﹣【考点】数量积表示两个向量的夹角.【分析】将|+|=1两边平方,结合已知条件可算出•=﹣,再用两个向量的夹角公式即可算出向量,夹角的余弦值.【解答】解:∵|+|=1,∴(+)2=2+2•+2=1∵||=||=1,得2=2=1∴代入上式得:2•=﹣1,•=﹣因此,向量,夹角的余弦为cosθ==﹣故选:B3.下列向量中与向量=(2,3)垂直的是()A.=(﹣2,3)B.=(2,﹣3)C.=(3,﹣2)D.=(﹣3,﹣2)【考点】数量积判断两个平面向量的垂直关系.【分析】由=﹣4+9=5,=4﹣9=﹣5,=6﹣6=0,=﹣6﹣6=﹣12,能求出与向量=(2,3)垂直的向量.【解答】解:∵=﹣4+9=5,=4﹣9=﹣5,=6﹣6=0,=﹣6﹣6=﹣12,∴与向量=(2,3)垂直的是.故选:C.4.已知复数z=lgm+(lgn)i,其中i是虚数单位.若复数z在复平面内对应的点在直线y=﹣x上,则mn的值等于()A.0 B.1 C.10 D.【考点】复数的代数表示法及其几何意义.【分析】复数z=lgm+(lgn)i,复数z在复平面内对应的点(lgm,lgn)在直线y=﹣x上,可得lgm=﹣lgn,化简即可得出.【解答】解:复数z=lgm+(lgn)i,复数z在复平面内对应的点(lgm,lgn)在直线y=﹣x上,∴lgm=﹣lgn,可得lg(mn)=0,可得mn=1.故选:B.5.复数=()A.2+i B.2﹣i C.1+2i D.1﹣2i【考点】复数代数形式的乘除运算.【分析】利用复数的运算法则即可得出.【解答】解:===1+2i,故选:C.6.设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为R,四面体S﹣ABC的体积为V,则R=()A.B.C.D.【考点】类比推理.【分析】根据平面与空间之间的类比推理,由点类比点或直线,由直线类比直线或平面,由内切圆类比内切球,由平面图形面积类比立体图形的体积,结合求三角形的面积的方法类比求四面体的体积即可.【解答】解:设四面体的内切球的球心为O,则球心O到四个面的距离都是R,所以四面体的体积等于以O为顶点,分别以四个面为底面的4个三棱锥体积的和.则四面体的体积为∴R=故选C.7.由曲线y=,直线y=x﹣2及y轴所围成的图形的面积为()A.B.4 C.D.6【考点】定积分在求面积中的应用.【分析】利用定积分知识求解该区域面积是解决本题的关键,要确定出曲线y=,直线y=x﹣2的交点,确定出积分区间和被积函数,利用导数和积分的关系完成本题的求解.【解答】解:联立方程得到两曲线的交点(4,2),因此曲线y=,直线y=x﹣2及y轴所围成的图形的面积为:S=.故选C.8.用反证法证明“如果a<b,那么”,假设的内容应是()A. B.C.且D.或【考点】反证法与放缩法.【分析】分析:反证法是假设命题的结论不成立,即结论的反面成立,所以只要考虑>的反面是什么即可.【解答】解:∵>的反面是≤,即=或<.故选D.9.已知双曲线﹣=1(a>b,b>0)的离心率为,则椭圆+=1的离心率为()A.B.C.D.【考点】双曲线的简单性质.【分析】根据双曲线的离心率建立方程关系求出a,b的关系,然后结合椭圆离心率的定义进行求解即可.【解答】解:在双曲线中c2=a2+b2,∵双曲线的离心率为,∴==,即4a2+4b2=5a2,即a2=4b2,则c2=a2﹣b2=4b2﹣b2=3b2,则e2===,即e=,故椭圆的离心率是,故选:C.10.在四面体P﹣ABC中,PA,PB,PC两两垂直,设PA=PB=PC=a,则点P到平面ABC的距离为()A.B.C.D.【考点】点、线、面间的距离计算.【分析】取BC中点D,连结AD,作PO⊥平面ABC,交AD于O,由此能求出点P到平面ABC的距离PO.【解答】解:∵在四面体P﹣ABC中,PA,PB,PC两两垂直,PA=PB=PC=a,∴AB=AC=BC=a,取BC中点D,连结AD,作PO⊥平面ABC,交AD于O,则AD==,∴AO=×=,∴点P到平面ABC的距离PO==.故选:B.11.已知函数f(x)=,则()A.B.C.D.【考点】定积分.【分析】先根据条件可化为(x+1)2dx+dx,再根据定积分以及定积分的几何意义,求出即可.【解答】解:(x+1)2dx+dx,∵(x+1)2dx=(x+1)3|=,dx表示以原点为圆心以1为为半径的圆的面积的四分之一,故dx=π,∴(x+1)2dx+dx==,故选:B12.设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图象如图所示,则下列结论中一定成立的是()A.函数f(x)有极大值f(2)和极小值f(1)B.函数f(x)有极大值f(﹣2)和极小值f(1)C.函数f(x)有极大值f(2)和极小值f(﹣2)D.函数f(x)有极大值f(﹣2)和极小值f(2)【考点】函数在某点取得极值的条件;函数的图象.【分析】利用函数的图象,判断导函数值为0时,左右两侧的导数的符号,即可判断极值.【解答】解:由函数的图象可知,f′(﹣2)=0,f′(2)=0,并且当x<﹣2时,f′(x)>0,当﹣2<x<1,f′(x)<0,函数f(x)有极大值f(﹣2).又当1<x<2时,f′(x)<0,当x>2时,f′(x)>0,故函数f(x)有极小值f (2).故选D.二、填空题(本大题共4个小题,每小题5分,共20分)13.已知函数f(x)=2f′(1)lnx﹣x,则f′(1)的值为1.【考点】导数的运算.【分析】求函数的导数,令x=1即可求出f′(1)的值.【解答】解:函数的导数为f′(x)=2f′(1)﹣1,令x=1得f′(1)=2f′(1)﹣1,即f′(1)=1,故答案为:114.抛物线y=4x2的准线方程为.【考点】抛物线的简单性质.【分析】先把抛物线方程整理成标准方程,进而求得p,再根据抛物线性质得出准线方程.【解答】解:整理抛物线方程得x2=y,∴p=∵抛物线方程开口向上,∴准线方程是y=﹣故答案为:.15.函数y=(1﹣sinx)2的导数是sin2x﹣2cosx.【考点】导数的运算.【分析】利用导数的运算法则即可得出.【解答】解:y′=2(1﹣sinx)•(1﹣sinx)′=2(1﹣sinx)•(﹣cosx)=sin2x﹣2cosx 故答案为:sin2x﹣2cosx16.与双曲线共渐近线且过点的双曲线的标准方程是.【考点】双曲线的简单性质.【分析】与﹣y2=1有相同的渐近线的方程可设为﹣y2=λ≠0,再把点P的坐标代入即可.【解答】解:依题设所求双曲线方程为﹣y2=λ≠0,∵双曲线过点(,2),∴1﹣4=λ,∴λ=﹣3,∴所求双曲线方程为.故答案为:三、解答题(共6个小题,第17题10分,其余各12分,共70分)17.用数学归纳法证明:,n∈N*.【考点】数学归纳法.【分析】利用数学归纳法的证明标准,验证n=1时成立,假设n=k是成立,证明n=k+1时等式也成立即可.【解答】证明:(1)当n=1时,左边=,右边=,等式成立.﹣﹣(2)假设当n=k时,等式成立,即++…+=﹣﹣﹣﹣﹣那么,当n=k+1时,左边=++…++=+=,这就是说,当n=k+1时等式也成立.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣根据(1)和(2),可知等式对任何n∈N*都成立.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣18.在边长为2的正方体ABCD﹣A′B′C′D′中,E是BC的中点,F是DD′的中点(1)求证:CF∥平面A′DE(2)求二面角E﹣A′D﹣A的平面角的余弦值.【考点】用空间向量求平面间的夹角;向量语言表述线面的垂直、平行关系.【分析】(1)分别以DA,DC,DD'为x轴,y轴,z轴建立空间直角坐标系,求出各顶点坐标后,进而求出直线CF的方向向量和平面A'DE的法向量,根据两个向量的数量积为0,得到两个向量垂直后,进而得到CF∥平面A'DE(2)结合正方体的几何特征,可得是面AA'D的法向量,结合(1)中平面A'DE的法向量为,代入向量夹角公式,即可求出二面角E ﹣A'D﹣A的平面角的余弦值.【解答】证明(1):分别以DA,DC,DD'为x轴,y轴,z轴建立空间直角坐标系,则A'(2,0,2),E(1,2,0),D(0,0,0),C(0,2,0),F(0,0,1),…则,设平面A'DE的法向量是,则,取,…,∵,∴,所以,CF∥平面A'DE.…解:(2)由正方体的几何特征可得是面AA'D的法向量又由(1)中向量为平面A'DE的法向量故二面角E﹣A'D﹣A的平面角θ满足;即二面角E﹣A'D﹣A的平面角的余弦值为…19.在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,PB与平面ABC成60°的角,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AB=BC=AD.(1)求证:平面PCD⊥平面PAC;(2)设E是棱PD上一点,且PE=PD,求异面直线AE与PB所成角的余弦值.【考点】异面直线及其所成的角;平面与平面垂直的判定.【分析】(1)由AB,AD,AP两两垂直,建立空间直角坐标系A﹣xyz.利用向量法能证明平面PCD⊥平面PAC.(2)求出=(0,,),=(1,0,﹣),利用向量法能求出异面直线AE与PB所成的角的余弦值.【解答】证明:(1)∵AB,AD,AP两两垂直,建立空间直角坐标系A﹣xyz.∵PA⊥平面ABCD,PB与平面ABC成60°,∴∠PBA=60°.∴PA=ABtan60°=.取AB=1,则A(0,0,0),B(1,0,0),C(1,1,0),P(0,0,),D(0,2,0).∵=(1,1,0),=(0,0,),=(﹣1,1,0),∴=﹣1+1+0=0,=0.∴AC⊥CD,AP⊥CD,∵AC∩AP=A,∴CD⊥平面PAC.又CD⊂平面PCD,∴平面PCD⊥平面PAC.解:(2)∵=,=(0,2,﹣),∴=+=(0,0,)+(0,2,﹣)=(0,,),∴E(0,,),∴=(0,,).又=(1,0,﹣),∴•=﹣2.∴cos<•>==﹣.∴异面直线AE与PB所成的角的余弦值为.20.椭圆C: +=1(a>b>0)的两个焦点为F1,F2,点P在椭圆C上,且PF1⊥F1F2,|PF1|=,|PF2|=.(Ⅰ)求椭圆C的方程;(Ⅱ)若直线l过点M(﹣2,1),交椭圆C于A,B两点,且M恰是A,B中点,求直线l的方程.【考点】直线与圆锥曲线的关系;椭圆的标准方程.【分析】(Ⅰ)根据椭圆的定义,可得a的值,在Rt△PF1F2中,|F1F2|=,可得椭圆的半焦距c=,从而可求椭圆C的方程为=1;(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2),设过点(﹣2,1)的直线l 的方程为y=k(x+2)+1,代入椭圆C的方程,利用A,B关于点M对称,结合韦达定理,即可求得结论.【解答】解:(Ⅰ)因为点P在椭圆C上,所以2a=|PF1|+|PF2|=6,a=3.在Rt△PF1F2中,|F1F2|=,故椭圆的半焦距c=,从而b2=a2﹣c2=4,所以椭圆C的方程为=1.(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2).若直线l斜率不存在,显然不合题意.从而可设过点(﹣2,1)的直线l的方程为y=k(x+2)+1,代入椭圆C的方程得(4+9k2)x2+(36k2+18k)x+36k2+36k﹣27=0.因为A,B关于点M对称,所以,解得k=,所以直线l的方程为,即8x﹣9y+25=0.经检验,△>0,所以所求直线方程符合题意.21.已知函数f(x)=x3﹣2ax2+bx+c.(Ⅰ)当c=0时,f(x)的图象在点(1,3)处的切线平行于直线y=x+2,求a,b的值;(Ⅱ)当时,f(x)在点A,B处有极值,O为坐标原点,若A,B,O三点共线,求c的值.【考点】利用导数研究函数的极值;利用导数研究曲线上某点切线方程.【分析】(Ⅰ)当c=0时,函数f(x)=x3﹣2ax2+bx.依题意可得f(1)=3,f'(1)=1,即可得到a,b的值;(Ⅱ)当时,f'(x )=3x 2﹣6x ﹣9,列表得到,当x=﹣1时,f (x )极大值=5+c ;当x=3时,f (x )极小值=﹣27+c .又由A ,B ,O 三点共线,则得到k OA =k OB ,进而得到c 的值.【解答】解:(Ⅰ) 当c=0时,f (x )=x 3﹣2ax 2+bx . 则f'(x )=3x 2﹣4ax +b由于f (x )的图象在点(1,3)处的切线平行于直线y=x +2, 可得f (1)=3,f'(1)=1, 即, 解得;(Ⅱ)当时,f (x )=x 3﹣3x 2﹣9x +c .所以f'(x )=3x 2﹣6x ﹣9=3(x ﹣3)(x +1) 令f'(x )=0,解得x 1=3,x 2=﹣1.当x 变化时,f'(x ),f (x )变化情况如下表:所以当x=﹣1时,f (x )极大值=5+c ;当x=3时,f (x )极小值=﹣27+c . 不妨设A (﹣1,5+c ),B (3,﹣27+c ) 因为A ,B ,O 三点共线,所以k OA =k OB . 即,解得c=3.故所求c 值为3.22.设函数f (x )=2lnx ﹣x 2.(1)求函数f (x )的单调递增区间;(2)若关于x 的方程f (x )+x 2﹣x ﹣2﹣a=0在区间[1,3]内恰有两个相异实根,求实数a 的取值范围.【考点】利用导数研究函数的单调性;函数的零点.【分析】求函数f(x)的导数,解f′(x)>0便得增区间.要使关于x的方程f (x)+x2﹣x﹣2﹣a=0在区间[1,3]内恰有两个相异实根,也就是让函数f(x)+x2﹣x﹣2﹣a在[1,3]内有两个零点,令g(x)=f(x)+x2﹣x﹣2﹣a=2lnx﹣x﹣2﹣a,下面要做的就是考查g(x)在区间[1,3]内最值情况,若有最大值,则限制最大值大于0,然后两个端点值都小于0,若有最小值,情况恰好相反.【解答】解:(1)f′(x)=,∵x>0,x∈(0,1)时,f′(x)>0,所以函数f(x)的单调递增区间是(0,1].(2)将f(x)代人方程f(x)+x2﹣x﹣2﹣a=0得2lnx﹣x﹣2﹣a=0,令g(x)=2lnx﹣x﹣2﹣a则g′(x)=;∴x∈[1,2)时,g′(x)>0;x∈(2,3]时,g′(x)<0;∴g(2)是g(x)的极大值,也是g(x)在[1,3]上的最大值;∵关于x的方程f(x)+x2﹣x﹣2﹣a=0在区间[1,3]内恰有两个相异实根;∴函数g(x)在区间[1,3]内有两个零点;则有:g(2)>0,g(1)<0,g(3)<0,所以有:解得:2ln3﹣5<a<2ln2﹣4,所以a的取值范围是(2ln3﹣5,2ln2﹣4).2017年3月5日。
内蒙古包头市第一中学2016-2017学年高二上学期期末考试英语试题含答案
包头市第一中学2016——2017学年度第一学期期末试题高二英语出题人:武瑞第I卷第一部分听力(共两节,满分30分)第一节(共5小题:每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题.每段对话仅读一遍。
1.What is the relationship between the two speakers?A.Customer and waiter.B.Husband and wife.C.Teacher and student.2.What time will the taxi come here?A.At 7:00 pm。
B。
At 7:10 pm。
C。
At 7:30 pm.3.How will the boy go to Beijing?A.By train。
B. By air。
C. By car。
4.What language isn't the girl good at?A.English。
B. German。
C。
French.5.Where are they talking?A.On a plane。
B.At the airport。
C.In the woman’s house。
第二节(共15小题,每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间.每段对话读两遍。
听第6段材料,回答第6、7题.6.How much is the ticket for a kid?A.50 dollars. B。
30 dollars. C。
20 dollars7.When will the bus tour start?A.At 9:00 am. B。
内蒙古包头市第一中学高二数学上学期期末考试试题 文
包头一中2015--2016学年度第一学期期末考试高二文科数学试题一.选择题:(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案涂在答题卡相应的位置.). 1.已知集合11M xx ⎧⎫=≤⎨⎬⎩⎭,{}260N x x x =--<,则M N I 为 ( ). A.{2x x -≤<0或}1x <≤3 B.{20x x -<<或}x 1≤<3 C.{2x x ≤-或}3x > D.{2x x <-或}3x ≥2.若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥-+≤-≤-020102y x y x ,则目标函数y x t 2-=的最大值为( )A.2 B .0 C .1 D . 1- 3.已知等比数列{}n a 满足114a =,()35441a a a =-,则2a = ( ) .2A .1B 1.2C 1.8D4.下列有关命题的说法错误的个数是 ( )①命题“若x 2=1,则x=1”的否命题为“若x 2=1,则x ≠1”②“x=-1”是“x 2-5x-6=0”的充分不必要条件③命题“存在x ∈R,使得x 2+x-1<0”的否定是:“任意x ∈R,均有x 2+x-1>0” ④命题“若x=y,则sin x=sin y ”的逆否命题为真命题 ⑤若“p 或q ”为真命题,则p 、q 均为真命题A.2B.3C.4D.5 5.抛物线24x y =上一点A 的纵坐标为4,则点A 与抛物线焦点的距离为A.5B.3C.4D.2 6. 已知双曲线与椭圆共顶点,且焦距是6,此双曲线的渐近线是( )A .B .C .D .7.函数12)(2+-=ax x x f 在(]2,∞-上是单调递减函数的必要不充分条件是( )A .2≥aB .6=aC .3≥aD .0≥a8.直线1y kx =-与双曲线221x y -=的左支有两个公共点,则k 的取值范围是( )A .(2,0)-B .(2,2)-C .(2,1)--D .(2,1]--9.如图,12,F F 是双曲线22221x y a b-=(0,0)a b >>的左、右焦点,过1F的直线l 与双曲线的左右两支分别交于点A 、B .若2ABF ∆为等边三角形,则双曲线的离心率为( )A .4B .7C .233D .3 10.在区间)2,1(上,不等式042<---mx x 有解,则m 的取值范围为( ) A .4->m B .4-<m C .5-<m D.5->m 11.若满足 2c =,cos sin a C c A =的三角形ABC 有两个,则边长BC 的取值范围是 ( )A .(1,2)B .(1,3)C .(3,2)D .(2,2)12.已知直线()()20y k x k =+>与抛物线C :x y 82=相交于A ,B 两点,F 为C 的焦点,若FB FA 2=,则k =( )A .13 B 2 C .23 D 22 二、填空题:(本大题共4小题,每小题5分,共20分。
内蒙古包头市2016_2017学年高二数学下学期期末考试试题理2017092602124
内蒙古包头市2016-2017学年高二数学下学期期末考试试题理2017年7月8日一、选择题:(本大题共12小题,每小题5分,共60分。
每题只有一个正确答案)1.设复数z满足(z-2i)(2-i)=5,则z=()A.2+3iB.2-3iC.3+2i D.3-2ie x2.函数f(x)=的递减区间为()x-23.在同一平面直角坐标系中,经过伸缩变换Error!后,曲线C变为曲线x′2+y′2=1,则曲线C的方程为()x2 y2A.25x2+9y2=1B.9x2+25y2=1C.25x+9y=1 D. +=125 9x2 y2 54.已知双曲线的方程为-=1(a>0,b>0),双曲线的一个焦点到一条渐近线的距离为c(ca2 b2 3为双曲线的半焦距长),则双曲线的离心率为()5 3 3 5 2A. B. C. D.2 2 5 35.已知圆(x+2)2+y2=36的圆心为M,设A为圆上任一点,N(2,0),线段AN的垂直平分线交MA于点P,则动点P的轨迹是()A.圆B.椭圆C.双曲线D.抛物线6.长方体的三个相邻面的面积分别为2,3,6,若这个长方体的顶点都在同一球面上,则这个球的表面积为()7A. πB.56πC.14πD.64π27.已知函数f(x)=Error!则f(x)d x=()1 3A. B.1C.2 D.2 28.f(x)=e x-x(e为自然对数的底数)在区间[-1,1]上的最大值是()1A.1+B.1C.e+1 D.e-1e19.在正方体ABCD-A1B1C1D1中,E是棱BB1中点,G是DD1中点,F是BC上一点且FB=BC,4则GB与EF所成的角为()A.30° B.120°C.60°D.90°10.已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是()3 5 11A. B.2C. D.35 51x2 y211.已知椭圆C:+=1的左、右焦点分别为F1,F2,椭圆C上的点A满足AF2⊥F1F2,若4 3→→点P是椭圆C上的动点,则F1P·F2A的最大值为()3 3 3 9 15A. B. C. D.2 2 4 412.函数f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-11)f′(x)<0,设a=f(0),b=f( ),c=f(3),则()2A.a<b<c B.c<a<b C.c<b<a D.b<c<a二.填空题:(本大题共4小题,每小题5分,共20分)ππ13.在极坐标系中,点(2,)到直线ρsin(θ-)=1的距离是6 6________.14.若某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为________.2x-a15.若f(x)=(x∈R)在区间[-1,1]上是增函数,则a的范围x2+2是.16.如图所示,在平面上,用一条直线截正方形的一个角,截下的是一个直角三角形,有勾股定理c2=a2+b2.空间中的正方体,用一平面去截正方体的一角,截下的是一个三条侧棱两两垂直的三棱锥,若这三个两两垂直的侧面的面积分别为S1,S2,S3,截面面积为S,类比平面的结论有________.三.解答题(共70分),写出必要的解题过程.17.(本题满分10分)在平面直角坐标系xOy中,已知直线l的参数方程为Error!(t为参数),直线l与抛物线y2=4x相交于A,B两点,求线段AB的长.18.(本题满分12分)2x2 y2如右图,已知椭圆+=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,a2 b2直线AF2交椭圆于另一点B.(1)若∠F1AB=90°,求椭圆的离心率;→→(2)若椭圆的焦距为2,且AF2=2F2B,求椭圆的方程.19.(本小题满分12分)如图所示,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2 3.(1)求证:AB∥平面MCD;(2)求平面ACM与平面BCD所成二面角的正弦值.20.(本小题满分12分)设函数f(x)=x+ax2+b ln x,曲线y=f(x)过P(1,0),且在P点处的切线斜率为2.(1)求a,b的值;(2)令g(x)=f(x)-2x+2,求g(x)在定义域上的最值.21.(本小题满分12分)已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A,B两点,O 为坐标原点.(1)若m=1,且直线l的斜率为1,求以线段AB为直径的圆的方程;1 1(2)问是否存在定点M,不论直线l绕点M如何转动,使得+恒为定值.|AM|2 |BM|23122.(本小题满分12分)已知函数f(x)=x2+a ln x.2(1)若a=-1,求函数f(x)的极值,并指出是极大值还是极小值;(2)若a=1,求函数f(x)在[1,e]上的最大值和最小值;2(3)若a=1,求证:在区间[1,+∞)上函数f(x)的图像在函数g(x)=x3的图像的下方.34包33中2016~2017学年度第二学期期末考试高二年级数学(理)试卷答案一、选择题:(本大题共12小题,每小题5分,共60分)题号 1 2 3 4 5 6 7 8 9 10 11 12答案 A C A B B C D D D B B B二、填空题(本大题共4小题,每小题5分,共20分)13.1 ;14. 22;15 1,1 ;16 ;S2 S2 S2 S2123三.解答题(本大题共6小题,共70分)2 217.解析将直线l的参数方程Error!代入抛物线方程y2=4x,得(2+t)2=4(1-t).解2 2得t1=0,t2=-8 2.2 x2 y218.答案(1) (2) +=12 3 2解析(1)若∠F1AB=90°,则△AOF2为等腰直角三角形.所以有|OA|=|OF2|,即b=c.c 2所以a=2c,e==.a 2(2)由题知A(0,b),F2(1,0),设B(x,y),9 b2→→ 3 b x2 y2 4 4由AF2=2F2B,解得x=,y=-.代入+=1,得+=1.2 2 a2 b2 a2 b29 1 x2 y2即+=1,解得a2=3.所以椭圆方程为+=1.4a2 4 3 219.解析(1)证明:取CD中点O,因为△MCD为正三角形,所以MO⊥CD.由于平面MCD⊥平面BCD,所以MO⊥平面BCD.又因为AB⊥平面BCD,所以AB∥MO.又AB⊄平面MCD,MO⊂平面MCD,所以AB∥平面MCD.(2)连接OB,则OB⊥CD,又MO⊥平面BCD.取O为原点,直线OC,BO,OM为x轴,y轴,z轴,建立空间直角坐标系如图所示.OB=OM=3,则各点坐标分别为C(1,0,0),M(0,0,3),B(0,-3,0),5A(0,-3,2 3).→→CM=(-1,0,3),CA=(-1,-3,2 3).设平面ACM的法向量为n1=(x,y,z),由Error!得Error!解得x=3z,y=z,取z=1,得n1=( 3,1,1).又平面BCD的法向量为n2=(0,0,1),n1·n2 1所以cos〈n 1,n2〉==.|n1|·|n2| 52 5设所求二面角为θ,则sinθ=.5b20.解析(1)f′(x)=1+2ax+(x>0),x又f(x)过点P(1,0),且在点P处的切线斜率为2,∴Error!即Error!解得a=-1,b=3.(2)由(1)知,f(x)=x-x2+3ln x,其定义域为(0,+∞),∴g(x)=2-x-x2+3ln x,x>0.3 x-1 2x+3则g′(x)=-1-2x+=-.x x当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.所以g(x)在(0,1)上单调递增,在(1,+∞)上单调递减.∴g(x)的最大值为g(1)=0,g(x)没有最小值.21.解析(1)设A,B两点坐标为A(x1,y1),B(x2,y2),AB中点P的坐标为P(x0,y0).由题意,得M(1,0),直线l的方程为y=x-1.由Error!得x2-6x+1=0.则x1+x2=6,x1x2=1,x1+x2且x0==3,y0=x0-1=2.2故圆心为P(3,2),直径|AB|=2|x1-x2|=2· x1+x2 2-4x1x2=8.∴以AB为直径的圆的方程为(x-3)2+(y-2)2=16.1 1(2)若存在这样的点M,使得+恒为定值,设直线l的方程为x=ky+m.|AM|2 |BM|2由Error!得y2-4ky-4m=0.于是y1+y2=4k,y1y2=-4m.又∵|AM|2=y21(1+k2),|BM|2=y2(1+k2),61 1 1 1 1∴+=( +)·y21 2|AM|2 |BM|2 y1+k2mk2+1 y1+y2 2-2y1y2 1 2=·=·.1+k2 y1y2 2 1+k2 m2m∵要与k无关,只需=1,即m=2,21 1 1进而+=.|AM|2 |BM|2 41 1 1∴存在定点M(2,0),不论直线l绕点M如何转动,+恒为定值.|AM|2 |BM|2 422.解析(1)由于函数f(x)的定义域为(0,+∞),1 x+1 x-1当a=-1时,f′(x)=x-=,x x令f′(x)=0,得x=1或x=-1(舍去).当x∈(0,1)时,函数f(x)单调递减,当x∈(1,+∞)时,函数f(x)单调递增,1所以f(x)在x=1处取得极小值,极小值为.2(2)当a=1时,易知函数f(x)在[1,e]上为增函数,1 1 所以f(x)min=f(1)=,f(x)max=f(e)=e2+1.2 21 2(3)证明:设F(x)=f(x)-g(x)=x2+ln x-x3,2 31 1-x 1+x+2x2则F′(x)=x+-2x2=,x x1 当x>1时,F′(x)<0,故F(x)在区间(1,+∞)上是减函数.又因为F(1)=-<0,所以在6区间[1,+∞)上F(x)<0恒成立,即f(x)<g(x)恒成立.因此,当a=1时,在区间[1,+∞)上函数f(x)的图像在函数g(x)图像的下方.7。
内蒙古包头市第一中学2017-2018学年高二下学期期末考试数学(理)试题 Word版含答案
包头一中2017-2018学年度第二学期期末考试高二年级理科数学试题一、选择题(共12小题,每小题5分,共60分.在每小题给出的四个选项中只有一项是最符合题目要求的,请将正确答案的序号填涂到答题卡上.)1.若曲线错误!未找到引用源。
在点错误!未找到引用源。
处的切线方程是错误!未找到引用源。
,则()(A)错误!未找到引用源。
(B) 错误!未找到引用源。
(C) 错误!未找到引用源。
(D) 错误!未找到引用源。
2.设复数错误!未找到引用源。
满足错误!未找到引用源。
则错误!未找到引用源。
=()(A)错误!未找到引用源。
(B)错误!未找到引用源。
(C)错误!未找到引用源。
(D)错误!未找到引用源。
3.已知随机变量错误!未找到引用源。
服从正态分布错误!未找到引用源。
,错误!未找到引用源。
,则错误!未找到引用源。
()A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D,错误!未找到引用源。
4.为了考察两个变量x和y之间的线性相关性,甲、乙两个同学各自独立地作10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2.已知在两个人的试验中发现对变量x的观测数据的平均值恰好相等,都为s,对变量y的观测数据的平均值也恰好相等,都为t.那么下列说法正确的是( )l2相交,但是交点未必是点(s,t)A.直线lB.直线l1和l2有交点(s,t)C.直线l1和l2由于斜率相等,所以必定平行D.直线l1和l2必定重合5.将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中,若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有()(A)12种(B) 18种(C) 36种(D) 54种6.在一组样本数据(x1,y1),(x2,y2),…,(x n,y n)(n≥2,x1,x2,…,x n不全相等)的散点图上,则这组样本数据中,若所有样本点(x i,y i)(i=1,2,…,n)都在直线错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
包头一中高二年级2016-2017年度第一学期期末考试
文科数学试卷
一.选择题(本大题共12小题,每小题5分,共计60分,在每小题给出的四个选项中,只有一项
是符合题目要求的.)
1.设有一个直线回归方程为2 1.5y x =-,则变量x 增加一个单位时 ( )
A .y 平均增加2个单位
B .y 平均增加1.5个单位
C .y 平均减少2个单位
D .y 平均减少1.5个单位
2.下列双曲线中,渐近线方程为2y x =±的是 ( )
A .2
212y x -= B .2
212x y -= C . 2214x y -= D . 2214
y x -= 3.从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是
( ) A. 12 B. 13 C.14 D.16 4.一组数据X 1,X 2,…,X n 的平均数是3,方差是5,则数据3X 1+2,3X 2+2,…,3X n +2 的平均
数和方差分别是 ( )
A. 11 ,45
B. 5 ,45
C. 3 ,5
D. 5 ,15
5.已知点A (1,3),B (4,-1),则与向量AB 同方向的单位向量为 ( )
A.⎝ ⎛⎭⎪⎫35,-45
B.⎝ ⎛⎭⎪⎫45,-35
C.⎝ ⎛⎭⎪⎫-35,45
D.⎝ ⎛⎭
⎪⎫-45,35 6.设,x y R ∈,则"0"x y >>是"1"x y
>的 ( ) A. 充分不必要条件 B.必要不充分条件
C. 充要条件
D.既不充分也不必要条件
7.()sin f x ax x =+是R 上的增函数,则实数a 的取值范围是 ( )
A .(,1]-∞
B .(,1)-∞
C .(1,)+∞
D .[1,)+∞
8.已知向量a =(k,3),b =(1,4),c =(2,1),且(2a -3b )⊥c ,则实数k 等于( )
A .-92
B .0
C .3 D.152
9.已知||4a =,||5b =,||21a b +=,则a b ∙= ( )
A .-8
B .-10
C .10
D .8
10.若直线l 过抛物线x y 42=的焦点,与抛物线交于A 、B 两点,且线段AB 中点的横坐标为2,则弦AB 的长为 ( )
A .2 B.4 C.6 D. 8
11.已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算机随机产生0到9之间取整数的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中,再以三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
807 966 191 925 271 932 812 458 569 683
489 257 394 027 556 488 730 113 537 741
根据以上数据,估计该运动员三次投篮恰好有两次命中的概率为 ( )
A. 0.20
B. 0.25
C. 0.30
D. 0.35
12.抛物线22(0)y px p =>的焦点为F ,直线l 过焦点F 且斜率为2,与抛物线交于A 、B (其中A 在第一象限)两点,(,0)2
p M -,则tan AMF ∠= ( ) A
B. 3
C.3
D.
二、填空题(本大题共4小题,每小题5分,共计20分)
13.命题“2,210x R x x ∀∈-+<”的否定形式为 .
14. 已知正方形ABCD 的边长为2,E 为CD 的中点,则AE AC =________.
15.已知双曲线
C 的离心率为12,F F ,点A 在曲线C 上,若12||3||F A F A =,则21cos _______AF F ∠=
16.已知32()31f x ax x =+-存在唯一的零点0x ,且00x <,则实数a 的取值范围是________。
