全等三角形经典例题整理课件.doc
12.1全等三角形(上课用)PPT精品文档

16
1.△ABO≌△DCO,试写 出这两个三角形中相等的 边和相等的角。
A
D
O
B
C
解:∵△ABO≌△DCO ∴AB=DC,BO=CO,AO=DO ∠A=∠ D,∠ABO=∠DCO,
∠AOB=∠DOC
课本4页练习
17
△ABC≌△DBF,找出图中的对应边,对应角.
B D
C
答:∠B的对应角是( ∠B ) ∠C的对应角是( ∠F )
B’
C’
△ABC≌ △A’ B’C’
对应边:相互重合的边。 对应角:相互重合的角。
(这里,符号“≌”表示 全等,读作“全等于”)
注意:对应顶点写在对应的位置上.
全等三角形的特征:
全等三角形的对应边、对应角分别相等.
全等三角形的识别:
边、角分别对应相等的两个三角形全等.
9
全等三角形的性质:对应边相等,对应角相等
26
27
11.1 全等三角形
1
观
同一张底片冲洗出来的两张照片
察
形状和大小有什么特征?
2
观察下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
能够完全重合的两个图形称为全等形.
3
及时反馈
观察下面两组图形,它们是不是全等形?
只有形状
(1)
相同
只有大小 相同
(2)
全等形的 形状和 大小 都相同
4
能够完全重合的两个三角形,叫做 全等三角形.
相等的式子。
BE
答:∠A=∠EDF,
∠B=∠E, ∠BCA=∠EFD A D
F C
规律1:全等三角形中,对应边所对的角是对应角
12-1 全等三角形 课件(共26张PPT)

知识梳理
例题 1:如图所示,△ ≌△ ,指出所有的对应边和对应角.
AB与DC,AC与DB,BC与CB是对应边;
∠ABC与∠DCB,∠A与∠D,∠ACB与∠DBC是对应角。
【解答】(1)已知△ABC≌△DCB,故公共边BC和CB
是对应边,它们所对的∠A和∠D是对应角,最短边
【结论】本题考查了全等三角形的性质及
比较角的大小,解题的关键是找到两全等
三角形的对应角、对应边.
80°
.
知识梳理
例题4:如图,将长方形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF = 60°,那么∠DAE= 15°
角
例题5:如图,△ ABC ≌△ ADE,则AB = AD ,∠E =
知识梳理
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合
的边叫做对应边,重合的角叫做对应角。例如,图中的△ 和△
全等,记作△ ≌ ,其中点和点,点和点,点
和点是对应顶点;和,和,和是对应边;∠和
∠,∠和∠,∠和∠是对应角.
∠BAE = 130°,∠BAD = 50°,则∠BAC=
。
80°
∠C
,若
知识梳理
例题6:如图,已知△ ABC ≌△ EBF,AB ⊥ CE,ED ⊥ AC,∠A = 24°,
则:(1)AB =
EB ,BC = BF ,∠C = 66 °,∠EFB = 66 °;
(2)若AB = 5cm,BC = 3cm,则AF = 2cm 。
AB和DC是对应边,它们所对的∠ACB和∠DBC是对应
角,余下的一对边和一对角分别是对应边和对应角.
(2)根据书写规范可知点A和点D,点B和点C,点C
全等三角形的基本模型复习(正式经典)PPT课件

2021
10
模型四 一线三垂直型 模型解读:基本图形如下:此类图形 通常告诉 BD⊥DE,AB⊥AC, CE⊥DE,那么一定有∠B=∠CAE.(常用到同(等)角的余角相等)
2021
11
4.如图,AD⊥AB于A,BE⊥AB于B,点C在AB上,且CD⊥CE,CD=CE. 求证:AB=AD+BE.
2021
2021
3
1.如图,AB∥DE,AC∥DF,BE=CF,求证:AB=DE.
2021
4
解:∵BE=CF,∴BE+EC=CF+EC,即 BC=EF, ∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F, 在△ABC 与△DEF 中 ∠B=∠DEF, BC=EF, ∠ACB=∠F, ∴△ABC≌△DEF(ASA) ∴AB=DE
2021
8
3.如图,AB⊥CD于B,CF交AB于E,CE=AD,BE=BD.求证:CF⊥AD.
2021
9
解:∵AB⊥CD,∴∠EBC=∠DBA=90°.在 Rt△CEB 与 Rt△ADB 中 CBEE= =ABDD,,∴Rt△CEB≌Rt△ADB(HL),∴∠C=∠A,又∵∠C+∠CEB= 90°,∠CEB=∠AEF,∴∠A+∠AEF=90°,∴CF⊥AD
12
解:∵AD⊥AB,BE⊥AB,CD⊥CE,∴∠DAC=∠CBE=∠DCE=90 °,又∵∠DCB=∠D+∠DAC=∠DCE+∠ECB,∴∠D=∠ECB.在△ACD
与△BEC 中,∠∠AD==∠∠BEC,B,∴△ACD≌△BEC(AAS),∴AC=BE,CB= DC=CE,
AD,∴AB=AC+CB=AD+BE
2021
5
模型二 翻折型 模型解读:将原图形沿着某一条直线折叠后,直线两边的部分能够完全重 合,这两个三角形称之为翻折型全等三角形.此类图形中要注意其隐含条件, 即公共边或公共角相等.
完整版-全等三角形总复习PPT教学课件

AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
2024/3/9
29
6. 如图A、B、C在一直线上,△ABD,△BCE都是等边 三角形,AE交BD于F,DC交BE于G,求证:BF=BG。
AB
=
DB
∠ABE = ∠ DBC
BE=BC ∴△ABE≌△DBC(SAS)
D
C
2
1
A
B
思路3: 已知一边一角(边与角相邻):
找夹这个角的另一边
AD=CB (SAS)
找夹这条边的另一角
∠ACD=∠CAB(ASA)
找边的对角
∠D=∠(B AAS)
15
如图,已知∠B= ∠E,要识别△ABC≌ △AED,需 要添加的一个条件是--------------
A
D
C
E
思路4:
找夹边
AB=AE (ASA)
∴ △ADC ≌ △EDB
D
C
∴ AC = EB
在△ABE中,AE < AB+BE=AB+AC
E
即 2AD < AB+AC
∴ AD 1 (AB AC) 2
2024/3/9
35
12.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA, CD过点E,则AB与AC+BD相等吗?请说明理由。
C A
∵ QD⊥OA,QE⊥OB,QD=QE(已知). ∴点Q在∠AOB的平分线上.(到角的两边的距
离相等的点在角的平分线上)
2024/3/9
10
2.如图, △ABC的角平分线BM,CN相交于点P, 求证:点P到三边AB、BC、CA的距离相等
全等三角形的讲义整理讲义

全等三角形专题一 全等三角形的性质【知识点1】能够完全重合的两个三角形叫做全等三角形。
(两个三角形全等是指两个三角形的大小和形状完全一样,与他们的位置没有关系。
)【知识点2】两个三角形重合在一起,重合的顶点叫做对应顶点;重合的边叫做 对应边;重合的角叫做对应角。
【例题1】如图,已知图中的两个三角形全等,填空:(1)AB 与 是对应边,BC 与 是对应边, CA 与 是对应边;(2)∠A 与 是对应角,∠ABC 与 是对应角, ∠BAC 与 是对应角【方法总结】在两个全等三角形中找对应边和对应角的方法。
(1)有公共边的,公 共边一定是对应边;(2)有公共角的,公共角一定是对应角;(3)有对顶角的,对顶角是对应角;(4)在两个全等三角形中,最长的边对最长的边,最短的边对最短的边,最大的角对最大的角,最小的角对最小的角。
【练习1】 如图,图中有两对三角形全等,填空: (1)△BOD ≌ ; (2)△ACD ≌ .【知识点3】 全等三角形的对应边相等,对应角相等。
(由定义还可知道,全等三角形的周长相等,面积相等,对应边上的中线和高相DABCOE ABCD等,对应角的角平分线相等)【例题2】 (海南省中考卷第5题) 已知图2中的两个三角形全等,则∠α度数是( )A.72°B.60°C.58°D.50°【例题3】(清远)如图,若111ABC A B C △≌△,且11040A B ∠=∠=°,°,则1C ∠= .【练习2】 如图,ACB A C B '''△≌△,BCB ∠'=30°,则ACA '∠的度数为( )A 20° B.30° C .35° D .40°【练习3】如图,△ABD 绕着点B 沿顺时针方向旋转90°到△EBC , 且∠ABD=90°。
初二数学《全等三角形完整复习》PPT课件

A O E C F
B
D
8、两块含30°角的相同直角三角板,按如图位置摆放,使得两条 相等的直角边AC、C1A1共线 (1)图中有多少对全等三角形?并将它们写出来; (2)选择其中一对(⊿ABC≌⊿A1B1C1除外)进行证明。
B1 O E F B
(1)3对
(2)⊿AEC1≌⊿A1FC
A
C1
C
A1
AC1=A1C
)
延长AD到E,使得AD=DE ⊿ABD≌⊿ECD AB=CE AE-AC<CE<AE+AC 8-5<CE<8+5 3<CE<13
B
A
D
C
E
(三角形中两边之和大于第三 边,两边之差小于第三边)
(2)当⊿DEF旋转至如图③位置时,(1)中的结论还成立吗?请说 A 明理由; A
C A E
O B
F B(E) C
⊿ABF≌⊿DBC
∠AFD=∠DCA
(3)在图③中,连接BO、AD,探索BO、AD之间有怎样的位置关系, A 并证明。
1 3
连接BO,AD
由(2)知:⊿ABC≌⊿DBF ∴∠1=∠2,AB=DB,AC=DF ∴∠3=∠4 AO=DO ∴AO=DO BA=BD BO=BO
B(E)
F C
O
4
2
D
⊿BAO≌⊿BDO ∠ABO=∠DBO
三角形全等
完整复习
知识点
三角形全等的证题思路:
找夹角 SAS 已知两边找直角 HL 找另一边 SSS 边为角的对边 找任一角 AAS 找夹角的另一边 SAS 已知一边一角 边为角的邻边找夹角的另一角 ASA 找边的对角 AAS
《全等三角形的判定》PPT习题课件(多种类型的解法)
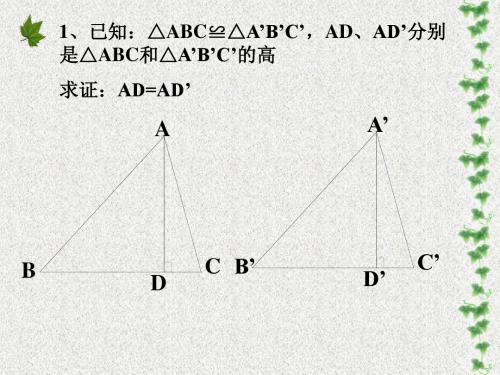
求证:AD=AD’
A
A’
B
D
C B’
D’
C’
2、已知:△ABC≌△A’B’C’,AD、AD’分别 是△ABC和△A’B’C’的角平分线
求证:AD=AD’
A
A’
B
D
C
B’
D’
C’
3、已知:△ABC≌△A’B’C’,AD、AD’分别 是△ABC和△A’B’C’的中线
求证:AD=AD’
A
A’
B
D
C B’
D’
C’
A
A’
C
B
C’
B’
如图,已知:Rt△ABC和Rt△A’B’C’,判断下列 条件能否使这两个三角形全等?并说明理由。
1、AB=A’B’,∠A=∠A’ 2、AB=A’B’,∠B=∠B’ 3、BC=B’C’,∠A=∠A’ 4、AC=A’C’,∠B=∠B’ 5、AC=A’C’,BC=B’C’
求证:AD=BC
A B
D
C
证明:延长DA、CB交于点E
已知:在△ABC中,AE=AF,CF⊥AB于F, BE⊥AC于E,BE、CF相交于O
求证: (1)FB=EC (2)FO=EO (3)AO⊥BC
F O B C E A
已知:AP∥BC,∠PAB的平分线与∠CBA的 平分线相交于E,CE的连线交AP于D
思考: AC=A’C’ AB=A’B’
已知:AC平分∠ DAB,E为AC上一点, AD=AB.
求证: ∠CDE=∠CBE .
D E
A
C
多种方法证明
B
已知:AB∥CD,AB=CD,O为AC的中点, 过O的直线交DA、BC的延长线于E、F
勾股定理全等三角形典型例题

勾股定理全等三角形典型例题哎呀,今天我们来聊聊一个老生常谈的话题——勾股定理。
说到勾股定理,很多人脑海中是不是就浮现出那幅经典的直角三角形图案?没错,就是那种底边和高边形成一个“L”型,斜边就像是那条梦想中的直线,正好把这两条边连起来。
是不是觉得一切都那么简单明了?这个小小的定理可谓是数学界的明星,真的是有一套哦。
勾股定理告诉我们,在一个直角三角形里,斜边的平方等于另外两边的平方之和。
简简单单几句话,却蕴含了无穷的奥秘。
大家想想,生活中有多少地方都能看到它的身影呢?比如说,你在测量一块地的时候,难免会用到它。
只要你把地的宽和高测出来,轻轻一算,斜边的长度就出来了!这简直就是“算得一手好账”的节奏啊。
有些同学可能会问,这个定理跟全等三角形有什么关系呢?嘿,这可是个大亮点!想象一下,两个三角形如果是全等的,咱们就可以说它们的边长、角度都是一模一样的。
用勾股定理来验证全等三角形,简直像是在做魔术!就像两个人手握相同的甜筒,吃起来的味道那叫一个美妙。
只要你知道其中一个三角形的边长,就能迅速推算出另一个三角形的边长,简直就是小聪明的表现。
那我们来看看几个典型例题。
比如说,有一个三角形,底边是3厘米,高边是4厘米,你觉得斜边是多少呢?没错,咱们先用勾股定理一算,斜边就等于√(3² + 4²) =√(9 + 16) = √25 = 5厘米。
听上去是不是特别简单?这就是勾股定理的魅力所在,瞬间让复杂的事情变得简单明了。
再来一个,想象一下,一个小孩在公园里跑,忽然停下来,看到前面有个直角三角形的石头。
他好奇地问,石头的底边和高边分别是6厘米和8厘米,那斜边又是多长呢?没问题,照样用勾股定理,一算就知道斜边是10厘米!这小孩肯定会惊呼:“哇,原来我可以用这个公式来解决问题,真是太神奇了!”生活中可不止有这些简单的例子。
勾股定理在建筑、设计、航海等各个领域都得到了广泛的应用。
想想那些高楼大厦,建筑师们可得用这个定理来确保结构的稳定性,避免“东倒西歪”的情况出现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的典型习题
一、全等在特殊图形中的运用
1、如图,等边△ABC中,D、E分别是AB、CA上的动点,AD=CE,试求
∠DFB的度数.
C
E
F
A D B
2、如下图所示,等边△ABC中,D、E、F是AB、BC、CA上动点,AD=
BE=CF,试判断△DEF的形状.
C
F
E
A D B
3、如图,△ABC和△ADE都是等边三角形,线段BE、CD相交于点H,线
段BE、AC相交于点G,线段BE、CD相交于点H.请你解决以下问题:
(1) 试说明BE=CD的理由;
(2) 试求BE和CD的夹角∠FHE的度数E
C
H
G
F
B
A D
1
Ex1、如下图所示,△ABC和△ADE都是等边三角形,且点B、A、D在同一
直线上,AC、BE相交于点G,AE、CD相交于点F,试说明AG=AF的理由.
E
C
G
F
B
A D
Ex2、如图,四边形ABCD与BEFG都是正方形,AG、CE相交于点O,AG、BC相交于点M,BG、CE相交于点N,请你猜测AG与CE的关系(数量关系
和位置关系)并说明理由.
D C
G
O
M
N
A B F
E
4、△ABC是等腰直角三角形,AB=AC,∠BAC=90°,∠B=∠C=45°,D是底边BC
的中点,DE⊥DF,试用两种不同的方法说明BE、CF、EF为边长的三角形是直角三角形。
A
E
F
B D C
2
二.证明全等常用方法(截长发或补短法)
5、如图所示,在△ABC中,∠ABC=2∠C,∠BAC的平分线交BC于点D.请
你试说明AB+BD=AC的理由.
A
B C
D
Ex1,∠C+∠D=180°,∠1=∠2,∠3=∠4.试用截长法说明AD+BC=AB.
C
E
D
1 4
23
A B Ex2、五边形ABCDE中,AB=AE,∠BAC+∠DAE=∠CAD,∠ABC+∠AED =180°,连结AC,AD.请你用补短法说明BC+DE=CD.(也可用截长法,
A 自己考虑)
E
B
D
C
6、如图,正方形ABCD中,E是AB上的点,F是BC上的点,且∠EDF=
45°.请你试用补短法说明AE+CF=EF.
D C
3
F
Ex1.、如图所示, 在△ ABC 中,边B C 在直线m 上,△ABC 外的四边形 ACDE 和四边形 ABFG 均为正方形, DN ⊥m 于 N ,FM ⊥m 于 M .请你说明 BC = FM +DN 的理由. (分别用截长法和补短法 ) (连结GE ,你能说明 S △ ABC =S
△AGE
吗?)
E
G
D
F
A
m
M
B
C
N
三.全等在探究题中的运用
7、数学课上,张老师出示了问题:如图1,四边形 ABCD 是正方形,点 E 是边
BC 的中点.
AEF 90 ,且 EF 交正方形外角
DCG 的平行线C F 于点 F ,求证:
AE= E F .经过思考,小明展示了一种正确的解题思路:取 AB 的中点 M ,连接 ME ,则
AM = E C ,易证△ AME ≌ △ ECF ,所以 AE
EF .
(1)请你写出说明△ ABC ≌ △ ECF 的理由; 在此基础上,同学们作了进一步的研究:
( 2)小颖提出:如图2,如果把“点 E 是边B C 的中点”改为“点 E 是边B C 上(除
B ,
C 外)的任意一点” ,其它条件不变,那么结论
“ AE=EF ”仍然成立,你认为小颖的 观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
( 3)小华提出:如图3,点 E 是 BC 的延长线上(除 C 点外)的任意一点,其他条件
不变,结论
“ AE=EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;
如果不正确,请说明理由.
F
A D
A
D
A
D
F
F
B E 图1
C G B E 图2 4 C G B 图3 C E
G
)
图(第2题
Ex1、如图1,一等腰直角三角尺GEF(∠EGF=90°, ∠GEF=∠GFE=45°,GE=GF)的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺
GEF 绕斜边EF 的中点O(点O 也是BD 中点)按顺时针方向旋转.
(1)如图2,当EF 与AB 相交于点M,GF 与BD 相交于点N 时,通过观察或测量BM,FN 的长度,猜想FN,BM 相等吗?并说明理由;
(2)若三角尺GEF 旋转到如图 3 所示的位置时,线段FE 的延长线与AB 的延长线相交
于点M,线段BD 的延长线与GF 的延长线相交于点N,此时,(1)中的猜想还成立吗?
请说明理由.
N
F
D( F )
C
D C
D C
F
N
O
O O
G
E
A( G ) B( E )
图1 A M B
E
图2
A
G
图3
B M
5
Ex2.在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度而
C
C
得到新位置图形的一种变换.
G
E
E
活动一:如图1,在Rt△ABC中,D为斜边
F
AB上的一点,AD=2,BD=1,且四边形DECF
A B
A B
是正方形,求阴影部分的面积.
D D
图1 图2
小明运用图形旋转的方法,将△DBF绕点D逆时针旋转90°,得到△DGE(如图 2 所示),
一眼就看出这题的答案,请你写出阴影部分的面积:.
活动二:如图3,在四边形ABCD中,AB=AD,∠BAD=∠C=90°,BC=5,C D=3,过点 A 作
AE⊥BC,垂足为点E,求AE的长.
小明仍运用图形旋转的方法,将△ABE绕点A逆时针旋转90°,得到△AD(G如图 4 所示),
则①四边形AECG是怎样的特殊四边形?答:.②AE的长是.
活动三:如图5,在四边形ABCD中,AB⊥AD,C D⊥AD,将BC按逆时针方向绕点 B 旋转
90°得到线段BE,连接AE.若AB=2,
D C=4,求△ABE的面积. A A G E
D
D
A B
B E 图 C
6 B C
图4
E
D 图5 C
四.动点问题中的全等、
8 如图,已知△ABC 中,AB AC 20 厘米,BC=16厘米,点 D 为AB 的中点.
(1)如果点P在线段 B C上以 6 厘米/ 秒的速度由B点向C点运动,同时,点Q在线段CA 上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,
请说明理由;
②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使
△BPD 与△CQP 全等?
A
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动
D 速度从点B同时出发,都逆时针沿△ABC 三边运动,求经过多
Q 长时间点P与点Q第一次在△ABC 的哪条边上相遇?
B
C
P
7
8。
