电路理论基础课后习题答案 陈希有主编 第五章
电路分析基础习题第五章答案

第5章选择题1、在关联参考方向下,R 、L 、C 三个元件的伏安关系可分别如( D )表示。
A. dtdi C u d i L u u Gu i C C tL L L R R =+==⎰ ,)(1)0( ,0ττ B. dtdi C u d i L u Ri u C C tL L R R =+==⎰ ,)(1 )0(u , 0L ττC. ⎰+===tC C C L L R R d i C u u dt di L u Gi u 0)(1)0( , ,ττ D. ⎰+===tC C C L L R R d i C u u dt di Lu Ri u 0)(1)0( , ,ττ 2、一阶电路的零输入响应是指( D )。
A. 电容电压V 0)0(≠-C u 或电感电压V 0)0(≠-L u , 且电路有外加激励作用B. 电容电流A 0)0(≠-C i 或电感电压V 0)0(≠-L u , 且电路无外加激励作用C. 电容电流A 0)0(≠-C i 或电感电压A 0)0(≠-L i , 且电路有外加激励作用D. 电容电压V 0)0(≠-C u 或电感电流A 0)0(≠-L i , 且电路无外加激励作用 3、若1C 、2C 两电容并联,则其等效电容C =( A )。
A. 21C C +B.2121C C C C +C.2121C C C C +D. 21C C4、已知电路如图 所示,电路原已稳定,开关闭合后电容电压的初始值)0(+C u 等 于( A )。
A. V 2-B. V 2C. V 6D. V 85、已知V 15)(τtC e t u -=,当s 2=t 时V 6=C u ,电路的时间常数τ等于( B )。
A. s 458.0B. s 18.2C. s 2.0D. s 1.06、二阶RLC 串联电路,当C L R 2____时,电路为欠阻尼情况;当CL R 2____时, 电路为临界阻尼情况( B )。
电路理论基础(哈尔滨工业大学陈希有第3版) 第1章-第5章

a 电位: 任选一点p作为电位参考点,电路中某点与参考点之间的电压称为该点的电 位,用 表示。有了电位的概念,两点之间的电压便等于这两点的电位之差。
uab Ec dl
a A
(a)
a A
(b)
u ab
u ba
A
(c)
a uA
b
b
b
电压参考方向的表示法
一个元件上的电压和电流的参考方向取成相同的,并称为关联参考方向。
2 基尔霍夫电流定律
基尔霍夫电流定律(Kirchhoff's Current Law,简称KCL)表述为:在集中 参数电路中,任一时刻流出(或流入)任一节点的支路电流代数和等于零, 即
i
k
0
( ik 表示第 k 条支路电流)
规定: ik 参考方向为流出节点时, ik 前面 取“+”号; 流入节点时, ik 前面取“-”号。
i1
A
i2
1、在集中参数电路中,任一时刻流出(或流入) 任一闭合边界 S 的支路电流代数和等于零。
KCL的其它表述
2、任一时刻,流出任一节点(或闭合边界)电 流的代数和等于流入该节点电流的代数和。
根据右图,列写KCL方程 1)基本表述方 式——对节点
3 i3
④
S
4 i4 i6 7 i7 ③
节点① :
① u1 1
u
电压降
= u电压升
6 ③ u6 l1 5 u5 l2 7 u7 ⑤ 基尔霍夫电压定律示例
u2
l3 ②
2
说明:平面电路网孔上的KVL方程是一组独立方程。设电路有b个支路n个节 点,可以证明:平面电路的网孔数即独立KVL方程的个数等于b-(n-1)。当然 取网孔列方程只是获得独立KVL方程的充分条件,而不是必要条件。
电路理论-第5章习题答案

5-1 电感和电容元件的电压u 、电流i 参考方向如题5-1图所示,已知 u C =10sin(10t +30o )V ,i L =5cos(10t -30o )A 。
试电流i C 和电压u L 。
+-5μF u C i C (a)-+i L u L 10mH(b)题 5-1 图解 应用元件VCR 关系时,要注意电压u 和电流i 的关联参考方向。
(a) 664C ()5105101010cos(1030)510cos(1030)A cdu i t t t dt ---=-⨯=-⨯⨯⨯+︒=-⨯+︒ (b) 33()10101010510(sin(1030))0.5cos(1060)V L L diu t t t dt--=⨯=⨯⨯⨯--︒=+︒5-2 已知一正弦电流的波形如题5-2图所示。
(1) 试求此正弦电流的幅值、周期、频率、角频率和初相; (2) 写出此正弦电流的瞬时函数表达式。
题 5-2 图解 (1) 由题5-2图所示正弦电流波,可以看出 12A,1m I T ms == 从而,有 21/1Hz,2000/f T k rad s Tπωπ==== 令()12cos()mA i i t t ωϕ=+当cos()0i t ωϕ+=时,由题5-2图看出 0.4t ms = 所以,得 310i ϕπ=-(2) 电流的瞬时函数表达式为 3()12cos(2000)mA 10i t t ππ=-5-4 写出对应于下列各相量的瞬时函数表达式,设角频率为ω。
12(1) 200120 V;(2)3000 V;(3)250(60)mA U U I =∠=∠=∠-o o o &&& 解 列写正弦量的瞬时函数表达式时要注意幅值、频率、初相位三个要素及两种表达式的对应关系。
(1) 1()120)V u t t ω=+︒(2) 2()V u t t ω=(3) ()60)mA i t t ω=-︒5-6 在题5-6图所示电路中,若电流i (t )=cos314t A ,试求电压()R u t 、()L u t 、()C u t 和()u t ,并绘出波形图和相量图。
电路理论基础第四版孙立山陈希有主编第5章习题答案详解

教材习题5答案部分(p151)答案略答案负载各相阻抗化为星形联接为设A相电源相电压为,A相负载线电流与电源相电流相等由三角形联接得相电流与线电流关系得即负载相电流为。
答案解:电路联接关系如图(a)所示。
负载断开时电源的输出线电压等于图中相电压的倍。
下面计算相电压。
设负载A相电压为,对于感性负载,由,得,则采用单相分析法,如图(b)所示。
电源相电压为当负载断开时,电源输出电压为答案略答案略答案略答案解:设电源为星形联接,电源A相电压相量为则电源线电压分别为,,。
(1)设电路联接如图(a)所示,化为单相计算,如图(b)所示。
因为负载为星形联接,所以负载相电压,,又因为,相电流电压、电流相量图如图(c)所示。
(2) C相断线时,,电源线电压降落在AB相上。
如图(d)所示。
(3) C相负载短路时,如图(e)所示。
,答案解:(1)电路模型如图(a)所示。
图题负载相电流负载线电流(2)设A相负载断路,如图(b)所示。
由图(b)可见,,B、C相负载因相电压不变,均为电源线电压,故电流(3)设端线A断路,如图(c)所示。
由图(c)可见答案解:电路如图所示:图题因为三相负载平均功率等于每相负载平均功率的3倍,所以答案解:星形接法时,三角形接法时负载每相承受电压为380V,是星形接法时的倍。
根据功率与电压的平方成正比关系可知,三角形联接时负载的平均功率是星形联接的3倍。
即解:由已知功率因数,可求得星形和三角形负载的阻抗角分别为:,方法一:因为负载端线电压所以星形负载相电流为星形负载阻抗三角形负载相电流为三角形负载阻抗将三角形联接等效成星形联接,设负载阻抗为,化为单相分析法,则电路如图 (b)所示。
设V,,A由KVL方程得,电源相电压为则电源线电压为V方法二:负载总平均功率负载总无功功率负载总功率因数因为负载线电流电源发出平均功率为无功功率为电源视在功率为答案略答案解:设电源电压则设负载为星形联接,如图(b)所示。
阻抗角为,则A相负载电流滞后电压的角度为,滞后的角度为,即功率表的读数由对称三相负载无功功率的计算公式得。
大学电工电子基础习题参考答案:第5章习题习题参考答案

第五章习题参考答案5.1 题5.1的图所示的是三相四线制电路,电源线电压l U =380V 。
三个电阻性负载接成星形,其电阻为1R =11Ω,2R =3R =22Ω。
(1)试求负载相电压、相电流及中性线电流,并作出它们的相量图;(2)如无中性线,求负载相电压及中性点电压;(3)如无中性线,当L1相短路时求各相电压和电流,并作出它们的相量图;(4)如无中性线,当L3相断路时求另外两相的电压和电流;(5)在(3),(4)中如有中性线,则又如何?1L 2L 3L N题5.1的图解: ○1各相负载两端电压都等于电源相电压,其值为:V V U U l P22033803===。
各负载相电流分别为:()()AI I I I I I A R UI A R U I A R U I N P P P 1030cos 30cos 30sin 30sin 10,10,202232132332211=︒-︒++︒-︒-=======相量图如图(b )所示。
○2因为三相电源对称,而三相负载不对称时,由于无中性线,将使电源和负载中点之间的电位差不为零,而产生中性点位移。
设 V U U ︒∠=011 ()()()V V U U U V V U U U VV U U U V V R R R R U R U R U U NN N N N N N N ︒∠=︒∠-︒∠=-=︒-∠=︒∠-︒-∠=-=︒∠=︒∠-︒∠=-=︒∠=++︒∠+︒-∠+︒∠=++++=131252055120220131252055120220016505502200552212211112212022022120220110220111''''3'32'21'1321332211○3若无中性线,1L 相短路,此时电路如图(c )所示,此时1L 相的相电压01=U ,2L 相、3L 相的相电压分别等于2L 、1L 之间、3L 、1L 之间的线电压,所以有:V U U V U U ︒∠==︒-∠=-=150380,150380313122 各相电流为:()()A A I I IV R U I VR U I ︒∠=︒∠+︒-∠-=+-=︒∠==︒-∠==0301503.171503.171503.171503.17321333222 相量图如图(d )所示○4若无中线,3L 相断路,电路如图(e )所示,1L ,2L 两相成了串联电路: V V R I UV V R I U AA R R U I I ︒∠=⨯︒∠=∙=︒∠=⨯︒∠=∙=︒∠=+︒∠=+==3025322305.113012711305.11305.11221130380222111211221 ○5当有中性线,1L 相短路或3L 相断路,其他相电压、电流均保持不变。
电路理论课后答案,带步骤
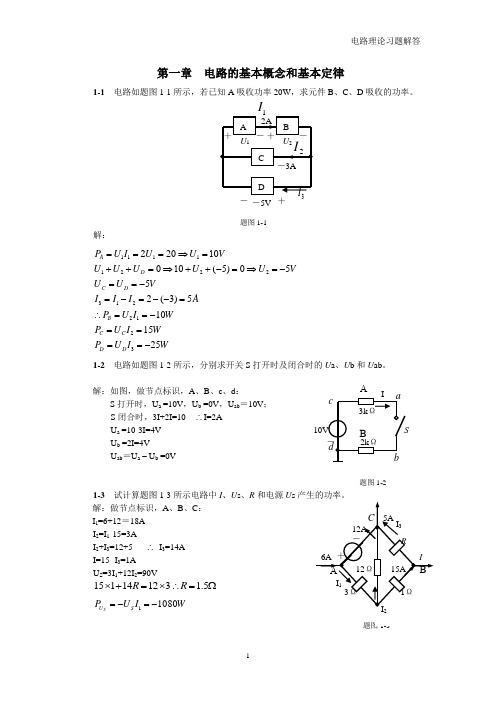
解:(1)该电路有三个网孔。设网孔电流分别为 、 ,
参考方向如图3-4所示。并设受控源两端电压为U。
(2)列写网孔方程:
辅助方程为:
联立求解得:
U= V
所以: mW
3-5电路如题图3-5所示,试用网孔分析法求电流 和电压 。
题图3-5题图3-5(b)
解:(1)将原图中20A电流源与2 电阻并联部分等效为40V电压源与2 电阻串联,如图3-5(b)所示。
(2)列写节点方程:
整理得:
求解得: V
V
所以: V
3-7电路如题图3-7所示,①试用节点分析法列写电路的节点方程;②该电路能否用网孔分析法分析?为什么?
题图3-7题图3-7(b)
①解:
(1)将原图中的 电压源与 串联部分等效为 电流源与 并联。
且 。如图3-7(b)所示。
(2)该电路有5个节点,以节点5为参考点,节点电压分别设为: 、 、 ,
Ua=10-3I=4V
Ub=2I=4V
Uab=Ua–Ub=0V
题图1-2
1-3试计算题图1-3所示电路中I、Us、R和电源Us产生的功率。
解:做节点标识,A、B、C:
I1=6+12=18A
I2=I1-15=3A
I2+I3=12+5 I3=14A
I=15- I3=1A
US=3I1+12I2=90V
题图1-3
2-15题图2-15所示电路,试问当电阻R等于何值时,可获得最大功率,最大功率等于多少?
题图2-15图2-15(b)
解:先将a,b与R断开,则
得:
所以:共戴维南等效电路为图(a)所示
所以:当 时,获得最大功率
电路理论基础课后习题答案 陈希有主编 第十到十四章
答案10.1解:0<t时,电容处于开路,故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得:V 20)0()0(==-+C C u u换路后一瞬间,两电阻为串联,总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得:m A5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解:0<t时电容处于开路,电感处于短路,Ω3电阻与Ω6电阻相并联,所以A3)363685(V45)0(=Ω+⨯++=-i,A 2)0(366)0(=⨯+=--i i LV 24)0(8)0(=⨯=--i u C由换路定律得:V24)0()0(==-+C C u u ,A 2)0()0(==-+L L i i由KVL 得开关电压:V8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解:0<t 时电容处于开路,0=i ,受控源源电压04=i ,所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C>t 时,求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R 时间常数s 1.0i ==C R τ0>t 后电路为零输入响应,故电容电压为:V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为:V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4 解:<t 时电感处于短路,故A 3A 9363)0(=⨯+=-L i ,由换路定律得: A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ,时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应,故电感电流为 A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t Lti Lt u --==)0(>t Ω3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为:W3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解:由换路定律得0)0()0(==-+L L i i ,达到稳态时电感处于短路,故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
电路理论基础(陈希有)课后题答案
答案11.1解: (1)2020001e 1e 1e e )()(-ssdt s stdt t t s F stst stst =-=+-==∞-∞-∞-∞----⎰⎰ε (2)20)(20)(00)(1e)(1e 1e e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s dts s t dt t t s F ts t s st st t答案11.2解:)/1(//1)(1τττ+=+-=s s A s A s A s F 由拉氏变换的微分、线性和积分性质得:)/1(/)()()/(]/)([)()]0()([)(22111112ττ+++=++=++-=-s s A c bs as s F s c b as s s F c s bF f s sF a s F答案11.3解:设25)}({)(11+==s t f s F L ,52)}({)(22+==s t f L s F 则)5)(2(10)()(21++=s s s F s F)(1t f 与)(2t f 的卷积为)e e (310]e 31[e 10e e 10e 2e 5)(*)(520350350)(5221t t t tt ttt d d t f t f --------=⨯==⨯=⎰⎰ξξξξξξ对上式取拉氏变换得:)5)(2(10)5121(310)}(*)({21++=+-+=s s s s t f t f L 由此验证)()()}(*)({2121s F s F t f t f =L 。
答案11.4解:(a)6512)(2+++=s s s s F 3221+++=s A s A3|31221-=++=-=s s s A , 3|31221-=++=-=s s s A 所以t t s s t f 321e 5e 3}3523{)(---+-=+++-=L(b))2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A 所以t t t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ (c)623)(2++=s s s F 22)5()1(5)5/3(++⨯=s 查表得)5sin(e 53)(t t f t-=答案11.5解:(a) 由运算电路(略)求得端口等效运算阻抗为:11262241)3/(142)]3/(14[21)(22i ++++=++++=s s ss s s s s s Z , 112611430)(22++++=s s s s s Z i (b) 画出运算电路如图11.5(c)所示U )(2s __在端口加电流,列写节点电压方程如下⎩⎨⎧-==++-=-+)2()]()([3)(3)()]5.0/(11[)()1()()()()1(2122s U s U s U s U s s U s I s U s U s由式(2)解得)(144)(2s U s ss U ⨯+=代入式(1)得)()()1221(s I s U s ss =+-+所以1212)(2i +++=s s s s Y答案11.6解:运算电路如图11.6(b)所示。
《电路理论基础》(第三版陈希有)习题答案
答案2.1解:本题练习分流、分压公式。
设电压、电流参考方向如图所示。
(a) 由分流公式得:23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得:3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解:电路等效如图(b)所示。
20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得:220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯=再对图(a)使用分压公式得:13==30V 1+3U U ⨯答案2.3解:设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1)由已知条件得如下联立方程:32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω再将3R 代入(1)式得210k 3R =Ω答案2.4解:由并联电路分流公式,得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解:首先将电路化简成图(b)。
图 题2.5120Ω(a)(b)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-=再由图(a)得321201A 360120I I =⨯=+由KVL 得,3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解:(a )设R 和r 为1级,则图题2.6(a)为2级再加x R 。
电路理论基础第四版孙立山陈希有主编答案
电路理论基础第四版孙立山陈希有主编答案1. 引言《电路理论基础(第四版)》是一本系统介绍电路基本理论和基本分析方法的教材。
本文档是《电路理论基础(第四版)》的答案,提供了教材中习题的解答。
通过这些答案,学生可以检验自己对电路理论的理解,巩固知识点,提高解题能力。
2. 电路理论基础答案2.1 第一章网孔法和节点法的基本概念2.1.1 习题1-1a)略b)略c)略…2.2 第二章电阻网络的基本性质2.2.1 习题2-1a)略b)略c)略…2.3 第三章基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)2.3.1 习题3-1a)略b)略c)略…2.4 第四章电流和电压的计算2.4.1 习题4-1a)略b)略c)略…2.5 第五章电阻串联与并联的简化2.5.1 习题5-1a)略b)略c)略…2.6 第六章电流分压和电压分流2.6.1 习题6-1a)略b)略c)略…2.7 第七章网格分析法2.7.1 习题7-1a)略b)略c)略…2.8 第八章直流电路的戴维南定理2.8.1 习题8-1a)略b)略c)略…2.9 第九章交流电路频率特性2.9.1 习题9-1a)略b)略c)略…2.10 第十章交流电阻、电感和电容的阻抗2.10.1 习题10-1a)略b)略c)略…2.11 第十一章交流电路的功率2.11.1 习题11-1a)略b)略c)略…2.12 第十二章交流电路分析方法2.12.1 习题12-1a)略b)略c)略…3. 结语本文档提供了《电路理论基础(第四版)》的答案,涵盖教材中的习题。
通过阅读答案,学生可以巩固和检验自己的理论知识和解题能力。
希望本答案对学生学习电路理论有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WL
1 2
LI L 2
1 2
0.2H (0.12A)2
1.44103V
答案 5.12
解:由互感元件的端口特性方程,得
0.2
diS dt
0.08
di2 dt
u1
(1)
0.1
di2
dt
0.08 diS dt
uS
(2)
将式(2)乘以 0.8,再与式(1)相减,从而消去 di2 得 dt
u1
L1
di1 dt
L3
d(i1 dt
i2 )
u2
L2
di2 dt
L3
d(i1 i2 ) dt
整理得
u1
(L1
L3 )
di1 dt
L3
di2 dt
u2
L3
di1 dt
(L2
L3 )
di2 dt
(1)
对图(b)电路,
u1
La
di1 dt
u1
u1
Lb
di1 dt
nu2
i1
1 n
i2
i1 i1 i1
的电压。
答案 5.3 解:电阻消耗的电能为
WR
0 pR (t)d
i2Rd
0
(
Ie
t RC
)2
Rd
0.5R2I 2C
0
电容最终储存的电荷为
qC () qC (0) 0 id
t
CuC (0) 0 (Ie RC )d RCI
电容最终储能为
WC
qC2 () 2C
0.5R 2 I
2C
u1
uS
(0.2
0.064)
diS dt
(3)
将 uS 及 iS 代入式(3)得
u1 (8te20t 0.816e10t )V
答案 5.13 解:由消去互感法可将图(a)电路等效成图(b)。
L1 M
M
+ i1
u Leq
-
i2 +
L2 M u2
-
i3
(b)
由电感的串、并联等效得:
Leq (L1 M ) (L2 M )∥M
(1 4n
n)u1
1 n 1 4n
解得
n 0.5
答案 5.17
解:图(a)电路,从 ab 端看过去,等效电阻 Req n2 8 48 32 电路等效
成图(b)所示。
a 10 i1
iS
30
32
b (b)
因为理想变压器为非能元件,图(b)电路中 32电阻消耗的功率与图(a)电路 8 电 阻消耗的功率相同。由分流公式得
u2
u1 n
解得
C n
d(u1 ) n dt
C n2
du1 dt
Ceq
du1 dt
Ceq
C n2
i(t) 1
0 u( )d 1
1
1.5d
1
t
(1)d
L
L0
L1
i(0) 1.5 1 (1 t) 0.5 0.5
(3)
6 2t
令 i(t) 0 ,得
t 3s
(2) t 4s 时,由式(3)得此时电流
i(4s)=6A-2 4A=-2A
故磁链及磁场能分别为
(4s) Li(4s) 0.5(2)Wb=-1Wb
u1
L1
d dt
(i1
i2
/
n)
L1
di1 dt
L1L2
di2 dt
(3)
由理想变压器特性还可得
1 u2 n u1
L1 L2
di1 dt
L2
di2 dt
方程(3)和(4)刚好是图(a)全耦合电感( M
等效。
(4) L1L2 )的特性方程,故图(a)、(b)相互
答案 5.15
解:证明:
对图(a)电路,列其端口特性方程
W (4s) 1 Li2 (4s) 1J 2
答案 5.9 解:由题意,电感两端电压为
u L diS dt
将电流源的电流表达式代入式(1),得
(1)
u L d iS dt
0 (2 6t)e3t
t0 t 0
(2)
由式(2)可知,当 t 0 时,电感上电压为 0,其绝对值仍为 0;当 t 0 时,令 du 0 , dt
uS u i 1 (2t 4)V
答案 5.7 解:设各元件电压、电流取关联参考方向,由 KVL 得
uR uC uL uL 0
即
iC R uC
(1 ) L diC dt
0
(1)
将
iC
C
duC dt
2e2tA
代入(1)式得
2e2t e2t (1 ) 4e2t 0
解得
0.75
答案 5.8 解:(1)由图(b)可知电感上电压的表达式为
1.5V 0 t 1s
u(t)
1V
t 1s
(1)
电感元件上电流与电压的关系可表示为
i(t) 1
t
u( )d
L
(2)
在 0 t 1s 内,电流在1.5V 电压作用下继续增加,只有在 t 1s 后,由于电压改
变极性,电流方开始减小,并在某一时刻达到零值。在 t 1s 后电流变化规律为
U3
U
2
C4 C3 C4
40 0.05 0.2 0.05
8V ,U4
U2
U3
32V
则各电容储存的电场能量为
WC1
1 2
C1U12
20J ,WC2
1 2
C2U
2 2
48J
,
WC3
1 2
C3U32
6.4J
, WC4
1 2
C4U
2 4
25.6J
注释:只有对联接到电路前均未充电的电容,才可按电容分压来计算串联电容
ui R
, uo
uC
故
uo
1 C
t
iC ( )d
1 C
0
iC
(
)d
1 C
t 0
iC
(
)d
1 C
t
0 iC ( )d uC (0)
1 RC
t
0 ui ( )d uC (0)
答案 5.5 解:取电容、电感上的电压、电流为关联参考方向,如图所示。由运算放大器
输入端口电流为零的条件可知
1A 2s t 3s
i(t) 的变化规律如图(d)所示。
i/A 1
o
1
2
3
t/s
-1
图 (d)
(2)在关联参考方向下,电容上电压与电流关系又可表示为
u(t) 1
t
i( )d
C
图(c)所示电流可描述为
1A 0 t 1s
i(t)
0 1s<t 0.5A 2s
2s t
3s
0 t 3s
i1
iS
(10
30 32 30)
0.25e10t A
则
p8 i12 32 (0.25e10tA)2 32 2e20t W
答案 5.18 解:求等效电容就是要求 i1 与 u1 的关系。为此可按如下步骤进行,其中要涉及
理想变压器和电容元件方程:
i1
1 n
i2
i2
C
du2 dt
1 (C du2 ) n dt
由此可知
WR WC
注释:当通过电阻给电容充电时,无论电阻为何值( R 0 ),被电阻损耗的能量 总等于电容最终储存的能量。
答案 5.4 解: 取电容、电感上的电压、电流为关联参考方向,如图所示。由运算放大器
输入端口电流为零的条件可知
iC iR
又由运算放大器输入端口电压为零的条件可知Leabharlann iRuR R即
(12 18t)e3t 0
可求得电感上电压的极值。由上式解得
t 1s 将 t 1s 代入式(2),
u(1s) 2e2V
因为该电流源表达式为分段连续函数,求最大值应该考虑间断点的函数值,即
limu(t) 2V , lim u(t) 0
t 0
t
比较极值点和间断点的函数值,可得
u 2V max
已知 q(0) 0.5C
由 q Cu
可求得 u(0) q(0) 0.5V C
当 t 3.5s 时,电容上的电压取决于电流在此刻前的历史,即
u(t) 1
0 i( )d 1
1
1Ad
1
2
0d
1
3
(0.5A)d
1
3.5
0d
C
C0
C1
C2
C3
u(0) (1 0 0.5 0)V
i Ψ 4A L
答案 5.11 解:图题电路为直流电路,电容相当于开路,电感相当于短路。
由分流公式得电感电流
IL
0.3A 12 (12 10 8)
0.12A
电容电压
UC IL 8 0.96V 电容储存的能量为
WC
1 2
CUC
2
1 2
0.5F (0.96V)2
0.2304J
电感储存的能量为
Lb
L32 L2 L3
n L3
L2 L3
答案 5.16 解:由变压器特性方程可知
u1 nu2
i1
1 n
i2
1 n
( u2 ) 16
(1)
对左回路应用 KVL 方程
u1 4i1 u1 4i1 nu2
(2)
将式(1)代入式(2),考虑到 u2 u1 ,可得
