全国自学考试信号与系统试题
全国2002年4月自考信号与系统试题参考答案
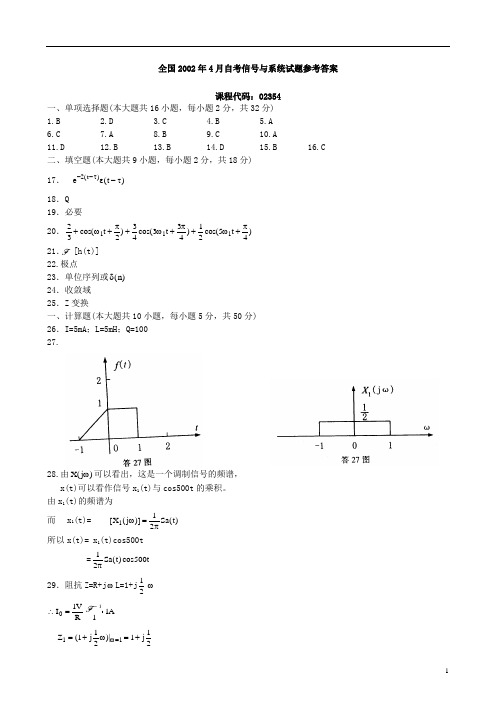
全国2002年4月自考信号与系统试题参考答案课程代码:02354一、单项选择题(本大题共16小题,每小题2分,共32分)1.B2.D3.C4.B5.A6.C7.A8.B9.C 10.A11.D 12.B 13.B 14.D 15.B 16.C二、填空题(本大题共9小题,每小题2分,共18分)17.t t ---2()()τετ18.Q19.必要20.232343341254111++++++cos()cos()cos()ωπωπωπt t t21. [h(t)]22.极点23.单位序列或δ()n24.收敛域25.Z 变换一、计算题(本大题共10小题,每小题5分,共50分)26.I=5mA ;L=5mH ;Q=10027.28.由X j ()ω可以看出,这是一个调制信号的频谱,x(t)可以看作信号x 1(t)与cos500t 的乘积。
由x 1(t)的频谱为而 x 1(t)= [()]()X j Sa t 112ωπ=所以x(t)= x 1(t)cos500t =12500πSa t t ()cos29.阻抗Z=R+j ωL=1+j 12ω∴===I V R A 01111Z j j 11112112=+=+=()|ωω∴=+=-∙I j j m 1111245112()则P I R W 002111==⋅=P I R W m 1122121245114125==+⋅=()()∴=+=+=P P P W 0112575302112212111222222.()()()()()()()()f t t t t t t t F s S S e S ee S s s s =---+--=-+=----εεε或用微分性质做:''=--+-=-+∴=-+=------f t t t t S F s e e F s e e S e S s s ss s ()()()()()()()δδδ2121212122222231.u c ()010-=伏开关到“2”之后的复频域模型为答31图 ()()()()10sc R I s u s E s c ++=-I s sss s s ()=-+=-+=-+110111011111 ∴=--i t t e t t ()()()δε1132.令y t dx t dt ()()=,则y(t)如图所示则Y j ()ω= [()]()sin()y t Sa ==ωωω222由于Y j ()|ωω==≠010,根据时域积分特性X j Y j j Y ()()()()ωωωπδω=+0 =⋅+⋅⋅2211sin()()ωωωπδωj =+222sin()()ωωπδωj33.F z z z z z z zz ()()()=+-=++-41121212f n n n n n n ()()()()([()]())=+-+-221211εεε或34121212122002.()()*()()()()()|()()()()y t f t h t e e t d e e d t e e t e e t f t t t t t t t ==⋅-=⋅⋅=-=-----∞+∞------⎰⎰ττττετετττεεε或y t h t f t e e e t d e e d t e e t e e t f t t tt t t t()()*()()()()()()()()()==⋅-=⋅=-=-----∞+∞----⎰⎰12121211222022ττττετττεεε35.方程两边拉氏变换得:[()()()][()()]()s Y s sy y sy s y Y s s 2003201253--'+-+=+---∴=+++++++Y s s s s s s s ()53321232321222y t f ()= [()()()][]()53112543112s s s e e e t t t+++=-+---εy t x ()= [()()][]()s s s e e t t t+++=-+--32112212εy t y t y t e e e t f x t tt ()()()[]()=+=-++---66123ε。
历年全国高等教育自学考试信号与系统考题

全国2001年10月系号与系统考试试题一、单项选择题(本大题共16小题,每小题2分,共32分)1.积分⎰+--0)()2(dt t t δ等于( )A.)(2t δ-B.)(2t ε-C. )2(-t εD. )2(2-t δ2. 已知系统微分方程为)(2)(2)(t f t y dt t dy =+,若)()(,34)0(t t f y ε==+,解得全响应为0,131)(2≥+=-te t y ,则全响应中t e 234-为( )A.零输入响应分量B.零状态响应分量C.自由响应分量D.强迫响应分量 3. 系统结构框图如下,该系统单位冲激响应)(t h 的表达式为( )A.⎰∞---td T x x T τττ)]()([1 B. )()(T t x t x --C. ⎰∞---td T T ττδτδ)]()([1 D. )()(T t t --δδ 4. 信号)(),(21t f t f 波形如图所示,设)()()(21t f t f t f *=则)0(f 为( ) A.0 B.1C.2D.3111001-)(1t f )(2t f tt5. 已知信号)(t f 如图所示,则其傅里叶变换为( )A.)21(-ωa S B. )21(+ωa SC. )1(-ωa SD. )1(+ωa S6. 已知)()]([ωj F t f =ℑ 则信号)52(-t f 的傅里叶变换为( )A. ωω5)2(21j e j F -B. ωω5)2(j ej F - C. 25)2(ωωj e j F - D. 25)2(21ωωjej F -7. 已知信号)(t f 的傅里叶变换)()()(00ωωεωωεω--+=j F 则)(t f 为( )A.)(00t S a ωπω B.)2(00tS a ωπω C. )(200t S a ωω D. )2(200tS a ωω8. 已知一线性时不变系统,当输入)()()(3t e et x t tε--+=时,其零状态响应是)()22()(4t e e t y t t ε---=,则该系统的频率响应为( )A.)521524(2++-++ωωωωj j j j B. )521524(2+++++ωωωωj j j jC. )521524(++-++ωωωωj j j j D. )521524(+++++ωωωωj j j j9. 信号)()(2t et f tε-=的拉氏变换及收敛域为( )A.2)Re(,21>+s s B. 2)Re(,21->+s s C.2)Re(,21>-s s D. 2)Re(,21->-s s10.信号)2()(2(sin )(0--=t t t f εω的拉氏变换为( )A.s e s s 2202-+ω B. se s s 222ω+ C. s e s 22020ωω+ D. s e s 22020-+ωω 11. 已知某系统的系统函数为)(s H ,唯一决定该系统单位冲激响应)(t h 函数形式的是( )A. )(s H 的零点B. )(s H 的极点C.系统的输入信号D.系统的输入信号与)(s H 的极点12. 若)()(),()(221t t f t et f tεε==-则)()(21t f t f *的拉氏变换为()A.⎪⎭⎫ ⎝⎛+-21121s s B. ⎪⎭⎫⎝⎛++-21121s s C.⎪⎭⎫ ⎝⎛++21121s s D. ⎪⎭⎫ ⎝⎛++-21141s s 13. 序列)]5()2([2cos)(---=n n nn f εεπ的正确图形是( )14. 已知序列)(1n x 和)(2n x 如图(a )所示,则卷积)()()(21n x n x n y *=的图形为图(b)中的( )15. 图(b)中与图(a)所示系统等价的系统是( )16.在下列表达式中:① )()()(z F z Y z H =②)()()(n f n h n y f *= ③=)(z H )]([n h ④=)(n y f )]()([z F z H离散系统的系统函数的正确表达式为( )A.①②③④B.①③C.②④D.④ 二、填空题(本大题共9小题,每小题2分,共18分)不写解答过程,将正确的答案写在每小题的空格内。
浙江省1月高等教育自学考试信号与系统试题及答案解析历年试卷及答案解析

浙江省2018年1月高等教育自学考试信号与系统试题课程代码:02354一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题3分,共30分)1.设:如图—1所示信号。
则:信号f(t)的数学表示式为( )。
(A)f(t)=t ε(t)-t ε(t-1)(B)f(t)=t ε(t)-(t-1)ε(t-1)(C)f(t)=(1-t)ε(t)-(t-1)ε(t-1)(D)f(t)=(1+t)ε(t)-(t+1)ε(t+1)2.设:两信号f 1(t)和f 2(t)如图—2。
则:f 1(t)与f 2(t)间变换关系为( )。
(A)f 2(t)=f 1(21t+3) (B)f 2(t)=f 1(3+2t)(C)f 2(t)=f 1(5+2t) (D)f 2(t)=f 1(5+21t)3.已知:f(t)=SgN(t)的傅里叶变换为F(j ω)=ωj 2, 则:F 1(j ω)=j πSgN(ω)的傅里叶反变换f 1(t)为( )。
(A)f 1(t)=t1 (B)f 1(t)=-t2 (C)f 1(t)=-t1 (D)f 1(t)=t2 4.周期性非正弦连续时间信号的频谱,其特点为( )。
(A)频谱是连续的,收敛的(B)频谱是离散的,谐波的,周期的(C)频谱是离散的,谐波的,收敛的(D)频谱是连续的,周期的5.设:二端口网络N 可用A 参数矩阵{a ij }表示,其出端与入端特性阻抗为Z c2、Z c1,后接负载Z L ,电源•U s 的频率为ωs ,内阻抗为Z s 。
则:特性阻抗Z c1、Z c2仅与( )有关。
(A){a ij },Z L(B){a ij },Z L ,Z s(C){a ij },ωs , *U s(D){a ij }6.设:f(t)↔F(j ω) 则:f 1(t)=f(at+b) ↔F 1(j ω)为( )(A)F 1(j ω)=aF(j a ω)e -jb ω (B)F 1(j ω)=a 1F(j a ω)e -jb ω (C)F 1(j ω)= a 1F(j a ω)ω-a bj e (D)F 1(j ω)=aF(j aω)ω-a b j e 7.已知某一线性时不变系统对信号X(t)的零状态响应为4dt)2t (dX -,则该系统函数H(S)=( )。
浙江7月高等教育自学考试信号与系统试题及答案解析

浙江省2018年7月高等教育自学考试信号与系统试题课程代码:02354一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题3分,共30分)1. 设:如图—1所示信号。
则:信号f(t)的数学表示式为( )。
(A)f(t)=t ε(t)-(t-1)ε(t-1)(B)f(t)=(1-t)ε(t)-(t-1)ε(t-1)(C)f(t)=t ε(t)-t ε(t-1)(D)f(t)=(t-1)ε(t)-(t-1)ε(t-1)2. 设:信号f 1(t)和f 2(t)如图—2。
则:f 1(t)与f 2(t)间关系为( )。
(A)f 2(t)=f 1(t+1)ε(t)(B)f 2(t)=f 1(t+1)ε(t+1)(C)f 2(t)=f 1(t)ε(t-1)(D)f 2(t)=f 1(t-1)ε(t-1)3. 设:g τ(t)↔G τ(j ω)则:g τ(t)t j 0e ω ↔G ω0τ(j ω)为( )(A)G ω0τ(j ω)=0ωτSa [2)(0τω-ω] (B)G ω0τ(j ω)=τSa [2)(0τω+ω] (C)G ω0τ(j ω)=τSa [2)(0τω-ω] (D)G ω0τ(j ω)= 0ωτSa [2)(0τω+ω] 4. 设:一非正弦周期电源为:u s (t)=u S0+u S1+u S2+…+u S N 其中:U S0为直流电压(V), u sn =U snm cosn ω0t n=1,2,…N ,U snm 为幅值(V)则:电源的平均功率P T 为( )。
(A)P T =∑=N 0n 21 U snm (B)P T =21U 2S0+∑=N 1n U snm(C)P T =U 2S0+∑=N 1n 21U snm (D)P T =U 2S0+∑=N 1n U 2snm 5. 设:一并联RLC 谐振回路,电感存在电阻R ,负载电阻R L ,信号源U&s 与内阻R s 串接,分别与回路并联连接。
(完整word版)信号与系统考试试题及答案,推荐文档

长沙理工大学拟题纸课程编号 1拟题教研室(或老师)签名 教研室主任签名 符号说明:)sgn(t 为符号函数,)(t δ为单位冲击信号,)(k δ为单位脉冲序列,)(t ε为单位阶跃信号,)(k ε为单位阶跃序列。
一、填空(共30分,每小题3分)1. 已知)()4()(2t t t f ε+=,求_______)("=t f 。
)('4)(2)("t t t f δε+2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ,求______)()(=*k h k f 。
}4,6,8,3,4,10,3{)()(-=*k h k f3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。
0)(t j Kej H ωω-=4. 若)(t f 最高角频率为m ω,则对)4(t f 取样的最大间隔是______。
m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。
101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =,试判断该系统是否为线性时不变系统______。
故系统为线性时变系统。
7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ,求该信号的傅立叶变换)(ωj F =______。
故傅立叶变换)(ωj F 不存在。
8. 已知一离散时间系统的系统函数2121)(---+=z z z H ,判断该系统是否稳定______。
故系统不稳定。
9. =+-+⎰∞∞-dt t t t )1()2(2δ______。
310. 已知一信号频谱可写为)(,)()(3ωωωωA e A j F j -=是一实偶函数,试问)(t f 有何种对称性______。
关于t=3的偶对称的实信号。
二、计算题(共50分,每小题10分)1. 已知连续时间系统的单位冲激响应)(t h 与激励信号)(t f 的波形如图A-1所示,试由时域求解该系 统的零状态响应)(t y ,画出)(t y 的波形。
浙江7月自考信号与系统试题及答案解析

1浙江省2018年7月高等教育自学考试信号与系统试题课程代码:02354一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题2分,共20分) 1.dtd[e -t ε(t)]=( )。
A.-e -t ε(t) B.δ(t) C.-e -t ε(t)+δ(t) D.-e -t ε(t)-δ(t) 2.已知y(n)=(-2)n ε(n)+δ(n)+ε(n)中,稳态响应分量为( )。
A.(-2)n ε(n) B.δ(n) C.ε(n) D.δ(n)+ε(n) 3.⎰∞-∞δ'(t)e-j ωtdt=( )。
A.j ωB.2πδ(ω)C.2πδ(t)D.jt4.已知F(s)=)3S 2(S 4+,则f(t)=( )。
A.34 (1-e t 23)B. 34(1-e t 23-)C. 34 (1+e t 23)D. 34(1+e t 23-)5.已知F(Z)=5.0Z 5.1Z Z 22+- (|Z|>1),则f(n)=( )。
A.(2-0.5n )B.(2-0.5 n )ε(n)C.0.5 nD.0.5 n ε(n) 6.f(t)=δ'(t),则F(j ω)=( )。
A.1 B.j ω C.-j ω D.δ(ω) 7.A 参数中的α12具有的单位是( )。
A.电压单位 B.电流单位 C.阻抗单位 D.导纳单位 8.RLC 串联谐振电路的通频带宽度,即BW=( )。
A.LR B.CR C.LC1D.LC9.瞬态响应分量应是( )。
A.零输入响应的全部 B.零状态响应的全部 C.全部的零输入响应和部分的零状态响应 D.全部的零输入响应和全部的零状态的响应 10.图1所示的理想变压器,其H 参数为( )。
A. ⎥⎦⎤⎢⎣⎡-0nn 0B. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-0n 1n 10 C. ⎥⎦⎤⎢⎣⎡-0n n 0D.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-0n1n 10 二、填空题(每空2分,共20分)21.系统方程为y(n)+3y(n-1)=0,其齐次解形式为_________。
7月全国信号与系统自考试题及答案解析
1全国2018年7月高等教育自学考试信号与系统试题课程代码:02354一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题2分,共20分)1. RLC 串联谐振电路的谐振频率f 0为( )。
A. LC 1 B. 02ωπ C. 2πLC D. LC 21π2. 已知系统的激励f(n)=n ε(n),单位序列响应h(n)=δ(n-2),则系统的零状态响应为( )。
A. (n-2)ε(n-2)B. n ε(n-2)C. (n-2)ε(n)D. n ε(n)3. 序列f(n)=δ(n)-81δ(n-3)的Z 变换为( )。
A. 1-81Z 3 B. 1-21Z 3 C. 1-21Z -3 D. 1-81Z -3 4. 题4图所示波形可表示为( )。
A. f(t)=ε(t)+ε(t-1)+ε(t-2)-ε(t-3)B. f(t)=ε(t)+ε(t+1)+ε(t+2)-3ε(t)C. f(t)=ε(t)+ε(t-1)+ε(t-2)-3ε(t-3)D. f(t)=2ε(t+1)+ε(t-1)-ε(t-2)5. 描述某线性时不变系统的微分方程为y ′(t)+3y(t)=f(t)。
已知y(0+)=23, f(t)=3ε(t), 则21e -3t ε(t)为系统的( )。
A. 零输入响应B. 零状态响应C. 自由响应D. 强迫响应 6. 已知某系统,当输入f(t)=e -2t ε(t)时的零状态响应y f (t)=e -t ε(t),则系统的冲激响应h(t)的表达式为( )。
A. δ(t)+e t ε(t)B. δ(t)+e t ε(-t)C. δ(t)+e -t ε(t)D. δ(t)+e -t ε(-t)7. 已知信号f(t)如题7图所示,则其傅里叶变换为( )。
2A. Sa(ω)+Sa(2ω)B. 2Sa(ω)+4Sa(2ω)C. Sa(ω)+2Sa(2ω)D. 4Sa(ω)+2Sa(2ω)8. 某系统的微分方程为y ′(t)+3y(t)=2f ′(t)则系统的阶跃响应g(t)应为( )。
(最新整理)7月全国自考信号与系统试题及答案解析
1全国2018年7月自学考试信号与系统试题课程代码:02354一、单项选择题(本大题共12小题,每小题2分,共24分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列参数的量纲仅为导纳的是( ) A.Z 参数 B.Y 参数 C.A 参数D.H 参数2.双口网络可以用四种不同的方程和参数来描述,这些参数仅决定于( ) A.信号源的方向或极性 B.信号源的幅度 C.负载的大小D.信号源的频率3.若连续LTI 系统的初始状态不为零,当激励信号增大一倍时,其零状态响应( ) A.增大一倍B.保持不变C.增大,但不能确定增大倍数D.增大两倍4.设f (t )为系统输入,y (t )为系统输出,则下列关系式中为线性时不变系统的是( ) A.y (t )=x (t )f (t ) B.y (t )=tf (t ) C.)()()()(22t f t f dt d t y t y dtd +=+D.y (t )=f (2t )5.式⎰∞∞-⎪⎭⎫⎝⎛-+6)sin (πδt t t dt 的值是( )A.6πB.6π-1 C.6π-21 D.6π+21 6.已知f (t )的傅里叶变换为F (j ω),y (t )=f ⎪⎭⎫⎝⎛+b a t ,其中a 、b 为常数,则Y (j ω)为( )A.|a |F (j ω)ωjab eB.|a |F (ja ω)ωjab e -C.||1a F (j aω)ωa b j e D.||1a F ⎪⎭⎫ ⎝⎛a j ωωa bj e -27.已知信号f (t )如题7图所示,其傅里叶变换为F (j ω),则F (0)为( ) A.2 B.π C.π21 D.48.信号t n ε(t )的拉普拉斯变换为( )A.1!+n Sn B.n S n !C.1!-n Sn D.1)!1(+-n S n9.已知拉普拉斯变换F (s )=)4(822+s s ,则原函数f (t )为( )A.[])()2sin(2t t t ε+B.[])()2sin(2t t t ε-C.[])()2cos(2t t t ε+D.[])()2cos(2t t t ε-10.已知某系统的系统函数H (s )=122++s s s,则该系统一定是( ) A.稳定系统 B.不稳定系统 C.临界稳定系统 D.不确定11.离散系统y (n )=∑=ni if 03(n -i )的单位序列响应h (n )是( )A.3δ(n )B.3n ε(n )C.3D.3ε(n )12.已知若f (n )的z 变换为F (z ),其收敛域为|z |>ρ0,则a -n f (n )的z 变换为( ) A.F (az ),|z |>||0a ρ B.F ,⎪⎭⎫⎝⎛a z |z |>|a |0ρC.F (-az ),|z |>||0a ρD. F ,⎪⎭⎫⎝⎛-a z |z |>|a |0ρ二、填空题(本大题共12小题,每小题2分,共24分)请在每小题的空格中填上正确答案,错填、不填均无分。
2020年7月全国自考信号与系统试卷及答案解析
全国自考2018年7月信号与系统试卷课程代码:02354一、单项选择题(本大题共12小题,每小题2分,共24分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.题1图所示二端口网络A参数中,a12为( )A.1B.ZC.0D.不存在2.RLC串联谐振电路,若串联谐振频率为f0,当输入信号频率f < f0时,此时电路性质为( )A.容性B.感性C.阻性D.无法测定3.原已充电到3V电压的电容,现通过强度为8δ(t)的冲激电流,则在冲激电流作用时刻,电容电压的跃变量为( )A.7VB.4VC.3VD.-4V4.信号f (6-3t)表示( )A.f (3t)左移6B.f (3t)左移2C.f (3t)右移6D.f (-3t)右移25.周期信号满足f (t)=-f (-t)时,其傅里叶级数展开式的结构特点是( )A.只有正弦项B.只有余弦项C.有直流分量D.正弦余弦项都有12 6.已知f (t)的傅里叶变换为F(j ω),则(t-a )f(t)的傅里叶变换为( ) A.)()(ω-ωωj aF d j dF B.)()(ω-ωω-j aF d j dFC.)()(ω-ωωj aF d j dF j D.)()(ω-ωω-j aF d j dF j7.信号ej2t δ′(t)的傅里叶变换为( )A.j(ω+2)B.2+j ωC.j(ω-2)D.j ω-28.已知系统的冲激响应h(t)=8e-3t ε(t),则系统函数H (s )为() A.S 8 B.38-SC.38+SD.S 39.因果系统的系统函数为H(s)=2322++S S ,则该系统是() A.稳定的 B.不稳定的C.临界稳定的D.不确定10.函数f (t)=δ(t-t0)的拉氏变换为( )A.1B.0st eC.)(e 0-st 0t t -εD.0-st e11.信号f (n-i),(i>0)表示为( )A.信号f (n)左移序iB.信号f (n)右移序iC.信号f (n)的翻转D.信号f (n)翻转再移序i12.序列an ε(n)的Z 变换为( )A.a Z -1B.a Z +1C.a Z Z -D.a Z Z+二、填空题(本大题共12小题,每小题2分,共24分)3 13.如题13图所示,二端口网络A 参数a11为__________。
全国自学考试信号与系统试题
中国自考人()——700门自考课程 永久免费、完整 在线学习 快快加入我们吧!全国2005年7月自学考试信号与系统试题课程代码:02354一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题3分,共30分)1. 设:如图—1所示信号f(t)。
则:f(t)的数学表示式为( )。
A.f(t)=t ε(t)-(t-1)ε(t-1)B.f(t)=(t-1)ε(t)-(1-t)ε(t-1)C.f(t)=t ε(t)-t ε(t-1)D.f(t)=(1-t)ε(t)-(t-1)ε(t-1)2. 设:两信号f 1(t)和f 2(t)如图—2。
则:f 1(t)和f 2(t)间的关系为( )。
A.f 2(t)=f 1(t-2)ε(t-2)B.f 2(t)=f 1(t+2)ε(t+2)C.f 2(t)=f 1(2-t)ε(2-t)D.f 2(t)=f 1(2-t)ε(t+2)3. 设:f(t)↔F(j ω)=ω+ωj a e 0t j ,则f(t)为( )。
A.f(t)=e )t t (a 0+-ε(t)B.f(t)=e )t t (a 0--ε(t+t 0)C.f(t)=e )t t (a 0--ε(t-t 0)D.f(t)=e )t t (a 0+-ε(t)4. 设:一有限时间区间上的连续时间信号,其频谱分布的区间是( )。
A.有限,连续区间B.无穷,连续区间C.有限,离散区间D.无穷,离散区间5. 设:一LC 串联谐振回路,电感有电阻R ,电源SU 的内阻为R S ,若电容C 上并接一负载电阻R L 。
要使回路有载品质因素Q L 提高,应使( )。
A.R s 、R L 、R 均加大B.R s 、R 减小,R L 加大C.R s 、R L 、R 均减小D.R s 、R L 加大,R 减小 6. 设:已知g τ(t)↔G τ(j ω)=τSa(2ωτ) 则:f(t)=g 2(t-1)↔F(j ω)为( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 中国自考人()——700门自考课程 永久免费、完整 在线学习 快快加入我们吧!
全国2004年4月高等教育自学考试
信号与系统试题
课程代码:02354
一、单项选择题(本大题共12小题,每小题2分,共24分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.已知信号f (t )的波形如题1图所示,则f (t )的表达式为( )
A .t ε(t)
B .(t-1)ε(t-1)
C .t ε(t-1)
D .2(t-1)ε(t-1)
2.积分式⎰-δ+δ++4
422)]dt -(t 2(t))[23(t t 的积分结果是( )
A .14
B .24
C .26
D .28
3.已知f(t)的波形如题3(a )图所示,则f (5-2t)的波形为( )
4.周期矩形脉冲的谱线间隔与( )
A .脉冲幅度有关
B .脉冲宽度有关
C .脉冲周期有关
D .周期和脉冲宽度有关
5.若矩形脉冲信号的宽度加宽,则它的频谱带宽( )
A .不变
B .变窄
C .变宽
D .与脉冲宽度无关
6.如果两个信号分别通过系统函数为H (j ω)的系统后,得到相同的响应,那么这两个信号(
) A .一定相同 B .一定不同
第 2 页
C .只能为零
D .可以不同
7.f(t)=)t (e t ε的拉氏变换为F (s )=
11-s ,且收敛域为( ) A .Re[s]>0
B .Re[s]<0
C .Re[s]>1
D .Re[s]<1 8.函数⎰-∞-δ=
2t dx )x ()t (f 的单边拉氏变换F (s )等于( ) A .1
B .s 1
C .e -2s
D .s 1e -2s 9.单边拉氏变换F (s )=2
2++-s e )
s (的原函数f(t)等于( ) A .e -2t ε(t-1)
B .e -2(t-1)ε(t-1)
C .e -2t ε(t-2)
D .e -2(t-2)ε(t-2) 10.已知f 1(n )=(
21)n ε(n),f 2(n )=ε(n )- ε(n -3),令y (n )=f 1(n )*f 2(n ),则当n=4时,y (n )为( ) A .
165 B .167 C .85 D .8
7 11.序列f(n)作用于一线性时不变离散时间系统,所得自由响应为y 1(n ),强迫响应为y 2(n ),零状态响应为y 3(n ),零输入响应为y 4(n )。
则该系统的系数函数H (z )为( )
12.若序列x (n )的Z 变换为X (z ),则(-0.5)n x (n )的Z 变换为( )
A .2X (2z )
B .2X(-2z)
C .X(2z)
D .X(-2z)
二、填空题(本大题共12小题,每小题2分,共24分)
请在每小题的空格中填上正确答案。
错填、不填均无分。
13.用同一组电阻、电感和电容,分别组成RLC 串联谐振电路和GCL 并联谐振电路,其谐振频率分别为ω1和ω2,则ω1与ω2的关系为_________________。
14.在RLC 串联谐振电路中,品质因数Q 值越大,则谐振电路的选择性越________________。
15.如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为_________。
16.如果一线性时不变系统的输入为f(t),零状态响应为y f (t )=2f (t-t 0),则该系统的单位冲激响应h(t)为_________________。
17.如果一线性时不变系统的单位冲激响应h(t)=ε(t),则当该系统的输入信号f (t )=t ε(t )时,其零状态响应为_________________。
第 3 页 18.如题18图所示周期脉冲信号的傅里叶级数的余弦项系数a n 为_________________。
19.已知x(t)的傅里叶变换为X (j ω),那么x (t-t 0)的傅里叶变换为_________________。
20.已知x 1(t)=δ(t-t 0),x 2(t)的频谱为π[δ(ω+ω0)+δ(ω-ω0)],且y(t)=x 1(t)*x 2(t),那么y(t 0)= _________________。
21.若已知f 1(t)的拉氏变换F 1(s )=)e (s
s --11,则f (t)=f 1(t)* f 1(t)的拉氏变换F (s )= _________________。
22.已知线性时不变系统的冲激响应为h(t)=(1-e -t )ε(t),则其系统函数H (s )=__________。
23.某线性时不变连续时间系统的模拟框图如题23图所示,初始状态为零,则描述该系统输入输出关系的S 域方程为_________________。
24.两线性时不变离散时间系统分别为S 1和S 2,初始状态均为零。
将激励信号f (n)先通过S 1再通过S 2,得到响应y 1(n);将激励信号f (n)先通过S 2再通过S 1,得到响应y 2(n)。
则y 1(n)与y 2(n)的关系为_________________。
三、计算题(本大题共10小题,题25-题32,每小题5分;题33-题34,每小题6分,共52分)
25.在题25图所示电路中,R =10Ω,L =0.01H ,C =1μF. 求电路谐振时的振荡频率ω0,品质因数Q ,以及通频带BW.(其中ω0和BW 的单位为rad/s )
26.已知一线性时不变系统的时域模拟框图如题26图所示。
(1)写出y (t)与f (t)之间的关系式;
(2)求该系统的单位冲激响应h(t)。
第 4 页
27.已知在题27图中,f(t)为输入电压,y (t)为输出电压,电路的时间常数RC =1.
(1)列出该电路的微分方程;
(2)求出该电路的单位冲激响应h(t)。
28.求抽样函数x(t)=Sa(2
t c ω)的傅里叶变换。
29.已知一线性时不变连续时间系统的单位冲激响应h(t)=δ(t-t 0),若x (t )的傅里叶变换为X(j ω)=
ω+j 11,用频域分析法求当输入为x(t)+x(t-1)时系统的零状态响应y f (t )。
30.已知一线性时不变系统的输入f(t)与输出y(t)的关系可用下列微分方程描述
)t (f )t (y dt )t (dy dt )t (y d =++232
2 若f(t)=2ε(t),用拉氏变换方法求该系统的零状态响应y f (t)。
31.已知一离散时间系统的差分方程为y(n)-2
1y(n-1)=f (n),试用Z 变换法 (1)求系统单位序列响应h(n);
(2)当系统的零状态响应为y(n)=3[(21)n -(3
1)n ]ε(n)时,求激励信号f (n)。
32.已知信号f 1(t)与f 2(t)如题32图所示,
(1)y(t)=f 1(t)* f 2(t),写出此卷积积分的一般表示公式;
(2)分段求出y(t)的表述式。
33.已知信号x(t)、y(t)的频谱X(j ω)、Y(j ω)如题图33(a)图及题33(b)图所示,求用x(t)表示的y(t)。
第 5 页
34.已知RLC 串联电路如题34图所示,其中R =2Ω,L =1H ,C =0.2F ,i(0-)=1A ,u c (0-)=1V ,输入信号u i (t)=ε(t)。
试画出该系统的复频域模型图,并计算出电流i(t)。
(提示:cos(ω0t) ←→ 202ω+s s
)
中国自考人()——改写昨日遗憾 创造美好明天!用科学方法牢记知识点顺利通过考试!。
