浙江工业大学材料力学第7章答案
材料力学第7章讲解
根据对材料的均匀、连续假设进一步推知，拉(压)杆横截面上的内力均匀分布，亦即横
衡方程： Fx 0
-FR + F2 F1 0
A
1 B 2C
FR=F2-F1=50-20=30kN
（2）计算各段轴力，研究AB段，假想
FR
1
2
F F N1
N2
F2
1-1截面将杆件分为两部分，取左端为研
A
究对象，画受力图，列方程：
1
2C
Fx 0 FN1-FR=0 FN1=FR=30kN
30kN
再研究BC段，假想2-2截面将杆件分为两部分， 取右端为研究对象，画受力图，列方程：
8
§7-2 轴向拉（压）时横截面上的内力
例题 试作此杆的轴力图。
40KN
55KN 25KN
20KN
解： 1、为求轴力方便，先求
出约束力 ∑Fx=0
-FR-F1+F2-F3+F4=0 FR=10KN
FR
取横截面1－1左边为分
A 600
B
C
300
500
D
E
400
1800 1 F1=40KN 2 F2=55KN3 F3=25KN 4 F4=20KN
截面法求内力 1）假想沿 m-m 横截面将杆切开，如图a。
2）杆件横截面 m-m 上的内力是一个分布的力系，其合力为 FN
3）由于外力的作用线沿杆的轴线，同二力平衡公理，FN的作用线 也必定沿杆的作用线。
4） FN 为杆件在横截面 m-m 上的轴力。取左半部分为研究对象图b。
Fx 0
FN F
FN F 0 图a F
§7-3 轴向拉（压）时横截面及斜截面上的应力 （1）轴向拉（压）时横截面上的应力
材料力学第七章课后题答案 弯曲变形
(a) (b)
7
该梁的位移边界条件为：
在x 0处， w0 dw 在x 0处， 0 dx 将条件(c)与(d)分别代入式(b)和(a)，得 D 0，C 0 4．建立挠曲轴方程 将所得 C 与 D 值代入式(b)，得挠曲轴的通用方程为
1 Fa 2 F 3 3Fa [ x x xa EI 4 6 4 由此得 AC 段、 CD 段和 DB 段的挠曲轴方程依次为 w
5．计算 wC 和 θ B 将 x a 代入上述 w1或w2 的表达式中，得截面 C 的挠度为
41qa 4 ( ) 240EI 将以上所得 C 值和 x 2a 代入式(a)，得截面 B 的转角为 wC θB qa 3 7 4 16 1 187 203qa 3 [ ] EI 24 24 24 720 720 EI ()
(4)
D1 0 ， C1
由条件（4） 、式（a）与（c） ，得
qa 3 12 EI
C2
由条件（3） 、式（b）与（d） ，得
qa 3 3EI
D2
7qa 4 24 EI
3. 计算截面 C 的挠度与转角 将所得积分常数值代入式（c）与（d） ，得 CB 段的转角与挠度方程分别为
q 3 qa 3 x2 6 EI 3EI 3 q qa 7 qa 4 4 w2 x2 x2 24 EI 3EI 24 EI 将 x2=0 代入上述二式，即得截面 C 的转角与挠度分别为
5．计算 wC 和 θ B 将 x a 代入上述 w1 或 w2 的表达式中，得截面 C 的挠度为
Fa 3 ( ) 12 EI 将以上所得 C 值和 x 3a 代入式(a)，得截面 B 的转角为 wC
材料力学作业答案(7-14)
D
6m 1m
B
a
800
20
620 120
解：求反力作剪力图 和弯矩图，如图 计算截面几何性质：
240 4803 230 8003 Iz 12 12 2.04 103 m 4
FS (kN)
M(kN.m)
640 820 640
IZ 2.04 10 3 WZ ymax 420 10 3 4.86 10 3 m3
2
1 x 33.3 45.9 79.2 MPa, x 2 y 66.7 MPa, 3 0
r 3 1 3 79.2MPa < [] 120MPa
8-7
A
500kN
500kN
40kN/m C
1m
660
240 20 10
FP
FN F1 F2 FP 120 100 77 297kN
I
40
I
z 20 40 20
M F1 0.2 F2 0.4 16kN .m
C max
FN M 297 103 16 103 1.82MPa, A Wz 0.208 0.0404 297 103 16 103 1.03MPa 0.208 0.0404
τ
7-3(c)
60 20MPa
30MPa 80MPa
30
A3 30 O 30 60 C 30 2α0 60
D1
σ
A1
D2
60°
80 20 80 20 2 1 ( ) 302 30 58.3 88.3MPa 2 2 80 20 80 20 2 3 ( ) 302 30 58.3 28.3MPa 2 2
材料力学部分答案
1.12若物体各部分均无变形，则物体内各点的应变均为零。(∨)
1.13若物体内各点的应变均为零，则物体无位移。(×)
1.14平衡状态弹性体的任意部分的内力都与外力保持平衡。(∨)
1.15题1.15图所示结构中，AD杆发生的变形为弯曲与压缩的组合变形。(∨)
1.16题1.16图所示结构中，AB杆将发生弯曲与压缩的组合变形。(×)
2.14两矩形截面木杆通过钢连接器连接(如图示)，在轴向力F作用下，木杆上下两侧的剪切面积A=2lb，切应力τ＝F/2lb；挤压面积Abs=2δb，挤压应力σbs=F/2δb。
2.15挤压应力与压杆中的压应力有何不同挤压应力作用在构件的外表面，一般不是均匀分布；压杆中的压应力作用在杆的横截面上且均匀分布。
3.7图示受扭圆轴，若直径d不变；长度l不变，所受外力偶矩M不变，仅将材料由钢变为铝，则轴的最大切应力（E），轴的强度（B），轴的扭转角（C），轴的刚度（B）。
A．提高 B．降低 C．增大 D．减小 E．不变
第四章弯曲内力
一、是非判断题
4.1杆件整体平衡时局部不一定平衡。（×）
4.2不论梁上作用的载荷如何，其上的内力都按同一规律变化。（×）
2.9图示三种情况下的轴力图是不相同的。(×)
2.10图示杆件受轴向力FN的作用，C、D、E为杆件AB的三个等分点。在杆件变形过程中，此三点的位移相等。(×)
2.11对于塑性材料和脆性材料，在确定许用应力时，有相同的考虑。（×）
2.12连接件产生的挤压应力与轴向压杆产生的压应力是不相同的。（∨）
二、填空题
正确答案是C。
1.3 等截面直杆其支承和受力如图所示。关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。
材料力学_高教第二版_范钦珊_第7篇习题答案
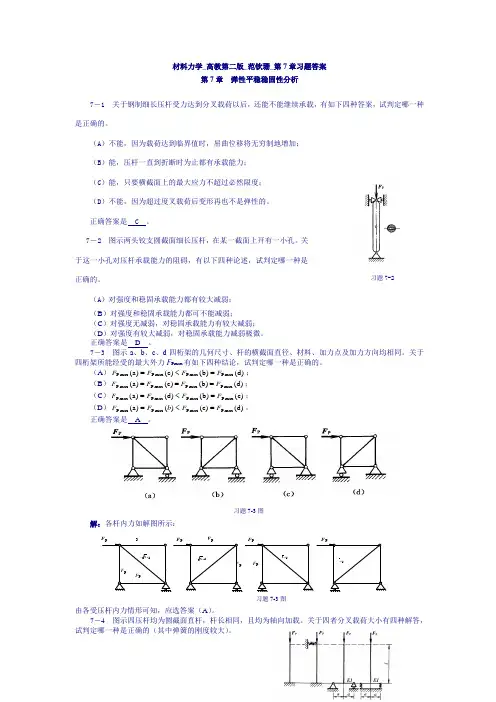
习题7-3图P F P F P F P F 0PF P -F P2F -P2FP2F -P2F 000P F P F P F P-F P -F P -F P F P F P F P F 0P F P -F P2F -P2FP2F -P2F00P F P F P F P -F P -F P-F 0习题7-3图 材料力学_高教第二版_范钦珊_第7章习题答案第7章 弹性平稳稳固性分析7－1 关于钢制细长压杆受力达到分叉载荷以后，还能不能继续承载，有如下四种答案，试判定哪一种是正确的。
（A ）不能，因为载荷达到临界值时，屈曲位移将无穷制地增加； （B ）能，压杆一直到折断时为止都有承载能力； （C ）能，只要横截面上的最大应力不超过必然限度； （D ）不能，因为超过度叉载荷后变形再也不是弹性的。
正确答案是 C 。
7－2 图示两头铰支圆截面细长压杆，在某一截面上开有一小孔。
关于这一小孔对压杆承载能力的阻碍，有以下四种论述，试判定哪一种是正确的。
（A ）对强度和稳固承载能力都有较大减弱；（B ）对强度和稳固承载能力都可不能减弱；（C ）对强度无减弱，对稳固承载能力有较大减弱； （D ）对强度有较大减弱，对稳固承载能力减弱极微。
正确答案是 D 。
7－3 图示a 、b 、c 、d 四桁架的几何尺寸、杆的横截面直径、材料、加力点及加力方向均相同。
关于四桁架所能经受的最大外力F Pmax 有如下四种结论，试判定哪一种是正确的。
（A ）)d ()b ()c ()a (max P max P max P max P F F F F =<=； （B ）)d ()b ()c ()a (max P max P max P max P F F F F ===； （C ）)c ()b ()d ()a (max P max P max P max P F F F F =<=；（D ）)d ()c ()()a (max P max P max P max P F F b F F =<=。
《材料力学》第7章应力状态和强度理论习题解..pdf
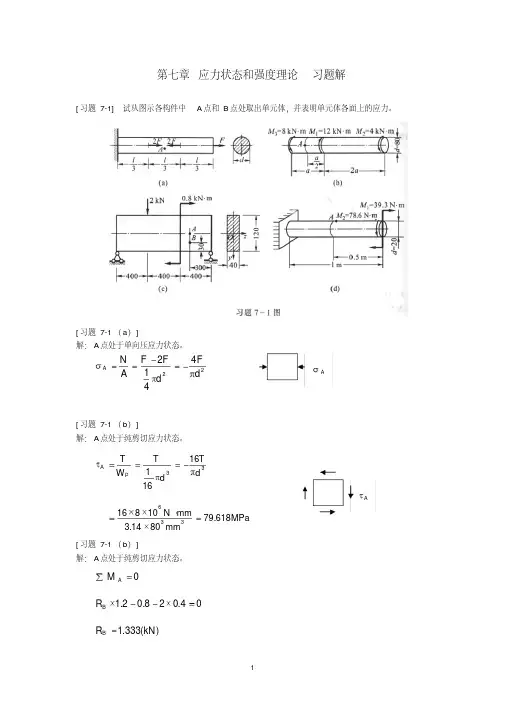
应力圆（ O.Mohr 圆）
主单元体图
[ 习题 7-9 （ c）] 解：坐标面应力： X（ -20 ， -10 ）； Y（ -50 ， 10）。根据以上数据作出如图所示的应
力圆。图中比例尺为 1cm 代表 10MPa 。按比例尺量得斜面的应力为：
1 0MPa , 2 16.25MPa ， 3 53.75MPa ； 0 16.10 。
1 d3
d3
16
6
16 8 10 N mm 3.14 803 mm3
79.618MPa
[ 习题 7-1 （ b）] 解： A 点处于纯剪切应力状态。
MA 0
RB 1.2 0.8 2 0.4 0
RB 1.333(kN )
1
A A
QA RB 1.333( kN)
Q A 1.5
A
1333N 1.5 40 120 mm2
单元体图
应力圆（ O.Mohr 圆）
主单元体图
[ 习题 7-9 （ d）] 解：坐标面应力： X（ 80， 30）； Y（ 160， -30 ）。根据以上数据作出如图所示的应
力圆。图中比例尺为 1cm 代表 20MPa 。按比例尺量得斜面的应力为：
1 170MPa , 2 70MPa ， 3 0MPa ； 0 71.60 。
第七章 应力状态和强度理论 习题解
[ 习题 7-1] 试从图示各构件中 A 点和 B 点处取出单元体，并表明单元体各面上的应力。
[ 习题 7-1 （ a）]
解： A 点处于单向压应力状态。
N F 2F 4F
A
A
1 d2
d2
4
[ 习题 7-1 （ b）] 解： A 点处于纯剪切应力状态。
材料力学答案第7章
∑F
及
n
= 0， σ α dA = 0
∑F
分别得到
t
= 0， τ α dA = 0
σ α = 0，τ α = 0
由于方位角 α 是任取的，这就证明了 A 点处各截面上的正应力与切应力均为零。 顺便指出，本题用图解法来证更为方便，依据 A 点上方两个自由表面上的已知应力（零 应力）画应力图，该应力圆为坐标原点处的一个点圆。至此，原命题得证。
由此可知，主应力各为
σ1 = 60.0MPa, σ 2 = σ 3 = 0
5
σ1 的方位角为
α0 = 0o
对于应力图(b),其正应力和切应力分别为
σB = τB =
| M | | y B | 12 × 20 × 10 3 × 0.050 N = = 3.00 × 10 7 Pa = 30.0MPa 3 2 Iz 0.050 × 0.200 m Fs S z (ω) 12 × 20 × 10 3 × 0.050 × 0.050 × 0.075 N = = 2.25 × 10 6 Pa = 2.25MPa 3 2 I zb 0.050 × 0.200 × 0.050m
σα = (
− 30 + 10 − 30 − 10 + cos45 o − 20sin45 o )MPa = −38.3MPa 2 2 − 30 − 10 τα = ( sin45 o + 20cos45 o )MPa = 0 2
(c)解：由题图所示应力状态可知，
σ x = 10MPa，σ y = −20MPa，τ x = 15MPa，α = −60 o
7-7
已知某点 A 处截面 AB 与 AC 的应力如图所示（应力单位为 MPa） ，试用图解法
7材料力学课后题答案
（二）作图题与计算题： 1、在图示各单元体中，试用解析法和图解法求斜截面 ab 上的应力。应力的单位 为 MPa。
A)
A) 解： σ x =70MPa ， σ y = − 70MPa ， τ x =0 ， α
B)
= 30o
σα =
cos 2α − τ x sin 2α 2 2 70 + ( −70 ) 70 − ( −70 ) = + cos(2 × 30°) − 0 × sin(2 × 30°) 2 2 = 35MPa + sin 2α + τ x cos 2α 2 70 − ( −70 ) = sin(2 × 30°) + 0 × cos(2 × 30°) 2 = 60.62MPa
解 ： σ 1 = σ t = 550MPa ， σ 2 = σ z = 420MPa ，
σ 3 = σ r = −350MPa σ r3 = σ 1 − σ 3 = 900MPa
σ r4 =
1⎡ 2 2 2 ( σ 1 − σ 2 ) + (σ 2 − σ 3 ) + (σ 3 − σ 1 ) ⎤ ⎣ ⎦ 2 = 842.56MPa
第七章应力状态（训练题）答案 （一）填空与改错题： 1、有 一 个 主 应力不为零时称为单向应力状态；当有 二 个 主 应力 不为零时称为二向应力状态或 平面 应力状态； 当 三 个 主 应力都不 为零时称为三向应力状态或 空间 应力状态； 2、构件受力如图所示，图A）的危险点在 固定端（如考虑自重），应力状态为 F 单向 应力状态，应力大小为（ σ = ） ；图B）的危险点在 BC段表面，应力 π 2 d 4 2M e 状态为 纯剪切应力状态，应力大小为（ τ max = ） ；图C）的危险点在 固定 π 3 d 16 Fl 端 上 下 边 缘 ， 应 力 状 态 为 二 向 应 力 状 态 ， 应 力 大 小 为 （ σ max = ， π 3 d 32 Me ） ；图D）的危险点在 轴表面 ，应力状态为 二向 应力状态，应力 τ max = π 3 d 16 Me F 大小为（ σ max = ， τ max = ） 。 π 2 π 3 d d 4 16
《材料力学》第七章课后习题参考答案
题目二
说明杆件在拉伸或压缩时，其 应力与应变的关系。
题目三
一矩形截面梁，长度为L，截面 积为A，弹性模量为E，泊松比 为v，求梁的临界截面转角。
题目四
一圆截面杆，直径为D，弹性模 量为E，泊松比为v，求杆的临 界截面转角。
答案
第一季度
第二季度
第三季度
第四季度
答案一
材料力学的研究对象是 固体，特别是金属和复 合材料等工程材料。其 基本假设包括连续性假 设、均匀性假设、各向 同性假设和小变形假设 。
解析四
圆截面杆的临界截面转角是指杆在受到扭矩作用 时发生弯曲变形的角度。通过弹性力学和材料力 学的知识，我们可以计算出这个角度的值。其中 ，D表示杆的直径，E表示杆的弹性模量，v表示 杆的泊松比。
03
习题三答案及解析
题目
• 题目：一矩形截面简支梁，其长度为L，截面高为h，宽度为b，且h/b=2，梁上作用的均布载荷q=100N/m，试求梁上最大 弯矩值Mmax。
解释了材料力学的基本假设，包括连续性假设、 均匀性假设、各向同性假设和线性弹性假设。这 些假设是材料力学中常用的基本概念，对于简化 复杂的实际问题、建立数学模型以及进行实验研 究具有重要的意义。
题目二解析
强调了材料力学在工程实践中的重要性，说明了 它为各种工程结构的设计、制造、使用和维护提 供了理论基础和实验依据，能够保证工程结构的 可靠性和安全性。这表明了材料力学在工程实践 中的实际应用价值。
题目四解析
解释了材料力学中的应力和应变概念，说明了应 力表示单位面积上的内力，应变表示材料在受力 过程中发生的变形程度。这些概念是材料力学中 的基本概念，对于理解和分析材料的力学行为具 有重要的意义。
THANK YOU
材料力学习题及答案
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。
解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。
1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。
解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量，并确定其大小。
图中之C点为截面形心。
解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。
解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。
材料力学课后题答案7-10
作业参考答案（7-10章）7-１ (a )已知：045201030=-===ατσσMPa MPaMPaxy y xMPa MPa xy yx xy yx yx 1045220452210302224045220452210302103022224545=︒⨯-︒⨯-=+-==︒⨯+︒⨯-++=--++=cos sin cos sin sin cos sin cos ατασστατασσσσσ (b )已知：05.67203010-=-=-==ατσσMPaMPa MPaxy y x567220567223010222343856722056722(-30)102(-30)102222=︒⨯--+︒⨯-+=+-=-=︒⨯-+︒⨯--++=--++=).cos()().sin(cos sin .).sin().cos(sin cos ατασστατασσσσσααxy y x xy yx y x MPa(d )已知：012003050-====ατσσxy y x MPaMPaMPa MPa xy yx xy yx yx 668240230502223524023050230502222..)sin(cos sin )cos(sin cos -=︒--=+-==︒--++=--++=ατασστατασσσσσαα7-2 (a )已知：MPa MPaMPaxy y x 202040===τσσ︒-=︒︒-=-=-⨯-=--====⎩⎨⎧=+⎪⎭⎫ ⎝⎛-±+=+⎪⎪⎭⎫ ⎝⎛-±+=⎩⎨⎧3587316116463222040202220647365264736522022040220402200003212222....tan ....min max αασστασσστσσσσσσyx xyxy y x y x xMPa MPa MPa MPa(a )7-3(a )解：MPaMPa MPaMPaMPa 6527060260703060311321=+=-===-===σστσσσσσmax max(b )解：给定应力状态中有一个主应力是已知的，即σz =30MPa 。
材料力学习题册_参考答案(1-9章)
（图 1）
（图 2）
3．有 A、B、C 三种材料，其拉伸应力—应变实验曲线如图 3 所示，曲线( B )材料
的弹性模量 E 大，曲线( A )材料的强度高，曲线( C )材料的塑性好。
4．材料经过冷作硬化后，其( D )。
A．弹性模量提高，塑性降低
B． 弹性模量降低，塑性提高
C．比例极限提AB 梁的中点
D 任意点
14. 轴向拉伸杆，正应力最大的截面和剪应力最大的截面 ( A )
A 分别是横截面、450 斜截面
B 都是横截面
C 分别是 450 斜截面、横截面
D 都是 450 斜截面
15. 设轴向拉伸杆横截面上的正应力为σ，则 450 斜截面上的正应力和剪应力( D )。
A σ＝Eε＝300MPa
B σ＞300MPa
C 200MPa＜σ＜300Mpa
D σ＜200MPa
21．图 9 分别为同一木榫接头从两个不同角度视图，则（ B ）。
A. 剪切面面积为 ab,挤压面面积为 ch； B. 剪切面面积为 bh,挤压面面积为 bc；
C. 剪切面面积为 ch,挤压面面积为 bc； D. 剪切面面积为 bh,挤压面面积为 ch。
F
p
.D
.
.
.
.
...
解：设每个螺栓受力为 F，由平衡方程得
根据强度条件，有 ［σ］≥
故螺栓的内径取为 24mm。 4．图示一个三角架，在节点 B 受铅垂荷载 F 作用，其中钢拉杆 AB 长 l1=2m，截面面
积 A1=600mm2，许用应力 [ ]1 160MPa ，木压杆 BC 的截面面积 A2=1000mm2，许 用应力 [ ]2 7MPa 。试确定许用荷载[F]。
材料力学课后答案07d
F = 10 kN 时杆件的轴向变形量，以及使杆件屈服的荷载。
解：材料屈服的荷载：
Fu
=
1 4
πd 2σ s
=
1 4
× 3.14 ×102
×180
= 14137
N。
故荷载 F = 10 kN 作用时杆件仍处于弹性阶段。由图可知，
E
=
180 0.2 ×10−2
= 90
GPa 。
杆件轴向变形量
σ (MPa) 180
ε y = −νε x 。
q
250
400
题 7-7 图
面积改变量
∆A = A(ε x + ε y ) = Aε x (1 −ν ) 。
故有
ν
=1−
∆A Aε x
=1−
56 400 × 250 × 8 ×10−4
= 0.3 。
7-8 某种材料的试件的应力应变曲线如图。图中上方曲线对应于横坐标中上一排应变标
识，下方曲线对应于下一排应变标识，即低应变区。试确定这种材料的类型，并确定其
弹性模量 E，屈服极限σ s ，强度极限σ b 与伸长率 δ 。
σ (MPa)
500
σ (MPa)
500
400
400
300
300
200
200
100
100
ε (%)
ε (%)
0
5
10 15 20 25 30
0
5
10 15 20 25 30
E．获取许用应力的安全系数必定是大于 1 的；
F． 获取许用应力的安全系数的大小主要取决于构件的尺寸，尺寸越大的构件安全
系数就应越大。
7-4 某杆件横截面为宽 b = 30 mm 、高 h = 50 mm 的矩形。杆件中有一法线方向与杆 轴 线 成 30o 角 的 斜 截 面 。 斜截 面 上 作 用有 均 布 正 应力 σ = 30 MPa 和 均 布切 应 力 τ = 20 MPa 。求该斜截面上所有应力的合力的大小与方位。
材料力学课后习题答案详细
CB
CB E
6.5MPa 10 103 MPa
6.5 104
（4）计算柱的总变形
l AC AC l AC CB lCB (2.5 1500 6.5 1500) 104 1.35(mm)
[ 习 题 2-9] 一 根 直 径 d 16mm 、 长 l 3m 的 圆 截 面 杆 ， 承 受 轴 向 拉 力
（2）作轴力图
N33 F 2F 2F F
轴力图如图所示。
1
（c）
解：（1）求指定截面上的轴力
N11 2F N22 F 2F F
（2）作轴力图
N33 2F F 2F 3F
轴力图如图所示。
（d）
解：（1）求指定截面上的轴力
N11 F
N 22
如以 表示斜截面与横截面的夹角，试求当 0o ,30o ,45o ,60o ,90o 时各斜截面
上的正应力和切应力，并用图表示其方
向。
解：斜截面上的正应力与切应力的公式
为：
5
0 cos 2
0 2
sin 2
式中， 0
N A
10000 N 100mm 2
100MPa ，把
AC
N AC A
100 103 N 200 200mm2
2.5MPa 。
CB
N CB A
260 103 N 200 200mm2
6.5MPa ，
（3）计算各段柱的纵向线应变
7
AC
AC E
2.5MPa 10 103 MPa
2.5 104
材料力学习题册答案-第7章 应力状态
第 七 章 应力状态 强度理论一、 判断题1、平面应力状态即二向应力状态，空间应力状态即三向应力状态。
(√)2、单元体中正应力为最大值的截面上，剪应力必定为零。
(√)3、单元体中剪应力为最大值的截面上，正应力必定为零。
(×) 原因：正应力一般不为零。
4、单向应力状态的应力圆和三向均匀拉伸或压缩应力状态的应力圆相同，且均为应力轴 上的一个点。
(×) 原因：单向应力状态的应力圆不为一个点，而是一个圆。
三向等拉或等压倒是为一个点。
5、纯剪应力状态的单元体，最大正应力和最大剪应力值相等，且作用在同一平面上。
(×) 原因：最大正应力和最大剪应力值相等，但不在同一平面上6、材料在静载作用下的失效形式主要有断裂和屈服两种。
(√)7、砖,石等脆性材料式样压缩时沿横截面断裂。
(×)8、塑性材料制成的杆件，其危险点必须用第三或第四强度理论所建立的强度条件来校核强度。
(×) 原因：塑性材料也会表现出脆性，比如三向受拉时，此时，就应用第一强度理论9、纯剪应力状态的单元体既在体积改变，又有形状改变。
(×) 原因：只形状改变，体积不变10、铸铁水管冬天结冰时会因冰膨胀被胀裂，而管内的冰不会被破坏，只是因为冰的强度比铸铁的强度高。
(×) 原因：铸铁的强度显然高于冰，其破坏原因是受到复杂应力状态 11．圆杆受扭时，杆内阁点处于纯剪切状态。
（√）12．受扭圆轴内最大拉应力的值和最大切应力的值相等。
(√)二、 选择题1、危险截面是（ C ）所在的截面。
A 最大面积B 最小面积C 最大应力D 最大内力2、关于用单元体表示一点处的应力状态，如下论述中正确的一种是( D )。
A 单元体的形状可以是任意的B 单元体的形状不是任意的，只能是六面体微元C 不一定是六面体，五面体也可以，其他形状则不行D 单元体的形状可以是任意的，但其上已知的应力分量足以确定任意方向面上的硬力 3、受力构件内任意一点，随着所截取截面方位不同，一般来说（ D ） A 正应力相同，剪应力不同 B 正应力不同，剪应力相同 C 正应力和剪应力均相同 D 正应力和剪应力均不同 4、圆轴受扭时，轴表面各点处于（ B ）A 单向应力状态B 二向应力状态C 三向应力状态D 各向等应力状态 5、分析处于平面应力状态的一点，说法正确的是（ B ）。
材料力学第七章答案 景荣春
课
后
答
案
网
ww
7-13 用塑性很好的低碳纲制成的螺栓，当拧过紧时，往往沿螺纹根部崩断，试分析其 破坏原因。 答 螺纹根部处于三向受拉应力状态，切有叫大的应力集中。脆断。
w.
102
kh
7-12 水管在冬天常发生冻裂，为什么冰不破碎而钢管却破裂？ 答 冰的密度比水小，结的冰成三向受压，呈现良好的塑性，不破碎；钢管因冰体积膨 胀受拉，加上温度低，呈现冷脆性，被拉断。
kh
τ yz τ zx
G G
1 ⎡σ x − μ (σ y + σ z ) ⎤ , ⎦ E⎣ 1 ⎡σ y − μ (σ z + σ x ) ⎦ ⎤, εy = ⎣ E 1 εz = ⎡ σ z − μ (σ x + σ y ) ⎤ ⎦, E⎣
εx =
上式称为一般应力状态下的广义胡克定律。 正应力只产生正应变， 并考虑横向变形效应 （泊松效应） ， 用叠加原理求得在 σ x ，σ y 和
w.
co
m
2 ⎧11.2 − 40 + (− 20 ) ⎛ − 40 + 20 ⎞ 2 d 解（1） σ 1,3 = ± ⎜ MPa ， σ 2 = 0 ⎟ + (− 40 ) = ⎨ 2 2 ⎝ ⎠ ⎩− 71.2 2 × (− 40 ) （2） tan 2α 0 = − = −4 ， α 01 = −38.0° − 40 − (− 20 ) σ −σ3 （3） τ max = 1 = 41.2 MPa 2
即
w. da
⎛σ x −σ y ⎞ 2 ⎟ τ max = ⎜ ⎜ ⎟ + τ xy = 35 2 ⎝ ⎠ σ x +σ y σ x −σ y + × (− 0.28) − τ xy × 0.96 = 0 2 2 σ x −σ y × 0.96 + τ xy × (− 0.28) = 0 2 2 ⎛σ x −σ y ⎞ 2 ⎜ ⎟ + τ xy = 1 225 ⎜ ⎟ 2 ⎠ ⎝
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
浙江工业大学材料力学第7章答案7.1一实心圆杆1，在其外依次紧套空心圆管2和3。
设三杆的抗拉刚度分别为E 1A 1、E 2A 2及E 3A 3，此组合杆承受轴向拉力F ，三杆之间无相对摩擦。
试求组合杆的伸长量。
解：平衡方程：F F F F N N N =++321（1）变形协调方程：333222111A E lF A E l F A E l F N N N == （2）方程（1）和（2）联立求解，得到：332211111AE A E A E AFE F N ++=332211222A E A E A E A FE F N ++= 332211333A E A E A E A FE F N ++=组合杆的伸长量为：332211111A E A E A E FlA E l F l N ++==∆7.2 在温度为2︒C 时安装铁轨，两相邻段铁轨间预留的空隙为Δ＝1.2mm 。
当夏天气温升为40︒C 时，铁轨内的温度应力为多少？已知：每根铁轨长度为12.5m ，E ＝200GPa ，线膨胀系数α＝12.5×10-6 m /m ⋅︒C 。
解：没有约束情况下，铁轨自由热膨胀时的伸长量mm9375.5m 109375.55.12)240(105.1236=⨯=⨯-⨯⨯=⋅∆⋅=∆--l T l T α （1）温度应力引起的铁轨长度变形为mm 0625.010200105.1233σσσσ=⨯⨯⨯===∆E l EA l F l N（温度应力σ的单位为MP a ） （2）变形协调条件为∆=∆-∆σl l T（3）方程（1）、（2）和（3）联立求解，可得MPa8.75=σ（压应力）7.3图示结构中，①、②和③三杆材料与截面相同，弹性模量为E ，横截面面积为A ，横杆CD 为刚体。
求三杆所受的轴力。
解：平衡方程F F F F N N N =++321（1）31=⋅-⋅a F a F N N （2）FF N 1F N 2F N 3变形协调方程：312l l l ∆+∆=∆ （3）物理方程：EAlF l N 112∆ EA l F l N 22=∆ EAl F l N 33=∆代入方程（3），可得补充方程 31231222N N N N N N F F F EAlF EA l F EA l F +=⇒+= （4） FC①②③DllaaF∆l 1∆l 2∆l 3DC①②③联立补充方程和平衡方程并求解，可得F F N 721= F F N 732= F F N 723= 7.4图示螺栓通过螺母拧紧套筒。
螺栓的螺距为0.65mm ，螺栓直径d 1=20mm ；套筒内径d 2=22mm ，外径D 2=32mm ；两者材料相同，E ＝200GPa 。
若将螺帽按拧紧方向再旋转60°，试求螺栓横截面上的正应力增加多少？不考虑螺母和螺栓头的变形。
解：拧紧螺帽后，螺栓受拉且轴力为1N F ，套筒受压且轴力为2N F ，平衡方程为021=-N N F F （1）螺母旋进60度后，则总位移为mm 108.065.036060=⨯=∆；假设螺栓伸长1l ∆，套筒缩短2l ∆，因而变形协调方程（如图）为∆=∆+∆21l l （2）物理方程为：211211111441d E lF d E l F EA l F l N N N ππ=⋅==∆（3）()()2222222222222441d D E l F d D E lF EA l F l N N N -=-⋅==∆ππ（4）方程（1）、（2）、（3）和（4）联立求解，可得250mm 套筒螺栓螺母kN641.151=N F螺栓横截面上的正应力为MPa 8.4920115644211=⨯⨯==πσA F N7.5 图示的刚性梁由三根钢杆联接，它们的截面积均为2cm 0.2=A ，钢的弹性模量E =200GPa ，其中杆3由于制造误差，其长度比杆1和杆2短l 0005.0=δ。
试求装配后各杆的应力。
解：平衡方程为0321=++N N N F F F（1）31=⋅-⋅a F a F N N （2）F N 1F N 2N 3变形协调方程为：()2312l l l ∆=-∆+∆δ，即δ=∆-∆+∆2312l l l （3）物理方程为EA lF l N 11=∆ EAl F l N 22=∆ EAlF l N ⋅=∆33（4）方程（4）代入方程（3），得到补充方程为δ=-+EA l F EA l F EA l F N N N 2312，即lEAF F F N N N δ=-+2312 （5） 补充方程联立平衡方程求解，可得 l EAF F N N 631δ==，lEA F N 32δ-=各杆的应力为l a a 123δ∆l 1∆l 2∆3①②③MPa 7.1660005.020*******=⨯===lll E δσσ MPa 3.3330005.020000031-=⨯-=-=ll l E δσ7.6图示结构的三根杆用同一材料制成，弹性模量为E ，杆1和杆3的截面积A A A ==31，杆2的截面积A A 22=。
试求载荷F 作用下各杆的内力。
解：受力图如下： 故平衡方程为 （1） θcos 60cos 21F F F N N =︒+ θsin 30cos 23F F F N N =︒⋅+ （2）根据结构变形图，有()()⎪⎪⎭⎫ ⎝⎛-=+=∆=∆⎪⎪⎭⎫ ⎝⎛+=-=∆ββδβδβδββδβδsin 21cos 2330cos cos sin 23cos 2160cos 321οοl l l故，变形协调条件为：2312321l l l ∆=∆+∆ （3）物理方程为 EAlF l N 11=∆，EAlF A E l F l N N 33230cos 222=⋅︒=∆，EAlF lN 33=∆ （4）方程（4）代入方程（3），得到补充方程为23132333N N N F F F =+（5）FFN 1FN 2FN 3θ方程（1）、（2）和（5）联立求解，可得()()F F N 6322sin 33cos 9341+-+=θθ，()F F N 632sin 33cos 32++=θθ，()()F F N 6322cos 33sin 3343+-+=θθ7.7 钢管壁厚δ1＝2mm ，直径d 1＝50mm ，套在直径为d 2＝25mm 的实心钢轴外，两端与刚性法兰盘焊接，如图所示。
焊接前，轴上加200N·m 的扭转力偶，并在焊接过程中保持该状态。
焊接完后解除扭转力偶，试求钢管横截面上的扭矩。
解：焊接前，实心钢轴右端相对于左端的扭转角为0ϕ，扭矩为0T 。
焊接完后解除初始力偶后，钢管右端相对于左端的扭转角为1ϕ，扭矩为1T ；实心钢轴右端相对于左端的扭转角为2ϕ，扭矩为2T 。
受力平衡方程为:21=-T T （1）变形协调方程为：21ϕϕϕ=+ （2）物理方程为：()324650441111-⋅==πϕG lT GI l T p ，322542222⋅⋅==πϕG lT GIl T p ，3225200004200⋅⋅==πϕG lGI l T p （3）方程（1）、（2）和（3）联立求解，可得m N 9.1631⋅=T7.8 图示两端固定的圆截面实心阶梯轴，承受扭转力偶作用，如图所示。
若材料的许用切应力MPa 50][=τ，试设计轴的直径D 2。
解：平衡方程为eBCABM T T =+ （1）变形协调方程为BCAB ϕϕ= （2）物理方程为3242D G l T ABAB AB πϕ⋅=，3241D G l T BCBC BCπϕ⋅=（3）BC 段的扭转强度条件：][1631τπτ≤=D T BCBC（4）方程（1）、（2）、（3）和（4）联立求解，可得：mm2.772≥D ，取mm782=D。
7.9EI 。
ABCqaalAABBBDCCFM eaFa al/2(a)(b)(c)(d)Al/2l/2题7.9图解：（a ）一次超静定梁。
F BABB CqaaACqaa解除多余支座约束B ，应用支反力BF 代替，得到图示静定基。
由叠加法可以得到截面B 的挠度为EIa q EI a F w BB384)2(548)2(43-= 变形协调方程为 0=Bw 于是可得45qaF B= 由0=∑AM可得0245)2(212=⋅+⋅+-a F a qa a q C ，()↑=83qaFC由结构几何与载荷的对称性，可知()↑=83qa F A（b ）一次超静定梁。
AB D CFaa aAB D CFaaaF B解除多余支座约束B ，应用支反力BF 代替，得到图示静定基。
由叠加法可以得到截面B 的挠度为[][]aEI a a a a Fa a EI a a a a a F w BB36)3(36)2()3(2222222⋅--⋅⋅-⋅--⋅⋅=变形协调方程为0=Bw于是可得F F B87= 由0=∑AM可得3287=⋅-⋅+-a F a F Fa C ，()↓=F FC41由竖直向的受力平衡方程，可得()↑=F F A 83（c ）一次超静定梁。
lABl/2(c)lABl/2F B解除多余支座约束B ，应用支反力BF 代替，得到图示静定基。
由叠加法可以得到截面B 的挠度为()EIl l Fl EI l l l F w B B 62336322⎪⎭⎫ ⎝⎛-⋅⋅--⋅=变形协调方程为 0=Bw于是可得F F B47= 由0=∑AM可得02347=⋅-⋅+l F l F M A ，FlMA41-=由竖直向的受力平衡方程，可得F F A 43=（d ）一次超静定梁。
BBAl/2l/2M Al/2l/2解除多余支座约束B ，应用支反力BF 代替，得到图示静定基。
有叠加法可以得到截面B 的挠度为l EI l M EI l M EI l F w e e B B 2121221323⋅⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=变形协调方程为 0=Bw于是可得lMF eB89= 由竖直向的受力平衡方程，可得lMF eA89= 由0=∑AM可得089=⋅+-l lM M M ee A ，eAM M 81-=7.10 图示悬臂梁AD 和BE ，通过钢杆CD 连接。
已知，kN 50=F ，梁AD 和BE 的抗弯刚度均为26m N 1024⋅⨯=EI ，CD 杆长m 5=l ，横截面面积24m 103-⨯=A ，弹性模量GPa 200=E 。
试求悬臂梁AD 在D 点的挠度。
解：一次超静定结构。
变形协调方程为CDD C l w w ∆=- （1）F C D AB 2m 2m E物理关系为EIa F w N D 33-=，()EIa F EI a a Fa w N C 36632+-⋅-=，EAlF l N CD=∆ （2）方程（1）和（2）联立求解，可得()kN454.45124533=+=EIlEAa EAFa F N 悬臂梁AD 在截面D 的挠度为mm05.51024320004545431233-=⨯⨯⨯-=-=EI a F w N D7.11 图示结构，AC 梁的EI 和CD 杆的EA 为已知，且a ＝l /2。