工程经济学 第10章例题
《工程经济学》(第二版)课后及补充习题 解答

《工程经济学》(第二版)课后及补充习题解答第一部分课后习题1.资金的时间价值习题(P27):13. 某企业获得8万元贷款,偿还期4年,年利率为10%,试就以下4种还款方式,分别计算各年的还款额(本金和利息)、4年还款总额及还款额的现值和终值:⑴每年年末还2万元本金和所欠利息;⑵每年末只还所欠利息,本金在第4年末一次还清;⑶每年末等额偿还本金和利息;⑷第4年末一次还清本金和利息。
【解】⑴利息:第1年末8000元,第2年末6000元,第3年末4000元,第4年末2000元。
∴4年还款总额=20000×4 +(8000+6000+4000+2000)=100000元各年的还款额(本金和利息):第1年末28000元,第2年末26000元,第3年末24000元,第4年末22000元.还款额的现值P = 28000(P/F,10%,1)+ 26000(P/F,10%,2)+ 24000(P/F,10%,3)+ 22000(P/F,10%,4)= 80000元还款额的终值F = 80000(F / P,10%,4)=117128元。
⑵利息:每年还利息8000元。
∴4年还款总额=80000 + 8000×4 =112000元各年的还款额(本金和利息):第1年末8000元,第2年末8000元,第3年末8000元,第4年末88000元.还款额的现值P = 8000(P/A,10%,4)+ 80000(P/F,10%,4)= 80000元还款额的终值F = 80000(F / P,10%,4)=117128元。
⑶各年的还款额(本金和利息)均为:A=80000(A/P,10%,4)=25240元。
∴4年还款总额= 25240×4 = 100960元。
还款额的现值:P = 25240(P/A,10%,4)= 80000元还款额的终值:F = 80000(F / P,10%,4)=117128元。
工程经济学课件例题汇总

01
直线计提折旧 加速折旧
提取方式主要有两种:
02
年折旧额=(原值-净残值)/ 折旧年限 其他:工作量法
直线计提折旧
折旧
加速折旧主要有两种
双倍余额递减法
年折旧率= 2/折旧年限 是直线计提折旧率的2倍 (双倍) 年折旧额=固定资产净值×年折旧率 从倒数第二年起按直线折旧(最后两年均摊): 年折旧额=(净值- 残值)/2 注:双倍余额递减法提折旧,最初不考虑净残值,只以净值提折旧。在其固定资产折旧年限到期前两年,将固定资产净值扣除预计净残值之后的净额平均摊销。
所以,P=F(P/F,i,n)=F(P/F,8%,6)=315.10(万元)
【解】这是一个已知年金求终值的问题,根据公式可得:
此题表示若全部资金是贷款得来,需要支付1.5亿元的利息。
某大型工程项目总投资10亿元,5年建成,每年末投资2亿元,年利率为7%,求5年末的实际累计总投资额。
F=A [(1+i)n-1]/i=11.5(亿元)
02
设乙银行复利率为r ,则由有关公司得:
03
[1+(r/12)]12 -1= 8.24%
04
解得:r=7.94%
05
答案
现在把500元存入银行,银行年利率为4%,计算3年后该笔资金的实际价值。(假设是一年定期自动转存) 【解】这是一个已知现值求终值的问题,由公式得: F=P(1+i)3=500×(1+4%)3=562.43(元) 即500元资金在年利率为4%时,经过3年后变为562.43元,增值62.43元。 这个问题也可以查表计算求解,由复利系数表可查得:(F/P,4%,3)=1.1249 所以,F=P(F/P,i,n)=P(F/P,4%,3)=500×1.1249=562.45
工程经济学课后习题答案计算题刘晓君答案
利用复利公式:(F / A,11.5%,10) (1 i)n 1 (111.5%)10 1 17.13
i
11.5%
利用复利系数表:当i1 10%, (F / A,10%,10) 15.9374 当i2 12%, (F / A,12%,10) 17.5487
11.5% 10% x 15.9374 12% 10% 17.5487 15.9374
4 700
350 0.5718 400.26 -365.18
5 800
1150 0.4972 397.76 32.58
解:(1)静态投资回收期 Pt = 4-1+(350/700)=3.5 (年) 动态投资回收期:Pt′= 5-1+(365.18/397.76)=4.92(年)
NPV04 2000 450(P / F,15%,1) 550(P / F,15%,2) 650(P / F,15%,3) 700(P / F,15,4) 365.18万元 NPV5 800(P / F,15%,5) 397.76万元 NPV05 365.18 397.76 32.58万元
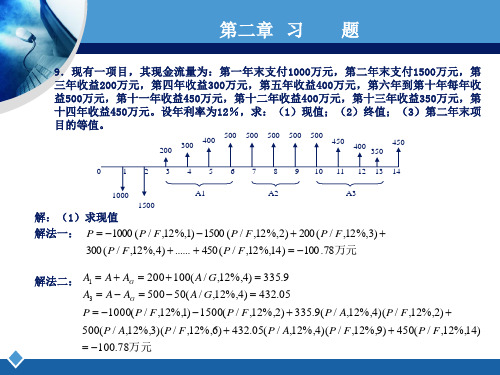
500(P / A,12%,3)(P / F,12%,6) 432.05(P / A,12%,4)(P / F,12%,9) 450(P / F,12%,14) 100.78万元
第二章 习 题
工程经济学 习题及答案解析[精品文档]
![工程经济学 习题及答案解析[精品文档]](https://img.taocdn.com/s3/m/b87106e1ce2f0066f53322a9.png)
第一部分工程经济学模拟测试题工程经济学模拟测试题(一)一、某项资产原值为50,000 元,预计使用5 年,预计净残值为2,000 元,分别用直线折旧法、双倍余额递减法、年数总和法和定率法求每年的折旧率和折旧额。
(20 分)折旧率和折旧额计算表二、某A 与某B 计划投资5 万元,为期10 年,年利率10%,若 A 按每年复利计算利息,而B 按连续复利计算利息,试分别计算此二人的未来值。
(10 分)三、某种产品的需求函数为X=3000-150P,供求平衡时的需求量为1200 单位。
现有新项目使该种产品的供给量增加了300 单位。
试绘图计算分析:(20 分)1、新项目的销售收入;2、新增消费者剩余;3、新项目的国民经济收益;4、原生产者收益的减少额。
四、如果年利率为12%,按每月计息一次,那么实际的年利率为多少?(10分)五、已知某项目设计生产能力为生产某种产品6,000 件,单位产品售价100元,总固定成本费用为200,000 元,单位变动成本费用为50 元,求:(20 分)1、盈亏平衡产量;盈亏平衡销售收入;2、盈亏平衡生产能力利用率;3、盈亏平衡销售价格;4、若企业的计划利润目标为100,000 元,求目标产量。
六、分别用以下方法评价表格所示的现金流量(按10%折现率)。
(20 分)1、净现值法;2、年值法;3、益/本比法;4、内部收益率法。
要求内部收益率精确到0.1%。
(备注:工程经济学模拟测试题(二)一、某项资产原值为2,500 元,预计使用5 年,预计净残值率为10%,分别用直线折旧法、双倍余额递减法、年数总和法和定率法求每年的折旧率和折旧额。
(20 分)折旧率和折旧额计算表二、试以下列方法计算比较每年2,000 元,连续10 年,年利率10%的现金流量的现值。
(备注:(P/A,10%,10)=6.1445)(10 分)1、按每年复利计算;2、按连续复利计算。
三、假设DD 为产品的价格与需求的关系曲线,由于需求规律的作用,需求量随价格的下降而增加。
《工程经济学》全套习题库(含)答案

3-11 某夫妇为自己的小孩设立一创业基金,从小孩 出生开始连续18年在每年末存入银行等额资金1万元, 若银行年利率为2%,则第18年末该创业基金总额为 多少?
解:已知A=10000元,i=2%,n=18,求F。
F
A
1
in
i
1
10000
1
2%18
2%
1
214120
(元)
也可查表计算: F=A(F/A,i,n)=10000(F/A,2%,18)=214120(元)
(元)
3-13 假如银行存款利率为3%,某人希望在第5 年末积累10000元的储蓄,则每年年末应等额 存入银行多少存款?
解:已知F=10000元,i=3%,n=5,求A。
因为A银行的计息周期为年,所以A银行的名义年利 率和实际年利率一致,均为5%;
B银行的计息周期为月,其实际年利率为:
i (1 r )m 1 (1 4%)12 1 4.07%
m
12
因为B银行的实际年利率要低于A银行,因此企业向
B银行贷款更合算。
3-8 某企业拟建一个工业项目,第1、2、3年初
ห้องสมุดไป่ตู้
分别投资100万元、150万元和130万元;第3年、
(2)双倍余额递减法:
l = {[2(VK-VL)/N*VK] /N*VK} × 100% ={2(100-20)/10*100} × 100%=16% • 第1年折旧额: 100×16%=16(万元) • 第2年折旧额:(100-16)×16%=13.44(万元) • 第3年折旧额:(100-16-13.44)×16%=11.29(万元) • 第4年折旧额: 9.48(万元) • 第5年折旧额: 7.966(万元) • 第6年折旧额: 6.692(万元) • 第7年折旧额: 5.621(万元) • 第8年折旧额: 4.722(万元) • 最后两年(第9、10年)折旧额为:2.3945(万元)
(完整版)工程经济学课后习题答案

第一章概论本章要求(1)熟悉工程经济活动的概念及其要素;(选择、判断)(2)了解工程经济学的性质、发展过程;(3)掌握工程经济学的基本原理;(简答)(4)熟悉工程经济分析的过程和步骤;(简答)(5)了解工程经济分析人员应具备的知识和能力本章重点(1)经济效果的含义(2)工程经济学的基本原理本章难点工程经济学的基本原理第二章现金流量构成与资金等值计算本章要求(1)熟悉现金流量的概念;(选择)(2)熟悉资金时间价值的概念;(选择、简答)(3)掌握资金时间价值计算所涉及的基本概念和计算公式;(选择、计算)(4)掌握资金等值计算及其应用。
(计算)本章重点(1)资金时间价值的概念、等值的概念和计算公式(2)名义利率和实际利率本章难点(1)等值的概念和计算(2)名义利率和实际利率第三章投资、成本、收入与利润本章要求(1)熟悉工程项目投资概念及构成;(建设期利息的计算)(2)熟悉成本费用的概念及构成;(折旧的计算)(3)掌握工程项目的收入和销售税金及附加的计算;(增值税的计算)(4)掌握利润总额、所得税的计算及净利润的分配顺序;(5)熟悉经营成本、固定成本和变动成本、机会成本的概念本章重点(1)工程项目投资的概念及构成(2)折旧的概念、计算及其与现金流量的关系(3)经营成本、固定成本和变动成本、机会成本的概念(4)销售税金及附加的内容、含义及计算(5)利润总额、所得税的计算及净利润的分配顺序本章难点(1)经营成本、机会成本的概念第四章工程项目经济评价方法※本章要求(1)熟悉静态、动态经济评价指标的经济含义、优缺点;(选择、判断)(2)掌握静态、动态经济评价指标计算方法和评价准则;(计算)(3)掌握不同类型投资方案适用的评价指标和方法。
(计算)※本章重点(1)投资回收期的概念和计算(2)净现值和净年值的概念和计算(3)净现值与收益率的关系(4)内部收益率的含义和计算(5)互斥方案的经济评价方法※本章难点(1)净现值与收益率的关系(2)内部收益率的含义和计算(3)互斥方案的经济评价方法第五章工程项目风险与不确定性分析※本章要求(计算、简答)(1)了解不确定性分析的目的和意义;(2)掌握盈亏平衡分析方法;(线性盈亏平衡、互斥方案的盈亏平衡分析)(3)掌握敏感性分析方法和步骤;(单因素敏感性分析)(4)熟悉风险估计的方法。
工程经济学例题_

1.某项设备购置及安装费共8000元,估计可使用6年,残值忽略不计。
使用该设备时,第1年维修操作费为1500元,但以后每年递增200元,假设年利率为10%,问该设备总费用现值、终值为多少?相当于每年等额总费用为多少? 解 (1)绘制现金流量图如下:(2)设备总费用的现值为:3)设备总费用的终值为:4)相当于每年的等额年金为:⏹ 2.某工程师获得10000元贷款,偿还期为5年,利率为10%。
在下列几种还款方式下,按复利计息计算此人还款总额和利息各是多少?⏹ 1)每年年末只偿还2000元本金,所欠利息第5年年末一次还清。
⏹ 2)每年年末偿还2000元本金和所欠利息。
⏹ 3)每年年末偿还所欠利息,第5年年末一次还清本金。
⏹ 4)第5年年末一次还清本利。
⏹ 5)每年末等额还本付息。
假定有某项财务活动,其现金流量如图所示,试求出按季度计息的等值将来值为多少(假定年利率为8%)。
按照计算期长于支付期的等值计算处理原则,将上图加以整理,得到等值的现金流量图,如下图所示123456789101112400100 100 100100100100250100( 月 ) ( 存)( 提)012346580001500170019002100230025005.1646868.9200355.415008000]%)101(6%)101%(101%)101([%101200]%)101%(101%)101([15008000])1()1(1)1([1])1(1)1([6666611=⨯+⨯+=+-+-+⨯++-++=+-+-+++-++=n n n n n i n i i i i G i i i A P P 2.29182772.15.16468%)101(5.16468)1(6=⨯=+⨯=+=n i P F 31.378212961.02.291821%)101(%102.291821)1(6=⨯=-+⨯=-+=n i i F A (季度)13422004001002503001003.假设你以4500元/平方米的价格购买了一套建筑面积为120平方米的住宅,并向金融机构申请了相当于房价的70%的按月等额还款的抵押贷款。
工程经济学习题+答案

名词解释1工程经济:以最低的代价可靠地实现目标的最佳或满意的活动方案。
2工程经济学:是以工程建设项目为主体,把经济学原理应用到与工程经济相关的问题和投资上,以技术—经济系统为核心,研究如何有效利用工程技术资源,促进经济增长的科学。
3资金的时间价值:不同时间发生的等额资金在价值上的差别4资金具有时间价值的内涵:资金在生产与交换过程中由于有劳动者的劳动使之产生了增值;5等值:一笔资金在运动过程中,在不同时刻它的数值时不同的,但它们的作用是相同的。
从实际价值来看,可以认为它们具有相等的经济价值。
6等值的概念:资金等值是指在不同时点绝对值不等而价值相等的资金。
7折现率是指在经济分析中,把根据未来的现金流量求现在现金流量时使用的利率8收益率:某个项目投产以后,每年的净收益与原来投资之比。
9折现(贴现):把将来某一时点上的资金金额换算成现在时点的等值金额的过程10现值(P):资金发生在某一特定时间序列开始点上的价值。
11终值(F):资金发生在某一特定时间序列终止点上的价值。
12年值(A):指各年等额收入或支出的金额,通常以等额序列表示,即在某一特定时间序列期内,每隔相同时间收入或支出的等额款项。
13利率:在单位时间内所得到利息额与原来本金之比。
其是衡量资金时间价值的相对尺度。
14单利:每期均按照原始本金来计算利息。
15复利:在计算利息时,某一计息周期的利息是由本金加先前周期上所累积利息之和来计算的。
16名义利率r:指实际计息周期利率与每年计息次数的乘积。
17利息:占用资金所付出的代价或者是放弃现期消费所得到的补偿。
其是衡量资金时间价值的绝对尺度。
18实际利率:利率的时间单位与实际计息期一致。
19折旧:固定资产在使用过程中由于逐渐磨损而转移到产品中的那部分价值20折旧费:根据固定资产的折旧费,从销售收入中按月提存,用于固定资产再生的那部分金额。
21摊销指对除固定资产之外,其他可以长期使用的经营性资产按照其使用年限每年分摊购置成本的会计处理办法. 22摊销费是指无形资产和递延资产在一定期限内分期摊销的费用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
假如某工程已有某台设备,目前的残值为7000元,估计还能使用3年。
若保留使用旧机器
现有一种较好的设备,原始费用为30000元,经济寿命为12年,12年末的残值为2000元,年度使用费固定为1000元,如果基准贴现率为15%,(1)问设备是否要马上更换?(2)如果旧设备不需要马上更换,那么何时更换最好?
解:
(1)根据新旧设备经济寿命时的等值年度费用确定旧设备是否马上更换:
AC(15%)新=(30000-2000(P/F,0.15,12))(A/P,0.15,12)+1000=6466(元)
旧设备的经济寿命:
旧设备再保留使用1年
AC(15%)=(7000-5000(P/F,0.15,1))*(A/P,0.15,1)+3000=6050(元)
旧设备再保留使用2年
AC(15%)=(7000-
3000*(P/F,0.15,2)+3000*(P/F,0.15,1)+4000*(P/F,0.15,2))*(A/P,0.15,2)=6375.58(元)
旧设备再保留使用3年
AC(15%)=(7000-2000*(P/F,0.15,3)+3000*(P/F,0.15,1)+4000*(P/F,0.15,2)+6000*(P/F,0.15,3)) *(A/P,0.15,3)=6684.99(元)
旧设备的经济寿命为1年,经济寿命时的等值年度费用AC(15%)旧=6050元,而新设备经济寿命时等值年度费用AC(15%)新=6466元,可见旧设备不需要马上更换。
(2)采用逐年比较确定旧设备何时更换为好
马上更换旧设备
AC(15%)=6466元
旧设备使用1年的情况
AC(15%)=6050元
旧设备使用2年,第1年的使用费用作为沉没成本,现在仅仅关注第2年得现金流,同新设备经济寿命期内的等值年度费用6466作比较。
AC(15%)=(5000-3000*(P/F,0.15,1))*(A/P,0.15,1)+4000=6750元
所以结论是旧设备使用一年后就应该更换。
某公司有一台设备,购于3年前,按直线法折旧,为保持生产能力,两年后需大修,大修成本为290000元,现在考虑是否要更新,新设备按年数总和法折旧,该公司所得税税率为33%,税后基准收益率为6%,其他有关资料如下表所示。
分别进行税前和税后更新比较。
解:都以计算期为4年比较净现值以决定方案的取舍。
(1)旧设备净现金流量计算
1)折旧的计算
年折旧额=1600000−160000
6
=240000(元)
2)0年末应纳所得税额的计算
旧设备处置收入(损失)=目前变现价值-账面价值
账面价值=1600000-240000×3=880000(元)
故旧设备处置收入=350000-880000=-530000(元)
损失但是由于保留旧设备,因此放弃扣减所得税的机会,所以应纳税所得额增加530000元,放弃了机会抵扣所得税174900元。
(530000×33%)
3)第4年末旧设备处置的所得税计算
第4年年末旧设备处置收入=70000-160000=-90000(元)
第4年年末所得税=-90000×33%=-29700(元)(少交)
税后净现金流量等于税前净现金流量减去所得税。
旧设备的税前和税后净现金流量计算结果如下表所示。
(2)新设备净现金流量计算
1)折旧的计算
第1年折旧额=(820000-82000)×4
4+3+2+1
=295200(元)
第2年折旧额=(820000-82000)×3
=221400(元)
4+3+2+1
=147600(元)第3年折旧额=(820000-82000)×2
4+3+2+1
第4年折旧额=(820000-82000)×1
=73800(元)
4+3+2+1
2)第4年年末新设备处置的所得税计算
第4年年末新设备处置收入=100000-82000=18000(元)第4年年末所得税=18000×33%=5940(元)
税后净现金流量等于税前净现金流量减去所得税。
新设备税前和税后净现金流量计算见下表。
(3)费用现值比较
税前
NPV(6%)旧=-843721
NPV(6%)新=-844744
按照税前现金流量继续使用旧设备
税后
NPV(6%)旧=-602168
NPV(6%)新=-598031
按照税后现金流量应该选择更新。
