第3章平面力系的合成与平衡精品PPT课件
合集下载
第三章平面力系的合成与平衡

【解】杆AB和BC都是二力杆,假设杆AB受拉力、杆BC 受压力,如图3.10(b)所示。
滑轮的受力图如图3.10(c)所示。
为了避免解联立方程,选直角坐标系如图所示,使x、 y轴分别与反力NBC、NAB垂直。
∑Fx=0,-NAB+Tcos60°-TBDcos30°=0 得 NAB=Tcos60°-TBDcos30°=-7.33kN NAB为负值,表示该力的实际指向与受力图中所假设 的指向相反。即杆AB受压力作用。再由
R Rx2 Ry2 ( Fx )2 ( Fy )2
tan Ry Fy
Rx
Fx
上式表明了合力在任一轴上的投影,等于各分 力在同一轴上投影的代数和。我们称之为合力投影 定理。
【例3.3】图3.7所示的吊环上作用有3个共面的拉力,各 力的大小分别是T1=3kN、T2=1kN、T3=1.5kN,方向如图
【解】绳AB作用于桩上的拉力是由绳BD传来的。因此先 取结点D为研究对象求出绳BD的拉力。
作用在结点D上的力有已知力F、绳DE的拉力TDE和 绳BD的拉力TDB,这三个力组成一平面汇交力系。结点D 的受力图如图3.11(b)所示。
选直角坐标系如图,使y轴与TDE垂直。列平衡方程
∑Fy=0,TDBsinα-Fcosα=0 得 TDB=Fcotα=4000N 再取结点B为研究对象。作用在结点B上的力有绳BC、 BD和BA的拉力TBC、TBD、TBA,绳BD给两结点D和B的 作用力应大小相等、方向相反,即有TBD=TDB=4000N。 力TBC、TBD、TBA组成一个平面汇交力系,结点B的受力 图如图3.11(c)所示。
3.1 平面汇交力系 3.1.1 力在坐标轴上的投影
设力F作用于物体的A点,如图3.4所示。
滑轮的受力图如图3.10(c)所示。
为了避免解联立方程,选直角坐标系如图所示,使x、 y轴分别与反力NBC、NAB垂直。
∑Fx=0,-NAB+Tcos60°-TBDcos30°=0 得 NAB=Tcos60°-TBDcos30°=-7.33kN NAB为负值,表示该力的实际指向与受力图中所假设 的指向相反。即杆AB受压力作用。再由
R Rx2 Ry2 ( Fx )2 ( Fy )2
tan Ry Fy
Rx
Fx
上式表明了合力在任一轴上的投影,等于各分 力在同一轴上投影的代数和。我们称之为合力投影 定理。
【例3.3】图3.7所示的吊环上作用有3个共面的拉力,各 力的大小分别是T1=3kN、T2=1kN、T3=1.5kN,方向如图
【解】绳AB作用于桩上的拉力是由绳BD传来的。因此先 取结点D为研究对象求出绳BD的拉力。
作用在结点D上的力有已知力F、绳DE的拉力TDE和 绳BD的拉力TDB,这三个力组成一平面汇交力系。结点D 的受力图如图3.11(b)所示。
选直角坐标系如图,使y轴与TDE垂直。列平衡方程
∑Fy=0,TDBsinα-Fcosα=0 得 TDB=Fcotα=4000N 再取结点B为研究对象。作用在结点B上的力有绳BC、 BD和BA的拉力TBC、TBD、TBA,绳BD给两结点D和B的 作用力应大小相等、方向相反,即有TBD=TDB=4000N。 力TBC、TBD、TBA组成一个平面汇交力系,结点B的受力 图如图3.11(c)所示。
3.1 平面汇交力系 3.1.1 力在坐标轴上的投影
设力F作用于物体的A点,如图3.4所示。
平面力系-PPT课件

力偶:两个大小相等、方向相反且不共线的平行力组成 的力系。 记作(F,F′) d 称为力偶臂 力偶所在的平面称为力偶的作用面。
2.4 平面力偶
(1)力偶不能合成为一个力,力偶也不能用一个力来平衡。因 此,力和力偶是静力学的两个基本要素
(2)力偶对作用面内任一点的矩,与矩心的位置无关。 力偶对点O的矩为Mo(F,F′),则 M o (F ,F ) M o (F ) M o (F ) F (x d ) F xF d 力偶矩是一个代数量,其绝对值等于力的 大小与力偶臂的乘积,正负号表示力偶的 转向:一般以逆时针转向为正,反之为负。
合力矩定理:平面汇交力系的合力对于平面内任一点之 矩等于所有各分力对于该点之矩的代数和。
n
MO(FR) MO(Fi) i1
上式适用于任何有合力存在的力系。
2.3 平面力系中力对点之矩的概念及计算
力矩的解析表达式 已知力F,作用点A(x,y)及夹角θ。 力F 对坐标原点O之矩
M O (F ) M O (F y) M O (F x)
Fx 0 FBAF1sin30F2sin60 0 Fy 0 FBC F1co3s0F2co6s0 0
F 1F2P2k0N 4.解方程
F B A 0 .3P 6 6 7 .3k 2N 1F BC 1.36 P 62.3 7k 2N FBC为正值,表示这力的假设方向与实际方向相同, 即杆BC受压。 FBA为负值,表示这力的假设方向与实际 方向相反,即杆AB也受压力。
结论:平面汇交力系可简化为一合力,其合力的大小与方向
等于各分力的矢量和(几何和),合力的作用线通过汇交点。
特殊情况:如力系中各力的作用线都沿同一直线,则
此力系称为共线力系它是平面汇交力系的特殊情况,该力
2.4 平面力偶
(1)力偶不能合成为一个力,力偶也不能用一个力来平衡。因 此,力和力偶是静力学的两个基本要素
(2)力偶对作用面内任一点的矩,与矩心的位置无关。 力偶对点O的矩为Mo(F,F′),则 M o (F ,F ) M o (F ) M o (F ) F (x d ) F xF d 力偶矩是一个代数量,其绝对值等于力的 大小与力偶臂的乘积,正负号表示力偶的 转向:一般以逆时针转向为正,反之为负。
合力矩定理:平面汇交力系的合力对于平面内任一点之 矩等于所有各分力对于该点之矩的代数和。
n
MO(FR) MO(Fi) i1
上式适用于任何有合力存在的力系。
2.3 平面力系中力对点之矩的概念及计算
力矩的解析表达式 已知力F,作用点A(x,y)及夹角θ。 力F 对坐标原点O之矩
M O (F ) M O (F y) M O (F x)
Fx 0 FBAF1sin30F2sin60 0 Fy 0 FBC F1co3s0F2co6s0 0
F 1F2P2k0N 4.解方程
F B A 0 .3P 6 6 7 .3k 2N 1F BC 1.36 P 62.3 7k 2N FBC为正值,表示这力的假设方向与实际方向相同, 即杆BC受压。 FBA为负值,表示这力的假设方向与实际 方向相反,即杆AB也受压力。
结论:平面汇交力系可简化为一合力,其合力的大小与方向
等于各分力的矢量和(几何和),合力的作用线通过汇交点。
特殊情况:如力系中各力的作用线都沿同一直线,则
此力系称为共线力系它是平面汇交力系的特殊情况,该力
第三章 平面力系的合成与平衡

得: FAy 2.32kN
M A 0 : M A M 2ql 2l FB sin 600 3l F cos300 4l 0
得: M A 10.37kN
第三章
24
例5:
已知:P=60kN,P1=20kN,P2=10kN, F=10kN,尺寸如图; 求:A、B处的约束力。
当把作用在M物体B 上 的MFB力(F平)行移F至d物体上任一
(点其时中,d为必F须方同向时过附A加点一的个连力线偶到,B点此的附垂加直力距偶离矩)
第三章等于F力对新作用点的力矩。
14
目 录
第三节 平面一般力系的合成
1. 平面一般力系向作用面内一点简化 · 主矢和主矩
主矢(合力): FR Fi
建筑力学
教学用书 周国瑾,施美丽,张景良.建筑力学.第三版.上海:同济大学出版社.2006
参考书目 乔宏洲.理论力学.第一版.北京:中国建筑工业出版社.2004 张如三,王天明.材料力学.第一版.北京:中国建筑工业出版社.2005
李家宝.结构力学.第三版.北京:高等教育出版社.2002
第三章
制作:陶钦贵
第三章
28
即: 75kN P3 350kN
当 P3 = 180kN 时:
M A 0, 4P3 2P2 14P1 4FB 0
解得: FB=870kN
Fiy 0, FA FB P1 P2 P3 0
解得: FA=210kN
第三章29目 录源自F2cos60
F3
cos45
F4
cos45
129.3N
FRy
F iy
F1 sin 30
M A 0 : M A M 2ql 2l FB sin 600 3l F cos300 4l 0
得: M A 10.37kN
第三章
24
例5:
已知:P=60kN,P1=20kN,P2=10kN, F=10kN,尺寸如图; 求:A、B处的约束力。
当把作用在M物体B 上 的MFB力(F平)行移F至d物体上任一
(点其时中,d为必F须方同向时过附A加点一的个连力线偶到,B点此的附垂加直力距偶离矩)
第三章等于F力对新作用点的力矩。
14
目 录
第三节 平面一般力系的合成
1. 平面一般力系向作用面内一点简化 · 主矢和主矩
主矢(合力): FR Fi
建筑力学
教学用书 周国瑾,施美丽,张景良.建筑力学.第三版.上海:同济大学出版社.2006
参考书目 乔宏洲.理论力学.第一版.北京:中国建筑工业出版社.2004 张如三,王天明.材料力学.第一版.北京:中国建筑工业出版社.2005
李家宝.结构力学.第三版.北京:高等教育出版社.2002
第三章
制作:陶钦贵
第三章
28
即: 75kN P3 350kN
当 P3 = 180kN 时:
M A 0, 4P3 2P2 14P1 4FB 0
解得: FB=870kN
Fiy 0, FA FB P1 P2 P3 0
解得: FA=210kN
第三章29目 录源自F2cos60
F3
cos45
F4
cos45
129.3N
FRy
F iy
F1 sin 30
3平面力系的合成与平衡PPT课件

You Know, The More Powerful You Will Be
谢谢你的到来
学习并没有结束,希望大家继续努力
Learning Is Not Over. I Hope You Will Continue To Work Hard
演讲人:XXXXXX 时 间:XX年XX月XX日
[b]
应用:平面一般力系平衡条件
一矩式:
MA 0 RB 4 Mo 0
RB 2kN
Fy 0 RB RA 0
RA 2kN
二矩式:
Fx 0 HA 0 MB 0 RA 4 Mo 0
[d]
应用:平面平行力系平衡条件
一矩式:
MA 0 MA F 2 Mo 0
0
条件:x 轴不AB 连线
三矩式:
M M
A(F ) B (F )
0 0
M
C (F )
0
条件:A,B,C不在 同一直线上
每一种表达式有三个独立方程,只能求出三个未知数。
解题步骤: ➢选取研究对象,画受力图 ➢建立直角坐标系 ➢列平衡方程并求解
[例] 已知:P, a , 求:A、B两点的支座反力?
①力线平移定理揭示了力与力偶的关系:力 力+力偶 ②力平移的条件是附加一个力偶m,且m与d有关,m=F•d ③力线平移定理是力系简化的理论基础。
3.3 平面一般力系的合成
平面任意力系:各力的作用线在同一平面内,既不汇交为一点 又不相互平行的力系叫∼。
[例]
力系向一点简化:把未知力系(平面任意力系)变成已知 力系(平面汇交力系和平面力偶系)
一般力系(任意力系)向一点简化汇交力系+力偶系
(未知力系)
(已知力系)
汇交力系
谢谢你的到来
学习并没有结束,希望大家继续努力
Learning Is Not Over. I Hope You Will Continue To Work Hard
演讲人:XXXXXX 时 间:XX年XX月XX日
[b]
应用:平面一般力系平衡条件
一矩式:
MA 0 RB 4 Mo 0
RB 2kN
Fy 0 RB RA 0
RA 2kN
二矩式:
Fx 0 HA 0 MB 0 RA 4 Mo 0
[d]
应用:平面平行力系平衡条件
一矩式:
MA 0 MA F 2 Mo 0
0
条件:x 轴不AB 连线
三矩式:
M M
A(F ) B (F )
0 0
M
C (F )
0
条件:A,B,C不在 同一直线上
每一种表达式有三个独立方程,只能求出三个未知数。
解题步骤: ➢选取研究对象,画受力图 ➢建立直角坐标系 ➢列平衡方程并求解
[例] 已知:P, a , 求:A、B两点的支座反力?
①力线平移定理揭示了力与力偶的关系:力 力+力偶 ②力平移的条件是附加一个力偶m,且m与d有关,m=F•d ③力线平移定理是力系简化的理论基础。
3.3 平面一般力系的合成
平面任意力系:各力的作用线在同一平面内,既不汇交为一点 又不相互平行的力系叫∼。
[例]
力系向一点简化:把未知力系(平面任意力系)变成已知 力系(平面汇交力系和平面力偶系)
一般力系(任意力系)向一点简化汇交力系+力偶系
(未知力系)
(已知力系)
汇交力系
-建筑力学第三章平面力系的合成与平衡

平面汇交力系合成与平衡的几何法小 结
几何法解题步骤:1. 取研究对象;2. 画受力图; 3. 作力多边形;4. 选比例尺; 5. 解出未知数。
几何法解题不足: 1. 精度不够,误差大; 2. 作图要求精度高; 3. 不能表达各个量之间的函数关系。
平面汇交力系合成与平衡的另一种方法: 解析法(重点掌 握)。
R0
Rx2
R
2 y
0
或:力系中所有力在各个坐标轴上投影的代
数和分别等于零。
Rx Fx 0 Ry Fy 0
为平衡的充要条件, 也叫平衡方程
解析法求解汇交力系平衡问题的一般步骤:
1.选-对像;即依需选分离体,分离体选取应最好含题设
的已知条件; 2.画-分离体受力图,作到准确无误;
应用力线平移定理,可将刚体上平面任意力系中各个力
的作用线全部平行移到作用面内某一给定点O 。从而这
力系被分解为平面汇交力系和平面力偶系。这种变换的
方法称为力系向给定点O 的简化。点O 称为简化中心。 R0 -----主矢,与简化中心选取无关; M0 ---主矩,与简化中心有关。
2、主矢和主矩 (1)主矢R0
F3 F2
D
C
F2 F4 F3
R
F4
R
F4
E
E
3、汇交力系的合成结果
汇交力系可以合成为一个力,合力作用在力系
的公共作用点,它等于这些力的矢量和,并可由这
力系的力多边形的封闭边表示。
矢量的表达式:R F1 F 2
F1
A F2
F4 F3
F1
A
B F2
R
C
F3
D
F4
n
第三章 平面力系的合成与平衡

上一页 下一页 返回
第一节 平面汇交力系
求解得到 负号表示受力图中S’BC的方向与实际相反,在斜杆中实为压力。
上一页
返回
第二节 平面力偶系
一、力对点的矩及合力矩定理
1.力对点的矩 从实践中知道,力对物体的作用效果除了能使物体移动外,还能使物体
转动。力对点的矩是很早以前人们在使用杠杆、滑轮、绞盘等机械搬运 或提升重物时所形成的一个概念。现以扳手拧螺母为例来加以说明。如 图3-9所示,在扳手上加一力F,可以使扳手绕螺母的轴线旋转。 实践经验表明扳手的转动效果不仅与力F的大小有关,而且还与O点到 力作用线的垂直距离d有关。当d保持不变时,力F越大,转动越快。当 力F不变时,d值越大,转动也越快。若改变力的作用方向,则扳手的转 动方向就会发生改变,因此,我们用F与d的乘积和适当的正负号来表示 力F使物体绕O点转动的效应。
上一页 下一页 返回
第一节 平面汇交力系
做法是:选取适当的比例尺表示力的大小,按选定的比例尺依次作出两个 分力矢量F1和F2,并使二矢量首尾相连。再从第一个矢量的起点向另一 矢量的终点引矢量R,它就是按选定的比例尺所表示的合力矢量,如图 3-5(b)所示。上述方法又称为力的三角形法则。
我们可以利用几何关系计算出合力R的大小和方向。如果给定两个分力 F1和F2的大小及它们之间的夹角α ,应用余弦定理,如图3-5 (b)所示, 可求得合力R的大小为
上一页 下一页 返回
第一节 平面汇交力系
= 20X0.+30 X 0. 866-10 X 0. 707-25X 0. 707 =11.24 (kN) (2)计算合力的大小与方向。
由于∑X>0,艺∑Y>0,所以合力R指向右上方,作用线通过原汇交力系的 汇交点O如图3-7所示。
第一节 平面汇交力系
求解得到 负号表示受力图中S’BC的方向与实际相反,在斜杆中实为压力。
上一页
返回
第二节 平面力偶系
一、力对点的矩及合力矩定理
1.力对点的矩 从实践中知道,力对物体的作用效果除了能使物体移动外,还能使物体
转动。力对点的矩是很早以前人们在使用杠杆、滑轮、绞盘等机械搬运 或提升重物时所形成的一个概念。现以扳手拧螺母为例来加以说明。如 图3-9所示,在扳手上加一力F,可以使扳手绕螺母的轴线旋转。 实践经验表明扳手的转动效果不仅与力F的大小有关,而且还与O点到 力作用线的垂直距离d有关。当d保持不变时,力F越大,转动越快。当 力F不变时,d值越大,转动也越快。若改变力的作用方向,则扳手的转 动方向就会发生改变,因此,我们用F与d的乘积和适当的正负号来表示 力F使物体绕O点转动的效应。
上一页 下一页 返回
第一节 平面汇交力系
做法是:选取适当的比例尺表示力的大小,按选定的比例尺依次作出两个 分力矢量F1和F2,并使二矢量首尾相连。再从第一个矢量的起点向另一 矢量的终点引矢量R,它就是按选定的比例尺所表示的合力矢量,如图 3-5(b)所示。上述方法又称为力的三角形法则。
我们可以利用几何关系计算出合力R的大小和方向。如果给定两个分力 F1和F2的大小及它们之间的夹角α ,应用余弦定理,如图3-5 (b)所示, 可求得合力R的大小为
上一页 下一页 返回
第一节 平面汇交力系
= 20X0.+30 X 0. 866-10 X 0. 707-25X 0. 707 =11.24 (kN) (2)计算合力的大小与方向。
由于∑X>0,艺∑Y>0,所以合力R指向右上方,作用线通过原汇交力系的 汇交点O如图3-7所示。
第三章.平面力系的合成与平衡

各力首尾相接
§3-1 平面汇交力系的合成与平衡
例4
已知:
系统如图,不计杆、轮自重,忽略滑轮大小,P=20kN; 求:系统平衡时,杆AB、BC受力。 解:AB、BC杆为二力杆, 取滑轮B(或点B),画受力图。
用解析法,建图示坐标系。
F
x
0
FBA F1 cos 60 F2 cos 30 0
Fy F cos F Fx Fy
Fx cos F
Fx
x
O
Fx
F Fx2 Fy2
cos
Fy F
§3-1 平面汇交力系的合成与平衡 3)合力投影定理 平面汇交力系,由三个力组成的力多边形 合力投影定理建立了合力投影与各分力投影的关系
FRx Fix
当 x轴与 y 轴不是正交轴时 :
F Fx Fy
力在坐标轴上的投影不等于力在这个轴上的分量。
§3-1 平面汇交力系的合成与平衡 2、平面汇交力系的解析法 2)力沿坐标轴的分解 当
Fx Fx
x y
y
Fy Fy
B
Fy
Fx F cos
Fy
A
β α
矢量和
θ
P
FNA 11.4kN FNB 10kN
F
FNB
F
θ P FNA
§3-1 平面汇交力系的合成与平衡 2、平面汇交力系的解析法 1)力在坐标轴上的投影 F力在 x 轴上的投影:
Fx F cosθ
Fy
Fx
F力在 y 轴上的投影:
Fy F cosβ
3 FR 2 FR1 F3 Fi i 1
第三章:平面力系的合成与平衡1
x
图b 力在坐标轴上的投影
由图b知,若已知力 F 的大小 和其与x轴、y轴的夹角为
、 ,则力在x、y轴上的投影为
Fx F cos
Fy F cos F sin
即力在某轴上的投影等于力的模乘以力与该轴的正向间夹
角的余弦。这样当 、 为锐角时, Fx、Fy 均为正值;
当 、 为钝角时, Fx、Fy可能为负值。
0 2 0 0 0 sin 3 0 0 2 0 7 N
第一节 汇交力系的合成与平衡
合力的大小:
FR
F
2 Rx
F
2 Ry
473
N
合力与轴x,y夹角的方向余弦为:
cos( FR , x)
cos
425 473
0.9
cos( FR , y ) cos
207 473
FA (b)
F F B sin q 1 0 k N , F A P F B c o s q 1 1 . 3 4 k N
(a)
FB
P FA
F
(c)
例题
FO
P
FB B
A
FA
FB
P
FA
c
F
2. 碾子能越过障碍的力学条
件是 FA=0, 得封闭力三角形abc。
由此可得
a
FB P
Fmin b
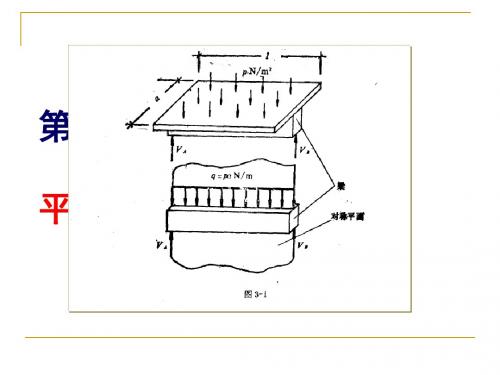
例如,厂房建筑中常采用刚架结构,取其中一个刚架 来考察,如图a所示,作用于其上的力可简化为图b所示的 平面力系。
第二节 平面任意力系的简化
有些空间力系的问题,可近似地简化为平面力系问 题来分析计算。
如水利工程上常见的重力坝,如图a所示。在对其进行 力学分析时,往往取单位长度(如1m)的坝段来考察, 而将坝段所受的力简化成为作用于坝段中央平面内的平面 力系,如图b所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1.2数解法
我们在第一章已讨论了力在坐标 轴上的投影规则和方法。现在我们 来讨论平面汇交力系各力投影与汇 交力系合力投影之间的关系。
设有一平面汇交力系F1、F2作用
在物体的A点,如图。根据平行四 边形法则可求得该力系的合力R 。
F1x ab1 F2x ab2 而 ab2 b1c
R x a c a b 1 b 1 c a b 1 a b 2 F 1 x F 2 x F1y ab1 F2y ab2 ab1 b2c
【例2】固定于墙内的环形螺钉上,作用有3个力
F1、
F
、
2
F
3
,各
力的方向如图所示,各力的大小分别为 F1 3kN, F2 4kN
F3 5kN。试求螺钉作用在墙上的力。
解:要求螺钉作用在墙上的力可先求作用在螺钉上三力合力。
R x F x F 1 x F 2 x F 3 x 0 4 5 c o s 3 0 8 . 3 3 k N
R y a c a b 2 b 2 c a b 2 a b 1 F 1 y F 2 y
R Rx2 Ry2
tan R y Rx
设有一平面汇交力系F1、F2、F3作用在物体的 点,如图。
根据平行四边形法则可求得该力系的合力 R 。 O
R F 1F 2F 3F i R23xF2xF3x Rx F1xR23x
3.1 平面汇交力系的合成与平衡 3.1.1平面汇交力系的概念和实例
在平面力系中,如果 平面汇交力系; 平面平行力系; 平面一般力系。
3.1 平面汇交力系的合成与平衡
3.1.1平面汇交力系的概念和实例
平面汇交力系是力系中最简单的一种,在工程中有很多实 例。例如,起重机起吊重物时,作用于吊钩C的三根绳索的
R R x 2 R y 21 2 3 .2 2 ( 2 6 3 .4 )2 2 9 0 .8 N
tan Ry 263.42.138
Rx 123.2
64.9
例1 如图所示,已知F1=20kN,F2=40kN,如果三个力F1、 F2、F3的合力R沿铅垂向下,试求力F3和R的大小。
解: 取直角坐标系如图所示。因已知合力R沿y轴向下,故
第3章 平面力系的合成与平衡
[内容提要]本章主要介绍了用解析法推出的平面力系平衡条件,以 及平衡条件的应用。
实际工程中,作用在构件或结构上的力系是多种多样的。但是 , 按照力作用线的分布情况,主要分为两类力系:凡各力的作用线都 在同一平面内的力系称为;凡各力的作用线不在同一平 面内的力系,称为。
在实际工程中,有些结构的某一尺寸比其它两个方向的尺
Rx=0,Ry= -R。由式(2-2)知,得
Rx Fx 0
0 F 1 F 2co s2 5 F 3co sa
020400.906F332442
F3 70.3kN
又由
Ry Fy
0 F2 sin 25 F3 sin
3 40 0.423 70.3
32 42 59.1kN
R Rx2Ry2 59.1kN
的荷载有一个共同的对称面 ,
那么,作用在结构上的力系 就可以简化为在对称面内的 平面力系,例如图所示沿直 线行驶的汽车,反力的合力RA
R面B,内都,总可组之简成,化平在到面工汽一程车般中的力,对系许称。多结构的力学问题,可以简化为平 面力系的问题来处理。本章将讨论平面力系的简化和平衡 问题。
当以各个铰结点(或称节点)为研究对象时,与结点相连接 的各杆作用于该节点上的力也组成一个平面汇交力系。例如
, 图b)就是结点C的受力图,它构成了一个平面汇交力系。
研究平面汇交力系,一方面可以解决一些简单的工程 实际问题,另一方面也为研究更复杂的力系打下基础。
• 平面汇交力系的合成问题可以采用几何法 和解析法进行研究。其中,平面汇交力系 的几何法具行直观、简捷的优点,但其精 确度较差,在力学中用得较多的还是解析 法。这种方法是以力在坐标轴上的投影的 计算为基础。
R y F y i F y 1 F y 2 F y 3 3 0 5 s i n 3 0 0 . 5 k N
且F1 250N,F2 200N,F3 100N, 3 0 , 60 。用数
解法求此平面汇交力系的合力R 。 解:
Rx F1xF2xF3x
0F2cosF3cos
200cos30100cos60 123.2N
RyF1yF2yF3yF1F2sinF3sin
250200sin30100sin60 263.4N
拉平力面汇T 交、T 力A 、系T B。都又在如同三一角平支面架内当,不且计汇杆交的于自一重点时,,就作组用成于了铰
B上的三个力FN1、FN2、T 也组成平面汇交力系。
又如图所示的屋架,它通常被看作为由一些在其两端用光 滑圆柱铰互相连接的直杆组成,而且由于各杆的自重比屋架 所承受的各个荷载小很多而可忽略不计,因此每根直杆都在 作用于其两端的两个力的作用下处于平衡。
注意:式中各分量的正负号选取。 从图中的几何关系可知,合力R的 大小和方向可由下式确定:
R Rx2 Ry2 (
Fx)2 (
Fy)2
tan Ry Fy
Rx
Fx
(3-5)
式中 为合力R与x轴所夹的锐角, 角在哪个象限由
F x 和 F y 的正负号来确定。
例3-3 已知作用在刚体上并交于o点的三力均在 x o y 平面内,
寸小的多或大得多。忽略次要因素后,我们可把这种结构看
成为平面结构。如图所示的挡土墙,考虑到它沿长度方向受
力情况大致相同,通常取1M长度的墙身作为研究对象,它所 受到的重力G、土压力P和地基反力R也都可简化到1M长墙身 的对称面上,组成平面力系。
还有些结构虽然明显不是 受平面力系作用,但如果本 身(包括支座)及其所承受
因此可得
RxF 1xF2xF3x
RyF1yF2yF3y
这一关系可推广到任意平面汇交力的情形,即
R x F 1 x F 2 x F n x F i x F x
(3-4)
R y F 1 y F 2 y F n y F i y F y
由此可见,合力在任一轴上的投影,等于各分力在同一 轴上投影的代数和。这就是合力投影定理。
