浙教版数学九年级上1.1反比例函数同步练习三

合集下载

2018-2019年初中数学浙教版《九年级上》《第一章反比例函数》《1.3 反比例函数的应用》同步

2018-2019年初中数学浙教版《九年级上》《第一章反比例函数》《1.3 反比例函数的应用》同步练习试卷【9】含答案考点及解析班级:___________ 姓名：___________ 分数：___________ 题号一二三总分得分注意事项： 1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上评卷人得分一、选择题 1.根据下图所示程序计算函数值，若输入的x的值为，则输出的函数值为 ( ) A．B．C．D．【答案】B【解析】∵x＝时，在2≤x≤4之间，∴将x＝代入函数y＝，得y＝. 2.如果反比例函数y＝的图象经过点(－1，－2)，则k的值是( ) A．2B．－2C．－3D．3 【答案】D 【解析】∵反比例函数图象过点(－1，－2)∴－2＝. k＝3.故选D.23.已知矩形的面积为20 cm，设该矩形一边长为y cm，另一边的长为x cm，则y与x之间的函数图象大致是( )【答案】B 【解析】∵矩形的面积＝长×宽∴xy＝20 y＝又∵这是一个实际问题，∴函数图象只能在第一象限，故选B.4.某村的粮食总产量为a(a为常数)吨，设该村的人均粮食产量为y 吨，人口数为x，则y与x 之间的函数关系式的大致图象应为()【答案】C【解析】因xy＝a，y＝，y与x成反比例，所以选C.333 5.一定质量的干木,当它的体积V=4m时,它的密度ρ=0.25×10kg/m,则ρ与V的函数关系式是 A．ρ=1000V B．ρ=V+1000C．ρ=D．ρ=【答案】D333【解析】由ρ=，体积V=4m时,密度ρ=0.25×10kg/m，则质量=1000kg，因为质量不变，所以有ρ=.6.若反比例函数y=﹣的图象经过点A（2，m），则m的值是（）A．-2B．2C．D．【答案】B.【解析】试题分析：∵点（2，m）在反比例函数y=的图象上，∴．故选B.考点: 反比例函数图象上点的坐标特征．7.当＞0，＜0时，反比例函数的图象在（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】C【解析】当时，反比例函数的图象在第一、三象限，当时，函数图象在第三象限，所以选C.8.反比例函数的图象在（）A．第一、三象限B．第一、二象限C．第二、四象限D．第三、四象限【答案】C【解析】试题分析：反比例函数：当时，图象位于第一、三象限；当时，图象位于第二、四象限.∴反比例函数的图象在第二、四象限故选C.考点：反比例函数的性质点评：本题是反比例函数的性质的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，难度一般.9.反比例函数的共同点是（）A．图象位于同样的象限B．自变量取值范围是全体实数C．图象关于直角坐标系的原点成中心对称.D．y随x的增大而增大【答案】C【解析】试题分析：根据反比例函数的图象的特点即可得所给函数的共同点．∵所给反比例函数的比例系数不同∴所在象限不同，自变量的取值范围应是非0数；图象关于直角坐标系的原点成中心对称；没有相应规律的函数的增减性故选C．考点：反比例函数的性质点评：本题是反比例函数的性质的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，难度一般.评卷人得分二、填空题10.如图，直线x=2与反比例函数y＝和y＝−的图象分别交于A、B两点，若点P是y轴上任意一点，则△PAB的面积是( )．【答案】【解析】先分别求出A、B两点的坐标，得到AB的长度，再根据三角形的面积公式即可得出△PAB的面积．解：∵把x=2分别代入y＝、y＝−，得y=1、y=-．∴A（2，1），B（2，-），∴AB=1-（-）=．∵P为y轴上的任意一点，∴点P到直线x=2的距离为2，∴△PAB的面积=AB×2=AB=．。

浙教版九年级上 1.1反比例函数(第一课时) 同步练习

第1章反比例函数第1课时反比例函数（1）【知识要点】1．形如(0)k y k x=≠的函数叫做反比例函数. 2．两个变量成反比例，则它们的积是一个不为零的常数.课内同步精练●A 组基础练习1．下列函数中是反比例函数的是（）A.y=-xB.(0)x y kk =≠ C.y = D.24y x = 2．下列说法正确的是（）A ．圆面积公式S=πr 2中，S 与r 成正比例关系B ．三角形面积公式S =12ah 中，当S 是常量时，a 与h 成反比例关系 C ．11y x=+中，y 与x 成反比例关系 D ．12x y -=中，y 与x 成正比例关系 3．矩形面积是40m 2，设它的一边长为x(m)，则矩形的另一边长y(m)与x 的函数关系是（ ) A.1202y x =- B.y=40x C.40y x = D.40x y = 4．s 、v 、t 分别表示路程、速度与时间，当v 为常数时, s 与t 的函数关系为，属于函数；s 为常数时v 与t 的函数关系式是 .5．九年级的全体师生500人准备用10000只纸鹤来表达对2008年北京奥运会的美好祝愿，如果每人每天折x 只，y 天能够完成，求y 关于x 的函数关系式．●B 组提高训练6.圆柱的侧面积是10π，则圆柱的高线长h 与圆柱的底面半径r 之间的函数关系是 .7.一个无盖的长方体木箱的体积是400O0cm 2, (1）如果它的底面积为acm ，高为hcm ，求h 关于a 的函数关系式．(2）如果这个长方体的底是边长为xcm 的正方形，求它的表面积S （cm 2）关于x 的函数关系式．课外拓展练习●A 组基础练习1.当路程一定时，速度v 与时间t 之间的函数关系是( )A ．正比例函数B ．反比例函数C ．一次函数D ．不能确定2.下列函数式中，属于反比例函数的是（ )A.y=x+2B.2x y =C.12y x =+D.1y x=- 3．当三角形面积是8cm 2时，它的底边上的高h (cm ）与底边长x(cm)之间的函数解析式是 .4．把23y x =-化为k y x=的形式为；比例系数为 .5．两个整数x 与y 的积为10 , (1)求y 关于x 的函数关系式； (2)写出比例系数；(3)写出自变量x 的取值范围．6．试写出一个实际生活中的反比例函数．●B 组提高训练7．一定质量的二氧化碳气体，当它的体积V=5m 2时，它的密度ρkg/m 3. (1）求ρ与V 的函数关系式；(2)当V=9m 3时二氧化碳的密度ρ8．某工厂生产化肥的总任务一定时，每天生产化肥y 吨和生产天数x 之间成反比例关系，如果每天生产化肥125吨，那么完成总任务需要7天．(l）求y关于x的函数关系式，并指出比例系数．(2）若要5天完成总任务，那么每天需要生产化肥多少吨？。

九年级(初三)上册数学作业本答案浙教版

九年级(初三)上册数学作业本答案浙教版第一章反比例函数【1.1(1)】1.否，是，是，是，否;/，3，1/2，-π，/2.x≠0的全体实数，1/4，-13.答案不唯一.如函数解析式为y=12/x，此时有(1)3 (2)3/2 (3)-3/24.(1)v=240/t (2)当t=3.2h时，v=75km/h5.(1)S=600/x (2)a=300/b6.(1)a=16/h，h取大于0的全体实数(2)上、下底的和为8cm，腰AB=CD=2√2cm，梯形的周长为(8+4√2)cm【1.1(2)】1.-122.y=10/x，x≠0的全体实数3.y=-√6/x.当x=√6时，y=-14.(1)y=2z，z=-3/x(2)x=-3/5，y=10(3)y=-6/x，是5.(1)D=100/S(2)150度6.(1)y=48/x，是，比例系数48的实际意义是该组矩形的面积都为48cm(2)设矩形的一边长是a(cm)，则另一边长是3a(cm).将x=a，y=3a代入y=48/x，可得a=4，故该矩形的周长是2(a+3a)=32(cm)【1.2(1)】1.y=-√2/x2.B3.(1)表略(2)图略4.(1)y=4/x(2)图略5.(1)反比例函数的解析式为y=8/x，一个交点的坐标为(2，4)，另一个交点的坐标为(-2，-4)6.根据题意得{3m-1>0，1-m>0，解得1/3。

数学：第1章《反比例函数》单元测试3(浙教版9年级上)

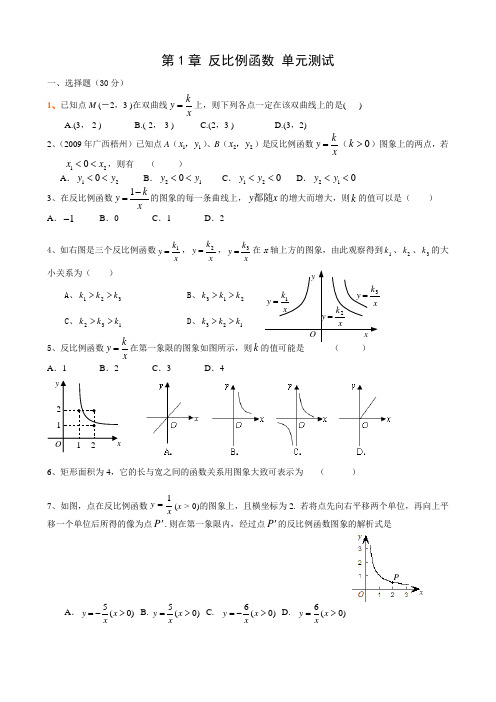
Oyxxky 1=xk y 2=xk y 3=第1章反比例函数单元测试一、选择题（30分）1、已知点M (－2，3 )在双曲线xky =上，则下列各点一定在该双曲线上的是( ) A.(3，-2 ) B.(-2，-3 ) C.(2，3 ) D.(3，2)2、（2009年广西梧州）已知点A （11x y ，）、B （22x y ，）是反比例函数xky =（0>k ）图象上的两点，若210x x <<，则有（）A ．210y y <<B ．120y y <<C ．021<<y yD ．012<<y y3、在反比例函数1ky x-=的图象的每一条曲线上，y x 都随的增大而增大，则k 的值可以是（）A ．1-B ．0C ．1D ．24、如右图是三个反比例函数x k y 1=，x k y 2=，xk y 3=在x 轴上方的图象，由此观察得到1k 、2k 、3k 的大小关系为（）A 、321k k k >>B 、213k k k >>C 、132k k k >>D 、123k k k >>5、反比例函数ky x=在第一象限的图象如图所示，则k 的值可能是（）A ．1B ．2C ．3D ．46、矩形面积为4，它的长与宽之间的函数关系用图象大致可表示为（）7、如图，点在反比例函数1y x =(x > 0)的图象上，且横坐标为2. 若将点先向右平移两个单位，再向上平移一个单位后所得的像为点P '.则在第一象限内，经过点P '的反比例函数图象的解析式是A ．)0(5>-=x xy B .)0(5>=x x y C . )0(6>-=x x y D . )0(6>=x x yP1 2 21 Oy x8、如图，直线y=mx 与双曲线y=xk交于A 、B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM,若ABM S ∆=2，则k 的值是（）A ．2B 、m-2C 、mD 、49、函数8y x=，若-4≤x<-2,则（） A 、2≤y<4 B 、-4≤y<-2 C 、-2≤y<4 D 、-4<y ≤-210．函数y 1=xk和y 2=kx-k 在同一坐标系中的图象大致是( )二、填空题（30分）11、（2009年台州市）请你写出一个图象在第一、三象限的反比例函数．答：．12、若反比例函数1232)12(---=k kx k y 的图象经过二、四象限，则k = _______；13、近视眼镜的度数y （度）与镜片焦距x （米）成反比例. 已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数y 与镜片焦距x 之间的函数关系式是_____________； 14、点A (2，1)在反比例函数y kx=的图像上，当y<2时，x 的取值范围是 15、如图4，反比例函数xky =)0(<k 的图象与经过原点的直线l 相交于A 、B 两点，已知A 点坐标为)1,2(-，那么B 点的坐标为 .16．正比例函数y=x 与反比例函数y=1x的图象相交于A 、C 两点.AB ⊥x 轴于B,CD ⊥y 轴于D(如图),则四边形ABCD 的面积为_______________三、解答题17．（本题8分）如图，第一象限的角平分线OM 与反比例函数的图象相交于点A ，已知OA =22.(1)求点xy 图41 A B O 1 lA 的坐标；(2)求此反比例函数的解析式.18、（2009肇庆）如图 7，已知一次函数1y x m =+（m 为常数）的图象与反比例函数 2ky x=（k 为常数， 0k ≠）的图象相交于点 A （1，3）．（1）求这两个函数的解析式及其图象的另一交点的坐标；（2）观察图象，写出使函数值12y y ≥的自变量的取值范围．19、（2009河池）为了预防流感，某学校在休息天用药熏消毒法对教室进行消毒．已知药物释放过程中，室内每立方米空气中的含药量（毫克）与时间（分钟）成正比例；药物释放完毕后，与成反比例，如图9所示．根据图中提供的信息，解答下列问题：（1）写出从药物释放开始，与之间的两个函数关系式及相应的自变量取值范围；（2）据测定，当空气中每立方米的含药量降低到0.45毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能进入教室？yB 1-1- 1 2 3 3 12 A （1，3）y20、(2009年达州)如图8，直线b kx y +=与反比例函数xk y '=（＜0）的图象相交于点A 、点B ，与x 轴交于点C ，其中点A 的坐标为（－2，4），点B 的横坐标为－4.（1）试确定反比例函数的关系式；（2）求△AOC 的面积.。

九年级上反比例函数同步训练1

九年级上反比例函数同步训练 1姓名： __________一•判断题1 .如果y 是x 的反比例函数，那么当 x 增大时，y 就减小（） 2 •当x 与y 乘积一定时，y 就是x 的反比例函数，x 也是y 的反比例函数（） 3 •如果一个函数不是正比例函数，就是反比例函数（）4.y 与x 2成反比例时y 与x 并不成反比例（） 5.y 与2x 成反比例时，y 与x 也成反比例（）x6 •已知y 与x 成反比例，又知当 x =2时，y =3，贝u y 与x 的函数关系式是 y （）6二.填空题k1. y=— （k z 0）叫 ____________ 函数.,x 的取值范围是 _____________ ；x2 •已知三角形的面积是定值 S ,则三角形的高h 与底a 的函数关系式是h = ______________ ,这时h 是a 的 ___________3 •如果y 与x 成反比例，z 与y 成正比例，则 z 与x 成 ______ __________ .;4•如果函数y=kx 2"永'是反比例函数，那么 k= _____________ ，此函数的解析式是 _____________ ; 三•辨析题（1 ）兄弟二人分吃一碗饺子，每人吃饺子的个数如下表:① 写出兄吃饺子数 y 与弟吃饺子数x 之间的函数关系式（不要求写 xy 的取值范围）② 虽然当弟吃的饺子个数增多时，兄吃的饺子数（y ）在减少，但y 与x 是成反例吗?（2）水池中有水若干吨，若单开一个出水口，水流速v与全池水放光所用时t如下表:① 写出放光池中水用时 t （小时）与放水速度v （吨/小时）之间的函数关系. ② 这是一个反比例函数吗？③ 与（1）的结论相比，可见并非反比例函数有可能“函数值随自变量增大而减小”，反之，所有的反比例函数都是“函数值随自变量的增大而减小吗？这个问题，你可以提前探索、尝试，也可以预习下一课时”反比例函数的图象和性质，也可以等到下一节课我们共同解决四•解答题：k1 .已知一次函数 y = -x • 6和反比例函数y （ k 丰0）x（1）k满足什么条件时这两个函数在同一坐标系xoy中图象有两个公共交点。

九年级数学上册( 反比例函数)同步练习(无答案) 浙教版试题

暑期专题复习第二讲反比例函数知识讲解1．反比例函数的图像是双曲线，故也称双曲线y=kx（k≠0）．2．反比例函数y=kx（k≠0）的性质（1）当k>0时⇔函数图像的两个分支分别在第一，三象限内⇔在每一象限内，y随x的增大而减小．（2）当k<0时⇔函数图像的两个分支分别在第二，四象限内⇔在每一象限内，y随x的增大而增大．（3）在反比例函数y=kx中，其解析式变形为xy=k，故要求k的值，•也就是求其图像上一点横坐标与纵坐标之积，•通常将反比例函数图像上一点的坐标当作某一元二次方程的两根，运用两根之积求k的值．（4）若双曲线y=kx图像上一点（a，b）满足a，b是方程Z2－4Z－2=0的两根，求双曲线的解析式．由根与系数关系得ab=－2，又ab=k，∴k=－2，故双曲线的解析式是y=2x-．（5）由于反比例函数中自变量x和函数y的值都不能为零，所以图像和x轴，y•轴都没有交点，但画图时要体现出图像和坐标轴无限贴近的趋势．例题解析例1如图，在直角坐标系中，O为原点，点A在第一象限，它的纵坐标是横坐标的3倍，反比例函数y=12x的图像经过点A，（1）求点A的坐标；（2）如果经过点A的一次函数图像与y轴的正半轴交于点B，且OB=AB，•求这个一次函数的解析式．例2 如图，已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数y=mx的图像在第一象限内的交点，且S△AOB=3．（1）该一次函数与反比例函数的解析式是否能完全确定？如能确定，•请写出它们的解析式；如不能确定，请说明理由．（2）如果线段AC的延长线与反比例函数的图像的另一支交于D点，过D作DE⊥x 轴于E，那么△ODE 的面积与△AOB的面积的大小关系能否确定？（3）请判断△AOD为何特殊三角形，并证明你的结论例3 如图，已知反比例函数y=kx（k<0）的图像经过点A（－3，m），•过点A作AB⊥x轴于点，且△AOB 的面积为3．（1）求k和m的值；（2）若一次函数y=ax+1的图像经过点A，并且与x轴相交于点C，求∠ACO•的度数为│AO│：│AC│的值．同步练习一、填空题1．（2006，南通）如图1，直线y=kx（k>0）与双曲线y=4x交于A（x1，y1），B（x2，y2）两点，•则2x1y2－7x2y1的值等于_______．图1 图2 图32．（2006，重庆）如图2，矩形AOCB的两边OC，OA分别位于x轴，y轴上，点B的坐标为B（－203，5），D是AB边上的一点，将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图像上，那么该函数的解析式是______．3．近视眼镜的度数y （度）与镜片焦距x （m ）成反比例，已知400•度近视眼镜镜片的焦距为0.25m ，则y 与x 的函数关系式为_______． 4．若y=2131a a a x--+中，y 与x 为反比例函数，则a=______．若图像经过第二象限内的某点，则a=______． 5．反比例函数y=k x的图像上有一点P （a ，b ），且a ，b 是方程t 2－4t －2=0的两个根，则k=_______；点P 到原点的距离OP=_______．6．已知双曲线xy=1与直线y=－x+b 无交点，则b 的取值范围是______． 7．反比例函数y=k x的图像经过点P （a ，b ），其中a ，b 是一元二次方程x 2+kx+4=0的两个根，那么点P 的坐标是_______．8．（2008，咸宁）两个反比例函数y=k x 和y=1x 在第一象限内的图像如图3所示，•点P 在y=kx的图像上，PC⊥x 轴于点C ，交y=1x 的图像于点A ，PD⊥y 轴于点D ，交y=1x 的图像于点B ，•当点P 在y=kx的图像上运动时，以下结论：①△ODB 与△OCA 的面积相等； ②四边形PAOB 的面积不会发生变化； ③PA 与PB 始终相等④当点A 是PC 的中点时，点B 一定是PD 的中点．其中一定正确的是_______（把你认为正确结论的序号都填上，•少填或错填不给分）．二、选择题9．（2008，济南）如图4所示，等腰直角三角形ABC 位于第一象限，AB=AC=2，直角顶点A 在直线y=x 上，其中A 点的横坐标为1，且两条直角边AB ，AC 分别平行于x 轴，y 轴，•若双曲线y=kx（k≠0）与△ABC 有交点，则k 的取值范围是（）A ．1<k<2B ．1≤k≤3C ．1≤k≤4 D．1≤k<4图4 图5 图6 10．反比例函数y=kx（k>0）的第一象限内的图像如图5所示，P 为该图像上任意一点，PQ 垂直于x 轴，垂足为Q ，设△POQ 的面积为S ，则S 的值与k 之间的关系是（） A ．S=4k B ．S=2kC ．S=kD ．S>k 11．如图6，已知点A 是一次函数y=x 的图像与反比例函数y=2x的图像在第一象限内的交点，点B 在x 轴的负半轴上，且OA=OB ，那么△AOB 的面积为（）A ．2B ．22C ．2D ．22 12．函数y=mx与y=mx －m （m≠0）在同一平面直角坐标系中的图像可能是（）13．如果不等式mx+n<0的解集是x>4，点（1，n ）在双曲线y=2x上，那么函数y=（n －1）x+2m 的图像不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 14．（2006，攀枝花）正比例函数y=2kx 与反比例函数y=1k x-在同一坐标系中的图像不可能是（）15．已知P为函数y=2x的图像上一点，且P到原点的距离为3，则符合条件的P点数为（ •）A．0个 B．2个 C．4个 D．无数个16．如图，A，B是函数y=1x的图像上关于原点O对称的任意两点，AC平行于y轴，•交x轴于点C，BD平行于y轴，交x轴于点D，设四边形ADBC的面积为S，则（）A．S=1 B．1<S<2 C．S=2 D．S>2三、解答题17．已知：如图，反比例函数y=－8x与一次函数y=－x+2的图像交于A，B两点，求：（1）A，B两点的坐标；（2）△AOB的面积．18．（2006，广州白云区）如图，已知一次函数y=kx+b的图像与反比例函数y=－8x的图像交于A，B两点，且点A的横坐标和点B的纵坐标都是－2，求：（1）一次函数的解析式；（2）△AOB的面积．19．已知函数y=kx的图像上有一点P（m，n），且m，n是关于x方程x2－4ax+4a2－6a－8=0•的两个实数根，其中a是使方程有实根的最小整数，求函数y=kx的解析式．20．（2006，北京市）在平面直角坐标系Oxy中，直线y=－x绕点O顺时针旋转90 °得到直线L．直线L与反比例函数y=kx的图像的一个交点为A（a，3），试确定反比例函数的解析式．21．（2008，南通）如图所示，已知双曲线y=kx与直线y=14x相交于A，B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线y=kx上的动点．过点B作BD∥y轴交x轴于点D．•过N（0，－n）作NC∥x轴交双曲线y=kx于点E，交BD于点C．（1）若点D的坐标是（－8，0），求A，B两点的坐标及k的值；（2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式；（3）设直线AM，BM分别与y轴相交于P，Q两点，且MA=pMP，MB=qMQ，求p－q的值．22．如图，在等腰梯形ABCD中，CD∥AB，CD=6，AD=10，∠A=60°，以CD•为弦的弓形弧与AD相切于D，P是AB上的一个动点，可以与B重合但不与A重合，DP•交弓形弧于Q．（1）求证：△CDQ∽△DPA；（2）设DP=x，CQ=y，试写出y关于x的函数关系式，并写出自变量x的取值范围；（3）当DP之长是方程x2－8x－20=0的一根时，求四边形PBCQ的面积．。

【九年级】九年级上册数学第1章反比例函数测试题(浙教版含答案)

【九年级】九年级上册数学第1章反比例函数测试题(浙教版含答案)第1章反比例函数检测题（本试卷满分：100分，时间：90分钟）一、（每小题3分，共30分）1.在以下选项中，如果是反比函数关系，则为（）a.在直角三角形中，30°角所对的直角边与斜边之间的关系b、在等腰三角形中，顶角和底角之间的关系c.圆的面积与它的直径之间的关系d、面积为20的钻石，一条对角线和另一条对角线之间的关系2.（2021哈尔滨中考）如果反比例函数的图象经过点(-1，-2)，则k的值是（）a、 2b.-2c.-3d。

三3.在同一坐标系中，函数和的图象大致是（）当图像的逆比例小于0（.0）时a.第一象限b.第二象限c.第三象限d.第四象限5.如果购买一个茶杯只需15元，那么一个茶杯的单价与a.（取实数）b.（取整数）c、（取自然数）d（取正整数）6.若反比例函数的图象位于第二、四象限，则的值是（）a、 0b。

0或1C0或2D四7．如图，a为反比例函数图象上一点，ab垂直于轴b点，若s△aob＝3，则的值为（）a、 6b。

3c。

d、不确定8.已知点、、都在反比例函数的图象上，则的大小关系是（）a、 b。

c.d.9.如果正比例函数和反比例函数的图像在两点a和C相交，ab⊥ X轴在点B和CD处⊥ X轴位于d点（如图所示），四边形ABCD的面积为（）a.1b.c.2d.10.（2022年福州市高中入学考试）如图所示，通过点C（1,2）分别画出x轴和y轴的平行线，相交线y=-x+6位于a点和B点。

如果反比例函数y=（x>0）的图像与△ ABC，K的取值范围为（）a.2≤k≤9b.2≤k≤8c、二,≤K≤5d。

5.≤K≤8.二、题（每小题3分，共24分）11.已知与当时成反比12．（2021山东潍坊中考）点p在反比例函数(k≠0)的图象上，点q（2,4）与点p 关于y轴对称，则反比例函数的解析式为.13.已知逆比例函数。

当时，其图像的两个分支位于第一象限和第三象限；在那个时候，它的图像随着每个象限中的亮度的增加而增加14.若反比例函数的图象位于第一、三象限内，正比例函数的图象过第二、四象限，则的整数值是________.15.有一批救灾物资需要从a市运送到B市。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.1 反比例函数同步练习
一、选择题：（5`×5=25`）
1、下列函数中，y 关于x 的反比例函数是：（） A. 1)2(=+y x B. 11+=x y C. 21x y = D.x
y 21
-= 2、如果函数x
k
y =
的图象经过（1，－1），则函数2-=kx y 的图象不经过象限是：（） A. 一 B. 二 C. 三 D. 四
3、点A （－2，1y ）与B （－1，2y ）都在反比例函数x
y 2
-=的图象上，则1y 与2y 的大小关系为：（）
A. 21y y <
B. 21y y >
C. 21y y =
D. 无法确定
4、如图，在函数x
y 1
=的图象上取三点A 、B 、C ，由这三点分别向x 轴、y 轴作垂线，设矩形AA 1OA 2、BB 1OB 2、、
CC 1OC 2的面积分别为S A 、S B 、S C ，则下列正确的是：（）
A. S A ＜S B ＜S C
B. S A ＞S B ＞S C
C. S A ＝S C ＝S B
D. S A ＜S C ＜S B 5、反比例函数x
k
y =
和一次函数k kx y -=在同一坐标系中的图象大致是：（）
二、填空题：（3`×5=15`） 6、若反比例函数m
x m y --=)1(的图象经过第二、四象限，则= .
7、已知反比例函数x
k
y =
的图象经过（－1，3），若点（2，m ）在这个图象上，则m = . 8、如图，点P 为反比例函数
x
y 2
-=上的任意一点，
作PC ⊥x 轴于C ，则△POC 的面积为 .
三、解答题：（60`）
9、已知,正比例函数y ax =图象上的点的横坐标与纵坐标互为相反数,反比例函数k
y x
=
在每一象限内y 随x 的增大而减小,一次函数24y x k a k =-++过点()2,4-.（1）求的值.（2）求一次函数和反比例函数的解析式.
10、在某一电路中，保持电压不变，电流I(安培)与电阻R(欧姆)成反比例，当电阻R=5欧姆时，电流I=2安培。

（1）求I 与R 之间的函数关系式；（2）当电流I=0.5安培时，求电阻R 的值.
11、已知：y = y 1－y 2，y 1与x 成反比例，y 2与x －2成正比例，且x = 1时，y =－1；x = 3时，y = 5，求x = 5时y 的值.
12、正比例函数x y =的图象与反比例函数x
k
y =
的图象有一个交点的纵坐标是2，求：（1）3-=x 时反比例函数的值；
（2）当13-<<-x 时反比例函数的取值范围.
13、已知反比例函数x k y =的图象经过点A （4，2
1），若一次函数1+=x y 的图象平移后经过该反比例函数图象上的点B （2，m ），求平移后的一次函数图象与轴的交点坐标.
14如图，Rt △ABO 的顶点A 是双曲线k
y x
=与直线()1y x k =--+在第二象限的交点，AB ⊥轴于B 且S △
ABO =3
2。

（1）求这两个函数的解析式（2）求直线与双曲线的两个交点A ，C 和直线AC 与x 轴的
交点D 的坐标和△AOC 的面积。