八年级上册第十一章至十三章数学提高题

合集下载

《常考题》初中八年级数学上册第十一章《三角形》提高练习(含答案解析)

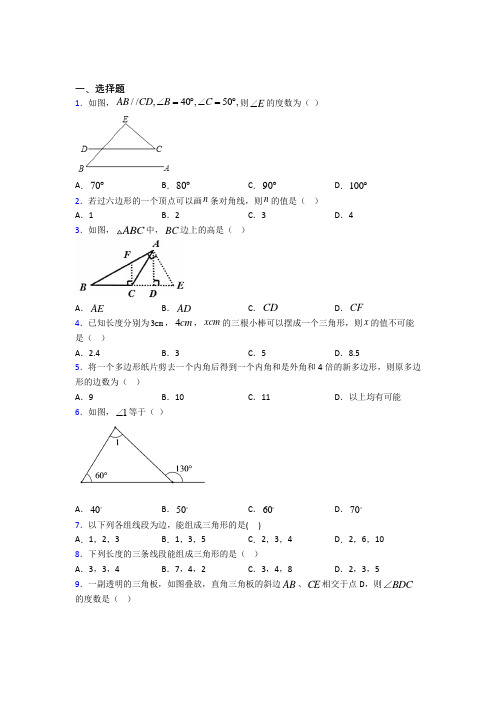
一、选择题1．如图，//,40,50,AB CD B C ∠=︒∠=︒则E ∠的度数为（）A ．70︒B ．80︒C ．90︒D ．100︒ 2．若过六边形的一个顶点可以画n 条对角线，则n 的值是（）A ．1B ．2C ．3D ．4 3．如图，ABC 中，BC 边上的高是（）A ．AEB ．ADC ．CD D ．CF 4．已知长度分别为3cm ，4cm ，xcm 的三根小棒可以摆成一个三角形，则x 的值不可能是（）A ．2.4B ．3C ．5D ．8.5 5．将一个多边形纸片剪去一个内角后得到一个内角和是外角和4倍的新多边形，则原多边形的边数为（）A ．9B ．10C ．11D ．以上均有可能 6．如图，1∠等于（）A ．40B ．50C ．60D ．70 7．以下列各组线段为边，能组成三角形的是( ) A ．1，2，3B ．1，3，5C ．2，3，4D ．2，6，10 8．下列长度的三条线段能组成三角形的是（） A ．3，3，4B ．7，4，2C ．3，4，8D ．2，3，5 9．一副透明的三角板，如图叠放，直角三角板的斜边AB 、CE 相交于点D ，则BDC∠的度数是（）A ．65︒B ．75︒C ．85︒D ．105︒ 10．做一个三角形的木架，以下四组木棒中，符合条件的是（） A ．4cm, 5cm,9cmB ．4cm, 5cm, 6cmC ．5cm,12cm,6cmD ．4cm,2cm,2cm 11．下列长度的四根木棒，能与3cm ，7cm 长的两根木棒钉成一个三角形的是（） A ．3cm B ．10cm C ．4cm D ．6cm 12．如图，盖房子时，在窗框没有安装之前，木工师傅常常先在窗框上斜钉一根木条，使其不变形，这种做法的根据是（）A ．两点之间线段最短B ．长方形的对称性C ．长方形四个角都是直角D ．三角形的稳定性 13．某多边形的内角和是其外角和的3倍，则此多边形的边数是（）A ．5B ．6C ．7D ．8 14．如图，王师傅用六根木条钉成一个六边形木框，要使它不变形，至少还要再钉上________根木条（）A ．2B ．3C ．4D ．515．如图，105DBA ∠=︒，125ECA ∠=︒，则A ∠的度数是（）A ．75°B ．60°C ．55°D ．50°二、填空题16．如图，已知//,AB CD E 是直线AB 上方一点，G 为直线AB 下方一点，F 为直线CD 上一点，148EAF ︒∠=，3BAF BAG ∠=∠，3DCE DCG ∠=∠，则E ∠和G ∠的数量关系为___________．17．对于一个四边形的四个内角，下面四个结论中，①可以四个角都是锐角；②至少有两个角是锐角；③至少有一个角是钝角；④最多有三个角是钝角；所有正确结论的序号是______．18．过n 边形的一个顶点有9条对角线，则n 边形的内角和为______．19．将正三角形、正四边形、正五边形按如图所示的位置摆放．如果147∠=︒，220∠=︒，那么3∠= __________．20．如图，∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H 的度数为___________．21．如图，将长方形纸片的一角折叠，使顶点A 落在F 处，折痕为BC ，FBD ∠的角平分线为BE ，将FBD ∠沿BF 折叠使BE ，BD 均落在FBC ∠的内部，且BE 交CF 于点M ，BD 交CF 于点N ，若BN 平分CBM ∠，则ABC ∠的度数为_________．22．如图所示，△ABC 中，∠BAC 、∠ABC 、∠ACB 的四等分线相交于D 、E 、F （其中∠CAD ＝3∠BAD ，∠ABE ＝3∠CBE ，∠BCF ＝3∠ACF ），且△DFE 的三个内角分别为∠DFE ＝60°、∠FDE ＝53°、∠FED ＝67°，则∠BAC 的度数为_________°．23．如图，则∠A+∠B+∠C+∠D+∠E+∠F+∠G ＝_____．24．如图，在ABC 中，已知66ABC ∠=︒，54ACB ∠=︒，BE 是AC 上的高，CF 是AB 上的高，H 是BE 和CF 的交点，EHF ∠的度数是________．25．如图，已知∠A ＝47°，∠B ＝38°，∠C ＝25°，则∠BDC 的度数是______．26．如图，ABC 面积为1，第一次操作：分别延长,,AB BC CA 至点111,,A B C 使111,,A B AB B C BC C A CA ===顺次结111,,A B C ，得到111A B C △，第二次操作：分别延长111111,,A B B C C A 至点222A B C ，使211121112111,,A B A B B C B C C A C A ===，顺次连结222,,A B C ，得到222A B C △…，按此规律，则333A B C △的面积为_______．三、解答题27．如图，BP 平分ABC ∠，交CD 于点F ，DP 平分ADC ∠交AB 于点E ，AB 与CD 相交于点G ，42A ∠=︒．（1）若60ADC ∠=︒，求AEP ∠的度数；（2）若38C ∠=︒，求P ∠的度数．28．如图，所有小正方形的边长都为1个单位，A 、B 、C 均在格点上．（1）过点A 画线段BC 的垂线，垂足为E ；（2）过点A 画线段AB 的垂线，交线段CB 的延长线于点F ；（3）线段BE 的长度是点到直线的距离；（4）线段AE 、BF 、AF 的大小关系是．（用“＜”连接）29．如图，在ABC 中，A ACB ∠=∠，CD 为ABC 的角平分线，CE 是ABC 的高．（1）若15DCB ∠=︒，求CBD ∠的度数；（2）若36DCE ∠=︒，求ACB ∠的度数．30．观察探究及应用．（1）如图，观察图形并填空：一个四边形有_______条对角线；一个五边形有_______条对角线；一个六边形有_______条对角线；（2）分析探究：由凸n 边形的一个顶点出发，可作_______条对角线，多边形有n 个顶点，若允许重复计数，共可作_______条对角线；（3）结论：一个凸n 边形有_______条对角线；（4）应用：一个凸十二边形有多少条对角线？。

2022-2023学年人教版八年级数学上学期期末复习通关练第十一章三角形(提高卷)(解析版)

2022-2023学年人教版八年级上册期末真题单元冲关测卷（提高卷）第十一章三角形一．选择题（共7小题，满分14分，每小题2分）1．（2分）（2020春•雨花区期末）如图，已知CD 和BE 是ABC ∆的角平分线，60A ∠=︒，则(BOC ∠= )A ．60︒B ．100︒C ．120︒D ．150︒【解答】解：60A ∠=︒，18060120ABC ACB ∴∠+∠=︒-︒=︒， CD 和BE 是ABC ∆的角平分线， 111()60222OBC OCB ABC ACB ABC ACB ∴∠+∠=∠+∠=∠+∠=︒， 180()120BOC OBC OCB ∴∠=︒-∠+∠=︒，故选：C ．2．（2分）（2020春•义乌市期末）如图，在ABC ∆中，B C α∠+∠=，按图进行翻折，使////B D C G BC ''，//B E FG '，则C FE '∠的度数是( )A ．2αB ．902α︒- C ．90α-︒ D ．2180α-︒【解答】解：设ADB γ∠'=，AGC β∠'=，CEB y ∠'=，C FE x ∠'=，//B D C G ''，B C γβα∴+=∠+∠=，//EB FG '，CFG CEB y ∴∠=∠'=，2180x y ∴+=︒①，2y B γ+=∠，2x C β+=∠，2y x γβα∴+++=，x y α∴+=②，②2⨯-①可得2180x α=-︒，2180C FE α∴∠'=-︒．故选：D ．3．（2分）（2020春•海淀区校级期末）如图，在ABC ∆中，90ACB ∠=︒，//CD AB ，36ACD ∠=︒，那么B ∠的度数为( )A ．144︒B ．54︒C ．44︒D ．36︒【解答】解：//AB CD ， 36A ACD ∴∠=∠=︒，90ACB ∠=︒，903654B ∴∠=︒-︒=︒，故选：B ．4．（2分）（2019秋•巴州区期末）若一个多边形截去一个角后，变成十四边形，则原来的多边形的边数可能为( )A ．14或15B ．13或14C ．13或14或15D ．14或15或16【解答】解：如图，n 边形，123n A A A A ⋯，若沿着直线13A A 截去一个角，所得到的多边形，比原来的多边形的边数少1，若沿着直线1A M 截去一个角，所得到的多边形，与原来的多边形的边数相等，若沿着直线MN 截去一个角，所得到的多边形，比原来的多边形的边数多1，因此将一个多边形截去一个角后，变成十四边形，则原来的四边形为13或14或15，故选：C ．5．（2分）（2019秋•潮州期末）如图，在ABC ∆中，32B ∠=︒，将ABC ∆沿直线m 翻折，点B 落在点D 的位置，则12∠-∠的度数是( )A ．32︒B ．45︒C ．60︒D ．64︒【解答】解：如图所示：由折叠的性质得：32D B ∠=∠=︒，根据外角性质得：13B ∠=∠+∠，32D ∠=∠+∠，1222264D B B ∴∠=∠+∠+∠=∠+∠=∠+︒，1264∴∠-∠=︒．故选：D ．6．（2分）（2019秋•兰州期末）ABC ∆的三个内角A ∠，B ∠，C ∠满足关系式3B C A ∠+∠=∠，则此三角形( )A ．一定是直角三角形B ．一定是钝角三角形C ．一定有一个内角为45︒D ．一定有一个内角为60︒【解答】解：180A B C ∠+∠+∠=︒又3B C A ∠+∠=∠，4180A ∴∠=∠︒，45A ∴∠=︒，ABC ∴∆一定有一个内角是45︒，故选：C ．7．（2分）（2019秋•义安区期末）如图，将ABC ∆沿DE 、HG 、EF 翻折，三个顶点均落在点O 处，若1131∠=︒，则2∠的度数为( )A ．49︒B ．50︒C ．51︒D ．52︒【解答】解：由折叠得：HOG B ∠=∠，DOE A ∠=∠，EOF C ∠=∠，180A B C ∠+∠+∠=︒，180HOG DOE EOF ∴∠+∠+∠=︒，12360HOG DOE EOF ∠+∠+∠+∠+∠=︒，12180∴∠+∠=︒，1131∠=︒，218013149∴∠=︒-︒=︒，故选：A ．二．填空题（共10小题，满分20分，每小题2分）8．（2分）（2020春•竞秀区期末）如图1，ABC ∆中，有一块直角三角板PMN 放置在ABC ∆上(P 点在ABC ∆内），使三角板PMN 的两条直角边PM 、PN 恰好分别经过点B 和点C ．（1）若52A ∠=︒，则12∠+∠= 38 ︒；（2）如图2，改变直角三角板PMN 的位置；使P 点在ABC ∆外，三角板PMN 的两条直角边PM 、PN 仍然分别经过点B和点C，1∠的关系是．∠与A∠，2【解答】解：（1）52A∠=︒，∴∠+∠=︒-︒=︒，18052128ABC ACBP∠=︒，90∴∠+∠=︒，PBC PCB90ABP ACP∴∠+∠=︒-︒=︒，1289038即1238∠+∠=︒．故答案为：38；（2）2190A∠-∠=︒-∠．理由如下：在ABCABC ACB A∠+∠=︒-∠，∆中，180∠=︒，MPN90PBC PCB∴∠+∠=︒，90ABC ACB PBC PCB A∴∠+∠-∠+∠=︒-∠-︒，()()18090即90∠+∠+∠-∠-∠-∠=︒-∠，ABC ACP PCB ABP ABC PCB A∴∠-∠=︒-∠．ACP ABP A90即2190A∠-∠=︒-∠；故答案为：2190A∠-∠=︒-∠．9．（2分）（2020春•鼓楼区期末）如图，直线a、b、c、d互不平行，以下结论正确的是①②③．（只填序号）①125∠+∠=∠；②134∠+∠=∠；③1236∠+∠+∠=∠；④3425∠+∠=∠+∠．【解答】解：由三角形外角的性质可知：512∠=∠+∠，413∠=∠+∠，64235∠=∠+∠=∠+∠， 6123∴∠=∠+∠+∠，故①②③正确，故答案为①②③．10．（2分）（2020春•裕华区期末）（1）新冠肺炎疫情发生以来，我国人民上下齐心，共同努力抗击疫情，逐渐取得了胜利．截止3月13日，我国各级财政安排的疫情防控投入已经达到了1169亿元，1169亿元用科学记数法表示 111.16910⨯ 元．（2）已知102m =，103n =，则210m n += ．（3）在ABC ∆中，4A B ∠=∠，且60C B ∠-∠=︒，则B ∠的度数是．（4）如图（1），在三角形ABC 中，38A ∠=，72C ∠=︒，BC 边绕点C 按逆时针方向旋转一周回到原来的位置（即旋转角0360)α︒︒，在旋转过程中（图2)，当//CB AB '时，旋转角为度；当CB 所在直线垂直于AB 时，旋转角为度．【解答】解：（1）1169亿8116910=⨯元111.16910=⨯（元)．故答案为111.16910⨯．（2）2222101010(10)(10)2318m n m n m n +=⨯=⨯=⨯=，故答案为18．（3）4A B ∠=∠，且60C B ∠-∠=︒，60C B ∴∠=︒+∠，460180B B B ∴∠+∠+︒+∠=︒，20B ∴∠=︒，故答案为20︒（4）在三角形ABC 中，38A ∠=︒，72C ∠=︒，180387270B ∴∠=︒-︒-︒=︒，如图1，当//CB AB '时，旋转角70B =∠=︒，当//CB AB ''时，38B CA A ∠''=∠=︒， ∴旋转角3603872250=︒-︒-︒=︒，综上所述，当//CB AB '时，旋转角为70︒或250︒；如图2，当CB AB '⊥时，907020BCB ∠''=︒-︒=︒，∴旋转角18020160=︒-︒=︒，当CB AB ''⊥时，旋转角180160340=︒+︒=︒，综上所述，当CB AB '⊥时，旋转角为160︒或340︒；故答案为：70或250；160或340．11．（2分）（2020春•雨花区期末）如图，若30A ∠=︒，105ACD ∠=︒，则EBC ∠= 105 ︒．【解答】解：ACD A ABC ∠=∠+∠，10530ABC ∴︒=︒+∠，75ABC ∴∠=︒，180105EBC ABC ∴∠=︒-∠=︒，故答案为105．12．（2分）（2015春•金牛区期末）如图，ABC ∆的外角平分线CP 和内角平分线BP 相交于点P ，若80BPC ∠=︒，则CAP ∠= 10︒ ．【解答】解：延长BA ，作PN BD ⊥于点N ，PF BA ⊥于点F ，PM AC ⊥于点M ，设PCD x ∠=︒， CP 平分ACD ∠，ACP PCD x ∴∠=∠=︒，PM PN =， BP 平分ABC ∠，ABP PBC ∴∠=∠，PF PN =，PF PM ∴=，80BPC ∠=︒，(80)ABP PBC x ∴∠=∠=-︒，2(80)(80)160BAC ACD ABC x x x ∴∠=∠-∠=︒-︒-︒-︒-︒=︒， 20CAF ∴∠=︒，在Rt PFA ∆和Rt PMA ∆中，PA PA PM PF =⎧⎨=⎩， Rt PFA Rt PMA(HL)∴∆≅∆，10FAP PAC ∴∠=∠=︒．故答案为10︒．13．（2分）（2011春•成都校级期末）ABC ∆中，A x ∠=，B ∠、C ∠的角平分线的夹角为y ，则y 与x 之间的关系可以表示为 1902y x =︒+．．【解答】解：PB 、PC 是B ∠、C ∠的角平分线，1122ABC ∴∠=∠=∠，1342ACB ∠=∠=∠， 11113()222ABC ACB ABC ACB ∴∠+=∠+∠=∠+∠， 180(13)y =︒-∠+∠，180ABC ACB x ∠+∠=︒-，11180(180)9022y x x ∴=︒-︒-=︒+．故答案为1902y x =︒+．14．（2分）（2019春•崇川区校级期末）如图，在ABC ∆中，40BAC ∠=︒，60ACB ∠=︒，D 为ABC ∆形外一点，DA 平分BAC ∠，且50CBD ∠=︒，求DCB ∠= 60︒ ．【解答】解：如图，延长AB 到P ，延长AC 到Q ，作DH AP ⊥于H ，DE AQ ⊥于E ，DF BC ⊥于F ．4060100PBC BAC ACB ∠=∠+∠=︒+︒=︒，50CBD ∠=︒， DBC DBH ∴∠=∠，DF BC ⊥，DH BP ⊥，DF DH ∴=，又DA 平分PAQ ∠，DH PA ⊥，DE AQ ⊥， DE DH ∴=，DE DF ∴=，CD ∴平分QCB ∠，18060120QCB ∠=︒-︒=︒，60DCB ∴∠=︒，故答案为60︒．15．（2分）（2018秋•沈河区期末）已知如图，BQ 平分ABP ∠，CQ 平分ACP ∠，BAC α∠=，BPC β∠=，则BQC ∠= 1()2αβ+ ．（用α，β表示）【解答】解：连接BC ， BQ 平分ABP ∠，CQ 平分ACP ∠，132ABP ∴∠=∠，142ACP ∠=∠， 12180β∠+∠=︒-，2(34)(12)180α∠+∠+∠+∠=︒-，134()2βα∴∠+∠=-， 1180(12)(34)180(180)()2BQC ββα∠=︒-∠+∠-∠+∠=︒-︒---，即：1()2BQC αβ∠=+．故答案为：1()2αβ+．16．（2分）（2016秋•成都期末）如图，已知ABC ∆ 中，60A ∠=︒，BD AC ⊥于D ，CE AB ⊥于E ，BD 、CE 交于点F ，FBC ∠、FCB ∠的平分线交于点O ，则BOC ∠的度数为 150︒ ．【解答】解：60A ∠=︒，BD AC ⊥于D ，CE AB ⊥于E ，30ACE ABD ∴∠=∠=︒，120ABC ACB ∠+∠=︒，60FBC FCB ∴∠+∠=︒，FBC ∠、FCB ∠的平分线交于点O ，30OBC OCB ∴∠+∠=︒，150BOC ∴∠=︒故答案为150︒．17．（2分）（2017春•高密市期末）如图，把一个三角尺的直角顶点D 放置在ABC ∆内，使它的两条直角边DE ，DF 分别经过点B ，C ，如果30A ∠=︒，则ABD ACD ∠+∠= 60︒ ．【解答】解：30∠=︒，A∴∠+∠=︒，ABC ACB150∠=︒，D90∴∠+∠=︒，90DBC DCB∴∠+∠=︒-︒=︒．1509060DBA DCA故答案为：60︒．三．解答题（共12小题，满分66分）18．（4分）（2020春•惠安县期末）已知：如图1，在ABC∠=∠．∆中，CD是AB边上的高，A DCB（1）试说明90∠=︒；ACB（2）如图2，如果AE是角平分线，AE、CD相交于点F．那么CFE∠的大小相等吗？请说明理∠与CEF由．【解答】（1）解：CD是AB边上的高，∴∠=︒，CDA90∴∠+∠=︒，A ACD90∠=∠，A DCBACB ACD BCD ACD A∴∠=∠+∠=∠+∠=︒；90（2）解：CFE CEF∠=∠，理由是：AE平分CAB∠，∴∠=∠，CAE BAE90CDA BCA ∠=∠=︒，180()DFA CDA BAE ∠=︒-∠+∠，180()CEA BCA CAE ∠=︒-∠+∠， CEF DFA ∴∠=∠，DFA CFE ∠=∠，CFE CEF ∴∠=∠．19．（4分）（2020春•海州区期末）已知如图，90COD ∠=︒，直线AB 与OC 交于点B ，与OD 交于点A ，射线OE 与射线AF 交于点G ．（1）若OE 平分BOA ∠，AF 平分BAD ∠，36OBA ∠=︒，则OGA ∠= 18 ︒．（2）若13GOA BOA ∠=∠，13GAD BAD ∠=∠，36OBA ∠=︒，则OGA ∠= ︒．（3）将（2）中的“36OBA ∠=︒”改为“OBA α∠=”，其它条件不变，求OGA ∠的度数．（用含α的代数式表示）（4）若OE 将BOA ∠分成1:4两部分，23GAD BAD ∠==∠，(1890)ABO αα∠=︒<<︒，求OGA ∠的度数．（用含α的代数式表示）【解答】解：（1）90BOA ∠=︒，36OBA ∠=︒，126BAD BOA ABO ∴∠=∠+∠=︒， AF 平分BAD ∠，OE 平分BOA ∠，90BOA ∠=︒，1632GAD BAD ∴∠=∠=︒，1452EOA BOA ∠=∠=︒， 634518OGA GAD EOA ∴∠=∠-∠=︒-︒=︒；故答案为：18︒；（2）90BOA ∠=︒，36OBA ∠=︒，126BAD BOA ABO ∴∠=∠+∠=︒，90BOA ∠=︒，13GOA BOA ∠=∠，13GAD BAD ∠=∠，42GAD ∴∠=︒，30EOA ∠=︒，423012OGA GAD EOA ∴∠=∠-∠=︒-︒=︒；故答案为12︒；（3）90BOA ∠=︒，OBA α∠=，90BAD BOA ABO α∴∠=∠+∠=︒+，90BOA ∠=︒，13GOA BOA ∠=∠，13GAD BAD ∠=∠， 1303GAD α∴∠=︒+，30EOA ∠=︒， 13OGA GAD EOA α∴∠=∠-∠=；（4）当:1:4EOD COE ∠∠=时，18EOD ∠=︒，90BAD ABO BOA α∠=∠+∠=+︒，23GAD BAD ∠=∠， 22(90)33FAD BAD α∴∠=∠=+︒， FAD EOD OGA ∠=∠+∠，218(90)3OGA α∴︒+∠=+︒，解得2423OGA α∠=+︒；当:4:1EOD COE ∠∠=时，72EOD ∠=︒，同理可得2123OGA α∠=-︒；综上所述，OGA ∠的度数为2423α+︒或2123α-︒．20．（4分）（2020春•淅川县期末）现有一张ABC ∆纸片，点D 、E 分别是ABC ∆边上两点，若沿直线DE折叠．研究（1）：如果折成图①的形状，使点A落在CE上，则1∠=∠．∠的数量关系是12A∠与A研究（2）：如果折成图②的形状，猜想12∠的数量关系是；∠+∠与A研究（3）：如果折成图③的形状，猜想1∠的数量关系，并说明理由．∠和A∠、2【解答】解：（1）如图1，12A∠=∠，理由是：由折叠得：A DA A∠=∠'，∠=∠+∠'，1A DA A∴∠=∠；12A故答案为：12A∠=∠；（2）如图2，猜想：122A∠+∠=∠，理由是：由折叠得：ADE A DE∠=∠'，AED A ED∠=∠'，∠+∠=︒，ADB AEC360∴∠+∠=︒-∠-∠'-∠-∠'=︒-∠-∠，ADE A DE AED A ED ADE AED 1236036022∴∠+∠=︒-∠-∠=∠；ADE AED A122(180)2故答案为：122A∠+∠=∠；（3）如图3，212DAE∠-∠=∠，理由是：AFE A∠=∠'+∠，∠=∠+∠，12AFE DAE∴∠=∠'+∠+∠，A DAE21∠=∠'，DAE A∴∠=∠+∠，221DAE∴∠-∠=∠．212DAE故答案为：（1）12A∠=∠；（2）122A∠+∠=∠．21．（4分）（2020春•马山县期末）如图，在三角形ABC中，AD BC∠，点E是⊥于点D，且AD平分BACBA的延长线上任一点，过点E作EF BC⊥于点F，与AC交于点G．（1）求证：//AD EF．（2）若36∠的度数．∠=︒，求BCGF（3）猜想E∠与AGE∠的大小关系，并证明你的猜想．【解答】（1）证明：AD BC⊥，⊥，EF BCADC EFC∴∠=∠=︒，90∴；//AD EF（2）//AD EF，36∠=︒，CGFCGF CAD∴∠=∠=︒，36AD平分BAC∠，∴∠=∠=︒，36BAD CAD∴∠=︒-∠-∠=︒；B BAD BDA18054（3）E AGE∠=∠，证明：理由是：//AD EF，∴∠=∠，AGE CADE BAD∠=∠，∠=∠，BAD CAD∴∠=∠．E AGE22．（5分）（2020春•赣榆区期末）[问题背景]（1）如图1的图形我们把它称为“8字形”，请说理证明A B C D ∠+∠=∠+∠．[简单应用]（可直接使用问题（1）中的结论）（2）如图2，AP 、CP 分别平分BAD ∠、BCD ∠，①若28ABC ∠=︒，20ADC ∠=︒，求P ∠的度数；②D ∠和B ∠为任意角时，其他条件不变，试直接写出P ∠与D ∠、B ∠之间数量关系．[问题探究]（3）如图3，直线BP 平分ABC ∠的邻外角FBC ∠，DP 平分ADC ∠的邻补角ADE ∠， ①若30A ∠=︒，18C ∠=︒，则P ∠的度数为 24︒ ；②A ∠和C ∠为任意角时，其他条件不变，试直接写出P ∠与A ∠、C ∠之间数量关系．[拓展延伸]（4）在图4中，若设C x ∠=，B y ∠=，14CAP CAB ∠=∠，14CDP CDB ∠=∠，试问P ∠与C ∠、B ∠之间的数量关系为；（用x 、y 的代数式表示)P ∠（5）在图5中，直线BP 平分ABC ∠，DP 平分ADC ∠的外角ADE ∠，猜想P ∠与A ∠、C ∠的关系，直接写出结论．【解答】解：（1）如图1中，180A B AOB ∠+∠+∠=︒，180C D COD ∠+∠+∠=︒，AOB COD ∠=∠， A B C D ∴∠+∠=∠+∠；（2）如图2中，设BAP PAD x ∠=∠=，BCP PCD y ∠=∠=，则有x B y P x P y D +∠=+∠⎧⎨+∠=+∠⎩， B P P D ∴∠-∠=∠-∠，11()(2820)2422P B D ∴∠=∠+∠=︒+︒=︒；（3）①如图3中，设CBJ JBF x ∠=∠=，ADP PDE y ∠=∠=．则有18021802P x A y A x C y∠+=∠+⎧⎨∠+︒-=∠+︒-⎩， 2P A C ∴∠=∠+∠，1(3018)242P ∴∠=︒+︒=︒；故答案为：24︒；②设CBJ JBF x ∠=∠=，ADP PDE y ∠=∠=．则有18021802P x A y A x C y ∠+=∠+⎧⎨∠+︒-=∠+︒-⎩， 2P A C ∴∠=∠+∠；（4）如图4中，设CAP α∠=，CDP β∠=，则3PAB α∠=，3PDB β∠=，则有33P C P B βααβ∠+=∠+⎧⎨∠+=∠+⎩， 43P C B ∴∠=∠+∠，1(3)4P x y ∴∠=+，故答案为1(3)4P x y ∠=+．（5）如图5中，延长AB 交PD 于J ，设PBJ x ∠=，ADP PDE y ∠=∠=．则有21802A x C y ∠+=∠+︒-，190()2x y C A ∴+=︒+∠-∠， 180P x A y ∠++∠+=︒，119022P C A ∴∠=︒-∠-∠．故答案为119022P C A ∠=︒-∠-∠．23．（5分）（2020春•西城区期末）在ABC ∆中，BD 是ABC ∆的角平分线，点E 在射线DC 上，EF BC ⊥于点F ，EM 平分AEF ∠交直线AB 于点M ．（1）如图1，点E 在线段DC 上，若90A ∠=︒，M α∠=．①AEF ∠= 1802α︒- ；（用含α的式子表示）②求证：//BD ME ；（2）如图2，点E 在DC 的延长线上，EM 交BD 的延长线于点N ，用等式表示BNE ∠与BAC ∠的数量关系，并证明．【解答】解：（1）①90A ∠=︒，M α∠=，1809090AEM αα∴∠=︒-︒-=︒-， EM 平分AEF ∠，21802AEF AEM α∴∠=∠=︒-，故答案为：1802α︒-；②证明：EF BC ⊥，90EFC ∴∠=︒，90A ∠=︒，90C ABC ∴∠+∠=︒，CEF ABC ∴∠=∠，1802AEF α∠=︒-，2CEF α∴∠=，2ABC α∴∠=， BD 是ABC ∆的角平分线，12ABD ABC α∴∠=∠=， ABD M ∴∠=∠，//BD ME ∴；（2）290BNE BAC ∠=︒+∠，证明：BD 平分ABC ∠，EM 平分AEF ∠，设ABD x ∠=，AEM y ∠=，2ABC x ∴∠=，2AEF y ∠=，180ABD BAD ADB ∠+∠=︒-∠，180NED END NDE ∠+∠=︒-∠，ADB NDE ∠=∠，ABD BAD NED END ∴∠+∠=∠+∠，x BAD y END ∴+∠=+∠，x y END BAD ∴-=∠-∠，同理，ABC BAC FEC EFC ∠+∠=∠+∠，22x BAC y EFC ∴+∠=+∠，22x y EFC BAC ∴-=∠-∠，EF BC ⊥，90EFC ∴∠=︒，2()90x y BAC ∴-=︒-∠，2()90END BAD BAC ∴∠-∠=︒-∠，即2()90BNE BAC BAC ∠-∠=︒-∠，290BNE BAC ∴∠=︒+∠．24．（5分）（2020春•润州区期末）已知ABC ∆中，90ABC ∠=︒，BD 是AC 边上的高，AE 平分BAC ∠，分别交BC 、BD 于点E 、F ．求证：BFE BEF ∠=∠．【解答】证明：AE 平分BAC ∠，BAE CAE ∴∠=∠，BD AC ⊥，90ABC ∠=︒，90BAE BEF CAE AFD ∴∠+∠=∠+∠=︒，BEF AFD ∴∠=∠，BFE AFD ∠=∠（对顶角相等）， BEF BFE ∴∠=∠25．（6分）（2019秋•市中区期末）已知将一块直角三角板DEF 放置在ABC ∆上，使得该三角板的两条直角边DE ，DF 恰好分别经过点B 、C ．（1）DBC DCB ∠+∠= 90 度；（2）过点A 作直线//MN DE ，若20ACD ∠=︒，试求CAM ∠的大小．【解答】解：（1）在DBC ∆中，180DBC DCB D ∠+∠+∠=︒，而90D ∠=︒，90DBC DCB ∴∠+∠=︒；故答案为90；（2）在ABC ∆中，180ABC ACB A ∠+∠+∠=︒，即180ABD DBC DCB ACD BAC ∠+∠+∠+∠+∠=︒，而90DBC DCB ∠+∠=︒，90ABD ACD BAC ∴∠+∠=︒-∠，9070ABD BAC ACD ∴∠+∠=︒-∠=︒．又//MN DE ，ABD BAN ∴∠=∠．而180BAN BAC CAM ∠+∠+∠=︒，180ABD BAC CAM ∴∠+∠+∠=︒，180()110CAM ABD BAC ∴∠=︒-∠+∠=︒．26．（7分）（2019秋•揭阳期末）探究与发现：如图①，在ABC ∆中，45B C ∠=∠=︒，点D 在BC 边上，点E 在AC 边上，且ADE AED ∠=∠，连接DE ．（1）当60BAD ∠=︒时，求CDE ∠的度数；（2）当点D 在BC （点B 、C 除外）边上运动时，试猜想BAD ∠与CDE ∠的数量关系，并说明理由．（3）深入探究：如图②，若B C ∠=∠，但45C ∠≠︒，其他条件不变，试探究BAD ∠与CDE ∠的数量关系．【解答】解：（1）ADC ∠是ABD ∆的外角，105ADC BAD B ∴∠=∠+∠=︒，30DAE BAC BAD ∠=∠-∠=︒，75ADE AED ∴∠=∠=︒，1057530CDE ∴∠=︒-︒=︒；（2）2BAD CDE ∠=∠，理由如下：设BAD x ∠=，45ADC BAD B x ∴∠=∠+∠=︒+，90DAE BAC BAD x ∠=∠-∠=︒-，902x ADE AED ︒+∴∠=∠=， 9014522x CDE x x ︒+∴∠=︒+-=， 2BAD CDE ∴∠=∠；（3）设BAD x ∠=，ADC BAD B B x ∴∠=∠+∠=∠+，1802DAE BAC BAD C x ∠=∠-∠=︒-∠-，12ADE AED C x ∴∠=∠=∠+， 11()22CDE B x C x x ∴∠=∠+-∠+=， 2BAD CDE ∴∠=∠．27．（7分）（2020春•泰州期末）已知在四边形ABCD 中，A x ∠=，C y ∠=，(0180,0180)x y ︒<<︒︒<<︒．（1）ABC ADC ∠+∠= 360x y ︒-- （用含x 、y 的代数式直接填空）；（2）如图 1 ，若90x y ==︒．DE 平分ADC ∠，BF 平分CBM ∠，请写出DE 与BF 的位置关系，并说明理由；（3）如图 2 ，DFB ∠为四边形ABCD 的ABC ∠、ADC ∠相邻的外角平分线所在直线构成的锐角． ①若120x y +=︒，20DFB ∠=︒，试求x 、y ．②小明在作图时，发现DFB ∠不一定存在，请直接指出x 、y 满足什么条件时，DFB ∠不存在．【解答】解：（1）360A ABC C ADC ∠+∠+∠+∠=︒，A x ∠=，C y ∠=，360ABC ADC x y ∴∠+∠=︒--．故答案为：360x y ︒--．（2）DE BF ⊥．理由：如图 1 ，DE 平分ADC ∠，BF 平分MBC ∠，12CDE ADC ∴∠=∠，12CBF CBM ∠=∠，又180180(180)CBM ABC ADC ADC ∠=︒-∠=︒-︒-∠=∠，CDE CBF ∴∠=∠，又DGC BGE ∠=∠，90BEG C ∴∠=∠=︒，DE BF ∴⊥；（3）①由（1）得：360(360)CDN CBM x y x y ∠+∠=︒-︒--=+， BF 、DF 分别平分CBM ∠、CDN ∠，1()2CDF CBF x y ∴∠+∠=+，如图 2 ，连接DB ，则180CBD CDB y ∠+∠=︒-，111180()180222FBD FDB y x y y x ∴∠+∠=︒-++=︒-+， 112022DFB y x ∴∠=-=︒，解方程组：120112022x y y x +=︒⎧⎪⎨-=︒⎪⎩，可得：4080x y =︒⎧⎨=︒⎩； ②当x y =时，1118018022FBD FDB y x ∠+∠=︒-+=︒， ABC ∴∠、ADC ∠相邻的外角平分线所在直线互相平行，此时，DFB ∠不存在．28．（7分）（2019秋•辽阳期末）已知如图①，BP 、CP 分别是ABC ∆的外角CBD ∠、BCE ∠的角平分线，BQ 、CQ 分别是PBC ∠、PCB ∠的角平分线，BM 、CN 分别是PBD ∠、PCE ∠的角平分线，BAC α∠=．（1）当40α=︒时，BPC ∠= 70 ︒，BQC ∠= ︒；（2）当α= ︒时，//BM CN ；（3）如图②，当120α=︒时，BM 、CN 所在直线交于点O ，求BOC ∠的度数；（4）在60α>︒的条件下，直接写出BPC ∠、BQC ∠、BOC ∠三角之间的数量关系：．【解答】解：（1）DBC A ACB ∠=∠+∠，BCE A ABC ∠=∠+∠，180220DBC BCE A ∴∠+∠=︒+∠=︒， BP 、CP 分别是ABC ∆的外角CBD ∠、BCE ∠的角平分线，1()1102CBP BCP DBC BCE ∴∠+∠=∠+∠=︒， 18011070BPC ∴∠=︒-︒=︒， BQ 、CQ 分别是PBC ∠、PCB ∠的角平分线，12QBC PBC ∴∠=∠，12QCB PCB ∠=∠， 55QBC QCB ∴∠+∠=︒，18055125BQC ∴∠=︒-︒=︒；（2）//BM CN ，180MBC NCB ∴∠+∠=︒， BM 、CN 分别是PBD ∠、PCE ∠的角平分线，BAC α∠=， ∴3()1804DBC BCE ∠+∠=︒，即3(180)1804α︒+=︒，解得60α=︒；（3）120α=︒，33()(180)22544MBC NCB DBC BCE α∴∠+∠=∠+∠=︒+=︒， 22518045BOC ∴∠=︒-︒=︒；（4）60α>︒，1902BPC α∠=︒-、 11354BQC α∠=︒-、 3454BOC α∠=-︒． BPC ∠、BQC ∠、BOC ∠三角之间的数量关系：113(90)(135)(45)180244BPC BQC BOC ααα∠+∠+∠=︒-+︒-+-︒=︒．故答案为：70，125；60；180BPC BQC BOC ∠+∠+∠=︒．29．（8分）（2019秋•长白县期末）Rt ABC ∆中，90C ∠=︒，点D 、E 分别是ABC ∆边AC 、BC 上的点，点P 是一动点．令1PDA ∠=∠，2PEB ∠=∠，DPE α∠=∠．（1）若点P 在线段AB 上，如图（1）所示，且50α∠=︒，则12∠+∠= 140 ︒；（2）若点P 在边AB 上运动，如图（2）所示，则α∠、1∠、2∠之间有何关系？（3）若点P 在Rt ABC ∆斜边BA 的延长线上运动()CE CD <，则α∠、1∠、2∠之间有何关系？猜想并说明理由．【解答】解：（1）如图，连接PC ，由三角形的外角性质，1PCD CPD ∠=∠+∠，2PCE CPE ∠=∠+∠，12PCD CPD PCE CPE DPE C ∴∠+∠=∠+∠+∠+∠=∠+∠，50DPE α∠=∠=︒，90C ∠=︒，125090140∴∠+∠=︒+︒=︒，故答案为：140︒；（2）连接PC ，由三角形的外角性质，1PCD CPD ∠=∠+∠，2PCE CPE ∠=∠+∠， 12PCD CPD PCE CPE DPE C ∴∠+∠=∠+∠+∠+∠=∠+∠， 90C ∠=︒，DPE α∠=∠，1290α∴∠+∠=︒+∠；（3）如图1，由三角形的外角性质，21C α∠=∠+∠+∠， 2190α∴∠-∠=︒+∠；如图2，0α∠=︒，2190∠=∠+︒；如图3，21C α∠=∠-∠+∠，1290α∴∠-∠=∠-︒．。

人教新版数学八年级上册第11-13章阶段性测评试卷(含答案解析)

A．∠B=∠CB．AD=AEC．BD=CED．BE=CD
10．一个三角形的三边长分别为2，5，x，另一个三角形的三边长分别为y，2，6，若这两个三角形全等，则x+y=（）
A．11B．7C．8D．13
二、填空题
11．下列图形中轴对称图形的个数是_____．
12．如图所示，在△ABC中，∠1＝∠2，G是AD的中点，延长BG交AC于点E，F为AB上一点，CF⊥AD交AD于点H.下列说法：①AD是△ABE的角平分线；②BE是△ABD的边AD上的中线；③CH为△ACD的边AD上的高；④AH是△ACF的角平分线和高线．其中正确的有_______．
A．66°B．36°C．56D．46°
3．点M（1，2）关于y轴对称点的坐标为（）
A．（﹣1，2）B．（﹣1，﹣2）C．（1，﹣2）D．（2，﹣1）
4．到三角形三个顶点的距离相等的点是三角形（）的交点．
A．三个内角平分线B．三边垂直平分线
C．三条中线D．三条高
5．如图，△ 中，，是中点，下列结论，不一定正确的是（）
【详解】
试题分析：根据线段垂直平分线上的点到两端点的距离相等解答．
解：到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点．
故选B．
点评：本题考查了线段垂直平分线上的点到两端点的距离相等的性质，熟记性质是解题的关键．
5．C
【分析】
根据等边对等角和等腰三角形三线合一的性质解答．
【详解】
解：∵AB=AC，
三、解答题
19．如图，∠B=∠C，AD平分∠BAC，求证：△ABD≌△ACD．若BD=3cm，则CD有多长？
证明：∵AD平分∠BAC，
∴∠=∠（角平分线的定义）．
在△ABD和△ACD中，

八年级数学上册第十一至十三章综合测试题

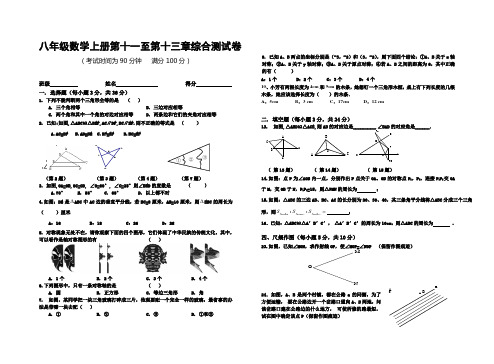
OMN八年级数学上册第十一至第十三章综合测试卷（考试时间为90分钟满分100分）班级姓名得分一. 选择题（每小题3分，共36分）1. 下列不能判断两个三角形全等的是（） A. 三个角相等 B. 三边对应相等 C. 两个角和其中一个角的对边对应相等 D. 两条边和它们的夹角对应相等2. 已知:如图,△ABC≌△DEF,AC∥DF,BC∥EF.则不正确的等式是（）A.AC=DFB.AD=BEC.DF=EFD.BC=EF（第2题）（第3题）（第4题）（第7题） 3. 如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED 的度数是 ( )A.70°B. 85°C. 65°D. 以上都不对4.如图：DE 是∆ABC 中AC 边的垂直平分线，若BC=8厘米，AB=10厘米，则∆EBC 的周长为（）厘米A ：16B ：18C ：26D ：285. 对称现象无处不在，请你观察下面的四个图形，它们体现了中华民族的传统文化，其中，可以看作是轴对称图形的有（）A. 1个B. 2个C. 3个D. 4个 6.下列图形中，只有一条对称轴的是（）A. 圆B. 正方形C. 等边三角形D. 角7. 如图，某同学把一块三角玻璃打碎成三片，他现要配一个完全一样的玻璃，最省事的办法是带哪一块去配（）A. ①B. ②C. ③D. ①和②9. 已知A 、B 两点的坐标分别是（-3，-2）和（3，-2），则下面四个结论：①A 、B 关于x 轴对称；②A 、B 关于y 轴对称；③A 、B 关于原点对称；④若A 、B 之间的距离为6，其中正确的有（）A ：1个B ：2个C ：3个D ：4个10、小芳有两根长度为4cm 和9cm 的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为（）的木条．A ．5cmB ．3 cmC ．17cmD ．12 cm二. 填空题（每小题3分，共24分）13. 如图,△ABD ≌△ACE,则AB 的对应边是_________,∠BAD 的对应角是______．EBC AD（第13题）（第14题）（第15题）14.如图：点P 为∠AOB 内一点，分别作出P 点关于OA 、OB 的对称点P 1，P 2，连接P 1P 2交OA 于M ，交OB 于N ，P 1P 2=15，则△PMN 的周长为；15.如图：△ABC 的三边AB 、BC 、AC 的长分别为20、30、40，其三条角平分线将△ABC 分成三个三角形，则=∆∆∆OAC OBC OAB S S S :: ；16．已知：△ABC ≌△A ′B ′C ′， △A ′B ′C ′的周长为10cm ，则△ABC 的周长为 .四、尺规作图（每小题5分，共10分）23.如图，已知∠MON ，求作射线OP ，使∠MOP=∠NOP （保留作图痕迹）24．如图，A 、B 是两个村镇，都在公路a 的同侧，为了方便运输，•要在公路边开一个岔路口通向A 、B 两地，问该岔路口建在公路边的什么地方，•可使所修的路最短，试在图中确定该点P （保留作图痕迹）a ABP2P 1PNMO BACEB DAC EDB O AOCBA③②①五、解答题（共35分）25. (7分)如图所示，AB ∥DE 且AB ＝DE ，BE ＝CF. 求证：AC ∥DF.26.（8分）如图, 已知：AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF ．求证：AB=ED ．27．（10分)如图，已知：E 是∠AOB 的平分线上一点，EC⊥OB，ED⊥OA，C ，D 是垂足，连接CD ，求证:（1）∠ECD=∠EDC；（2）OD=OC ；（3）OE 是CD 的中垂线.28. （10分）平面直角坐标系中，△ABC 的三个顶点坐标分别为A （0,0），B （3,4），C （3，2）.（1）试在平面直角坐标系中，标出A 、B 、C 三点；（2）求△ABC 的面积.（3）若111C B A 与△ABC 关于Y 轴对称，写出1A 、1B 、1C 的坐标.C ED B AO FG E DCB A A BCDE F。

《第11章三角形》同步专题提升训练(附答案)2021-2022学年八年级数学人教版上册

2021-2022学年人教版八年级数学上册《第11章三角形》同步专题提升训练（附答案）1．在下列各图的△ABC中，正确画出AC边上的高的图形是（）A．B．C．D．2．如图中三角形的个数是（）A．6B．7C．8D．93．如图，△ABC的角平分线AD、中线BE相交于点O，则①AO是△ABE的角平分线；②BO是△ABD的中线；③DE是△ADC的中线；④ED是△EBC的角平分线的结论中正确的有（）A．1个B．2个C．3个D．4个4．如果三角形的两边长分别为7和9．那么第三边的长可能是下列数据中的（）A．2B．13C．16D．185．如图，在△ABC中，∠B＝32°，将△ABC沿直线m翻折，点B落在点D的位置，则∠1﹣∠2的度数是（）A．32°B．45°C．60°D．64°6．如图，△ABC中，∠A＝20°，沿BE将此三角形对折，又沿BA′再一次对折，点C落在BE上的C′处，此时∠C′DB＝74°，则原三角形的∠C的度数为（）A．27°B．59°C．69°D．79°7．如图，AE是△ABC的角平分线，AD⊥BC于点D，若∠BAC＝76°，∠C＝64°，则∠DAE的度数是（）A．10°B．12°C．15°D．18°8．如图，在△ABC中，∠ACB＝90°，过点C作CD∥AB交∠ABC的平分线于点D，若∠ABD＝20°，则∠ACD的度数为（）A．20°B．30°C．40°D．50°9．如图，△ABC中，∠BAC＝90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC．给出下列结论：①∠BAD＝∠C；②∠AEF＝∠AFE；③∠EBC＝∠C；④AG⊥EF．正确结论有（）A．1个B．2个C．3个D．4个10．将若干个大小相等的正五边形排成环状，如图所示是前3个五边形，要完成这一圆环还需_______个正五边形（）A．6B．7C．8D．911．如图，△ABC中，∠ABC、∠ACB的三等分线交于点E、D，若∠E＝90°，则∠BDC 的度数为（）A．120°B．125°C．130°D．135°12．一副三角板如图放置，则∠1+∠2的度数为（）A．22.5°B．30°C．45°D．60°13．如图，△ABC的角平分线CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②∠ADC＝∠GCD；③CA平分∠BCG；④∠DFB＝∠CGE．其中正确的结论的个数是（）A．1B．2C．3D．414．若多边形的边数由n增加到n+1（n为大于3的正整数），则其内角和的度数（）A．增加180°B．减少180°C．不变D．不能确定15．小明把一副含45°，30°的直角三角板如图摆放，其中∠C＝∠F＝90°，∠A＝45°，∠D＝30°，则∠α+∠β等于（）A．280°B．285°C．290°D．295°16．若一个三角形三条高的交点在这个三角形的顶点上，则这个三角形是三角形．17．木工师傅在做完门框后为防止变形，常如图所示那样钉上两条斜拉的木板条，这样做的数学依据是．18．如图，把一张三角形纸片（△ABC）进行折叠，使点A落在BC上的点F处，折痕为DE，点D，点E分别在AB和AC上，DE∥BC，若∠B＝75°，则∠BDF的度数为．19．一个多边形的一个外角为α，且该多边形的内角和与α的和等于840°，则这个多边形的边数为，α＝度．20．如图，在△ABC中，∠A、∠B的平分线相交于点I，若∠C＝70°，则∠AIB＝度，若∠AIB＝155°，则∠C＝度．21．如图，在△ABC中，∠B＝∠C，∠BAD＝40°，且∠ADE＝∠AED，求∠CDE的度数．22．如图，在Rt△ABE中，∠AEB＝90°，C为AE延长线上的一点，D为AB边上的一点，DC交BE于F，若∠ADC＝80°，∠B＝30°，求∠C的度数．23．如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB＝50°，∠C＝60°，求∠DAE和∠BOA的度数．24．已知：如图，△ABC中，∠BAD＝∠EBC，AD交BE于F．（1）试说明：∠ABC＝∠BFD；（2）若∠ABC＝35°，EG∥AD，EH⊥BE，求∠HEG的度数．25．如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．（1）如果∠A＝80°，求∠BPC的度数；（2）如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q、∠A之间的数量关系．（3）如图③，延长线段BP、QC交于点E，△BQE中，存在一个内角等于另一个内角的2倍，求∠A的度数．参考答案1．解：AC边上的高就是过B作垂线垂直AC交AC的延长线于D点，因此只有C符合条件，故选：C．2．解：∵图中三角形有：△ECA，△EBD，△FBA，△FCD，△AFD，△ABD，△ACD，△AED，∴共8个．故选：C．3．解：∵△ABC的角平分线AD、中线BE相交于点O，∴∠BAD＝∠CAD，AE＝CE，①在△ABE中，∠BAD＝∠CAD，∴AO是△ABE的角平分线，故①正确；②AO≠OD，所以BO不是△ABD的中线，故②错误；③在△ADC中，AE＝CE，DE是△ADC的中线，故③正确；④∠ADE不一定等于∠EDC，那么ED不一定是△EBC的角平分线，故④错误；正确的有2个选项．故选：B．4．解：∵三角形的两边长分别为7和9，∴9﹣7＜第三边的长＜9+7，即2＜第三边的长＜16，选项中只有，13符合题意．故选：B．5．解：如图所示：由折叠的性质得：∠D＝∠B＝32°，根据外角性质得：∠1＝∠3+∠B，∠3＝∠2+∠D，∴∠1＝∠2+∠D+∠B＝∠2+2∠B＝∠2+64°，∴∠1﹣∠2＝64°．故选：D．6．解如图，∵△ABC沿BE将此三角形对折，又沿BA′再一次对折，点C落在BE上的C′处，∴∠1＝∠2，∠2＝∠3，∠CDB＝∠C′DB＝74°，∴∠1＝∠2＝∠3，∴∠ABC＝3∠3，在△BCD中，∠3+∠C+∠CDB＝180°，∴∠3+∠C＝180°﹣74°＝106°，在△ABC中，∵∠A+∠ABC+∠C＝180°，∴20°+2∠3+（∠3+∠C）＝180°，即20°+2∠3+106°＝180°，∴∠3＝27°，∴∠ABC＝3∠3＝81°，∠C＝106°﹣27°＝79°，故选：D．7．解：∵AE平分∠BAC，∴∠CAE＝∠CAB＝×76°＝38°，∵AD⊥BC，∴∠ADC＝90°，∴∠CAD＝90°﹣∠C＝90°﹣64°＝26°，∴∠DAE＝∠EAC﹣∠CAD＝38°﹣26°＝12°，故选：B．8．解：∵BD平分∠ABC，∴∠ABD＝∠DBC＝20°，∴∠ABC＝40°，∵∠ACB＝90°，∴∠A＝90°﹣∠ABC＝90°﹣40°＝50°，∵CD∥AB，∴∠ACD＝∠A＝50°，故选：D．9．解：∵∠BAC＝90°，AD⊥BC，∴∠C+∠ABC＝90°，∠BAD+∠ABC＝90°，∴∠BAD＝∠C，故①正确；∵BE是∠ABC的平分线，∴∠ABE＝∠CBE，∵∠ABE+∠AEF＝90°，∠CBE+∠BFD＝90°，∴∠AEF＝∠BFD，又∵∠AFE＝∠BFD（对顶角相等），∴∠AEF＝∠AFE，故②正确；∵∠ABE＝∠CBE，∴只有∠C＝30°时∠EBC＝∠C，故③错误；∵∠AEF＝∠AFE，∴AE＝AF，∵AG平分∠DAC，∴AG⊥EF，故④正确．综上所述，正确的结论是①②④．故选：C．10．解：五边形的内角和为（5﹣2）•180°＝540°，所以正五边形的每一个内角为540°÷5＝108°，如图，延长正五边形的两边相交于点O，则∠1＝360°﹣108°×3＝360°﹣324°＝36°，360°÷36°＝10，∵已经有3个五边形，∴10﹣3＝7，即完成这一圆环还需7个五边形．故选：B．11．解：在△BEC中，∵∠BEC＝90°，∴∠EBC+∠ECB＝90°，∵∠ABC、∠ACB的三等分线交于点E、D，∴∠DBC＝∠EBC，∠DCB＝∠ECB，∴∠DBC+∠DCB＝×90°＝45°，∴∠BDC＝180°﹣（∠DBC+∠DCB）＝135°，故选：D．12．解：标上字母如图，连接BA并延长到C，∵∠DAC是△ABD的外角，∠EAC是△ABE的外角，∴∠DAC＝∠1+∠ABD，∠EAC＝∠2+∠ABE，∴∠DAE＝∠1+∠2+∠DBE，∴∠1+∠2＝90°﹣60°＝30°．故选：B．13．解：∵EG∥BC，∴∠CEG＝∠ACB，∵CD平分∠ACB，∴∠ACB＝2∠DCB，∴∠CEG＝2∠DCB，故①正确；∵∠A＝90°，∴∠ACD+∠ADC＝90°，∵EG∥BC，且CG⊥EG于G，∴∠CGE＝∠GCB＝90°，∴∠GCD+∠BCD＝90°，∵CD平分∠ACB，∴∠ACD＝∠BCD，∴∠ADC＝∠GCD，故②正确；无法证明CA平分∠BCG，故③错误；∵∠EBC+∠ACB＝∠AEB，∠DCB+∠ABC＝∠ADC，∴∠AEB+∠ADC＝90°+（∠ABC+∠ACB）＝135°，∴∠DFE＝360°﹣135°﹣90°＝135°，∴∠DFB＝45°＝∠CGE，故④正确；所以其中正确的结论为①②④共3个，故选：C．14．解：n边形的内角和是（n﹣2）•180°，n+1边形的内角和是（n+1﹣2）•180°＝（n﹣1）•180°，则（n﹣1）•180°﹣（n﹣2）•180°＝180°，故选：A．15．解：∵∠C＝∠F＝90°，∠A＝45°，∠D＝30°，∴∠2+∠3＝180°﹣∠D＝150°，∵∠α＝∠1+∠A，∠β＝∠4+∠C，∵∠1＝∠2，∠3＝∠4，∴∠α+∠β＝∠A+∠1+∠4+∠C＝∠A+∠C+∠2+∠3＝45°+90°+150°＝285°，故选：B．16．解：若一个三角形三条高的交点在这个三角形的顶点上，则这个三角形是直角三角形．故答案为直角．17．解：木工师傅在做完门框后为防止变形，常如图所示那样钉上两条斜拉的木板条，这样做的数学依据是三角形具有稳定性，故答案为：三角形具有稳定性．18．解：∵DE∥BC，∴∠ADE＝∠B＝75°，又∵∠ADE＝∠EDF＝75°，∴∠BDF＝180°﹣75°﹣75°＝30°，故答案为30°．19．解：∵840÷180＝4…120，∴这个多边形的边数为：4+2＝6，α＝120°，故答案为：六；120．20．解：连接CI并延长交AB于P．∵AI平分∠CAP，∴∠1＝∠2．∵BI平分∠CBP，∴∠3＝∠4，∴∠1+∠3＝（∠CAB+∠CBA）＝×（180°﹣70°）＝55°，∴∠7+∠8＝∠1+∠3+∠5+∠6＝55°+70°＝125°．∵∠AIB＝155°，∴∠2+∠4＝180°﹣155°＝25°，又∵∠CAP、∠CBP的平分线，相交于点I，∴∠CAP+∠CBP＝2×25°＝50°，∴∠ACB＝180°﹣50°＝130°．21．解：∵∠CDE+∠C＝∠AED，∠ADE＝∠AED，∴∠C+∠CDE＝∠ADE．又∵∠B+∠BAD＝∠ADC，∴∠B+40°＝∠C+∠CDE+∠CDE．∵∠B＝∠C，∴2∠CDE＝40°，∴∠CDE＝20°．22．解：∵在Rt△ABE中，∠AEB＝90°，∠B＝30°∴∠A＝90°﹣∠B＝60°，∵在△ADC中，∠A＝60°，∠ADC＝80°∴∠C＝180°﹣60°﹣80°＝40°，答：∠C的度数为40°．23．解：∵∠CAB＝50°，∠C＝60°∴∠ABC＝180°﹣50°﹣60°＝70°，又∵AD是高，∴∠ADC＝90°，∴∠DAC＝180°﹣90°﹣∠C＝30°，∵AE、BF是角平分线，∴∠CBF＝∠ABF＝35°，∠EAF＝25°，∴∠DAE＝∠DAC﹣∠EAF＝5°，∠AFB＝∠C+∠CBF＝60°+35°＝95°，∴∠BOA＝∠EAF+∠AFB＝25°+95°＝120°，∴∠DAC＝30°，∠BOA＝120°．故∠DAE＝5°，∠BOA＝120°．24．解：（1）∵∠BFD＝∠ABF+∠BAD，∠ABC＝∠ABF+∠FBC，∵∠BAD＝∠EBC，∴∠ABC＝∠BFD；（2）∵∠BFD＝∠ABC＝35°，∵EG∥AD，∴∠BEG＝∠BFD＝35°，∵EH⊥BE，∴∠BEH＝90°，∴∠HEG＝∠BEH﹣∠BEG＝55°．25．（1）解：∵∠A＝80°．∴∠ABC+∠ACB＝100°，∵点P是∠ABC和∠ACB的平分线的交点，∴∠P＝180°﹣（∠ABC+∠ACB）＝180°﹣×100°＝130°，（2）∵外角∠MBC，∠NCB的角平分线交于点Q，∴∠QBC+∠QCB＝（∠MBC+∠NCB）＝（360°﹣∠ABC﹣∠ACB）＝（180°+∠A）＝90°+∠A∴∠Q＝180°﹣（90°+∠A）＝90°﹣∠A；（3）延长BC至F，∵CQ为△ABC的外角∠NCB的角平分线，∴CE是△ABC的外角∠ACF的平分线，∴∠ACF＝2∠ECF，∵BE平分∠ABC，∴∠ABC＝2∠EBC，∵∠ECF＝∠EBC+∠E，∴2∠ECF＝2∠EBC+2∠E，即∠ACF＝∠ABC+2∠E，又∵∠ACF＝∠ABC+∠A，∴∠A＝2∠E，即∠E＝∠A；∵∠EBQ＝∠EBC+∠CBQ＝∠ABC+∠MBC＝（∠ABC+∠A+∠ACB）＝90°．如果△BQE中，存在一个内角等于另一个内角的2倍，那么分四种情况：①∠EBQ＝2∠E＝90°，则∠E＝45°，∠A＝2∠E＝90°；②∠EBQ＝2∠Q＝90°，则∠Q＝45°，∠E＝45°，∠A＝2∠E＝90°；③∠Q＝2∠E，则90°﹣∠A＝∠A，解得∠A＝60°；④∠E＝2∠Q，则∠A＝2（90°﹣∠A），解得∠A＝120°．综上所述，∠A的度数是90°或60°或120°．。

八年级数学上册第11章三角形提高题培优练习(word版 )

八年级数学上册第11章三角形提高题培优练习(word版 )1.在三角形ABC中，E是BC上的一点，且EC=2BE。

D是AC的中点。

设三角形ABC、ADF、BEF的面积分别为S1、S2、S3，且S1=24.求S2-S3的值。

2.在四边形ABCD中，对角线AC⊥BD于O点。

证明S四边形ABCD=1/2AC·BD。

3.已知三角形三边长为15、20、25.求三条高的比。

4.在图中，A、B、C分别是线段A1B、B1C、C1A的中点。

若三角形ABC的面积为1，则三角形A1B1C1的面积为1/4.5.化简|a-b+c|-|a-b-c|=|2c-a-b|。

6.在三角形ABC中，O是内部一点，连接OA、OB、OC，得到三个小三角形。

证明：___<OA+OB+OC<___。

7.在三角形ABC中，∠B=∠C，∠BAD=44，并且∠ADE=∠___。

求∠___的度数。

8.(1) 已知四边形ABCD，证明：∠D=∠A+∠B+∠C。

2) 在四边形ABCD中，BE平分∠ABD，CE平分∠ACD，且∠A=60，∠E=100.求∠D的度数。

9.在三角形ABC中，D为BC上一点，∠1=∠2，∠3=∠4，且∠BAC=124.求∠___的度数。

10.在图中，∠xOy=90，点A、B分别在射线Ox、Oy上移动，BE是∠ABy的平分线，BE的反向延长线与∠OAB的平分线交于点C。

问∠___的大小是否发生变化。

11.在图中，∠A=55，∠B=85，将纸片的一角折叠，使点C落在△ABC外，且∠2=25.求∠1的度数。

12.在图中，将△___纸片沿DE折叠，使点A落在四边形BCDE的内部，且∠A=45.求∠1+∠2的度数。

13.在图中，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，且∠___。

求∠CAP的度数。

14.在图中，∠ABC=α，∠ABC和∠ACD的平分线交于点A1，得到∠A1；∠___和∠A1CD的平分线相交于点A2，得到∠A2；……；∠A2015BC和∠A2015CD的平分线相交于点A2016，得到∠A2016.求∠A2016的度数。

2021-2022学年人教版八年级数学上册第十一章三角形单元提升测试卷

第十一章三角形提升卷时间：60分钟满分：l00分一、选择题（共10小题，每小题3分，共30分，每小题有四个选项，其中只有一个选项符合题意）1.（2020·浙江嘉兴期末）如果一个三角形的两边长分别为3和4，那么第三边的长可能是（）A.12B.10C.8D.62.（2020·北京二模）用三角板作△ABC的BC边上的高，下列三角板的摆放位置正确的是（）3.（2020·河北邢台期末）下面给出的四个三角形都有一部分被遮挡，其中不能确定三角形类型的是（）4.（2021·山西太原期末）如图，CE是△ABC的外角∠ACD的平分线，CE交BA的延长线于点E，若∠B=35°，∠E=25°，则∠ACD的度数为（）A.100° B.110° C.120° D.130°（第4题）（第5题）5.（2021·广东中山期末）如图，在△ABC中，∠A=90°，若沿图中虚线截去∠A，则∠1+∠2的度数为（）A.90°B.180°C.270°D.300°6.如图，已知BD是△ABC的中线，AB=5.BC=3，且△ABD的周长为11，则△BCD的周长是（）A.9B.14C.16D.不能确定7.（2021·湖北武汉青山区期末）如图，AD，AE分别为△ABC的高线和角平分线，DFLAE于点F，当∠ADF=69，∠C=65时，∠B的度数为（）A.21°B.23°C.25°D.30°（第7题）（第8题）8.如图，在△ABC中，D，E，F分别是BC，AD，CE的中点，若S∆ABC=4cm2，则S∆BEF =A.0.5cm2B.1cm2C.1.5cm2D.2cm29.（2021·河北唐山路北区期末）若一个多边形截去一个角后，形成的新多边形的内角和是1620°，则原来多边形的边数可能是（）A.10或11B.11C.1l或12D.10或11或1210.（2020·河南郑州期末）如图，△ABC的外角平分线BP，CP相交于点P，若∠P=60°，则∠A的大小为（）A.30°B.60°C.90°D.120°二、填空题（共6小题，每小题3分，共18分）。

人教版八年级数学上册第11--13章检测题含答案)

人教版八年级数学上册第十一章检测题11.1 与三角形有关的线段一、选择题（本大题共12道小题）1. 三角形按边分类可分为()A.不等边三角形、等边三角形B.等腰三角形、等边三角形C.不等边三角形、等腰三角形、等边三角形D.不等边三角形、等腰三角形2. 人字梯中间一般会设计一“拉杆”，这样做的道理是()A．两点之间，线段最短B．垂线段最短C．两直线平行，内错角相等D．三角形具有稳定性3. 已知在△ABC中，AB=6，BC=4，那么边AC的长可能是下列哪个值()A. 11B. 5C. 2D. 14. 课堂上,老师把教学用的两块三角尺叠放在一起,得到如图所示的图形,其中三角形的个数为()A.2B.3C.5D.65. 已知等腰三角形的腰和底的长分别是一元二次方程x2－6x＋8＝0的根，则该三角形的周长为()A. 8B. 10C. 8或10D. 126. 如图，已知AD是△ABC的中线，且△ABD的周长比△ACD的周长大3 cm，则AB与AC的差为()A．2 cm B．3 cm C．4 cm D．6 cm7. 如图，已知P为直线l外一点，点A，B，C，D在直线l上，且PA＞PB＞PC ＞PD，则下列说法正确的是()A．线段PD的长是点P到直线l的距离B．线段PC可能是△PAB的高C．线段PD可能是△PBC的高D．线段PB可能是△PAC的高8. 下列关于三角形的分类，有如图K－1－4所示的甲、乙两种分法，则()A．甲、乙两种分法均正确B．甲分法正确，乙分法错误C．甲分法错误，乙分法正确D．甲、乙两种分法均错误9. 如图，六根木条钉成一个六边形框架ABCDEF，要使框架稳固且不活动，至少还需要添加木条()A．1根B．2根C．3根D．4根10. 长为9，6，5，4的四根木条，选其中三根组成三角形，选法有()A．1种B．2种C．3种D．4种11. 将一个三角形纸片剪开分成两个三角形，这两个三角形不可能()A．都是直角三角形B．都是钝角三角形C．都是锐角三角形D．是一个直角三角形和一个钝角三角形12. 某木材市场上木棒规格与对应单价如下表:规格 1 m 2 m 3 m 4 m 5 m 6 m单价(元/根) 10 15 20 25 30 35小明的爷爷要做一个三角形的木架养鱼用，现有两根长度分别为3 m和5 m的木棒，还需要到该木材市场去购买一根木棒，则小明的爷爷至少带的钱数应为()A.10元B.15元C.20元D.25元二、填空题（本大题共6道小题）13. 如图，自行车的主框架采用了三角形结构，这样设计的依据是________________．14. 如图，AE是△ABC的中线，已知EC＝8，DE＝3，则BD＝________．15. 已知一个等腰三角形两边的长分别为3和6，则该等腰三角形的周长是.16. 如图，在△ABC中，AD⊥BC于点D，点E在CD上，则图中以AD为高的三角形有______个．17. 已知三角形的三边长分别为3，8，x，若x为偶数，则x＝____________．18. 如图，将△ABC沿直线DE折叠，使点C与点A重合，已知AB＝7，BC＝6，则△BCD的周长为________．三、解答题（本大题共3道小题）19. 如图，用钉子把木棒AB，BC和CD分别在端点B，C处连接起来，AB，CD 可以转动，用橡皮筋把AD连接起来，橡皮筋始终绷直，设橡皮筋AD的长是x cm.(1)若AB=5 cm，CD=3 cm，BC=11 cm，求x的最大值和最小值;(2)在(1)的条件下要围成一个四边形，你能求出x的取值范围吗?20. 数学活动课上，老师让同学们用长度分别是20 cm，90 cm，100 cm的三根木棒搭一个三角形的木架，小明不小心把100 cm的木棒折去了35 cm，他发现：用折断后剩下的木棒与另两根木棒怎么也搭不成三角形．(1)你知道为什么吗？(2)100 cm长的木棒至少折去多长后剩余的部分就不能与另两根木棒搭成三角形？21. 观察探究观察并探求下列各问题．(1)如图①，在△ABC中，P为边BC上一点，则BP＋PC________AB＋AC(填“＞”“＜”或“＝”)；(2)将(1)中的点P移到△ABC内，如图②，试观察比较△BPC的周长与△ABC的周长的大小，并说明理由；(3)将(2)中的点P变为两个点P1，P2，如图③，试观察比较四边形BP1P2C的周长与△ABC的周长的大小，并说明理由．人教版八年级数学11.1 与三角形有关的线段课时训练-答案一、选择题（本大题共12道小题）1. 【答案】D2. 【答案】D3. 【答案】B4. 【答案】C5. 【答案】B【解析】解一元二次方程x2－6x＋8＝0，得x1＝2，x2＝4.当三角形三边为2，2，4时，∵2＋2＝4，∴不符合三边关系，应舍去；当三角形三边为2，4，4时，∵2＋4>4，符合三边关系，∴三角形的周长为10，故选B.6. 【答案】B[解析] ∵AD是△ABC的中线，∴BD＝CD.∴△ABD与△ACD的周长之差＝(AB＋AD＋BD)－(AC＋AD＋CD)＝AB－AC. ∵△ABD的周长比△ACD的周长大3 cm，∴AB与AC的差为3 cm.7. 【答案】C[解析] 由于PA＞PB＞PC＞PD，因此PD可能是钝角三角形PBC 中BC边上的高．8. 【答案】C9. 【答案】C[解析] 添加3根木条以后成为如右所示图形，其由若干三角形组成，具有稳定性．10. 【答案】C11. 【答案】C[解析] 如图①，沿虚线剪开即可得到两个直角三角形．如图②，钝角三角形沿虚线剪开即可得到两个钝角三角形．如图③，直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形．因为剪开的边上的两个角互补，故这两个三角形不可能都是锐角三角形．12. 【答案】C[解析] 由三角形三边大小关系可得第三根木棒的长度应该大于2 m 且小于8 m，所以满足要求的木棒有3 m，4 m，5 m，6 m，其中买3 m木棒用钱最少，为20元.二、填空题（本大题共6道小题）13. 【答案】三角形具有稳定性14. 【答案】5[解析] ∵AE是△ABC的中线，EC＝8，∴BE＝EC＝8.∵DE＝3，∴BD＝BE－DE＝8－3＝5.15. 【答案】15[解析] 若腰长为3，3+3=6，∴3，3，6不能组成三角形;若腰长为6，3+6=9>6，∴3，6，6能组成三角形，该三角形的周长为3+6+6=15.16. 【答案】617. 【答案】6或8或10[解析] 由三角形三边关系可知5<x<11.因为x为偶数，所以x的值为6或8或10.18. 【答案】13【解析】由折叠的性质可得：CD＝AD，∴△BCD的周长＝BC ＋CD＋BD＝BC＋AD＋BD＝BC＋BA＝6＋7＝13.三、解答题（本大题共3道小题）19. 【答案】解:(1)x的最大值是5+3+11=19，最小值是11-3-5=3.(2)由(1)得x的取值范围为3<x<19.20. 【答案】解：(1)把100 cm的木棒折去了35 cm后还剩余65 cm.∵20＋65＜90，∴20 cm，65 cm，90 cm长的三根木棒不能构成三角形．(2)设折去x cm后剩余的部分不能与另两根木棒搭成三角形．根据题意，得20＋(100－x)≤90，解得x≤30，∴100 cm长的木棒至少折去30 cm后剩余的部分就不能与另两根木棒搭成三角形．21. 【答案】解：(1)＜(2)△BPC的周长＜△ABC的周长．理由：如图①，延长BP交AC于点M.在△ABM中，BP＋PM＜AB＋AM.在△PMC中，PC＜PM＋MC.两式相加，得BP＋PC＜AB＋AC，∴△BPC的周长＜△ABC的周长．(3)四边形BP1P2C的周长＜△ABC的周长．理由：如图②，分别延长BP1，CP2交于点M.由(2)知，BM＋CM＜AB＋AC.又∵P1P2＜P1M＋P2M，∴BP1＋P1P2＋P2C＜BM＋CM＜AB＋AC.∴四边形BP1P2C的周长＜△ABC的周长．11.2三角形-与三角形有关的角一、选择题1.若一个三角形三个内角度数的比为2：3：4，那么这个三角形是( )A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形2.如图所示，BD平分∠ABC，DE∥BC，且∠D=30°，则∠AED的度数为（）。

人教版八年级数学上册提高题11(因式分解).docx

u初中数学试卷桑水出品初二上数学提高题11（整式乘除）班级姓名座号1. 若4)1(22+--x m x 是一个完全平方式，则m ＝．2. 若14)5)((2222=-++b a b a ，则=+22b a ．3. 无论x 、y 取什么值，4012422+++-y y x x 的值都是．4. 化简=-+-+n n 212)2(2)2( ． 5. 若0132=-+x x ，则=+221x x ，=+xx 1 ． 6.阅读理解题：（因式分解的方法补充）分组分解方法：将多项式先分组，分别变形，再进行分解因式的方法叫分组分解法．如 mx nx my ny +++=))(()()()()(y x n m n m y n m x ny my nx mx ++=+++=+++试一试：(1)44ax ay x y --+ (2) b b a a 3322+--拆项法：如)1()1)(1(313314333---+=+--=+-y y y y y y y y y )133)(1(2-+-=y y y ．试一试： (1) 893+-x x 你有几种方法？添项法：如)22)(22()2()2(4)44(4222222244+++-=-+=-++=+x x x x x x x x x x试一试：（1）644+x （2）4224y y x x ++7.若2011=a ，2012=b ，2013=c 求ac bc ab c b a ---++222的值．8.试说明四个连续整数的积加上1是一个整数的平方．9. 如图，在直角梯形ABCD 中，AB ∥CD ，∠B ＝90°，E 是BC 上的一点，连结AE ，DE ，且AE=DE ，∠AED=90°．（1）求证：△ABE ≌△ECD ；（2）若△AED 的面积是225，直角梯形ABCD 的面积是249，求△ABE 的周长；（3）若△AED 的面积是a ，直角梯形ABCD 的面积是b ，试判断b 与a 2的大小，并说明理由． E DCB A。

2023-2024学年八年级上学期人教版数学阶段限时训练卷(第11~13章)(含解析)

2023-2024学年八年级上学期人教版数学阶段限时训练卷（第11~13章）一．选择题（共10小题，满分30分，每小题3分）1．（3分）下面有4个汽车标致图案，其中不是轴对称图形的是（）A．B．C．D．2．（3分）下列每组数据分别是三根小木棒的长度，用这些木棒能摆成三角形的是（）A．5cm，5cm，11cm B．13cm，12cm，20cmC．8cm，7cm，15cm D．3cm，4cm，8cm3．（3分）如图，工人师傅门时，常用木条EF固定长方形门框，使其不变形，这样做的根据是（）A．三角形的稳定性B．两点确定一条直线C．两点之间，线段最短D．四边形的不稳定性4．（3分）下列条件不能得到等边三角形的是（）A．有两个内角是60°的三角形B．三个外角都相等的三角形C．有两个角相等的等腰三角形D．有一个角是60°的等腰三角形5．（3分）如图，AB∥CD，∠AFE＝135°，∠D＝80°，则∠E等于（）A．55°B．45°C．80°D．50°6．（3分）如图，已知AC∥BD，∠A＝∠C，则下列结论不一定成立的是（）A．∠B＝∠D B．OA＝OCC．OA＝OD D．AD＝BC7．（3分）如图，已知MB＝ND，∠MBA＝∠NDC，下列条件中不能判定△ABM≌△CDN的是（）A．∠M＝∠N B．AM∥CNC．AB＝CD D．AM＝CN8．（3分）等腰三角形一腰上的高与另一腰的夹角为60°，则等腰三角形的底角度数为（）A．15°B．30°C．15°或75°D．30°或150°9．（3分）如图所示，在Rt△ACB中，∠C＝90°，AD平分∠BAC，若BC＝16，BD＝10，则点D到AB的距离是（）A．9B．8C．7D．610．（3分）如图，BE、CF是△ABC的角平分线，∠A＝50°，BE、CF相交于D，则∠BDC的度数是（）A．115°B．110°C．100°D．90°二．填空题（共7小题，满分28分，每小题4分）11．（4分）点P（2，﹣3）关于y轴对称的点的坐标是．12．（4分）已知在△ABC中，∠A＝40°，∠B﹣∠C＝40°，则∠C＝．13．（4分）已知a，b是等腰三角形的两边长，且a，b满足（a+b﹣13）2＝0，则此等腰三角形的周长为．14．（4分）如图，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，则∠ABD＝．15．（4分）如图Rt△ABC中，∠A＝30°，AB+BC＝12cm，则AB＝cm．16．（4分）一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为．17．（4分）如图，等边△ABC中，E是AC边的中点，AD是BC边上的中线，P是AD上的动点，若AD＝6，则EP+CP的最小值为．三．解答题（共8小题，满分62分）18．（6分）如图，AE＝CF，AD＝CB，DF＝BE，求证：△ADF≌△CBE．19．（6分）一个多边形的内角和比它的外角和的2倍还大180度，求这个多边形的边数．20．（6分）如图，已知AC＝AE，∠B＝∠D，∠1＝∠2，求证：AB＝AD．21．（8分）如图，△ABC的周长为20，其中AB＝8，（1）用直尺和圆规作AB的垂直平分线DE交AC于点E，垂足为D，连接EB；（保留作图痕迹，不要求写画法）（2）在（1）作出AB的垂直平分线DE后，求△CBE的周长．22．（8分）如图，在平面直角坐标系中，A（﹣3，2），B（﹣4，﹣3），C（﹣1，﹣1）．（1）在图中作出与△ABC关于y轴对称的△A1B1C1（要求点A与A1，点B与点B1，点C和点C1相对应）；写出点A1，B1，C1的坐标（直接写答案）：A1；B1；C1；（2）请直接写出△A1B1C1的面积是．23．（8分）如图，在△ABC中，已知AB＝AC，BD平分∠ABC，AE为BC边的中线，AE、BD相交于点D，其中∠ADB＝125°，求∠BAC的度数．24．（10分）如图，△ABC中，AB＝AC，D、E、F分别为AB、BC、AC上的点，且BD＝CE，∠DEF＝∠B．（1）求证：∠BDE＝∠CEF；（2）当∠A＝60°时，求证：△DEF为等边三角形．25．（10分）（1）如图①，把△ABC纸片沿DE折叠，使点A落在四边形BCED的内部点A′的位置，试说明2∠A＝∠1+∠2；（2）如图②，若把△ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，此时∠A与∠1、∠2之间的等量关系是（无需说明理由）；（3）如图③，若把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部点A′、D′的位置，请你探索此时∠A、∠D、∠1与∠2之间的数量关系，写出你发现的结论并说明理由．2023-2024学年八年级上学期人教版数学阶段限时训练卷（第11~13章）参考答案与试题解析一．选择题（共10小题，满分30分，每小题3分）1．【解答】解：A．是轴对称图形，故此选项不合题意；B．是轴对称图形，故此选项不合题意；C．是轴对称图形，故此选项不合题意；D．不是轴对称图形，故此选项符合题意；故选：D．2．【解答】解：A、5+5＜11，不能组成三角形，故此选项错误；B、13+12＞20，能组成三角形，故此选项正确；C、8+7＝15，不能组成三角形，故此选项错误．D、3+4＜8，不能够组成三角形，故此选项错误；故选：B．3．【解答】解：用木条EF固定长方形门框，得到了△AEF，使其不变形，这样做的根据是三角形的稳定性，故选：A．4．【解答】解：A、两个内角为60°，因为三角形的内角和为180°，可知另一个内角也为60°，故该三角形为等边三角形；故本选项不符合题意；B、三个外角相等说明该三角形中三个内角相等，故该三角形为等边三角形；故本选项不符合题意；C、等腰三角形的两个底角是相等的，故不能确定该三角形是等边三角形．故本选项符合题意；D、有一个角是60°的等腰三角形是等边三角形，故本选项不符合题意；故选：C．5．【解答】解：∵AB∥CD，∠AFE＝135°，∴∠DGF＝∠AFE＝135°，∴∠DGE＝180°﹣∠DGF＝45°，∵∠D＝80°，∴∠E＝180°﹣∠D﹣∠DGE＝55°，故选：A．6．【解答】解：A、∵AC∥BD，∴∠A＝∠D，∠C＝∠B，∵∠A＝∠C，∴∠B＝∠D，正确，故本选项不符合题意；B、∵∠A＝∠C，∴OA＝OC，正确，故本选项不符合题意；C、根据已知不能推出OA＝OD，错误，故本选项符合题意；D、∵∠A＝∠C，∠B＝∠D，∴OA＝OC，OD＝OB，∴OA+OD＝OC+OB，即AD＝BC，正确，故本选项不符合题意；故选：C．7．【解答】解：A、∠M＝∠N，符合ASA，能判定△ABM≌△CDN，故A选项不符合题意；B、AM∥CN，得出∠MAB＝∠NCD，符合AAS，能判定△ABM≌△CDN，故B选项不符合题意．C、AB＝CD，符合SAS，能判定△ABM≌△CDN，故C选项不符合题意；D、根据条件AM＝CN，MB＝ND，∠MBA＝∠NDC，不能判定△ABM≌△CDN，故D选项符合题意；故选：D．8．【解答】解：在等腰△ABC中，AB＝AC，BD为腰AC上的高，∠ABD＝40°，当BD在△ABC内部时，如图1，∵BD为高，∴∠ADB＝90°，∴∠BAD＝90°﹣46°＝30°，∵AB＝AC，∴∠ABC＝∠ACB（180°﹣30°）＝75°；当BD在△ABC外部时，如图2，∵BD为高，∴∠ADB＝90°，∴∠BAD＝90°﹣60°＝30°，∵AB＝AC，∴∠ABC＝∠ACB，而∠BAD＝∠ABC+∠ACB，∴∠ACB∠BAD＝15°，综上所述，这个等腰三角形底角的度数为75°或15°．故选：C．9．【解答】解：∵BC＝16，BD＝10∴CD＝6由角平分线的性质，得点D到AB的距离等于CD＝6．故选：D．10．【解答】解：∵∠A＝50°，∴∠ABC+∠ACB＝180°﹣50°＝130°，∵BE、CF是△ABC的角平分线，∴∠EBC∠ABC，∠FCB∠ACB，∴∠EBC+∠FCB（∠ABC+∠ACB）＝65°，∴∠BDC＝180°﹣65°＝115°，故选：A．二．填空题（共7小题，满分28分，每小题4分）11．【解答】解：点P（2，﹣3）关于y轴对称的点的坐标为：（﹣2，﹣3）．故答案为：（﹣2，﹣3）．12．【解答】解：∵在△ABC中，∠A＝40°，∴∠B+∠C＝140°①，∵∠B﹣∠C＝40°②，∴①﹣②得，2∠C＝100°，解得∠C＝50°．故答案为：50°．13．【解答】解：∵（a+b﹣13）2＝0，∴a﹣b+3＝0，a+b﹣13＝0，∴a＝5，b＝8，∵a，b是等腰三角形的两边长，∴等腰三角形的三边长为5，5，8或5，8，8，∴5+5+8＝18或5+8+8＝21，∴等腰三角形的周长为18或21，故答案为：18或21．14．【解答】解：设∠ABD＝x，∵BC＝AD，∴∠A＝∠ABD＝x，∵BD＝BC，∴∠C＝∠BDC，根据三角形的外角性质，∠BDC＝∠A+∠ABD＝2x，∵AB＝AC，∴∠ABC＝∠C＝2x，在△ABC中，∠A+∠ABC+∠＝180°，即x+2x+2x＝180°，解得x＝36°，即∠ABD＝36°．故答案为：36°．15．【解答】解：∵Rt△ABC中，∠A＝30°，∴BC AB．设BC＝xcm，则有AB＝2xcm∴x+2x＝12，∴x＝4，∴AB＝8cm．故答案为：8．16．【解答】解：如图∠NPM＝180°﹣70°﹣40°＝70°，∵向北的方向线是平行的，∴∠M＝70°，∴∠NPM＝∠M，∴NP＝MN＝40海里×2＝80海里，故答案为：80海里．17．【解答】解：作点E关于AD的对称点F，连接CF，∵△ABC是等边三角形，AD是BC边上的中线，∴AD⊥BC，∴AD是BC的垂直平分线，∴点E关于AD的对应点为点F，∴CF就是EP+CP的最小值．∵△ABC是等边三角形，E是AC边的中点，∴F是AB的中点，∴CF是△ABC的中线，∴CF＝AD＝6，即EP+CP的最小值为6，故答案为6．三．解答题（共8小题，满分62分）18．【解答】证明：∵AE＝CF，∴AE﹣EF＝CF﹣EF，∴AF＝CE．在△ADF和△CBE中，∴△ADF≌△CBE（SSS）．19．【解答】解：设这个多边形的边数为n，由题意得，（n﹣2）•180°＝2×360°+180°，解得n＝7，答：这个多边形的边数是7．20．【解答】证明：∵∠1＝∠2，∴∠1+∠CAD＝∠2+∠CAD，∴∠BAC＝∠DAE，在△ADF和△CBE中，，∴△ADF≌△CBE（AAS），∴AB＝AD．21．【解答】解：（1）如图，BE为所作；（2）∵DE是AB的垂直平分线，∴EA＝EB，∴EB+EC＝EA+EC＝AC，∵△ABC的周长为20，∴AC+BC＝20﹣AB＝20﹣8＝12，∴△CBE的周长＝BE+EC+BC＝AE+EC+BC＝AC+BC＝12．22．【解答】解：（1）如图所示，△A1B1C1即为所求；故答案为：（3，2），（4，﹣3），（1，﹣1）；（2）如图所示，S△ABC＝S梯形BCDE﹣S△ACD﹣S△ABE3×（5+3）2×31×5＝12﹣2.5﹣3＝6.5．故答案为：6.523．【解答】解：∵AB＝AC，AE为BC边的中线，∴AE⊥BC，∴∠AEB＝90°，又∵∠ADB＝125°，∴∠DBE＝∠ADB﹣∠AEB＝35°，∵BD平分∠ABC，∴∠ABC＝2∠DBE＝70°，∵AB＝AC，∴∠C＝∠ABC＝70°，∴∠BAC＝180°﹣∠ABC﹣∠C＝40°．24．【解答】证明：（1）∵∠DEC是△BDE的一个外角，∴∠B+∠BDE＝∠DEF+∠CEF，∵∠DEF＝∠B，∴∠BDE＝∠CEF；（2）由（1）可知∠BDE＝∠CEF，∵AB＝AC，∠A＝60°∴∠B＝∠C＝60°，∴∠DEF＝60°，在△BDE和△CEF中∴△BDE≌△CEF（ASA），∴DE＝EF，∴△DEF为等边三角形．25．【解答】解：（1）如图，根据翻折的性质，∠3（180﹣∠1），∠4（180﹣∠2），∵∠A+∠3+∠4＝180°，∴∠A（180﹣∠1）（180﹣∠2）＝180°，整理得，2∠A＝∠1+∠2；（2）根据翻折的性质，∠3（180﹣∠1），∠4（180+∠2），∵∠A+∠3+∠4＝180°，∴∠A（180﹣∠1）（180+∠2）＝180°，整理得，2∠A＝∠1﹣∠2；（3）根据翻折的性质，∠3（180﹣∠1），∠4（180﹣∠2），∵∠A+∠D+∠3+∠4＝360°，∴∠A+∠D（180﹣∠1）（180﹣∠2）＝360°，整理得，2（∠A+∠D）＝∠1+∠2+360°．。

人教版八年级上册数学第十一章三角形单元提高训练题 (15)(有解析)

第十一章三角形单元提高训练题 (15)一、单选题1．下列说法：①三角形的外角大于内角；②各条边都相等，各个角都相等的多边形是正多边形；③三角形的三条高相交于一点；④如果a>b，那么m2a>m2b，其中说法正确的有( )．A．1个B．2个C．3个D．4个2．已知一个正多边形的每个外角等于60，则这个正多边形是（）A．正五边形B．正六边形C．正七边形D．正八边形3．不是利用三角形稳定性的是A．自行车的三角形车架 B．三角形房架C．照相机的三角架 D．矩形门框的斜拉条4．以下列各组长度的线段为边（单位：cm），能组成三角形的是（）A．3，4，7 B．2.5，3.5，7.5C．6，4，9 D．8，3，35．如图，△ABC的两条内角平分线BD与CD交于点D，设∠A的度数为x，∠BDC的度数为y，则y关于x的函数图象是（）A．B．C．D．6．如图，直线l1∥l2，∠1＝35°，∠2＝80°，则∠3等于（）A．55°B．60°C．65°D．70°7．如图，在△ABC中，DE是AC的垂直平分线，且分别交BC，AC于点D和E，∠B＝60°，∠C＝25°，则∠BAD为（）A ．50°B ．70°C ．75°D ．80° 8．如果一个三角形的两边长分别是2和5，则第三边可能是（）A ．2B ．3C ．5D ．8 9．如果一个多边形的每一个内角都是135°，那么这个多边形的边数是（） A ．5B ．6C ．8D ．10 10．如果一个三角形中的其中一个外角等于与它相邻的内角，那么这个三角形是( ) A ．直角三角形B ．锐角三角形C ．钝角三角形D ．无法确定 11．如果等腰三角形有一个内角为70，则其底角的度数是（） A ．55B ．70C ．55或70D ．不确定12．如图，在ABC ∆中，AB AC =，A 40︒∠=，将ABC ∆沿CD 折叠，使点B 落在边AC 上的点E 处，则ADE ∠的度数是（）A ．40︒B ．30︒C ．60︒D ．70︒二、填空题13．若一个多边形的内角和与外角和之和是1800°，则此多边形是___边形.14．如图1六边形的内角和123456∠+∠+∠+∠+∠+∠为m 度，如图2六边形的内角和123456∠+∠+∠+∠+∠+∠为n 度，则m n -=________．15．如图，D 、E 分别是△ABC 边AB 、BC 上的点，AD=2BD ，BE=CE ，若S △ABC =18,设△ADF 的面积为S 1，△CEF 的面积为S 2，则S 1-S 2的值是______.16．在△ABC 中，∠C ＝30°，∠A ﹣∠B ＝30°，则∠A ＝_____．17．如图，D 是△ABC 的边BC 上任意一点，E 、F 分别是线段AD 、CE 的中点．若△ABC 的面积为m ，则△BEF 的面积为_____．18．如图，AB ∥GF ，若∠ABH=30°，∠MFG=28°，则∠H+∠L+∠M=____度．三、解答题19．如图，在△ABC 中，AD 是BC 边上的高，BE 平分∠ABC 交AC 边于E ，∠DAC ＝26°，∠CBE ＝22°．求∠BAC 的度数．20．如图①，BE 、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠，设BAD ∠=α，BCD β∠=．（1）若110αβ+=︒，则MBC NDC ∠+∠= ︒；（2）若BE 与DF 相交于点G ，且25BGD ∠=︒，求α、β所满足的等量关系式，并说明理由；（3）如图②，若αβ=，试判断BE 、DF 的位置关系，并说明理由．21．如图，在六边形ABCDEF 中，AF ∥CD ，AB ∥DE ，BC ∥EF ，且∠A ＝120°，∠B ＝80°，求∠C 及∠D 的度数．22．证明“三角形的外角和等于360°”．23．一个多边形的内角和与某一个外角的度数总和为1350°，求这个多边形的边数．24．（问题背景）（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；（简单应用）（2）如图2， AP、CP分别平分∠BAD．∠BCD，若∠ABC=46°，∠ADC=26°，求∠P的度数；（问题探究）（3）如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．（拓展延伸）（4）①在图4中，若设∠C=α，∠B=β，∠CAP=13∠CAB，∠CDP=13∠CDB，试问∠P与∠C、∠B之间的数量关系为：（用α、β表示∠P）；②在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论．25．（1）如图1，△ABC中，BO平分∠ABC，CO平分∠ACB，∠A=56°，求∠BOC的度数；（2）如图2，若点P为△ABC外部一点，PB平分∠ABC，PC平分外角∠ACD，先写出∠A 和∠P的数量关系，并证明你的结论．26．如图所示，OD是∠AOB的平分线，OE是∠BOC的平分线，且∠AOC=150，求∠DOE 的度数【答案与解析】一、单选题1．A解析：A根据三角形的外角性质，正多边形的定义，三角形的高及不等式的性质可得出答案.三角形的外角大于与它不相邻的内角，故①错误；各条边都相等，各个角都相等的多边形是正多边形，故②正确；三角形的三条高所在的直线交于一点，三条高不一定相交，故③错误；因为m可能为0，所以存在m2a=m2b，故④错误；故选择A项.【点睛】本题考查三角形的外角性质，正多边形的定义，三角形的高及不等式的性质，解题的关键是熟悉三角形的外角性质，正多边形的定义，三角形的高及不等式的性质.2．B解析：B分析：根据多边形的外角和为360°即可得出答案．详解：360°÷60°=6，即六边形，故选B．点睛：本题主要考查的是正多边形的外角和定理，属于基础题型．多边形的内角和定理为(n－2)×180°，多边形的外角和为360°．3．C解析：C试题分析：关键是分析能否在同一平面内组成三角形．解：照相机的三脚架构成的是立体图形，不是三角形.故选C.4．C解析：C根据三角形两边之和大于第三边进行判断即可．在A选项中，3+4=7，不符合三角形的三边关系，故A不能；在B选项中，2.5+3.5＜7.5，不符合三角形的三边关系，故B不能；在C选项中，4+6＞9，符合三角形的三边关系，故C能；在D选项中，3+3＜8，不符合三角形的三边关系，故D不能；故选：C．【点睛】本题考查三角形的三边关系，掌握三角形的两边之和大于第三边，两边之差小于第三边是解题的关键．5．B解析：B首先根据△ABC 的两条内角平分线的性质，可得出∠DBC ＝12∠ABC ，∠DCB ＝12∠ACB ，进而得出∠BDC ＝90°+12A ∠，再根据∠A ＞0°且180°＞90°+12A ∠＞0°，可得其取值范围0°＜∠A ＜180°，即可得出函数解析式. ∵△ABC 的两条内角平分线BD 与CD 交于点D∴∠DBC ＝12∠ABC ，∠DCB ＝12∠ACB ∴∠BDC ＝180°﹣∠DBC ﹣∠DCB ＝180°﹣()12ABC ACB +∠∠＝180°﹣()1801-2A ︒∠＝90°+12A ∠，∵∠A ＞0°且180°＞90°+12A ∠＞0° ∴解得0°＜∠A ＜180°，即：y ＝90+12x ，0＜x ＜180，故选：B ．【点睛】此题主要考查三角形内角平分线的性质，关键是列出两角的关系式.6．C解析：C由平行可得∠5的度数，利用三角形的内角和与∠2的对顶角，求出∠3．解：如图，∵l 1∥l 2，∴∠1＝∠4＝35°． ∵∠2＝∠5＝80°，又∵∠3+∠5+∠4＝180°， ∴∠3＝180°-∠5-∠4 ＝180°-80°-35° ＝65°．故选：C ．【点睛】本题考查了三角形的内角和定理及平行线的性质．利用平行线的性质得到∠4的度数，是解决本题的关键．7．B解析：B分析：根据线段垂直平分线的性质得到DA=DC，根据等腰三角形的性质得到∠DAC=∠C，根据三角形内角和定理求出∠BAC，计算即可．详解：∵DE是AC的垂直平分线，∴DA=DC，∴∠DAC=∠C=25°，∵∠B=60°，∠C=25°，∴∠BAC=95°，∴∠BAD=∠BAC-∠DAC=70°，故选B．点睛：本题考查的是线段垂直平分线的性质、等腰三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．8．C解析：C试题分析：设第三边长为x，则由三角形三边关系定理得5﹣2＜x＜5+2，即3＜x＜7．故选C．考点：三角形三边关系．9．C解析：C已知每一个内角都等于135°，就可以知道每个外角是45度，根据多边形的外角和是360度就可以求出多边形的边数．多边形的边数是：n＝360180135︒︒-︒＝8，即该多边形是八边形．故选：C．【点睛】本题考查了多边形的内角与外角，熟练掌握多边形的外角和、多边形的每一个外角的度数、多边形的边数三者之间的关系是解题的关键．10．A解析：A根据三角形的一个外角等于和它不相邻的两个内角的和与三角形的内角和等于180°可以求出与这个外角相邻的内角等于90°．根据题意，与这个外角相邻的内角等于180°÷2=90°，所以这个三角形是直角三角形．故选：A．【点睛】本题主要考查三角形的外角性质和三角形的内角和定理，熟练掌握性质和定理是解题的关键．11．C解析：C根据等腰三角形的性质和三角形的内角和定理解答即可．解：当顶角为70°时，则底角的度数是：(180°-70°)÷2=55°，当底角为70°时，则底角的度数是70°，故选：C．【点睛】此题考查等腰三角形的性质，关键是根据等腰三角形的性质和三角形的内角和定理解答．12．B解析：B根据等腰三角形两底角相等求出∠B，再根据翻折的性质可得∠CED＝∠B，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．∵AB＝AC，∠A＝40°，∴∠B＝12（180°−∠A）＝12（180°−40°）＝70°，∵△ABC沿CD折叠，点B落在边AC上的点E处，∴∠CED＝∠B＝70°，由三角形的外角性质得，∠ADE＝∠CED−∠A＝70°−40°＝30°．故选：B．【点睛】本题考查了翻折变换的性质，等腰三角形的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，要注意折叠前后对应角相等．二、填空题13．十解析：十试题分析：设所求n边形边数为n，先根据多边形的外角和为360度得到多边形的内角和，再根据多边形的内角和公式，即可得到结果．由题意得多边形的内角和为1800°-360°=1440°，设所求n边形边数为n，则180°(n-2)=1440°，解得n=10，则此多边形是十边形.考点：本题考查的是多边形的内角和公式，多边形的外角和点评：解答本题的关键是熟练掌握多边形的内角和公式：180°(n-2)，任意多边形的外角和均是360度，与边数无关．14．0解析：0将两个六边形分别进行拆分，再结合三角形的内角和和四边形的内角和计算即可得出答案.如图1所示，将原六边形分成了两个三角形和一个四边形，∴123456m=∠+∠+∠+∠+∠+∠=180°×2+360°=720°如图2所示，将原六边形分成了四个三角形∴123456n=∠+∠+∠+∠+∠+∠=180°×4=720°∴m-n=0故答案为0.【点睛】本题考查的是三角形的内角和和四边形的内角和，难度适中，解题关键是将所求六边形拆分成几个三角形和四边形的形式进行求解.15．3解析：3根据AD=2BD，BE=CE，且S△ABC=12，从而求出△ABE的面积和△BCD的面积，又因为S△ADF-S△CEF=S△ABE-S△BCD，所以即可求解S1-S2的值．解：∵BE=CE，∴BE=12 BC，∵S△ABC=18，∴S△ABE=12S△ABC=12×18=9．∵AD=2BD，S△ABC=18，∴S△BCD=12S△ABC=6，∵S△ABE-S△BCD=（S△ADF+S四边形BEFD）-（S△CEF+S四边形BEFD）=S△ADF-S△CEF，即S△ADF-S△CEF=S△ABE-S△BCD=9-6=3．故答案为：3．【点睛】本题考查了三角形的面积，通过高相等时，面积等于底边的比，从而可求出三角形的面积．16．90°解析：90°．根据三角形内角和得到∠A+∠B+∠C＝180°，而∠C＝30°，则可计算出∠A+∠B+＝150°，由于∠A﹣∠B＝30°，把两式相加消去∠B即可求得∠A的度数．解：∵∠A+∠B+∠C＝180°，∠C＝30°，∴∠A+∠B+＝150°，∵∠A﹣∠B＝30°，∴2∠A＝180°，∴∠A＝90°．故答案为：90°．【点睛】本题考查了三角形内角和定理：三角形内角和是180°．主要用在求三角形中角的度数．①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．17．m解析：14m．根据三角形的中线把三角形分成两个面积相等的三角形解答即可．∵点E是AD的中点，∴S△ABE=12S△ABD，S△ACE=12S△ADC，∴S△ABE+S△ACE=12S△ABC=12m，∴S△BCE=12S△ABC=12m，∵点F是CE的中点，∴S△BEF=12S△BCE=12×12m=14m．故答案为14 m．【点睛】本题考查了三角形的面积，主要利用了三角形的中线把三角形分成两个面积相等的三角形，原理为等底等高的三角形的面积相等．18．418解析：418连接BF，由平行线的性质得到∠ABF+∠BFG=180°，将∠H+∠L+∠M转化为五边形B HL MF 的内角和+（∠ABH+∠MFG）－（∠ABF+∠BFG），结合多边形的内角和定理求解即可．连接BF．∵AB∥GF，∴∠ABF+∠BFG=180°．∠H+∠L+∠M=五边形B HL MF的内角和+（∠ABH+∠MFG）－（∠ABF+∠BFG）=540°+（30°+28°）﹣180°=418°．故答案为418．【点睛】本题考查了平行线的性质及多边形的内角和，注意掌握平行线的性质及一个n 边形的内角和为：（n ﹣2）×180°．三、解答题19．72°根据直角三角形两锐角互余求出∠C 的度数，根据角平分线的定义求出∠ABC 的度数，然后根据∠BAC=180°-∠ABC-∠C 求解即可.解：∵AD 是BC 边上的高，∴∠ADC ＝90°，∵∠DAC ＝26°，∴∠C ＝90°﹣26°＝64°，∵BE 平分∠ABC ，∠CBE ＝22°，∴∠ABC ＝2∠CBE ＝22°×2＝44°，∴∠BAC ＝180°﹣∠ABC ﹣∠C ＝72°．【点睛】本题考查三角形内角和定理，直角三角形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．20．（1）110；（2）50βα-=︒，理由见解析；（3）BE DF ∥，理由见解析（1）根据四边形的内角和与邻补角的性质即可求解；（2）连接BD ，先得到1()2CBG CDG αβ∠+∠=+，再根据三角形的内角和得到角度的关系即可求解；（3）由（1）有，∠MBC ＋∠NDC ＝αβ+，BE 、DF 分别平分四边形的外角∠MBC 和∠NDC ，则∠CBE ＋∠CDH ＝12（αβ+），∠CBE ＋β−∠DHB ＝12（αβ+），根据α＝β，则有∠CBE ＋β−∠DHB ＝12（β＋β）＝β，得到∠CBE ＝∠DHB ，故可得到BE ∥DF ．解：（1）∵∠ABC ＋∠ADC ＝360°−（αβ+）＝250°，∴∠MBC ＋∠NDC ＝180°−∠ABC ＋180°−∠ADC ＝360°-（∠ABC ＋∠ADC ）=αβ+＝110°．故答案为：110；（2）50βα-=︒．理由如下：如解图①，连接BD ，由（1）知，MBC NDC αβ∠+∠=+， BE、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠， ∴12CBG MBC ∠=∠，12CDG NDC ∠= ()1111()2222CBG CDG MBC NDC MBC NDC αβ∴∠+∠=∠+=∠+=+．在△BCD 中，∠BDC ＋∠CBD ＝180°−∠BCD ＝180°−β，在△BDG 中，∠GBD ＋∠GDB ＋∠BGD ＝180°，∴∠CBG ＋∠CBD ＋∠CDG ＋∠BDC ＋∠BGD ＝180°，∴（∠CBG ＋∠CDG ）＋（∠BDC ＋∠CBD ）＋∠BGD ＝180°，∴12（αβ+）＋180°−β＋25°＝180°，整理得50βα-=︒；（3）BE DF ∥．理由如下，如解图②所示，延长BC 交DF 于点H ，由（1）、（2）可知，MBC NDC αβ∠+∠=+，1()2CBE CDH αβ∠+∠=+．BCD CDH DHC ∠=∠+∠，CDH BCD DHC DHC β∴∠=∠-∠=-∠，1()2CBE DHC βαβ∴∠+-∠=+．αβ=， 1()2CBE DHB ββββ∴∠+-∠=+=，CBE DHB ∴∠=∠，BE DF ∴∥．【点睛】此题考查了平行线的性质及其判定，多边形的内角和公式，利用多边形的内角和公式倒角为解题关键．21．∠D ＝120°，∠C ＝160°如图D11-6，向两边延长AB ，CD ，EF ，分别交于点H ，M ，G .∵∠BAF =120°，∠ABC =80°，∴∠GAF =60°，∠HBC =100°.∵AF ∥CD ，∴∠H =∠GAF =60°.∴∠BCD=∠H+∠HBC =60°+100°=160°.又∵AB ∥DE ，∴∠EDM =∠H =60°.∴∠CDE =180°-∠EDM =180°-60°=120°.22．见解析.先写出已知，求证，再根据平角的定义得到∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=540°，再根据三角形内角和定理和角的和差关系即可得到结论如图，∠BAE ，∠CBF ，∠ACD 是△ABC 的三个外角．求证：∠BAE+∠CBF+∠ACD=360°．证明：∵∠1+∠EAB=180︒∴∠EAB=180︒-∠1同理∠FBC=180︒ -∠2∠ACD=180︒ -∠3∴∠E AB +∠F BC +∠AC D = 180︒-∠1 + 180︒-∠2 + 180︒-∠3= 540︒-(∠1 +∠2 +∠3)在△ABC 中，∠1 +∠2 +∠3 = 180︒∴∠E A B +∠F BC +∠ACD = 540︒-(∠1 +∠2 +∠3)=360︒【点睛】本题考查了多边形的外角和：n边形的外角和为360°．也考查了三角形内角和定理和外角性质．23．九试题分析：根据多边形的内角和公式可知180×7=1260＜1350＜180×8=1440，所以一个外角只能为1350﹣1260=90，由此得出多边形的边数为7+2=9求得问题．试题解析：解：设这个多边形的边数为n，180×（n﹣2）=1350﹣360n，180×7=1260＜1350＜180×8=1440，所以一个外角只能为1350﹣1260=90，由此得出多边形的边数为7+2=9．点睛：此题考查多边形的内角和计算方法：180°×（n﹣2）；以及从这个多边形的一个顶点出发的对角线条数，多边形的外角和为360°．24．（1）见解析；（2）36°；（3）26°，理由见解析；（4）①∠P=23αβ+②∠P=1802B D︒+∠+∠（1）根据三角形内角和定理即可证明；（2）直接利用（1）中的结论两次，两式相加，然后根据角平分线的性质求解即可；（3）由AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，推出∠1=∠2，∠3=∠4，推出∠PAD=180°﹣∠2，∠PCD=180°﹣∠3，由∠P+（180°﹣∠1）=∠D+（180°﹣∠3），∠P+∠1=∠B+∠4，推出2∠P=∠B+∠D，即可解决问题．（4）①同法利用（1）种的结论列出方程即可解决问题．②同法利用（1）种的结论列出方程即可解决问题．（1）在△AEB中，∠A+∠B+∠AEB=180°．在△CED中，∠C+∠D+∠CED=180°．∵∠AEB=∠CED，∴∠A+∠B=∠C+∠D；（2）由（1）得：∠1+∠B=∠3+∠P，∠4+∠D=∠2+∠P，∴∠1+∠B+∠4+∠D =∠3+∠P+∠2+∠P．∵∠1=∠2，∠3=∠4，∴2∠P=∠B+∠D=46°+26°=72°，∴∠P=36°．（3）∠P=26°，理由是：如图3：∵AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，∴∠1=∠2，∠3=∠4，∴∠PAD=180°﹣∠2，∠PCD=180°﹣∠3．∵∠PAB=∠1，∠P+∠PAB =∠B+∠4，∴∠P+∠1=∠B+∠4．∵∠P+（180°﹣∠2）=∠D+（180°﹣∠3），∴2∠P=∠B+∠D，∴∠P=12（∠B+∠D）=12×（36°+16°）=26°．（4）①设∠CAP=m，∠CDP=n，则∠CAB=3m，，∠CDB=3n，∴∠PAB=2m，∠PDB=2n．∵∠C+∠CAP=∠P+∠PDC，∠P+∠PAB=∠B+∠PDB，∵∠C=α，∠B=β，∴α+m=∠P+n，∠P+2m=β+2n，∴α－∠P = n－m，∠P－β=2n－2m=2（n－m），∴2α+β=3∠P∴∠P=23αβ+．故答案为：∠P=23αβ+．②设∠BAP=x，∠PCE=y，则∠PAO=x，∠PCB=y．∵∠PAO+∠P=∠PCD+∠D，∠B+∠BAO=∠OCD+∠D，∴x+∠P=180°－y+∠D，∠B+2x=180°－2y+∠D，∴∠P=1802B D︒+∠+∠．故答案为：∠P=1802B D︒+∠+∠．【点睛】本题考查了三角形内角和，三角形的外角的性质、多边形的内角和等知识，解题的关键是学会用方程的思想思考几何问题，属于中考常考题型．25．（1）∠BOC=118°；（2）∠A=2∠P，理由见解析（1）根据角平分线的定义和三角形的内角和定理求出∠OBC+∠OCB的值，再利用三角形的内角和定理求出∠BOC的值；（2）根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC，∠PCD=∠P+∠PBC，根据角平分线的定义可得∠PCD=12∠ACD，∠PBC=12∠ABC，然后整理得到2∠PCD=∠A．解：（1）∵∠A=56°，∴∠ABC+∠ACB=180°-∠A=124°，∵BO、CO分别是∠ABC和∠ACB的角平分线，∴∠CBO=∠ABO，∠ACO=∠BCO，∴∠CBO+∠BCO=12（∠ABC+∠ACB）=12×124°=62°，∴∠BOC=180°-（∠CBO+∠BCO）=118°；（2）∵BP、CP分别是∠ABC和∠ACB的角平分线，∴∠ABC=2∠PBC，∠ACD=2∠PCD，∴∠ACD-∠ABC=2（∠PCD-∠PBC），∵∠A=∠ACD-∠ABC，∠P=∠PCD-∠PBC，∴∠A=2∠P．【点睛】本题考查了三角形内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，熟记定理与性质并求出∠PCD=12∠A是解题的关键．26．75°利用角平分线的定义得出∠AOD=∠BOD，∠BOE=∠COE，进而求出∠DOE的度数．解：∵OD是∠AOB的平分线，OE是∠BOC的平分线，且∠AOC=150°，∴∠AOD=∠BOD=12∠AOB，∠BOE=∠COE=12∠BOC，∴∠DOE=∠BOD+∠BOE=12∠AOC=75°．【点睛】本题考查角平分线的定义，得出∠DOE=12∠AOC是解题关键．。

人教版初中八年级数学上册第十一章《三角形》提高卷(含答案解析)(1)

一、选择题1．已知实数x 、y 满足|x －4|+ 8y -＝0，则以x 、y 的值为两边长的等腰三角形周长是（）A ．20或16B ．20C ．16D ．182．如图，在△ABC 中，∠ACB=90°，D 在AB 上，将△ABC 沿CD 折叠，点B 落在AC 边上的点B′处，若'20ADB ∠=︒，则∠A 的度数为（）A ．25°B ．30°C ．35°D ．40° 3．将一副三角板的直角顶点重合按如图所示方式放置，得到下列结论，其中正确的结论有（）①13∠=∠； ②180BAE CAD ∠+∠=︒；③若//BC AD ，则230∠=︒；④若150CAD ∠=︒，则4C ∠=∠．A ．1个B ．2个C ．3个D ．4个4．将一副三角板和一张对边平行的纸条按图中方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则1∠的度数是（）A ．10°B ．15°C ．20°D ．25°5．下列说法正确的是（）A ．射线AB 和射线BA 是同一条射线B ．连接两点的线段叫两点间的距离C ．两点之间，直线最短D ．七边形的对角线一共有14条 6．已知两条线段15cm a =，8cm b =，下列线段能和a ，b 首尾相接组成三角形的是（）A ．20cmB ．7cmC ．5cmD ．2cm 7．内角和为720°的多边形是（）．A ．三角形B ．四边形C ．五边形D ．六边形8．如图，线段BE 是ABC 的高的是( )A ．B ．C ．D ．9．下列长度的三条线段能组成三角形的是（）A ．3，3，4B ．7，4，2C ．3，4，8D ．2，3，5 10．一副透明的三角板，如图叠放，直角三角板的斜边AB 、CE 相交于点D ，则BDC∠的度数是（）A ．65︒B ．75︒C ．85︒D ．105︒11．在ABC 中，若一个内角等于另两个内角的差，则（）A ．必有一个内角等于30°B ．必有一个内角等于45°C ．必有一个内角等于60°D ．必有一个内角等于90°12．如图，直线//,65,30AB CD A E ∠=︒∠=︒，则C ∠等于（）A ．30°B ．35°C ．40°D ．45°13．设四边形的内角和等于a ，五边形的外角和等于b ，则a 与b 的关系是（）．A ．a b =B ．180a b =+°C ．180b a =+︒D ．360b a =+︒ 14．以下列各组线段为边，能组成三角形的是（） A ．1，2，3B ．2，3，4C ．2，5，8D ．6，3，3 15．如图，在ABC 中，70B ∠=，D 为BC 上的一点，若ADC x ∠=，则x 的度数可能为（）A ．30°B ．60°C ．70°D ．80°二、填空题16．已知ABC 的三边长分别为a ，b ，c ，则a b c b c a c a b --+--+-+=______．17．如图，C 为∠AOB 的边OA 上一点，过点C 作CD ∥OB 交∠AOB 的平分线OE 于点F ，作CH ⊥OB 交BO 的延长线于点H ，若∠EFD ＝α，现有以下结论：①∠COF ＝α；②∠AOH ＝180°﹣2α；③CH ⊥CD ；④∠OCH ＝2α﹣90°．其中正确的是__（填序号）．18．如果三角形的三边长分别为5，8，a ，那么a 的取值范围为__．19．如图，点D ，E ，F 分别是边BC ，AD ，AC 上的中点，若图中阴影部分的面积为3，则ABC 的面积是________．20．如图，在Rt ACB ∆中，90ACB ∠=︒，25A ∠=︒，D 是AB 上一点，将Rt ABC ∆沿CD 折叠，使点B 落在AC 边上的B '处，则ADB '∠等于_______．21．设三角形三内角的度数分别为,,x y z ︒︒︒，如果其中一个角的度数是另一个角的度数的2倍、那我们称数对(,)()y z y z <是x 的和谐数对，当150x =时，对应的和谐数对有一个，它为(10,20)；当66x =时，对应的和谐数对有二个，它们是__________．当对应的和谐数对(,)y z 有三个时，请写出此时x 的范围_______．22．对于一个四边形的四个内角，下面四个结论中，①可以四个角都是锐角；②至少有两个角是锐角；③至少有一个角是钝角；④最多有三个角是钝角；所有正确结论的序号是______．23．如图，把ABC 折叠，点B 落在P 点位置，若12120∠+∠=︒，则B ∠=______．24．如图，AD 、AE 分别是ABC 的高和角平分线，且76B ∠=︒，36C ∠=︒，则DAE ∠的度数为_________．25．如图，AB BE ,分别是ABC 中,BC AC 边上的高，6cm BC ，4cm AC =，若3cm =AD ，则BE 的长为__________cm ．26．如图，线段AD ，BE ，CF 两两相交于点H ，I ，G ，分别连接AB ，CD ，EF ．则A B C D E F ∠+∠+∠+∠+∠+∠=____．三、解答题27．△ABC 中，三个内角的平分线交于点O ，过点O 作OD ⊥OB ，交边BC 于点D ．（1）如图1，猜想∠AOC 与∠ODC 的关系，并说明你的理由；（2）如图2，作∠ABC 外角∠ABE 的平分线交CO 的延长线于点F ．①求证：BF ∥OD ；②若∠F ＝35°，求∠BAC 的度数．28．已知：如图，在△ABC 中，∠ACB=90°，AE 是角平分线，CD 是高，AE 、CD 相交于点F ．（1）若∠DCB=48°，求∠CEF 的度数；（2）求证：∠CEF=∠CFE ．29．如图，A 、O 、B 三点在同一直线上，OE ，OF 分别是∠BOC 与∠AOC 的平分线．求：（1）当∠BOC=30°时，∠EOF 的度数；（2）当∠BOC=60°时，∠EOF 等于多少度？（3）当∠BOC=n°时，∠EOF 等于多少度？（4）观察图形特点，你能发现什么规律？30．已知在四边形ABCD 中，90A C ∠=∠=︒．（1）如图1，若BE 平分ABC ∠，DF 平分ADC ∠的邻补角，请写出BE 与DF 的位置关系并证明；（2）如图2，若BF 、DE 分别平分ABC ∠、ADC ∠的邻补角，判断DE 与BF 位置关系并证明；（3）如图3，若BE 、DE 分别五等分ABC ∠、ADC ∠的邻补角（即11,55CDE CDN CBE CBM ∠=∠∠=∠），求E ∠度数．。

内蒙古包头市八年级数学上册第十一章《三角形》提高卷(含答案)

一、选择题1．如图，在ABC中，AB边上的高为（）A．CG B．BF C．BE D．AD A解析：A【分析】在ABC中，过C点向AB所在的直线作垂线，顶点与垂足之间的线段是AB上的高，由此可得答案．【详解】CG解：ABC中，AB边上的高为：.故选：.A【点睛】本题考查的是三角形的高的含义，掌握钝角三角形的高是解题的关键．2．将一副三角板和一张对边平行的纸条按图中方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边的度数是（）上，则1A．10°B．15°C．20°D．25°B解析：B【分析】延长两三角板重合的边与直尺相交，根据两直线平行，内错角相等求出∠2，再利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．【详解】解：如图，由平行线的性质可得∠2=30°，∠1=∠3-∠2=45°-30°=15°．故选：B．【点睛】本题考查了平行线的性质及三角形外角的性质，三角板的知识，熟记平行线的性质，三角板的度数是解题的关键．3．已知三角形的两边长分别为1和4，则第三边长可能是（）A ．3B ．4C ．5D ．6B解析：B【分析】根据三角形的三边关系“第三边大于两边之差，而小于两边之和”，求得第三边的取值范围．【详解】解：根据三角形的三边关系，设第三边的长为x ，∵三角形两边的长分别是1和4，∴4-1＜x ＜4+1，即3＜x ＜5．故选：B ．【点睛】此题考查了三角形的三边关系，关键是正确确定第三边的取值范围．4．如图，ABC 中，55,B D ∠=︒是BC 延长线上一点，且130ACD ∠=︒，则A ∠的度数是（）A ．50︒B ．65︒C ．75︒D ．85︒C解析：C【分析】根据三角形的外角性质求解．【详解】解：由三角形的外角性质可得：∠ACD=∠B+∠A ，∴∠A=∠ACD-∠B=130°-55°=75°，故选C ．【点睛】本题考查三角形的外角性质，熟练掌握三角形的外角性质定理并能灵活运用是解题关键．5．如图，ABC 中，将A ∠沿DE 翻折，若30A ∠=︒，25BDA '∠=︒，则CEA '∠多少度（）A ．60°B ．75°C ．85°D ．90°C解析：C【分析】根据折叠前后对应角相等可得ADE A DE '∠=∠，AED A ED '∠=∠，再运用平角的定义和三角形内角和定理依次求得ADE ∠、AED ∠，再次运用平角的定义即可求得CEA '∠．【详解】解：∵将A ∠沿DE 翻折，∴ADE A DE '∠=∠，AED A ED '∠=∠，∵D 是线段AB 上的点，25BDA '∠=︒，∴180ADE A D B E DA '∠+∠-'∠=︒，即251280ADE ︒=∠-︒，解得102.5ADE ∠=︒，∵30A ∠=︒，180A AED ADE ∠+∠+∠=︒，∴180180102.53047.5AED ADE A ∠=︒-∠-∠=︒-︒-︒=︒，∴18018047.547.585CEA AED A ED ''∠=︒-∠-∠=︒-︒-︒=︒．故选：C ．【点睛】本题考查折叠的性质，三角形内角和定理，平角的定义．理解折叠前后对应角相等是解题关键．6．以下列各组线段为边，能组成三角形的是( )A ．1，2，3B ．1，3，5C ．2，3，4D ．2，6，10C解析：C【分析】根据三角形三边关系逐一进行判断即可．【详解】A 、1+2=3，不能构成三角形，故不符合题意；B 、1+3=4＜5，不能构成三角形，故不符合题意；C 、2+3=5>4，可以构成三角形，故符合题意；D 、2+6=8＜10，不能构成三角形，故不符合题意，故选：C ．【点睛】本题主要考查三角形的三边关系，比较简单，熟记三边关系定理是解决本题的关键． 7．在下列长度的四根木棒中，能与2m 、5m 长的两根木棒钉成一个三角形的是（） A ．2mB ．3mC ．5mD ．7m C解析：C【分析】判定三条线段能否构成三角形，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．【详解】解：设三角形的第三边为x m ，则5-2＜x ＜5+2即3＜x ＜7，∴当x=5时，能与2m 、5m 长的两根木棒钉成一个三角形，故选：C ．【点睛】本题考查了三角形的三边关系的运用，解题时注意：三角形两边之和大于第三边，三角形的两边差小于第三边．8．如图，在ABC ∆中，AD 是ABC ∆的角平分线，DE AC ⊥，若40,60B C ︒︒∠=∠=，则ADE ∠的度数为（）A ．30︒B ．40︒C ．50︒D ．60︒C解析：C【分析】根据三角形内角和180︒求出∠BAC ，再由AD 是ABC ∆的角平分线求得∠DAC ，最后利用直角三角形的两个锐角互余求出∠ADE ，问题得到解决．【详解】解：∵40,60B C ︒︒∠=∠=，∴BAC=180B-C=80∠︒-∠∠︒，∵AD 是ABC ∆的角平分线， ∴1DAC=BAC=402∠∠︒， ∵DE AC ⊥，∴90DAC=50ADE ∠=︒-∠︒，【点睛】本题考查了三角形的内角和定理，三角形的角平分线定义，直角三角形的两个锐角互余，正确理解三角形中角之间的关系是解本题的关键．9．在△ABC中，∠A＝x°，∠B＝(2x＋10)°，∠C的外角大小(x＋40)°，则x的值等于（）A．15 B．20 C．30 D．40A解析：A【分析】根据三角形的一个外角等于与它不相邻的两个内角的和，列出方程求解即可．【详解】解：∵∠C的外角=∠A+∠B，∴x+40=2x+10+x，解得x=15．故选：A．【点睛】本题考查了三角形的外角性质，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．10．下列四个图形中，线段CE是ABC的高的是（）A．B．C．D． B解析：B【分析】利用三角形高的定义逐一判断选项，可得答案．【详解】A．CE不垂直AB，故CE不是ABC的高，不符合题意，B．CE是ABC中AB边上的高，符合题意，C．CE不是ABC的高，不符合题意，D．CE不是ABC的高，不符合题意．故选B．【点睛】此题主要考查了三角形的高，关键是掌握从三角形的一个顶点向对边作垂线，垂足与顶点之间的线段叫做三角形的高．二、填空题11．如果三角形的三边长分别为5，8，a，那么a的取值范围为__．3<a<13【分析】根据三角形的三边关系解答【详解】由题意得：8-5<a<8+5∴3<a<13故答案为：3<a<13【点睛】此题考查三角形的三边关系：三角形任意两边的和大于第三边解析：3<a<13根据三角形的三边关系解答．【详解】由题意得：8-5<a<8+5，∴3<a<13，故答案为：3<a<13．【点睛】此题考查三角形的三边关系：三角形任意两边的和大于第三边．12．设三角形三内角的度数分别为,,x y z ︒︒︒，如果其中一个角的度数是另一个角的度数的2倍、那我们称数对(,)()y z y z <是x 的和谐数对，当150x =时，对应的和谐数对有一个，它为(10,20)；当66x =时，对应的和谐数对有二个，它们是__________．当对应的和谐数对(,)y z 有三个时，请写出此时x 的范围_______．（3876）（3381）【分析】根据和谐数对的定义求出当x=66时的两组数对；再分当时当时当时三种情况讨论从而得出结论【详解】解：当时180-66=114则114÷3=3838×2=76此时和谐数对解析：（38，76），（33，81） 060x ︒<<︒【分析】根据“和谐数对”的定义求出当x=66时的两组数对；再分当060x ︒<<︒时，当60120x ︒<︒时，当120180x ︒<︒时，三种情况讨论，从而得出结论．【详解】解：当66x =时，180-66=114，则114÷3=38，38×2=76，此时和谐数对为（38，76），或66÷2=33，114-33=81，此时和谐数对为（33，81），若对应的和谐数对(,)y z 有三个，当060x ︒<<︒时，它的和谐数对有(1803,2)x x ︒-，3(,180)22x x ︒-，180(3x ︒-，2(180))3x ︒-；当60120x ︒<︒时，它的和谐数对有3(,180)22x x ︒-，180(3x ︒-，2(180))3x ︒-，当120180x ︒<︒时，它的和谐数对有180(3x ︒-，2(180))3x ︒-， ∴对应的和谐数对(,)y z 有三个时，此时x 的范围是060x ︒<<︒，故答案为：（38，76），（33，81）；060x ︒<<︒．【点睛】本题考查三角形内角和定理，解题的关键是明确题意，找出所求问题需要的条件，利用分类讨论的数学思想解答问题．13．如图，将纸片ABC 沿DE 折叠，点A 落在点P 处，已知12124+∠=∠︒，A ∠=___________．【分析】根据折叠得到由此得到利用计算得出再根据三角形的内角和定理求出结果【详解】解：∵∴∴∵∴∴故答案为：【点睛】此题考查折叠的性质三角形内角和定理正确理解折叠的性质得到对应角相等是解题的关键解析：62︒．【分析】根据折叠得到ADE EDP ∠=∠，AED DEP ∠=∠，由此得到122()360ADE AED ∠+∠+∠+∠=︒，利用12124+∠=∠︒，计算得出118ADE AED ∠+∠=︒，再根据三角形的内角和定理求出结果．【详解】解：∵ADE EDP ∠=∠，AED DEP ∠=∠，∴1222180180ADE AED ∠+∠+∠+∠+︒=︒，∴122()360ADE AED ∠+∠+∠+∠=︒，∵12124+∠=∠︒，∴118ADE AED ∠+∠=︒，∴180()62A ADE AED ∠=︒-∠+∠=︒．故答案为：62︒．【点睛】此题考查折叠的性质，三角形内角和定理，正确理解折叠的性质得到对应角相等是解题的关键．14．若,,a b c 是△ABC 的三边长,试化简a b c a c b +-+--= __________．2b 【分析】先根据三角形三边关系确定>0<0再去绝对值化简即可【详解】∵是△ABC 的三边长∴>0<0=+=2b 故答案填：2b 【点睛】本题主要考查三角形三边关系绝对值的性质和化简问题根据三角形三边关系解析：2b【分析】先根据三角形三边关系，确定a b c +->0，()a b c -+<0，再去绝对值化简即可．【详解】∵,,a b c 是△ABC 的三边长∴a b c +->0，()a b c -+<0，a b c a c b +-+--=a b c +-+b c a +-=2b ，故答案填：2b ．【点睛】本题主要考查三角形三边关系、绝对值的性质和化简问题，根据三角形三边关系定理正确去绝对值是解决本题的关键．15．如果点G 是ABC ∆的重心，6AG =，那么BC 边上的中线长为_______________________．【分析】根据三角形的重心到一顶点的距离等于到对边中点距离的2倍求得DG=3继而求得边上的中线长为9【详解】∵三角形的重心到顶点的距离是其到对边中点的距离的2倍∴DG=AG=×6=3∴AD=AG+GD 解析：9【分析】根据三角形的重心到一顶点的距离等于到对边中点距离的2倍求得DG=3，继而求得BC 边上的中线长为9．【详解】∵三角形的重心到顶点的距离是其到对边中点的距离的2倍，∴DG=12AG=12×6=3， ∴AD=AG+GD=6+3=9．即BC 边上的中线长为9．故答案为：9．【点睛】本题考查的是三角形重心的性质，熟知三角形的重心到顶点的距离是其到对边中点的距离的2倍是解决问题的关键．16．如图，在ABC ∆中，4ACB A ∠=∠，点D 在边AC 上，将BDA ∆沿BD 折叠，点A 落在点A '处，恰好BA AC '⊥于点E 且//BC DA '，则BDC ∠的度数为__________度．54°【分析】根据折叠的性质及题意可在Rt △BEC中求解∠C 及∠CBE 的度数从而计算∠ABD 的度数则∠BDC=∠A+∠ABD 即可计算出结果【详解】由题意可得：∠A=∠∠=∠CBE ∴则在Rt △BEC 中解析：54°【分析】根据折叠的性质及题意，可在Rt △BEC 中求解∠C 及∠CBE 的度数，从而计算∠ABD 的度数，则∠BDC=∠A+∠ABD ，即可计算出结果．【详解】由题意可得：∠A=∠A '，∠A '=∠CBE ，∴44ACB A CBE ∠=∠=∠，则在Rt △BEC 中，∠C+∠CBE=90°，即：5∠CBE=90°，∠CBE=18°，∴∠A=18°，∠C=72°，∠ABC=90°，∴72ABA ABC CBE '=-=︒∠∠∠，由折叠性质可知，ABD A BD '∠=∠，∴=36ABD A BD '∠=∠︒，∴54BDC ABD A ∠=∠+∠=︒故答案为：54°．【点睛】本体三角形的折叠问题，平行线的性质及三角形的外角定理，理解图形变化中的特点，准确结合题意计算是解题关键．17．如图，Rt △ABC 中，∠ACB ＝90°，∠A ＝50°，将其折叠，使点A 落在边CB 上A′处，折痕为CD ，则A DB '∠=________．10°【分析】由对折可得：∠A=∠CA′D=50°∠ACD=∠A′CD=45°再利用三角形的内角和求解【详解】解：由对折可得：∠A=∠CA′D=50°∠ACD=∠A′CD=×90°=45°∴∠ADC解析：10°【分析】由对折可得：∠A=∠CA ′D=50°，∠ACD=∠A ′CD=45°，再利用三角形的内角和求解．【详解】解：由对折可得：∠A=∠CA′D=50°，∠ACD=∠A′CD=12×90°=45°， ∴∠ADC=∠A′DC=180°−45°−50°=85°，∴∠A′DB=180°−85°×2=10°．故答案为：10°．【点睛】本题利用对折考查轴对称的性质，三角形的内角和定理，掌握以上知识是解题的关键． 18．如图，在ABC 中，已知66ABC ∠=︒，54ACB ∠=︒，BE 是AC 上的高，CF 是AB 上的高，H 是BE 和CF 的交点，EHF ∠的度数是________．120°【分析】先根据三角形内角和定理求出∠A 的度数再根据CF是AB 上的高得出∠ACF 的度数再由三角形外角的性质即可得出结论【详解】解：∵∠ABC=66°∠ACB=54°∴∠A=60°∵CF 是AB 上解析：120°【分析】先根据三角形内角和定理求出∠A 的度数，再根据CF 是AB 上的高得出∠ACF 的度数，再由三角形外角的性质即可得出结论．【详解】解：∵∠ABC=66°，∠ACB=54°，∴∠A=60°，∵CF 是AB 上的高，∴在△ACF 中，∠ACF=180°-∠AFC-∠A=30°，在△CEH 中，∠ACF=30°，∠CEH=90°，∴∠EHF=∠ACF+∠CEH=30°+90°=120°．故答案为120°．【点睛】本题考查的是三角形内角和定理及三角形外角的性质、三角形的高线等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．19．如图中，36B ∠=︒，76C ∠=︒，AD 、AF 分别是ABC 的角平分线和高，DAF ∠=________．【分析】根据三角形内角和定理及角平分线的性质求出∠BAD 度数再由三角形内角与外角的性质可求出∠ADF 的度数由AF ⊥BC 可求出∠AFD=90°再由三角形的内角和定理即可解答【详解】∵AF 是的高∴在中∴ 解析：20︒【分析】根据三角形内角和定理及角平分线的性质求出∠BAD 度数，再由三角形内角与外角的性质可求出∠ADF 的度数，由AF ⊥BC 可求出∠AFD=90°，再由三角形的内角和定理即可解答．【详解】∵AF 是ABC 的高，∴90AFB ∠=︒，在Rt ABF 中，36B ∠=︒，∴90BAF B ∠=︒-∠9036=︒-︒54=︒．又∵在ABC 中，36B ∠=︒，76C ∠=︒，∴18068BAC B C ∠=︒-∠-∠=︒，又∵AD 平分BAC ∠， ∴11683422BAD CAD BAC ∠=∠=∠=⨯=︒， ∴DAF BAF BAD ∠=∠-∠5434=︒-︒ 20=︒．故答案为：20︒．【点睛】本题考查了三角形内角和定理、三角形的高线、及三角形的角平分线等知识，难度中等． 20．如图，ABC ∆的面积是2，AD 是BC 边上的中线，13AE AD =，12BF EF =．则DEF ∆的面积为_________．【分析】直接根据高相等的三角形面积之比等于底之比【详解】解：∵是边上的中线∴BD=DC 又∵的面积是2和的高相等∴∵和的高相等∴∴又∴同理：故答案为：【点睛】此题主要考查根据高相等的三角形面积之比等于解析：49【分析】直接根据高相等的三角形，面积之比等于底之比．【详解】解：∵AD 是BC 边上的中线∴BD=DC又∵ABC ∆的面积是2，D AB ∆和D A C ∆的高相等∴D DC S =S =1AB A ∆∆∵13AE AD = E AB ∆和BDE ∆的高相等∴E BDE ABD 11S =S =S 23AB ∆∆∆ ∴BDE 2S =3∆ 又12BF EF =，∴1B 3BF E =，同理： DEF BFD BDE 24S =2S =S =39∆∆∆ 故答案为：49．【点睛】此题主要考查根据高相等的三角形，面积之比等于底之比求三角形的面积，解题的关键是正确理解高相等的三角形之间的关系．三、解答题21．如图，直线//PQ MN ，点C 是PQ 、MN 之间（不在直线PQ ，MN 上）的一个动点．（1）如图1，若∠1与∠2都是锐角，请写出∠C 与∠1，∠2之间的数量关系并说明理由．（2）把Rt △ABC 如图2摆放，直角顶点C 在两条平行线之间，CB 与PQ 交于点D ，CA 与MN 交于点E ，BA 与PQ 交于点F ，点G 在线段CE 上，连接DG ，有∠BDF ＝∠GDF ，求AEN CDG∠∠的值．（3）如图3，若点D 是MN 下方一点，BC 平分∠PBD ，AM 平分∠CAD ，已知∠PBC ＝25°，求∠ACB +∠ADB 的度数．解析：（1）12C ∠=∠+∠，理由见解析；（2）12；（3）75︒．【分析】（1）过C 作//l MN ，标注字母，如图1所示，根据平行线公理证明//l PQ ，再根据平行线的性质即可求解．（2）先证明∠GDF ＝∠PDC ，可得∠CDG +2∠PDC ＝180°，即∠PDC ＝1902CDG ︒-∠，再证明∠AEN ＝∠CEM 90PDC =︒-∠，再代入AEN CDG∠∠计算即可得到答案；（3）利用角平分线的定义与平行线的性质求解：∠ADB ＝50BKA MAD CAM ∠-∠=︒-∠，再利用（1）的结论可得，∠ACB ＝∠PBC +∠CAM ，从而可得答案．【详解】解：（1）∠C ＝∠1+∠2，证明：过C 作//l MN ，标注字母，如图1所示，∵//l MN ，∴∠4＝∠2（两直线平行，内错角相等），∵//l MN ，//PQ MN ，∴//l PQ ，∴∠3＝∠1（两直线平行，内错角相等），∴∠3+∠4＝∠1+∠2，∴12DCE ∠=∠+∠；（2）如图2，∵∠BDF ＝∠GDF ，∠BDF ＝∠PDC ，∴∠GDF ＝∠PDC ，∵∠PDC +∠CDG +∠GDF ＝180°，∴∠CDG +2∠PDC ＝180°，∴∠PDC ＝1902CDG ︒-∠，由（1）可得，∠PDC +∠CEM ＝∠C ＝90°，∠AEN ＝∠CEM ，1909090122CDG AEN CEM PDC CDG CDG CDG CDG ⎛⎫︒-︒-∠ ⎪∠∠︒-∠⎝⎭∴====∠∠∠∠；（3）如图3，标注字母，∵BC 平分∠PBD ，AM 平分∠CAD ，∠PBC ＝25°，∴∠PBD ＝2∠PBC ＝50°，∠CAM ＝∠MAD ，∵//PQ MN ，∴BKA ∠＝∠PBD ＝50°，∴∠ADB ＝5050BKA MAD MAD CAM ∠-∠=︒-∠=︒-∠，由（1）可得，∠ACB ＝∠PBC +∠CAM ，∴∠ACB +∠ADB ＝∠PBC +∠CAM 50255075CAM +︒-∠=︒+︒=︒．【点睛】本题考查的是平行公理的应用，平行线的性质，角平分线的定义，平角的定义，三角形的外角的性质，掌握以上知识是解题的关键．22．△ABC 中，三个内角的平分线交于点O ，过点O 作OD ⊥OB ，交边BC 于点D ．（1）如图1，猜想∠AOC 与∠ODC 的关系，并说明你的理由；（2）如图2，作∠ABC 外角∠ABE 的平分线交CO 的延长线于点F ．①求证：BF ∥OD ； ②若∠F ＝35°，求∠BAC 的度数．解析：（1）∠AOC ＝∠ODC ，理由见解析；（2）①见解析；②70°【分析】（1）根据角平分线的定义得到∠OAC ＋∠OCA ＝12（180°−∠ABC ），∠OBC ＝12∠ABC ，由三角形的内角和得到∠AOC ＝90°＋∠OBC ，∠ODC ＝90°＋∠OBD ，于是得到结论；（2）①由角平分线的性质得到∠EBF ＝90°−∠DBO ，由三角形的内角和得到∠ODB ＝90°−∠OBD ，于是得到结论；②由角平分线的性质得到∠FBE ＝12（∠BAC ＋∠ACB ），∠FCB ＝12ACB ，根据三角形的外角的性质即可得到结论．【详解】（1）∠AOC ＝∠ODC ，理由：∵三个内角的平分线交于点O ，∴∠OAC+∠OCA ＝12（∠BAC+∠BCA ）＝12（180°﹣∠ABC ）， ∵∠OBC ＝12∠ABC ， ∴∠AOC ＝180°﹣（∠OAC+∠OCA ）＝90°+12∠ABC ＝90°+∠OBC ， ∵OD ⊥OB ，∴∠BOD ＝90°，∴∠ODC ＝90°+∠OBD ，∴∠AOC ＝∠ODC ；（2）①∵BF 平分∠ABE ，∴∠EBF ＝12∠ABE ＝12（180°﹣∠ABC ）＝90°﹣∠DBO ， ∵∠ODB ＝90°﹣∠OBD ，∴∠FBE ＝∠ODB ，∴BF ∥OD ；②∵BF 平分∠ABE ，∴∠FBE ＝12∠ABE ＝12（∠BAC+∠ACB ）， ∵三个内角的平分线交于点O ， ∴∠FCB ＝12∠ACB ， ∵∠F ＝∠FBE ﹣∠BCF ＝12（∠BAC+∠ACB ）﹣12∠ACB ＝12∠BAC ， ∵∠F ＝35°，∴∠BAC ＝2∠F ＝70°．【点睛】本题考查了平行线的性质和判定，角平分线的定义，三角形的内角和，三角形的外角的性质，熟练掌握三角形的外角的性质是解题的关键．23．阅读下面内容，并解答问题在学习了平行线的性质后，老师请学们证明命题：两条平行线被第三条直线所截，一组同旁内角的平分线互相垂直．小颖根据命题画出图形并写出如下的已知条件．已知：如图1，//AB CD ，直线EF 分别交AB ，CD 于点E ，F ，BEF ∠的平分线与DFE ∠的平分线交于点G ．（1）直线EG ，FG 有何关系？请补充结论：求证：“__________”，并写出证明过程；（2）请从下列A 、B 两题中任选一题作答，我选择__________题，并写出解答过程． A ．在图1的基础上，分别作BEG ∠的平分线与DFG ∠的平分线交于点M ，得到图2，求EMF ∠的度数．B ．如图3，//AB CD ，直线EF 分别交AB ，CD 于点E ，F ．点O 在直线AB ，CD 之间，且在直线EF 右侧，BEO ∠的平分线与DFO ∠的平分线交于点P ，请猜想EOF ∠与EPF ∠满足的数量关系，并证明它．解析：（1）EG ⊥FG ，证明见解析；（2）A ．45；B .2EOF EPF ∠=∠（在A 、B 两题中任选一题即可）【分析】（1）由AB ∥CD ，可知∠BEF 与∠DFE 互补，由角平分线的定义可得90GEF GFE ∠+∠=︒，由三角形内角和定理可得∠G ＝90︒，则EG FG ⊥；（2）A ．由（1）可知90BEG DFG ∠+∠=︒，根据角平分线的定义可得45MEG MFG ∠+∠=︒,故135MEF MFE ∠+∠=︒，根据三角形的内角和即可求出EMF ∠=45︒；B ．设OEF α∠=，OFE β∠=，故EOF ∠=180αβ︒--，再得到180BEO DFO αβ∠+∠=--︒，根据角平分线的定义可得190122PEO PFO αβ︒-∠+∠=-，则119022PEF PFE αβ∠+∠=︒++，再求出EPF ∠，即可比较得到结论．【详解】解：（1）由题意可得，求证：“EG ⊥FG”，证明过程如下∵//AB CD∴∠BEF ＋∠EFD=180° EG 平分BEF ∠，FG 平分DFE ∠，12GEF BEF ∴∠=∠，12GFE DFE ∠=∠， 1111()180902222GEF GFE BEF DFE BEF DFE ∴∠+∠=∠+∠=∠+⨯︒∠==︒．在EFG 中，180GEF GFE G ∠+∠+∠=︒，180()1809090G GEF GFE ∴∠=-∠+∠=-︒=︒︒︒，EG FG ∴⊥．（2）A ．由（1）可知=90BEG DFG GEF GFE ∠+∠=∠+∠︒，∵BEG ∠的平分线与DFG ∠的平分线交于点M∴∠MEG=12∠BEG ，∠MFG=12∠DFG ∴()111190452222MEG MFG BEG DFG BEG DFG ∠+∠=∠+∠=∠+∠=⨯︒=︒ 则4591350MEF MFE ︒+∠︒=+∠=︒， ∴EMF ∠=180135︒-︒=45︒故答案为：A ，45；B.设OEF α∠=，OFE β∠=，∴EOF ∠=180αβ︒--，∵//AB CD∴∠BEF ＋∠EFD=180°则180BEO DFO αβ∠+∠=--︒∵BEO ∠的平分线与DFO ∠的平分线交于点P∴190122PEO PFO αβ︒-∠+∠=-, ∴111190902222PEF PFE αβαβαβ∠+∠=︒--++=︒++， ∴EPF ∠=111809022αβ⎛⎫︒-︒++ ⎪⎝⎭=121902αβ︒--， ∵EOF ∠=1118029022αβαβ⎛⎫︒--=︒-- ⎪⎝⎭，故2EOF EPF ∠=∠故答案为：B ，2EOF EPF ∠=∠．（在A 、B 两题中任选一题即可）【点睛】本题考查了平行线的性质、角平分线的定义、三角形内角和定理，熟练掌握平行线的性质和角平分线的定义是解题的关键．24．如图，∠CBF ，∠ACG 是△ABC 的外角，∠ACG 的平分线所在的直线分别与∠ABC ，∠CBF 的平分线BD ，BE 交于点D ，E ．（1）若∠A=70°，求∠D的度数；（2）若∠A=a，求∠E；（3）连接AD，若∠ACB= ，则∠ADB= ．解析：（1）35°；（2）90°-12α；（3）12β【分析】（1）由角平分线的定义得到∠DCG=12∠ACG，∠DBC=12∠ABC，然后根据三角形外角的性质即可得到结论；（2））根据角平分线的定义得到∠DBC=12∠ABC，∠CBE=12∠CBF，于是得到∠DBE=90°，由（1）知∠D=12∠A，根据三角形的内角和得到∠E=90°-12α；（3）根据角平分线的定义可得，∠ABD=12∠ABC，∠DAM=12∠MAC，再利用三角形外角的性质可求解．【详解】解：（1）∵CD平分∠ACG，BD平分∠ABC，∴∠DCG=12∠ACG，∠DBC=12∠ABC，∵∠ACG=∠A+∠ABC，∴2∠DCG=∠ACG=∠A+∠ABC=∠A+2∠DBC，∵∠DCG=∠D+∠DBC，∴2∠DCG=2∠D+2∠DBC，∴∠A+2∠DBC=2∠D+2∠DBC，∴∠D=12∠A=35°；（2）∵BD平分∠ABC，BE平分∠CBF，∴∠DBC=12∠ABC，∠CBE=12∠CBF，∴∠DBC+∠CBE=12（∠ABC+∠CBF）=90°，∴∠DBE=90°，∵∠D=12∠A，∠A=α，∴∠D=12α，∵∠DBE=90°，∴∠E=90°-12α；（3）如图，∵BD 平分∠ABC ，CD 平分∠ACG ，∴AD 平分∠MAC ，∠ABD=12∠ABC ， ∴∠DAM=12∠MAC ， ∵∠DAM=∠ABD+∠ADB ，∠MAC=∠ABC+∠ACB ，∠ACB=β，∴∠ADB=12∠ACB=12β．故答案为：12β．【点睛】本题主要考查三角形的角平分线，三角形外角的性质，灵活运用三角形外角的性质是解题的关键．25．如图BC 平分∠ABE ，DC 平分∠ADE ，求证：∠E+∠A=2∠C解析：证明见解析．【分析】如图（见解析），先根据角平分线的定义可得12,34∠=∠∠=∠，再根据三角形的外角性质可得13,42A C E C ∠+∠=∠+∠∠+∠=∠+∠，然后两式相加化简即可得．【详解】如图，BC 平分ABE ∠，DC 平分ADE ∠，12,34∴∠=∠∠=∠，由三角形的外角性质得：153462A C E C ∠+∠=∠=∠+∠⎧⎨∠+∠=∠=∠+∠⎩，即1342A C E C ∠+∠=∠+∠⎧⎨∠+∠=∠+∠⎩，两式相加得：14223A E C ∠+∠+∠+∠=∠+∠+∠，14214A E C ∴∠+∠+∠+∠=∠+∠+∠，2E A C ∴∠+∠=∠．【点睛】本题考查了角平分线的定义、三角形的外角性质等知识点，熟练掌握三角形的外角性质是解题关键．26．（1）已知△ABC 中，∠B=5∠A ，∠C-∠B=15°，求∠A ，∠B ，∠C 的度数．（2）在△ABC 中，∠A=50°，BD ，CE 为高，直线BD ，CE 交于点H ，求∠BHC 的度数．解析：（1）∠A=15°，∠B=75°，∠C =90°；（2）130°【分析】（1）将∠C 用∠A 表示，然后利用三角形内角和即可求解∠A ，然后在依次求出∠B ，∠C 即可；（2）根据题意作出示意图，然后根据四边形内角和即可求出∠DHE ，根据对顶角相等即可求解∠BHC ．【详解】（1）∵∠C-∠B=15°，即∠C =15°+∠B又∵∠B=5∠A∴∠C =15°+5∠A∵∠A+∠B+∠C=180°∴∠A+5∠A +15°+5∠A =180°解得∠A=15°∴∠B=75°，∠C =90°∴∠A=15°，∠B=75°，∠C =90°（2）根据题意作出下图，∵BD AC ⊥，CE AB ⊥∴∠BDA =90°，∠CEA=90°∵在四边形AEHD中，∠A+∠HDA+∠HEA+∠DHE =360°∴∠DHE=360°-∠A-∠HAD-∠HEA=360°-50°-90°-90°=130°∴∠BHC=∠DHE=130°∴∠BHC =130°．【点睛】本题考查了三角形的内角和和四边形内角和，重点是熟记多边形内角和公式．27．如图，AB∥CD，点E是CD上一点，连结AE．EB平分∠AED，且DB⊥BE，AF⊥AC，AF与BE交于点M．（1）若∠AEC＝100°，求∠1的度数；（2）若∠2＝∠D，则∠CAE＝∠C吗？请说明理由．解析：（1）40°；（2）∠CAE＝∠C，理由见解析．【分析】（1）根据邻补角的定义可求∠AED，再根据角平分线的定义和平行线的性质可求∠1的度数；（2）根据三角形内角和定理可求∠BED＝∠C，根据平行线的判定可知AC∥BE，根据平行线的性质可得∠CAE＝∠AEB，根据角平分线的定义和等量关系即可求解．【详解】（1）∵∠AEC＝100°，∴∠AED＝80°，∵EB平分∠AED，∴∠BED＝40°，∵AB∥CD，∴∠1＝∠BED＝40°；（2）∵DB⊥BE，AF⊥AC，∴∠EBD＝∠CAF＝90°，∵∠2＝∠D，∴∠BED＝∠C，∴AC∥BE，∴∠CAE＝∠AEB，∵EB平分∠AED，∴∠AEB＝∠BED，∴∠CAE ＝∠C ．【点睛】本题考查平行线的判定和性质，邻补角的定义，角平分线的定义，三角形内角和定理．熟悉相应的性质和定义是解答本题的关键．28．如图，AD 、AE 分别是ABC 的高和角平分线．（1）已知∠B ＝40°，∠C ＝60°，求∠DAE 的度数；（2）设∠B ＝α，∠C ＝β(α＜β)，请用含α，β的代数式表示∠DAE ，并证明．解析：（1）10°；（2）12DAE，证明见解析．【分析】（1）根据三角形的内角和等于180︒列式求出BAC ∠，再根据角平分线的定义求出BAE ∠，根据直角三角形两锐角互余求出BAD ∠，然后根据DAE BAD BAE ∠=∠-∠代入数据计算即可得解；（2）根据三角形的内角和等于180︒列式表示出BAC ∠，再根据角平分线的定义求出BAE ∠，根据直角三角形两锐角互余求出BAD ∠，然后根据DAE BAD BAE ∠=∠-∠整理即可得解．【详解】解：（1）40B ∠=︒，60C ∠=°，180180406080BAC B C ∴∠=︒-∠-∠=︒-︒-︒=︒， AE ∵是角平分线， 11804022BAE BAC ，AD 是高，90904050BADB ， 504010DAE BAD BAE ；（2）1()2．B α∠=，()C βαβ∠=<，180()BAC ，AE ∵是角平分线， 1190()22BAE BAC ，AD 是高，9090BADB ， 1190[90()]()22DAE BAD BAE ．【点睛】本题考查了三角形的内角和定理，角平分线的定义，直角三角形两锐角互余的性质，熟练掌握定理与概念并准确识图理清图中各角度之间的关系是解题的关键．。

人教版八年级上册数学第十一章三角形单元提高训练题 (1)(有解析)

第十一章三角形单元提高训练题 (1)一、单选题1．一个多边形的每一个外角都等于40°，那么这个多边形的内角和为（）A．1260°B．900°C．1620°D．360°2．如图，△ABC中，BD⊥AC，AE⊥BC，AE、BD交于点O，连接CO，∠ABC=54°，∠ACB=48°，则∠COD=（）A．51°B．66°C．78°D．88°3．在△ABC中，∠A=2∠B=75°，则∠C=（）A．30°B．67.5°C．105°D．135°4．为估计池塘两岸A，B间的距离，杨阳在池塘一侧选取了一点P，测得PA=16m，PB=12m，那么AB间的距离不可能是（）A．15m B．17m C．20m D．28m5．图中，三角形的个数为（）A．5 B．6 C．7 D．86．一正多边形的内角和与外角和的和是1440°，则该正多边形是（）A．正六边形B．正七边形C．正八边形D．正九边形7．现有2根长度分别为1米，4米的钢管，若再选一根钢管首尾顺次连接，焊成一个三角形的固定架(接头不计)，则下列符合条件的钢管长为()A．2米B．3米C．4米D．5米8．从n边形的一个顶点出发可以连接8条对角线，则n （）A．8 B．9 C．10 D．119．如图，已知：在△ABC中，AB＝AC，D是BC边上任意一点，DF⊥AC于点F，E在AB边上，ED⊥BC于D，∠AED＝155°，则∠EDF等于（）A ．50°B ．65°C ．70°D ．75°10．如图，用一条宽度相等的足够长的纸条打一个结（如图1所示），然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE ，图2中，BAC ∠的大小是（）A ．72B ．36C ．30D ．5411．下列长度的三条线段能组成三角形的是（）A ．5 cm ，3 cm ，1 cmB ．2 cm ，5 cm ，8 cmC ．1 cm ，3 cm ，4 cmD ．1.5 cm ，2 cm ，2.5 cm 12．已知等腰三角形的腰和底边长分别为5cm 和4cm ，则它的周长等于（）A ．9 cmB ．13 cmC ．14 cmD ．13 cm 或14 cm二、填空题13．一个六边形的六个内角都是120°，连续四边的长依次为2.31，2.32，2.33，2.31，则这个六边形的周长为_____．14．如图，AB CD ∥，BE 交CD 于点D ，CE BE ⊥于点E ，若34B ∠=︒，则C ∠的大小为__________度．15．已知三角形两边长是方程x 2﹣5x +6＝0的两个根，则三角形的第三边c 的取值范围是_____．16．如图，在△ABC 中，EF ∥BC ，∠ACG 是△ABC 的外角，∠BAC 的平分线交BC 于点D ，记∠ADC=α，∠ACG=β，∠AEF=γ，则：α、β、γ三者间的数量关系式是______.17．如图，BP 平分∠ABC ，CP 平分∠ACB ，∠A ＝100°，则∠P ＝_____．18．如图∆ABC 中， AB = 2 ， BC = 4 ， CD ⊥ AB 于 D ， AE ⊥ BC 于 E ，则AE : CD = ．三、解答题19．如图，点F 是ABC 的边BC 的延长线上一点，FD AB ⊥于点D ，30A ∠=︒，40F ∠=︒，求ACB ∠的度数．20．已知点D 为ABC ∆ 内部（包括边界但非A 、B 、C ）上的一点．（1）若点D 在边AC 上，如图①，求证：AB + AC> BD + DC （2）若点D 在ABC ∆内，如图②，求证：AB + AC> BD + DC （3）若点D 在ABC ∆内，连结DA 、DB 、DC ，如图③求证：12(AB + BC + AC) < DA + DB + DC < AB + BC + AC21．如图，在△ABC 中，∠B=63°，∠C=51°，AD 是BC 边上的高，AE 是∠BAC 的平分线，求∠DAE 的度数.22．如图，点O是△ABC内一点，∠A=80°，∠1=15°，∠2=40°，则∠BOC等于？（提示：可作辅助线）23．如图，△ABC 中，∠A=44°，∠C=76°.BD 平分∠ABC,交 AC于D 点，求∠BDC的度数.24．如图，已知，在平面直角坐标系中S△ABC=24,OA=OB,BC=12.（1）求出三个顶点坐标.（2）若P点为y轴上的一动点，且△ABP的面积等于△ABC的面积，求点P的坐标. 25．(1)如图①，已知△ABC为直角三角形，∠A＝90°，若沿图中虚线剪去∠A，则∠1＋∠2等于( )A．90° B．135° C．270° D．315°(2)如图②，已知△ABC中，∠A＝40°，剪去∠A后成四边形，则∠1＋∠2＝________°；(3)根据(1)与(2)的求解过程，请你归纳猜想∠1＋∠2与∠A的关系是______________．26．（1）如图1所示，△ABC中，∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F；①若∠B＝90°则∠F＝；②若∠B＝a，求∠F的度数（用a表示）；（2）如图2所示，若点G是CB延长线上任意一动点，连接AG，∠AGB与∠GAB的角平分线交于点H，随着点G的运动，∠F+∠H的值是否变化？若变化，请说明理由；若不变，请求出其值．【答案与解析】一、单选题1．A解析：A先利用360°÷40°求出多边形的边数，再根据多边形的内角和公式（n-2）•180°计算即可求解．360°÷40°=9，∴（9-2）•180°=1260°．故选A．【点睛】主要考查了正多边形的外角与边数的关系，求出多边形的边数是解题的关键．2．C解析：C延长CO与AB交于点F，利用三角形内角和定理和三角形三条高所在直线交于一点可求得∠COD=∠OBE+∠OCE=∠OAD+∠OAF=∠BAC=78°。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级上册数学期中考试培优题1、△ABC中，AB=AC，AC上的中线BD把△ABC的周长分为24㎝和30㎝两部分，求三角形的三边长.2、如图，AF，AD分别是△ABC的高和角平分线，BE是△ABC的角平分线，AD、BE交于点O，且∠ABC=36°，∠C=76°，求∠DAF和∠DOE的度数.3.在边长为3的等边△ABC的AB边上任取一点D，作DF⊥AC交AC于F，在BC的延长线上截取CE=AD，连接DE交AC于G，求FG的值。

4.（1）如图所示，已知△ABC中，∠ABC、∠ACB的平分线相交于点O，试说明∠BOC=90°+21∠A。

（2）如图所示，在△ABC中，BD、CD分别是∠ABC、∠ACB的外角平分线，试说明∠D=90°-21∠A。

（3）如图所示，已知BD为△ABC的角平分线，CD为△ABC外角∠ACE的平分线，且与BD交于点D，试说明∠A=2∠D。

FDEBAGABCDE图2FEC AD5．已知，AC⊥CE，AC=CE，∠ABC=∠EDC=900，证明：BD=AB+ED.6. 如图,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF＝90°.求证：BE＝CF.7.（1）把一大一小两个等腰直角三角板（即EC=CD,AC=BC）如图1放置，点D在BC上，连结BE，AD，AD的延长线交BE于点F，求证：（1）ΔACD≌ΔBCE （2）AF⊥BE．AB COAB CDAB CD(1)(2)(3)EDCAHFC（2）把左边的小三角板逆时针旋转一定的角度如图2放置，问AF 与BE 是否垂直？并说明理由．8. 如图，已知点B 、C 、D 在同一条直线上，△ABC 和△CDE•都是等边三角形．BE 交AC 于F ，AD 交CE 于H ，①求证：△BCE ≌△ACD ；②求证：CF=CH ；判断△CFH•的形状并说明理由；④FH||BD.9.已知：在⊿ABC 中，∠A=900，AB=AC ，在BC 上任取一点P ，作PQ ∥AB 交AC 于Q ，作PR ∥CA 交BA 于R ，D 是BC 的中点，求证：⊿RDQ 是等腰直角三角形。

CB10.已知：在⊿ABC 中，∠A=900，AB=AC ，D 是AC 的中点，AE ⊥BD ，AE 延长线交BC 于F ，求证：∠ADB=∠FDC 。

11.已知：在⊿ABC 中BD 、CE 是高，在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ，求证：MA ⊥NA 。

12、在Rt △ABC 中，AB ＝AC ，∠BAC =90°，O 为BC (1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明)； (2)如果点M 、N 分别在线段AB 、AC 上移动，在移动中保持AN ＝BM ，请判断△OMN 的形状，并证明你的结论。

13、如图，△ABC为等边三角形，延长BC到D，延长BA到E，AE=BD，连结EC、ED，求证：CE=DE14、如图，等腰三角形ABC中，AB＝AC，∠A＝90°，BD平分∠ABC，DE⊥BC且BC＝10，求△DCE的周长。

15. 已知：如图2，在∆ABC中，AB AC>，AM是BC边的中线。

求证：()AM AB AC>-12CAMBD图216. 如图3，∠B＝∠C＝90°，M是BC的中点，DM平分∠ADC。

求证：AM平分DAB。

17. 已知如图4，△ABC是边长为1的等边三角形，△BDC是顶角（∠BDC）为120°的等腰三角形，以D为顶点作一个60°的角，它的两边分别交AB于M，交AC于N，连结MN。

求证：∆AMN的周长等于2。

A BCOMN18. 如图5，已知：点C 是∠FAE 的平分线AC 上一点，CE ⊥AE ，CF ⊥AF ，E 、F 为垂足。

点B 在AE 的延长线上，点D 在AF 上。

若AB ＝21，AD ＝9，BC ＝DC ＝10。

求AC 的长。

19. 已知：如图6，∆ABC 中，AB ＝AC ，∠ACB ＝90°，D 是AC 上一点，AE 垂直BD 的延长线于E ，AE BD =12。

求证：BD 平分∠ABC20. 某小区结合实际情况建了一个平面图形为正三角形的花坛。

如图7，在正三角形ABC花坛外有满足条件PB＝AB的一棵树P，现要在花坛内装一喷水管D，点D的位置必须满足条件AD＝BD，∠DBP＝DBC，才能使花坛内全部位置及树P均能得到水管D的喷水，问∠BPD为多少度时，才能达到上述要求？21. 如图所示，AB＝AC，∠BAC＝90°，M是AC中点，AE⊥BM。

求证：∠AMB＝∠CMD22. 如图，已知在等边三角形ABC 中，D 是AC 的中点，E 为BC 延长线上一点，且CE ＝CD ，DM ⊥BC ，垂足为M 。

求证：M 是BE 的中点。

E23. 如图，已知：AB C ∆中，AC AB =，D 是BC 上一点，且CA DC DB AD ==，，求BAC ∠的度数。

ABCD24. 已知：如图，AB C ∆中，AB CD AC AB ⊥=，于D 。

求证：DCB 2B AC ∠=∠。

C25. 如图，AB C ∆中， 100=∠=A AC AB ，，BD 平分ABC ∠。

求证：B C B D AD =+。

AD1 B 2E FC26、（1）已知△ABC 中， AE 为角平分线，D 为AE 上一点，且∠BDE =∠CDE ，求证：AB =AC.（2）若把（1）中“AE 角平分线”换为“AE 为高线”，其它条件不变，结论还会成立吗？如果成立，请说明；若不成，也请说明理由．27、（1）已知如图①，△ABC 和△ADE 中，AB=AC ，AD=AE ，且∠CAB=∠DAE,连结CE 、BD ，求证：CE=BD 。

（2）将△ADE 绕着A 点旋转，当点C 、E 、D 在一条直线时如图②，上述结论是否成立？（3）旋转到图③时，上述结论成立吗？（4）旋转到图④时，此时点B 、E 、D 在一条直线上，上述结论成立吗？若成立，请就（2）（3）（4）中的一种情况加以说明．28、如图，在R t △ABC 中，∠ACB =450，∠BAC =900，AB =AC ，点D 是AB 的中点，AF ⊥CD 于H 交BC 于F ，BE∥AC 交AF 的延长线于E ，求证：BC 垂直且平分DE.29、已知：三角形ABC 中，∠A ＝90°，AB ＝AC ，D③DBECAABCED②A CBE④DBADE①CEDCB A为BC 的中点，（1）写出点D 到的三个顶点A 、B 、C 的距离关系（不要证明）；（2）如图，E ，F 分别是AB ，AC 上的点，且BE ＝AF ，判定△DEF 的形状，并加以证明；（3）若E ，F 分别为AB ，CA 延长线上的点，仍有BE ＝AF ，其他条件不变，那么（2）的结论是否仍然成立？证明你的结论．30、已知四边形ABCD 中，AB AD ⊥，BC CD ⊥，AB BC =，120ABC =∠，60MBN =∠，MBN ∠绕B 点旋转，它的两边分别交AD DC ，（或它们的延长线）于E F ，．当MBN ∠绕B 点旋转到AE CF =时（如图1），易证AE CF EF +=．当MBN ∠绕B 点旋转到AE CF ≠时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE CF ，，EF 又有怎样的数量关系？请写出你的猜想，不需证明．31. 直线CD 经过BCA ∠的顶点C ，CA=CB ．E 、F 分别是直线CD 上两点，且BEC CFA α∠=∠=∠．（1）若直线CD 经过BCA ∠的内部，且E 、F 在射线CD 上，请解决下面问题：如图1，若90,90BCA α∠=∠=，则EF AF -（填“>”，“<”或“=”号）；（2）如图2，若直线CD 经过BCA ∠的外部，BCA α∠=∠，请探究EF 、与BE 、AF 三条线段的数量关系，并给予证明．（图1）A B CDEFM N（图2）AB CDE FMN（图3）AB C D EF MN32、如图，在△ABC 中，,120,AB AC A AB =∠=︒边上的垂直平分线交BC 于D 点，求证：3BC BD =.33、如图，△ABC 中，,120,AB AC BAC D =∠=︒是BC 的中点，DE AB ⊥于E ，求:AE EB 的值.34. 如图:在△ABC 中,AB=AC,P 为BC 边上任意一点,PF⊥AB 于F,PE⊥AC 于E,若AC 边上的高BD=a . (1)试说明PE ＋PF=a ;(2)若点P 在BC 的延长线上,其它条件不变,上述结论还成立吗?如果成立请说明理由;如果不成立,请重新给出一个关于PE ，PF ，a 的关系式,并明理由.。