解析几何第四版吕林根课后习题答案第五章
解析几何第五章习题及解答

第五章 正交变换和仿射变换习题5.1 1.证明变换的乘法适合结合律,即 123123()().σσσσσσ=证明:设:,1,2,3.i S S i σ→=,显然都是S 的变换,对任给a S ∈,有123123123[()]()[()()][(())],a a a σσσσσσσσσ== 123123123[()]()()[()][(())],a a a σσσσσσσσσ==因此 123123[()]()[()](),a a σσσσσσ= 从而 123123()().σσσσσσ= 2.求出平面上对直线y x =的反射公式。
解:在直角坐标系中,设点(,)P x y 关于直线y x =的对称点是(,)P x y ''',则,P P '的中点在直线y x =上,且PP '与直线垂直,因此有:,22()()0,x x y yx x y y ''++⎧=⎪⎨⎪''-+-=⎩ 得到,,x y y x '=⎧⎨'=⎩即平面上对直线y x =的反射公式:01.10x x y y '⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪'⎝⎭⎝⎭⎝⎭3.设平面上直线l 的方程0Ax By C ++=,求平面对于直线l 的反射的公式。
解:在直角坐标系中,设点(,)P x y 关于直线0Ax By C ++=的对称点是(,)P x y ''',则,P P '的中点在直线0Ax By C ++=上,且PP '与直线垂直,因此有:0,22()()0,x xy y A B C x x B y y A ''++⎧++=⎪⎨⎪''---=⎩ 解此方程得到平面对于直线l 的反射的公式:222222221[()22],1[2()2].x B A x ABy AC A B y ABx A B y BC A B⎧'=---⎪⎪+⎨⎪'=-+--⎪⎩+4. 设12,l l 是平面上两条平行直线,而12,σσ分别是平面对于直线12,l l 的反射,证明12σσ是一个平移。
解析几何第四版吕林根课后习题答案一至三章

第一章向量与坐标§1.1 向量的概念1.下列情形中的向量终点各构成什么图形?(1)把空间中一切单位向量归结到共同的始点;(2)把平行于某一平面的一切单位向量归结到共同的始点;(3)把平行于某一直线的一切向量归结到共同的始点;(4)把平行于某一直线的一切单位向量归结到共同的始点.[解]:(1)单位球面;(2)单位圆(3)直线;(4)相距为2的两点2. 设点O是正六边形ABCDEF的中心,在向量OA、、OC、、、OF、、BC、CD、、EF和FA中,哪些向量是相等的?[解]:如图1-1,在正六边形ABCDEF中,相等的向量对是:图1-1.DEOFCDOEABOCFAOBEFOA和;和;和;和;和3. 设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB、BC、CD、DA的中点,求证:KL=. 当ABCD是空间四边形时,这等式是否也成立?[证明]:如图1-2,连结AC, 则在∆BAC中,21AC. KL与AC方向相同;在∆DAC中,21AC. NM与AC方向相同,从而KL=NM且KL与NM方向相同,所以KL=.4. 如图1-3,设ABCD-EFGH是一个平行六面体,在下列各对向量中,找出相等的向量和互为相反向量的向量:(1) AB、; (2) AE、; (3) 、;(4) AD、; (5) BE、.[解]:相等的向量对是(2)、(3)和(5);互为反向量的向量对是(1)和(4)。
§1.2 向量的加法1.要使下列各式成立,向量ba,应满足什么条件?(1-=+(2+=+(3-=+(4+=-E(5=[解]:(1),-=+(2),+=+(3≥且,=+ (4),+=-(5),≥-=-§1.3 数量乘向量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从向量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出向量→x ,→y . 解 ⑴→→→→→→→→→→→→→→-=+-+---+=-⋅+--⋅-ay b x b y a y b x a x b y a y b x a x b a y x b a y x 22)()()()(⑵ →→→→→→→→→→+=+-+-+=+3132132142232e e e e e e e e b a ,→→→→→→→→→→→-+-=+---+=-321321321342)223(2e e e e e e e e e b a , →→→→→→→→→→→-+-=+---+=-3213213217103)223(2)2(323e e e e e e e e e b a . 2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF .解 →→→→→→→→→→→-+=-+-+=+=c b a c a c b a AB CD EF 533)2(21)865(212121.3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线,又∵B 为公共点,从而A 、B 、D 三点共线.4 在四边形ABCD 中,→→→+=b a AB 2,→→→--=b a BC 4,→→→--=b a CD 35,证明ABCD 为梯形.证明∵→→→→→→→→→→→→→=--=-+--++=++=BC b a b a b a b a CD BC AB AD 2)4(2)35()4()2( ∴→AD ∥→BC ,∴ABCD 为梯形.6. 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点,证明:三中线向量AL , BM ,可 以构成一个三角形.[证明]: )(21+=)(21BC BA BM +=)(21+=0)(21=+++++=++∴CB CA BC BA AC AB CN BM AL从而三中线向量CN BM AL ,,构成一个三角形。
解析几何-吕林根-课后习题解答一到五
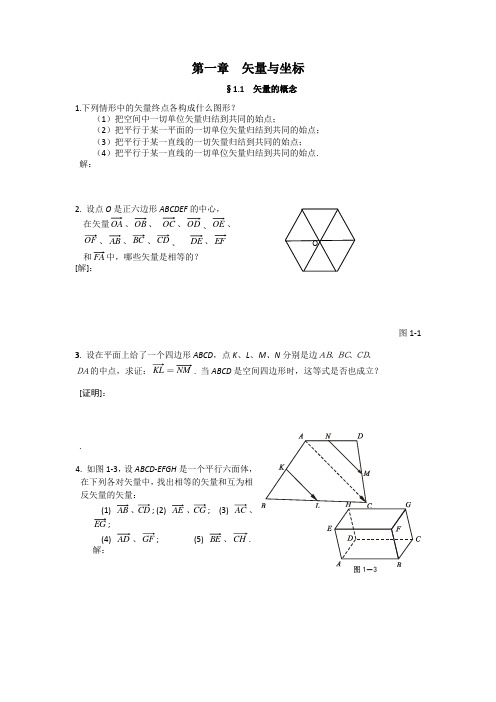
第一章矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点;(3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点.解:2. 设点O是正六边形ABCDEF的中心,在矢量OA、OB、OC、OD、OE、OF、AB、BC、CD、DE、EF和FA中,哪些矢量是相等的?[解]:图1-13. 设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB、BC、CD、DA的中点,求证:KL=NM. 当ABCD是空间四边形时,这等式是否也成立?[证明]:.4. 如图1-3,设ABCD-EFGH是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB、CD; (2) AE、CG; (3) AC、EG;(4) AD、GF; (5) BE、CH.解:§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件? (1=+ (2+=+ (3-=+ (4+=- (5= 解:§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解:2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF . 解:3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 解:4 在四边形ABCD中,→→→+=baAB2,→→→--=baBC4,→→→--=baCD35,证明ABCD为梯形.解:6. 设L、M、N分别是ΔABC的三边BC、CA、AB的中点,证明:三中线矢量AL, BM, CN可以构成一个三角形.7. 设L、M、N是△ABC的三边的中点,O是任意一点,证明OBOA++OC=OL+OM+ON.解:8. 如图1-5,设M是平行四边形ABCD的中心,O是任意一点,证明OA+OB+OC+OD=4OM.解:9在平行六面体ABCDEFGH(参看第一节第4题图)中,证明→→→→=++AGAHAFAC2.证明:.10.用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.解11. 用矢量法证明,平行四边行的对角线互相平分.解12. 设点O 是平面上正多边形A 1A 2…A n 的中心,证明: 1OA +2OA +…+n OA =0.解,13.在12题的条件下,设P 是任意点,证明 证明:§1.4 矢量的线性关系与矢量的分解1.在平行四边形ABCD 中,(1)设对角线,,b BD a AZ ==求.,,,DA CD BC AB 解(2)设边BC 和CD 的中点M 和N ,且q AN P AM ==,求CD BC ,。
1-5解析几何吕林根第四版

因为M1为P2 P3的中点,故M1(
x2
+ 2
x3
,y2
+ 2
y3 ,z2
+ 2
z3
),又因为G为重心,
故有P1G 2= GM1,即重心G把中线分成定比λ 2,
P1
利用定比分点坐标公式可得
x x= 1 + x2 + x3 ,y y= 1 + y2 + y3 ,z
3
3
z1 + z2 + z3 . G 3
e1, e2 , e3 两两相互垂直的笛卡尔标架叫做笛卡尔直角标架;简称直角标架;
在一般情况下,叫做仿射标架.
P
e3 r
e1 O
e2
e3 e1 O e2
e3 e1 O e2
注: (1) 标架{O; e1, e2 , e3}中的向量 e1, e2, e3 是有顺序的,交换它们
的次序将会得到另一标架.
(2) 空间标架有无穷多个.
e3
e1 O
e2
e3
e2 O
e1
右手(旋)标架
左手(旋)标架
二、坐标
{ } 定义 1.5.2 (1)式中的 x, y, z 叫做向量 r 关于标架 O;e1, e2, e3 的
坐标或称为分量,记做 r{x, y, z} 或{x, y, z} .
{ } 定义 1.5.3 对于取定了标架 O;e1,e2,e3 的空间中任意点 P ,向量 OP { } 叫做点 P 的向径,或称点 P 的位置向量,向径 OP 关于标架 O;e1,e2,e3 的坐 { } 标 x, y, z 叫做点 P 关于标架 O;e1,e2,e3 的坐标,记做 P ( x, y, z) 或 ( x, y, z).
1-4解析几何吕林根第四版

证明: AG = λGD; BG = µGE;
CG = AG − AC = λ AD − AC
=
λ
•
1
(
1+ λ
AB + AC)
−
AC
1+λ 2
= λ AB − λ + 2 AC
2(1 + λ) 2(1 + λ)
CG = BG − BC = µ BE − BC 1+ µ
= µ • (AE − AB) − BC 1+ µ
八、共面向量的条件
定理1.4.7 三向量共面的充要条件是它们线性相关. 定理1.4.8 空间任何四个向量总是线性相关.
推论 空间四个以上向量总是线性相关.
例6
设 p = a − b + 5 − 1 b + b − 3a , q = 4a + 5b,
2
5
试证明 : p // q.
证明:
p
=
(1
−
5
组合,即
r = xe1 + ye2 + ze3 ,
C
并且其中系数 x, y, z 被
e1, e2, e3, r 惟一确定.
P
向量 e1, e2, e3 叫做空间向量的基底.
E3 e3 r
E1 e1 O e2 E2
B
A
例1 已知三角形OAB,其中= OA a= , OB b, 而M、N分别
是三角形OA,OB 两边上的点,且有OM= λ a (0 < λ < 1) ,
线性相关.
推论 一组向量如果含有零向量,那么这组向量必线性相关.
七、共线向量的条件
解析几何_苏大第四版 课后答案(吕林根_许子道)

1 ∵ AL = ( AB + AC ) 2 1 BM = ( BA + BC ) 2 1 CN = (CA + CB) 2 1 ∴ AL + BM + CN = ( AB + AC + BA + BC + CA + CB ) = 0 2 从而三中线矢量 AL, BM , CN 构成一个三角形。
OA + OB + OC = OL + OM + ON .
PA + PB + PC = 0 . [证明]: “ ⇒ ” 若 P 为△ABC 的重心,则
CP =2 PE = PA + PB ,
从而 即
PA + PB - CP = 0 , PA + PB + PC = 0 .
图 1-9
“ ⇐ ” 若 PA + PB + PC = 0 , 则 PA + PB =- PC = CP , 取 E,F,G 分别为 AB,BC,CA 之中点,则有
1 m , μ= 1+ m 1+ m 1 m + =1. 从而 λ+μ= 1+ m 1+ m
λ=
“ ⇐ ” 设 λ+μ=1. 则有 OC =λ OA +μ OB =λ OA +(1-λ) OB = OB +λ( OA - OB ),
OC - OB =λ( OA - OB ),
所以
BC =λ BA ,
F
OF 、 AB 、 BC 、 CD 、
DE 、 EF
和 FA 中,哪些矢量是相等的? [解]:如图 1-1,在正六边形 ABCDEF 中, 相等的矢量对是:
解析几何第四版吕林根课后习题答案

解析几何第四版吕林根课后习题答案Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#第三章 平面与空间直线§ 平面的方程1.求下列各平面的坐标式参数方程和一般方程:(1)通过点)1,1,3(1-M 和点)0,1,1(2-M 且平行于矢量}2,0,1{-的平面(2)通过点)1,5,1(1-M 和)2,2,3(2-M 且垂直于xoy 坐标面的平面;(3)已知四点)3,1,5(A ,)2,6,1(B ,)4,0,5(C )6,0,4(D 。
求通过直线AB 且平行于直线CD 的平面,并求通过直线AB 且与ABC ∆平面垂直的平面。
解: (1) }1,2,2{21--=M M ,又矢量}2,0,1{-平行于所求平面, 故所求的平面方程为:一般方程为:07234=-+-z y x(2)由于平面垂直于xoy 面,所以它平行于z 轴,即}1,0,0{与所求的平面平行,又}3,7,2{21-=M M ,平行于所求的平面,所以要求的平面的参数方程为: 一般方程为:0)5(2)1(7=+--y x ,即01727=--y x 。
(3)(ⅰ)设平面π通过直线AB ,且平行于直线CD : }1,5,4{--=,}2,0,1{-= 从而π的参数方程为:一般方程为:0745910=-++z y x 。
(ⅱ)设平面π'通过直线AB ,且垂直于ABC ∆所在的平面∴}1,5,4{--=AB , }1,1,1{4}4,4,4{}1,1,0{}1,5,4{==-⨯--=⨯AC AB均与π'平行,所以π'的参数式方程为: 一般方程为:0232=--+z y x . 2.化一般方程为截距式与参数式:042:=+-+z y x π.解: π与三个坐标轴的交点为:)4,0,0(),0,20(),0,0,4(--, 所以,它的截距式方程为:1424=+-+-z y x . 又与所给平面方程平行的矢量为:}4,0,4{},0,2,4{-,∴ 所求平面的参数式方程为:3.证明矢量},,{Z Y X =平行与平面0=+++D Cz By Ax 的充要条件为:0=++CZ BY AX . 证明: 不妨设0≠A ,则平面0=+++D Cz By Ax 的参数式方程为: 故其方位矢量为:}1,0,{},0,1,{ACA B --, 从而v 平行于平面0=+++D Cz By Ax 的充要条件为:v ,}1,0,{},0,1,{ACA B --共面⇔ ⇔ 0=++CZ BY AX .4. 已知连接两点),12,0(),5,10,3(z B A -的线段平行于平面0147=--+z y x ,求B 点的z 坐标.解: }5,2,3{z AB +-= 而AB 平行于0147=--+z y x 由题3知:0)5(427)3(=+-⨯+⨯-z 从而18=z .5. 求下列平面的一般方程.⑴通过点()1,1,21-M 和()1,2,32-M 且分别平行于三坐标轴的三个平面; ⑵过点()4,2,3-M 且在x 轴和y 轴上截距分别为2-和3-的平面; ⑶与平面0325=+-+z y x 垂直且分别通过三个坐标轴的三个平面;⑷已知两点()()1,2,4,2,1,321--M -M ,求通过1M 且垂直于21,M M 的平面; ⑸原点O 在所求平面上的正射影为()6,9,2-P ;⑹求过点()1,5,31-M 和()2,1,42M 且垂直于平面0138=-+-z y x 的平面.解:平行于x 轴的平面方程为001011112=--+-z y x .即01=-z .同理可知平行于y 轴,z 轴的平面的方程分别为01,01=-+=-y x z . ⑵设该平面的截距式方程为132=+-+-c z y x ,把点()4,2,3-M 代入得1924-=c 故一般方程为02419812=+++z y x .⑶若所求平面经过x 轴,则()0,0,0为平面内一个点,{}2,1,5-和{}0,0,1为所求平面的方位矢量,∴点法式方程为001215000=----z y x ∴一般方程为02=+z y .同理经过y 轴,z 轴的平面的一般方程分别为05,052=-=+y x z x .⑷{}2121.3,1,1M M --=M M →垂直于平面π, ∴该平面的法向量{}3,1,1--=→n ,平面∂通过点()2,1,31-M , 因此平面π的点位式方程为()()()02313=--+--z y x . 化简得023=+--z y x . (5) {}.6,9,2-=→op∴ .116cos ,119cos ,112cos -===∂γβ 则该平面的法式方程为:.011116119112=--+z y x既 .0121692=--+z y x(6)平面0138=-+-z y x 的法向量为{}3,8,1-=→n ,{}1,6,121=M M ,点从()2,1,4写出平面的点位式方程为0161381214=----z y x ,则,261638-=-=A74282426,141131,21113-=++⨯-=====D C B ,则一般方程,0=+++D Cz By Ax 即:.037713=---z y x 6.将下列平面的一般方程化为法式方程。
解析几何全册课件(吕林根版)精选全文完整版

(1)交换律:
(2)结合律:
(3)
上一页
下一页
返回
O
A1
A2
A3
A4
An-1
An
这种求和的方法叫做多边形法则
上一页
下一页
返回
向量减法
上一页
下一页
返回
A
B
C
上一页
返回
例2 试用向量方法证明:对角线互相平分的四边形必是平行四边形.
证
上一页
下一页
返回
解
设
为直线上的点,
6、线段的定比分点坐标
上一页
下一页
返回
由题意知:
上一页
下一页
返回
定理1.5.4 已知两个非零向量
7、其它相关定理
则
共线的充要条件是
定理1.5.6 已知三个非零向量
,则
共面的充要条件是
上一页
返回
空间一点在轴上的投影(Projection)
§1.6 向量在轴上的射影
解
根据题意有
所求方程为
上一页
下一页
返回
根据题意有
化简得所求方程
解
上一页
下一页
返回
例4 方程 的图形是怎样的?
根据题意有
图形上不封顶,下封底.
解
以上方法称为截痕法.
上一页
下一页
返回
以上几例表明研究空间曲面有两个基本问题:
线为
的连
的中点
对边
一组
设四面体
证
e
e
e
AP
e
AD
e
AC
e
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 二次曲线一般的理论§5.1二次曲线与直线的相关位置1. 写出下列二次曲线的矩阵A 以及1(,)F x y ,2(,)F x y 及3(,)F x y .(1)22221x y a b +=;(2)22221x y a b -=;(3)22y px =;(4)223520;x y x -++=(5)2226740x xy y x y -+-+-=.解:(1)22100100001a A b ⎛⎫ ⎪⎪ ⎪= ⎪ ⎪- ⎪ ⎪⎝⎭;121(,)F x y x a =221(,)F x y y b=3(,)1F x y =-;(2)22100100001a A b ⎛⎫ ⎪⎪ ⎪=- ⎪ ⎪- ⎪ ⎪⎝⎭;121(,)F x y x a =221(,)F x y y b =-;3(,)1F x y =-.(3)0001000p A p -⎛⎫⎪= ⎪ ⎪-⎝⎭;1(,)F x y p =-;2(,)F x y y =;3(,)F x y px =-;(4)51020305022A ⎛⎫ ⎪⎪=- ⎪ ⎪ ⎪⎝⎭;15(,)2F x y x =+;2(,)3F x y y =-;35(,)22F x y x =+;(5)1232171227342A ⎛⎫-- ⎪ ⎪ ⎪=-⎪ ⎪ ⎪-- ⎪⎝⎭;11(,)232F x y x y =--;217(,)22F x y x y =-++;37(,)342F x y x y =-+-. 2. 求二次曲线22234630x xy y x y ----+=与下列直线的交点.(1)550x y --=(2)220x y ++=;(3)410x y +-=;(4)30x y -=;(5)2690x y --=.提示:把直线方程代入曲线方程解即可,详解略(1)15(,),(1,0)22-;(2⎝⎭,⎝⎭;(3)二重点(1,0);(4)11,26⎛⎫⎪⎝⎭;(5)无交点.3. 求直线10x y --=与222210x xy y x y -----=的交点. 解:由直线方程得1x y =+代入曲线方程并解方程得直线上的所有点都为交点. 4 .试确定k 的值,使得(1)直线50x y -+=与二次曲线230x x y k -+-=交于两不同的实点; (2)直线1,{x kt y k t=+=+与二次曲线22430x xy y y -+-=交于一点; (3)10x ky --=与二次曲线22(1)10xy y k y -+---=交于两个相互重合的点;(4)1,{1x t y t=+=+与二次曲线222420x xy ky x y ++--=交于两个共轭虚交点.解:详解略.(1)4k <-;(2)1k =或3k =(3)1k =或5k =;(4)4924k >. §5.2二次曲线的渐进方向、中心、渐进线1. 求下列二次曲线的渐进方向并指出曲线属于何种类型的(1)22230xxy y x y ++++=;(2)22342250x xy y x y ++--+=;(3)24230xy x y --+=.解:(1)由22(,)20X Y X XY Y φ=++=得渐进方向为:1:1X Y =-或1:1-且属于抛物型的; (2)由22(,)3420X Y X XY Y φ=++=得渐进方向为:(2:3X Y =-且属于椭圆型的; (3)由(,)20X Y XY φ==得渐进方向为:1:0X Y =或0:1且属于双曲型的.2. 判断下列曲线是中心曲线,无心曲线还是线心曲线.(1)22224630x xy y x y -+--+=;(2)22442210x xy y x y -++--=;(3)2281230y x y ++-=;(4)2296620x xy y x y -+-+=.解:(1)因为2111012I -==≠-,所以它为中心曲线; (2)因为212024I -==-且121241-=≠--,所以它为无心曲线; (3)因为200002I ==且004026=≠,所以它为无心曲线; (4)因为293031I -==-且933312--==-,所以它为线心曲线; 3. 求下列二次曲线的中心.(1)225232360x xy y x y -+-+-=;(2)222526350x xy y x y ++--+=;(3)22930258150x xy y x y -++-=.解:(1)由510,3302x y x y --=⎧⎪⎨-++=⎪⎩得中心坐标为313(,)2828-; (2)由5230,2532022x y x y ⎧+-=⎪⎪⎨⎪+-=⎪⎩得中心坐标为(1,2)-; (3)由91540,15152502x y x y -+=⎧⎪⎨-+-=⎪⎩知无解,所以曲线为无心曲线. 4. 当,a b 满足什么条件时,二次曲线226340x xy ay x by ++++-=(1)有唯一中心;(2)没有中心;(3)有一条中心直线.解:(1)由330,2302x y b x ay ⎧++=⎪⎪⎨⎪++=⎪⎩知,当9a ≠时方程有唯一的解,此时曲线有唯一中心;(2)当9,9a b =≠时方程无解,此时曲线没有中心;(3)当9a b ==时方程有无数个解,此时曲线是线心曲线.5. 试证如果二次曲线22111222132333(,)2220F x y a x a xy a y a x a y a =+++++= 有渐进线,那么它的两个渐进线方程是Φ00(,)x x y y --=221101200220()2()()()0a x x a x x y y a y y -+--+-=式中00(,)x y 为二次曲线的中心.证明:设(,)x y 为渐进线上任意一点,则曲线的的渐进方向为00:():()X Y x x y y =--,所以Φ00(,)x x y y --=221101200220()2()()()0a x x a x x y y a y y -+--+-=.6. 求下列二次曲线的渐进线.(1)226310x xy y x y --++-=;(2)2232340x xy y x y -++-+=;(3)2222240x xy y x y ++++-=.解:(1)由1360,2211022x y x y ⎧-+=⎪⎪⎨⎪--+=⎪⎩得中心坐标13(,)55-.而由2260X XY Y --=得渐进方向为:1:2X Y =或:1:3X Y =-,所以渐进线方程分别为210x y -+=与30x y += (2)由310,22332022x y x y ⎧-+=⎪⎪⎨⎪-+-=⎪⎩得中心坐标13(,)55-.而由22320X XY Y -+=得渐进方向为:1:1X Y =或:2:1X Y =,所以渐进线方程分别为20x y -+=与210x y --=(3)由10,10x y x y ++=⎧⎨++=⎩知曲线为线心曲线,.所以渐进线为线心线,其方程为10x y ++=.7. 试证二次曲线是线心曲线的充要条件是230I I ==,成为无心曲线的充要条件是230,0I I =≠. 证明:因为曲线是线心曲线的充要条件是131112122223a a a a a a ==也即230I I ==;为无心曲线的充要条件是131112122223a a a a a a =≠也即230,0I I =≠. 8. 证明以直线1110A x By C ++=为渐进线的二次曲线方程总能写成111()()0A x By C Ax By C D +++++=. 证明:设以1110A x By C ++=为渐进线的二次曲线为 22111222132333(,)2220F x y a x a xy a y a x a y a =+++++=,则它的渐进线为Φ00(,)x x y y --=221101200220()2()()()0a x x a x x y y a y y -+--+-=,其中00(,)x y 为曲线的中心, 从而有Φ00(,)x x y y --=111()()0A x By C Ax By C ++++= ,而Φ00(,)x x y y --=0 因为00(,)x y 为曲线的中心, 所以有11012013a x a y a +=-,12022023a x a y a +=- 因此Φ000033(,)(,)(,)x x y y F x y x y a φ--=+-, 令0033(,)x y a D φ-=-,代入上式得 即111(,)()()F x y A x By C Ax By C D =+++++, 所以以1110A x By C ++=为渐进线的二次曲线可写为111()()0A x By C Ax By C D +++++=.9.求下列二次曲线的方程.(1)以点(0,1)为中心,且通过(2,3),(4,2)与(-1,-3); (2)通过点(1,1),(2,1),(-1,-2)且以直线10x y +-=为渐进线. 解:利用习题8的结论即可得: (1)40xy x --=; (2)2223570x xy y x ---+=.§5.3二次曲线的切线1. 求以下二次曲线在所给点或经过所给点的切线方程.(1)曲线223457830x xy y x y ++---=在点(2,1); (2)曲线曲线223457830x xy y x y ++---=在点在原点; (3)曲线22430x xy y x y +++++=经过点(-2,-1); (4)曲线225658x xy y ++=经过点(); (5)曲线222210x xy y x y -----=经过点(0,2).解:(1)910280x y +-=; (2)20x y -=; (3)10,30y x y +=++=; (4)1150,0x y x y +-=-+=; (5)0x =.2. 求下列二次曲线的切线方程并求出切点的坐标.(1)曲线2243530x xy y x y ++--+=的切线平行于直线40x y +=; (2)曲线223x xy y ++=的切线平行于两坐标轴.解:(1)450x y +-=,(1,1)和480x y +-=,(4,3)-; (2)20y ±=,(1,2),(1,2)--和20x ±=,(2,1),(2,1)--. 3. 求下列二次曲线的奇异点.(1)22326410x y x y -+++=; (2)22210xy y x +--=; (3)2222210x xy y x y -+-++=.解:(1)解方程组330,220x y +=⎧⎨-+=⎩得奇异点为(1,1)-; (2)解方程组10,0y x y -=⎧⎨+=⎩得奇异点为(1,1)-.4.试求经过原点且切直线4320x y ++=于点(1,-2)及切直线10x y --=于点(0,-1)的二次曲线方程. 解:利用(5.3-5)可得226320x xy y x y +-+-=.5.设有共焦点的曲线族2222221x y a h b h+=++,这里h 是一个变动的参数,作平行于已知直线y mx =的曲线的切线,求这些切线切点的轨迹方程. 解:设切点坐标为00(,)x y ,则由(5.3-4)得曲线的切线为0022221x x y ya hb h+=++, 因为它平行与y m x =,所以有2220000x b my a h x my +=-+, 代入220022221x y a h b h +=++整理得222220000(1)()0m x m x y m y m a b +----=, 所以切点的轨迹为22222(1)()0mx m xy my m a b +----=.§5.4二次曲线的直径1. 已知二次曲线223754510x xy y x y +++++=.求它的(1)与x 轴平行的弦的中点轨迹; (2)与y 轴平行的弦的中点轨迹; (3)与直线10x y ++=平行的弦的中点轨迹.解:(1)因为x 轴的方向为:1:0X Y =代入(5.4-3)得中点轨迹方程6740x y ++=; (2)因为y 轴的方向为:0:1X Y =代入(5.4-3)得中点轨迹方程71050x y ++=; (3)因为直线10x y ++=的方向为:1:1X Y =-代入(5.4-3)得中点轨迹方程310x y ++=. 2.求曲线224260x xy x y +---=通过点(8,0)的直径方程,并求其共轭直径. 解:(1)把点(8,0)代入(2)(21)0X x Y y -+-= 得:1:6X Y =,再代入上式整理得直径方程为1280x y +-=,其共轭直径为122230x y --=.3.已知曲线22310xy y x y --+-=的直径与y 轴平行,求它的方程,并求出这直径的共轭直径. 解:直径方程为10x -=,其共轭直径方程为230x y -+=.4.已知抛物线28y x =-,通过点(-1,1)引一弦使它在这点被平分. 解:430x y ++=.5. 求双曲线22164x y -=一对共轭直径的方程,已知两共轭直径间的角是45度. 解:设直径和共轭直径的斜率分别为',k k ,则'23kk =.又因为它们交角45度,所以''11k k kk -=+,从而13k =-或2,'2k =-或13,故直径和共轭直径的方程为30x y +=和20x y -=或20x y +=和30x y -=.6.求证:通过中心曲线的直线一定为曲线的直径;平行于无心曲线渐进方向的直线一定为其直径. 证明:因为中心曲线直径为中心线束,因此过中心的直线一定为直径;当曲线为无心曲线时,它们的直径属于平行直线束,其方向为渐进方向,所以平行于无心曲线渐进方向的直线一定为其直径. 7.求下列两条曲线的公共直径.(1)223234440x xy y x y -+++-=与2223320x xy y x y --++=; (2)220x xy y x y ----=与2220x xy y x y ++-+=. 解:(1)210x y -+=;(2)5520x y ++=.8.已知二次曲线通过原点并且以下列两对直线 320,5540x y x y --=⎧⎨--=⎩与530,210y x y +=⎧⎨--=⎩为它的两对共轭直径,求该二次曲线的方程. 解:设曲线的方程为22111222132333(,)2220F x y a x a xy a y a x a y a =+++++=,则由(5.4-3)和(5.4-5)可得1112221323331111,,1,,,0222a a a a a a ==-=-=-=-=,所以曲线的方程为220x xy y x y ----=.§5.5二次曲线的主直径与主方向1.分别求椭圆22221x y a b +=,双曲线22221x y a b-=,抛物线22y px =的主方向与主直径.解:椭圆的主方向分别为1:0和0:1,主直径分别为0,0x y ==;双曲线的主方向分别为1:0和0:1,主直径分别为0,0x y ==;抛物线的主方向分别为0:1和1:0,主直径分别为0y =. 2.求下列二次曲线的主方向与主直径. (1)22585181890x xy y x y ++--+=; (2)22210xy x y -+-=; (3)229241618101190x xy y x y -+--+=.解:(1)曲线的主方向分别为1:(-1)和1:1,主直径分别为0,20x y x y -=+-=; (2)其主方向分别为1:1和1:(-1),主直径分别为0,20x y x y +=-+=; (3)其主方向分别为3:(-4)和4:3,主直径分别为3470x y -+=; (4)任何方向都是其主方向,过中心的任何直线都是其主直径.3.直线10x y ++=是二次曲线的主直径,点(0,0),(1,-1),(2,1)在曲线上,求该曲线的方程.解:设二次曲线方程为22111222132333(,)2220F x y a x a xy a y a x a y a =+++++=, 把点坐标(0,0),(1,-1),(2,1)分别代入上面方程同时利用直线10x y ++=为其主直径可得111222132333774,,4,,4,022a a a a a a ==-==-==,所以所求曲线方程为22474780x xy y x y -+-+=.4.试证二次曲线两不同特征根确定的主方向相互垂直.证明:设12,λλ分别曲线的两不同特征根,由它们确定的主方向分别为11:X Y 与22:X Y 则1111211112122111,,a X a Y X a X a Y Y λλ+=⎧⎨+=⎩与1121222212222222,a X a Y X a X a Y Y λλ+=⎧⎨+=⎩,所以11211211112121212212()()X X YY a X a Y X a X a Y Y λλ+=+++11212211222221221221()(),a X a Y X a X a Y X X X Y Y λλ=+++=+从而有121212()()0X X YY λλ-+=,因为12λλ≠,所以12120X X YY +=,由此两主方向11:X Y 与22:X Y 相互垂直.§5.6二次曲线方程的化简与分类1. 利用移轴与转轴,化简下列二次曲线的方程并写出它们的图形.(1)225422412180x xy y x y ++--+=;(2)222410x xy y x y ++-+-=;(3)25122212190x xy x y +---=;(4)222220x xy y x y ++++=. 解(1)因为二次曲线含xy 项,我们先通过转轴消去xy ,设旋转角为α,则324ctg α=,即21324tg tg αα-=,所以12tg α=或-2.取2tg α=-,那么sin α=,cos α=,所以转轴公式为''''2),2).x x y y x y ⎧=+⎪⎪⎨⎪=-+⎪⎩代入原方程化简再配方整理得新方程为''2''26120x y +-=;类似的化简可得 (2)''2''250y +=;(3)''2''294360x y --=;(4)''2210x -=.2.以二次曲线的主直径为新坐标轴,化简下列方程,并写出的坐标变换公式与作出它们的图形.(1)22845816160x xy y x y +++--=;(2)22421040x xy y x y --++=;(3)22446830x xy y x y -++-+=;(4)2244420x xy y x y -++-=. 解:(1)已知二次曲线的距阵是 8242584816⎛⎫ ⎪- ⎪ ⎪--⎝⎭, 18513I =+=,2823625I ==, 所以曲线的特征方程为213360λλ-+=,其特征根为14λ=,29λ=,两个主方向为11:1:2X Y =-,22:2:1X Y =;其对应的主直径分别为8200x y -+=,7740x y +-=. 取这两条直线为新坐标轴得坐标变换公式'''')1,2) 2.x x y y x y ⎧=--⎪⎪⎨⎪=++⎪⎩代入已知曲线方程并整理得曲线在新坐标系下的方程为 '2'294360x y +-=.(2)已知二次曲线的距阵是 225222520-⎛⎫ ⎪- ⎪ ⎪⎝⎭坐标变换公式''''2)1,) 2.x x y y x y ⎧=--⎪⎪⎨⎪=++⎪⎩代入已知曲线方程并整理得曲线在新坐标系方程为'2'23210x y-+-=. (3)已知二次曲线的距阵是423214343-⎛⎫⎪--⎪⎪-⎝⎭,坐标变换公式''''92),101).5 x x yy x y⎧=--⎪⎪⎨⎪=++⎪⎩代入已知曲线方程并整理得曲线在新坐标系下的方程为'2'50y x-=. (4)坐标变换公式''''22),51).5x x yy x y⎧=--⎪⎪⎨⎪=++⎪⎩代入已知曲线方程并整理得曲线在新坐标系下的方程为'2510y-=.3.试证在任意转轴下,二次曲线的新旧方程的一次项系数满足关系式'2'22213231313a a a a+=+.证明:设旋转角为α,则''131323cos sina a aαα=-,''231323sin cosa a aαα=+,两式平方相加得'2'22213231313a a a a+=+.4.试证二次曲线222ax hxy ay d++=的两条主直径为220x y-=,曲线的两半轴的长分别为. 证明:求出曲线的两主直径并化简即可得.§5.7应用不变量化简二次曲线的方程1. 利用不变量与半不变量,判断下列二次曲线为何种曲线,并求出它的化简方程与标准方程. (1)2266210x xy y x y++++-=;(2)223234440x xy y x y-+++-=;(3)2243220x xy y x y-++-=;(4)22442210x xy y x y-++--=;(5)222246290x xy y x y-+--+=;(6);(7)2222240x xy y x y++++-=;(8)224412690x xy y x y-++-+=.解:(1)因为12I=,213831I==-,13331116311=-,322II=-,而特征方程2280λλ--=的两根为124,2λλ==-,所以曲线的简化方程(略去撇号)为224220x y --=曲线的标准方程为 2221012x y --=,曲线为双曲线; 类似地得下面:(2)曲线的简化方程(略去撇号)为 222480x y +-=,曲线的标准方程为 22142x y +=,曲线为椭圆; (3)曲线的简化方程(略去撇号)为22(2(20x y +=,曲线的标准方程为22011x y -=, 曲线为两相交直线;(4)曲线的简化方程(略去撇号)为250y -=, 双曲线的标准方程为2y =, 曲线为抛物线; (5)曲线的简化方程(略去撇号)为2233((022x y +=, 曲线的标准方程为220x y +=, 曲线为一实点或相交与一实点的两虚直线;(6)曲线的简化方程(略去撇号)为220,0,0)y x a y a -=≤≤≤≤(, 曲线的标准方程为2y =,0,0)x a y a ≤≤≤≤( 曲线为抛物线的一部分;(7)曲线的简化方程(略去撇号)为 2250y -=, 曲线的标准方程为 252y =,曲线为两平行直线;(8)曲线的简化方程(略去撇号)为 250y =,曲线的标准方程为 20y =, 曲线为两重合直线.2. 当λ取何值时,方程 2244230x xy y x y λ++---= 表示两条直线.解:方程 2244230x xy y x y λ++---=表示两条直线当且仅当3222110213I λ-=-=---, 即4λ=.3. 按实数λ的值讨论方程2222250x xy y x y λλ-+-++= 表示什么曲线.解:因为12I λ=,2(1)(1)I λλ=-+,3(53)(1)I λλ=+-,12(51)K λ=-,所以当λ的值变化时,1231,,,I I I K 也随着变化,它们的变化关系如下表:4. 设221112221323332220a x a xy a y a x a y a +++++= 表示两条平行直线,证明这两条直线之间的距离是d =. 证明:曲线的方程可简化为:这里当曲线表示两条平行的实直线时,10K <.所以这两条直线之间的距离是d =5. 试证方程 221112221323332220a x a xy a y a x a y a +++++= 确定一个实圆必须且只须212124,0I I I I =<.证明:当曲线 221112221323332220a x a xy a y a x a y a +++++=表示一个实圆的充要条件是其特征方程2120I I λλ-+=有相等实根且120I I <,即21240I I ∆=-=且120I I <,从而方程确定一个实圆必须且只须212124,0I I I I =<.6. 试证如果二次曲线的10I =,那么20I <. 证明:因为111220I a a =+=即1122a a =-,所以1112222211221211121222()a a I a a a a a a a==-=-+,而11122,,a a a 不全0,所以有20I <. 7. 试证如果二次曲线的230,0I I =≠,那么10I ≠,而且120I I <.证明:当230,0I I =≠时,由5.2节习题7知,曲线为无心曲线,从而有10I ≠,而且120I I <.。
