《流体力学习题解》学生用
流体力学题解

2-1 两高度差z =20cm 的水管,与一倒U 形管压差计相连,压差计内的水面高差h =10cm ,试求下列两种情况A 、B 两点的压力差:(1)γ1为空气;(2)γ1为重度9kN/m 3的油。
已已知知::z=20cm ,h=10cm 。
解析:设倒U 型管上部两流体分界点D 处所在的水平面上的压力为p ',BC 间的垂直距离为l ,则有)(A z l h p p +++'=水γ;l h p p 水γγ++'=1B 以上两式相减,得 h z h p p 1B A )(γγ-+=-水(1) 当γ1为空气时,气柱的重量可以忽略不计,则A 、B 两点的压力差为 Pa 2943)2.01.0(9810)(B A =+⨯=+=-z h p p 水γ (2) 当γ1为重度9kN/m 3的油时,A 、B 两点的压力差为Pa 20431.09000)2.01.0(9810)(1B A =⨯-+⨯=-+=-h z h p p γγ水2-2 U 形水银压差计中,已知h 1=0.3m ,h 2=0.2m ,h 3=0.25m 。
A 点的相对压力为p A =24.5kPa ,酒精的比重为0.8,试求B 点空气的相对压力。
已已知知::h 1=0.3m ,h 2=0.2m ,h 3=0.25m 。
p A =24.5kPa ,S=0.8。
解析:因为左右两侧的U 型管,以及中部的倒U 型管中1、2、3点所在的水平面均为等压面,依据题意列静力学方程,得3B 3h p p 汞γ+=, 232h p p 酒精γ-=, 221h p p 汞γ+=, 121A )(p h h p =++水γ 将以上各式整理后,可得到B 点空气的相对压力为Pa10906.2)]25.02.0(6.132.08.0)2.03.0[(9810105.24)()(4332221A B ⨯-=+⨯-⨯++⨯+⨯=+-+++=h h h h h p p 汞酒精水γγγ 以mH 2O 表示为 O mH 96.2981010906.224B-=⨯-==水γp h2-3 如图所示,一洒水车等加速度a=0.98m/s2向前平驶,求水车内自由表面与水平面间的夹角a ;若B点在运动前位于水面下深为h=1.0m ,距z 轴为xB= -1.5m ,求洒水车加速运动后该点的静水压强。
(完整版)流体力学习题解析
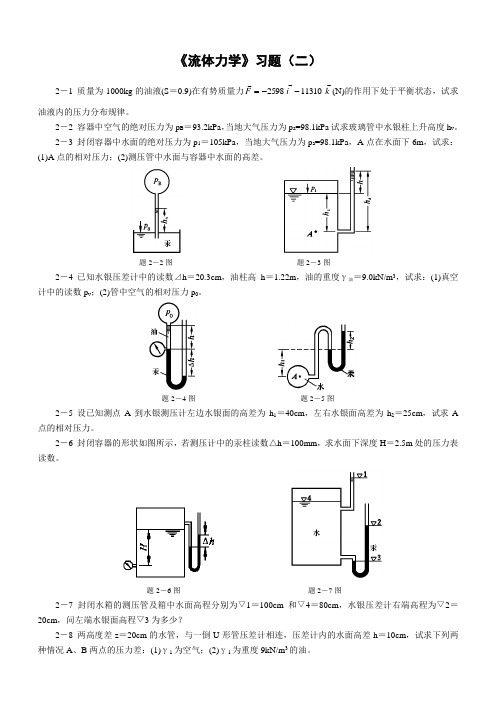
《流体力学》习题(二)2-1 质量为1000kg 的油液(S =0.9)在有势质量力k i F 113102598--=(N)的作用下处于平衡状态,试求油液内的压力分布规律。
2-2 容器中空气的绝对压力为p B =93.2kPa ,当地大气压力为p a =98.1kPa 试求玻璃管中水银柱上升高度h v 。
2-3 封闭容器中水面的绝对压力为p 1=105kPa ,当地大气压力为p a =98.1kPa ,A 点在水面下6m ,试求:(1)A 点的相对压力;(2)测压管中水面与容器中水面的高差。
题2-2图 题2-3图 2-4 已知水银压差计中的读数⊿h =20.3cm ,油柱高h =1.22m ,油的重度γ油=9.0kN/m 3,试求:(1)真空计中的读数p v ;(2)管中空气的相对压力p 0。
题2-4图 题2-5图 2-5 设已知测点A 到水银测压计左边水银面的高差为h 1=40cm ,左右水银面高差为h 2=25cm ,试求A 点的相对压力。
2-6 封闭容器的形状如图所示,若测压计中的汞柱读数△h =100mm ,求水面下深度H =2.5m 处的压力表读数。
题2-6图 题2-7图 2-7 封闭水箱的测压管及箱中水面高程分别为▽1=100cm 和▽4=80cm ,水银压差计右端高程为▽2=20cm ,问左端水银面高程▽3为多少?2-8 两高度差z =20cm 的水管,与一倒U 形管压差计相连,压差计内的水面高差h =10cm ,试求下列两种情况A 、B 两点的压力差:(1)γ1为空气;(2)γ1为重度9kN/m 3的油。
题2-8图题2-9图2-9 有一半封闭容器,左边三格为水,右边一格为油(比重为0.9)。
试求A、B、C、D四点的相对压力。
2-10 一小封闭容器放在大封闭容器中,后者充满压缩空气。
测压表A、B的读数分别为8.28kPa和13.80kPa,已知当地大气压为100kPa,试求小容器内的绝对压力。
流体力学习题讲解(修)

【3-3】 水流通过如图所示管路流入大气,已知:U形测压管中水银柱高差Δh=0.2m,h1=0.72m H2O,管径d1=0.1m,管嘴出口直径d2=0.05m,不计管中水头损失,试求管中流量qv。 【解】 首先计算1-1断面管路中心的压强。因为A-B为等压面,列等压面方程得: 则 (mH2O) 列1-1和2-2断面的伯努利方程
1-5:如 图 所 示 容 器, 上 层 为 空 气, 中 层 为 的 石 油, 下 层 为 的 甘 油, 试 求: 当 测 压 管 中 的 甘 油 表 面 高 程 为 时 压 力 表 的 读 数。
已知:H = 1 m h = 5 m D = 50 mm 喷嘴 d = 30 mm 不计摩擦损失 求: 1、真空室中的 压强 p2 , 2、排出水的流量 qV 。
解:取 5 个过流断面如图。
对1—1,3—3 断面列伯努利方程得:
流体力学-习题
1-1. 一 底 面 积 为45x50cm2 , 高 为 1cm 的 木 块, 质 量 为5kg , 沿 涂 有 润 滑 油 的斜 面 向 下 作 等 速 运 动, 木 块 运 动 速 度u=1m/s , 油 层 厚 度1cm , 斜 坡 角 22.620 (见 图 示), 求 油 的 粘 度 。
则:
由连续方程知:
即:
再对 1—1,2—2 断面列伯努利方程得:
解得:
真空室压强 p2 低于大气压,降至 0.345105 Pa 后, 蓄水池中的水被压上来。
流量为:
v — 吸水管中的流速
对 4—4 和 5—5 断面列伯努利方程求 v :
解得:
排出水的流量:
3-2:注 液 瓶 为 了 使 下 部 管 口 的 出 流 量 不 随 时 间 而 变, 在 上 部 瓶 塞 中 插 人 通 气 管, 试 分 析 出 流 量 恒 定 的 原 理 和 调 节。
流体力学习题解答4

习 题 四1. 油(μ=3⨯103-kg/m*s )和水(μ=1.14⨯103-kg/m*s )在管径d=100mm 的圆管中流动,如果压力降相同,流态都是层流,试求这两种流动中管轴线上的流速之比。
2. 动力粘度μ=0.072kg/m*s 的油在管径d=0.1m 的圆管中作层流运动,流量Q=3⨯103-m 3/s ,试计算管壁切应力τ0。
3. 水(运动粘度υ=106-m2/s )在直径d=200mm ,长l=20m 的圆管流动,流量Q=24⨯103-m 3/s ,如果管壁粗糙度∆=0.2mm ,求沿程水头损失。
4. 圆管直径d=80mm ,当流量很大时,测得沿程损失系数是一个常数,其值为λ=0.025,试计算管壁的粗糙度∆。
5. 一条管道,新使用时,相当粗糙度∆/d=104-,使用多年后,发现在水头损失相同的情况下,流量减少了35%,试估算此旧管的相对粗糙度。
6. 如图,串联管道由两段管组成,其长度和直径分别为l 1=500m ,d 1=300mm ,l 2=400m ,d 2=250mm ,壁面粗糙度都是∆=0.6mm ,水位H=10m ,如果沿程损失系数按阻力平方区计算,求流量Q 。
11题图7. 一段水管,长l=150m ,流量Q=0.12 m 3/s ,该管段内总的局部损失系数为ζ=5,沿程损失系数那λ=3.002.0d计算,如果要求水头损失h=3.96m ,求管径d 。
8. 为了测量截面突然扩大的局部损失系数ζ和管道沿程损失系数λ,在管道三个截面上装有测压管,其中测压管1在扩大前端,其余两个测压管等距离地安装在下游,已知三支测压管液面读数为h 1=156.5mm, h 2=163mm, h 3=113mm ,管径d=15mm ,D=20mm ,长度l=100mm ,测得流量Q=2.65⨯104-m 3/s ,求ζ和λ的值。
15题图9. 一条输油管道,直径d=250mm ,长l=6.5km ,壁面粗糙度∆=0.8mm ,流量Q=0.06 m 3/s ,油的运动粘度υ=2.4⨯106-m 2/s ,求沿程损失。
流体力学习题解答

2.在现实生活中可视为牛顿流体的有水 和空气 等。
3.流体静压力和流体静压强都是压力的一种量度。
它们的区别在于:前者是作用在某一面积上的总压力;而后者是作用在某一面积上的平均压强或某一点的压强。
4.均匀流过流断面上压强分布服从于水静力学规律。
5.和液体相比,固体存在着抗拉、抗压和抗切三方面的能力。
7.流体受压,体积缩小,密度增大 的性质,称为流体的压缩性 ;流体受热,体积膨胀,密度减少 的性质,称为流体的热胀性 。
8.压缩系数β的倒数称为流体的弹性模量 ,以E 来表示 12.液体静压强分布规律只适用于静止、同种、连续液体。
13.静止非均质流体的水平面是等压面,等密面和等温面。
14.测压管是一根玻璃直管或U 形管,一端连接在需要测定的容器孔口上,另一端开口,直接和大气相通。
16.作用于曲面上的水静压力P 的铅直分力z P 等于其压力体内的水重。
17.通过描述物理量在空间的分布来研究流体运动的方法称为欧拉法。
18. 流线不能相交(驻点处除外),也不能是折线,因为流场内任一固定点在同一瞬间只能有一个速度向量,流线只能是一条光滑的曲线或直线。
20.液体质点的运动是极不规则的,各部分流体相互剧烈掺混,这种流动状态称为紊流。
21.由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速k v ',其中kv '称为上临界速度,k v 称为下临界速度。
23.圆管层流的沿程阻力系数仅与雷诺数有关,且成反比,而和管壁粗糙无关。
25.紊流过渡区的阿里特苏里公式为25.0)Re68(11.0+=d k λ。
26.速度的大小、方向或分布发生变化而引起的能量损失,称为局部损失。
29.湿周是指过流断面上流体和固体壁面接触的周界。
31.串联管路总的综合阻力系数S 等于各管段的阻抗叠加。
32.并联管路总的综合阻力系数S 与各分支管综合阻力系数的关系为3211111s s s s++=。
管嘴与孔口比较,如果水头H 和直径d 相同,其流速比V 孔口/V 管嘴等于82.097.0,流量比Q 孔口/Q 管嘴等于82.060.0。
《流体力学》课后习题答案.pdf

得:T1 = t1 + 273 = 50 + 273 = 323K ,T2 = t2 + 273 = 78 + 273 = 351K
根据
p
=
mRT V
,有:
p1
=
mRT1 V1
,
p2
=
mRT2 V2
得: V2 V1
=
p1 p2
T2 T1
=
9.8067 104 5.8840 105
351 323
=
0.18
设管段长度 l,管段表面积: A = dl
单位长度管壁上粘滞力: = A u = dl u − 0 = 3.14 0.025 0.03
l y l
0.001
1-8 解: A = 0.8 0.2 = 0.16m2 ,u=1m/s, = 10mm , = 1.15Pa s
T = A u = A u − 0 = 1.15 0.16 1 = 18.4N
1
=
T1 b
=
A b
u
−0 −h
=
0.7 0.06b b
15 − 0 0.04 − 0.01
=
21N
/m,方向水平向左
下表面单位宽度受到的内摩擦力:
2
=
T2 b
=
Au−0 b h−0
=
0.7 0.06b 15 − 0
b
0.01− 0
= 63N
/m,方向水平向左
平板单位宽度上受到的阻力:
= 1 + 2 = 21+ 63 = 84N ,方向水平向左。
h1 = 5.6m
2.4 解:如图 1-2 是等压面,3-4 是等压面,5-6 段充的是空气,因此 p6 = p5 ,6-7 是等压面,
流体力学习题解答

《流体力学》选择题库第一章 绪论1.与牛顿内摩擦定律有关的因素是:A 、压强、速度和粘度;B 、流体的粘度、切应力与角变形率;C 、切应力、温度、粘度和速度;D 、压强、粘度和角变形。
2.在研究流体运动时,按照是否考虑流体的粘性,可将流体分为:A 、牛顿流体及非牛顿流体;B 、可压缩流体与不可压缩流体;C 、均质流体与非均质流体;D 、理想流体与实际流体。
3.下面四种有关流体的质量和重量的说法,正确而严格的说法是 。
A 、流体的质量和重量不随位置而变化;B 、流体的质量和重量随位置而变化;C 、流体的质量随位置变化,而重量不变;D 、流体的质量不随位置变化,而重量随位置变化。
4.流体是 一种物质。
A 、不断膨胀直到充满容器的;B 、实际上是不可压缩的;C 、不能承受剪切力的;D 、在任一剪切力的作用下不能保持静止的。
5.流体的切应力 。
A 、当流体处于静止状态时不会产生;B 、当流体处于静止状态时,由于内聚力,可以产生;C 、仅仅取决于分子的动量交换;D 、仅仅取决于内聚力。
6.A 、静止液体的动力粘度为0; B 、静止液体的运动粘度为0;C 、静止液体受到的切应力为0;D 、静止液体受到的压应力为0。
7.理想液体的特征是A 、粘度为常数B 、无粘性C 、不可压缩D 、符合RT p ρ=。
8.水力学中,单位质量力是指作用在单位_____液体上的质量力。
A 、面积B 、体积C 、质量D 、重量 9.单位质量力的量纲是A 、L*T -2B 、M*L 2*TC 、M*L*T(-2)D 、L(-1)*T 10.单位体积液体的重量称为液体的______,其单位。
A 、容重N/m 2B 、容重N/M 3C 、密度kg/m 3D 、密度N/m 311.不同的液体其粘滞性_____,同一种液体的粘滞性具有随温度______而降低的特性。
A 、相同降低 B 、相同升高 C 、不同降低 D 、不同升高 12.液体黏度随温度的升高而____,气体黏度随温度的升高而_____。
流体力学习题解答(参考)

习题解答2-9解L H L H H ⋅⋅=⋅⋅⋅=αγαγsin 2sin 2P 2左()()()αααααααsin 32sin 6sin 2 sin /sin /2/12/sin /sin 2 3H H H L H H H HAZ J ZC Z C C D =+=+=+= ααsin 3sin H x Z H x x D D -=⎪⎭⎫⎝⎛--= ⎪⎭⎫ ⎝⎛-⋅⋅⋅=⎪⎭⎫ ⎝⎛-⋅=⋅ααγαsin 3sin 2sin 3P P 2H x L H H x x D 左左L h ⋅⋅=αγsin 2P 2右 αs i n 32'h Z D = ⎪⎭⎫ ⎝⎛-⋅⋅⋅=⎪⎭⎫ ⎝⎛-⋅=⋅ααγαsin 3sin 2sin 3P P 2'h x L h h x x D右右平衡时有:⎪⎭⎫ ⎝⎛-⋅⋅⋅⎪⎭⎫ ⎝⎛-⋅⋅⋅ααγααγsin 3sin 2sin 3sin 222h x L h H x L H = 所以 ⎪⎭⎫⎝⎛-⋅⎪⎭⎫ ⎝⎛-⋅ααs i n 3s i n 322h x h H x H =有 m h H h H x 795.060sin )4.02(34.02sin )(322332233=︒--=--=α2-13解L d L d L d Ry 22216316181γπγπγπ=+=()L d d d L H H L H L H Rx 22222212221834121212121γγγγγ=⎪⎭⎫ ⎝⎛-=-=+=N 9236100.49.810001632=⨯⨯⨯⨯=π+Ry N 5880100.49.81000832=⨯⨯⨯⨯=RxN 588010949923658802222==+=+=y x R R R︒=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=50.5758809236arctg arctg x yR R θ 2-16解(不能直接利用教材上的公式)盖板上任意点上的压力()⎪⎪⎭⎫⎝⎛+=︒+=z h z h p 2245sin γγ ()A z J J J A z h dA z dA z h zdA z h z p c c z z c A AAD ⋅+=⋅+⋅⋅⋅+=︒+=⋅⎰⎰⎰22 222245sin ,=γγγγγ其中:42244332322542213223222224442 22d d d d J d d d b a J d ab A d z z c c ππππππππ=⋅+==⋅⎪⎪⎭⎫ ⎝⎛=====,434232543225224222d d h d d d h z p D γππγπγπγ+⋅⋅=⋅+⋅⋅⋅=⋅433254d hd z p d T D γπγπ+=⋅=⋅ ()()6587N0.6528320.69.81000 583232542232==⨯+⨯⨯⨯⨯⨯+=+=h d h d d hd T ππγγπγπ2-17解r d r H 3 4==,,由图可知 21h h =球冠edc 和fgh 的体积分别为:()321 2456/41r r r r V ππ=-=球冠edc 曲面上的压力体为abedc ,重量为γπγππγπ33221244924533411341r r r r V r d F =⎪⎭⎫⎝⎛-⋅⋅=⎪⎭⎫ ⎝⎛-⋅=部分球面ef -rg 上作用力等于同体积水的重量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 流体运动的基本方程组3.1 写出下列各量的数学表达式:(1)单位时间内以n 为法向的面积元dA 上的流体体积流量; (2)t ∇时间内经固定不动空间τ的表面S 净流入τ的质量; (3)流体体积τ内的动量、动能的随体导数。
[解](1)设流速为V ,单位时间令为“1”,则解为:dA n ν⋅(2)设流体密度为ρ,n 为其单位法向量,流速为ν,则解为:t dA n ∇⋅-⎰νρ(3)动量的随体导数:()⎰τνρτd DtD动能的随体导数:⎪⎪⎭⎫ ⎝⎛⎰τνρτd Dt D 22 (解完)3.2 写出下列情况的连续性方程: (a) yz 平面上稳定可压缩性流体。
(b) 在xz 平面上不稳定、不可压缩流体。
(c) 仅在y 方向上不稳定的可压缩流体。
(d) 在平面极坐标上的稳定、可压缩流体。
[解](a) yz 平面上稳定可压缩性流体:0)()(=∂∂+∂∂w zv y ρρ(b) 在xz 平面上不稳定、不可压缩流体:0=∂∂+∂∂zwx u(c) 仅在y 方向上不稳定的可压缩流体:0)(=∂∂+∂∂v zt ρρ(d) 在平面极坐标上的稳定、可压缩流体。
0)()(=∂∂+∂∂θρρv zrv r r (解完)3.3 一不可压流场为2Kxz u =,Cy w =,式中的K 与C 均为定值。
试由连续性方程导出速度分量v 。
[解] 由连续性方程:0=∂∂+∂∂+∂∂z w y v x u ⇒ 002=+∂∂+yvKz ⇒2Kz yv-=∂∂ ⇒ ),,(2t z x f Kyz v +-=(解完)3.4 一不可压流场具有如下的圆柱坐标分量:Cr v =θ,)(22r R K v z -=,0=r v ,式中C 与K 为常数,且R r ≤,L z ≤。
此流动满足连续方程吗?物理上,此流场代表什么?[解] 由连续性方程:0)()(1)(1=∂∂+∂∂+∂∂z r v zv r rv r r θθ ⇒0)]([)(1)0(122=-∂∂+∂∂+⋅∂∂r R K z Cr r r r r θ ⇒ 00=故此速度分布满足连续性方程。
此流场可能是一圆柱中之流体,由于圆柱底盘转动所带动的粘性流。
(解完)3.5 在流体中取一任意形状的控制体,由此求连续性方程。
[解] 取一任意形状控制体(流场中),其体积为τ,表面积为S,密度为()t z y x ,,,ρ,左方流入流体质量dAn s νρ⎰⋅-1,右方流出流体质量dA n s νρ⎰⋅2,净流量为dA n s νρ⎰⋅-1-dA n s νρ⎰⋅2=dA n s νρ⎰⋅-据质量守恒有:dA n d t p s νρττ⎰⎰⋅-=∂∂,即0=⋅+∂∂⎰⎰dA n d tps νρττ (解完)3.6 流体作有自由面的三维波动,底面为平面且流体等深,波动幅度小,求连续性方程。
[解] 取一控制体(如上图):x方向:左端流入()t dy h u ∆+ξρ,右端流出()()()xt dy h u t dy h u ∂∆+∇+∆+ξρξρ,净流量()()t dxdy h u x∆+∂∂ξρ y方向:同理有:净流量()()t dxdy h u y∆+∂∂ξρ 控制体内质量变化为:()()t dxdy h u y∆+∂∂ξρ 据质量守恒:()()()()0)(=∆+∂∂+∆+∂∂+∆∂+∂t dxdy h yt dxdy h u x t dxdy t h ξρνξρξ 约去t dxdy ∆,且h为常量,整理得:()()()0)(=+∂∂++∂∂+∂∂ξρνξρξh yh u x t (解完)3.7 某一二维近壁剪切流如图示。
速度分量为: )2(222xa y ax y U u -=而a 为一常数,试由连续性导出速度分量),(y x v ,假设0=y ,近壁处0=v 。
[解]0=∂∂+∂∂yv x u)22(2222xa y ax y U y v +--=∂∂)()32(22222x f xa y ax y U v +-=由于,0)0,(≡x v ,∴ 0)(=x f)32(),(22222xa y ax y U y x v -=(解完)3.8 若z 轴向上,速度场ay u =,bx v =,0=w 为上不可压流动的连续性方程和N -S 方程的精确解,则常数a ,b 有何条件。
[解] 将ay u =,bx v =,0=w 代入:0000=++=∂∂+∂∂+∂∂zw y v x u ,故满足连续性方程。
代入N -S 方程:)()(222222zu w y u v x u u t u z u y u x u x p g x ∂∂+∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂-ρμρ⇒abx xpρ-=∂∂, 同理:aby y p -=∂∂,g zp ρ-=∂∂(静水压强)02=∂∂∂yx p,故其满足N -S 方程。
因此,a ,b 为任意数均可同时满足连续性方程和N -S 方程。
(解完)3.9 证明:图中两平板间的Couette 流动(h Vy u /=,0==w v )为不可压流动的N -S 方程式之解,并求出流体中唯一的非零剪应力。
[解] N -S 方程式:V p g DtV D2∇+∇-=μρρ 代入:i y h V V=,得:⇒ 0=∂∂xp0=∂∂yp0=∂∂zp(忽略重力) 因此,若流场内无压力变人,则流动合于N -S 方程。
并且,唯一的剪力为:hV x v y u xy μμτ=∂∂+∂∂=)((解完)3.10流体在两平板间入口处速度为均匀,4==U u cm/sec ,继续下流后,发展成为抛物线形状的层流运动,速度分布为)(0z z az u -=,a 是一个常数。
若0z =1cm ,且流体为甘油,在20︒C 稳定流动情况下,求m ax u ,以cm/sec 表示。
[解] 4)2)(2(2000max az z z z a U =-=∴ 20max /4z U a =6)(2000az dz z z z a udz Q z z =-==⎰⎰∴ 6230max ==U U cm/sec(解完)3.11 在平板中之完全发展的层流,与习题3.10相同,其速度分布为200max /)(4z z z z u u -=,0==w v 为N -S 方程之恰当解,不计重力。
计算压力分布),(z x p 及剪应力之分布),(z x τ,利用m ax u ,0z ,μ为参数。
为何最大剪应力产生于板壁,为何密度不出现在参数中?[解] 200max /)(4z z z z u u -=,0==w v代入动量方程式:20max 280)(z u u u V z pμμρ-=∇+∇⋅-=∂∂故=∂∂zp常数z z u p z p p 2max8)0()(μ-==)2(4020maxz z z u z u -=∂∂=μμτ(线性分布)max4z u w μτ=因为加速度为0,故与密度无关。
(解完)3.12 对于在极坐标中的不可压缩流体,由N -S 方程求出一旋转流Um ax u 0z z =0=z)(r v θ,0==z r v v 的通式。
流体在两固定的同心圆柱中没有滑动。
[解] 假设)(r v v θθ=,不考虑压力梯度与重力,代入N -S 方程式中有:])(1[1)(2rv r u r r r g p r v V θθθθνθρ-∂∂∂∂++∂∂-=∇⋅ rv dr dv r dr d θθ=)( rCr C v 21+=θ边界条件:a C a C a v 210)(+==θ;bC b C b v 210)(+==θ 解得:021==C C故0=θv 。
(解完)3.13 一固定厚度的薄膜粘性液体以层流的方式流下一夹解为θ的平板,如图示。
速度分布为:)2(y h Cy u -=,0==w v ,求常数C 以比重、粘滞系数、及角度θ表出,并求出每单位宽的体积流量Q 以ρ、μ、θ表出。
[解] θsin g g x = )2(y h Cy u -=u g xpu V x 2)(∇++∂∂-=∇⋅μρρ)2(sin 00C g -++=μθρ∴ μθρ2sin g C =30032)2(Ch dy y h Cy udy Q hh=-==⎰⎰最后得:μθρ3sin 3h g Q =(每单位宽度)(解完)3.14 一个无穷宽平板,置于静止的粘性流体中,平板在正弦波形做往复运动。
如图示,在远离平板的流体为静止。
试做出简化的假设,建立一微分方程式及边界条件,以求出流体的速度场u 。
(不必解出)[解] 因板子为非常长且非常宽,故:),(t y u u =,0=∂∂xp,0==w v 代入动量方程式中:)()(222222zw y u x u g x p z w w y u v x u u t u x ∂∂+∂∂+∂∂++∂∂-=∂∂+∂∂+∂∂+∂∂μρρ∴ 22yut u ∂∂=∂∂ν (1)边界条件:当0=y 时,t U t u ωsin ),0(0=当∞=y 时,),(t u ∞=0已知:t U t u ωsin ),00=可设一变量*U ,令t U t U ωcos ),0(0*=于是:2*2*yU V t U ∂∂=∂∂ (4)满足:),(**t y U U =边界条件:t U t U ωcos ),0(0*=0),(*=∞t U),(),(),(*t y iu t y U t y W +≡=复速度(4)式+(1)⨯i :)()(*22*iu U y iu U t +∂∂=+∂∂22yW V t W ∂∂=∂∂(5)故:)],([t y W I U m =,即U 为W 的虚部。
由*U 及U 边界条件得:)sin (cos ),0(),0(0*t i t U t iu t U ωω+=+∴ 边界条件:t i e U t W ω0),0(=;0),(=∞t W平板速度不可压缩粘性流体tU ωsin 0t i e y F t G y F t y W ω)()()(),(≡=(6)将(6)式分别微分后,代入(5):0)()(=-''y F ri y F ω其解为:ri ri eC e C y F ωω21)(+=进一步化简:2)1(22112i i i +=+-=,∴21ii +=由边界条件得知:t i t i e U e F t W ωω0)0(),0(== ∴ 0)0(U F =(7a )0)(),(=∞=∞t i e F t W ω ∴ 0)(=∞F(7b )(7a )代入(6)得:021)0(U C C F =+=(7b )代入(6)得:0)(1==∞∞e C F ∴ 1C = 0,02U C =故 yry ri y ri eU eU eU y F 202100)(ωωω-+--=== (8)(8)代入(6):)2(20)(),(y r t i y rti eeU ey F t y W ωωωω--==已知:)],([),(t y W I t y u m =∴ )2sin(),(20y rt eU t y u yrωωω-=-(解完)3.15 如图示,两平板间的层流速度分布为:2max )(4h y h y u u -=,0==w u若两壁面间的温度均为0T ,试采用不可压流 动的能量方程式解两板间的温度分布。
