南京航空航天大学结构力学课后习题集规范标准答案第1章
结构力学课后习题答案
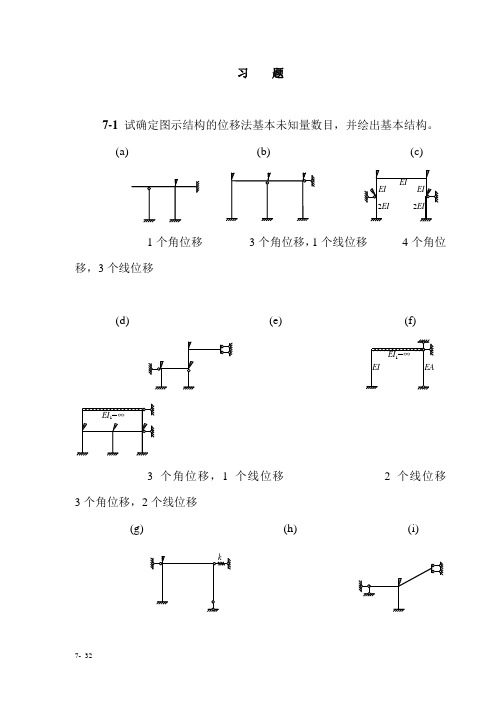
习题7-1 试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a) (b) (c)1个角位移3个角位移,1个线位移4个角位移,3个线位移(d) (e) (f)3个角位移,1个线位移2个线位移3个角位移,2个线位移(g) (h)(i)7- 327- 33一个角位移,一个线位移 一个角位移,一个线位移 三个角位移,一个线位移7-2 试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?7-3 试说出位移法方程的物理意义,并说明位移法中是如何运用变形协调条件的。
7-4 试回答:若考虑刚架杆件的轴向变形,位移法基本未知量的数目有无变化?如何变化?7-5 试用位移法计算图示结构,并绘出其内力图。
(a)解:(1)确定基本未知量和基本结构有一个角位移未知量,基本结构见图。
lll7- 34Z 1M 图(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==(4)画M 图M 图(b)4m4m 4m7- 35解:(1)确定基本未知量1个角位移未知量,各弯矩图如下1Z =1M 图32EIp M 图(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程 1115,352p r EI R ==- 153502EIZ -=114Z EI=(4)画M 图()KNm M ⋅图(c)6m6m9m7- 36解:(1)确定基本未知量一个线位移未知量,各种M 图如下1M 图243EI 243EI 1243EI p M 图F R(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程 1114,243p pr EI R F ==- 140243p EIZ F -=12434Z EI=(4)画M 图7- 3794M 图(d)解:(1)确定基本未知量一个线位移未知量,各种M 图如下11Z1111r 252/25EA a 简化a2a a2aa F P7- 38图1pR pp M(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程 11126/,55p pr EA a R F ==-126055p EA Z F a -=13a Z EA=(4)画M 图图M(e)l7- 39解:(1)确定基本未知量两个线位移未知量,各种M 图如下图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M p(2)位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++=(3)确定系数并解方程7- 4011122122121,1,0p p p EA r r r l EA r l R F R ⎛=== ⎝⎭⎛=+ ⎝⎭=-=代入,解得12p p lZ F EAlZ F EA=⋅=⋅(4)画M 图图M p7-6 试用位移法计算图示结构,并绘出M 图。
结构力学课后习题答案

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学1-9章答案
1 8
2 36
1 4
3 ( 1 3 2 1 6 2 (3) 1 (6))
6EI 2
2
+ 2 6 1 2 5 ()
6EI
2EI
(c)
2kN/m 6m
2kN 2kN
B 2EI C
EI
EI
1
A
D
3m 3m 3m
1 6
2
2
3
3
42
18
36
30
6
MP
M
xc
6
3 2EI
(2
18
2
0
C
F RC [( 1 ) a] a (方向与图示一致)
h
h
(b)
c1 c2 c3
A A′
2a
BC
D
B′ C′
D′
Δ C
a
2a
1
0.5
1.5
0
FR 图
yc
t h
M ds
t
5 4
5
+t 5 5 t (1) 12 t ( 1 4 3 2 4 3)
4
2
h2
54.5t()
5-10 试求图示结构在支座位移作用下的位移:(a) ΔC ;(b) ΔyC , ΔC 。 (a)
C D
D′
E E′
C′ΔC
h
b
A
l 2
B
B′
l 2
a
1
1
1
h
h
0
A
B
C
D
E
FG
H
2m 2m 2m 2m 2m 2m 2m 3m
A
M 7.5
南京航空航天大学材料力学习题集

第二章 拉伸、压缩与剪切
学号(
) 姓名(mm的两快盖板相联接。各零件材料相同,许用应力均为 [ σ ]=80MPa,[τ ]=60MPa,[ σ bs]=160MPa。若拉杆的厚度t =15mm,拉力P =120kN,试设 计螺栓直径d及拉杆宽度b。
△R R
题 1.12 图
.
第二章 拉伸、压缩与剪切
学号(
) 姓名(
)4
第二章 拉伸、压缩与剪切
一、是非题
2.1 使杆件产生轴向拉压变形的外力必须是一对沿杆件轴线的集中力。
()
2.2 轴力越大,杆件越容易被拉断,因此轴力的大小可以用来判断杆件的强度。 ( )
2.3 内力是指物体受力后其内部产生的相互作用力。
()
2.15 变形与位移关系描述正确的是( )
A. 变形是绝对的,位移是相对的
B. 变形是相对的,位移是绝对的
C. 两者都是绝对的
D. 两者都是相对的
2.16 轴向拉压中的平面假设适用于( )
A. 整根杆件长度的各处
B. 除杆件两端外的各处
C. 距杆件加力端稍远的各处
2.17 变截面杆如图,设F1、F2、F3分别表示杆件中截面 1-1、2-2、3-3 上的内力,则下
A
B
l
题 1.10 图
第一章 绪论
学号(
) 姓名(
)3
1.11 图示三角形薄板因受外力作用而变形,角点 B 垂直向上的位移为 0.03mm,但 AB 和 BC 仍保持为直线。试求沿 OB 的平均应变,并求 AB,BC 两边在 B 点的角度改变。
B
45º
45º
A
O
C
240
题 1.11 图
结构力学课后习题答案
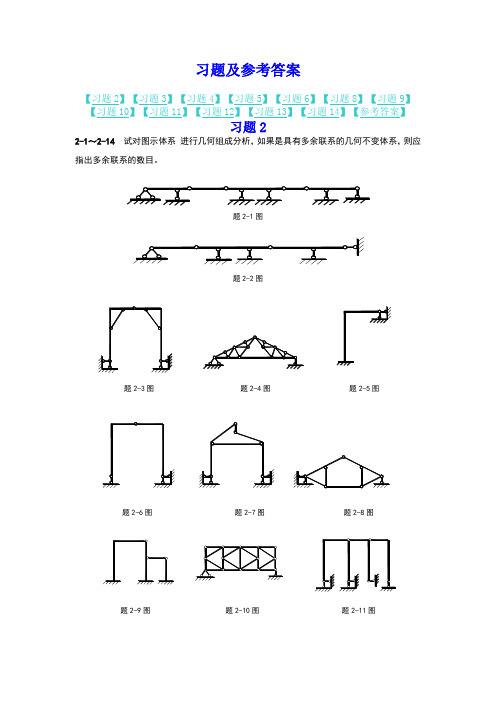
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)8kN /m20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6检查下列刚架的M图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1图示抛物线三铰拱轴线方程xxllfy)(42-=,试求D截面的内力。
题5-1图5-2带拉杆拱,拱轴线方程xxllfy)(42-=,求截面K的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)P题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学课后习题答案
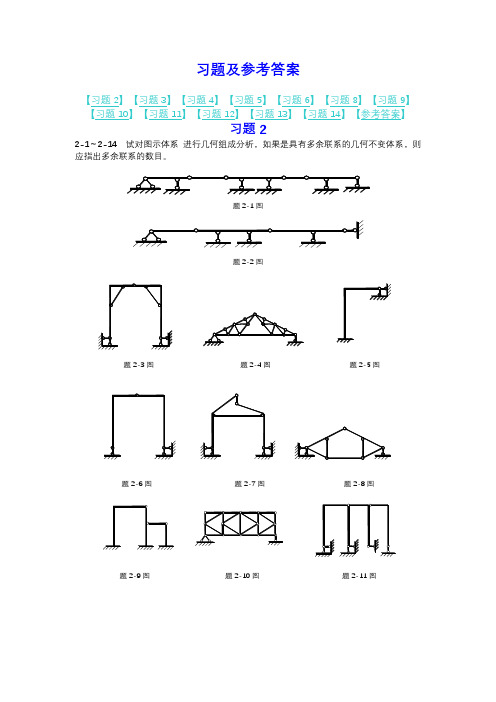
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
题3-1图3-2 试不计算反力而绘出梁的M 图。
题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
题4-1图4-2 作图示刚架的M 图。
(b)(a)20kN40kN20kN/m40kN(b)5kN/m40kN(a)(c)(b)(a)题4-2图4-3 作图示三铰刚架的M 图。
题4-3图4-4 作图示刚架的M 图。
题4-4图4-5 已知结构的M 图,试绘出荷载。
P(e)(d)(a)(b)(c)/4kN(b)(a)(a)(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
题4-6图习题55-1 图示抛物线三铰拱轴线方程,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程,求截面K 的弯矩。
题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(e)(g)(h)P(d)(c)(a)(b)(f)x x l l fy )(42-=x x l lfy )(42-=C题6-1图6-2 用结点法计算图示桁架中各杆内力。
题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(b)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学课后习题答案[1]
![结构力学课后习题答案[1]](https://img.taocdn.com/s3/m/8c0493dc80eb6294dd886c23.png)
)e( 移位线个 1�移位角个 3 移位角个 1
)d(
)c(
。构结本基出绘并�目数量知未本基法移位的构结示图定确试 1-7
)b(
) a(
题
习
33 -7
下如图矩弯各�量知未移位角个 1 m4 m4
量知未本基定确�1� �解 C IE
m4
D Nk01
IE
B
IE2 m/Nk5.2
A )b(
图M
42 lq 2 5
图矩弯终最画�4� 得解�入代
61.53
IE
3
0 � p 2 R , 0 3 � p 1R 6 � 2 2r IE � 1 2r � 2 1r , I E 2 � 1 1r
程方解并数系定确�3�
p2
11
1
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
N K 0 3 � � p 2 R , N K 0 3 � p 1R 4 � � 2 2r 0 � 1 2r � 2 1r , i1 1 � 1 1r
p2
得解�入代
i3
程方解并数系定确�3�
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
程方型典法移位�2�
程方型典法移位�2�
0�
p1
图p M
03 � p 1R � 0 � p 1R
03
04 -7
m2
m2 数常=IE F
B E
m2
m2
D
A
m2
Nk03
C )c(
90.92 55.43
图M
81.8 19.02 54.57 02
《结构力学》习题解答(内含解答图)

解:将固定铰支座换为单铰,如图(b),由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结BF为刚片Ⅱ,铰结△CDE为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆AB和支撑杆F相连,虚铰在无穷远处,刚片Ⅰ与刚片Ⅲ是由杆AC和支撑杆E相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是由杆BC和杆FD相连,虚铰在两杆的延长线的交点处。此时,三铰不共线,该体系为几何不变体,且无多余约束。
所以,体系是几何不变得,且无多余约束。
习题2-2试对图示体系进行几何组成分析。
解:从图2-15(b)可知,杆件CD和链杆3及铰D构成二元体,可以去掉;取杆件CB为刚片Ⅰ,基础作为刚片Ⅱ,根据规则一,两刚片是通过杆AB、链杆1、2组成几何不变体。所以,整个体系为几何不变体系,且无多余约束。
习题2-2图习题2-2解答图
习题2-10试对图示体系进行几何组成分析。
习题2-10图习题2-10解答图
解:由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结△ABF为刚片Ⅱ,铰结△BCD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆EA和支撑杆F相连,虚铰在两杆的延长线的交点处,刚片Ⅰ与刚片Ⅲ是由杆EC和支撑杆D相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是铰B相连。此时,三铰不共线,该体系为几何不变体,且无多余约束。
习题2-26图习题2-26解答图
解:将链杆截断,截断一处,去掉一个约束,共去掉四个约束;再将刚性联结杆截断,截断一处,去掉三个约束,共去掉十二个约束,如图(b)。此时,体系变成与基础独立相连的三个单一杆件,见图(b)。所以,该体系具有十六个多余约束的几何不变体。
2.3.2提高题
提高题2-1 试对图示体系作几何组成分析。
所以,由规则一知,体系是几何不变体,且无多余约束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 弹性力学基础(习题解答)1-1 上端悬挂、下端自由的等厚度薄板,其厚度为1,容重为ρ。
试求在自重作用下的位移分量表达式。
解:如图1-1建立坐标系.利用x σ沿y 方向均匀分布及x 方向的力平衡条件0=∑x 可得,⎪⎩⎪⎨⎧==-= x l xyy x 00)(τσρσ 又因为1()()x y u u l x x E Eρσσ∂=-=-∂ )()(1x l Eu u E y vx y --=-=∂∂ρσσ 积分得)()21(12y f x lx u +-=Eρ)()(2x f y x l uv +--=Eρ又由对称性 0)(020=⇒==x f v y 由 2110()2xy u v f y uy y x Eτρ∂∂=+=⇒=-∂∂ 综上所述有2221)21(uy Ex lx u ρρ--=Ey x l uv )(--=Eρ(方法二:只分析出x σ,再求应力函数,然后求其他。
)1-2 写出图1-2所示平面问题的应力边界条件。
解:上表面为力边界,100=,=,=,m l q lxl X --=Y 。
代入x xy xy y l m Xl m Yσττσ⎧+=⎪⎨+=⎪⎩ 中得到上表面的边界条件为00=--=xy y x q lxl τσσ;=; 下表面为自由边,边界条件为000==xy y x τσσ;=;侧面为位移边界。
1-3 矩形板厚为1。
试用应力函数22A xy ϕ=求解。
(并画出面力分布图)解:应力函数22A xy ϕ=满足应力函数表示的变形协调方程,可以作为解。
在无体力的情况下,矩形板的应力为22x Ax yϕσ∂==∂220y xϕσ∂==∂2xyAy x yϕτ∂=-=-∂∂根据应力边界条件公式x xy xy y l m X l m Yσττσ+=+=各边的应力边界为a d 边: 0,1l m == 20A X Ay h Y ⎧=-=-⎪⎨⎪=⎩ c b 边: 0,1l m ==- 20A X Ay h Y ⎧==-⎪⎨⎪=⎩a b 边: 1,0l m =-= 0X Y Ay ⎧=⎪⎨=⎪⎩c d 边: 1,0l m == X Ax AlY Ay⎧==⎪⎨=-⎪⎩根据以上各边的应力边界条件,可画出矩形板的面力分布图如图1-3a 。
1-4 如图1-4设三角形悬臂梁只受重力作用,梁容重为ρ。
试用完全三次多项式的应力函数求解其应力分量。
解:设完全三次多项式应力函数为3223Ax Bx y Cxy Dy ϕ=+++ (1)显然应力函数满足变形协调方程40ϕ∇=则应力分量:2226x Xx Cx Dy yϕσ∂=-=+∂ (2)2262y Yy Ax By y xϕσρ∂=-=+-∂ (3)222xyBx Cy x yϕτ∂=-=--∂∂ (4)利用边界条件来确定应力函数中的系数根据上表面的边界条件,当0y =时00()0,()0y y xy y στ====代入(3)、(4)得0A =; 0B =根据斜边的边界条件,当tan y x α=⋅时,面力0X Y ==,即x xy xy y l m X l m Y σττσ⎧+==⎪⎨+==⎪⎩ (5)其中:cos(,)cos(90)sin cos(,)cos l N x m N y ααα︒==+=-==代入(5)得sin (26tan )cos (2tan )0Cx Dx Cx αααα-++-= (6)cos (tan )sin (2tan )0x Cx αρααα---= (7)联立(6)、(7)得到tan 2C c ρα=⋅2tan 3D c ρα=⋅-将各系数代入应力分量表达式中,得到应力各分量为2tan 2tan tan x y xy x c y c y y c σραρασρτρα=⋅-⋅=-=-⋅1-5 对图1-5所示简支梁,试验证应力函数Fxy Ex Dxy y Cx xy B y Ax +++++=333533ϕ成立,并求解各系数和应力分量。
解:由Fxy Ex Dxy y Cx xy B y Ax +++++=333533ϕ可知:)1(0530244224444B A yy x x =+⇒=∂∂+∂∂∂+∂∂=∇ϕϕϕϕ应力分量:F Dy Cx By y Ax y xEx Cxy Axy x Dxy Bxy y Ax y xy y x (*)335966662062242223223322⎪⎪⎪⎩⎪⎪⎪⎨⎧-----=∂∂∂-=++=∂∂=++=∂∂=ϕτϕσϕσ 利用边界条件来确定待定系数上表面2h y =: )2(6343030 lq E hC A h q lx y -=++⇒-=σ F Dh Cx Bh x Ah xy -----==22422433165490τ ⎪⎩⎪⎨⎧=++=+⇒)4(043165)3(0349242F D h B hC A h下表面2hy -=:)5(0634303 E hC A h y =+--⇒=σ弯矩:)6(0220)(2222D B h A l ydy Mlx hh x lx =++⇒===-=⎰σ联立(1)~(6)可解得l h q h l q l q h l q lh q D lh q lhq lh q A 8041231045300030003030---=--==;=;;=;=;F E C B代入(*)式可得各应力分量()()222232332222223232;103243420x y xy q xy h x y l lh q xh y h lhq h h y x y l lh σστ︒︒︒⎛⎫=--+ ⎪⎝⎭=--⎛⎫=---+ ⎪⎝⎭34y ;1-6图1-6所示悬臂梁受自重作用,试用应力函数22335Ax y Bx y Cy Dy ϕ=+++求解。
并将所得应力分量与材料力学的结果进行比较。
解:应力函数必须满足变形协调条件,满足40ϕ∇=即444422420x x y yϕϕϕ∂∂∂++=∂∂∂∂ 将应力函数代入上式,得50B D += (1)应力分量22326620x Bx y Cy Dy yϕσ∂==++∂23222y Yy Ay By y xϕσρ∂=-=+-∂2226xyAx Bxy x yϕτ∂=-=--∂∂利用边界条件确定待定系数当2hy =±时,22()0()0y h y xy h y στ=±=±==得到23202A Bh += (2)2142A Bh ρ+= (3)联立方程(1)、(2)、(3)可解得4A ρ=2B h ρ=25D hρ=-在待定系数中,C 还没有求出。
现根据0x =截面上的条件来求C 值;因为0()0x x σ=≠,应用圣维南原理得202()0h h x x dy σ=-⎰=因为被积函数是y 的奇次函数,积分必恒等于零,此积分等式一定成立。
此外,尚需满足202()0h h x x ydy σ=-=⎰即322(620)0h h Cy Dy ydy -+=⎰得到352222240h h h h CyDy--+=2210h C D ρ=-=将各个系数代入应力分量表达式,得22226320153x y x y y h h ρσρ⎛⎫=+- ⎪⎝⎭ 22412y y y h ρσ⎛⎫=-- ⎪⎝⎭223412xy y x h τρ⎛⎫=- ⎪⎝⎭材料力学的解答:设载荷q h ρ=,故在某一截面上的弯矩为21()2M x hx ρ=剪力为Q hx ρ=由此得226x M x y y J hρσ==0y σ=(假设纤维间不存在挤压)22232124341212xy h hx y QS y x h Jb h ρτρ⎛⎫⋅- ⎪⎛⎫⎝⎭===- ⎪⎝⎭ 现将弹性力学的解答化为下列形式以便于材料力学解答进行比较:22320153x M y y y J h σρ⎛⎫=+- ⎪⎝⎭(与材料力学解不同) 22412y y y h ρσ⎛⎫=-- ⎪⎝⎭(与材料力学解不同)xy QSJbτ=(与材料力学解一致)1-7 用图1-7所示45︒应变花测得650010x ε-=⨯,680010y ε-=⨯,64530010ε︒-=⨯试求:(1)xy γ; (2)1ε和2ε,及主方向。
解:(1)根据材料力学公式cos 2sin 2222x yx yxyαεεεεγεαα+-=+-将45α︒=,x ε,y ε,45ε︒的值带入上式。
可得645270010xy x y γεεε-︒=+-=⨯(2)主应变的计算公式122x yεεεε+⎧⎫=±⎨⎬⎩⎭可得61103010ε-=⨯,6227010ε-=⨯利用公式tan 2xyx yγθεε=-- 则17arctan 23θ=得到156.6θ︒=-,233.4θ︒=1-8 如图1-8,已知平面圆环的应力为212,0,0rA r r πτσσθθ===试检查这组 应力存在的可能性。
并阐明其边界条件。
(体力不计)解:方法(一) 因为212,0,0r A r r πτσσθθ===,由022=∂∂=r ϕσθ积分得:设)()(21θθϕf r f +=由0)()()(112''2''11222=++=∂∂+∂∂=rf r f r f r r r r θθθθϕϕσ⎩⎨⎧==+⇒f f f 0)(0)()(''2''11θθθ 由2'2212)(1)1(r A f rr r r πθθϕτθ==∂∂∂∂-= 于是可得 c Af b a f +=+=θπθθθθ2)()cos sin ()(21; 即),,(2)cos sin (为任意常数;c b a c Ar b a +++=θπθθϕ 将ϕ代入变形协调方程检验可知ϕ满足变形协调条件。
因此为212,0,0rA r r πτσσθθ===可以存在。
边界条件为:212,0,0a A a r r r πτσσθθ====时,212,0,0bA b r r r πτσσθθ====时, 1-8 题方法(二)将212,0,0rA r r πτσσθθ===代入平衡方程 ⎪⎩⎪⎨⎧=++∂∂+∂∂=+-+∂∂+∂∂K r r r K r r r r r r r r r 02101θθθθθθττθσσσθτσ 中检验⎪⎩⎪⎨⎧=+-=++ r A r A 0110000033ππ 成立;由物理方程可得,将21)1()1(2,0)(1,0)(1rE u A E u u E u E r r r r r πτγσσεσσεθθθθθ-=+==-==-= 代入变形协调方程θθγθθεθεr r r r rr r r r r r )11()11()2(2222222∂∂∂+∂∂=∂∂-∂∂+∂∂+∂∂ 中检验,显然成立,因此这组应力可以存在。
