计量经济学(第三章多元线性回归)
计量经济学 第三章

3-2.答:变量非线性、系数线性;变量、系数均线性;变量、系数均 线性;变量线性、系数非线性;变量、系数均为非线性;变量、系数均 为非线性;变量、系数均为线性。 3-3.答:多元线性回归模型与一元线性回归模型的区别表现在如下几 方面:一是解释变量的个数不同;二是模型的经典假设不同,多元线性 回归模型比一元线性回归模型多了“解释变量之间不存在线性相关关
方和较大,但相对来说其AIC值最低,所以我们选择该模型为最优的模
型。
(4)随着收入的增加,我们预期住房需要会随之增加。所以可以预
期β3>0,事实上其估计值确是大于零的。同样地,随着人口的增加,
住房需求也会随之增加,所以我们预期β4>0,事实其估计值也是如
此。随着房屋价格的上升,我们预期对住房的需求人数减少,即我们预
其中:——某天慢跑者的人数 ——该天降雨的英寸数 ——该天日照的小时数 ——该天的最高温度(按华氏温度) ——第二天需交学期论文的班级数Байду номын сангаас
请回答下列问题:(1)这两个方程你认为哪个更合理些,为什么? (2)为什么用相同的数据去估计相同变量的系数得
到不同的符号? 3-18.对下列模型: (1)
(2) 求出β的最小二乘估计值;并将结果与下面的三变量回归方程的最小二 乘估计值作比较:
(1) 检验模型A中的每一个回归系数在10%水平下是否为零(括 号中的值为双边备择p-值)。根据检验结果,你认为应该把 变量保留在模型中还是去掉?
(2) 在模型A中,在10%水平下检验联合假设H0:i =0(i=1,5,6,7)。说明被择假设,计算检验统计值,说明其 在零假设条件下的分布,拒绝或接受零假设的标准。说明你 的结论。
(3) ,你认为哪一个估计值更好? 3-19.假定以校园内食堂每天卖出的盒饭数量作为被解释变量,盒饭 价格、气温、附近餐厅的盒饭价格、学校当日的学生数量(单位:千 人)作为解释变量,进行回归分析;假设不管是否有假期,食堂都营 业。不幸的是,食堂内的计算机被一次病毒侵犯,所有的存储丢失,无 法恢复,你不能说出独立变量分别代表着哪一项!下面是回归结果(括 号内为标准差):
计量经济学多元线性回归

调整过的R2(The Adjusted R-squared)
因此, R2增加并不意味着加入新的变量一定 会提高模型拟合度。
调整过的R2是R2一个修正版本,当加入新的 解释变量,调整过的R2不一定增加。
R 21(SS /n (R (k 1 ) )1n(k 1 )SSR
SS /n (T 1 )
定义:
y i y 2 to su to a s m flqS ua S总 rT es平
y ˆi y 2exp slu o as m ifq nu e Sd a Sr解 E es释 u ˆi2 ressiu d os m u fq au S l a SrR 残 es 差平
SST= SSE + SSR
3
重新定义变量
为什么我们想这样做? 数据测度单位变换经常被用于减少被估参数小数
点后的零的个数,这样结果更好看一些。 既然这样做主要为了好看,我们希望本质的东西
不改变。
4
重新定义变量:一个例子
以下模型反映了婴儿出生体重与孕妇吸烟量和家 庭收入之间的关系:
(1) b w g h t ˆ 0 ˆ 1 c ig s ˆ 2 fa m in c
explog考虑如果我们想知道时的百分比变化我们不能只报告因为所以22含二次式的模型u的模型我们不能单独将b解释为关于xy变化的度量我们需要将b如果感兴趣的是给定x的初始值和变动预测y的变化那么可以直接使用1
课堂提纲
重新定义变量的影响
估计系数 R 平方 t 统计量
函数形式
对数函数形式 含二次式的模型 含交叉项的模型
24
wage
7.37
3.73
24.4
exper
25
对含二次式模型的进一步讨论
第三章多元线性回归模型(计量经济学,南京审计学院)

Yˆ 116.7 0.112X 0.739P
R2 0.99
(9.6) (0.003) (0.114)
Y和X的计量单位为10亿美元 (按1972不变价格计算).
P
食品价格平减指数 总消费支出价格平减指数
100,(1972
100)
3
多元线性回归模型中斜率系数的含义
上例中斜率系数的含义说明如下: 价格不变的情况下,个人可支配收入每上升10
c (X X )1 X D
从而将 的任意线性无偏估计量 * 与OLS估计量 ˆ 联系
起来。
28
cX I
由
可推出:
(X X )1 X X DX I
即 I DX I
因而有 D X 0
cc (X X )1 X D (X X )1 X D ( X X )1 X D X ( X X )1 D
第三章 多元线性回归模型
简单线性回归模型的推广
1
第一节 多元线性回归模型的概念
在许多实际问题中,我们所研究的因变量的变动 可能不仅与一个解释变量有关。因此,有必要考虑线 性模型的更一般形式,即多元线性回归模型:
Yt β0 β1X1t β2 X 2t ... βk X kt ut t=1,2,…,n
Yt
ˆ0
βˆ 1
X
1t
... βˆ K X Kt
2
为最小,则应有:
S
S
S
ˆ0 0, ˆ1 0, ..., ˆ K 0
我们得到如下K+1个方程(即正规方程):
13
β0 n
β1 X1t ...... β K X Kt Yt
β 0 X 1t β1 X 1t 2 ...... β K X 1t X Kt X 1tYt
《计量经济学》第3章数据

《计量经济学》各章数据第3章 多元线性回归模型例3.1.1 经过研究,发现家庭书刊消费水平受家庭收入及户主受教育年数的影响。
现对某地区的家庭进行抽样调查,得到样本数据如表3.1.1所示,其中y 表示家庭书刊消费水平(元/年),x 表示家庭收入(元/月),T 表示户主受教育年数。
下面我们估计家庭书刊消费水平同家庭收入、户主受教育年数之间的线性关系。
回归模型设定如下: t t t t u T b x b b y +++=210(t =1,2, …)表3.1.1 某地区家庭书刊消费水平及影响因素的调查数据表例3.4.1根据表3.4.1给出的中国1980-2003年间总产出(用国内生产总值GDP度量,单位:亿元),劳动投入L(用从业人员度量,单位为万人),以及资本投入K(用全社会固定投资度量,单位:亿元),试建立我国的柯布——道格拉斯生产函数。
表3.4.1 1980-2003年中国GDP、劳动投入与资本投入数据例3.4.2 某硫酸厂生产的硫酸透明度一直达不到优质要求,经分析透明度低与硫酸中金属杂质的含量太高有关。
影响透明度的主要金属杂质是铁、钙、铅、镁等。
通过正交试验的方法发现铁是影响硫酸透明度的最主要原因。
测量了47组样本值,数据见表3.4.3。
试建立硫酸透明度(y)与铁杂质含量(x)的回归模型。
表3.4.3 硫酸透明度(y)与铁杂质含量(x)数据例3.4.3假设某企业在15年中每年的产量Y(件)和总成本X(元)的统计资料表3.4.7所示,试估计该企业的总成本函数模型。
表3.4.7 某企业15年中每年总产量与总成本统计资料3.6.1 案例1——中国经济增长影响因素分析根据表3.6.1给出的1980-2003年间总产出(用国内生产总值GDP度量,单位:亿元),最终消费CS(单位:亿元),投资总额I(用固定资产投资总额度量,单位:亿元),出口总额(单位:亿元)统计数据,试对中国经济增长影响因素进行回归分析。
庞皓《计量经济学》(第4版)章节题库-第3章 多元线性回归模型【圣才出品】

2
2
而 1-α 的置信度下 Y0 的置信区间为:
Yˆ0 t ˆ
1
X0
X
X
1
X
0
Y0
Yˆ0
t
ˆ
1
X0
X
X
1
X
0
2
2
6.多元回归模型中的解释变量个数为 k,那么回归方程显著性检验的 F 统计量的第一 自由度为 n-k-1,第二自由度为 k。( )
【答案】× 【解析】多元回归模型中的解释变量个数为 k,那么回归方程显著性检验的 F 统计量 的第一自由度为 k,第二自由度为 n-k-1。
2 / 22
圣才电子书
十万种考研考证电子书、题库视频学习平
台
【解析】在变量显著性检验中,针对某变量 Xj(j=1,2,…,k)设计的原假设与备
择假设为 H0:βj=0,H1:βj≠0。给定显著性水平 α 之后,可根据|t|>tα/2(n-k-1)
(或|t|≤tα/2(n-k-1))来决定拒绝(或接受)原假设 H0,从而判定对应的解释变量是
三、简答题 1.多元线性回归模型的基本假设是什么?试说明在证明最小二乘估计量的无偏性和 有效性的过程中,哪些基本假设起了作用? 答:(1)针对普通最小二乘法,多元线性回归模型的基本假设主要有以下三大类: ①关于模型设定的基本假设: 假定回归模型的设定是正确的,即模型的变量和函数形式均为正确的。 ②关于随机扰动项的基本假设: 假定随机扰动项满足条件零均值、条件同方差、条件序列不相关性以及服从正态分布。
2.调整的多重可决系数 Error!2 与多重可决系数 R2 的关系为( )。 A.Error!2=R2(n-1)/(n-k-1) B.Error!2=1-R2(n-1)/(n-k-1) C.Error!2=1-(1+R2)(n-1)/(n-k-1) D.Error!2=1-(1-R2)(n-1)/(n-k-1) 【答案】D 【解析】在样本容量一定的情况下,增加解释变量必定使得自由度减少,为了剔除变 量个数对拟合优度的影响,调整的多重可决系数是将残差平方和与总离差平方和处以各自
第三章 多元线性回归模型

i = 1,2, L , n
回归剩余(残差): 回归剩余(残差):
ˆ ei = Yi - Yi
21
二、多元线性回归模型的矩阵表示
k 1个解释变量的多元线性回归模型的 n (通常大
于k)个观测 样本, 样本,可表示为
Y1 = β1 + β2 X21 + β3 X31 + ... + βk Xk1 + u1
如收入、价格、费用、道路状况、能源、政策环境等) (如收入、价格、费用、道路状况、能源、政策环境等)
各种因素对汽车销量影响的性质怎样?(正、负) 各种因素对汽车销量影响的性质怎样? 各种因素影响汽车销量的具体数量关系是什么? 各种因素影响汽车销量的具体数量关系是什么? 所得到的数量结论是否可靠? 所得到的数量结论是否可靠? 中国汽车行业今后的发展前景怎样? 中国汽车行业今后的发展前景怎样?应当如何制定汽车的 产业政策? 产业政策? 很明显,只用一个解释变量已很难分析汽车产业的发展, 很明显,只用一个解释变量已很难分析汽车产业的发展 还需要寻求有更多个解释变量情况的回归分析方法。 还需要寻求有更多个解释变量情况的回归分析方法。下面 多元线性回归模型。 介绍——多元线性回归模型。 介绍
11
怎样分析多种因素的影响? 怎样分析多种因素的影响?
分析中国汽车行业未来的趋势,应具体分析这样一些问题: 分析中国汽车行业未来的趋势 应具体分析这样一些问题: 应具体分析这样一些问题 中国汽车市场发展的状况如何? 用销售量观测) 中国汽车市场发展的状况如何?(用销售量观测) 影响中国汽车销量的主要因素是什么? 影响中国汽车销量的主要因素是什么?
假定4:随机扰动项与解释变量不相关 假定4
12
计量经济学
第三章 多元线性回归模型 思考题

第三章 多元线性回归模型 思考题3.1 若要将一个被解释变量对两个解释变量做线性回归分析; 1) 写出总体回归函数和样本回归函数; 2)写出回归模型的矩阵表示; 3) 说明对此模型的古典假定;4)写出回归系数及随机扰动项方差的最小二乘估计式 , 并说明参数估计式的性质。
3.2 什么是偏回归系数 ? 它与简单线性回归的回归系数有什么不同 ? 3.3 多元线性回归中的古典假定与简单线性回归时有什么不同 ?3.4 多元线性回归分析中 , 为什么要对可决系数加以修正 ? 修正可决系数与 F 检验之间有何区别与联系 ?3.5 什么是方差分析 ? 对被解释变量的方差分析与对模型拟合优度的度量有什么联系和 区别 ?3.6 多元线性回归分析中 ,F 检验与 t 检验的关系是什么 ? 为什么在做了 F 检验以后还要做 t 检验?3.7 试证明 : 在二元线性回归模型i Y =1β+2β2i X +33i X β+i u 中 , 当 2X 和3X 相互独立时,对斜率系数2β和3β的OLS 估计值 , 等于i Y 分别对2X 和3X 做简单线性回归时斜率系数的OLS 估计值。
3.8 对于本章开始提出的“中国汽车终极保有量会达到2.4亿-2.5 亿辆吗?”你认为可建立什么样的计量经济模型去分析?3.9 说明用Eviews 完成多元线性回归分析的具体操作步骤。
练习题3.1 为研究中国各地区入境旅游状况,建立了各省市旅游外汇收入(Y,百万美元)、旅行社职工人数 (1X ,人)、国际旅游人数(Xz,万人次)的模型 , 用某年31 个省市的截面数据估计结果如下ˆiY =-151.0263+0.11791i X +1.54522i X t=(-3.)(6.)(3.)2R =0. 2R =0.92964 F=191.1894 n=311) 从经济意义上考察估计模型的合理性。
2) 在 5% 显著性水平上 , 分别检验参数1β,2β的显著性。
庞皓计量经济学第三章多元线性回归模型学习辅导
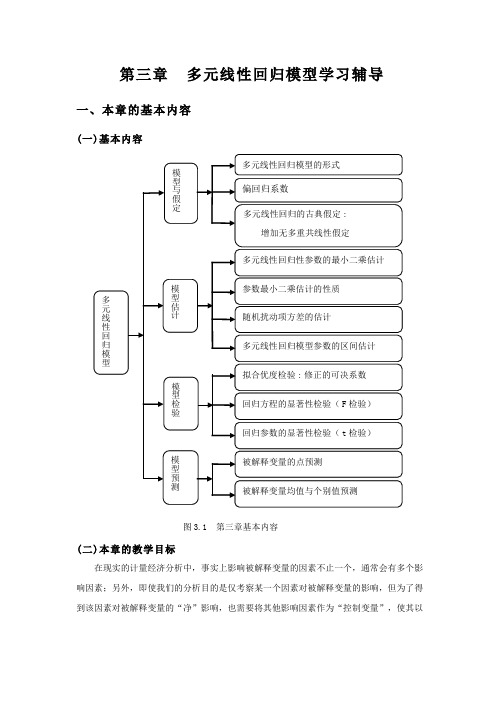
第三章 多元线性回归模型学习辅导一、本章的基本内容(一)基本内容图3.1 第三章基本内容(二)本章的教学目标在现实的计量经济分析中,事实上影响被解释变量的因素不止一个,通常会有多个影响因素;另外,即使我们的分析目的是仅考察某一个因素对被解释变量的影响,但为了得到该因素对被解释变量的“净”影响,也需要将其他影响因素作为“控制变量”,使其以显性形式出现在模型中,以提高模型估计精度。
因此,在对现实经济问题进行计量经济分析时,通常需要建立包含两个及两个以上解释变量的计量模型,此类模型称为多元回归模型。
多元回归模型是在简单回归模型理论基础上的扩展,其建模的理论基础、基本思路、模型估计等与一元回归模型基本一致,只是因解释变量增多,从而带来一些新的内容,比如模型整体显著性检验(F 检验)、修正的可决系数(2R )以及解释变量之间多重共线性等问题。
本章的教学目标是:深刻理解建立多元回归模型的目的;掌握多元线性回归模型估计、检验的理论与方法;熟练掌握多元线性回归EViews 输出结果的解释。
二、重点与难点分析1.对多元线性回归模型参数意义的理解多元线性回归模型的参数与简单线性回归模型的参数有重要区别。
在多元线性回归模型中,解释变量对应的参数是偏回归系数,表达的是控制其他解释变量不变的条件下,该解释变量的单位变动对被解释变量平均值的“净”影响。
为了更深刻理解偏回归系数,可以两个解释变量的多元线性回归模型为例加以说明1。
例如,被解释变量Y 与解释变量2X 和3X 都有关,如果分别建立模型:多元线性回归: 12233i i i i Y X X u b b b =+++简单线性回归 : 1221i i i Y a a X u =++由于Y 与3X 有关,可以作回归:1332i i i Y b b X u =++,若用OLS 估计其参数,并计算残差213333ˆˆˆi i i i i e Y b b X y b x =--=-,这里的2i e 表示除去3i X 影响后的i Y 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
取值范围:0-1
3.1.3 修正可决系数 R2
为什么要修正?
可决系数随解释变量个数的增加而增大。易 造成错觉:要模型拟合得越好,就应增加解 释变量。然而增加解释变量会降低自由度, 减少可用的样本数。并且有时增加解释变量 是不必要的。
导致解释变量个数不同模型之间对比困难。
可决系数只涉及变差,没有考虑自由度。
多元样本回归函数:
Y i 0 1 X1i 2 X 2i...... k X ki
回归剩余(残差):ei Yi Y i
多元线性回归模型的矩阵表示
Y1
Y
Y2
,
Yn
1
X
1
X12 X13
X 22 X 23
1 X n2 X n3
X1k X 2k
X nk
1
2
,
1.1.1 多元线性回归模型形式
一般形式(随机扰动形式,注意X的下 标):
Yi 0 1 X1i 2 X 2i ......k X ki ui 模型中,(j j 1, 2,..., k)是偏回归系数:
控制其他解释变量不变的条件下, 第j个解释变量的单位变动对应变量平均 值的影响。
其中:k为解释变量的数目,j称为回归参
源于回归 源于残差 总变差
2
ESS (Y i Y )
2
RSS (Yi Y i )
2
TSS (Yi Y )
K n-k-1 n-1
ESS / k RSS /(n k 1)
TSS /(n 1)
3.3.2 F-检验(单侧检验)
(1) H0 : 1 3 ... k 0 H1 : 1, 2,..., k不全为0
如何才能缩小置信区间?
• 增大样本容量n,因为在同样的样本容量下, n越大,t分布表中的临界值越小,同时,增大 样本容量,还可使样本参数估计量的标准差减 小;
• 提高模型的拟合优度,因为样本参数估计量 的标准差与残差平方和呈正比,模型优度越高, 残差平方和应越小。
提高样本观测值的分散度,也就是说变量必 须变化大。
(2)选择、(根据样本)计算统计量
F ESS / k ~ F(k, n k 1) RSS /(n k 1)
(3)给出显著性水平,查表,得F (k, n k 1);
(4)判断:若F F (k, n k 1),拒绝原假设, 接受备择假设,。反之则反。
3.4 各种检验之间的关系
3.4.1 经济意义检验和其他检验的关系 联 系: 判断一个回归模型是否正确,首先要看 模型是否具有合理的经济意义,其次才是 统计检验。
对多元线性回归方程的最小二乘估计和 分析是一元情形的推广。所使用的前提 假定、估计方法、估计结果的性质等等 都同于一元的情形。
OLS:原则、求解、结果
OLS原则: min
ei2
(Yi ( 0 1 X1i ... k X ki ))2
求解:
由
ei2
0,
j 0,1, 2,..., k,可得X 'e 0;
是Y的线性函数 j 正态)
2.4 随机扰动项方差的估计
2
扰动项的方差 2估计:
ei2
n k 1
其中n为样本容量,k为待估参数个数。
2
(比较:一元情形:
ei2 ,待估参数有2个)
n2
第三节 多元线性回归模型的 检验
本节主要介绍:
3.1 拟合优度检验(多重可决系数及其修正) 3.2 回归参数的显著性检验(t-检验) 3.3 回归方程的显著性检验(F-检验) 3.4 拟合优度、t-检验、F-检验的关系
(所以在一元情形,只需要进行一种检验) 多元中,不存在以上关系。
第四节 多元线性回归模型的 预测
4.1 应变量平均值的点预测、区间预测; 4.2 应变量个别值的点预测、区间预测;
4.1 应变量平均值的点预测、区间预测
4.1.1 Y平均值的点预测 将解释变量预测值代入估计的方程便可:
Y F 1 2 X F 2 3 X F3 ... k X Fk
假定5 正态性。假定 ui ~ N (0, 2 ) i 1,2,...,k
第二节 多元线性回归模型的 估计
本节主要介绍 2.1 参数的最小二乘估计(OLS); 2.2 OLS回归线的性质 2.3 参数的最小二乘估计量的性质; 2.4 随机扰动项的方差估计。
2.1 参数的最小二乘估计(OLS)
以下给出t-检验的具体过程
(1) 提出假设:H0: j 0 H1: j 0 j 1, 2,..., k
(2)
根据样本计算t
j jj0Fra bibliotekjc jj c jj c jj
(3) 给出显著水平,查表,得临界值t /2 (n k 1)
(4) 判断:若|t| t /2 (n k 1), 拒绝原假设,接受 备择假设。反之则反。
Var(U ) 2In
模型的古典假定(二)
假定3 随机扰动项与解释变量不相关。
即 Cov( X ji , ui ) 0 j 2,3,...... , k
假定4 无多重共线性。
此即假定解释变量向量之间线性无关,
这样,解释变量矩阵X列满秩:R(X)=k。
此时,有
R( X ' X ) k, X ' X可逆。
自由度:n-1
n-k-1 k
对以上自由度的分解的说明
3.1.2 可决系数 R2
可决系数的定义:
TSS RSS ESS 1 RSS ESS TSS TSS
R2
ESS TSS
1
RSS TSS
意义:可决系数越大,自变量对因变量的解释
程度越高,自变量引起的变动占总变动的百分
比高。观察点在回归直线附近越密集。
3.4.2 拟合优度和F检验的关系
(1)都是对回归方程的显著性检验; (2)都是把总变差分解,以构成统计量进
行检验;
(3)两者同增同减,具有一致性。
在数量上,它们有如下关系
2
F
n
k k
1
R
2
1 R
,
2
R 1
n 1
n k 1 kF
拟合优度和F检验的关系(续)
区别: (1)F检验中使用的统计量有精确的分布,
或者
Y
F
=X
' F
4.2.2应变量个别值的区间预测
选取残差变量eF=YF Y F
易证得:eF~N
(0,
2 [1
X
F
(
X
'
X
)1
X
' F
])
2
用 代替 2,构造统计量:
t
eF
0
YF Y F
~ t(n k 1)
se(eF )
[1
X
F
(X
'
X
)1
X
' F
]
给定显著水平,查表....(.. 步骤方法完全同上)
计式 具有最小方差。
结论:在古典假定下,OLS估计式 是最佳线性
无偏估计(BLUE)
OLS估计量的性质(续)
(4)在古典假定下, j ~ N ( j ,Var( j )), j 1,2,...,k
其中,Var( j ) 2c jj , c jj是(X'X)1中对角线上第j
个元素。
(ui正态,Y是ui的线性函数 Y正态,又 j
5. 案例分析
实验
第五节 受约束回归
在建立回归模型时,有时根据经济理论需对 模型中变量的参数施加一定的约束条件。
模型施加约束条件后进行回归,称为受约束 回归(restricted regression);
不加任何约束的回归称为无约束回归 (unrestricted regression)。
3.3 回归方程的显著性检验 ——(F检验)
回归系数的t检验,检验了各个解释变 量Xj单独对应变量Y是否显著;我们还需 要检验:所有解释变量联合在一起,是 否对应变量Y也显著?
这即是下面所要进行的F检验。
3.3.1 方差分析表
以下用表格的形式列出变差、自由度、方差
变差来源 平方和 自由度
方差
Y平均值的区间预测 ——具体作法
可证明: Y F ~ N (E(YF ),
2[ 1 n
(XF
X xi2
)2
])
用
2
代替
2,得 se(Y
F )。构造统计量:t
Y
F
E(YF )
~
t(n
k
1)
se(Y F )
给出临界值,查表得t /2 (n k 1),则:
P[Y F t /2 (n k 1) se(Y F ) E(YF ) Y F t /2 (n k 1)) se(Y F )] 1
第三章 多元线性回归模型
本章主要内容
第一节 多元线性回归模型及古典假定 第二节 多元线性回归模型的估计 第三节 多元线性回归模型的检验 第四节 多元线性回归模型的预测 第五节 实例
第一节 多元线性回归模型及 古典假定
主要介绍 1.1 多元线性回归模型及其矩阵表示 1.2 模型的古典假定
或者
Y
F
=X
' F
4.1.2 Y平均值的区间预测
基本思想
(1)由于存在抽样波动,预测的平均值 Y F 也是个变量, 不一定等于真实平均值E(YF / X F );还需要对真实平均 值作区间估计;
(2)为此,需要确定预测的平均值 Y F 的抽样分布,
以及找出与 Y F 和E(YF / X F )均有关的统计量。
从而得到E(YF )得区间估计:
[Y F t /2 (n k 1) se(Y F ), Y F t /2 (n k 1)) se(Y F )]
