人教版初中数学三年级下册《相似三角形的性质》图文课件

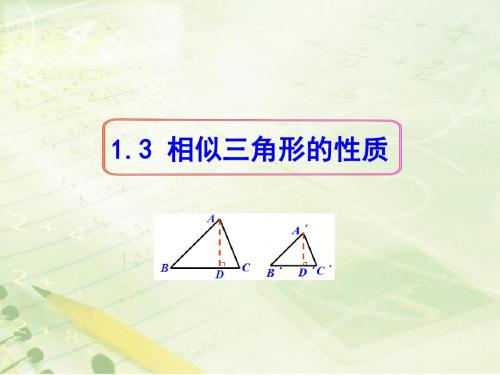
A
边成比例的两个三角形叫作相似三角形。
C B D
相似比：相似三角形对应边的比k叫做相似比 (求相似三角形的相似比要注意顺序性)
F
如右图所示:△ABC相似于△DEF就可表示为： E “△ABC∽△DEF”读作“△ABC相似于△DEF” 对应顶点一定要写在对应位置，这样可以准 确地找出相似三角形的对应角和对应边。
探 索2:
A
三组对应边成比例
A’
B C
B’
C’
A' B' B' C' A' C' ＝ ＝ AB BC AC
是否有△ABC∽△A’B’C’？
动手：
1、请同学们在所发的方格纸上任意画一个△ABC, 使点A、B、C三点均在格点上。
2、作△A‘B’C‘，使A‘、B’、C‘各点也在格 点上。且A'B'=kAB,B'C'=kBC,A'C'=kAC.(k取一个大于0 且便于画图的数）
(三边对应成比例的两个三角形相似)
练习1: 已知△ABC和 △DEF,根据下列 条件判断它们是否相似. 否 (1) AB=3，
BC=4， AC＝6 DE＝6， EF＝8， DF＝9
是 (2) AB=4，
BC=8， AC＝10 DE＝20， EF＝16， DF＝8
否 (3) AB=12，
BC=15， AC＝24 DE＝16， EF＝20， DF＝30
相似三角形的性质
蓦然回首
1、什么叫做全等三角形？ 能够完全重合的两个三角形叫做全等三 角形。（如右图△ABC≌△DEF）
B
A D C E F

2、全等三角形的对应边、对应角之 间各有什么关系？
对应边相等、对应角相等。
3.怎样判定两个三角形全等？
SAS，ASA，AAS，SSS，（HL）.
探究新知
定义：三个角对应角相等、三条边对应
1、如果两个三角形全等，则它们必相似。 √ 2、三角形的三条中位线围成的三角形与原 三角形相似，且相似比为1/2。 √ 3、如果两个三角形均与第三个三角形相 √ 似，则这两个三角形必相似。 4、相似的两个三角形必定大小不等。 × 5、两个等边三角形必定相似。
√
试一试身手
填一填 ： 1、若△ABC与△A′B′C′相似，一组对应边的长为 AB=3 cm，A′B′=4 cm，那么△A′B′C′与△ABC的 4︰ 3 相似比是____; 2、若△ABC 的三条边长为3cm、5cm、6cm,与其相似 的另一个△A′B′C′的最小边长为12 cm， 那么 24cm △A′B′C′的最大边长是_____; 3、若△ABC的三条边长3cm,4cm,5cm,且 直角三角形 △ABC∽△A1B1C1，那么△A1B1C1的形状是 ____ __.
感悟与反思
通过前面的动手、探索与展示，我们又得到 识别两个三角形相似的一个方法：
判定定理1 三边对应成比例的两 个三角形相似
如图: 如果
图 18.3.3
AB = A'B'
BC AC = A'C' B'C'
那么
△ABC∽△A'B'C'
例题赏析
例1、在△ABC和△A′B′C′中，已知：AB＝6cm，BC＝8cm， AC＝10cm，A′B′＝18cm，B′C′＝24 cm，A′C′＝ 30cm．试判定△ABC与△A′B′C′是否相似，并说明理 由。
1.相似三角形的定义、性质
及相似比；
注意顺序 喔！
2.相似三角形的判定定理1.
要做两个形状相同的三角形框架，其中一个三角形框架 的三边的长分别为4、5、6，另一个三角形框架的一边长 为2，请你想一想应该怎样选择材料可使这两个三角形相 似？你有几种选材方案？
解：设另一个三角形的另两边的长分别为x、y。因为这两个三
1、如图所示如果△ADE∽△ABC，那么哪些角是对应角？哪 些边是对应边？对应角有什么关系？对应边呢？
C E
A
D
B
对应角相等即∠A=∠A， ∠ADE=∠B ，∠AED=∠C AD AE DE 对应边成比例 = =
AB AC BC
两个全等三角形一定相似吗？为什么？它 与相似三角形有什么关系？
两个全等三角形的对应边相等，对应角相等，由 对应边相等可知对应边一定成比例，且相似比为 1， 因此满足相似三角形的两个条件，所以两个全等 三角形一定相似。全等三角形是相似三角形的特 殊形式！
相等 3、∠A=∠A'吗？ ∠B=∠B'吗？ ∠C=∠C'吗？
4、两个三角形三边对应比例，它们的对应角相等吗？
两个三角形三边对应成比例，它们的对应角相等。 5、△ABC与△A’B’C’相似吗？为什么？
相似。由定义可知三边对应成比例，且对应角相等的两 个三角形是相似三角形。
6、三边对应成比例的两个三角形相似吗？
3、分别量出∠A、∠B、 ∠C与∠A'、∠B'、∠C'的 度数。
探究：
A' B ' B' C' A' C ' 1、 AB , BC , AC
A ' B ' B 'C ' A 'C ' = = AB BC AC
A ' B ' B 'C ' A'C ' 相等吗？AB = BC = AC = k 相等
2、A‘B’、B‘C'、A'C'与AB、BC、AC对应成比例吗？
解： AB <BC<AC, A'B'<B'C'<A'C',
AB 6 1 BC 8 1 AC 10 1 = = , = = , = = , A ' B ' 18 3 B ' C ' 24 3 A ' C ' 30 3 AB BC AC \ = = , A' B ' B 'C ' A'C ' \ D ABC D A'B'C'
角形相似，所以
2 x y 1， = = ， 4 5 6
2 x y 3, = = ， 6 5 4 10 4 解得：x=2.5 y=3. 解得：x=1.8 y=2.4. 解得：x= y= . 3 3 4 答：有三种方案即另两边长分别为2.5、或 3 1.8、 2.4或10 、 3 3。
2 x y 2, = = ， 5 4 6
（温馨提示：大对大，小对小，中对中）
练习2：如图在正方形网格上 有△A1 B1C1和△ A2 B2 C 2， 它们相似吗？如果相似 ，求出相似比；如果 不相似，请说明理由。
解：设正方形边长为1，由图及勾股定理可得：
A1 B1 = 2 2, A1C1 = 4, B1C1 = 2 10 A2 B2 = 2, A2C2 = 2, B2C2 = 10 A1 B1 A1C1 B1C1 = 2, = 2, = 2, A2 B2 A2C2 B2C2 A1B1 A1C1 B1C1 \ = = A2 B2 A2C2 B2C2 \ D A1B1C1 D A 2 B2C2 (三边对应成比例的两个三角形相似）