第21章 Logistic 回归分析
logistic regression法

logistic regression法
(原创实用版)
目录
1.线性回归概述
2.Logistic 回归法的原理
3.Logistic 回归法的应用
4.Logistic 回归法的优缺点
正文
线性回归是一种常见的统计分析方法,主要用于研究因变量和自变量之间的关系。
在线性回归中,因变量通常是连续的,而自变量可以是连续的或离散的。
然而,当因变量为二分类或多分类时,线性回归就不再适用。
这时,Logistic 回归法就被引入了。
Logistic 回归法是一种用于解决分类问题的统计方法,其原理是基于逻辑斯蒂函数。
逻辑斯蒂函数是一种 S 型函数,其取值范围在 0 到 1 之间,可以用来表示一个事件发生的概率。
在 Logistic 回归法中,我们通过将自变量输入逻辑斯蒂函数,得到一个概率值,然后根据这个概率值来判断因变量所属的类别。
Logistic 回归法广泛应用于二分类和多分类问题中,例如信用风险评估、疾病预测、市场营销等。
在我国,Logistic 回归法也被广泛应用于各种领域,如金融、医疗、教育等。
Logistic 回归法虽然具有很多优点,但也存在一些缺点。
首先,Logistic 回归法对于自变量过多或者数据量过小的情况不太适用,因为这样容易导致过拟合。
其次,Logistic 回归法的计算过程比较复杂,需要用到特种数学知识,对计算资源的要求也比较高。
总的来说,Logistic 回归法是一种重要的分类方法,具有广泛的应
用前景。
logistic回归

概念
logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同 之处。它们的模型形式基本上相同,都具有 w‘x+b,其中w和b是待求参数,其区别在于他们的因变量不同,多 重线性回归直接将w‘x+b作为因变量,即y =w‘x+b,而logistic回归则通过函数L将w‘x+b对应一个隐状态p, p =L(w‘x+b),然后根据p与1-p的大小决定因变量的值。如果L是logistic函数,就是logistic回归,如果L是 多项式函数就是多项式回归。
感谢观看
logistic回归
一种广义的线性回归分析模型
01 概念
目录
02 主要用途
logistic回归又称logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘,疾病自动诊断, 经济预测等领域。例如,探讨引发疾病的危险因素,并根据危险因素预测疾病发生的概率等。以胃癌病情分析为 例,选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群必定具有不同的体征与生活方式等。因此因变量 就为是否胃癌,值为“是”或“否”,自变量就可以包括很多了,如年龄、性别、饮食习惯、幽门螺杆菌感染等。 自变量既可以是连续的,也可以是分类的。然后通过logistic回归分析,可以得到自变量的权重,从而可以大致 了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。
实际上跟预测有些类似,也是根据logistic模型,判断某人属于某病或属于某种情况的概率有多大,也就是 看一下这个人有多大的可能性是属于某病。
这是logistic回归最常用的三个用途,实际中的logistic回归用途是极为广泛的,logistic回归几乎已经 成了流行病学和医学中最常用的分析方法,因为它与多重线性回归相比有很多的优势,以后会对该方法进行详细 的阐述。实际上有很多其他分类方法,只不过Logistic回归是最成功也是应用最广的。
logistic回归模型分析和总结

含有名义数据的logit
含有名义数据的logit
• 例:某地25岁及以上人中各类婚姻状况居民的死
亡情况见表,试建立死亡率关于年龄和婚姻状况
的logit模型。
ln p 1 p
A 1M1
2M 2
3M3
• 其中,A表示年龄(取中值),M1、M2、M3表示婚 姻状况
• 于是,估计的logit方程为:
多项logit模型
【例】研究三个学校、两个课程计划对学生偏好何 种学习方式的影响。调查数据见表:
• 其中,三个学校对应两个哑变量x1和x2,两个课 程计划为常规(x3=1)和附加(x3=0),学习方式分 为:自修(y=1)、小组(y=2)、上课(y=3)
• 从题目可以看出,响应变量是学习方式有三类, 属于多项逻辑斯蒂回归问题。于是,建模为:
ln ln
p1 p3 p2 p3
10 11x1 12 x2 13 x3 20 21x1 22 x2 23x3
多项logit模型
多项logit模型
• 应用统计软件可以得到模型的参数估计和回归方程:
ln
p1 p3
0.5931.134 x1 0.618 x3
ln
p2 p3
0.603 0.635 x3
ln p A E
1 p
• 其中A为年龄,E为文化程度
含有有序数据的logit
含有有序数据的logit
• 于是,估计的logit方程为:
ln p 11.637 0.124A 0.164E 1 p
• 其中,年龄的系数0.124,说明年龄越大死亡率会 越高;
• 文化程度的系数-0.164,说明文化程度与死亡率 呈负相关,文化程度越高,死亡率越低。
logistic回归分析

第二节 条件Logistic回归
概念: 用配对设计获得病例对照研究资料,计算的Logistic
回归模型为条件Logistic回归。
成组(未配对)设计的病例对照研究资料,计算的
Logistic回归模型为非条件Logistic回归。
例:见265页 区别:
条件Logistic回归的参数估计无常数项(β0),主要用 于危险因素的分析。
Parame Estimate Error Chi-Square Pr
常数 -1.9037 0.5982 10.127 0.0015 性别 1.4685 0.575 6.508 0.0107
药物 1.7816 0.518 11.794 0.0006
Odds Ratio Estimates Point 95% Wald
第1页,共86页。
问题提出:
医学研究中常研究某因素存在条件下某结果是否发 生?以及之间的关系如何?
因素(X)
疾病结果(Y)
x1,x2,x3…XK
发生
Y=1
不发生 Y=0
例:暴露因素 高血压史(x1):有 或无 高血脂史(x2): 有 或 无 吸烟(x3): 有或无
冠心病结果 有 或无
第2页,共86页。
研究问题可否用多元线性回归方法?
yˆ a b1x1 b2x2 bmxm
1.多元线性回归方法要求 Y 的取值为计量 的连续性随机变量。
2.多元线性回归方程要求Y与X间关系为线 性关系。
3.多元线性回归结果 不能回答“发生 与否”
logistic回归方法补充多元线性回归的不足
第3页,共86页。
Logistic回归方法
几个logistic回归模型方程
Logistic回归分析

[例]饮酒与食道癌发病关系的分析
1977年Tuyns等在法国llle-et-Vilaine(Brittany) 地区的一所医院收集了200例食道癌患者与775 例对照进行病例—对照研究,探讨饮食与发病 的关系,考虑到年龄这一混杂因素的干扰,按 每10岁一组共分为6组。危险因素饮酒分为两 个水平:每天饮酒量少于80克者为非接触 (x=0),≥80克为接触(x=1),年龄组范围 为:1组:25~,2组:35~,3组:45~,4组: 55~,5组:65~,6组:75~ (数据集为logit)
计算中心
Logistic回归分析
Logistic回归模型: Logit(p)=ln(p/(1-p))=β0+β1x1+β2x2+βnxn Y=Logit(p) 的图形如下 (随p由0变到1,Y的值由-∞单调上升到∞)
计算中心
Logistic回归分析
上模型称为Logistic回归模型.其中最简单的情况
作业 关于食管癌与使用咸菜关系的病例-对照研究
不考虑年龄的因素,仅对“吃咸菜”一个变量作 Logistic回归
病例 吃咸菜 110 对照 吃咸菜 不吃咸菜 8 98 24 186 32 148 28 139 18 88 0 31 110 690
zi = zi =
1 , 当x取第i种状态, 0 , 其它. (i =1,…,k-1).
计算中心
例
下表记录了某公司在过去6个月中的顾客信息.其 中包括顾客的性别(gender:0=男和1=女),顾 客的年龄(AGE),顾客的年收入(income:1= 低,2=中和3=高)和购买价值(PURCHASE: 0=小于100元,1=大于等于100元),共记录了 431位顾客的资料,数据集为sales1。
图文举例详细讲解Logistic曲线的回归分析
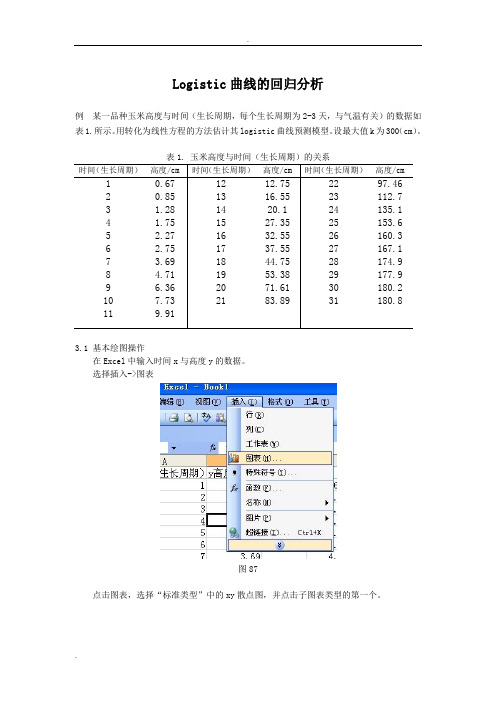
Logistic 曲线的回归分析例 某一品种玉米高度与时间(生长周期,每个生长周期为2-3天,与气温有关)的数据如表1.所示。
用转化为线性方程的方法估计其logistic 曲线预测模型。
设最大值k 为300(cm )。
表1. 玉米高度与时间(生长周期)的关系时间(生长周期) 高度/cm 时间(生长周期) 高度/cm 时间(生长周期) 高度/cm12 3 4 5 6 7 8 9 10 11 0.67 0.85 1.28 1.75 2.27 2.75 3.69 4.71 6.36 7.73 9.9112 13 14 15 16 17 18 19 20 21 12.75 16.55 20.1 27.35 32.55 37.55 44.75 53.38 71.61 83.89 22 23 24 25 26 27 28 29 30 31 97.46 112.7 135.1 153.6 160.3 167.1 174.9 177.9 180.2 180.83.1 基本绘图操作在Excel 中输入时间x 与高度y 的数据。
选择插入->图表图87点击图表,选择“标准类型”中的xy 散点图,并点击子图表类型的第一个。
图88 点击下一步,得到如图89。
图 89点击下一步。
图90分别点击标题、网格线、图例进行修改,然后点击下一步。
图91点击完成。
图92右击绘图区,修改绘图区格式,双击做表格,修改坐标轴刻度,最后的散点图。
图93观察散点图,其呈S 型曲线,符合logistic 曲线。
采用转化为线性方程的方法求解模型。
3.2 Logistic 曲线方程及线性化Logistic 曲线方程为:1atk y me-=+ (12)(1) 将数据线性化及成图转化为线性方程为:01'y a a t =+ (13)其中,'ln(/1)y k y =-,0ln a m =,1a a =-具体操作为:向excel 表格中输入y ’数据。
logistic回归分析

队列研究(cohort study):也称前瞻性研究、随访研究等。是一种由因及果的研
究,在研究开始时,根据以往有无暴露经历,将研究人群分为暴露人群和非暴 露人群,在一定时期内,随访观察和比较两组人群的发病率或死亡率。如果两 组人群发病率或死亡率差别有统计学意义,则认为暴露和疾病间存在联系。队 列研究验证的暴露因素在研究开始前已存在,研究者知道每个研究对象的暴露 情况。
调查方向:追踪收集资料 暴露 疾病 +
人数
比较
aபைடு நூலகம்
b c
+
研究人群
a/(a+b)
+ -
-
c/(c+d)
d
队列研究原理示意图
暴露组 非暴露组
病例 a c
非病例 b d
合计 n1=a+b n0=c+d
发病率 a/ n1 c/ n0
相对危险度(relative risk, RR)也称危险比(risk ratio) 或率比(rate ratio) RR I e a / n1 、 I e a / n1 、 I 0 c / n2 。
研究,先按疾病状态确定调查对象,分为病例(case)和对照 (control)两组,然后利用已有的记录、或采用询问、填写调查表 等方式,了解其发病前的暴露情况,并进行比较,推测疾病与 暴露间的关系。
调查方向:收集回顾性资料
比较 a/(a+b)
人数 a b c
暴露 +
疾病 病例
+ 对照 -
c/(c+d) d
二、 logistic回归模型的参数估计
logistic 回归模型的参数估计常采用最大似然估计。 其基本思想是先建立似然函数与对数似然函数, 求使对数似然函数最大时的参数值,其估计值即 为最大似然估计值。 建立样本似然函数:
logistic回归分析及其应用-41页文档资料

21.03.2020
2
F(y) :因变量的logit值
1.00
0.75
0.50
0.25
0.00 -4.00 -2.00 0.00 2.00 4.00
X:自变量
21.03.2020
如果一定要进 行直线回归也 可以做出结果, 但此时效果不 佳。当自变量 取一定值时, 因变量的预测 值可能为负数。
21.03.2020
14
2.哑变量的设置和引入
哑变量,又称指示变量或设计矩阵。 有利于检验等级变量各个等级间的变 化是否相同,但主要适合于无序分类变 量。 一个k分类的分类变量,可以用k-1个 哑变量来表示。
21.03.2020
15
哑变量的设置
教育程度:文盲,小学,初中,高中以上
教育程度 X1
X2
X3
文盲:0 0
0
0
小学:1 1
0
0
初中:2 0
1
0
高中:3 0
0
1
以文盲作为参考组
21.03.2020
16
以高中作为参照
教育程度
X1
X2
X3
文盲:010 Nhomakorabea0
小学:1
0
1
0
初中:2
0
0
1
高中:3
0
0
0
21.03.2020
17
SPSS提供的方法
Indicator: 默认。以第1 或最后1类作对照,其他每类 与对照比较; Sample: 以第1 或最后1类作对照,其他每类与对照比 较,但反映平均效应。 Difference: 除第1类外各分类与其前各类平均效应比较; Helmert: 除最后1类外各分类与其前各类平均效应比较; Repeated: 除第1类外各分类与其前一类比较; Polynomial: 假设类间距相等,用于数值型变量。 Deviation: 以第1 或最后1类作对照,其余每类与总效 应比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( 1) 1 1 1 1 1 ,当概率π≠1,π增大时,Odds增大,
特别当π趋于1时,Odds趋于+∞;反之,π减小Odds亦减小, π=0时,Odds=0,Odds与概率π是一一对应和单调递增关系。
当π1= π0时,由Odds1=Odds0,对应的OR=1;
P(Y 1| X 1) 1 P(Y 0 | X 1) 1 1
,对应的样本估计
”比“不发生出血症状”的优势(odds),取值范围是0至+∞。
类似地,在未服用该药品条件下,记π0=P(Y=1|X=1),样本估计 值为P0,发生出血症状比不发生出血症状的优势为
Odds0
P(Y 1| X 0) 0 P(Y 0 | X 0) 1 0
P0 c 0.0022 其样本估计值为 1 P0 d
服用该药品人群“发生出血症状”比“不发生出血症状”的优势
Odds1与未服用该药品人群“发生出血症状”比“不发生出血症状
”的优势Odds0之比,称优势比(Odds Ratio,OR),具有概率风险的 含义。
表21-1 上消化道出血症状与非甾体类抗炎药的关系 出血例数(Y=1) 服用该药(X=1) 未用该药(X=0) 155(a) 96(c) 未出血例数(Y=0) 46981(b) 44538(d) 合计 47136(a+b) 44634(c+d)
服用非甾体类抗炎药(有暴露史)人群中,发生上消化道出血症
logistic回归概率模型,一般简称为二分类logistic回归模型。
当参数β1为正数时,该函数的集合形状呈拉长的“S”行曲线, 时间发生概率π随X的增加二单调增加,称自变量X为事件发生的 危险因素;
当β1为负数时,为拉长的反“S”型曲线,π随X的增加而单调减 小,称自变量X为事件发生的保护因素。
j 0 bj 2 W Sb j
2
H0 成立时,统计量近似服从自由度为1 的2分布。
6. logistic回归模型的拟合程度评价
1ogistic回归模型的拟合优度是通过比较模型预测的与实际观测的事件 发生和不发生的频数有无差别来进行检验。如果预测值与实际观测值
四、 多自变量logistic回归
例21-2 为探讨糖尿病与血压、血脂等因素的关系,某研究者对56 例糖尿病患者和65例对照者进行病例-对照研究,收集了性别、年 龄、职业、体重指数、家族史、吸烟、血压、总胆固醇、甘油三 脂、高密度脂蛋白、低密度脂蛋白11个因素的资料,各因素的赋
值见表21-1下表,数据见表21-2。
以未包含某个或几个变量的模型为基础,保留模型中参数的估 计值,并假设新增加的参数为零,计算对数似然函数的一价偏 导数(又称有效计分)及信息距阵,两者乘积即为计分检验的 统计量S 。样本量较大时, S近似服从自由度为待检验变量个
数的2分布。
③
Wald检验 (wald test)
针对单个回归系数的假设检验。 检验假设H0: 检验统计量
t j t j m m
j (a b)
即
ORj exp[ j (a b)]
调整优势比(adjusted odds ratio)
1 如果 Xj 赋值为 X j 0
暴露 非暴露
则暴露组与非暴露组的优势比为
OR j exp( j )
βj=0时, ORj =1,对疾病发生不起作用; βj0时, ORj 1是一个危险因子;
Wald检验 (Wald test)
① 似然比检验(likelihood ratio test)
当一个模型能够从另一个模型中通过令若干自变量的系数为0得到,
称这个模型嵌套于另一模型。自变量较多的模型称为“完全”模型, 相应的另一个模型称为“简化”模型。
似然比统计量计算公式为:
log(odds) = + 1x1 + 2x2 + 3x3 + 4x4 log(odds) = + 1x1 + 2x2 (model 1) (model 2)
e ( 0 1 X 1 2 X 2 m X m ) 1 e ( 0 1 X 1 2 X 2 m X m )
2. logistic回归模型参数的意义 某一自变量的两个不同取值Xj1=a、 Xj2=b
Pa /(1 Pa ) lnOR j ln P /(1 P ) b b ( 0 j a t X t ) ( 0 j b t X t )
OR
1 (1 1 ) 0 (1 0 )
其样本估计值为 OR
P1 (1 P ad 1) = 1.5306 P0 (1 P0 ) bc
其含义是以未服用该药品人群作为参照类,服用该药品人 群“发生出血症状”的优势是参照类“发生出血症状”优 势的1.5306倍。 由于 Odds 1
状的条件概率P(Y=1|X=1)=π1,其样本估计值为 P1 a b ;
a
服用该药品人群中,不发生上消化道出血症状的条件概率
P(Y=1|X=1)=1-π1,相应的样本估计值为 1 P1 a b ;
b
上述两个条件概率之比,Odds 值为
1
P a 1 0.0033 ,这两个条件概率之比,称为“发生出血症状 1 P b 1
exp(bj Z / 2 SE(bj ))
5. 回归系数整体检验
检验模型中的所有自变量整体来看是否与所研究事件的对数优势比存
在线性关系。
检验假设H0: 检验的方法:
0
1 2 m
似然比检验(likelihood ratio test)
计分检验 (score test)
医学统计学
医学统计学
第二十一章
logistic 回归分析
公共卫生学院卫生统计学教研室 裴磊磊
Email:peileilei424@
章节概要
第一节 非条件logistic回归
第二节 条件logistic回归
第三节 logistic回归的应用及其注意事项
logistic回归分析
渐近正态性:随着样本量增大,最大似然参数估计值的分布 趋近于正态分布。因此可对参数进行假设检验和计算参数的 置信区间。
4. 优势比OR的区间估计
当样本量较大时,logistic回归模型参数的最大似然估计具有渐近正 态性。所以可以利用正态近似法计算总体回归系数的100(1- )% 可信区间。 计算公式为 b j Z / 2 SE (b j ) 其中 SE (b j ) 为回归系数,bj 为渐进标准误, Z / 2 为标准正态分布的 界值。 OR的100(1- )%可信区间为
当 P << 1,优势比可以作为相对危险度的近似估计。
P1 /(1 P1 ) P1 OR RR P0 /(1 P0 ) P0
二、Logit变换与单自变量Logistic方程
概率π的Logit变换,记为logit π,并有
log it ln 1
ln Odds
0 1X
公式两边同时做以e为底的指数变换
x Odds x exp( 0 1X) 1 x
初等数学变换
exp( 0 1X) P(Y 1| X) x 1 exp( 0 1X)
上述三式是等价的,两者均可称为以Y(取值为0和1)为因变量的
势为β0+ β1。
ln(OR) ln 1 ln 0 ( 0 1 1) ( 0 1 0) 1 1 1 1 0
常数项β0是未服用该药品人群发生出现症状优势的自然对数, 自变量回归系数β1是优势比的自然对数。
二分类反应变量 多分类有序反应变量 多分类无序反应变量
第一节 非条件logistic回归
一、优势与优势比
例21-1 非甾体类抗炎药上市前的研究中,已知可能引起亚临床上消 化道出血症状。因此,1980年Strom和Carson开展了大样本上市后 安全性评价,以确定该药品是否引起上消化道出血不良反应。回顾 性跟踪调查的47136例服用该药的患者中,由155例上消化道出血; 同期没有服用该药的44634例对照中,由96例上消化道出血。
βj<0时, ORj < 1是一个保护因子。
3. logistic回归的参数估计
采用最大似然估计MLE(maximum likelihood estimate)估计
logistic回归模型的参数,即建立一个样本的似然函数。
最大似然估计就是确定模型中的参数使得在一次抽样中获得现
有样本的概率为最大,即似然函数达到最大值。对似然函数的
三、 回归系数的解释
以例21-1为例,建立logistic回归方程:
x log it x ln 1 x
0 1X
在未服用该药品条件下(X=0),记上消化道出血与不出血的对数 优势为β0,即ln(Odds0)=β0;
在服用该药品条件下(X=1),记上消化道出血与不出血的对数优
由于Odds取值范围时0至+∞, logit π取值范围时-∞到+ ∞,并 且是概率π的单调增函数, π的任何变化都会反映为logit π的改 变,于是可以把logit π假设为自变量X的线性函数。
x log it x ln 1 x
0 1X
x log it x ln 1 x
