结构力学课件--6力法3.ppt
合集下载
结构力学 (1)

X1 3EI 3 l
基本结构已 为何为 0 无支座位移
5. 内力计算(静定结构)
M M1 X1 M P
内力全部由多余未知力引 起
31
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
M M 1 X 1 (
3EI ) x; 0 x l 3 l
3EI 3EI ) 3 2 l l
对于支座位移
A B
1. 超静定结构支座移动、温度改变使结构产生变形,同时产生内力。
C
C
A
B
C’
FyC
静定结构 无内力和支座反力
超静定结构 有内力和支座反力
23
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
对于温度变化
A
t t
B
C
A
t t
B
C
C’
FyC
静定结构 无内力和支座反力
X2
X3
X1
a 0 11 X 1 12 X 2 13 X 3 1C 0 2 C b 0 21 X 1 22 X 2 23 X 3 0 X X X 0 3C 31 1 32 2 33 3 0
1 P 1C 0 11 X 1 12 X 2 13 X 3 P 基本结构由支座 2P X X X 0 位移引起的 21 1 22 2 23 3 22 CP X X X 0 3P i 方向位移 3 P 31 1 32 2 33 3 3 C
29
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
基本结构(II)
基本结构已 为何为 0 无支座位移
5. 内力计算(静定结构)
M M1 X1 M P
内力全部由多余未知力引 起
31
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
M M 1 X 1 (
3EI ) x; 0 x l 3 l
3EI 3EI ) 3 2 l l
对于支座位移
A B
1. 超静定结构支座移动、温度改变使结构产生变形,同时产生内力。
C
C
A
B
C’
FyC
静定结构 无内力和支座反力
超静定结构 有内力和支座反力
23
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
对于温度变化
A
t t
B
C
A
t t
B
C
C’
FyC
静定结构 无内力和支座反力
X2
X3
X1
a 0 11 X 1 12 X 2 13 X 3 1C 0 2 C b 0 21 X 1 22 X 2 23 X 3 0 X X X 0 3C 31 1 32 2 33 3 0
1 P 1C 0 11 X 1 12 X 2 13 X 3 P 基本结构由支座 2P X X X 0 位移引起的 21 1 22 2 23 3 22 CP X X X 0 3P i 方向位移 3 P 31 1 32 2 33 3 3 C
29
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
基本结构(II)
结构力学——6力法ppt课件

的位移条件,首先求出多余未知力,然后再由平
衡条件计算其余反力、内力的方法,称为力法。 力法整个计算过程自始至终都是在基本结构 上进行的,这就把超静定结构的计算问题,转化
为已经熟悉的静定结构的内力和位移的计算问题。 11
§6—4 力法的典型方程 用力法计算超静定结构的关键,是根据位移条件建立力法方 程以求解多余未知力,下面首先以三次超静定结构为例进行推导。 P P 1. 三次超静定问题的力法方程 ↓ ↓ 首先选取基本结构(见图b) 基本结构的位移条件为: 原结构 基本结构 △1=0 △2=0 A B X1 A X2 △3=0 → (b) B ↑ (a) X 3 设当X 1 、 X 1 、 X 1 和荷载 P 1 2 3 分别作用在结构上时, 沿X 方向: 、 、 和△ ; 1 11 12 1P 13 A点的位移 沿X2方向:21、22、23和△2P ; 沿X3方向:31、32、33和△3P 。 据叠加原理,上述位移条件可写成 △1=11X1 +12X2+13X3 +△1P=0 △2=21X1+22X2+23X3+△2P=0 (8—2) 12 △3=31X1+32X2+33X3+△3P=0
多余未知力: 多余联系中产生的力称为多余未 知力(也称赘余力)。 多余联系与多余未知力的选择。
3. 超静定结构的类型 (1)超静定梁; (2)超静定桁架; ⑶ (3)超静定拱; (4)超静定刚架; (5)超静定组合结构。 4. 超静定结构的解法 ⑷
求解超静定结构,必须 综合考虑三个方面的条件: (1)平衡条件; ⑸ (2)几何条件; (3)物理条件。 5 具体求解时,有两种基本(经典)方法—力法和位移法。
↑
X1
结构力学课件--6力法3
2
内容回顾
对称荷载:
反对称荷载:
EI
P EI
EI P P
EI
P EI
EI P P
B.有中柱对称结构(偶数跨结构) 对称荷载:
反对称荷载:
EI EI
P EI
EI P P
EI EI
P EI EI EI P P
EI/2
2019/7/14
课件
3
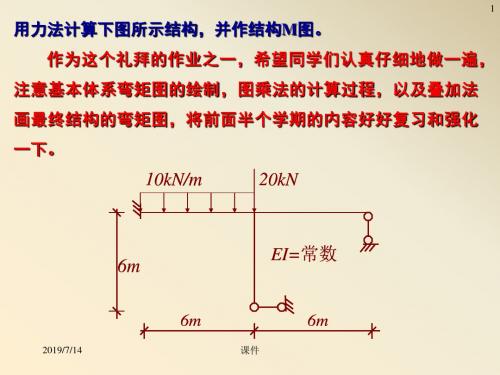
用力法计算下图所示结构,并作结构M图。
1 kN/m EI
EI
EI 2m
可能使: 21 = 12 = 0
即得:
课件
11X1 1P = 0 22 X 2 2P = 0 33 X 3 3P = 0
y y´
12
X2
X2 y
X1 X1 a
y
O
x
x'
1
y
x
X1 = 1
y
X2 =1
M1 =1 N1 = 0 Q1 = 0
12 =
15
4m
a
y
2EI
EI
EI
x
8m
X1 X1
X2 X2 X3
a
=
y
1 EI
ds
1 EI
ds
=
1 2EI
8 4
2( 1 EI
4 2)
=
8
=
2.667m
1 8 2( 1 4)
3
2019/7/14
2EI
EI 课件
§6-7 支座移动和温度改变时的内力计算
16
一、支座移动时的计算
(a 11
1 2
力法 ppt课件

力法课件包含了大量的信息和内容,可能 导致学生无法消化和理解,造成信息过载 。
替代传统教学
技术更新快
力法课件虽然可以辅助教学,但不能完全 替代传统的教学方式,过分依赖课件可能 影响学生的思考能力和实践能力。
力法课件所依赖的技术更新换代较快,导 致课件的维护和更新成本较高,对学校和 教师提出了更高的要求。
扩展应用领域
随着研究的深入和技术的发展,展望
更高效的求解算法
针对大规模、复杂问题,寻 求更快速、稳定的求解算法 是力法未来的重要研究方向 。
跨学科交叉融合
力法将与其它工程学科、数 学方法及计算科学进一步交 叉融合,形成更综合、系统 的分析方法。
力法的基本原理
总结词
力法的基本原理包括虚功原理、虚位移原理和最小势能原理。
详细描述
力法的基本原理包括虚功原理、虚位移原理和最小势能原理。虚功原理是力法的基本依据,它表明在平衡状态下 ,实功和虚功相等;虚位移原理表明在平衡状态下,虚位移和外力所做的虚功相等;最小势能原理则表明结构的 平衡状态对应于势能的最小值。
结果分析
解析解的意义
对求解得到的力学模型结果进行深入分析,理解其物理意义 ,并评估其对实际问题的指导价值。这一步骤有助于将力学 模型解转化为实际应用的指导。
03
力法的应用实例
桥梁结构的力法分析
总结词
桥梁结构的力法分析是利用力学原理对桥梁结构进行受力 分析和评估的过程。
计算模型
力法分析基于力学原理建立计算模型,通过计算和分析桥 梁结构的内力和变形,评估其承载能力和稳定性。
详细描述
通过力法分析,可以确定桥梁结构的承载能力、稳定性以 及在不同载荷下的变形情况。这对于确保桥梁安全运行和 预防潜在的损坏至关重要。
结构力学力法ppt课件

EI E2I
2 E2I
2 M E 2 M d I x E 1 2 6 I 6 0 1 2 9 3 2 6 0 1 2 9 3 2 E 28 I80
力法
(4) 求多余未知力
18
将系数和自在项代入力法方程,并消去 EI 2 ,得
28X17X2 600 7X132X2 1600
假设X1知,根本体系就是一个静定构造。
怎样 求X1 呢?
力法
二、力法的根本方程
FP
位移条件:根本构造转 化为原构造的条件是:根 本构造在原有荷载和多余
A 原构造
未知力共同作用下,在去
掉多余约束处的位移应与
原构造中相应的位移相等。
A
即
1 0
根本体系
〓
FP 当ΔB=Δ1=0
B
FB
B
X1 =><>=> FB
Δ1P
δ11——根本构造在X1=1单独作用下,B点沿X1方向 的位移。
1 11 10 力法根本方程
Δ11=δ11X1
δ1X 111P0
δ11和Δ1P都是静定的根本构造在知力作用下的位移,均可用“单位 荷载法〞求得。
力法
用图乘法计算δ11和Δ1P
பைடு நூலகம்δ11
X1=1
Fl
EI
2
↓
B
Δ1P
l
X1=1
M1
MP图
5Fl3 0 48EI
X1
5 16
F
最后的弯矩图可按叠加原理由下式求得: MM1X1M
力法
Fl
EI
2
l
X1=1
M1
MP图
MA
l
5 16
结构力学第六章力法

正对称荷载作用下,沿对称轴截面 上反对称内力为0
3)反对称荷载作用下
2P 3P 0
11 X 1 22 X 2
1P 23
0 X3
0
32 X 2 33 X 3 0
X121X1
1P X3 0
0
反对称荷载作用下, 沿对称轴截面上正对称内力为0
例:
FP
FP/2 FP/2
FP/2
FP/2 FP/2
M,FN,FQ,R任一基本结构力 下下 的的 单内 位力和反力
3 温度变化
E M Ih t,E F N A t0,kG F Q A
M EM IdxFN EFA NdxFQ GFQ Adx MhtdxFNt0dx
4 综合因素下位移公式
M EM IdxFN EFA NdxFQ GFQ Adx MhtdxFNt0dxRC
(2 2)FPa EA
X1
2FP 2
FNX1FN1FNP
二 组合结构
实体梁和加劲杆组成加劲梁,基本结构一般由切断二力杆得到。
计算系数要按梁式杆和二力杆分别处理。
2
2
ii
M i dx N i l
EI
EA
ij
M i M j dx N i N j l
EI
EA
iP
M i M P dx N i N P l
FNDA
FNBD=-23FP/40 FNDC=9FP/80
2 铰接排架 计算柱子内力时,通常将屋架视为一根轴向EA为∞的杆件
(横梁)。阶梯式的变截面柱,上端与横梁铰接,下端与基础刚接。 铰接排架超静定次数等于排架跨数,其基本结构由切断各跨横 梁得到。
典型方程: 11 X11P0
110.12E 3l3I,1P
3)反对称荷载作用下
2P 3P 0
11 X 1 22 X 2
1P 23
0 X3
0
32 X 2 33 X 3 0
X121X1
1P X3 0
0
反对称荷载作用下, 沿对称轴截面上正对称内力为0
例:
FP
FP/2 FP/2
FP/2
FP/2 FP/2
M,FN,FQ,R任一基本结构力 下下 的的 单内 位力和反力
3 温度变化
E M Ih t,E F N A t0,kG F Q A
M EM IdxFN EFA NdxFQ GFQ Adx MhtdxFNt0dx
4 综合因素下位移公式
M EM IdxFN EFA NdxFQ GFQ Adx MhtdxFNt0dxRC
(2 2)FPa EA
X1
2FP 2
FNX1FN1FNP
二 组合结构
实体梁和加劲杆组成加劲梁,基本结构一般由切断二力杆得到。
计算系数要按梁式杆和二力杆分别处理。
2
2
ii
M i dx N i l
EI
EA
ij
M i M j dx N i N j l
EI
EA
iP
M i M P dx N i N P l
FNDA
FNBD=-23FP/40 FNDC=9FP/80
2 铰接排架 计算柱子内力时,通常将屋架视为一根轴向EA为∞的杆件
(横梁)。阶梯式的变截面柱,上端与横梁铰接,下端与基础刚接。 铰接排架超静定次数等于排架跨数,其基本结构由切断各跨横 梁得到。
典型方程: 11 X11P0
110.12E 3l3I,1P
结构力学课件 力法

(5)叠加原理作M图
M1(m)
M A 360 6 ( 22) 228 M C 6 ( 22) 132
90
228
132
桁架
P
a
(1)基本体系 —基本未知量 (2)位移协调条件 —写力法基本方程 (3)求系数和自由项 —单位荷载法
a
(4)解力法方程 —求基本未知量
P
→ X1 ↑
拆开一个单铰,相当于去掉两个联系。
X1
X 1 ← → ↑ → X2
(3) 在刚结处作一切口,或去掉一个固定端,相当于去掉 三个联系。 X
X1
←→
X2
(4)将刚结改为单铰联结,相当于去掉一个联系。
X1 X1
← →
3
例1: 确定图示结构的超静定次数。
2
1 3
n=6
例2: 确定图示结构的超静定次数。 对于具有较多框格的结构, 可按框格的数目确定,因为一
q a
A
B X1
A
2 力法的基本概念
力法的基本体系
q
A B A
q a
力法的基本未知量
a
B X1
B点的位移条件Δ1=0
变形协调条件
q
A
B A
变形协调条件
Δ1=Δ1P+Δ11=0
Δ1P:基本体系在荷载q单独
a q
A B Δ1P
Δ11 B X1
作用下沿X1方向产生的位移;
Δ11:基本体系在荷载X1单 独作用下沿X1方向产生的 位移;
X1
X1
(1)基本体系 —基本未知量 (2)位移协调条件 —写力法基本方程
a
a
1P 11 X 1 0
结构力学第6章力法3ppt课件

作业:
• P268 6-5 (a)、6-6
•X1= - ⊿1P / δ11 = - 38746 N= - 38.746kN
按以下公式计算最后内力
• M = - 38.746 M1+MP • FN = - 38.746FN1+FN P
FP 2.469
- 38.746 61.263
54.416 61.263
M 图〔kN ·m〕 FN1 ( kN )
√2a √2a 2(1+√2)a
FN1FNPl
0 FP·a /√2 FP·a /√2
0 2FP·a
0 (√2+2)
×FБайду номын сангаас·a
FN
+FP /2 - FP /2 - FP /2 +FP /2 √2FP/2 -√2FP/2
讨论:
• 1、桁架中的杆件(EA=常数)不是 去掉而是截断,计算δij时,不能忘记 被截断杆的轴力。
作M1图,并求各 杆轴力。
3/2
A
C
B
-√10/2 -√10/2 D X1=
M1 图〔1m〕FN1
FP 55.65
A
C
B
作MP图。
83.475
D
MP 图〔kN·m〕FNP=
求系数和自在项。 0
• δ11=∑ FN12 l /EA+∑∫M12 dx/EI = 29.7869×10 -8 m/N
• ⊿1P=∑ FN1 FNP l /EA+∑∫M1MP dx/EI =1154.1290×10 -5 m
F N X 1 F N 1 F NP
2 2
FP
FN1
F NP
FPFNP FP
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
kQ 12ds GA
=(1NQ)
M12 ds EI
通常可以略去Q
2020/11/4
课件
二、带拉杆的两铰拱
E、I、A
10
为什么要用拉杆? 推力减少了拱肋弯矩 使墙、柱不承担弯矩
X1=1
E1、A1
11 X1X1 1P=0
M 1 N1
MP
其中
11=
M12d s EI
N12d s l N12dx EA 0E1A1
1 kN/m EI
2m EA=
EI 2m
EI
2m
2020/11/4
课件
4
EI A
aP
P
EA= P
2
EI
EI EI
a
a
a
Pa
2
1
PP 22
P 2 MP
2020/11/4
X1 =1 M1
课件
P 2
1
X2 =1 M2
5
Pa 2
P 2 MP
1
X1 =1 M1
2020/11/4
1 1 1=E 1 I(a 1 11 2a 12 3)=3 4 E a I
2
内容回顾
对称荷载:
反对称荷载:
EI
P EI
EI P P
EI
P EI
EI P P
B.有中柱对称结构(偶数跨结构) 对称荷载:
反对称荷载:
EI EI
P EI
EI P P
EI EI
P EI EI EI P P
EI/2
2020/11/4
课件
3
用力法计算下图所示结构,并作结构M图。
1 kN/m EI
EI
EI 2m
=
y
EI 1
EI
ds ds
=
a
。
y y
(b)
y ds
等截面时 a =
ds
要点202:0/111/、4 先计算a;2、将未知力放课在件弹性中心;3、独立方程, 22考虑N。
14
例1、试确定图示园弧拱的弹性中心,EI=常数,半径R=6.25m 。
y
x
2.5m
a
=
y 1 EI
ds
1 EI
ds
0 0
1P =
M1MP EI
ds=
1P
l N12dx= l 12 dx= l
0E1A1
0E1A1 E1A1
1 1 =M E 1 2d I sN E 1 2d A sE 1 lA 1=1 1E 1 lA 1
两类拱的比较: 无拉杆 H = 1P
11
E1A1 H H 相当于无拉杆
有拉杆
H
=
11
y与的计算
8
X1
X1=1
在竖向荷载作用下
9
MP=M° M1 = y N1 =cos
M =M M 1X 1=M Hy
Q=Qco sHsin N=QsinHcos
H = 1P
11
计算特点: 和 只能积分; H——推力由变形条件求得;
关于位移计算简化的讨论;
11 =
M 12d s EI
N12d s EA
l=10m
y
y
y=Rcos ds=Rd
x
2
a= 0
2RcoRsdRd=Rsi0n0
0
sin0=lR /2=6.525=0.8
a=5.39m
0=0.927(r3a)d
2020/11/4
x 课件
a=5.39m
3m 3m q=1kN/m
3 2I
2I
1
4 I 2
X1
3m 3m
2
4.33
1.33
X2
X1=2.67kN
5.66 3.56
MkNm
如计算第4点的水平位移
H 4
X2 =1.11kN
1
6m
1
6m
3m
M
H4
=
MMdx EI
M
2020/11/4
课件
§6-6 超静定拱
一、两铰拱计算
11 X11P=0
1P =
X 2 = 1 22=E 1I(1 2a12 3)=3E aI
M2
12=E 1I(1 2a11 3)=6E aI
11P a 1P a 2 5 P a 2 1 P= E I(2 2 a 1 2 2 a 3 )= 1 2 E I
2P=E 1I1 2P 2aa1 3)=1P 2a E 2I
课件
Pa 2
y y´
12
X2
X2 y
X1 X1 a
y
O
x
x'
Q2
1 y N2
y
x
X1 =1
y
y x
X2 =1
M1 =1 N1 = 0 Q1 = 0
12 =
y ds EI
M2 =y N2 =cos Q2 =sin
另选座标 xoy 则 y=ya
2020/11/4
12 = yE ad I= 课s件 E yd I s aE 1dIs
1
用力法计算下图所示结构,并作结构M图。
作为这个礼拜的作业之一,希望同学们认真仔细地做一遍,
注意基本体系弯矩图的绘制,图乘法的计算过程,以及叠加法
画最终结构的弯矩图,将前面半个学期的内容好好复习和强化
一下。
10kN/m
20kN
X1
6m
EI=常数
2020/11/4
6m
6m
课件
A.无中柱对称结构(奇数跨结构)
EI= (c)
(a)与(c)具有完全等效关系。 此时将图(c)在对称轴位置截断, 对于两对称内力:X1、X2而言: X1=1作用下,基本体系同侧受拉; X2=1作用下,基本体系异侧受拉。 当附加竖向刚臂长度变化时,就
可能使: 21 = 12 = 0
即得:
课件
11 X 1 1P = 0 22 X 2 2 P = 0 33 X 3 3P = 0
M1MP ds EI
略去剪力的影响;
当f< l /3 时,考虑
轴力的影响。
f l
P 状态
y
1
y x
x X1=1状态
11=
M1M1ds EI
N1N1ds EA
MP=M°
M1 = y
1P =
My ds EI
列方程
N1 =cos
11=
y2 ds EI
co2s
ds EA
X1
= 1P
11
=H
2020当/11/4f /l<1/4 时,可取ds=dx 课件
适当加202大0/1E1/14A1使H*较大,可减小拱肋M课,件 H求出后,计算内力公式与前面一样。
三、对称无铰拱的计算
11
(a)
X2 X1 X2
X3
(b) (1)利用对称性
11X1 12X2 1P = 0 21X1 22X2 2P = 0 2020/11/4 33X3 3P = 0
y y´
令 12=0 则
13
X2
X1
X2 y
X1 a
y
O
x
x'
a
=
y 1 EI
ds
1 EI
ds
即:若取刚臂端点到x’轴
12 =yE ad I= s E yd I s aE 1dIs
距离为a,则 12=0 ,该点
称为弹性中心。
形象解释
EI
1 EI
(a)
1 EI
ds
y
=
1 EI
ds y
y
P 2 MP
1
X1 =1 M1
2020/11/4
6
1
X2 =1
Pa M 2
5 Pa 10
3 10 Pa
4 3 1 6
X1 X1
1 6 1 3
X2 X2
5 12 1 12
Pa Pa
= =
0 0
X X
1 2
= =
3 10
1 10
Pa Pa
课件
§6-8 超静定结构的位移计算
7
荷载作用
P=3kN
