初中数学总复习-函数
初中数学总复习专题12 三角函数
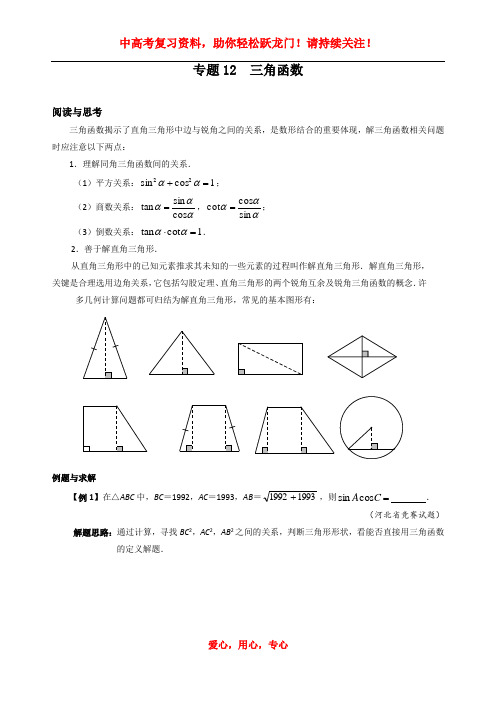
专题12 三角函数阅读与思考三角函数揭示了直角三角形中边与锐角之间的关系,是数形结合的重要体现,解三角函数相关问题时应注意以下两点:1.理解同角三角函数间的关系. (1)平方关系:1cos sin 22=+αα; (2)商数关系:αααcos sin tan =,αααsin cos cot =; (3)倒数关系:1cot tan =⋅αα.2.善于解直角三角形.从直角三角形中的已知元素推求其未知的一些元素的过程叫作解直角三角形.解直角三角形, 关键是合理选用边角关系,它包括勾股定理、直角三角形的两个锐角互余及锐角三角函数的概念.许多几何计算问题都可归结为解直角三角形,常见的基本图形有:例题与求解【例1】在△ABC 中,BC =1992,AC =1993,AB =19931992+,则=C A cos sin .(河北省竞赛试题)解题思路:通过计算,寻找BC 2,AC 2,AB 2之间的关系,判断三角形形状,看能否直接用三角函数的定义解题.【例2】某片绿地形状如图所示,其中∠A =600,AB ⊥BC ,AD ⊥CD ,AB =200m ,CD =100m . 求AD ,BC 的长.(精确到1m ,732.13≈)图2图1F EAE AABDDBDB解题思路:本题的解题关键是构造直角三角形,构造的原则是不能破坏∠A ,所以连结AC 不行.延长AD 和BC 交于一点E (如图1),这样既构造出了直角三角形,又保全了特殊角∠A ;或过点D 作矩形ABEF (如图2)来求解.【例3】如图,已知正方形ABCD 中,E 为BC 上一点.将正方形折叠起来,使点A 和点E 重合,折痕为MN .若31tan =∠AEN ,DC +CE =10. (1)求△ANE 的面积; (2)求ENB ∠sin 的值.解题思路:将31tan =∠AEN 与DC +CE =10结合起来,可求出相关线段的长,为解题铺平道路.【例4】如图,客轮沿折线A —B —C 从A 出发经B 再到C 匀速航行,货轮从AC 的中点D 出发沿某一方向匀速直线航行,将一批物品送达客轮.两船同时起航,并同时到达折线A —B —C 上的某点E 处.已知AB =BC =200海里,∠ABC =900,客轮速度是货轮速度的2倍.(1)选择:两船相遇之处E 点( )A .在线段AB 上 B .在线段BC 上C .可以在线段AB 上,也可以在线段BC 上(2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)(南京市中考试题)解题思路:对于(2),过D 作DF ⊥CB 于F ,设DE =x ,建立关于x 的方程.【例5】若直角三角形的两个锐角A ,B 的正弦是方程02=++q px x 的两个根. (1)那么,实数p ,q 应满足哪些条件?(2)如果p ,q 满足这些条件,方程02=++q px x 的两个根是否等于直角三角形的两个锐角A ,B 的正弦?(江苏省竞赛试题)解题思路:解本例的关键是建立严密约束条件下的含不等式、等式的混合组,需综合运用一元二次方程,三角函数的知识与方法.C【例6】设a ,b ,c 是直角三角形的三边,c 为斜边,整数n≥3.求证:nnnc b a <+.(福建省竞赛试题)解题思路:由直角三角形的边可以转化为三角函数正余弦来解.其不等关系可以利用正弦、余弦的有界性来证明.能力训练A 级1.如图,D 是△ABC 的边AC 上一点,CD =2AD ,AE ⊥BC 于E .若BD =8,43sin =∠CBD ,则AE = . 2.已知00900≤≤α,则ααsin sin 45+-=y 的最大值是 ,最小值是 .(上海市理科实验班招生考试试题)3.如图,在△ABC 中,∠C =900,∠BAC =300,BC =1,D 为BC 边上的一点,ADC ∠tan 是方程2)1(5)1(322=+-+xx x x 的一个较大的根,则CD = .东第5题图第1题图第3题图E BAO4.已知△ABC 的两边长a =3,c =5,且第三边长b 为关于x 的一元二次方程042=+-m x x 的两个正整数根之一,则A sin 的值为 . (哈尔滨中考试题) 5.如图,小雅家(图中点O 处)门前有一条东西走向的公路,经测得有一水塔(图中点A 处)在她家北偏东600距离500m 处,那么水塔所在的位置到公路的距离AB 是( ) A .250mB .3250mC .33500mD .2250m6.如图,在△ABC 中,∠C =900,∠ABC =300,D 是AC 的中点,则DBC ∠cot 的值是( ) A .3B .32C .23D .43 (大连市中考试题)7.一渔船上的渔民在A 处看见灯塔M 在北偏东600方向,这艘渔船以28海里/时的速度向正东航行.半小时后到B 处,在B 处看见灯塔M 在北偏东150方向,此时灯塔M 与渔船的距离是( ) (黄冈市中考试题) A .27海里B .214海里C .7海里D .14海里8.如图,四边形ABCD 中,∠A =600,∠B =∠D =900,AD =8,AB =7,则BC +CD 等于( ) A .36B .35C .34D .33第7题图第6题图第8题图东北BA OA9.如图是某品牌太阳能热水器的实物图和横断面示意图.已知真空集热管AB 与支架CD 所在直线相交于水箱横断面⊙O 的圆心,支架CD 与水平面AE 垂直,AB =150厘米,∠BAC =300,另一根辅助支架DE =76厘米,∠CED =600.(1)求垂直支架CD的长度(结果保留根号);(2)求水箱半径OD的长度(结果保留三位有效数字,参考数据:73.13,41.12≈≈).(扬州市中考试题)图2图1BA EOD10.若α为锐角,求证:4cossin1cos1sin1>⋅++αααα.(宁波市竞赛试题)11.如图,已知AB=CD=1,∠ABC=900, ∠CBD=300,求AC的长.(加拿大数学奥林匹克竞赛试题)12.如图,在△ABC中,∠ACB=900,CD⊥AB于点D,CD=1.若AD,BD的长是关于x的方程02=++qpxx的两根,且2tantan=-BA,求p,q的值并解此二次方程.ABCB 级1.若0300<<θ,且31sin +=km θ(k 为常数,k <0),则m 的取值范围是 . 2.设00450<<α,1673cos sin =⋅αα,则=αsin . (武汉市选拔赛试题) 3.已知在△ABC 中,∠A ,∠B 是锐角,且2tan ,135sin ==B A ,AB =29cm ,则△ABC 的面积等于 . (“祖冲之杯”邀请赛试题)4.如图,在正方形ABCD 中,N 是DC 的中点,M 是AD 上异于D 的点,且MBC NMB ∠=∠,则有=∠ABM tan . (全国初中数学联赛试题) 5.如图,在Rt △ABC 中,∠C =900, ∠CAB =300,AD 平分∠CAB ,则CDACCD AB -的值为( ) A .3B .33C .33-D .326-(湖北省选拔赛试题)第4题图第5题图NBAB AMD6.如图,在梯形ABCD 中,AD//BC ,AD ⊥CD ,BC =CD =2AD ,E 是CD 上一点,∠ABE =450,则AEB∠tan的值等于( ) (天津市竞赛试题) A .23 B .2 C .25D .3 7.如图,在等腰Rt △ABC 中,∠C =900, ∠CBD =300,则DCAD=( ) A .33 B .22C .12-D .13-(山东省竞赛试题)第7题图第6题图BA BDE8.如图是一座人行天桥的引桥部分的示意图,上桥通道是由两段互相平行并且与地面成370角的楼梯AD ,BE 和一段水平天台DE 构成.已知天桥高度BC =4.8米,引桥水平跨度AC =8米. (1)求水平天台DE 的长度;(2)若与地面垂直的平台立柱MN 的高度为3米,求两段楼梯AD 与BE 的长度之比.(参考数据:取75.037tan ,80.037cos ,60.037sin 0===) (长沙市中考试题)NA9.在△ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的对边,且c =35.若关于x 的方程0)35(2)35(2=-+++b ax x b 有两个相等的实根,又方程0sin 5)sin 10(22=+-A x A x的两实数根的平方和为6,求△ABC 的面积.(武汉市中考试题)10.如图,EFGH 是正方形ABCD 的内接四边形,两条对角线EG 和FH 所夹的锐角为θ,且BEG ∠与CFH ∠都是锐角.已知,,l FH k EG ==四边形EFGH 的面积为S .(1)求证:klS2sin =θ; (2)试用S l k ,,来表示正方形ABCD 的面积.(全国初中数学联赛试题)GF11.如图,在直角梯形ABCD 中,AD//BC ,∠A =900,BC =CD =10,54sin =C . (1) 求梯形ABCD 的面积;(2)点E ,F 分别是BC ,CD 上的动点,点E 从点B 出发向点C 运动,点F 从点C 出发向点D 运动.若两点均以每秒1个单位的速度同时出发,连接EF ,求△EFC 面积的最大值,并说明此时E ,F 的位置.(济宁市中考试题)A DFB C 12.如图,甲楼楼高16米,乙楼坐落在甲楼的正北面.已知当冬至中午12时太阳光线与水平面的夹角为300,此时,求:(1)如果两楼相距20米,那么甲楼的影子落在乙楼上有多高?(2)如果甲楼的影子刚好落在乙楼上,那么两楼的距离应当是多少?(山东省竞赛试题)。
初中数学函数知识点归纳

初中数学函数知识点归纳初中数学中,函数是一个重要的概念。
在学习函数时,主要包括函数的定义、函数的基本性质、函数的图像以及函数的应用等方面的内容。
一、函数的定义在初中数学中,函数通常被理解为一种数学关系。
具体地说,如果存在一个规则,它能够将一个数集的每个元素与另一个数集的唯一元素相对应,那么我们就称这个规则为函数。
数集的每个元素称为自变量,相对应的元素称为函数值或因变量。
例如,y=2x就是一个函数的表示方式,其中y是因变量,x是自变量。
这个函数的规则是将自变量x乘以2得到对应的y值。
二、函数的基本性质1.定义域和值域:函数的定义域指的是自变量的取值范围,而值域指的是因变量的取值范围。
定义域和值域的确定可以通过函数的解析式,也可以通过函数的图像来确定。
2.单调性:函数的单调性是指函数在一些区间内是递增还是递减。
对于递增的函数,当自变量增加时,因变量也增加;对于递减的函数,当自变量增加时,因变量减少。
3.奇偶性:奇函数和偶函数是函数的一种分类。
当函数满足f(-x)=-f(x)时,我们称这个函数为奇函数;当函数满足f(-x)=f(x)时,我们称这个函数为偶函数。
4.对称轴:对于偶函数,它的图像关于y轴对称;对于奇函数,它的图像关于原点对称。
因此,对称轴就是y轴或者原点。
5.零点:函数的零点指的是函数取0的自变量值,也叫做函数的根。
求零点的方法有很多,例如用图像法、方程求解法等。
三、函数的图像1. 直线函数:直线函数的图像是一条直线。
其解析式通常为y = kx + b,其中k是斜率,表示直线的倾斜程度,b是截距,表示直线与y轴的交点。
2.常函数:常函数的图像是一条水平的直线。
它的解析式为y=c,其中c是常数。
3. 平方函数:平方函数的图像是一条抛物线。
其解析式通常为y = ax^2 + bx + c,其中a、b、c都是常数。
4.开方函数:开方函数是平方函数的反函数。
其图像是一条拋物線的一部分,始终在x轴的非负值上。
数学初中函数知识总结

数学初中函数知识总结函数是数学中的基础概念之一,也是中学数学中的重要内容。
在初中阶段,学生们开始接触函数的概念和相关知识,逐渐深入探讨函数的性质和应用。
本文将对初中函数的知识进行总结和梳理,包括函数的定义、性质、图像和应用等方面。
一、函数的定义函数是以某个变量(自变量)为输入,通过某种规则或算法得到另一个变量(因变量)为输出的关系。
简单来说,函数就是一种对应关系。
用符号表示函数的一般形式为:y = f(x),其中x是自变量,y是因变量,f(x)代表函数关系。
二、函数的性质1. 定义域和值域:函数的定义域是自变量可能取得的值的集合,值域是因变量可能取得的值的集合。
在定义函数时,需要确定函数的定义域和值域。
2. 奇偶性:对于函数f(x),如果对于任意x,有f(-x) = f(x),则该函数是偶函数;如果对于任意x,有f(-x) = -f(x),则该函数是奇函数;否则,函数既不是偶函数也不是奇函数。
3. 单调性:函数的单调性描述了函数的增减规律。
如果函数的自变量增大时,对应的因变量也增大,则该函数是递增的;如果函数的自变量增大时,对应的因变量减小,则该函数是递减的。
三、函数的图像函数的图像是函数的可视化表示,可以通过画出函数的图像来更好地理解和分析函数的性质。
1. 直线函数:直线函数的图像是一条直线,可以通过确定直线上两个点或一个点和斜率来确定直线函数的图像。
2. 平方函数:平方函数的图像是一条抛物线,开口方向取决于平方项系数的正负。
平方函数的顶点是抛物线的最低点或最高点,也是抛物线的对称轴与x轴的交点。
3. 一次函数:一次函数的图像是一条斜率不变的直线,可以通过确定直线上两个点或一个点和斜率来确定一次函数的图像。
四、函数的应用函数是数学中的一个强大工具,不仅在数学中有广泛的应用,还可以在实际生活和其他学科中得到应用。
1. 函数的模型建立:通过观察和分析实际问题,可以建立函数模型来解决问题。
例如,利用一次函数模型可以描述物体的匀速直线运动,二次函数模型可以描述物体的自由落体运动。
初中数学-函数详解

初中数学-函数详解我选择介绍初中数学中的函数的概念、性质和应用。
一、函数的概念函数是一种特殊的数学关系,表示两个数集之间的一种映射关系。
简单来说,函数就是将一个数集中的每一个元素映射到另一个数集中的一个唯一元素的规律。
二、函数的性质1)定义域和值域函数的定义域是指所有可以作为自变量的数的集合,函数的值域是指所有可能的函数值所构成的集合。
2)单调性函数的单调性指函数在其定义域内的增减规律,分为单调递增和单调递减。
3)奇偶性函数的奇偶性是指当自变量为负数时,函数值是否与自变量为正数时的函数值相同。
4)周期性函数的周期性是指函数图像在某个区间内重复出现的规律。
三、函数的应用函数在数学中应用广泛,例如在物理学、经济学和工程学等方面,都是重要的数学工具。
下面是两个应用例题:例题1:一辆汽车从A地出发,行驶一段距离后达到B 地,再从B地出发,返回A地,设汽车行驶的速度为v1和v2,A、B两地之间的距离为d,求汽车来回所需的时间。
解:设汽车从A到B的时间为t1,从B返回A的时间为t2。
由于路程相同,因此可以列出以下等式:v1t1 = v2t2v1t1 + v2t1 = d解出t1和t2的表达式如下:t1 = d / (v1 + v2)t2 = d / (v2 - v1)因此,汽车来回所需时间为t = t1 + t2 = 2d / (v2 - v1)。
例题2:一个球从地面上抛出,下落后又反弹回来,每次反弹的高度都是原来高度的一半,求球弹起第四次所达到的高度。
解:设球第一次弹起的高度为h,则球第二次弹起的高度为h/2,第三次弹起的高度为h/4,第四次弹起的高度为h/8。
因此,球弹起第四次所达到的高度为h/8。
我们可以将球弹起的高度与弹起次数建立函数关系:h(n) = h/2^(n-1),n 为弹起次数。
通过以上的例题,我们可以了解到函数的概念、性质和应用,深入了解函数的应用可以帮助我们解决生活中实际问题。
初中数学函数知识点

数学函数知识点1.常量和变量在某变化过程中可以取不同数值的量叫做变量.在某变化过程中保持同一数值的量或数,叫常量或常数.2.函数设在一个变化过程中有两个变量x与y,如果对于x在某一范围的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是x的函数.3.自变量的取值范围(1)整式:自变量取一切实数.(2)分式:分母不为零.(3)偶次方根:被开方数为非负数.(4)零指数与负整数指数幂:底数不为零.4.函数值对于自变量在取值范围内的一个确定的值,如当x=a时,函数有唯一确定的对应值,这个对应值,叫做x=a时的函数值.5.函数的表示法(1)解析法;(2)列表法;(3)图象法.6.函数的图象把自变量x的一个值和函数y的对应值分别作为点的横坐标和纵坐标,可以在平面直角坐标系内描出一个点,所有这些点的集合,叫做这个函数的图象.由函数解析式画函数图象的步骤:(1)写出函数解析式及自变量的取值范围;(2)列表:列表给出自变量与函数的一些对应值;(3)描点:以表中对应值为坐标,在坐标平面内描出相应的点;(4)连线:用平滑曲线,按照自变量由小到大的顺序,把所描各点连接起来.7.一次函数(1)一次函数如果y=kx+b(k、b是常数,k≠0),那么y叫做x的一次函数.特别地,当b=0时,一次函数y=kx+b成为y=kx(k是常数,k≠0),这时,y叫做x的正比例函数.(2)一次函数的图象一次函数y=kx+b的图象是一条经过(0,b)点和点的直线.特别地,正比例函数图象是一条经过原点的直线.需要说明的是,在平面直角坐标系中,“直线”并不等价于“一次函数y=kx+b(k≠0)的图象”,因为还有直线y=m(此时k=0)和直线x=n(此时k不存在),它们不是一次函数图象.(3)一次函数的性质当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.直线y=kx+b与y轴的交点坐标为(0,b),与x轴的交点坐标为.(4)用函数观点看方程(组)与不等式①任何一元一次方程都可以转化为ax+b=0(a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:一次函数y =kx+b(k,b为常数,k≠0),当y=0时,求相应的自变量的值,从图象上看,相当于已知直线y=kx+b,确定它与x 轴交点的横坐标.②二元一次方程组对应两个一次函数,于是也对应两条直线,从“数”的角度看,解方程组相当于考虑自变量为何值时两个函数值相等,以及这两个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线的交点的坐标.③任何一元一次不等式都可以转化ax+b>0或ax+b<0(a、b为常数,a≠0)的形式,解一元一次不等式可以看做:当一次函数值大于0或小于0时,求自变量相应的取值范围.8.反比例函数(1)反比例函数如果 (k是常数,k≠0),那么y叫做x的反比例函数.(2)反比例函数的图象反比例函数的图象是双曲线.(3)反比例函数的性质①当k>0时,图象的两个分支分别在第一、三象限内,在各自的象限内,y随x的增大而减小.②当k<0时,图象的两个分支分别在第二、四象限内,在各自的象限内,y随x的增大而增大.③反比例函数图象关于直线y=±x对称,关于原点对称.(4)k的两种求法①若点(x0,y0)在双曲线上,则k=x0y0.②k的几何意义:若双曲线上任一点A(x,y),AB⊥x轴于B,则S△AOB(5)正比例函数和反比例函数的交点问题若正比例函数y=k1x(k1≠0),反比例函数,则当k1k2<0时,两函数图象无交点;当k1k2>0时,两函数图象有两个交点,坐标分别为由此可知,正反比例函数的图象若有交点,两交点一定关于原点对称.1.二次函数如果y=ax2+bx+c(a,b,c为常数,a≠0),那么y叫做x 的二次函数.几种特殊的二次函数:y=ax2(a≠0);y=ax2+c(ac≠0);y =ax2+bx(ab≠0);y=a(x-h)2(a≠0).2.二次函数的图象二次函数y=ax2+bx+c的图象是对称轴平行于y轴的一条抛物线.由y=ax2(a≠0)的图象,通过平移可得到y=a(x-h)2+k(a≠0)的图象.3.二次函数的性质二次函数y=ax2+bx+c的性质对应在它的图象上,有如下性质:(1)抛物线y=ax2+bx+c的顶点是,对称轴是直线,顶点必在对称轴上;(2)若a>0,抛物线y=ax2+bx+c的开口向上,因此,对于抛物线上的任意一点(x,y),当x< 0时,y随x的增大而减小;当x>0 时,y随x的增大而增大;当x= y时有最小值;若a<0,抛物线y=ax2+bx+c的开口向下,因此,对于抛物线上的任意一点(x,y),当x< 0,y随x的增大而增大;当x >0时,y随x的增大而减小;当x= y时有最大值;(3)抛物线y=ax2+bx+c与y轴的交点为(0,c);(4)在二次函数y=ax2+bx+c中,令y=0可得到抛物线y=ax2+bx+c与x轴交点的情况:∆<0时,抛物线y=ax2+bx+c与x轴没有公共点.∆=0时,抛物线y=ax2+bx+c与x轴只有一个公共点,即为此抛物线的顶点;当∆=b2-4ac>0,抛物线y=ax2+bx+c与x轴有两个不同的公共点,它们的坐标分别是和,这两点的距离为;当∆当4.抛物线的平移抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)、向左(右)平移,可以得到抛物线y=a(x -h)2+k.平移的方向、距离要根据h、k的值来决定.函数知识点总结(掌握函数的定义、性质和图像) (一)平面直角坐标系1、定义:平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系2、各个象限内点的特征:第一象限:(+,+)点P(x,y),则x>0,y>0;第二象限:(-,+)点P(x,y),则x<0,y>0;第三象限:(-,-)点P(x,y),则x<0,y<0;第四象限:(+,-)点P(x,y),则x>0,y<0;3、坐标轴上点的坐标特征:x轴上的点,纵坐标为零;y轴上的点,横坐标为零;原点的坐标为(0 , 0)。
初中数学知识归纳函数的概念和性质的归纳

初中数学知识归纳函数的概念和性质的归纳初中数学知识归纳:函数的概念和性质函数在数学中占据着重要的地位,它是数学中最基本的概念之一。
通过对函数的学习,我们可以更好地理解和应用各类数学知识。
本文将对函数的概念和性质进行归纳,帮助初中生更好地掌握这一内容。
一、函数的概念函数是一种特殊的关系,它将一个集合中的每个元素和另一个集合中的唯一元素相对应。
这里,我们通常将前一个集合称为自变量的定义域,后一个集合称为函数值的值域。
函数用符号f(x)表示,其中x为自变量,f(x)为对应的函数值。
1. 定义域和值域函数的定义域是指所有自变量可能的取值范围,而值域是指函数所有可能的函数值。
在解决函数题目时,我们需要明确定义域和值域的范围。
例如,函数f(x) = 2x + 1中,自变量x可以是任意实数,所以定义域为全体实数集R;函数值为对应x的表达式2x + 1的值,即f(x) = 2x + 1的值域也是全体实数集R。
2. 函数的图象函数的图象是函数在平面直角坐标系上的表示,用于描述函数的性质和变化规律。
函数的图象通常是一条曲线,通过观察图象可以得到函数的一些重要信息。
二、函数的性质函数有许多重要的性质,这些性质帮助我们更深入地理解和分析函数的特点。
1. 奇偶性如果对于函数f(x),对于任意实数x,有f(-x) = f(x),则称函数f(x)为偶函数;如果对于任意实数x,有f(-x) = -f(x),则称函数f(x)为奇函数。
例如,函数f(x) = x^2是一个偶函数,因为对于任意实数x,都有f(-x) = (-x)^2 = x^2 = f(x);函数g(x) = x^3是一个奇函数,因为对于任意实数x,都有g(-x) = (-x)^3 = -x^3 = -g(x)。
2. 单调性函数的单调性描述了函数值随自变量的变化而变化的规律。
函数可以是增函数、减函数或者不变函数。
增函数是指随着自变量的增大,函数值也随之增大;减函数则是指随着自变量的增大,函数值减小;不变函数则是指自变量的改变不会导致函数值的变化。
八年级上册数学函数知识点_初中数学函数知识必看

八年级上册数学函数知识点_初中数学函数知识必看八年级上册数学函数知识点一、函数:一般地,在某一变化过程中有两个变量x与y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。
二、自变量取值范围使函数有意义的自变量的取值的全体,叫做自变量的取值范围。
一般从整式(取全体实数),分式(分母不为0)、二次根式(被开方数为非负数)、实际意义几方面考虑。
三、函数的三种表示法及其优缺点(1)关系式(解析)法两个变量间的函数关系,有时可以用一个含有这两个变量及数字运算符号的等式表示,这种表示法叫做关系式(解析)法。
(2)列表法把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系,这种表示法叫做列表法。
(3)图象法用图象表示函数关系的方法叫做图象法。
四、由函数关系式画其图像的一般步骤(1)列表:列表给出自变量与函数的一些对应值(2)描点:以表中每对对应值为坐标,在坐标平面内描出相应的点(3)连线:按照自变量由小到大的顺序,把所描各点用平滑的曲线连接起来。
五、正比例函数和一次函数1、正比例函数和一次函数的概念一般地,若两个变量x,y间的关系可以表示成(k,b为常数,k0)的形式,则称y是x的一次函数(x为自变量,y为因变量)。
特别地,当一次函数中的b=0时(即)(k为常数,k0),称y是x的正比例函数。
2、一次函数的图像:所有一次函数的图像都是一条直线3、一次函数、正比例函数图像的主要特征:一次函数的图像是经过点(0,b)的直线;正比例函数的图像是经过原点(0,0)的直线。
八年级上册数学函数知识考点归纳大全我们称数值变化的量为变量(variable)。
有些量的数值是始终不变的,我们称它们为常量(constant)。
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们说x是自变量(independentvariable),y是x的函数(function)。
初中数学函数知识点汇总

初中数学函数知识点汇总在初中数学学习中,函数是一个重要的概念,它涉及到数学中的关系与变化。
函数不仅在数学中有着广泛的应用,还在其他学科和实际生活中都有着重要的作用。
本文将对初中数学中的函数知识点进行汇总,并进行简要的介绍和解释。
一、函数的定义和表示方法函数是一种特殊的关系,它将一个数集中的每个数与另一个数集中的唯一一个数相关联。
函数通常用f(x)方式表示,其中x为自变量,f(x)为因变量。
二、函数的性质1. 定义域和值域:函数的定义域是自变量的取值范围,值域是因变量的取值范围。
2. 单调性:函数可以是递增的(严格递增和非严格递增)或递减的(严格递减和非严格递减)。
3. 奇偶性:函数可以是奇函数(f(-x)=-f(x))或偶函数(f(-x)=f(x))。
4. 周期性:函数可以是周期函数,即存在正数T,使得f(x+T)=f(x)。
三、常见函数的图像和性质1. 线性函数:f(x)=kx+b,其中k为斜率,b为截距。
线性函数的图像是一条直线。
2. 二次函数:f(x)=ax²+bx+c,其中a≠0。
二次函数的图像为抛物线。
3. 幂函数:f(x)=xⁿ,其中n为正整数。
幂函数的图像随着n的不同而有所变化。
4. 开方函数:f(x)=√x,其中x≥0。
开方函数的图像是一条非负的曲线。
5. 绝对值函数:f(x)=|x|。
绝对值函数的图像是一个V字形。
6. 正弦函数和余弦函数:f(x)=sinx和f(x)=cosx。
它们的图像是典型的周期函数。
四、函数的运算1. 函数的四则运算:给定两个函数f(x)和g(x),可以进行加、减、乘、除等运算得到新的函数。
f(x)+g(x)、f(x)-g(x)、f(x)×g(x)、f(x)/g(x)2. 复合函数:将一个函数的输出作为另一个函数的输入,即f(g(x))。
复合函数的运算结果是一个新的函数。
五、函数的应用函数在数学中有着广泛的应用,同时也在其他学科和实际生活中有着重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x 2 0 【自主解答】选C.根据题意得: x 3 0,
解得x≥2且x≠3.
【答题关键指导】 常见的自变量的取值范围的求法
所给代数式 自变量的取值范围 的形式
整式
分式 偶次根式
一切实数
使分母不为零的一切实数,注意不能随意约分, 同时注意“或”和“且”的含义 被开方数应满足大于或等于0
(3,5).
2.(2018·武汉中考)点A(2,-5)关于x轴对称的点的坐 标是 ( )
A.(2,5)
C.(-2,-5)
B.(-2,5)
D.(-5,2)
【解析】选A.点A(2,-5)关于x轴对称的点的坐标是 (2,5).
3.(2018·东营中考)在平面直角坐标系中,若点 P(m-2,m+1) 在第二象限,则m的取值范围是( )
)
(2)(2018·乌鲁木齐中考)在平面直角坐标系xOy中,将 点N(-1,-2)绕点O旋转180°,得到的对应点的坐标是
(
)
B.(-1,2) D.(1,-2)
A.(1,2) C.(-1,-2)
(3)(2018·长沙中考)在平面直角坐标系中,将点 A(-2,3)向右平移3个单位长度,再向下平移2个单位
A.m<-1
C.-1<m<2
B.m>2
D.m>-1
m 2<0, 【解析】选C.根据题意得 解得-1<m<2. m 1>0,
考点二 确定函数自变量的取值范围
x2 【示范题3】(2018·娄底中考)函数y= 中自变 x 3
量x的取值范围是 (
A.x>2 C.x≥2且x≠3
)
B.x≥2 D.x≠3
长度,那么平移后对应的点A'的坐标是________.
【自主解答】(1)选A.关于y轴对称点的坐标,其横坐标 互为相反数,纵坐标不变即为(1,2).
(2)选A.在平面直角坐标系xOy中,将点N(-1,-2)绕点O
旋转180°,得到的对应点的坐标是(1,2).
(3)∵将点A(-2,3)向右平移3个单位长度, ∴得到(1,3),∵再向下平移2个单位长度,
二、函数的定义 1.常量与变量:在某一变化过程中,始终保持不变的量 常量 数值变化的量叫做_____. 变量 叫做_____,
2.函数:在一个变化过程中,如果有两个变量x和y,并且 唯一 确定的值与其对 对于x的每一个确定的值,y都有_____ x 是自变量,__ y 是__ x 的函数. 应,那么就说__ 如果当x=a时y=b,那么b叫做当自变量的值为a时的 函数值 _______.
3 则m> . 2
(√ )
2.若y轴上的点A到x轴的距离为3,则点A的坐标为 (3,0). (× )
3.等腰三角形的底边长和面积不是函数关系.
(√ )
5 4.在函数y= 中,自变量x的取值范围x≥2. ( × ) x2
考点一 平面直角坐标系及点的坐标变换
【考情分析】平面直角坐标系及点的坐标变换的层级 为理解坐标系内点的坐标特点及能根据图形变换写出
∴平移后对应的点A'的坐标是(1,1).
答案:(1,1)
【答题关键指导】 1.坐标系内具有特殊位置关系的两点的坐标特征
两点的位置 关于x轴对称 关于y轴对称 坐标特征 横坐标相同,纵坐标互为相反数 横坐标互为相反数,纵坐标相同
关于原点对称 两点连线与x轴平行 两点连线与y轴平行
横、纵坐标都互为相反数 纵坐标相同 横坐标相同
变换后的点的坐标,能用有序数对表示位置,在各地中
考试题中均有体现,是函数初步的一个重要考向,一般与
图形的平移、轴对称、中心对称、位似及旋转结合考 查,各种题型均有体现.
命题角度1:坐标系内点的坐标特征 【示范题1】(2018·广安中考)已知点P(1-a,2a+6)在
第四象限,则a的取值范围是 (
三、函数的图象 1.列表:根据解析式列出自变量x与函数y之间的对应值
表.
坐标 在平面直角坐 2.描点:每组对应值就是一个点的_____, 标系中描出这些点.
3.连线:用光滑曲线(或直线)连接这些点,这些点组成 的图形就是这个函数的图象.
【自我诊断】(打“√”或“×”) 1.在平面直角坐标系中,点(-2,-2m+3)在第三象限,
第九讲
函 数 初 步
一、平面直角坐标系 1.各象限点的坐标的符号特征:
(-,+) 第一象限(+,+);第二象限______;
(+,-) 第三象限(-,-);第四象限______.
纵坐标 为0;y轴上 2.坐标轴上点的坐标特征:x轴上的点_______ 横坐标 为0;原点的坐标为______. (0,0) 的点_______
A.a<-3 C.a>-3 B.-3<a<1 D.a>1
)
【自主解答】选A.由第四象限的符号特征为(+,-),得 1-a>0,2题角度2:图形变换与坐标 【示范题2】(1)(2018·湘潭中考)如图,点A的坐标为
(-1,2),则点A关于y轴的对称点的坐标为 (
A.(1,2) C.(1,-2) B.(-1,-2) D.(2,-1)
2.平移变换与点的坐标特征 (1)左右平移,横坐标左减右加,纵坐标不变.
(2)上下平移,纵坐标上加下减,横坐标不变.
【跟踪训练】 1.(2018·成都中考)在平面直角坐标系中,点P(-3,-5)
关于原点对称的点的坐标是 (
A.(3,-5) C.(3,5) B.(-3,5) D.(-3,-5)
)
【解析】选C.关于原点对称的点的坐标,横、纵坐标都 互为相反数,∴点P(-3,-5)关于原点对称的点的坐标是
2.(2018·岳阳中考)函数y= x 3 中自变量x的取值范 围是 ( )
A.x>3
B.x≠3
C.x≥3
D.x≥0
【解析】选C.根据题意可得x-3≥0,解得x≥3.
3.(2018·内江中考)已知函数y= x 1 ,则自变量x的
所给代数式的 形式 0次幂或负整数 指数幂
自变量的取值范围 底数不为零
复合形式 具有实际意义
列不等式组,使所有式子同时有意义 使实际问题有意义
【跟踪训练】 1.(2018·永州中考)函数y= 1 中自变量x的取值范围
x 3
是
(
)
B.x<3 C.x≠3 D.x=3
A.x≥3
【解析】选C. 根据题意得:x-3≠0, 解得:x≠3.
