(完整版)五种灰色关联度分析matlab代码
(整理)灰色关联度分析法
灰色关联度分析法为了适应瞬息万变的市场需求, 企业不断调整自己的核心能力, 在产品的开发设计中更重视供应商的作用。
作为供应链合作关系运行的基础, 供应商的评价选择是一个至关重要的问题, 供应商的业绩对企业的影响越来越大,影响着企业的生存与发展。
因此, 进行科学全面的供应商评价就显得十分必要。
(1)确定比较对象产品质量、技术水平、供应能力、经济效益、市场影响度指标属于效益型指标;产品价格、地理位置、售后服务指标属于成本型指标。
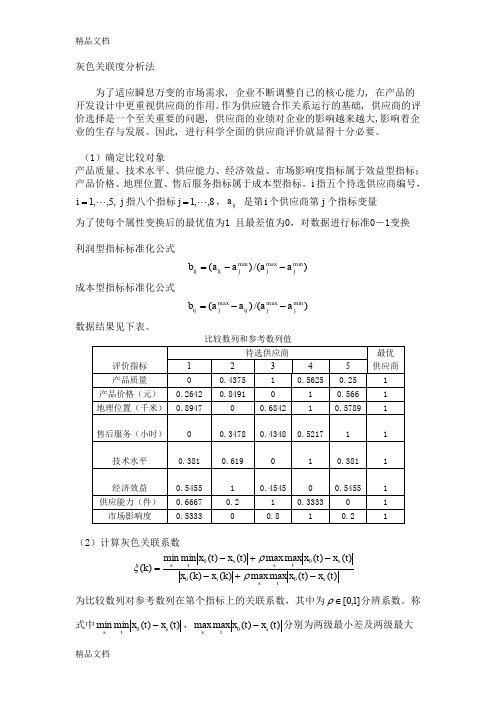
i 指五个待选供应商编号,,5,,1 =i j 指八个指标8,,1j =,ij a 是第i 个供应商第j 个指标变量为了使每个属性变换后的最优值为1 且最差值为0,对数据进行标准0-1变换利润型指标标准化公式)/()(min maxmin j j j ij ij a a a a b --=成本型指标标准化公式)/()(min max max j j ij j ij a a a a b --=数据结果见下表。
(2)计算灰色关联系数)()(max max )()()()(max max )()(min min )(0000t x t x k x k x t x t x t x t x k s tsi s ts s ts -+--+-=ρρξ为比较数列对参考数列在第个指标上的关联系数,其中为]1,0[∈ρ分辨系数。
称式中)()(min min 0t x t x s ts-、)()(max max 0t x t x s ts-分别为两级最小差及两级最大差。
一般来讲,分辨系数ρ越大,分辨率越大;ρ越小,分辨率越小。
在这里ρ取0.5。
(3)计算灰色加权关联度 灰色加权关联度的计算公式为∑==nk i i k w r 1)(ξ这里i r 为第i 个评价对象对理想对象的灰色加权关联度。
关联系数和关联度值(4)评价分析根据灰色加权关联度的大小,对各评价对象进行排序,可建立评价对象的关联序,关联度越大其评价结果越好。
(完整版)五种灰色关联度分析matlab代码

(完整版)五种灰色关联度分析matlab代码灰色邓氏关联度分析% P12 -- The Study on the Grey Relational Degree and Its Application function r1 = gld_deng(x)s = size(x);len = s(2);num = s(1);ro = 0.5;for i = 1: numx(i,:) = x(i,:)./x(i,1);enddx(num,len) = 0;for i = 2 : numfor k = 1 : lendx(i,k) = abs(x(1,k) - x(i,k));endendmax_dx = max(max(dx));min_dx = min(min(dx));r(1,1:len-1) = 1;for i = 2 : numfor k = 1 : lenr(i,k) = (min_dx + ro*max_dx)/(dx(i,k) + ro*max_dx);endendr1 = sum(r(2:num,:),2)/(len);改进灰色绝对关联度分析% P11 -- The Study on the Grey Relational Degree and Its Application function r1 = gld_gjjd(x)s = size(x);len = s(2);num = s(1);for i = 1: numx(i,:) = x(i,:)./x(i,1);enddx(num,len-1) = 0;for i = 1 : numfor j = 1 : len - 1dx(i,j) = x(i,j+1) - x(i,j);endendc = 1;beta(1,1:len-1) = 0;w(1,1:len-1) = 0;for i = 2 : numtemp = sum(abs(x(i,:) - x(1,:)),2);for k = 1 : len - 1beta(i,k) = atan((dx(i,k) - dx(1,k))/(1 + dx(i,k)*dx(1,k)));if beta(i,k) < 0beta(i,k) = pi + beta(i,k);endw(i,k) = 1 - abs(x(i,k) - x(1,k))/temp;endendr = c./(c + tan(beta./2));wr = w.*r;r1 = sum(wr(2:num,:),2)/(len - 1);灰色绝对关联度分析% P18 -- The Study on the Grey Relational Degree and ItsApplication function r1 = gld_jd(x)s = size(x);len = s(2);num = s(1);for i = 1: numx(i,:) = x(i,:)./x(i,1);enddx(num,len-1) = 0;for i = 1 : numfor j = 1 : len - 1dx(i,j) = x(i,j+1) - x(i,j);endendr(1,1:len-1) = 1;for i = 2 : numfor k = 1 : len - 1r(i,k) = 1/(1 + abs(dx(1,k) - dx(i,k)));endendr1 = sum(r(2:num,:),2)/(len - 1);灰色T型关联度分析% P19 -- The Study on the Grey Relational Degree and Its Application function r1 = gld_t(x)s = size(x);len = s(2);num = s(1);dx(num,len-1) = 0;for i = 1 : numfor j = 1 : len - 1dx(i,j) = abs(x(i,j+1) - x(i,j));d_x = sum(dx(i,:),2)/(len - 1);x(i,:) = x(i,:)./d_x;enddx(num,len-1) = 0;for i = 1 : numfor j = 1 : len - 1dx(i,j) = x(i,j+1) - x(i,j);endendr(1,1:len-1) = 1;for i = 2 : numfor k = 1 : len - 1if dx(1,k)*dx(i,k) == 0r(i,k) = sign(dx(1,k)*dx(i,k));elser(i,k) = sign(dx(1,k)*dx(i,k))*min(abs(dx(1,k)),abs(dx(i,k))) / max(abs(dx(1,k)),abs(dx(i,k)));endendendr1 = sum(r(2:num,:),2)/(len - 1);灰色斜率关联度分析% P20 -- The Study on the Grey Relational Degree and Its Application function r1 = gld_xl(x)s = size(x);len = s(2);num = s(1);for i = 1: numx(i,:) = x(i,:)./x(i,1);dx(num,len-1) = 0;for i = 1 : numfor j = 1 : len - 1dx(i,j) = x(i,j+1) - x(i,j);endendr(1,1:len-1) = 1;for i = 2 : numfor k = 1 : len - 1r(i,k) = 1/(1 + abs(dx(1,k)/x(1,k+1) - dx(i,k)/x(i,k+1))); endendr1 = sum(r(2:num,:),2)/(len - 1);。
matlab 灰度算法 -回复

matlab 灰度算法-回复Matlab灰度算法在Matlab中,灰度算法是图像处理中应用最广泛的一种算法之一。
灰度图像通常被用于减少图像的复杂性,保留图像中的重要信息,同时提高图像处理的速度和效率。
本文将介绍Matlab中常用的灰度算法,以及如何逐步实现这些算法。
一、图像的灰度化图像的灰度化是将彩色图像转换为灰度图像的过程。
Matlab中提供了多种灰度化方法,比较常用的是平均值法和加权平均值法。
1. 平均值法平均值法是将RGB三个分量的平均值作为灰度值,公式如下:灰度值= (R + G + B) / 3在Matlab中,可以使用rgb2gray函数将彩色图像转换为灰度图像。
2. 加权平均值法加权平均值法是根据颜色对灰度的贡献程度不同,对RGB分量进行加权求和得到灰度值。
一般情况下,红色对灰度的贡献最高,绿色次之,蓝色最低。
公式如下:灰度值= 0.299 * R + 0.587 * G + 0.114 * B同样地,在Matlab中可以使用rgb2gray函数实现加权平均值法。
二、图像的灰度直方图灰度直方图是衡量图像亮度分布的工具。
它将图像中所有像素的灰度值分布在不同的亮度级别上,并统计每个亮度级别的像素数量。
在Matlab中,可以使用imhist函数计算图像的灰度直方图。
1. 计算灰度直方图matlabim = imread('image.jpg'); 读取图像gray_image = rgb2gray(im); 灰度化imhist(gray_image); 计算灰度直方图这段代码首先读取名为image.jpg的图像,然后将其转换为灰度图像gray_image,最后使用imhist函数计算灰度直方图。
2. 绘制灰度直方图matlabim = imread('image.jpg'); 读取图像gray_image = rgb2gray(im); 灰度化hist_array = imhist(gray_image); 计算灰度直方图bar(hist_array); 绘制直方图xlabel('灰度级别'); x轴标签ylabel('像素数量'); y轴标签title('灰度直方图'); 标题这段代码在计算灰度直方图的基础上,使用bar函数绘制直方图,然后通过xlabel、ylabel和title函数设置相应的标签和标题。
matlab 灰度算法 -回复

matlab 灰度算法-回复【MATLAB灰度算法】灰度算法是一种将彩色图像转化为黑白图像的方法,在计算机视觉和图像处理领域被广泛使用。
MATLAB是一种强大的数学计算工具,它提供了丰富的图像处理函数和工具箱,可用于实现灰度算法。
本文将逐步回答如何使用MATLAB实现灰度算法,并介绍一些常用的灰度算法技术。
# 第一步:图像读取与显示在MATLAB中,可以使用`imread`函数读取图像,使用`imshow`函数显示图像。
我们首先需要读取一张彩色图像,并将其显示出来。
matlab读取彩色图像rgbImage = imread('image.jpg');显示彩色图像imshow(rgbImage);title('Original Image');# 第二步:转化为灰度图像灰度图像是一种每个像素只有一个灰度值(亮度值)的图像。
在MATLAB中,可以使用`rgb2gray`函数将彩色图像转化为灰度图像。
matlab将彩色图像转化为灰度图像grayImage = rgb2gray(rgbImage);显示灰度图像imshow(grayImage);title('Grayscale Image');# 第三步:灰度化算法选择灰度化算法决定了如何将彩色图像中的RGB信息转化为灰度图像中的灰度值。
常用的灰度化算法有平均值法、加权平均法和分量最大法等。
下面分别介绍这些算法并给出MATLAB代码实现。
平均值法平均值法是最简单的灰度化算法之一,它将彩色图像的RGB分量的平均值作为灰度值。
具体实现如下:matlab平均值法灰度化averageGrayImage = (rgbImage(:, :, 1) + rgbImage(:, :, 2) + rgbImage(:, :, 3)) / 3;显示平均值法灰度图像imshow(averageGrayImage);title('Average Grayscale Image');加权平均法加权平均法是一种考虑了RGB分量的亮度影响的灰度化算法。
灰色模型预测GM(1,1)MATLAB程序代码

灰⾊模型预测GM(1,1)MATLAB程序代码版权所有引⽤请注明出处function gmcal=gm1(x)%% ⼆次拟合预测GM(1,1)模型%x = [5999,5903,5848,5700,7884];sizexd2 = size(x,2);%求数组长度k=0;for y1=xk=k+1;if k>1x1(k)=x1(k-1)+x(k);%累加⽣成z1(k-1)=-0.5*(x1(k)+x1(k-1));%z1维数减1,⽤于计算Byn1(k-1)=x(k);elsex1(k)=x(k);endend%x1,z1,k,yn1sizez1=size(z1,2);%size(yn1);z2 = z1';z3 = ones(1,sizez1)';YN = yn1'; %转置B=[z2 z3];au0=inv(B'*B)*B'*YN;au = au0';afor = au(1);ufor = au(2);ua = au(2)./au(1);constant1 = x(1)-ua;afor1 = -afor;x1t1 = 'x1(t+1)';estr = 'exp';tstr = 't';leftbra = '(';rightbra = ')';strcat(x1t1,'=',num2str(constant1),estr,leftbra,num2str(afor1),tstr,rightbra,'+',leftbra,num2str(ua),rightbra) %输出时间响应⽅程k2 = 0;for y2 = x1k2 = k2 + 1;if k2 > kelseze1(k2) = exp(-(k2-1)*afor);endendsizeze1 = size(ze1,2);z4 = ones(1,sizeze1)';G=[ze1' z4];X1 = x1';au20=inv(G'*G)*G'*X1;au2 = au20';Aval = au2(1);Bval = au2(2);strcat(x1t1,'=',num2str(Aval),estr,leftbra,num2str(afor1),tstr,rightbra,'+',leftbra,num2str(Bval),rightbra) %输出时间响应⽅程nfinal = sizexd2-1 + 1; %决定预测的步骤数5 这个步骤可以通过函数传⼊%nfinal = sizexd2 - 1 + 1;%预测的步骤数 1for k3=1:nfinalx3fcast(k3) = constant1*exp(afor1*k3)+ua;end%⼀次拟合累加值for k31=nfinal:-1:0if k31>1x31fcast(k31+1) = x3fcast(k31)-x3fcast(k31-1);elseif k31>0x31fcast(k31+1) = x3fcast(k31)-x(1);elsex31fcast(k31+1) = x(1);endendendx31fcast%⼀次拟合预测值for k4=1:nfinalx4fcast(k4) = Aval*exp(afor1*k4)+Bval;end%x4fcastfor k41=nfinal:-1:0if k41>1x41fcast(k41+1) = x4fcast(k41)-x4fcast(k41-1);elseif k41>0x41fcast(k41+1) = x4fcast(k41)-x(1);elsex41fcast(k41+1) = x(1);endendendx41fcast,x%⼆次拟合预测值%***精度检验p C************//////////////////////////////////k5 = 0;for y5 = xk5 = k5 + 1;if k5 > sizexd2elseerr1(k5) = x(k5) - x41fcast(k5);endend%err1%绝对误差xavg = mean(x);%xavg%x平均值err1avg = mean(err1);%err1avg%err1平均值k5 = 0;s1total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2elses1total = s1total + (x(k5) - xavg)^2;endends1suqare = s1total ./ sizexd2;s1sqrt = sqrt(s1suqare);%s1suqare,s1sqrt%s1suqare 残差数列x的⽅差 s1sqrt 为x⽅差的平⽅根S1k5 = 0;s2total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2elses2total = s2total + (err1(k5) - err1avg)^2;endends2suqare = s2total ./ sizexd2;%s2suqare 残差数列err1的⽅差S2Cval = sqrt(s2suqare ./ s1suqare);Cval%nnn = 0.6745 * s1sqrt%Cval C检验值k5 = 0;pnum = 0 ;for y5 = xk5 = k5 + 1;if abs( err1(k5) - err1avg ) < 0.6745 * s1sqrtpnum = pnum + 1;%ppp = abs( err1(k5) - err1avg )elseendendpval = pnum ./ sizexd2;pval%p检验值%arr1 = x41fcast(1:6)%预测结果为区间范围预测步长和数据长度可调整程序参数进⾏改进。
灰色关联模型 python代码

灰色关联模型python代码摘要:1.灰色关联模型的概念2.灰色关联模型的Python 代码实现3.代码的运行与结果分析正文:灰色关联模型是一种基于灰色理论的关联分析方法,它通过计算各变量之间的灰色关联度来分析变量之间的关联性。
该模型广泛应用于工程、经济、社会等领域,对于数据挖掘、预测和决策具有重要意义。
下面我们将通过Python 代码实现灰色关联模型,并分析运行结果。
首先,我们需要安装`greyTheory`库,这是一个用于灰色关联分析的Python 库。
在命令行中输入以下命令进行安装:```pip install greyTheory```接下来,我们编写Python 代码来计算灰色关联度:```pythonimport numpy as npimport pandas as pdfrom greyTheory.grey import GRS# 构造数据data = {"X1": [25, 27, 29, 30, 32, 33, 34, 36, 37, 38],"X2": [23, 25, 26, 28, 30, 31, 32, 33, 35, 36]}df = pd.DataFrame(data)# 计算灰色关联度grs = GRS()result = grs.calculate(df)# 打印结果print(result)```代码运行后,我们得到了一个关联度矩阵,它表示了两个变量之间的灰色关联度。
关联度值的范围为-1 到1,值越接近1,表示两个变量之间的关联性越强;值越接近-1,表示两个变量之间的关联性越弱。
在上述示例中,我们构造了两组数据(X1 和X2),并计算了它们之间的灰色关联度。
灰色预测MATLAB程序

灰色预测心设尹曲⑴#为原始数列,其1次累<加生成数列为炉=(孝①宀2\S,其中©=2^°:⑺卫=12…止i-1尋定文沙的灰导数为d(Jt)=玄㈣(Jt)=尤⑴的-工⑴(*-1).令尹为数列壬⑴的邻值生成数列,即尹)(町=加小(町十(1—a)x山(k-1).于是定文GM(1T1)的灰微分方程模型为d(k)+az①(上)=&_即或.严⑹+盘⑴懐)=乩⑴在式(1)中口①的称为灰导数’熬称为发展系数'弧称为白化背景值,b称为灰作用量。
将时刻表庄=23…用代入(O式有j<0)(2)-az⑴(2)=工®⑶—俺叫巧=»于是GMIL)樫型可表示为r=现在问题归结为求巧h在值。
用一元绒性回归,即最小二垂進求它们的估计值住=[]卜护跖护F奕厢上回归分析中求诂计值是用软件计算的,有标淮程博求解,如山訥甜等。
GM(1.1)的白化型对于的(1-1)的获微分方程⑴,如果将解导教矿悶的时報=%…屮观対连续叢里"则工⑴衩为时间i函敕卅®,于是-<'W耐应于导敕重级必%),白化背杲值刃(時对应于导數申⑴。
于是GM(1,1)的换微分方嗨对应于的白微分方程为写®4曲%「)=也⑵GAI(1>1)换色预刪的步叢1-數堀的椅噓弓处理为了保证©M(B1)屋複方达的可行性・需要対已却皴堀锁必要的检峻处Ho 设療皓数攥列为了-计算埶列的级比如果所有的级比都落在可容覆盖区间盂-內・则數摒列X糾可咲建立G*ICL-1)複型且可以避行页色预测。
否则,丙軌据懺适当的叢换处理,如平移銮换:取C使得敕培列严⑹二工蚀盘)+匚用二12…”的级比都落在可啓禎盖内。
(1)残差檢验:计算相对薙差Z 建立GM (L T 1)複型不妬设少弋以m 叫唠霸足上面的要求,以它芮議堀列建立GM(1>1)型蛊(仍(i)+血C1\A)=b ・用回归分祈求得目上的估计值"于是相应的白化模型为 气^十小卄工解为工叱)=0)①—勺中1-色-⑶ 应Q于是停到预测值壬⑴(上+1)=0叫1)一勺>加+仝血二12…卫一1=aa伙而相应地得到预«=x co \t +1)=x 0)(t+l)-x a)(i)3i =1,2,-?n-l ?如果对所有的^<0.1・则认为达到鞭嵩的要求:否则,若耐所有的|^)1<0^,则认対达到一般要求©(2)级比偏差値桧验:计算能)=1-呂学©如果对所有的|,则认为达列较高的要求孑吾则若对斫有的,则认为达到一般要求O灰色预测计算实例^…;=:=-■■■■昏例北方某城市1986—1992年道路交通噪声平均声级数据见表6序号年吶寺表拆市近年来交通噪声数据[眶(应)]二諾;二319S872.4第—爭:级比检验建立丢通噪屛均声级数锯时间序列如下:4198972.1j 1990?1.4 619?17201199771.6艸=(•严①卫购(2)厂卅⑺) =(711,72.4.71.4,72.1.71.4,7UQ.71.6)些(1)求级比k(k)忠防护住T)2=(几⑵山⑶.…也⑺)g=(0.982JJ.0042J.0098-0.9917J.0056)(2)级比判断由于所有的X.(10e[0.982J.009S],k=2,3.6故可以用双0)作满意的GM(1,1)建模’第二步:GM(1,1)建模(1)对原始数据X®作一次累加,即卞⑴=(71.L143.5215.9.288359.4.431.4,503)(2)构造数据矩阵B及数据向量Y-2)—H 弋3/>1⑶讦算1T心求解得F'⑴=(工倒〔1〉_-)e 弋Q f+-1*^+1)=0<l,U)--)£-t +-=-3092^--^+31000⑶求生咸数列值歸型齊看:n令“is 那血由上面的碉醯数可甲得,其中取菱由龙⑴(i}=恥壮曲5加得丁I —"炉閃=进悶-进德-尊(71儿72.4.72.2:72.1:71.9:71.7,71.6)^}=(s"a >亍⑴⑵,…,网⑺A<第三步;模型检验•>模型的各种检验指标值的计算结果见表工 •t*表7GM(1检验表<序号年俯原始值模型值残差相对误差级比偏差•>1 19S6 71.1 71.1<219S7 72.4 72.4 -0.0057 0.01%0.0023 <3 19S S 72.4 72.2 0.163S 0.23%0.0203 •>4 19S9 72.1 72.1 0.0329 0.05%-O.(K H8 •>5199071.4 71.9 -0-49S4 0.7%-0.0074 <61991 72.0 71.7 0.21599 037%0.0107<71992 71.6 71.6 0.037S0.05%-0.0032于是得到目=山的餡,立欖型7-B)'1B TY=(dt0.0023 72.6573dt+0.002ix (1>=72.657^心经验证・该模型的精度较高.可进行预测和预报计算的Matlab 程序如下:仃坝测和预报n=length(x); z=0;%取输入数据的样本量for i=1:nz=z+x(i,:)be(i,:)=z; %计算累加值,并将值赋予矩阵beend for i=2:n %对y(i-1,:)=x(i,:)%对原始数列平行移位 endfor i=1:n-1%计算数据矩阵B 的第一列数据c(i,:)=-0.5*(be(i,:)+be(i+1,:)); clCjdearxO=[71H 72.472A 72J71477m c n.lengthtxO);*'b%注意这里为列帖lamda =xD(l :n-1),A0(2:n)%计算级比range =minmaxflamda f )%计算级比的范阖 X1=cumsum(xO);%累加运算B=['0,5*(xl(l ;n ^l)+xl(2:n))t ones(n -1,1)]TY 二甸(2:町;口=B\Y%拟合参数u(l>=a .u(2)=bx=dsolve (+a 'x =b\f x(0)-xO^J ;%求徴分方程的特号解x =subs(xJ*a\,b r /xO ,Mu(l)P u(2)t xO(l)|)i%代入荷计痹擞值和初蜡值yucel =subs %求巳知数擁的扳测位y-vpa(x,6)奄其中的石表示显不白位数字yuce=[x0(l)T diff(yucel)]%羔分运算,还原数据 epsiIon=-yuce%计算战羞作用:求累加数列、求ab 的值、求预测方程、求残差clc %清屏,以使结果独立显示x=[71.172.472.472.171.472.071.6]; format long ;%设置计算精度if length(x(:,1))==1%对输入矩阵进行判断,如不是一维列矩阵,进行转置变换x=x endM.I-JTVorhlllst 模型endfor j=1:n-1%计算数据矩阵B的第二列数据e(j,:)=1;endfor i=1:n-1%构造数据矩阵BB(i,1)=c(i,:);B(i,2)=e(i,:);endalpha=inv(B'*B)*B'*y;%计算参数矩阵即ab的值for i=1:n+1%计算数据估计值的累加数列,如改为n+1为n+m可预测后m-1个值ago(i,:)=(x(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1,:)*(i-1))+alpha( 2,:)/alpha(1,:);%显示输出预测值的累加数列endvar(1,:)=ago(1,: )for i=1:n%显示输出预测值%如改n为n+m-1,可预测后m-1个值var(i+1,:)=ago(i+1,:)-ago(i,:);%估计值的累加数列的还原,并计算出下一预测值endfor i=1:nerror(i,:)=x(i,:)-var(i,:);%计算残差endc=std(error)/std(x);%调用统计工具箱的标准差函数计算后验差的比值cago alpha var%显示输出预测值的累加数列%显示输出参数数列%显示输出预测值error %显示输出误差c %显示后验差的比值作用:数据处理判断是否可以用灰色预测、求级比、求累加数列、求ab的值、求预测方程clc,clearx0=[71.172.472.472.171.472.071.6]';%注意这里为列向量n=length(x0);lamda=x0(1:n-1)./x0(2:n)%计算级比range=minmax(lamda')%计算级比的范围x1=cumsum(x0)%累加运算B=[-0.5*(x1(1:n-1)+x1(2:n)),ones(n-1,1)];Y=x0(2:n);u=B\Y%拟合参数u(1)=a,u(2)=bx=dsolve('Dx+a*x=b','x(0)=x0');%求微分方程的符号解x=subs(x,{'a','b','x0'},{u(1),u(2),x0(1)})%代入估计参数值和初始值yuce1=subs(x,'t',[0:n-1]);%求已知数据的预测值y=vpa(x,6)%其中的6表示显示6位数字yuce=[x0(1),diff(yuce1)]%差分运算,还原数据。
灰色预测MATLAB代码

function hsyc(x0)%灰色模型GM(1,1)matlab代码在建立灰色模型前应对原始数据进行求%%%级比%%%%重要%输入原始时序列x0,输出各种所需参数%%%%实际使用该程序时应改变图像坐标轴%%%%%x0代表原始数据;x1代表x0经累加后;B代表所够造的矩阵B;Y代表向量Yn;au代表系数a,u构成的矩阵n=size(x0,2); %计算x0的列数x1=cumsum(x0,2); %将x0进行累加得到矩阵x1for k=1:n-1;b(k)=-0.5*(x1(k+1)+x1(k));y(k)=x0(k+1); %计算得到向量Y的转置矩阵yenda=ones(n-1,1);B=[b',a]; %计算得到矩阵BY=y'; %计算得到向量Yau=inv(B'*B)*B'*Y; %计算得到系数a,u构成的矩阵auA=au';k=1:n+10;X1(k)=(x0(1)-A(2)/A(1))*exp(-A(1)*(k-1))+A(2)/A(1); %计算预测累加数列的值X0(1)=X1(1);k=1:n+9;X0(k+1)=X1(k+1)-X1(k); %计算预测累加数列的还原值,即预测值for k=2:n;e(k)=X0(k)-x0(k); %计算残差E(k)=(X0(k)-x0(k))/x0(k); %计算预测值与实测值的差值跟实测值的比值,即残差与实测值的比值j(k)=x0(k-1)/x0(k); %计算实测数据的级比endk=1:n;p(k)=1-(1-0.5*A(1))*j(k)/(1+0.5*A(1)); %计算级比偏差e(k)、p(k)<0.1则说明模型达到较高要求,0.2>e(k)、p(k)>0.1则说明模型达到一般要求m=min(abs(e)); %计算残差中的最小值M=max(abs(e)); %计算残差中的最大值k=1:n;g(k)=(m+0.5*M)./(abs(e(k))+0.5*M); %计算关联系数R=sum(g')/(n-1); %计算关联度v=[1,5,120,185];axis(v);grid onplot([1996:2005],x0,'o-',[1996:2015],X0,'*:'); %画出原始数据跟时间序列的图像及预测数据跟时间序列的图像legend('原始数据','预测数据',4)au %输出参数a,u的值X0 %输出预测数列e %输出残差E %输出残差与原始数据的比值,定义的残差j %输出原始数据的级比p %输出偏比差R %输出关联度程度X1end。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色邓氏关联度分析
% P12 -- The Study on the Grey Relational Degree and Its Application function r1 = gld_deng(x)
s = size(x);
len = s(2);
num = s(1);
ro = 0.5;
for i = 1: num
x(i,:) = x(i,:)./x(i,1);
end
dx(num,len) = 0;
for i = 2 : num
for k = 1 : len
dx(i,k) = abs(x(1,k) - x(i,k));
end
end
max_dx = max(max(dx));
min_dx = min(min(dx));
r(1,1:len-1) = 1;
for i = 2 : num
for k = 1 : len
r(i,k) = (min_dx + ro*max_dx)/(dx(i,k) + ro*max_dx);
end
end
r1 = sum(r(2:num,:),2)/(len);
改进灰色绝对关联度分析
% P11 -- The Study on the Grey Relational Degree and Its Application function r1 = gld_gjjd(x)
s = size(x);
len = s(2);
num = s(1);
for i = 1: num
x(i,:) = x(i,:)./x(i,1);
end
dx(num,len-1) = 0;
for i = 1 : num
for j = 1 : len - 1
dx(i,j) = x(i,j+1) - x(i,j);
end
end
c = 1;
beta(1,1:len-1) = 0;
w(1,1:len-1) = 0;
for i = 2 : num
temp = sum(abs(x(i,:) - x(1,:)),2);
for k = 1 : len - 1
beta(i,k) = atan((dx(i,k) - dx(1,k))/(1 + dx(i,k)*dx(1,k)));
if beta(i,k) < 0
beta(i,k) = pi + beta(i,k);
end
w(i,k) = 1 - abs(x(i,k) - x(1,k))/temp;
end
end
r = c./(c + tan(beta./2));
wr = w.*r;
r1 = sum(wr(2:num,:),2)/(len - 1);
灰色绝对关联度分析
% P18 -- The Study on the Grey Relational Degree and Its Application function r1 = gld_jd(x)
s = size(x);
len = s(2);
num = s(1);
for i = 1: num
x(i,:) = x(i,:)./x(i,1);
end
dx(num,len-1) = 0;
for i = 1 : num
for j = 1 : len - 1
dx(i,j) = x(i,j+1) - x(i,j);
end
end
r(1,1:len-1) = 1;
for i = 2 : num
for k = 1 : len - 1
r(i,k) = 1/(1 + abs(dx(1,k) - dx(i,k)));
end
end
r1 = sum(r(2:num,:),2)/(len - 1);
灰色T型关联度分析
% P19 -- The Study on the Grey Relational Degree and Its Application function r1 = gld_t(x)
s = size(x);
len = s(2);
num = s(1);
dx(num,len-1) = 0;
for i = 1 : num
for j = 1 : len - 1
dx(i,j) = abs(x(i,j+1) - x(i,j));
end
d_x = sum(dx(i,:),2)/(len - 1);
x(i,:) = x(i,:)./d_x;
end
dx(num,len-1) = 0;
for i = 1 : num
for j = 1 : len - 1
dx(i,j) = x(i,j+1) - x(i,j);
end
end
r(1,1:len-1) = 1;
for i = 2 : num
for k = 1 : len - 1
if dx(1,k)*dx(i,k) == 0
r(i,k) = sign(dx(1,k)*dx(i,k));
else
r(i,k) = sign(dx(1,k)*dx(i,k))*min(abs(dx(1,k)),abs(dx(i,k))) / max(abs(dx(1,k)),abs(dx(i,k)));
end
end
end
r1 = sum(r(2:num,:),2)/(len - 1);
灰色斜率关联度分析
% P20 -- The Study on the Grey Relational Degree and Its Application function r1 = gld_xl(x)
s = size(x);
len = s(2);
num = s(1);
for i = 1: num
x(i,:) = x(i,:)./x(i,1);
end
dx(num,len-1) = 0;
for i = 1 : num
for j = 1 : len - 1
dx(i,j) = x(i,j+1) - x(i,j);
end
end
r(1,1:len-1) = 1;
for i = 2 : num
for k = 1 : len - 1
r(i,k) = 1/(1 + abs(dx(1,k)/x(1,k+1) - dx(i,k)/x(i,k+1)));
end
end
r1 = sum(r(2:num,:),2)/(len - 1);。
