六年级下学期数学 用比例解决行程问题 答案
六年级简单的比例问题及答案练习题及答案

六年级简单的比例问题及答案练习题及答案题目一:比例的基本性质问题一:小明一天走了6公里,小红一天走了18步,已知1步约等于0.1公里,那么小明走了多少步?问题二:小李一天能做6个分数题,小王一天能做18个分数题,那么小李比小王慢多少倍?答案一:问题一的答案是60步。
解析:小明走的6公里可以转换成60步,因为1公里等于10步,所以6公里等于60步。
答案二:问题二的答案是3倍。
解析:小李每天做6个分数题,而小王每天做18个分数题,所以小李比小王慢3倍。
题目二:比例的应用问题一:一本书有100页,小明一天读10页,小红一天读20页,那么小明比小红慢多少倍?问题二:一个水桶装满水需要12升,小王用2个小时装满水,而小李用6个小时装满水,那么小李比小王慢多少倍?答案一:问题一的答案是1倍。
解析:小明一天读10页,小红一天读20页,两人读书的速度一样,所以小明比小红慢1倍。
答案二:问题二的答案是3倍。
解析:小王每小时装满12/2=6升,而小李每小时装满12/6=2升,所以小李比小王慢3倍。
题目三:比例的变化问题一:按照1:2的比例放大一个正方形,原来的边长是4厘米,放大后的边长是多少厘米?问题二:小李把1元钱分成两个部分,第一个部分是第二个部分的3倍,那么第一个部分是多少钱?答案一:问题一的答案是8厘米。
解析:按照1:2的比例放大一个正方形,原来的边长是4厘米,放大后的边长是4*2=8厘米。
答案二:问题二的答案是0.75元。
解析:假设第一个部分是x元钱,根据题意可得x=3*(1-x),解方程可得x=3/4=0.75元。
题目四:比例的逆运算问题一:小明买了4个苹果,一共花了12元,那么小明买一个苹果需要多少元?问题二:小红搭了6辆出租车,一共用了30元,那么小红搭一辆出租车需要多少元?答案一:问题一的答案是3元。
解析:小明买了4个苹果,一共花了12元,所以小明买一个苹果需要12/4=3元。
答案二:问题二的答案是5元。
六年级数学 用比例解行程问题 PPT带答案

练习6
一辆汽车从甲地开往乙地,如果车速提高 20%可以提前1小时到 达.如果按原速行驶一段距离后,再将速度提高 30% ,也可以提前 1小时到达,那么按原速行驶了全部路程的几分之几?
例题7
甲、乙两人同时从 A地出发到 B 地,经过 3 小时,甲先到 B 地,乙 还需要 1 小时到达 B 地,此时甲、乙共行了 35 千米.求 A, B 两 地间的距离.
练习1
欢欢和贝贝是同班同学,并且住在同一栋楼里.早晨 7 : 40 ,欢欢 从家出发骑车去学校, 7 : 46 追上了一直匀速步行的贝贝;看到身 穿校服的贝贝才想起学校的通知,欢欢立即调头,并将速度提高到原 来的 2倍,回家换好校服,再赶往学校;欢欢 8 : 00赶到学校时,贝 贝也恰好到学校.如果欢欢在家换校服用去 6分钟且调头时间不计, 那么贝贝从家里出发时是几点几分.
例题8 如右图,A,B 是圆的直径的两端,甲在 A 点,乙在 B 点同时出发 反向而行,两人在 C 点第一次相遇,在 D 点第二次相遇.已知 C 离 A 有 80 米,D 离 B 有 60 米,求这个圆的周长.
根据总结可知,第二次相遇时,乙一共走了 80×3=240 米,两人的总路程和为一周 半,又甲所走路程比一周少 60 米,说明乙的路程比半周多 60 米,那么圆形场地的 半周长为 240-60=180 米,周长为 180×2=360 米.
例题6
王叔叔开车从北京到上海,从开始出发,车速即比原计划的速度提高 了1/9,结果提前一个半小时到达;返回时,按原计划的速度行驶 280 千米后,将车速提高1/6,于是提前1 小时 40 分到达北京.北 京、上海两市间的路程是多少千米?
从开始出发,车速即比原计划的速度提高了1/9,即车速为原计划的10/9,则所用时 间为原计划的1÷10/9=9/10,即比原计划少用1/10的时间,所以一个半小时等于原计 划时间的1/10,原计划时间为:1.5÷1/10=15(小时);按原计划的速度行驶 280 千米 后,将车速提高1/6,即此后车速为原来的7/6,则此后所用时间为原计划的 1÷7/6=6/7,即此后比原计划少用1/7的时间,所以1 小时 40 分等于按原计划的速度 行驶 280 千米后余下时间的1/7,则按原计划的速度行驶 280 千米后余下的时间为: 5/3÷1/7=35/3(小时),所以,原计划的速度为:84(千米/时),北京、上海两市间的 路程为:84 ×15= 1260(千米).
六年级奥数第20讲比例中的行程问题

比例中的行程问题例一、张师傅计划加工1200个零件,实际由于工作效率提高了20%,结果提前1小时完成,张师傅计划每小时加工多少个零件?分析:工作总量一定,工作时间与工作效率成反比例,计划与实际工作效率比是1:(1+20%)=5:6,计划与与实际工作时间相差1小时,可求出计划时间,再求出计划的工作效率。
计划工效:实际工效=1 ,(1+20%)=5:6计划时间:实际时间=6 :5计划时间1÷(6-5)×6=6(时)计划工效1200÷6=200(个/时)答:张师傅计划每小时加工500 个零件。
1、李师傅计划加工1000 个零件,实际由于工作效率提高25%,结果提前1小时完成。
李师傅计划每小时加工多少个零件?,这样就比计划多烧2天。
计划2、食堂运来900 千克煤,由于每天比计划节约用煤110每天烧煤多少千克?,结果提前1小时到达甲地。
甲、乙两3、一列火车从甲地开往乙地,返回时,速度提高15地相距440 千米,求这列火车往返的平均速度。
例二、甲、乙两人同时加工批零件,已知甲、已工作效率的比是4 :5,完成任务时,乙比甲多加工120个零件,这批零件共有多少个?分析:甲、乙两人加工零件的时间相同,所以工作总量与工作效率成正比例,即甲、乙工作总量的比应等于他们工作效率的比,又已知乙比甲多加工120个零件,这样就可求出这批零件的个数。
120÷(54+5-44+5)=1080(个)答:这批零件共有1080个。
巩固练习21、甲、乙两人同时加工一批零件,完成任务时,乙比甲多加工200 个,已知甲、乙工作效率的比是5 :7,这批零件共有多少个?2、甲、乙两车同时从A、B 两地同时出发相向而行,两车在距中点36 千米处相遇,已知甲、乙两车的速度比是4 :5,求A、B 两地之间的路程。
3、甲、乙两车同时从A 地开往B 地,速度比是7 :9,当乙车到达B 地后立即返回,在距B地24 千米处与甲车相遇。
苏教版数学六年级下册专项~比例解决问题【含答案】
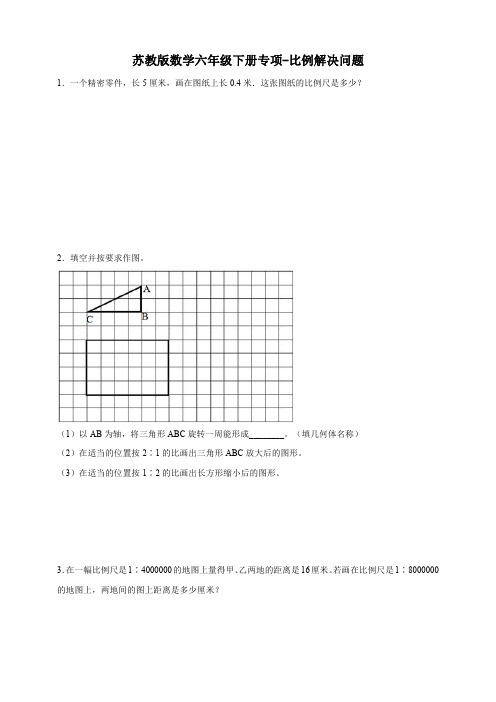
苏教版数学六年级下册专项-比例解决问题1.一个精密零件,长5厘米,画在图纸上长0.4米.这张图纸的比例尺是多少?2.填空并按要求作图。
(1)以AB为轴,将三角形ABC旋转一周能形成________。
(填几何体名称)(2)在适当的位置按2∶1的比画出三角形ABC放大后的图形。
(3)在适当的位置按1∶2的比画出长方形缩小后的图形。
3.在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。
若画在比例尺是1∶8000000的地图上,两地间的图上距离是多少厘米?4.画一画,填一填。
(1)按3∶1的比画出图形A放大后得到的图形B。
(2)按1∶2的比画出图形B缩小后得到的图形C。
我发现:放大或缩小前后的图形()变了,但()没有变,而且图形各部分长度是按一定的比变化的。
5.在一张比例尺是1∶150的建筑图纸上,量得一座大楼的长是6分米,这座大楼的实际长与宽的比是3∶1,这座大楼的实际宽是多少米?6.下图中小平行四边形按比放大后得到大平行四边形,求大平行四边形的高。
(单位:分米)12.根据图中提供的信息,完成下列问题。
(1)自来水厂要从水库取水,取水管道怎样铺最短,请在图中画出来。
(2)自来水厂到城区的送水管道经测算最短是2000米,请你测算:自来水厂到水库的取水管道最短需多少米?13.在一幅地图上,用5厘米长的线段表示实际距离100千米,这幅地图的比例尺是多少?如果甲市至乙市的铁路线路长150千米,那么这段铁路线路在这幅地图上的长度是多少厘米?14.江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。
广场绿地面积与铺装面积的比是6∶5,其中铺装面积共5000平方米,绿地面积有多少平方米?15.甲乙两城相距150千米,在一幅地图上量得甲乙两城之间的距离是5厘米,同时在这幅地图上量得乙丙两城之间的距离是8厘米。
乙丙两城之间的实际距离是多少千米?20.下图中A点是游乐场所在的位置,B点是电影院所在的位置,两地实际距离相距2千米。
2023-2024年人教版六年级下册数学小升初分班考专题:行程问题(含答案)

2023-2024年人教版六年级下册数学小升初分班考专题:行程问题一、单选题1.在比例尺是1:8000000的地图上量得A、B两地相距12厘米,若甲、乙两车同时从A、B两地相对开出,甲车与乙车的速度比是9:11,且两车6小时后在途中相遇,则甲车比乙车每小时慢( )千米。
A.72B.88C.16D.322.小军和小航住在同一个小区,他们为了锻炼身体每天都骑自行车去同一学校。
小军要8分钟,小航要6分钟。
小军和小航的速度比是( )A.3:4B.4:3C.8:6D.6:83.甲、乙二人同时从A地去B地,甲每分钟走60米,乙每分钟走90米,乙到达B地后立即返回,在离B地180米处与甲相遇,AB两地相距( )米。
A.900B.720C.540D.10804.一辆汽车前2小时行了75千米,后2.5小时平均每小时行42千米,这辆汽车平均每小时行多少千米?下面算式中正确的是( )。
A.(75÷2+42)÷2B.(75+42×2.5)÷(2+2.5)C.(75+42)÷(2+2.5)D.(75×2+42×2.5)÷(2+2.5)5.有甲、乙、丙三人同时同地出发,绕个花圃行走,乙、丙二人同方向行走,甲与乙相背而行,甲每分钟走40米,乙每分钟走38米,丙每分钟走35米,在途中,甲和乙相遇后3分钟和丙相遇。
问:这个花圃的周长是多少米?( )A.1000米B.1147米C.5850米D.10000米6.甲、乙两地相隔一座山岭,某人从甲地到乙地用6.5小时,从乙地回到甲地用7.5小时,他往返途中上山速度是3千米/时,下山速度是4千米/时,则甲、乙两地间的山岭路程有( )千米。
A.24.5B.24C.49D.48二、填空题7.两地相距600千米,甲、乙两车同时从两地相对出发,甲车每小时行驶70千米,乙车每小时行驶50千米, 小时后两车在途中相遇。
8.一列特快列车30分钟行驶60千米,它的速度是 ,李叔叔从嘉兴坐特快列车到北京需要14小时,嘉兴到北京的铁路线长 千米。
六年级数学行程问题应用题及参考答案

六年级数学行程问题应用题及参考答案1、甲乙两车同时从AB 两地相对开出。
甲行驶了全程的5/11,如果甲每小时行驶4.5千米,乙行了5小时。
求AB 两地相距多少千米?2、一辆客车和一辆货车分别从甲乙两地同时相向开出。
货车的速度是客车的五分之四,货车行了全程的四分之一后,再行28千米与客车相遇。
甲乙两地相距多少千米?3、甲乙两人绕城而行,甲每小时行8千米,乙每小时行6千米。
现在两人同时从同一地点相背出发,乙遇到甲后,再行4小时回到原出发点。
求乙绕城一周所需要的时间?4、甲乙两人同时从A 地步行走向B 地,当甲走了全程的41时,乙离B 地还有640米,当甲走余下的65时,乙走完全程的107,求AB 两地距离是多少米?5、甲,乙两辆汽车同时从A ,B 两地相对开出,相向而行。
甲车每小时行75千米,乙车行完全程需7小时。
两车开出3小时后相距15千米,A,B 两地相距多少千米?6、甲,已两人要走完这条路,甲要走30 分,已要走20 分,走3 分后,甲发现有东西没拿,拿东西耽误 3 分,甲再走几分钟跟乙相遇?7、甲,乙两辆汽车从A 地出发,同向而行,甲每小时走36 千米,乙每小时走48 千米,若甲车比乙车早出发 2 小时,则乙车经过多少时间才追上甲车?8、甲乙两人分别从相距36 千米的ab 两地同时出发,相向而行,甲从a 地出发至1 千米时,发现有物品遗忘在a 地,便立即返回,取了物品又立即从a 地向b 地行进,这样甲、乙两人恰好在a,b 两地的中点处相遇,又知甲每小时比乙多走0.5 千米,求甲、乙两人的速度?9、两列火车同时从相距400 千米两地相向而行,客车每小时行60 千米,货车小时行40千米,两列火车行驶几小时后,相距有100 千米?10、甲每小时行驶9 千米,乙每小时行驶7 千米。
两者在相距 6 千米的两地同时向背而行,几小时后相距150 千米?11、甲乙两车从相距600 千米的两地同时相向而行,已知甲车每小时行42 千米,乙车每小时行58 千米,两车相遇时乙车行了多少千米?12、一辆客车和一辆货车相向而行,6小时相遇,后经4小时,客车到达,货车还有188千米,问两地相距多少千米?13、甲乙两地相距600千米,客车和货车从两地相向而行,6小时相遇,已知货车的速度是客车的三分之二,求二车的速度?14、小兔和小猫分别从相距40千米的A、B两地同时相向而行,经过4小时候相距4千米,再经过多长时间相遇?15、甲、乙两车分别从a b两地开出,甲车每小时行50千米,乙车每小时行40千米,甲车比乙车早1小时到,两地相距多少?16、两辆车从甲乙两地同时相对开出,4时相遇。
行程问题之比例的应用 非常完整版 超详细解析+答案

行程问题之比例的应用【知识点总结】当速度一定时,时间和路程成正比例关系当时间一定时,速度和路程成正比例关系当路程一定时,时间和速度成反比例关系【例题讲解】例1一列客车和一列货车同时从甲乙两地同时相向而行,客车与货车的速度比是11∶8,甲乙两地相距380千米。
求相遇时,客车比货车多行了多少千米?解答:在时间相同时,速度与路程成正比例V客:V货=11:8S客:S货=11:8按比例分配:380÷(11+8)=20(千米)客车比火车多行的路程:20×(11-8)=60(千米)举一反三1、小军和小明同时从A、B两地相向而行,A、B两地相距600米,小军和小明的速度比是3∶2,相遇时,小明走了多少米?解答:在时间相同时,速度与路程成正比例V军:V明=3:2S军:S明=3:2按比例分配:600÷(3+2)=120(千米)小明走的路程:120×2=240(千米)2、哥哥和弟弟同时从家和学校相向而行,哥哥和弟弟的速度比是5∶3,相遇时哥哥比弟弟多走了200米,求家离学校有多少米?解答:在时间相同时,速度与路程成正比例V哥:V弟=5:3S哥:S弟=5:3按比例分配:200÷(5-3)=100(千米)总路程:100×(5+3)=800(千米)3、聪聪和明明的速度比是6∶5,聪聪在明明后面20米,他们同时同向出发,聪聪要走多少米就可以追上明明?解答:在时间相同时,速度与路程成正比例V聪:V明=6:5S聪:S明=6:5按比例分配:20÷(6-5)=20(千米)聪聪走的路程:20×6=120(米)例2一辆货车从甲城开往乙城,又立即按原路从乙城返回到甲城,一共用了9小时,去时每小时行40千米,返回时每小时行50千米。
甲乙两城相距多少千米?解答:去和返回所走的总路程相同,在路程相同前提下,速度和时间成反比例V去:V回=40:50=4:5t去:t回=5:4,总时间时9小时,按比例分配得:9÷(5+4)=1(小时)t去:1×5=5(小时)总路程:5×40=200(千米)举一反三1、一架侦查飞机最多能带飞行18小时的汽油,它从基地带满油到某地去侦察(中途没有加油站),去时顺风每小时飞行1500千米,回时逆风飞行每小时飞行1200千米。
人教版六年级数学下册比例中的行程问题(1)

比例中的行程问题典型例题1一辆汽车从甲地开往乙地,每小时行40千米,返回时每小时行50千米,结果返回时比去的时间少了48分钟,求甲、乙两地之间的路程。
巩固练习11.一辆汽车从甲地开往乙地,去时每小时行48千米,返回时,每小时行56千米,返回比去时少用1小时,求甲、乙两地的路程。
2.某人从A城步行到B城办事,每小时走5千米,回来时骑自行车,每小时行15千米,往返用6小时,求A、B 两城之间的路程。
3.一辆汽车从甲地去乙地,每小时行45千米,返回时每小时多行20%。
往返共用去11小时。
甲地到乙地共有多少千米?典型例题2甲、乙两车分别从A、B两地同时出发,相向而行,甲车每小时行48千米,乙车每小时行42千米。
当乙车行至全程的错误!时,甲车距中点还有24千米,A、B两地相距多少千米?巩固练习21.甲、乙两车分别从A、B两地同时出发,相向而行,甲车每小时行40千米,乙车每小时行48千米,当乙车行至全程的错误!时,甲车距中点还有30千米。
求A、B 两地的路程。
2.甲、乙两车分别从A、B两地同时出发,相向而行,甲车每小时行56千米,乙车每小时行40千米,当乙车行至全程的错误!时,甲车已超过中点12千米。
求两地的路程。
3.把一批零件按2:3分配给甲、乙两人,甲每小时加工12个,乙每小时加工16个,当甲完成时,乙还有24个未加工,这批零件共多少个?典型例题3甲、乙两车同时从A地开往B 地,当甲车行至全程的错误!处时,乙车行了全程的错误!;当乙车到达B地时,甲车距B地还有20千米,求A、B两地的路程。
巩固练习31.甲、乙两车同时从A地开往B地,当甲车行了全程的错误!时,乙车正好行了全程的错误!,当甲车到达B 地时,乙车距B地还有30千米,求A、B两地之间的路程。
2.甲、乙两车同时从A地开往B地,当甲车行至中点时,乙车行了80千米;当甲车到达B地时,乙车距B 地还有全程的错误!。
求A、B两地的路程。
3.甲、乙两车同时从A地开往B地,当甲车行至中点时,乙车行了全程的错误!;当甲车到达B地时,乙车已超过B地24千米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
演练四:一架侦察飞机最多能带飞机18小时的汽油,它从基地 带满油到某地去侦察(中途没有加油站),去时顺风每小时飞 行1500千米,回时逆风飞行1200千米。那么这架飞机最多能 侦查多远才能按原路返回?
解析:第一次相遇后均提速,算出速度比,量率对应
板书:相遇前,V甲:V乙=3:2
பைடு நூலகம்
相遇时,甲、乙分别走了全程的3/5,2/5
相遇后,V 甲1:V 乙1=(3×120%):(2×130%)=18:13
14
÷(53
-
2 5
13 18
)=14
÷
14 45
=45km
比例行程
预备题 1、泡泡和乐乐的速度比为3:4,他们进行百米赛跑所花的时间比是( ) 2、泡泡和乐乐的速度比为3:4,他们从8:00到9:30所走的路程比为( ) 3、泡泡和乐乐从家到学校所花的时间比为3:4,他们的速度一样,那泡泡
和乐乐家距学校的距离比是( )
答案: 1、 4:3 2、 3:4 3、 3:4
(1)客车和货车的速度比为1:2,所花的时间比为2:3,那么所走的路程比是多少?
(2)客车和货车的速度比为1:2,所走的路程比为2:3,那么所花的时间比是多少?
(3)客车和货车的运动时间比为1:2,所走的路程比为2:3,那么速度比是多少?
板书: (1)速度比: 1 : 2
时间比: 2 : 3 路程比:(1×2):(2×3)=2:6=1:3 (2)速度比: 1 : 2 路程比: 2 : 3 时间比:(2÷1):(3÷2)=4:3 (3)时间比:1 : 2 路程比:2 : 3 速度比:(2÷1):(3÷2)=4:3
解析:相遇时,速度与路程成正比;距离中点3千米处相遇,客车比货车多行驶6千米 板书: V货:V客=S货:S客=9:10 S总=(3×2)÷(10—9)×(10+9)=114千米 114 x(1—9/10)=11.4千米 答:货车离乙站11.4千米。
演练五:货车的速度是客车的4/5,两车分别从甲、乙两站同时相向而行,在 两站中点20千米处相遇,相遇后,两车分别用原来的速度继续前进,到达 乙、甲两站。当客车到达甲站时,货车还离乙站有多远?
解析:时间相同,路程就与速度成正比;路程相同,速度就与时间成反比 板书:时间相同 V甲:V乙= 100:(100-10)=10:9 路程相同 T甲:T乙=9:10
演练三: 甲乙两人进行百米赛跑,当甲到达终点时,乙在甲后面 20米处,如果两人各自速度不变,要使甲,乙两人同时到达终 点,甲的起跑线应比原起跑线后移多少米?
板书:V货:V客=S货:S客=4:5 S货:S总=4:9 S客:S总=5:9 S总=20×2÷(5/9—4/9)=360千米 360 x(1—4/5)=72千米
例6、甲、乙两人分别从A、B两地同时出发,相向而行,出发 时他们速度比为3:2,他们第一次相遇后,甲速提高20%,乙速 提高30%,这样,当甲到达B地时,乙离A还有14千米,那么A, B两地的距离是多少千米?
例1、求出下列几个比例
(1)泡泡和乐乐的速度比为3:4,所花的时间比为5:6,那么所走的路程比是多少?
(2)泡泡和乐乐的速度比为3:4,所走的路程比为5:6,那么所花的时间比是多少?
(3)泡泡和乐乐的时间比为3:4,所走的行程比为5:6,那么速度比是多少?
解析:速度比、时间比、路程比之间的关系
板书: (1)速度比: 3 : 4
板书:时间相同 V甲:V乙= 100:(100-20)=5:4 要使两人同时到达终点,时间相同,路程比等于速度比 S甲:S乙=5:4 后移:100÷4×5-100=25(米)
例4、一辆货车从甲城开往乙城,又立即按原路从乙城返回到甲城, 一共用了9小时,去时每小时行40千米,返回时每小时行50千米。 甲、乙两城相距多少千米?这辆货车往返于甲、乙两城的平均速度 是多少?
演练二: 泡泡和欢欢同时从A、B两地相对而行,A、B两地相距600米,泡 泡和欢欢的速度比是3:2,相遇时,欢欢走了多少米?
板书:相遇时,泡泡和欢欢的路程比:3:2 一份:600÷(3+2)=120(米) 欢欢:120×2=240(米)
例3、甲、乙两人进行百米赛跑,当甲到达终点时,乙离终点还有10米远, 他们两人的速度比是多少?他们跑一百米所用的时间比是多少?
例2、一列客车和一列货车同时从甲、乙两地相向而行,客车与货车的速度 比为11:8,甲乙两地相距380千米。求相遇时,客车比货车多行了多少千米?
解析:相遇时,客车和货车的行驶时间相同,路程就与速度成正比,得到路程比,再分配
板书:相遇时,客车与货车的路程比:11:8 一份:380÷(11+8)=20(千米) 多行了:20×(11-8)=60(千米)
解析:去回的速度比5:4,路程一定,时间与速度成反比 去回的时间比为4:5 去的时间:18÷(5+4)×4=8小时 全程:8×1500=12000千米
例5、货车的速度是客车的9/10,两车分别从甲,乙两站同时 相向而行,在两站中点3千米处相遇,相遇后,两车分别用原 来的速度继续前进,到达乙、甲两站。那么当客车到达甲站时, 货车还离乙站有多远?
时间比: 5 : 6 路程比:(3×5):(4×6)=15:24=5:8 (2)速度比: 3 : 4 路程比: 5 : 6 时间比:(5÷3):(6÷4)=20:18=10:9 (3)时间比: 3 : 4 路程比: 5 : 6 速度比:(5÷3):(6÷4)=20:18=10:9
演练一:求出下面几个比例:
