2014考研西北工业大学《821自动控制原理》模拟题解析部分
西北工业大学自动控制理论模拟卷四(含答案)

图解 1 根Biblioteka 迹图根据 计算,可绘制出系统根轨迹如图所示 由根轨迹图解 1(a)可 看出,当 0 ≤ a ≤ 0.4147 时,多项式的根全 实数
当 a < 0 时,需绘制 0o 根轨迹 实轴 的根轨迹区段 (− ∞,−3],[− 2,−1],
[0, ∞)
由根轨迹图图解 1(b)可 看出,当 a < 0 时,多项式的根全 实数 因 所求参 数 a 的范围 0 ≤ a ≤ 0.4147 或 a < 0
6
3.
已知系统开环传递函数
G(s)
=
10(s 2 − 2s (s + 2)(s −
+ 5) 0.5)
试概略绘制幅相特性曲线,并根
据奈氏判据判定闭环系统的稳定性
4. 设单
反馈系统的开环传递函数
G(s)
=
s(s
K + 1)(0.25s
+ 1)
,要求校
后系统
的静态速度误差系数Kv≥5(rad/s),相角裕度 γ≥45°,试设计串联迟后校 装置
Gc (s)
=
s ωD
s ω
E
+1 +1
=
s +1 0.06
s +1 0.0072
5( s + 1)
校 后系统开环传递函数
Gc (s) ⋅ G(s)
=
s(s
0.06 + 1)( s +1)(
s
+ 1)
4 0.0072
5
验算
图解 3
γ
′
=
180°
+
∠Gc
(
jω
′
西北工业大学《827信号与系统》历年考研真题汇编

目 录2014年西北工业大学827信号与系统考研真题(回忆版)2011年西北工业大学432信号与系统(A)考研真题2010年西北工业大学827信号与系统(A)考研真题2009年西北工业大学信号与系统(B)考研真题2008年西北工业大学827信号与系统(A)考研真题2007年西北工业大学432信号与系统(A)考研真题2006年西北工业大学432信号与系统(A)考研真题2005年西北工业大学信号与系统考研真题2004年西北工业大学432信号与系统考研真题2003年西北工业大学432信号与系统考研真题2002年西北工业大学536信号与系统考研真题版)西北工业大学201!年攻波硕士学位删究生入学专试试题试题名称:信号与系统(A )说 明:明节答迎•律七在答题维上科目代码:432 第I 页共』页—、口o 分)系统如图1-1欧不,请何该系统是若为:即KI 的? <4分)以}因果的?(4分〉线性的? C4^J E )时求先的,《4分) 壬)稳定的? 3分〉;并蚀分别说叫厕的-二、f 15分)某螃性时不变系统当轿人叫,)肘,扎亨状态痢应为:fP [|.,(心话别如园3-2.圈3-3和国3足所:芥.⑴ 用图解法求Y (»; <12分,f2)吗招丫口心的散学表达式.I分)COSift^r七』-广5}宙+门-]1-<“"奸丁),成中T 为常数L 试利用脂积的性质求彼系玩的冲噩响应h ⑴、"20分旧物系统如图3-1所示,系统输入』。
的敏业叶变换F (j*》以及11J 问>y(t)~X(t)COSr» £I 顷九}乘法器西北工业大学2011年攻读硕士学位研究生入学君试试题试题名称「信号与系统(A)科目代码:432说呱所有答题一供吗在答题纸上弟2页兵4弟图3-3叫、HQ分)图4-【区示系统.r.U)=12V,LTH,O1F.R,=3Q.R^2Q b R.1Q.坤升美s断升时.搦电捋已经处干起余*1o时.升美sfflrr:求s件]mm<i)总两端电压的客状态响曲.%(“m林(2)R,两端电翼的零输入响应.5>16分此西北工业大学20]I年攻读硕士学在研究生入学考试试题试题名称:信导与系统(A)科目代码:432说明:所有答魅•律”在答逅纸上第3页共,1页图4-]五」20分)在连瓣时间系统中.RG电路可以构成将通滤波嚣:在抽样素统中.可以利用也容的充放电特性来构成吓关电容滤波器■图5-1-个开美屯容就波簪的原理小摄图,屯容CI和C2两靖的起始电压为零,如果在nT时茉,开美黝接通,英咻而百订十9虬开关$1断开,维接通<n^0)t电容Cl和C2的充放电时间近小于「(1)对于激励*和响晌写出侔IS-1所示系统的爸分方程:门3图5-1西北工业大学20】I年攻读硕士学位研究生入学考试拭题试题名称,信号与系统(对科目代码:432说明:所亏答.腿神写在答题纸上第』讯其4训F若粉入代耳浏卜叫),求系统的零状态响应孔曲丁)槌分L六、<20分〕已知:.y J jj)-6)].-u(ji+6}"W(Jt+l)-求;J1J s(n)=i<14)⑵而出序列瓦皿(65»七、"。
西工大821试题解析

3 1 6 . 2 3 1 6 . 2 = 2 G ( j w )= ) - j w ( j w+ 1 0 w+ 1 0 j w
2 + 1 0 j w ) - 3 1 6 . 2 1 0 j 3 1 6 . 2 (- w = 2 + = 4 2 2 w + 1 0 0 w w+ 1 0 0 w ( w + 1 0 0 )
2× 1 - ξ %= e 1 0 0 %= 4 0 %, σ 槡 - π ξ
3 . 5 t = 0 . 7 s= w ξ n 3 1 . 6 2 ( 3 ) 开环传递函数为: G ( s )= s s ( + 1 ) 1 0 — 3—
考试点( w w w . k a o s h i d i a n . c o m ) 名师精品课程 电话: 4 0 0 6 8 8 5 3 6 5
西北工业大学 - 8 2 1自动控制原理真题、 典型题解析篇
第 1讲 2 0 0 2年真题( 一)
1 . ( 1 0分) 已知系统结构图如图所示:
图B . 1 系统结构图
( 1 ) 求前向通道传递函数 ( 2 ) 求系统闭环传递函数
C ( s ) ; E ( s ) C ( s ) ; R ( s )
- π ξ 1 . 2- 0 . 9 5 2 1 - ξ × 1 0 0 %= 2 6 . 3 %= e %= ② σ 槡 9 5 0 .
根据以上两式, 得ξ = 0 . 3 9 w 3 . 4 n= 1 1 . 0 7 s )= 2 Φ( s+ 2 . 6 7 s + 1 1 . 6 5 K 1 1 . 0 7 1 9 = G ( s )= =2 ( T s + 1 )× ( T s + 1 ) s 4 . 1 7 s + 1 )× ( 0 . 4 1 1 6 s + 1 ) + 2 . 6 7 s + 0 . 5 8 ( 1 2
《自动控制原理》西北工业大学参考题整理

《自动控制原理》西北工业大学参考题整理西北工业大学《自动控制原理》参考习题1-3、1-4;2-1(c)&(d)、2-6、2-8、2-10、2-11、2-12、2-133-1、3-3、3-4、3-6、3-7、3-9、3-11、3-13、3-15、3-16、3-17、3-21、3-22、3-23、3-24、3-28(1)、3-38、3-394-2、4-3(1)&(3)5-1、5-2(1)、5-3、5-6、5-9(1)&(2)&(3)、5-11(1)、5-13(1)~(4)6-2、6-3、6-4、6-5(1)、6-6、6-7、6-8、6-10(1)、6-12、6-13、6-16第一章习题及答案1-3、1-41-3 题1-3图为工业炉温自动控制系统的工作原理图。
分析系统的工作原理,指出被控对象、被控量和给定量,画出系统方框图。
题1-3图 炉温自动控制系统原理图解 加热炉采用电加热方式运行,加热器所产生的热量与调压器电压c u 的平方成正比,c u 增高,炉温就上升,c u 的高低由调压器滑动触点的位置所控制,该触点由可逆转的直流电动机驱动。
炉子的实际温度用热电偶测量,输出电压f u 。
f u 作为系统的反馈电压与给定电压r u 进行比较,得出偏差电压e u ,经电压放大器、功率放大器放大成a u 后,作为控制电动机的电枢电压。
在正常情况下,炉温等于某个期望值T °C ,热电偶的输出电压f u 正好等于给定电压r u 。
此时,0=-=f r e u u u ,故01==a u u ,可逆电动机不转动,调压器的滑动触点停留在某个合适的位置上,使c u 保持一定的数值。
这时,炉子散失的热量正好等于从加热器吸取的热量,形成稳定的热平衡状态,温度保持恒定。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下的控制过程:控制的结果是使炉膛温度回升,直至T °C 的实际值等于期望值为止。
(NEW)西北工业大学《821自动控制原理》历年考研真题汇编(含部分答案)

目 录
2014年西北工业大学821自动控制原理考研试题(回忆版)
2013年西北工业大学821自动控制原理考研试题(回忆版)
2012年西北工业大学821自动控制原理考研试题(回忆版)
2011年西北工业大学821自动控制原理(B)考研真题
2010年西北工业大学821自动控制原理(A)考研真题
2009年西北工业大学821自动控制原理(B)考研真题
2008年西北工业大学427自动控制原理(A)考研真题
2007年西北工业大学427自动控制原理(A)考研真题
2006年西北工业大学427自动控制原理(A)考研真题(含答案)
2005年西北工业大学427自动控制原理(B)考研真题(含答案)
2004年西北工业大学427自动控制原理(A)考研真题(含答案)
2003年西北工业大学427自动控制原理考研真题(含答案)
2002年西北工业大学541自动控制原理考研真题(含答案)
2001年西北工业大学自动控制原理考研真题(含答案)。
西北工业大学821自动控制原理重难点解析课程讲义

G G G G G G G G G G G G G G G G G G G G H 1 2 3 4+ 1 2 4+ 2 3 4 5+ 2 4 5- 3 4 6- 2 4 6 2 s )= Φ( 1- G H + G G G G H + G G G H 2 2 1 2 3 4 1 1 2 4 1 【 例6 】 已知系统结构图, 求 C ( s ) = ? ) R ( S
西北工业大学 8 2 1自动控制原理重难点解析篇
第 1讲 控制系统的数学模型
拉普拉斯变换有关内容 拉氏变换的几个重要定理 ( 1 ) 线性性质 L [ a f ( t )± b f ( t ) ]= a F ( s )± b F ( s ) 1 2 1 2 ( 2 ) 微分定理 L [ f ′ ( t ) ]= s ·F ( s )- f ( 0 )
2 t / 2 - a t e
1 1 / s
2 1 / s 3 1 / s
1 / ( s + a )
2 2 / ( s + ω ω) 2 2 s / ( s + ω)
s i n t ω c o s t ω
线性定常微分方程求解 【 例1 】 R- C电路计算 u R i + u r= c
· i = c u u ( t )= E ·1 ( t ) c r 0
考试点( w w w . k a o s h i d i a n . c o m ) 名师精品课程 电话: 4 0 0 6 8 8 5 3 6 5
其中初条件引起的自由响应部分 C C - 41 1 1 - ( s + 5 ) 1 2 C = + = + ( s )= 0 ) s + 1 s + 4 3s + 1 3s + 4 ( s + 1 ) ( s + 4
C i m 1 =l
西北工业大学自动控制原理模拟题与答案胡祝兵
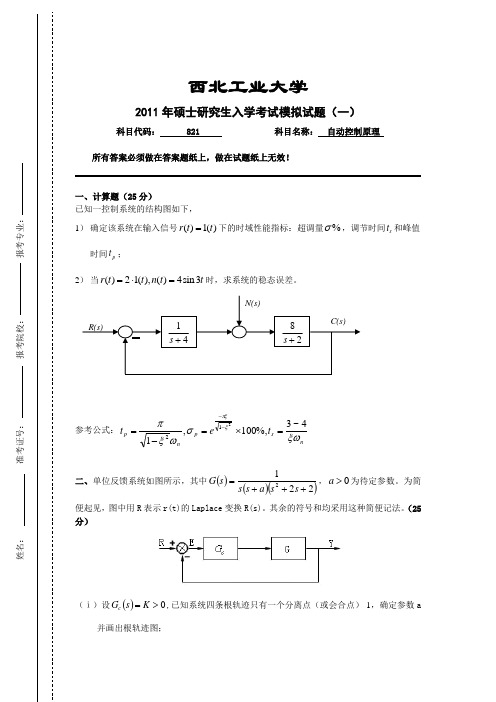
西北工业大学2011年硕士研究生入学考试模拟试题(一)科目代码: 821 科目名称: 自动控制原理所有答案必须做在答案题纸上,做在试题纸上无效!一、计算题(25分)已知一控制系统的结构图如下,1) 确定该系统在输入信号()1()r t t =下的时域性能指标:超调量%σ,调节时间s t 和峰值时间p t ;2) 当()21(),()4sin3r t t n t t =⋅=时,求系统的稳态误差。
参考公式:ns p np t et ξωσωξπξπξ4~3%,100,1212=⨯=-=--二、单位反馈系统如图所示,其中()()()2212+++=s s a s s s G ,0>a 为待定参数。
为简便起见,图中用R 表示r(t)的Laplace 变换R(s)。
其余的符号和均采用这种简便记法。
(25分)(ⅰ)设()0>=K s G c ,已知系统四条根轨迹只有一个分离点(或会合点)-1,确定参数a并画出根轨迹图;14s +82s +R(s)N(s)C(s)(ⅱ)确定根轨迹和虚轴的交点并由此确定使闭环系统稳定的K 值。
(ⅲ)确定系统输出无衰减振荡分量时的闭环传递函数。
三、已知最小相位系统的开环对数幅频特性渐近线如图所示,c ω位于两个交接频率的几何中心。
(25分)1) 计算系统对阶跃信号、斜坡信号和加速度信号的稳态精度。
计算超调量%σ和调节时间s t四、某火炮指挥系统结构如下图所示,()(0.21)(0.51)KG s s s s =++系统最大输出速度为2r/min ,输出位置的容许误差小于2,(25分)求:1) 确定满足上述指标的最小K 值,计算该K 值下的相位裕量和幅值裕量; 2) 前向通路中串联超前校正网络0.41()0.081c s G s s +=+,试计算相位裕量。
()G s ()R s ()E s ()C s五、已知系统的结构图如图所示。
(25分)(ⅰ)求出系统的闭环脉冲传递函数。
823自动控制原理答案2014

河南科技大学2014年硕士研究生入学考试试题答案及评分标准考试科目代码: 823 考试科目名称: 自动控制原理一、 解:1. ╳ 2. ╳ 3. √ 4. ╳ 5. ╳ 6. √ 7. ╳ 8. √ 9. √ 10. ╳ 每小题2分,共20分 二、简单计算题(共30分)1.(8分)解:1) 系统信号流图为:——3分2)前项通道1条:4321G G G G P =单独回路3个:211G G L -=,322G G L -=,343G G L -= 两个互不接触回路1个:432121G G G G L L =由梅森增益公式得到系统的总传递函数为432143322143211)(/)(G G G G G G G G G G G G G G s R s C k ++++=∆∆=——8分2.(5分)解:由0=+N ,1=-N ,2)(22=--=-=-+N N P N P Z闭环系统不稳定,其s 右半平面的闭环极点数为2 ——5分 3.(6分)解:(a) 稳定, 存在稳定的自激振荡 ——3分(b) 稳定, 不存在自激振荡 ——6分 4.(6分)解:由开环传递函数可得13.16/0.1582n nωξω====(弧度秒)——2分1212%100%60.5%()2()0111()0.1lim ()100.1ss ss v ss ss ss er t t e r t t e K sG s e e e σ=⨯==I =======+=时 系统为型系统时——6分5.(5分)解:[]11Q 1c a BAB b +⎡⎤==⎢⎥⎣⎦1c Q b a =-- 所以当10b a --≠时,系统完全能控。
——5分三、(10分)解:系统的特征方程为02012)(23=+++=K s s s s D列劳斯表⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-Ks K s K s s 0231224012201 可知系统稳定要求劳斯表的第一列大于零,即0240K << ——6分 系统为I 型系统当1)(=t r 时,稳态误差01=ss e 当t t r =)(时,稳态误差KK e s sG s vss 2011)(lim 02===→ 由2.02021≤=+=Ke e e ss ss ss 得K 的取值范围为100240K ≤<——10分 四、(15分)解:1. 系统的根轨迹方程为32()560D s s S s K *=+++= ——1分2. 根轨迹绘制如下:① 实轴上的根轨迹:[]3,-∞-,[]0,2-② 渐近线: ⎪⎪⎩⎪⎪⎨⎧=+=-=--=ππππϕσ35,,33)12(353320k a a③ 分离点:031211=++++d d d 解得分离点坐标为:用试探法可得 78.01-=d ,54.22-=d (舍去) 分离角为2/3,2//)12(πππ=+l k 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专业课模拟题解析课程第1讲模拟题一解析(一)一、(25分)某系结构图如下图所示,该系统的单位阶跃响应如右图。
(1)求该系统结构图中未知参量v,k,T.e (2)当T不等于零时,求a的值,使该系统的单位斜坡误差1ss考点:(1)阶跃响应的导数是脉冲响应,脉冲响应的s域表达式就是系统的传递函数。
(2)稳态误差的算法解:,a s Ts s a s K Ts s a s Ts s a s K s vvv++++=+++++=Φ)1()()1(1)1()()(⎩⎪⎨⎧===1110T v K ⎩⎪⎨⎧===0210T v K或者(2)由梅森公式可得,该系统的误差传递函数为:221()21(1)e s ss s a s s a s s φ+==+++++ 22220011lim *()*lim **12e s s s s s s s s s s a sφ→→+==++ a=1二、(25分)已知系统结构图,K *= 0→∞,绘制系统根轨迹并确定: (1)使系统稳定且为欠阻尼状态时开环增益 K 的取值范围; (2) 当3λ =-5 时,1,2λ=?相应 K=?解:①实轴上的根轨迹:[-∞,-4], [-2,0]②渐近线:*()(2)(4)KG ss s s=++*81K Kv⎧=⎨=⎩11124d d d++=++③ 分离点:整理得:舍去第二个结果,可得: ④ 虚轴交点:231280d d ++=120.845; 3.155d d =-=-0.845*24 3.08d d K d d d =-=++=*32*()(2)(4)680D s s s s K s s s K =+++=+++=使系统稳定且为欠阻尼状态时开环增益 K 的取值范围:(2)由题意,可用长除法进行运算:则三、(25分)已知最小相角系统 L(w) 如图所示,试确定(1) 开环传递函数G(s);(2) 由 γ 确定系统的稳定性;32*()68D s s s s K =+++2(5)(3)s s s =+++1,20.5 1.6583j λ=-±*15K =*8158 1.875K K ===(3) 将 L(w) 右移10倍频,讨论对系统的影响。
考点:利用伯德图,分析系统性能。
解:(1)由系统伯德图,可得该系统的开环传递函数为:(2)要计算系统的相角裕度,必须得到系统的截止频率。
截止频率可直接由图中确定。
)120)(11.0(10)(++=s s s s GGH jw e ,二阶环节四、(25分)一系统的开环传递函数为1()asGH jw轨迹图如下图所示,试求:1()(1)使闭环系统稳定的a的取值范围(2)若a=0,当系统输入r(t)=sin(t)时,求系统输出考点:利用奈奎斯特图确定系统传递函数形式。
解:根据该幅相曲线可知,其初始为平行负虚轴的无穷远处,所以为1型系统。
又因为单调变化,以180度终止于原点,且是二阶环节,所以含有一惯性环节无零点。
(1)1()(1)KGH S s Ts =+122()(1)(1)K kTw jk GH jw jw Tjw w T w --==++ 则幅频和相频特性为:022(),()90arctan 1K A w w Tww T w ϕ==--+则由幅相曲线可知,当w=2时有00(2)2,(2)145(2)90arctan 2145=0.5(2)=2421+1A T T KA K ϕϕ==-=--=-==得:,得加上延迟环节求截止频率01, 2.5=--arctan 0.5*2.5-2.5*57.31800.27A w a a ϕ==><204(w )=可得w 1+0.25w 另该点的相角(2.5)90得,(2)由第一问可知,K=1,a=0,T=0.5,所以可得幅频和相频特性分别为:04(1) 3.58,(1)90arctan 0.5116.61*10.25*1A ϕ===--=-+所以可得,系统输出为:3.58sin(116.6)t -五、(25分)已知系统结构图 (T=0.25), r(t)=2·1(t)+t,(1)该系统稳定时,求K 的范围 (2)使e(∞)<0.5, 求K 范围 考点:离散系统的判稳与求误差 解:(1)离散系统判定稳定性,用朱莉判据。
(2)求稳态误差用静态系数法可得:六、(25分)非线性系统结构图如右图所示,已知:(1) 自振时,调整K 使求此时的K 值和自振参数(A,w)以及输出振幅A c 。
(2)定性分析K 增大后自振参数(A,w)的变化规律。
考点:考查非线性系统的像平面分析法2()135(1)K G s s s ⎛⎫∠=∠=-︒ ⎪+⎝⎭解:(1)由题意得专业课模拟题解析课程第2讲模拟题二解析(二)一、(25分)已知一个单位反馈的三阶系统,对单位加速度输入的稳态误差为0。
该系统本身稳定,最多只有一个零点。
变化k,使该系统在w=3处会发生恒定的正弦波动。
(1)若该系统闭环特征方程有一根为-1,求其开环传递函数(2)在(1)的条件下,讨论使该系统特征根位于-1之左的情况考查点:劳斯公式本身内容及劳斯公式的特殊情况解:(1)该系统稳定,那么特征方程中就不会缺项。
从而可以设该系统的开环传递函数为: 2(1)()()k as G s s s b +=+则该系统的闭环传递函数为:32(1)()k as s s bs kas kφ+=+++从而系统的闭环特征方程为:32()D s s bs kas k =+++ 列出劳斯表可得: 3210100s ka s b k s kab k sk-要出现恒定的震荡,则kab-k=0此时震荡频率为3,则辅助方程20bs k +=的解为3s j =+从而k=9b,ab=1。
将s=-1带如特征方程,可得-1+b-ka+k=0 三个式子联合可得b=1,a=1,k=9 (2)在(1)的条件下,令s=S-1则相当于讨论在S 域中系统的稳定情况。
带入特征跟,得32()(1)(1)(1)D S S S k S k =-+-+-+ 列劳斯表,讨论S 域中系统的稳定情况。
二、(25分)某系统框图如下所示:(1)绘制当K*= 0→∞时系统的根轨迹;(2)使复极点对应的阻尼角为60o时的 K 及 考点:利用开环根轨迹,分析系统性能。
解:(1)可以先将系统开环传递函数进行化简:(2)可以使用待定系数法:三、(25分)某单位反馈系统的开环幅相曲线如下图所示,且(1)当输入r(t)=1(t)时,求输出量c(t)的最大值及稳态误差(2)当输入r(t)=5sin(2t)时,求系统的稳态误差考点:奈奎斯特图求系统开环传递函数;正弦输入时输出的求法解:(1)由图可得系统的开环传递函数为:将带入得到:则有:所以有:即有:得到自然震荡频率和阻尼比分别为:超调为:又因为:(终值定理)所以系统稳定误差为(静态误差系数法):(2)误差传递函数为:即有:所以误差响应为:四、(25分)已知非最小相位系统的开环伯德图如下图所示,开环增益K>0,(1)确定系统开环传递函数G(S)(2)用奈奎斯特稳定判据确定使系统稳定的K的范围。
考点:利用伯德图确定系统传递函数;奈奎斯特稳定判据解:(1)首先确定系统有一个微分环节(因为系统伯德图一开始就以20dB的斜率上升)在w=1处,系统的斜率变化-40dB,对应二阶积分环节,因此系统传递函数可设为:又因为:,可求出:(2)由已知,当当Z=P-2N=-2N时,系统才稳定,所以可得N=1。
且K/2>1,推得K>2时系统稳定。
五、(25分)已知离散系统结构图,K=10, T=0.2求:(1)系统的稳定性(2) r(t)=1(t)时系统的e(∞)。
考点:离散系统的稳定性和稳态误差的求法 解:先求系统的传递函数⎥⎦⎤⎢⎣⎡⋅-+⎥⎦⎤⎢⎣⎡⋅-==--s K s e Z s K s e Z z E z C z G Ts Ts 5.0111)()()(2⎥⎦⎤⎢⎣⎡⋅-+⎥⎦⎤⎢⎣⎡⋅-=--21311)1(5.011)1(s Z K z s Z K z 232)1(15.01)1(2)1(1-⋅-+-+⋅-=z Tz K z z z z z T z z K 1121)1(1222-⋅+-+⋅=z KT z z KT)1()1(2.02.010-+===z z z T K )1()1(2.011)(11)()()(-++=+==Φz z z z G z R z E z e 2.08.0)1()1(2.0)1()1(2+--=++--=z z z z z z z z z 02.08.0)(2=+-=z z z D所以系统稳定。
(2)由系统开环传递函数可得,稳态误差为: 六、(25分)非线性系统结构图如下图所示,已知: 214.02.08.0)1()1()1(lim )(2212==+--⋅-⋅-=∞→T z z z z z Tz z T e z 1221(),()(1)4()1()K G s G s s s s M h N A A h A A π⎧==⎪+⎪⎨⎛⎫⎪=-≥ ⎪⎪⎝⎭⎩(1) 时,系统是否自振?确定使系统自振的K 的范围。
考点:非线性系统的自振及其稳定性的讨论 解 先将系统结构图化为典型结构 特征方程法:3()1G s =11231()1G s G G G N G Φ=++1231()10D s G G G N G =++=123111G G G NG =-+1231()1G G G G s G =+专业课模拟题解析课程第3讲模拟题三解析(3)一、(25分)如下图所示,图中F(t)=1(t)N为输入量,位移y(t)为输出量。
m=1kg,f=2,K=1.(1)求该系统的传递函数;(2)求该系统的超调量和调节时间考查点:利用物理背景,求系统的传递函数。
解:(1)对小车单独进行受力分析,由牛顿第二定律可得:利用微分方程与传递函数的关系,可得:2()1()Y S F S ms fs K=++2121s s =++(2)由(1)可知,该系统的 1n w ξ== 带入超调和调节时间公式即可。
二、(25分)控制系统如下图所示:(1)取,绘制时的根轨迹。
(2)欲使系统闭环主导极点为,求12,K K 的值。
考点:主导极点法求系统性能。
解:(1)当时,副回路闭环传递函数为:因此,系统的开环传递函数为:渐近线与实轴交点为:可得,渐近线的角度为:36,108,180,252,324(2)系统副回路的闭环传递函数为:所以系统的开环传递函数为:要使系统的主导极点如题中所给,那么又设:所以有:从而:三、(25分)已知单位反馈系统开环传递函数为:(1)用奈奎斯特曲线求使系统稳定时参数K的范围(2)若希望系统的闭环极点全部位于s=-1之左,试用奈奎斯特判据判定此时K的取值范围。
