全等三角形的判定证明题sss、sas
全等三角形的判定证明题sss、sas讲课教案

全等三角形的判定证明题s s s、s a s全等三角形的判定训练题(SSS、SAS)判定定理1:简单的表示为:SSS数学语言:在△ABC和△A'B'C'中AC=A'C'(已知)BC=B'C'(已知)AB=A'B'(已知)∴△ABC≌△A'B'C'(SSS)1、若AB=CD,AC=DB,可以判定哪两个三角形全等?请证明。
2、△ABC中,AB=AC,AD是BC边上的中线,∠B与∠C有什么关系?请证明。
3、点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,则AB和DE有怎样的位置关系?请证明。
C4、已知AB=CD,BE=DF,AF=CE,则AB与CD有怎样的位置关系?5、如图,AC=DF,BC=EF,AD=BE,∠BAC=80o,∠F=60o,求∠ABC6、如图,AC=AD,BC=BD,∠1=35o,∠2=65o,求∠C精品资料7、如图,△ABC 中,AD=AE , BE=CD ,AB=AC ,说明△ABD ≌△ACE判定定理2: 简单的表示为:SAS 数学语言:在△ABC 和△A 'B 'C ' 中 AB=A 'B ' (已知) ∠B=∠B ' (已知) BC=B 'C '(已知) ∴△ABC ≌△A 'B 'C '(SSS )8、如图,已知AC ,BD 相交于O ,AO=DO ,BO=CO ,证明:∠A=∠D9.如图,AE 是,BAC 的平分线 AB=AC.证明 △ABD ≌△ACDC10、已知:如图,AB=AC,AD=AE,求证:BE=CD.11、如图,已知:点D、E在BC上,且BD=CE,AD=AE,∠1=∠2,求证:△ADB≌△AEC12、如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,求证: BE=DCDABQCPADBEC13、 如图,点C 是AB 中点,CD ∥BE ,且CD=BE ,试探究AD 与CE 的关系。
八年级数学—全等三角形判定一(SSS,SAS)(基础)巩固练习【名校试题+详细解答】

【巩固练习】一、选择题1. △ABC 和△'''A B C 中,若AB =''A B ,BC =''B C ,AC =''A C .则( )A.△ABC ≌△'''A C BB. △ABC ≌△'''A B CC. △ABC ≌△'''C A BD. △ABC ≌△'''C B A2. 如图,已知AB =CD ,AD =BC ,则下列结论中错误的是( )A.AB ∥DCB.∠B =∠DC.∠A =∠CD.AB =BC3. 下列判断正确的是( )A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4. 如图,AB 、CD 、EF 相交于O ,且被O 点平分,DF =CE ,BF =AE ,则图中全等三角形的对数共有( )A. 1对B. 2对C. 3对D. 4对5. 如图,将两根钢条'AA ,'BB 的中点O 连在一起,使'AA ,'BB 可以绕着点O 自由转动,就做成了一个测量工件,则''A B 的长等于内槽宽AB ,那么判定△OAB ≌△''OA B 的理由是( )A.边角边B.角边角C.边边边D.角角边6. 如图,已知AB ⊥BD 于B ,ED ⊥BD 于D ,AB =CD ,BC =ED ,以下结论不正确的是( )A.EC ⊥ACB.EC =ACC.ED +AB =DBD.DC =CB二、填空题7. 如图,AB =CD ,AC =DB ,∠ABD =25°,∠AOB =82°,则∠DCB =_________.8. 如图,在四边形ABCD中,对角线AC、BD互相平分,则图中全等三角形共有_____对.9. 如图,在△ABC和△EFD中,AD=FC,AB=FE,当添加条件_______时,就可得△ABC≌△EFD(SSS)10. 如图,AC=AD,CB=DB,∠2=30°,∠3=26°,则∠CBE=_______.11. 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B =20°,则∠C=_______.12. 已知,如图,AB=CD,AC=BD,则△ABC≌,△ADC≌ .三、解答题13. 已知:如图,四边形ABCD中,对角线AC、BD相交于O,∠ADC=∠BCD,AD=BC,求证:CO=DO.14. 已知:如图,AB ∥CD ,AB =CD .求证:AD ∥BC .分析:要证AD ∥BC ,只要证∠______=∠______,又需证______≌______.证明:∵ AB ∥CD ( ),∴ ∠______=∠______ ( ),在△______和△______中,⎪⎩⎪⎨⎧===),______(______),______(______),______(______ ∴ Δ______≌Δ______ ( ).∴ ∠______=∠______ ( ).∴ ______∥______( ).15. 如图,已知AB =DC ,AC =DB ,BE =CE 求证:AE =DE.【答案与解析】一.选择题1. 【答案】B ;【解析】注意对应顶点写在相应的位置.2. 【答案】D ;【解析】连接AC 或BD 证全等.3. 【答案】D ;4. 【答案】C ;【解析】△DOF ≌△COE ,△BOF ≌△AOE ,△DOB ≌△COA.5. 【答案】A ;【解析】将两根钢条'AA ,'BB 的中点O 连在一起,说明OA ='OA ,OB ='OB ,再由对顶角相等可证.6. 【答案】D ;【解析】△ABC ≌△EDC ,∠ECD +∠ACB =∠CAB +∠ACB =90°,所以EC ⊥AC ,ED +AB =BC +CD =DB.二.填空题7. 【答案】66°;【解析】可由SSS 证明△ABC ≌△DCB ,∠OBC =∠OCB =82412︒=︒, 所以∠DCB = ∠ABC =25°+41°=66°8. 【答案】4;【解析】△AOD ≌△COB ,△AOB ≌△COD ,△ABD ≌△CDB ,△ABC ≌△CDA.9. 【答案】BC =ED ;10.【答案】56°;【解析】∠CBE =26°+30°=56°.11.【答案】20°;【解析】△ABE ≌△ACD (SAS )12.【答案】△DCB ,△DAB ;【解析】注意对应顶点写在相应的位置上.三.解答题13.【解析】证明:在△ADC 与△BCD 中,,,,DC CD ADC BCD AD BC =⎧⎪∠=∠⎨⎪=⎩()...ADC BCD SAS ACD BDC OC OD ∠=∠=∴△≌△∴∴14. 【解析】3,4;ABD ,CDB ;已知;1,2;两直线平行,内错角相等;ABD ,CDB ;AB ,CD ,已知;∠1=∠2,已证;BD =DB ,公共边;ABD ,CDB ,SAS ;3,4,全等三角形对应角相等;AD ,BC ,内错角相等,两直线平行.15.【解析】证明:在△ABC 和△DCB 中D C BAAB DC AC DB BC =CB ⎧⎪⎨⎪⎩==∴△ABC ≌△DCB (SSS ) ∴∠ABC =∠DCB , 在△ABE 和△DCE 中ABC DCB AB DC BE CE =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△DCE (SAS ) ∴AE =DE.。
全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)
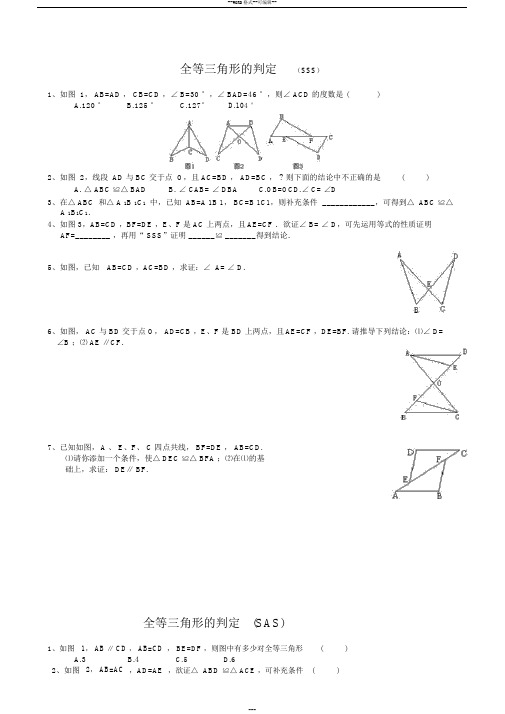
全等三角形的判定(SSS)1、如图 1, AB=AD , CB=CD ,∠ B=30 °,∠ BAD=46 °,则∠ ACD 的度数是 ()A.120 °B.125 °C.127°D.104 °2、如图 2,线段 AD 与 BC 交于点 O,且 AC=BD , AD=BC , ? 则下面的结论中不正确的是()A. △ ABC ≌△ BADB. ∠ CAB= ∠ DBAC.OB=OCD.∠ C= ∠D3、在△ ABC 和△ A 1B 1C1中,已知 AB=A 1B 1, BC=B 1C1,则补充条件 ____________,可得到△ ABC ≌△A 1B1C1.4、如图 3,AB=CD ,BF=DE ,E、F 是 AC 上两点,且AE=CF .欲证∠ B= ∠ D,可先运用等式的性质证明AF=________ ,再用“ SSS”证明 ______≌ _______得到结论.5、如图,已知AB=CD ,AC=BD ,求证:∠ A= ∠ D.6、如图, AC 与 BD 交于点 O, AD=CB ,E、F 是 BD 上两点,且AE=CF ,DE=BF. 请推导下列结论:⑴∠ D=∠B ;⑵ AE ∥CF.7、已知如图,A 、 E、F、 C 四点共线, BF=DE , AB=CD.⑴请你添加一个条件,使△ DEC ≌△ BFA ;⑵在⑴的基础上,求证: DE∥ BF.全等三角形的判定(SAS)1、如图1, AB ∥ CD , AB=CD, BE=DF ,则图中有多少对全等三角形()A.3B.4C.5D.62、如图2, AB=AC,AD=AE,欲证△ABD≌△ ACE ,可补充条件()A. ∠ 1= ∠23、如图 3, AD=BCA.AB ∥ CDB.∠ B= ∠ C,要得到△ ABDB.AD ∥ BCC.∠ D= ∠ ED. ∠BAE= ∠CAD 和△CDB 全等,可以添加的条件是 ( C.∠A=∠ C D. ∠ABC= ∠ CDA)4、如图 4, AB 与 CD 交于点 O, OA=OC , OD=OB ,∠ AOD=________ , ? 根据 _________可得到△ AOD≌△ COB,从而可以得到AD=_________ .5、如图 5,已知△ ABC 中, AB=AC , AD 平分∠ BAC ,请补充完整过程说明△∵ AD 平分∠ BAC ,∴∠ ________=∠ _________(角平分线的定义).在△ ABD 和△ ACD 中,∵ ____________________________ ,∴△ ABD≌△ ACD(ABD)≌△ ACD的理由.6、如图 6,已知 AB=AD , AC=AE ,∠ 1= ∠ 2,求证∠ ADE= ∠ B.7、如图,已知AB=AD ,若 AC 平分∠ BAD ,问 AC 是否平分∠ BCD ?为什么?BA CD8、如图,在△ABC 和△ DEF 中, B 、 E、 F、 C,在同一直线上,下面有 4 个条件,请你在其中选 3 个作为题设,余下的一个作为结论,写一个真命题,并加以证明.①AB=DE ;② AC=DF ;③∠ ABC= ∠ DEF ;④ BE=CF.9、如图⑴, AB ⊥ BD , DE⊥ BD ,点 C 是 BD 上一点,且BC=DE , CD=AB .⑴试判断AC 与 CE 的位置关系,并说明理由.⑵如图⑵,若把△CDE 沿直线 BD 向左平移,使△CDE 的顶点 C 与 B 重合,此时第⑴问中的位置关系还成立吗?(注意字母的变化)AC与BE全等三角形(三) AAS和 ASA【知识要点】1.角边角定理( ASA):有两角及其夹边对应相等的两个三角形全等.2 .角角边定理( AAS):有两角和其中一角的对边对应相等的两个三角形全等.【典型例题】例 1.如图, AB∥ CD, AE=CF,求证: AB=CDD FC O例 2.如图,已知: AD=AE,ACD ABE ,求证:BD=CE.AE BAD E例 3.如图,已知:CD . BAC ABD ,求证:OC=OD.B CD COA B例 4.如图已知: AB=CD,AD=BC,O是 BD中点,过 O点的直线分别交DA和 BC的延长线于E,F. 求证: AE=CF.FDCOAB例 5.如图,已知123 ,AB=AD.求证:BC=DE.EA2E1OB D 3C例6.如图,已知四边形 ABCD中, AB=DC,AD=BC,点 F 在 AD 上,点 E 在 BC上, AF=CE, EF 的对角线 BD 交于 O,请问 O点有何特征?A F DOB EC【经典练习】1. △ ABC和△A B C中,A A' , BC B C ,C C 则△ABC与△ A B C.2.如图,点 C,F 在 BE上,12, BC EF ,请补充一个条件,使△ABC≌DFE,补充的条件是.A DB 12EC F3.在△ ABC和△A B C中,下列条件能判断△ABC和△A B C全等的个数有()① A AB B , BC B C② AA , B B , AC A C③ A AB B , AC B C④ AA , B B , AB A CA . 1 个 B. 2 个 C. 3 个 D. 4 个4.如图,已知 MB=ND,MBA NDC ,下列条件不能判定是△ABM≌△CDN的是()A.M NB. AB=CD M NC. AM=CND. AM∥ CN5.如图 2 所示,∠E=∠ F=90°,∠ B=∠ C, AE=AF,给出下列结论:①∠ 1=∠2② BE=CF③△ ACN≌△ ABM④ CD=DN A C B D 其中正确的结论是_________ _________ 。
全等三角形的判定精选练习题分SSSSASAASASAHL分专题

全等三角形的判定(SSS)1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是()A。
120°B.125°C。
127° D。
104°2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )A.△ABC≌△BAD B。
∠CAB=∠DBA C.OB=OC D。
∠C=∠D3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论。
5、如图,已知AB=CD,AC=BD,求证:∠A=∠D.6、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.7、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.全等三角形的判定(SAS)1、如图1,AB∥CD,AB=CD,BE=DF,则图中有多少对全等三角形( )A.3 B。
4 C.5 D。
6CBA 2、如图2,AB=AC ,AD=A E,欲证△A BD ≌△A CE ,可补充条件( ) A 。
∠1=∠2B .∠B=∠C C.∠D=∠ED 。
∠BAE=∠C AD 3、如图3,AD=B C,要得到△AB D和△CD B全等,可以添加的条件是( )A .AB∥CD B。
AD ∥B CC .∠A=∠C D.∠ABC =∠CDA4、如图4,AB 与CD 交于点O ,O A=OC ,OD =OB ,∠A OD =________,•根据_________可得到△AOD ≌△COB ,从而可以得到AD=_________.5、如图5,已知△ABC 中,AB=AC ,A D平分∠BAC ,请补充完整过程说明△A BD≌△ACD 的理由。
08-16全等三角形的判定精选练习题SSS、SAS、AAS、ASA、HL分专题

全等三角形的判定 (SSS )3、在△ ABC 和△A 1B 1C 1 中,已知 AB=A 1B 1,BC=B 1C 1,则补充条件 ___________ ,可得到△ ABC ≌△A 1B 1C 1 .4、如图 3,AB=CD ,BF=DE ,E 、F 是 AC 上两点,且 AE=CF .欲证∠ B= ∠ D ,可先运用等式的性质证明AF= ________ ,再用“ SSS ”证明 _______ ≌ _________ 得到结论. 5、如图, AB=AC , BD=CD ,求证:∠ 1= ∠ 2.6、如图,已知 AB=CD ,AC=BD ,求证:∠ A=∠ D .7、如图, AC 与BD 交于点 O ,AD=CB ,E 、F 是 BD 上两点,且 AE=CF ,DE=BF.请推导下列结论:⑴∠8、已知如图, A 、E 、F 、C 四点共线, BF=DE ,AB=CD. ⑴请你添加一个条件,使△ DEC ≌△BFA ; ⑵在⑴的基础上,求证: DE ∥ BF.1、如图 1, AB=AD ,CB=CD ,∠A.120 °B.125°2、如图 2,线段 AD 与 BC 交于点 B. ∠ CAB= ∠DBA A.△ABC ≌△BAD AD=BC C.OB=OC , ?则下面的结论中不正确的是 ( D.∠C=∠ D D= ∠B ;⑵ AE ∥CF .B=30°C.127°O ,且AC=BD ,全等三角形的判定 (SAS )1、如图 1, AB ∥ CD , AB=CD , BE=DF ,则图中有多少对全等三角形 ( )A. 3B.4C.5D.62、如图 2,AB=AC ,AD=AE ,欲证△ ABD ≌△ACE ,可补充条件 ( ) A.∠1=∠2 B.∠B=∠CC.∠D=∠ED. ∠BAE= ∠CAD3、如图 3, AD=BC ,要得到△ ABD 和△ CDB 全等,可以添加的条件是 ( )A.AB ∥CDB.AD ∥BCC.∠A=∠CD. ∠ABC= ∠CDA4、如图 4,AB 与 CD 交于点 O ,OA=OC ,OD=OB ,∠ AOD= ________ ,?根据 _________ 可得到△ AOD ≌△ COB ,从而可以得到 AD= ________ .5、如图 5,已知△ ABC 中,AB=AC ,AD 平分∠ BAC ,请补充完整过程说明△ ABD ≌△ACD 的理由. ∵AD 平分∠ BAC , ∴∠ _______ = ∠ __________ (角平分线的定义 ). 在△ABD 和△ ACD 中,∵ __________________________________ , ∴△ ABD ≌△ ACD ( ) 6、如图 6,已知 AB=AD , AC=AE ,∠1=∠2,求证∠ ADE= ∠B.7、如图,已知 AB=AD ,若 AC 平分∠ BAD ,问 AC 是否平分∠ BCD ?为什么?8、如图,在△ ABC 和△ DEF 中, B 、E 、F 、C ,在同一直线上,下面有 为题设,余下的一个作为结论,写一个真命题,并加以证明 . ① AB=DE ; ②AC=DF ; ③∠ ABC= ∠ DEF ; ④ BE=CF.9、如图⑴, AB ⊥BD ,DE ⊥BD ,点C 是BD 上一点,且 BC=DE ,CD=AB . ⑴试判断 AC 与 CE 的位置关系,并说明理由.⑵如图⑵,若把△ CDE 沿直线 BD 向左平移,使△ CDE 的顶点 C 与 B 重合,此时第⑴问中 AC 与 BE 的位置关系还成立吗? (注意字母的变化 )4 个条件,请你在其中选 3 个作C全等三角形(三) AAS 和 ASA知识要点 】1.角边角定理( ASA ):有两角及其夹边对应相等的两个三角形全等 2 .角角边定理( AAS ):有两角和其中一角的对边对应相等的两个三角形全等【典型例题 】例 1.如图, AB ∥ CD , AE=CF ,求证: AB=CD例 2 .如图,已知: AD=AE , ACD ABE ,求证: BD=CE.例 4.如图已知: AB=CD ,AD=BC ,O 是 BD 中点,过 O 点的直线分别交 DA 和 BC 的延长线于 E ,F. 求证:AE=CF.例 5.如图,已知 1 23 , AB=AD.求证: BC=DE.例 6.如图,已知四边形 ABCD 中, AB=DC ,AD=BC ,点 F 在 AD 上,点 E 在 BC 上, AF=CE ,EF 的对角线 BD 交于 O ,请问 O 点有何特征?例 3.如图,已知: C D. BAC ABD ,求证:OC=OD.CABE【经典练习】1. △ABC 和△ ABC 中, AA ',BC BC , C C 则△ ABC 与△ A BC.2.如图,点C ,F 在 BE 上, 12,BC EF ,请补充一个条件, 使△ ABC ≌DFE,补充的条件是.3.在△ ABC 和△ AB C 中,下列条件能判断△ ABC 和△ ABC 全等的个数有( )①A A B B , BC BC ②A A , B B , AC AC③A A B B , AC BC ④A A , BB , AB AC A . 1 个B. 2 个C. 3 个D. 4 个4.如图,已MB=ND , MBA NDC , 下列条件不能判定ABM ≌△ CDN 的是( )6.如图 3 所示,在△ ABC 和△ DCB 中, AB =DC ,要使△ ABO ≌DCO ,请你补充条件 一个你认为合适的条件 ).7. 如图,已知∠ A=∠ C ,AF=CE ,DE ∥BF ,求证:△ ABF ≌△ CDE.A MNB. AB=CDC . AM=CND. AM ∥ CN5.如图 2 所示, ∠E =∠F =90°,∠ B =∠C ,AE =AF ,给出下列结论:①∠1=∠2 ② BE=CF ③△ ACN ≌△ ABM ④CD=DN( 注:将你认为正确的结论填上 ) 其中正确的结B图28.如图, CD ⊥AB ,BE ⊥AC ,垂足分别为 D 、E ,BE 交 CD 于 F ,且 AD=DF ,求证: AC= BF 。
专题12.3 全等三角形判定一(SSS,SAS)(知识讲解)(人教版)

专题12.3 全等三角形判定一(SSS,SAS )(知识讲解)【学习目标】1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定1——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).要点诠释:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .要点二、全等三角形判定2——“边角边”1. 全等三角形判定2——“边角边” 两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.【典型例题】类型一、全等三角形的判定1——“边边边”1、已知:如图,△RPQ 中,RP =RQ ,M 为PQ 的中点.求证:RM 平分∠PRQ .【思路点拨】由中点的定义得PM =QM ,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM =QM在△RPM 和△RQM 中,()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边 ∴△RPM ≌△RQM (SSS ).∴ ∠PRM =∠QRM (全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.类型二、全等三角形的判定2——“边角边”2、如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.【思路点拨】根据等腰直角三角形的性质得出CE=CD,BC=AC,再利用全等三角形的判定证明即可.【答案与解析】证明:∵△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,∴CE=CD,BC=AC,∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,∴∠ECB=∠DCA,在△CDA与△CEB中,∴△CDA≌△CEB.【总结升华】本题考查了全等三角形的判定,熟记等腰直角三角形的性质是解题的关键,同时注意证明角等的方法之一:利用等式的性质,等量加等量,还是等量.举一反三:【变式】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.求证:△ACD≌△BCE.【答案】证明:∵C是线段AB的中点,∴AC=BC,∵CD 平分∠ACE ,CE 平分∠BCD ,∴∠ACD=∠ECD ,∠BCE=∠ECD ,∴∠ACD=∠BCE ,在△ACD 和△BCE 中,∴△ACD ≌△BCE (SAS ).3、如图,将两个一大、一小的等腰直角三角尺拼接 (A 、B 、D 三点共线,AB =CB ,EB =DB ,∠ABC =∠EBD =90°),连接AE 、CD ,试确定AE 与CD 的位置与数量关系,并证明你的结论.【答案与解析】AE =CD ,并且AE ⊥CD证明:延长AE 交CD 于F ,∵△ABC 和△DBE 是等腰直角三角形∴AB =BC ,BD =BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△CBD (SAS )∴AE =CD ,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC =90°∴AE ⊥CD【总结升华】通过观察,我们也可以把△CBD 看作是由△ABE 绕着B 点顺时针旋转90°得到的.尝试着从变换的角度看待全等.举一反三:【变式】已知:如图,AP平分∠BAC,且AB=AC,点Q在PA上,求证:QC=QB【答案】证明:∵AP平分∠BAC∴∠BAP=∠CAP在△ABQ与△ACQ中∵∴△ABQ≌△ACQ(SAS)∴QC=QB类型三、全等三角形判定的实际应用4、如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的角平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.【思路点拨】只要证明轮船与D点的连线平分∠ADB就说明轮船没有偏离航线,也就是证明∠ADC=∠BDC.要证明角相等,常常通过把角放到两个三角形中,利用题目条件证明这两个三角形全等,从而得出对应角相等.【答案与解析】解:此时轮船没有偏离航线.理由:由题意知:DA=DB,AC=BC,在△ADC和△BDC中,,∴△ADC≌△BDC(SSS),∴∠ADC=∠BDC,即DC为∠ADB的角平分线,∴此时轮船没有偏离航线.【总结升华】本题考查了全等三角形的应用,解答本题的关键是:根据条件设计三角形全等,巧妙地借助两个三角形全等,寻找对应角相等.要学会把实际问题转化为数学问题来解决.举一反三:【变式】工人师傅经常利用角尺平分一个任意角,如图所示,∠AOB是一个任意角,在边OA,边OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D、E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线,你能先说明△OPE与△OPD 全等,再说明OP平分∠AOB吗?【答案】证明:在△OPE与△OPD中,∵OE OD OP OP PE PD=⎧⎪=⎨⎪=⎩∴△OPE≌△OPD (SSS)∴∠EOP=∠DOP(全等三角形对应角相等)∴OP平分∠AOB.。
浙教版全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)

全等三角形的判定(SSS)1、如图1.AB=AD.CB=CD.∠B=30°.∠BAD=46°.则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2.线段AD与BC交于点O.且AC=BD.AD=BC.•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中.已知AB=A1B1.BC=B1C1.则补充条件____________.可得到△ABC≌△A1B1C1.4、如图3.AB=CD.BF=DE.E、F是AC上两点.且AE=CF.欲证∠B=∠D.可先运用等式的性质证明AF=________.再用“SSS”证明______≌_______得到结论.5、如图.AB=AC.BD=CD.求证:∠1=∠2.6、如图.已知AB=CD.AC=BD.求证:∠A=∠D.7、如图.AC与BD交于点O.AD=CB.E、F是BD上两点.且AE=CF.DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.8、已知如图.A、E、F、C四点共线.BF=DE.AB=CD.⑴请你添加一个条件.使△DEC≌△BFA;⑵在⑴的基础上.求证:DE∥BF.DC BA全等三角形的判定(SAS)1、如图1.AB ∥CD.AB=CD.BE=DF.则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2.AB=AC.AD=AE.欲证△ABD ≌△ACE.可补充条件( ) A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD3、如图3.AD=BC.要得到△ABD 和△CDB 全等.可以添加的条件是( ) A.AB ∥CD B.AD ∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4.AB 与CD 交于点O.OA=OC.OD=OB.∠AOD=________.•根据_________可得到△AOD ≌△COB.从而可以得到AD=_________.5、如图5.已知△ABC 中.AB=AC.AD 平分∠BAC.请补充完整过程说明△ABD ≌△ACD 的理由. ∵AD 平分∠BAC. ∴∠________=∠_________(角平分线的定义). 在△ABD 和△ACD 中.∵____________________________. ∴△ABD ≌△ACD ( ) 6、如图6.已知AB=AD.AC=AE.∠1=∠2.求证∠ADE=∠B.7、如图.已知AB=AD.若AC 平分∠BAD.问AC 是否平分∠BCD ?为什么?8、如图.在△ABC 和△DEF 中.B 、E 、F 、C.在同一直线上.下面有4个条件.请你在其中选3个作为题设.余下的一个作为结论.写一个真命题.并加以证明.①AB=DE ; ②AC=DF ; ③∠ABC=∠DEF ; ④BE=CF.9、如图⑴.AB ⊥BD.DE ⊥BD.点C 是BD 上一点.且BC=DE.CD=AB .⑴试判断AC 与CE 的位置关系.并说明理由.⑵如图⑵.若把△CDE 沿直线BD 向左平移.使△CDE 的顶点C 与B 重合.此时第⑴问中AC 与BE 的位置关系还成立吗?(注意字母的变化)全等三角形(三)AAS 和ASA【知识要点】1.角边角定理(ASA ):有两角及其夹边对应相等的两个三角形全等.2.角角边定理(AAS ):有两角和其中一角的对边对应相等的两个三角形全等. 【典型例题】例1.如图.AB ∥CD.AE=CF.求证:AB=CD例2.如图.已知:AD=AE.ABE ACD ∠=∠.求证:BD=CE.例3.如图.已知:ABD BAC D C ∠=∠∠=∠..求证:OC=OD. 例4.如图已知:AB=CD.AD=BC.O 是BD 中点.过O 点的直线分别交DA 和BC 的延长线于E.F.求证:AE=CF.例5.如图.已知321∠=∠=∠.AB=AD.求证:BC=DE.AABDC O12 3例6.如图.已知四边形ABCD 中.AB=DC.AD=BC.点F 在AD 上.点E 在BC 上.AF=CE.EF 的对角线BD 交于O.请问O 点有何特征?【经典练习】1.△ABC 和△C B A '''中.C B C B A A ''='∠=∠,'.C C '∠=∠则△ABC 与△C B A ''' .2.如图.点C.F 在BE 上.,,21EF BC =∠=∠请补充一个条件.使△ABC ≌DFE,补充的条件是 .3.在△ABC 和△C B A '''中.下列条件能判断△ABC 和△C B A '''全等的个数有( ) ①A A '∠=∠ B B '∠=∠.C B BC ''= ②A A '∠=∠.B B '∠=∠.C A C A ''=' ③A A '∠=∠ B B '∠=∠.C B AC ''= ④A A '∠=∠.B B '∠=∠.C A B A ''=' A . 1个 B. 2个 C. 3个 D. 4个4.如图.已知MB=ND.NDC MBA ∠=∠.下列条件不能判定是△ABM ≌△CDN 的是( )A . N M ∠=∠ B. AB=CD C . AM=CN D. AM ∥CN 5.如图2所示. ∠E =∠F =90°.∠B =∠C .AE =AF .给出下列结论:①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是_________ _________。
三角形全等的判定(SSS,SAS,ASA)
全等三角形性质及判定(SSS,SAS,ASA) 1.了解三角形全等,对应角,对应边的概念
教学目标
2.掌握全等三角形的性质(对应元素相等)及判定(主要是 SSS,SAS,ASA) 3.学会书写证明题的思路及主要格式,养成数学推理思想 1.确定全等三角形的对应元素,掌握找对应元素的方法 2.理解 SSS,SAS,ASA 的涵义,会利用这三种方法判定三角形全等,并熟练掌
A D B E
C
F
练习 5:如图,已知 AB=AC,AD=AE,求证:BD=CE。 A
B D
E C
练习 6:如图,在 △ ABC 中, AB AC,BAC 40° ,分别以 AB,AC 为边作两个等腰直 角三角形 ABD 和 ACE ,使 BAD CAE 90° . (1)求 DBC 的度数;(2)求证: BD CE 。
3.已知:如图 T-3,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB=________度. 4.如下右图所示,AB = AD,∠1 = ∠2,添加一个适当的条件,使△ABC ≌ △ADE,则需要添加 的条件是________
O B E D
T-3
A C
A
5.已
E O
知:如图,DC∥AB,且 DC=AE,E 为 AB 的中点,求证:△AED≌△EBC.
B
1 2 3 4
A
O D
C
练习 9:如图,在 ABC 中, BAC 90 ,AB=AC,BD 是∠ABC 的角平分线,BD 的延长线 垂直于过点 C 的直线于 E,直线 CE 交 BA 的延长线于点 F。 求证:BD=2CE.(提示:等腰三角形底边上的高和中线重合,将底边平均分成两段)
F A E D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的判定训练题(SSS 、SAS)
判定定理1: 简单的表示为:SSS 数学语言:在△ABC 和△A 'B 'C ' 中 AC=A 'C ' (已知) BC=B 'C ' (已知)
AB=A 'B ' (已知) ∴△ABC ≌△A 'B 'C '
(SSS ) 1、若AB=CD,AC=DB ,可以判定哪两个三角形全等?请证明。
2、△ABC 中,AB=AC ,AD 是BC 边上的中线,∠B 与∠C 有什么关系?请证明。
3、点B 、E 、C 、F 在同一条直线上,AB=DE ,AC=DF ,BE=CF ,则AB 和DE 有怎样的位置关系?请证明。
A
C
4、已知AB=CD,BE=DF,AF=CE,则AB与CD有怎样的位置关系?
5、如图,AC=DF,BC=EF,AD=BE,∠BAC=80o,∠F=60o,求∠ABC
6、如图,AC=AD,BC=BD,∠1=35o,∠2=65o,求∠C
.
7、如图,△ABC 中,AD=AE , BE=CD ,AB=AC ,说明△ABD ≌△ACE
判定定理2: 简单的表示为:SAS 数学语言:在△ABC 和△A 'B 'C ' 中 AB=A 'B ' (已知) ∠B=∠B ' (已知)
BC=B 'C '
(已知)
∴△ABC ≌△A 'B 'C '
(SSS ) 8、如图,已知AC ,BD 相交于O ,AO=DO ,BO=CO ,证明:∠A=∠D
9.如图,AE 是,BAC 的平分线 AB=AC.证明 △ABD ≌△ACD
C
D
E
1 2
10、已知:如图,AB=AC,AD=AE,求证:BE=CD.
11、如图,已知:点D、E在BC上,且BD=CE,AD=AE,∠1=∠2,求证:△ADB≌△AEC
12、如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,求证: BE=DC
13、如图,点C是AB中点,CD∥BE,且CD=BE,试探究AD与CE的关系。
D
A
B
Q
C
P
E
A
D
A
D
B
E
C
14、如图:已知AC,BD相交于O,OA=OB,OC=OD.证明:△ABC≌△BAD。
