经典医学统计学统计描述.ppt
合集下载
医学统计学(统计图表)ppt课件

案例三
不同治疗方案对患者生存 率的影响。通过饼图展示 各治疗方案的生存率,比 较方案优劣。
前沿动态和未来发展趋势
数据可视化技术的创新应用
01
如交互式图表、动态图表等,提高数据呈现效果和用
户体验。
大数据在医学领域的应用
02 利用大数据技术分析海量医学数据,挖掘潜在规律和
关联,为医学研究和实践提供支持。
相关系数计算
用于量化两个变量之间的线性关系强度和方向。常见的相关系数包括皮尔逊相关 系数、斯皮尔曼相关系数和肯德尔相关系数等。通过计算相关系数,可以对两个 变量之间的关系进行定量分析和假设检验。
03 推断性统计图表
假设检验原理及流程
假设检验的基本原理
通过设定原假设和备择假设,根据样 本数据对原假设进行检验,判断其是 否成立。
临床意义
AUC值越大,说明待评价试验的诊断价值越高。同时,AUC值还可以用来比较不同诊断性试验的诊断价值,以及 在同一诊断性试验中比较不同临界值的诊断价值。此外,AUC值还可以用来估计诊断性试验的阳性似然比和阴性 似然比等参数,为临床决策提供更多的信息。
05 生存分析与寿命 表制作
生存分析基本概念
计算灵敏度和特异度
根据金标准和待评价试验的结果,计算出不同临界值下的 灵敏度和特异度。
绘制ROC曲线
以特异度为横坐标,灵敏度为纵坐标,将不同临界值下的 灵敏度和特异度描绘在坐标图上,连接各点即得ROC曲线 。
AUC值计算和临床意义
AUC值计算
通过计算ROC曲线下的面积得到AUC值,其取值范围在0.5~1之间。当AUC=0.5时,说明待评价试验完全无效; 当AUC=1时,说明待评价试验具有完美的诊断价值。
人工智能在统计图表分析中的应用
图文《医学统计学》PPT课件

步骤
提出假设、构造检验统计量、确定拒绝域、计算p值、做出决策。
t检验和方差分析
t检验
用于比较两组均数是否有差别,包括单样本t检验、配对样本t检验和独立样本t检验。
方差分析
用于比较多组均数是否有差别,包括单因素方差分析和多因素方差分析。
卡方检验和秩和检验
卡方检验
用于推断两个或多个总体率或构成比之 间有无差别,多用于分类资料的统计分 析。
特点
以医学为背景,以数据为基础, 运用统计学方法揭示医学现象的 数量特征和规律。
发展历程及现状
发展历程
医学统计学经历了从描述性统计到推 断性统计,再到现代多元统计分析的 发展历程。
现状
随着计算机技术的发展和大数据时代 的到来,医学统计学在医学研究和实 践中发挥着越来越重要的作用。
研究对象与任务
研究对象
样本量
样本中所包含的个体数目 。
随机抽样与非随机抽样
随机抽样
按照随机原则从总体中抽取样本的方法,保证每个个体被抽 中的机会相等。
非随机抽样
根据研究者的主观意愿或方便性选择样本的方法,可能导致 选择偏倚。
变量与数据类型
变量
研究中观察或测量的特征或属性。
数据类型
根据变量的性质可分为定量数据和定性数据。定量数据包括连续型数据和离散型 数据,定性数据包括分类数据和顺序数据。
医学统计学的研究对象包括生物医学数据、临床医学数据、公共卫生数据等。
任务
医学统计学的任务包括描述医学数据的分布特征、比较不同组别间的差异、分 析影响医学现象的因素、预测医学现象的发展趋势等。
02
医学统计学基本概念
总体与样本
01
02
03
总体
提出假设、构造检验统计量、确定拒绝域、计算p值、做出决策。
t检验和方差分析
t检验
用于比较两组均数是否有差别,包括单样本t检验、配对样本t检验和独立样本t检验。
方差分析
用于比较多组均数是否有差别,包括单因素方差分析和多因素方差分析。
卡方检验和秩和检验
卡方检验
用于推断两个或多个总体率或构成比之 间有无差别,多用于分类资料的统计分 析。
特点
以医学为背景,以数据为基础, 运用统计学方法揭示医学现象的 数量特征和规律。
发展历程及现状
发展历程
医学统计学经历了从描述性统计到推 断性统计,再到现代多元统计分析的 发展历程。
现状
随着计算机技术的发展和大数据时代 的到来,医学统计学在医学研究和实 践中发挥着越来越重要的作用。
研究对象与任务
研究对象
样本量
样本中所包含的个体数目 。
随机抽样与非随机抽样
随机抽样
按照随机原则从总体中抽取样本的方法,保证每个个体被抽 中的机会相等。
非随机抽样
根据研究者的主观意愿或方便性选择样本的方法,可能导致 选择偏倚。
变量与数据类型
变量
研究中观察或测量的特征或属性。
数据类型
根据变量的性质可分为定量数据和定性数据。定量数据包括连续型数据和离散型 数据,定性数据包括分类数据和顺序数据。
医学统计学的研究对象包括生物医学数据、临床医学数据、公共卫生数据等。
任务
医学统计学的任务包括描述医学数据的分布特征、比较不同组别间的差异、分 析影响医学现象的因素、预测医学现象的发展趋势等。
02
医学统计学基本概念
总体与样本
01
02
03
总体
医学统计学课件:02_统计描述(定量定性)

中位数(median,M)
将一组观察值从小到大按顺序排列,居于中心位置 的数值。在全部观察值中有半数的值比M大,另有半数 的值比M小。 适用于当大部分观测值比较集中,少数观测值偏向 一侧时;或资料分布情况不清楚时;或数据的最大值
(最小值)无准确测量数据时。如传染病的潜伏期。任
何分布的定量数据均可用中位数描述其分布的集中趋势, 使用范围广。
2003年4月22日全国SARS发病人数频数表
发病地区 北京 山西 广东 河北 内蒙 天津 广西 其他省市 频数 105 16 14 6 3 2 1 0 频率/% 71.4 10.9 9.5 4.1 2.0 1.4 0.7 0.0 累积频数 105 121 135 141 144 146 14移,向右侧拖尾
负偏态(左偏态)
峰向右偏移,向左侧拖尾
集中趋势的特征值
—— 平均水平的度量
算术均数(arithmetic mean,M)
适用于正态分布和近似正态分布的资
料。
总体均数用µ表示;样本均数用 x 表示。
直接计算法
将所有观察值直接相加再除以观察值的个数。
f i lg X i f1 lg X 1 f 2 lg X 2 f n lg X n 1 lg G lg f f i i
1
频数表资料的几何均数
抗体滴度 ⑴
人数,f ⑵
滴度倒数,X ⑶
lgX ⑷
f· lgX ⑸
累积频率/%
71.4 82.3 91.8 95.9 98.0 99.3 100.0 100.0
合计
147
100.0
某药物疗效的频数表
治疗效果 治愈 频数 65 频率/% 43.3 累积频数 65
[医学]医学统计学课件PPT
![[医学]医学统计学课件PPT](https://img.taocdn.com/s3/m/686e15a59ec3d5bbfd0a74ca.png)
• (1)、同质(homogeneity):根据研 究目的给研究单位确定的相同性质。
• 研究长沙市2004年7岁 男孩身高的正常值范围?
• 同质:同长沙市、同7岁、同男孩、同无 影响身高的疾病。
2020/12/5
二、统计学中的几个基本概念
• (2)、变异 (variation)
• 变异 (variation):同质研究单位中变 量值间的差异。
二、统计学中的几个基本概念
变量值(value of variable) : 变量的观察结果。 例如:研究7岁男孩身高 变量值:测得的身高值 (
120.2cm,118.6cm,121.8cm,…) 研究某人群性别构成 变量值:男、女。
2020/12/5
二、统计学中的几个基本概念
• 2、同质(homogeneity)和变异 ( variation)
医学统计学 Medical Statistics
2020/12/5
医学统计学讲授内容
第一章 绪论 第二章 计量资料的统计描述 第三章 总体均数的估计与假设检验 第四章 多个样本均数比较的方差分析 第五章 计数资料的统计描述 第六章 几种离散型变量的分布及其应用
第七章 2 检验
第八章 秩转换的非参数检验 第九章 双变量回归与相关 第十章 统计表与统计图
睛
研究水污染情况 水
研究细胞变性 胞
研究肝癌的地区分布
一个人 一只眼 一毫升 一个细 一个地区
2020/12/5
二、统计学中的几个基本概念
(2)变量(variable): 研究单位的研究特
征。
例如:研究7岁 男孩身高的正常值范围
变量:
身高
(3)变量值(value of variable
• 研究长沙市2004年7岁 男孩身高的正常值范围?
• 同质:同长沙市、同7岁、同男孩、同无 影响身高的疾病。
2020/12/5
二、统计学中的几个基本概念
• (2)、变异 (variation)
• 变异 (variation):同质研究单位中变 量值间的差异。
二、统计学中的几个基本概念
变量值(value of variable) : 变量的观察结果。 例如:研究7岁男孩身高 变量值:测得的身高值 (
120.2cm,118.6cm,121.8cm,…) 研究某人群性别构成 变量值:男、女。
2020/12/5
二、统计学中的几个基本概念
• 2、同质(homogeneity)和变异 ( variation)
医学统计学 Medical Statistics
2020/12/5
医学统计学讲授内容
第一章 绪论 第二章 计量资料的统计描述 第三章 总体均数的估计与假设检验 第四章 多个样本均数比较的方差分析 第五章 计数资料的统计描述 第六章 几种离散型变量的分布及其应用
第七章 2 检验
第八章 秩转换的非参数检验 第九章 双变量回归与相关 第十章 统计表与统计图
睛
研究水污染情况 水
研究细胞变性 胞
研究肝癌的地区分布
一个人 一只眼 一毫升 一个细 一个地区
2020/12/5
二、统计学中的几个基本概念
(2)变量(variable): 研究单位的研究特
征。
例如:研究7岁 男孩身高的正常值范围
变量:
身高
(3)变量值(value of variable
医学统计学-定量资料统计描述集中离散PPT课件
5.27~5.47
例数 2 3 9 14 22 30 21 15 10 6 4 2
.2章
25
算术均数
组段 3.07~ 3.27~ 3.47~ 3.67~ 3.87~ 4.07~ 4.27~ 4.47~ 4.67~ 4.87~ 5.07~ 5.27~5.47 合计
频数 2 3 9 14 22 30 21 15 10 6 4 2 138
7—
连续型定量变量的频数分布
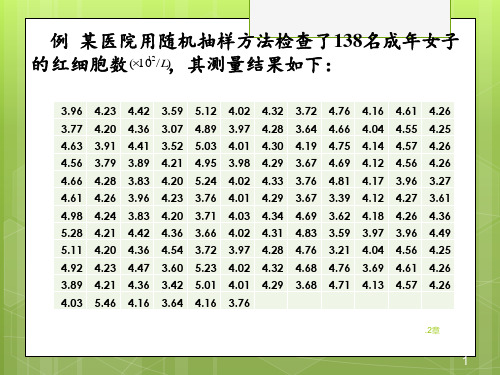
连续型定量变量(continuous variable)通 常是指取值连续的定量变量,可以取数轴上 的任意数值
例如身高、体重、血压、血清胆固醇值等 例:某医院用随机抽样方法检查了138名成
年女子的红细胞数
.2章
8
理想的描述结果
RBC 3.07~ 3.27~ 3.47~ 3.67~ 3.87~ 4.07~ 4.27~ 4.47~ 4.67~ 4.87~ 5.07~ 5.27~5.47
组中值 3.17 3.37 3.57 3.77 3.97 4.17 4.37 4.57 4.77 4.97 5.17 5.37 —
.2章
频数×组中值 6.34 10.11 32.13 52.78 87.34
125.10 91.77 68.55 47.70 29.82 20.68 10.74 583.06
.2章
20
1.算术均数
算术均数arithmetic mean (μ总体均数 ,
x 样本均数)简称均数,在已知各观察单 位具体变量值时,可以采用直接法计算,公 式如下:
XX1X2 n
n
Xn i1 Xi
n
.2章
21
直接法:
.
例4.3 利用例4.2的155名6月龄婴儿的SOS资 料,计算均数。
例数 2 3 9 14 22 30 21 15 10 6 4 2
.2章
25
算术均数
组段 3.07~ 3.27~ 3.47~ 3.67~ 3.87~ 4.07~ 4.27~ 4.47~ 4.67~ 4.87~ 5.07~ 5.27~5.47 合计
频数 2 3 9 14 22 30 21 15 10 6 4 2 138
7—
连续型定量变量的频数分布
连续型定量变量(continuous variable)通 常是指取值连续的定量变量,可以取数轴上 的任意数值
例如身高、体重、血压、血清胆固醇值等 例:某医院用随机抽样方法检查了138名成
年女子的红细胞数
.2章
8
理想的描述结果
RBC 3.07~ 3.27~ 3.47~ 3.67~ 3.87~ 4.07~ 4.27~ 4.47~ 4.67~ 4.87~ 5.07~ 5.27~5.47
组中值 3.17 3.37 3.57 3.77 3.97 4.17 4.37 4.57 4.77 4.97 5.17 5.37 —
.2章
频数×组中值 6.34 10.11 32.13 52.78 87.34
125.10 91.77 68.55 47.70 29.82 20.68 10.74 583.06
.2章
20
1.算术均数
算术均数arithmetic mean (μ总体均数 ,
x 样本均数)简称均数,在已知各观察单 位具体变量值时,可以采用直接法计算,公 式如下:
XX1X2 n
n
Xn i1 Xi
n
.2章
21
直接法:
.
例4.3 利用例4.2的155名6月龄婴儿的SOS资 料,计算均数。
医学医学统计学PPT课件

样本量估算
根据研究目的、效应大小、显著性水平 和把握度等因素,合理估算所需样本量。
随机化方法
介绍简单随机化、分层随机化、整群随 机化等随机化方法,以确保试验组和对 照组的可比性。
数据分析与解读
运用统计学方法对试验数据进行描述性 统计、推断性统计和生存分析等,正确 解读分析结果。
观察性数据分析与处理
误差和提高实验效率。
方差分析基本思想
将总变异分解为组间变异和组内变 异,通过比较组间变异与组内变异 的相对大小,推断各因素对结果的 影响是否显著。
方差分析步骤
建立假设、计算检验统计量、确定P 值、作出推断结论。
04
医学统计学在医学研究中 的应用
临床试验设计与分析
试验设计类型
包括随机对照试验、交叉设计、析因设 计等,以及各种设计类型的优缺点和适 用场景。
03
样本容量
样本中所包含的个体数目。
变量与数据类型
变量
研究中观察或测量的特征或属性, 可以是定量的或定性的。
数据类型
根据变量的性质可分为定量数据和 定性数据,其中定量数据又可分为 离散型和连续型。
统计பைடு நூலகம்与抽样分布
03
统计量
用于描述样本特征的数值,如样本均值、 样本标准差等。
抽样分布
由样本统计量所形成的分布,用于推断总 体参数。常见的抽样分布有t分布、F分布 和卡方分布等。
03
多重比较与假设检验的误用
Hochberg校正
02
01
控制FDR(False Discovery Rate) 的方法
统计模型的选择与评估
统计模型的选择
1
2
根据研究目的和数据类型选择合适的统计模型
医学统计学统计描述课件.ppt

合计
1468
448
100.00
因为60-岁组的患病年龄构成为30.13%,在五个组中最大,因 此60-岁组患白内障的机率最大,其次是50-岁组,最低是80岁组。这种说法成立吗?
。
• 2.计算相对数应有足够数量即分母不宜太小 ,例数很少的情况下最好用绝对数直接表示
Ⅰ期患者22例,确诊后未予治疗的5例 患者中1例进展,3例自愈,1例部分缓解; 确诊后即予激素治疗的17例患者中,9例 完全缓解,1例进展至Ⅱ期
。
结节病59例治疗及随访分析
目的 探讨结节病的治疗、影响预后的因素及预 后
方法 回顾1984年1月-2003年1月北京协和医院住 院治疗且随访≥2年的59例结节病临床资料
结果 随访时间(61.9±49.4)个月
讨论:随访时间可能为偏态分布资料,以均数与标 准差表示是否适合?
。
描述集中位置的统计指标
。
描述离散程度的统计指标
变异系数 表示方法:CV,它实际上是标准差的另一种表达方式, 即将标准差转化为均数的倍数,以百分数的形式表示。
计算公式:
适用情况: (1)比较度量衡单位不同的多组资料的变异度 (2)比较均数相差悬殊的多组资料的变异度。
。
描述离散程度的统计指标 指标的联用 正态分布:算术均数 ±标准差 偏态分布:中位数 与 四分位数间距
。
计量资料的统计描述
主要内容 1 描述集中位置的指标 23 描述离散程度的指标
。
描述集中位置的统计指标
平均数(average)
算术均数(mean) 几何均数(geometric mean) 中位数(median)
。
描述集中位置的统计指标
算术均数
医学统计学PPT课件

验结果,每次都有如此好的吻合. 的概率约10万分之4。 6
绪论 Introduction
讲授内容:
一、医学统计学的意义
二、统计学中的几个基本概念
三、统计资料的类型
四、医学统计工作的基本步骤
五、学习医学统计学应注意的问题
.
7
一、医学统计学的意义
• 1.统计学(statistics):应用数学的原理与 方法,研究数据的搜集、整理与分析的科 学,对不确定性数据作出科学的推断。
例如:某药治疗高血压患者30名
样本含量(n)为30
.
21
二、统计学中的几个基本概念
• 4、参数(parameter)和统计量(statistic)
• (1)参数(parameter):根据总体个体 值统 计计算出来的描述总体的特征量。
• 一般用希腊字母表示
• (2)、统计量(statistic):根据样本个体值统 计计算出来的描述样本的特征量。
(120.2cm,118.6cm,121.8cm,…)
研究某人群性别构成 变量值:男、女。
.
15
二、统计学中的几个基本概念
• 2、同质(homogeneity)和变异 (variation)
• (1)、同质(homogeneity):根据研究 目的给研究单位确定的相同性质。
• 研究长沙市2004年7岁 男孩身高的正常值范围?
.
27
二、统计学中的几个基本概念
• (3)、抽样误差(sampling error):由 于抽样所造成的样本统计量与总体参数 的差别。
• 例如:=120.0cm
n=100
•
N=5万 → X =118.6cm
• 特点:1)不可避免性
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P50:第50百分位数,即中位数。
。
描述离散程度的统计指标
方差 表示方法:总体方差用σ2表示,样本方差用S2表示。 计算公式: 特点:方差越大,离散程度越大。适用于正态分 布的资料
。
描述离散程度的统计指标
标准差 表示方法:总体标准差用σ表示,样本标准差用S表示。 计算公式:
特点:标准差越大,离散程度越大。适用于正态分布 的资料
。
结节病59例治疗及随访分析
目的 探讨结节病的治疗、影响预后的因素及预 后
方法 回顾1984年1月-2003年1月北京协和医院住 院治疗且随访≥2年的59例结节病临床资料
结果 随访时间(61.9±49.4)个月
讨论:随访时间可能为偏态分布资料,以均数与标 准差表示是否适合?
。
描述集中位置的统计指标
。
自体外周血干细胞移植术后早期感染的分析
目的 研究自体外周血干细胞移植(APBSCT) 后早期 感染的发生率、危险因素、治疗 对策和预后转归
方法 回顾性分析120例 APBSCT 患者早期感 染的相关临床资料
结果 感染持续的中位时间为2(1~23)d。
。
描述离散程度的统计指标
四分位数 间距 表示方法:Q
正常
有效
异常
有效
异常
无效
…
正常 无效
。
两个分类因素的交叉频数表
A、B 两组高血压患者疗效比较
组别 治愈 显效 有效 无效 合计 A 29 17 6 4 56 B 17 12 12 11 52
多采用软件进行汇总形成频数表,如EXCEL, SAS,SPSS等
。
常用相对数
绝对数:计数资料常见的数据形式,如某病的出院人 数、治愈人数、死亡人数等。反映事物的实际发生 情况。
主要内容
统计描述
计量资料统计描述 计数资料统计描述
。
案例:自体外周血干细胞移植术后早期感染的分析
目的 研究自体外周血干细胞移植(APBSCT)后早期 感染的发生率、危险因素、治疗对策和预后转归
方法 回顾性分析120例 APBSCT 患者早期感染的相 关临床资料
结果 早期感染发生率为57.5%(69/120) 死亡2.5%(3/120)(是病死率而非死亡率) 首次发生感染的中位时间为移植后6d 感染持续的中位时间为2(1~23)d。 血培养阳性率为16.0%(11/69)
。
计量资料的统计描述
主要内容 1 描述集中位置的指标 23 描述离散程度的指标
。
描述集中位置的统计指标
平均数(average)
算术均数(mean) 几何均数(geometric mean) 中位数(median)
。
描述集中位置的统计指标
算术均数
表示方法 总体均数:μ ,样本均数:X
计算公式 适用资料:适用于对称分布,特别是正态分布的资料
。
计数资料的统计描述
主要内容 1
常用相对数
2 相对数应用时的注意事项
。
例:108例高血压患者治疗后临床记录
编号 1 2 3 4 …
108
年龄 37 45 43 59
54
性别 男 女 男 女
男
治疗组 A B A B
… B
舒张压 11.27 12.53 10.93 14.67
16.80
心电图 正常
疗效 显效
几何均数
表示方法 G
计算公式
适用资料:观察值变化范围跨越多个数量级,成等 比增长(倍ቤተ መጻሕፍቲ ባይዱ变化),或在取对数后成正态分布 (即对数正态分布)的资料。
。
描述集中位置的统计指标
中位数 定义: 将n个数据从小到大排列,位置居中的那个数 表示方法:中位数用M或Md表示 计算公式 适用资料:主要适用于偏态分布的资料。
缺点:绝对数通常不具有可比性。
相对数:是两个有关绝对数之比,统称为相对数。 优点:消除基数影响,便于事物间的比较。
常用相对数有三大类:相对比、构成比、率
。
相对比
• 相对比:反映两个指标(指标可为绝对数、相对数;性 质相同或不同)相比的倍数或百分数。
结论 ………….
。
结节病59例治疗及随访分析
目的 探讨结节病的治疗、影响预后的因素及预 后
方法 回顾1984年1月-2003年1月北京协和医院住 院治疗且随访≥2年的59例结节病临床资料
结果 随访时间(61.9±49.4)个月 0期患者7例,均在确诊后即口服糖皮质激素治疗,
其中4例完全缓解,Ⅰ期患者22例,确诊后未予治 疗的5例患者中1例进展,3例自愈,1例部分缓解; 确诊后即予激素治疗的17例患者中,9例完全缓解 ,1例进展至Ⅱ期,Ⅱ期……. ,Ⅲ期 ……Ⅳ期 结论 ………
极差(range),又称全距 四分位数间距(quartile) 方差(variance) 标准差(standard deviation) 变异系数(coefficient of variation)
。
描述离散程度的统计指标
极差 表示方法:R
计算公式: R = 最大值 - 最小值
特点:极差越大离散程度越大。简单,较适用于 说明传染病、食物中毒等的最短、最长潜伏期等。 不稳定,没有全部观察值的信息,易受极端值的 影响,受样本含量的影响。
。
自体外周血干细胞移植术后早期感染的分析
目的 研究自体外周血干细胞移植(APBSCT)后早期 感染的发生率、危险因素、治疗对策和预后转归
方法 回顾性分析120例 APBSCT 患者早期感染的相 关临床资料
结果 首次发生感染的中位时间为移植后6d 感染持续的中位时间为2(1~23)d。
。
描述离散程度的统计指标
计算公式: Q= P75 - P25 P75 :第75百分位数 P25 :第25百分位数
特点:四分位数间距越大离散程度越大。比极差 稳定,但仍没有利用全部观察值的信息。主要适 用于偏态分布的资料
。
描述离散程度的统计指标 百分位数(percentile)
百分位数(percentile):是一种位置指标,以Px表 示,把一组数据从小到大排列,一个百分位数Px将数 据分成两部分,有x%的数值小于Px,有1-x%的数值大 于Px。如P25。
。
描述离散程度的统计指标
变异系数 表示方法:CV,它实际上是标准差的另一种表达方式, 即将标准差转化为均数的倍数,以百分数的形式表示。
计算公式:
适用情况: (1)比较度量衡单位不同的多组资料的变异度 (2)比较均数相差悬殊的多组资料的变异度。
。
描述离散程度的统计指标 指标的联用 正态分布:算术均数 ±标准差 偏态分布:中位数 与 四分位数间距
。
描述离散程度的统计指标
方差 表示方法:总体方差用σ2表示,样本方差用S2表示。 计算公式: 特点:方差越大,离散程度越大。适用于正态分 布的资料
。
描述离散程度的统计指标
标准差 表示方法:总体标准差用σ表示,样本标准差用S表示。 计算公式:
特点:标准差越大,离散程度越大。适用于正态分布 的资料
。
结节病59例治疗及随访分析
目的 探讨结节病的治疗、影响预后的因素及预 后
方法 回顾1984年1月-2003年1月北京协和医院住 院治疗且随访≥2年的59例结节病临床资料
结果 随访时间(61.9±49.4)个月
讨论:随访时间可能为偏态分布资料,以均数与标 准差表示是否适合?
。
描述集中位置的统计指标
。
自体外周血干细胞移植术后早期感染的分析
目的 研究自体外周血干细胞移植(APBSCT) 后早期 感染的发生率、危险因素、治疗 对策和预后转归
方法 回顾性分析120例 APBSCT 患者早期感 染的相关临床资料
结果 感染持续的中位时间为2(1~23)d。
。
描述离散程度的统计指标
四分位数 间距 表示方法:Q
正常
有效
异常
有效
异常
无效
…
正常 无效
。
两个分类因素的交叉频数表
A、B 两组高血压患者疗效比较
组别 治愈 显效 有效 无效 合计 A 29 17 6 4 56 B 17 12 12 11 52
多采用软件进行汇总形成频数表,如EXCEL, SAS,SPSS等
。
常用相对数
绝对数:计数资料常见的数据形式,如某病的出院人 数、治愈人数、死亡人数等。反映事物的实际发生 情况。
主要内容
统计描述
计量资料统计描述 计数资料统计描述
。
案例:自体外周血干细胞移植术后早期感染的分析
目的 研究自体外周血干细胞移植(APBSCT)后早期 感染的发生率、危险因素、治疗对策和预后转归
方法 回顾性分析120例 APBSCT 患者早期感染的相 关临床资料
结果 早期感染发生率为57.5%(69/120) 死亡2.5%(3/120)(是病死率而非死亡率) 首次发生感染的中位时间为移植后6d 感染持续的中位时间为2(1~23)d。 血培养阳性率为16.0%(11/69)
。
计量资料的统计描述
主要内容 1 描述集中位置的指标 23 描述离散程度的指标
。
描述集中位置的统计指标
平均数(average)
算术均数(mean) 几何均数(geometric mean) 中位数(median)
。
描述集中位置的统计指标
算术均数
表示方法 总体均数:μ ,样本均数:X
计算公式 适用资料:适用于对称分布,特别是正态分布的资料
。
计数资料的统计描述
主要内容 1
常用相对数
2 相对数应用时的注意事项
。
例:108例高血压患者治疗后临床记录
编号 1 2 3 4 …
108
年龄 37 45 43 59
54
性别 男 女 男 女
男
治疗组 A B A B
… B
舒张压 11.27 12.53 10.93 14.67
16.80
心电图 正常
疗效 显效
几何均数
表示方法 G
计算公式
适用资料:观察值变化范围跨越多个数量级,成等 比增长(倍ቤተ መጻሕፍቲ ባይዱ变化),或在取对数后成正态分布 (即对数正态分布)的资料。
。
描述集中位置的统计指标
中位数 定义: 将n个数据从小到大排列,位置居中的那个数 表示方法:中位数用M或Md表示 计算公式 适用资料:主要适用于偏态分布的资料。
缺点:绝对数通常不具有可比性。
相对数:是两个有关绝对数之比,统称为相对数。 优点:消除基数影响,便于事物间的比较。
常用相对数有三大类:相对比、构成比、率
。
相对比
• 相对比:反映两个指标(指标可为绝对数、相对数;性 质相同或不同)相比的倍数或百分数。
结论 ………….
。
结节病59例治疗及随访分析
目的 探讨结节病的治疗、影响预后的因素及预 后
方法 回顾1984年1月-2003年1月北京协和医院住 院治疗且随访≥2年的59例结节病临床资料
结果 随访时间(61.9±49.4)个月 0期患者7例,均在确诊后即口服糖皮质激素治疗,
其中4例完全缓解,Ⅰ期患者22例,确诊后未予治 疗的5例患者中1例进展,3例自愈,1例部分缓解; 确诊后即予激素治疗的17例患者中,9例完全缓解 ,1例进展至Ⅱ期,Ⅱ期……. ,Ⅲ期 ……Ⅳ期 结论 ………
极差(range),又称全距 四分位数间距(quartile) 方差(variance) 标准差(standard deviation) 变异系数(coefficient of variation)
。
描述离散程度的统计指标
极差 表示方法:R
计算公式: R = 最大值 - 最小值
特点:极差越大离散程度越大。简单,较适用于 说明传染病、食物中毒等的最短、最长潜伏期等。 不稳定,没有全部观察值的信息,易受极端值的 影响,受样本含量的影响。
。
自体外周血干细胞移植术后早期感染的分析
目的 研究自体外周血干细胞移植(APBSCT)后早期 感染的发生率、危险因素、治疗对策和预后转归
方法 回顾性分析120例 APBSCT 患者早期感染的相 关临床资料
结果 首次发生感染的中位时间为移植后6d 感染持续的中位时间为2(1~23)d。
。
描述离散程度的统计指标
计算公式: Q= P75 - P25 P75 :第75百分位数 P25 :第25百分位数
特点:四分位数间距越大离散程度越大。比极差 稳定,但仍没有利用全部观察值的信息。主要适 用于偏态分布的资料
。
描述离散程度的统计指标 百分位数(percentile)
百分位数(percentile):是一种位置指标,以Px表 示,把一组数据从小到大排列,一个百分位数Px将数 据分成两部分,有x%的数值小于Px,有1-x%的数值大 于Px。如P25。
。
描述离散程度的统计指标
变异系数 表示方法:CV,它实际上是标准差的另一种表达方式, 即将标准差转化为均数的倍数,以百分数的形式表示。
计算公式:
适用情况: (1)比较度量衡单位不同的多组资料的变异度 (2)比较均数相差悬殊的多组资料的变异度。
。
描述离散程度的统计指标 指标的联用 正态分布:算术均数 ±标准差 偏态分布:中位数 与 四分位数间距
