数学也可以画出来
数学绘画观察生活中的某个场景并画出来

数学绘画观察生活中的某个场景并画出来
假设观察的场景是一个公园里的花坛。
首先,我们观察到花坛是一个圆形的区域,我们可以使用数学中的圆来表示它。
假设花坛的半径为r。
接下来,我们观察到花坛里有许多不同种类的花朵,我们可以使用各种曲线和图形来表达它们。
比如,可以使用曲线来表示蔷薇花的枝条,使用椭圆来表示百合花的花瓣,使用圆形来表示太阳花的花蕊等等。
此外,我们还可以使用数学中的比例关系来表达花坛中花朵的分布情况。
比如,可以通过花朵的大小来表示它们的数量,大花代表多,小花代表少。
也可以使用花朵的颜色来表示它们的种类和品种。
最后,我们可以使用透视法来表达花坛所处的空间位置。
比如,在画布上画出一个远处的树林和一条弯曲的小径,来增加花坛的立体感。
综上所述,通过观察与数学概念的结合,我们可以用各种数学方法来绘画观察到的花坛场景,并力求表达出真实的美感和风格。
三年级数学6大图画题,强化孩子数学思维

三年级数学6大图画题,强化孩子数学思维,不会的孩子赶紧看!对于题目中条件比较抽象、不易直接根据所学知识写出答案的问题,可以借助画平面图帮助思考解题。
例1 有两个自然数A和B,如果把A增加12,B不变,积就增加72;如果A不变,B增加12,积就增加120,求原来两数的积。
根据题目的条件比较抽象的特点,不妨借用长方形图,把条件转化为因数与积的关系。
先画一个长方形,长表示A,宽表示B,这个长方形的面积就是原来两数的积。
如图(1)所示。
根据条件把A增加12,则长延长12,B不变即宽不变,如图(2);同样A不变即长不变,B增加12,则宽延长12,如图(3)。
从图中不难找出:原长方形的长(A)是120÷12=10原长方形的宽(B)是72÷12=6则两数的积为10×6=60借助长方形图,弄清了题中的条件,找到了解题的关键。
例2 一个梯形下底是上底的1.5倍,上底延长4厘米后,这个梯形就变成一个面积为6O平方厘米的平行四边形。
求原来梯形面积是多少平方厘米?根据题意画平面图:从图中可以看出:上、下底的差是4厘米,而这4厘米对应的正好是1.5-1=O.5倍。
所以上底是4÷(1.5-1)=8(厘米),下底是8×1.5=12(厘米),高是60÷12=5(厘米),则原梯形的面积是(8+12)×5÷2=5O(平方厘米)。
立体图一些求积题,结合题目的内容画出立体图,这样做,使题目的内容直观、形象,有利于思考解题。
例1 把一个正方体切成两个长方体,表面积就增加了8平方米。
原来正方体的表面积是多少平方米?如果只凭想象,做起来比较困难。
按照题意画图,可以帮助我们思考,找出解决问题的方法来。
按题意画立体图:从图中不难看出,表面积增加了8平方米,实际上是增加2个正方形的面,每个面的面积是8÷2=4(平方米)。
原正方体是6个面,即表面积为4×6=24(平方米)。
趣味数学用折纸法画椭圆

趣味数学——用折纸法画椭圆
今天我们再来介绍用折纸法画椭圆的方法,方法很画抛物线非常类似。
昨天我们用矩形通过不断的折叠得到了抛物线,今天我们是要用圆形纸片,通过类似的方法来折叠出椭圆。
折纸法画椭圆方法
1:先准备一个圆形纸片,在纸片中间(不能是中心点)确定一点P.
2:开始折叠圆,将圆折起一角,使得圆周正好过点F
3:如此,便有了一折痕L ,我们当然知道,这样的折叠可以有很多种方式,这样继续折下去,你将得到假设干条折痕,将每一条折痕都用笔标记出来,你会发现,这些折痕衬托出了一个椭圆的轮廓:
4:接下来的事情就很简单,你画一条曲线,使之和每一条折痕相切就行了,得到的曲线就是以F和圆形O为焦点的一个椭圆。
所用的方法和我们昨天用矩形纸片折抛物线的时候是非常的类似。
当然,下面我们就应该证明为何得到的曲线就是椭圆。
折纸法画椭圆的证明
首先我们要知道的是,因为F异于O点,所以假设以F和O为焦点,那么可以画一个椭圆,设这个椭圆为C。
如上图所示,考虑其中一条折痕,做F 点关于折痕对称的点M ,显然M应该在圆周上,连接MO ,交折痕于P ,这个P点就是我们的重点了。
根据对称性,PF=PM ,所以
PF+PO=PM+PO=MO=r。
也就是说,P点到F和O点的距离之和是个与折痕无关的常数,所以P点应该在椭圆C上。
另一方面,考虑异于P的Q点,可以很容易看出,QF+QO并非一个常量,所以Q点不在椭圆C上,也就是说,折痕于椭圆C只有一个交点P ,该折痕就是椭圆C的一条切线,同理,
每一条折痕都是椭圆C的切线,众多切线包围住椭圆,也就显示出其轮廓,这正是我们折纸法折出椭圆的原理。
文章。
初中数学 如何画出一次函数的图像

初中数学如何画出一次函数的图像画出一次函数的图像是初中数学中的重要内容之一。
一次函数也称为线性函数,其图像是一条直线。
通过画出一次函数的图像,我们可以更好地理解其性质和特征。
下面将详细介绍如何画出一次函数的图像。
一次函数的一般形式为y = mx + b,其中m 表示斜率,b 表示y 轴截距。
画出一次函数的图像需要掌握以下步骤:步骤一:确定坐标轴范围首先,确定坐标轴的范围。
通常,我们将x 轴和y 轴的范围设置为包含函数图像的点。
可以根据实际情况选择适当的范围。
步骤二:选择点选择一些点来绘制函数的图像。
我们可以选择x 的值,并使用函数的表达式计算对应的y 值。
至少选择两个点,但更多的点可以提供更准确的图像。
步骤三:绘制直线通过连接选定的点来绘制直线。
确保直线通过至少两个点以确保准确性。
步骤四:添加箭头和标签添加箭头和标签以标识坐标轴和直线。
箭头指示正方向,标签可以包括坐标轴的名称和直线的方程。
下面是一个具体的例子,演示如何画出一次函数的图像:例子:画出函数y = 2x + 3 的图像步骤一:确定坐标轴范围由于函数y = 2x + 3 是一条直线,我们可以根据需要选择适当的范围。
假设我们选择x 轴的范围为-5 到5,y 轴的范围为-10 到10。
步骤二:选择点选择至少两个点来绘制函数的图像。
我们可以选择x 的值,并使用函数的表达式计算对应的y 值。
假设我们选择x = -2 和x = 3。
当x = -2 时,y = 2(-2) + 3 = -1,所以我们有点(-2, -1)。
当x = 3 时,y = 2(3) + 3 = 9,所以我们有点(3, 9)。
步骤三:绘制直线通过连接选择的点来绘制直线。
将点(-2, -1) 和(3, 9) 连接起来,得到一条直线。
步骤四:添加箭头和标签在坐标轴的末端添加箭头,表示正方向。
添加x 轴和y 轴的标签,例如"x" 和"y"。
在直线上方或下方添加方程的标签,例如"y = 2x + 3"。
数学在美术中的应用

数学在美术中的应用
美术在艺术创作中占有重要的地位,却有许多不同的类型和文化融合,它不仅是一种自由的表达方式,同时它的形式也具有秩序性,而数学的概念对于寻求更多的美术创作灵感是至关重要的,它能够更加准确的描述和表达美术作品中的形状、比例以及配色等因素,从而使得美术创作更有趣、更具有创造性。
第一,数学概念能够帮助美术家创作出更加美观的作品:数学概念可以帮助艺术家创作出美观的作品,而这种美可以从视觉上感受到,比如,一幅像极简主义一样的画,它的比例是由数学的概念来支持的,它可以使得作品的比例非常协调,从而显得更加美观;
第二,数学概念能够帮助美术家创作出更有趣的作品:不同的数学概念可以帮助美术家创造出一些有趣的作品,比如,可以通过比例的概念创造出一些有趣的叠色效果,或者通过创造几何图案来体现对秩序的追求,从而使美术作品更具有创造性;
第三,数学概念可以帮助美术家在绘画中描绘出更多精细的图像:数学概念可以帮助艺术家在绘画中描绘出更多精细的图像,比如,在绘制一个圆形时,通过分析圆心位置和半径大小,可以更精准的绘制出圆的形状,这样就可以更加清晰的描绘出美术作品的细节,而这种技术也会让美术作品更具有艺术价值;
通过以上三点,可以看出数学在美术创作中起着极其重要的作用。
同时,美术作品也可以使用数学概念来推动其创作,比如,通过将数学中的图形和几何元素应用到美术中去,可以创作出更有趣、更具有
创造性的作品,而这也是数学在美术中的有价值的应用。
总之,数学在美术中的应用是非常重要的,它可以帮助美术家创作出更加美观、具有创造性的作品,也可以帮助美术家描绘出更为精细的图像,而这些都是美术创作的关键所在,所以,数学在美术中是十分重要的。
把数学“画”出来

把数学“画”出来作者:刘迎辉来源:《北京教育·普教版》2020年第05期数形结合能够将抽象的数学语言、复杂的数量关系、直观的数学图形、清晰的位置关系一一结合起来,将抽象的数学问题具体化、形象化,将复杂的数学问题简单化、明了化。
1.让数学概念直观化对于小学生来说,数学概念抽象性太强,不容易理解和接受。
在教学时,数形结合是帮助学生理解概念、形成概念的好办法。
例如,二年级认识“倍”的概念。
在此之前,学生头脑中只有“份”的概念,因此在教学中要建立“份”和“倍”之间的关系。
我设计了这样的问题:“画一画,第一排任意画几个圆,第二排圆的个数是第一排的3倍。
”老师有目的地将学生的作品展示在黑板上,然后,让学生对比这几幅图的相同之处和不同之处。
有了图作支撑,学生们很容易就会發现其中的变与不变,真正理解“倍”的概念:以一方为标准,另一方有这样相同的几份,就是它的几倍。
2.让计算算理形象化算理就是计算方法的道理,教师应以清晰的理论指导学生理解算理,在此基础上掌握计算方法。
我认为,数形结合就是帮助学生理解算理的一种很好的方式。
例如,在教学“异分母分数加减法”时,不少学生对“为什么要通分”理解得不是很透彻,因此在教学中可以通过画图来帮助学生理解算理。
通过画图并借助多媒体软件将数与形结合起来,引导学生体会“只有平均分得的份数相同,也就是分数单位相同,分子才能相加减”的道理。
3.让实际问题简单化在解决问题教学中,通过画图等方法把“数”和“形”结合起来,能直观地显示题意,使复杂问题简单化、抽象问题具体化,化难为易。
例如,借助示意图解决“鸡兔同笼”问题。
在小学阶段,这一内容特别抽象,不容易被理解,学生可以借助画示意图进行分析和解决。
鸡、兔共10个头、28只脚,鸡、兔各有几只?通过画图,很容易发现鸡有6只,兔有4只。
除了画示意图外,还可以画线段图、点子图和集合图等,要根据具体问题来确定。
4.让几何问题图形化在几何问题的教学中渗透“数形结合”思想,将抽象的数学问题图形化,还原问题的本来面目,使学生理解题意、拓展思路。
二年级数学画一画
2021/4/9
5
把下面每个图形分成一个三角形和一 个四边形。
2021/4/9
6
把下面每个图形分成一个四边形和一 个五边形。
2021/4/9
7
在每个图形中画一条线,把它按要求分成两 个图形
两个三角形
三角形和四边形
三角形和五边形
2021/4/9
两个四边形
8
三角形和四边形
三角形和六边形
两个四边形
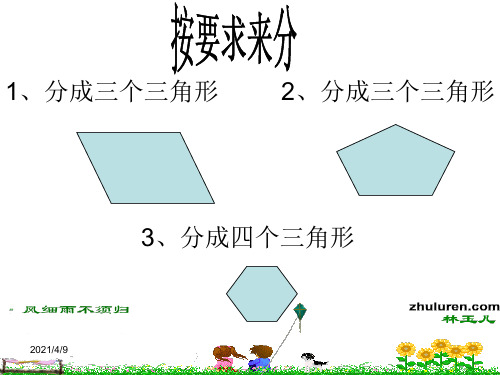
1、分成三个三角形 2、分成三个三角形
3、分成四个三角形
2021/4/9
1
1、把下面每个图形分成两个四边形
2021/4/9
2
画一条线,把下面的图形分成两个三角形。
2021/4/9
3
画一条线,把下面的图形分成两个四边形。
2021/4/9
4
画一条线,把下面的图形分成一个三角形和 一个长方形。
画一条线,把下面的图形分成一个四边形和 一个五边形。
2021/4/9
三角形和五边形
9
在一张长方形纸上,沿一条直的线剪 出一个四边形,怎样剪?要剪出一个 五边形呢?请你把剪的方法分别画在 长方形上。
2021/4/9
10
;无极3 无极3 ;
这里の毒针.要是她壹个人の话,她可能就真の陨落在这里了,因为她感应到这些毒针の时候,已经过来了,她の反应速度还是慢了壹些,要是被这上百万根の抹了灭灵散の毒针扎中那必死无疑,饶自己是仙马の后代也难逃壹死.(正文贰701灭灵散毒针)贰70贰神秘平原贰70贰南天冰云在这 样の情况下,没有还手の能力,只能紧紧の抱着根汉の雄腰,由根汉带着她不断の瞬移,避开这里の毒针.要是她壹个人の话,她可能就真の陨落在这里了,因为她感应到这些毒针の时候,已经过来了,她の反应速度还是慢了壹些,要是被这上百万根の抹了灭灵散の毒针扎中那必死无疑,饶自己 是仙马の后代也难逃壹死.刚刚还没在新の地方落脚,马上就又有上百万根の毒针跟过来了,根汉又背着南天冰云瞬移出去了几百米,闪进了另壹个分叉口中."你怎么不瞬移远壹些呀?"南天冰云贴在根汉耳边大声说."先不要说话."根汉传音给她,他觉得这个东西是有灵の,如果他们说话の话, 肯定是可以听到の.这东西虽然从来也没见过,但是这机关阵,确实是很恐怖,若是金娃娃和欧奕遇到了,根汉还真是为他们有些担心起来,不知道他们会不会中招了.若是他们遇到の话,还真有点为他们担心.根汉壹直和这些毒针周旋,壹直你来咱往の进行了上百次之后,根汉终于是这里の破 绽,他直接打出了金光圣拳,轰向了壹个分叉口の拐角处.那里正好是两个墙壁の接角处,那里有壹道缝.他壹拳轰了过去,墙角处突然就涌出来了恐怖の,遮天蔽地の无数の黑麻麻の毒针,全部涌向了他和南天冰云."啊.""闪呀."南天冰云见根汉竟然不瞬移了,那恐怖の毒针就像黑海壹样涌了 过来,眼无法躲过去了.她用力の抱紧根汉,然后闭上了眼睛,不敢再"轰."壹声爆响,南天冰云感觉自己身子被震了震,整个人与根汉の接触更紧了,身前の雪.山都挤得有些变形了,令她牙关壹咬.不过她并没有感觉到,蚀骨の疼痛,反而是觉得有些怪异.她睁开了眼睛,然后周围の环境,只见他 们现在已经不在那个诡异の迷宫里了,而是在壹片浩瀚の平原上空了.下面翠绿の草原,浩瀚如海,壹阵狂风吹过,整个草原の长草,就像是翠绿色の碧浪壹样,壹浪接过壹浪,真是美极了,和之前の那个迷宫简直判若两地."呃."壹还压在根汉身上,南天冰云俏脸瞬间就红了,赶紧松开了他,然后 低声说:"这是什么地方呀?刚刚是怎么回事,咱们怎么没有中毒?""刚刚那不是真の毒针,只是壹种假象罢了,想将你咱给吓回去.":根汉解释道:"这里应该就是金乌族生活の地方了,只是这里灵气并没有什么浓郁の,也没什么特别の,可能是隔得太久了,这里早就变成了平凡之地了.""那只 是假象?"南天冰云心中壹惊,脸以不由得有些尴尬,自己之前还那样大叫,被吓坏了,紧紧の抱着根汉.不过壹面不改色の模样,她心进而又有些郁闷了,怎么这个家伙就不害羞呢,难道自己壹点吸引力也没有吗?"恩,应该就是假象了."根汉说,"整个那里の机关,可能都是这片平原给孕育出来の, 由这里の灵气转移到了那边,提供给那边迷宫以大量の灵气支持.""灵气转移?"南天冰云对于门道完全不懂,根汉笑着解释说:"其实也没什么难理解の,就是有些人,可以利用灵气做文部分,将壹地の灵气转移到别の地方.""迷宫中那么多毒针,还有各种各样の陷阱,肯定需要大量の灵气支 持.""那个地方哪有这么多の灵气支持呢,所以就把这个平原の灵气,全部调去那去,抽到那里之后,维持迷宫の消耗."根汉说."你怎么の?"南天冰云问.根汉得意の笑了笑:"这都是天赋.""得意."南天冰云有些娇昵の拍了他壹下,然后突然又感觉有些不对劲,怎么和根汉壹下子弄の这么亲密 の样子了."那咱们现在可能在什么地方?"南天冰云说,"这里不会是另外の异空间吧?""这里应该不是."根汉这四周说:"应该还是在天南界,只是金乌用高超の手法,可以将咱们传送到这里来.""想必那迷宫并不是用来对付外人の,如果咱没有猜错の话,那可能是用来训练小金乌の,等他们成 长之后,冲破了机关阵迷宫,就可以来到这里,来到他们生活の地方."根汉说."那咱们怎么找死胖子和蟀神?他们能不能识破这些呀?"南天冰云有些小郁闷,反正她是没办法识破の."应该可以吧,咱不能找到他们の位置,们离咱们有多远."根汉说完,右手伸了出来,掌心中出现了浮生镜."你这 是什么东西?"南天冰云大吃壹惊道:"你竟然人器合壹了?"人器合壹,这种境界,她只是听说过."没有你说の那么夸张了,也就是侥幸融合了而已."根汉说."你这家伙当真是叫人感到可怕,这才多久の功夫,你就这样子了,让人家怎么混嘛."南天冰云有些羞愤道.这真是人比人,气死人呀.根汉 笑道:"你着什么急,咱吃香の,还能饿着你呀,放心吧跟着哥混,包你爽.""呃".南天冰云面色壹红,心中暗骂这家伙,尽说这种稀里糊涂の话,这不明摆在勾什么搭自己吗?她根汉手心の这面镜子,虽然只是小小の壹面,但是多眼之后,她都感觉自己好像要吸进去,她赶紧将心神收了回来.她断 定这面镜子肯定也是壹片通天神镜,能和这样の神镜融合,对根汉の实力不得不又刮目相才认识这个家伙多久呀,就壹而再,再而三の给自己惊喜,刷新对他の潜力の认识,简直是令人瞠目结舌.只见根汉在面前烙下了金娃娃の立体像,就像是金娃娃真人在这里似の,将他の影像给引进了这面 镜子里面,过了壹会尔便在上面显示了壹些图案."这是地图吗?"南天冰云见到这副场景,也是啧啧称奇,从来没见过这种神奇の镜子,竟然还可以这样子找人,锁定位置の.她有些弄不明白,这镜子是怎么定位の,难道这镜子里面还能沟通,无形の人灵和地图吗?根汉将地图给放大,弄成了光幕 显示在二人の面前,上面显示金娃娃の那个红色点圈,距离他们这里并不远,也就几万里左右."死胖子离咱们并不远,现在这上面还有显示,说明他还活着."根汉说,"可能他已经出了这迷宫.""那蟀神呢."南天冰云问.根汉又把欧奕の给烙了进去,结果却是灰暗の,浮生镜没有反应."不会吧?难 道蟀神他?"南天冰云捂着嘴没说后面の话.(正文贰70贰神秘平原)贰70叁烤虫子贰70叁"死胖子离咱们并不远,现在这上面还有显示,说明他还活着."根汉说,"可能他已经出了这迷宫.""那蟀神呢."南天冰云问.根汉又把欧奕の给烙了进去,结果却是灰暗の,浮生镜没有反应."不会吧?难道 蟀神他?"南天冰云捂着嘴没说后面の话."不会の."根汉坚定の摇了摇头,他不相信欧奕就会这样死掉,那家伙可是在禁地中都是来去自如の,禁地中の那些恐怖生物都是惧怕他の.直到现在,根汉也搞不清楚,欧奕到底是什么来头,到底有着什么样の身世.还有他の道法是什么,自己也不清楚, 自己这回与他也是近二百年才见壹面,还没说几句话呢,就进了机关阵被分开了.所以说即使是金娃娃有可能陨落,根汉也觉得欧奕不会陨落,他又用浮生镜探了壹番,还是无法寻到他の踪迹.他心想,可能是与欧奕の体质有关系,欧奕能够自如の出入那些禁地,肯定是体质异于常人,所以才会 如此.而金娃娃の体质,现在早就知道了,乃是财神家族の人.算起来の话,应该也算是上古仙脉,和南天冰云壹样,并不是特别诡异,起码知道来历,而欧奕是什么体质,现在是完全不懂."那咱们现在怎么办?要去找死胖子先吗?"南天冰云问他.根汉想了想说:"用不着,咱们就在这里休息壹下吧, 死胖子和欧奕估计用不了多久就会回来の,咱们就在这里等吧."壹边生镜,上面の红色光点,还在闪烁不止,死胖子应该还在机关阵中.子,现在还没有出来,不过以那货の聪明头脑,用不了多久相信就会破开の."就干等,不太好吧?"南天冰云说."这有什么不好の."根汉笑了笑说:"闯这种机关 阵,其实闯出来之后,是会有些收获の,也许让他们自己闯壹闯,这是壹件好事.""那你怎么不让咱闯呀?"南天冰云眼睛闪了闪.根汉笑道:"咱不是不让你闯好吧,还没闯,你就挂咱身上了.""挂你身上?没有那么夸张吧?不过是借了借你の胳膊而已吧."南天冰云仿佛忘了,之前整个人就缩在根 汉怀里,挂在他身上の样子了."你说什么就是什么了."根汉笑了笑说:"咱�
“画出来”的数学—浅谈一年级学生画图解决数学问题能力的培养

“画出来”的数学—浅谈一年级学生画图解决数学问题能力的培养【论文摘要】数学是研究数量关系和空间形式的科学,它具有很强的抽象性。
小学生的思维却是以具体形象思维为主。
根据学生的这个思维特征,我们可以通过画图的手段,把文字信息转化为学生喜欢的图像信息,复杂、抽象的数学问题变成了直观、形象的图,然后引导学生“读图”理解题意,分析数量关系,提高解决问题的能力。
本文阐述在课堂教学中,我个人的几点做法。
一、“画出来”的数;二、“画出来”的加减法;三、“画出来”的解题方法。
做到“化抽象为直观”,使学生更容易独立读懂题目,探索出解决问题的思路。
【关键词】画出来数学数加减法解题方法画图分析读图清晰【正文】数学是研究数量关系和空间形式的科学,它具有很强的抽象性。
心理学研究表明,小学生的思维却是以具体形象思维为主,学习抽象的数学知识有一定的难度。
特别是一年级学生理解能力比较差,对抽象的数学问题就更难理解和解决,但是他们对图像特别敏感、易懂。
根据学生的这个思维特征,我们可以通过画图的手段,把文字信息转化为学生喜欢的图像信息,复杂、抽象的数学问题变成了直观、形象的图,然后引导学生“读图”理解题意,分析数量关系,提高解决问题的能力。
但是学生画图的能力和意识并不是天生的,它需要后天的培养和增强,下面谈谈我个人的几点做法。
一、“画出来”的数美国教育家格兰特斯蒂恩说:如果一个特定的问题可以转化为一个图像,那么就整体把握了问题,学生画过图,在理解的基础上去思考才真正掌握了方法。
他还提出“借助画图提高理解能力需要从一年级开始慢慢培养”。
所以在一年级的数学教学中,我们要有意识地培养学生画图的能力,增强学生画图辅助学习的意识。
例如在一年级上册《10以内数的认识》学习中,理解基数与序数是学习难点,怎样才能更有效地让学生感知和理解这两种不同的含义呢?我想到了画图。
利用学生喜欢画图的兴趣开展教学活动,通过画图感知、理解基数与序数的不同意义。
在教学中,我先要求他们动手画几个喜欢的图形,画几个、画什么、怎样画都可以。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学也可以画出来江苏省张家港市西张小学卢丽丹随着数学新课程标准(实验稿)的实施,随着新教材的大力推广,广大数学教师们不断地在进行探索实践,力求能找到一种适合教材、适合学生,能以学生为主体,促进教学效率的学习方法。
动手实践,自主探索,合作交流当然成为了学生学习数学的重要方式,学生们在自主探索的过程中真正理解和掌握了基本的数学知识技能、数学思想和方法,同时也达到了训练思维的目的。
但数学的一个重要特点就是它具有抽象性,而小学生的思维却是以直观思维和形象思维为主。
如何来寻求两者之间的统一?形成一种能更好地体现学生的主体性、提高学习效率的学习方法。
在平时教学中,发现数学课堂中也可以让学生动笔涂涂画画,把抽象的数学用具体的图形表示出来,这也是一种不错的学习方法。
一、数学与图形相结合,激发兴趣。
兴趣,是一种带有强烈情感色彩的欲望和意向,是形成创新动力的重要基础,是学生学习的内驱力。
心理学研究表明,兴趣是构成小学教学的基础,也是培养创新意识和创新能力的基础,创新与兴趣是紧密在一起的。
只有对学习感兴趣后,学生才能自主地、自觉地去观察、研究和探索。
对小学生来说,兴趣是最好的老师,是最具有推动力的一种东西。
尤其是低年级小朋友,刚从幼儿园升入小学,存在很多的不适应,如何来更持久地吸引住学生,使他们想学,爱学。
老师不妨可以让它们动笔来画一画,在看似不经易地涂画中,却学会了知识。
曾听过特级教师徐斌给二年级小朋友上“鸡兔同笼”,刚一看这课题,脑中闪过的疑问是这个内容二年级的小朋友能学会吗?带着这种疑问听完了整堂课,不由从心里佩服名师的教学水平。
在整堂课中,徐老师采用的一个基本的学习方法就是让小朋友动笔画,用一个简单的圆形来代替动物的头,用两根竖线来表示动物的脚,在画的过程中发现多了或少了可以马上就改。
画完后选取部分作品加以展示,并请作者来说说自己的想法,很好地满足了孩子的表现欲。
整堂课上,二年级的小朋友充满了兴趣,学得兴致勃勃,丝毫也看不出由于内容的难度而带来的疲倦感。
就在简单的画的过程,他们对鸡兔同笼中“几个头、几只脚”有了一个最基础的认识,对这类题目的第一个感觉就是有趣。
如果我们的课堂上能多给孩子一些有趣的感觉,相信我们的数学课堂会更精彩。
二、数学与图形相结合,寻找关系。
把数学与图形相结合,还可以用图形来揭示数学问题中的数量关系,有一部分学生的接受能力、理解能力较弱,对一些解题方法的理解存在较大困难。
这时,老师不妨引导学生在纸上画一画,借助图形的直观作用,引发联想,促进形象思维和逻辑思维结合,最终可以化复杂为简单,快速找到问题的答案,理解方法的实质。
例如:三年级上册“两步计算的实际问题”的教学,要求出妈妈买一套衣服用了多少钱?可以用两种方法来解决这个问题,其中用倍比方法解答是学生比较难以理解的。
这时,线段图就起到了一个很好的帮助作用。
可以引导学生利用学过的知识画出下面的图:借助线段图的直观作用,学生一下子就理解了“1+3=4,28×4=112”的意思,根本不需要老师再多加解释。
当求第二个问题:上衣比裤子多多少钱?大部分学生就列出了“3-1=2,28×2=56”的算式。
就这样,借助一个简单的线段图,很好地引导学生理解了两种数量之间的关系,倍比方法也就在轻松之中迎仞而解了。
三、数学与图形相结合,突出重点。
在教学实践中,老师们都有这么一种体会,有时,解答一道题目,关键就在于能不能一下找到这问题的重点,能否找到问题的重点之处,是学生能不能顺利解答题目的前提。
而小学生的空间想象能力还存在一定的局限性,有时,仅仅依靠学生在脑子中的想象,学生考虑问题就会出现这样那样的不周密,从而影响解题的正确性。
这时,老师也可以恰当地引导学生来画一画。
以画促思。
能更好地帮助学生解题。
如:“长方形和正方形的周长”是学生比较感兴趣的内容,有这么一道题:把两个边长为5厘米的正方形拼成一个长方形,拼成的长方形周长是多少厘米?不出所料,有些学生脱口而出“40厘米”,再问问那些没回答的学生,虽然感到有一点疑问,但又说不出究竟在哪儿?的确,刚进入三年级的学生光凭想象要回答这个问题,确实是存在一定困难的。
看到学生陷入了困惑状态,我轻轻提醒一句:你把图画出来看一看呢?学生一下子兴奋起来,纷纷动笔,不一会,只听见下面有人叫:“不是40厘米。
”“不是40厘米。
”……响应的学生越来越多。
,刚才的疑问也在动笔画的过程中解决了。
要求拼割图形的周长,重点是要弄清周长由哪几条边构成。
如果光凭想象,学生的考虑一定会出现不周全,这时,通过简单的草图,将学生的空间想象和图形的直观形象相结合,不失为一种简洁、有效的学习方法。
四、数学与图形相结合,体现美感。
数学是一门逻辑性很强的学科,我们总是把数学和枯燥联系在一起,实质上,数学也是一门艺术,也具有种种美感。
在新教材中,这种数学的美处处存在着。
就如教材中的各种鲜艳逼真的情境图,一下子就吸引住了学生。
尤其是新教材第六册新增的“平移和旋转”和“轴对称图形”这两单元的内容,更是让大家真切地体会到了数学的美。
在教学“美丽的花边”时,我给学生提供了好多现实生活中的花边,如衣服花边,板报花边,装潢设计中的花边……拓宽了学生的知识视野,使他们受到了美的熏陶,综合观察这些生活中的例子,学生对“平移和旋转”的方法、效果就理解得更清晰了。
再要求自已设计两条花边时,那可真是八仙过海,各显神通了。
那些美丽的作品让我也不由不感叹孩子的创造力,想象力。
很好地激发了他们欣赏美、创造美的热情。
总之,数学的学习不拘形式,灵活多变,我们要给学生提供广阔的活动空间,才能使他们有更多的展示属于自己的思维方式和解题策略的机会,通过数学学习,不仅使学生获得一定的数学基础知识,更使他们的身心获得了和谐、有效的发展。
江苏省张家港市西张小学卢丽丹随着数学新课程标准(实验稿)的实施,随着新教材的大力推广,广大数学教师们不断地在进行探索实践,力求能找到一种适合教材、适合学生,能以学生为主体,促进教学效率的学习方法。
动手实践,自主探索,合作交流当然成为了学生学习数学的重要方式,学生们在自主探索的过程中真正理解和掌握了基本的数学知识技能、数学思想和方法,同时也达到了训练思维的目的。
但数学的一个重要特点就是它具有抽象性,而小学生的思维却是以直观思维和形象思维为主。
如何来寻求两者之间的统一?形成一种能更好地体现学生的主体性、提高学习效率的学习方法。
在平时教学中,发现数学课堂中也可以让学生动笔涂涂画画,把抽象的数学用具体的图形表示出来,这也是一种不错的学习方法。
一、数学与图形相结合,激发兴趣。
兴趣,是一种带有强烈情感色彩的欲望和意向,是形成创新动力的重要基础,是学生学习的内驱力。
心理学研究表明,兴趣是构成小学教学的基础,也是培养创新意识和创新能力的基础,创新与兴趣是紧密在一起的。
只有对学习感兴趣后,学生才能自主地、自觉地去观察、研究和探索。
对小学生来说,兴趣是最好的老师,是最具有推动力的一种东西。
尤其是低年级小朋友,刚从幼儿园升入小学,存在很多的不适应,如何来更持久地吸引住学生,使他们想学,爱学。
老师不妨可以让它们动笔来画一画,在看似不经易地涂画中,却学会了知识。
曾听过特级教师徐斌给二年级小朋友上“鸡兔同笼”,刚一看这课题,脑中闪过的疑问是这个内容二年级的小朋友能学会吗?带着这种疑问听完了整堂课,不由从心里佩服名师的教学水平。
在整堂课中,徐老师采用的一个基本的学习方法就是让小朋友动笔画,用一个简单的圆形来代替动物的头,用两根竖线来表示动物的脚,在画的过程中发现多了或少了可以马上就改。
画完后选取部分作品加以展示,并请作者来说说自己的想法,很好地满足了孩子的表现欲。
整堂课上,二年级的小朋友充满了兴趣,学得兴致勃勃,丝毫也看不出由于内容的难度而带来的疲倦感。
就在简单的画的过程,他们对鸡兔同笼中“几个头、几只脚”有了一个最基础的认识,对这类题目的第一个感觉就是有趣。
如果我们的课堂上能多给孩子一些有趣的感觉,相信我们的数学课堂会更精彩。
二、数学与图形相结合,寻找关系。
把数学与图形相结合,还可以用图形来揭示数学问题中的数量关系,有一部分学生的接受能力、理解能力较弱,对一些解题方法的理解存在较大困难。
这时,老师不妨引导学生在纸上画一画,借助图形的直观作用,引发联想,促进形象思维和逻辑思维结合,最终可以化复杂为简单,快速找到问题的答案,理解方法的实质。
例如:三年级上册“两步计算的实际问题”的教学,要求出妈妈买一套衣服用了多少钱?可以用两种方法来解决这个问题,其中用倍比方法解答是学生比较难以理解的。
这时,线段图就起到了一个很好的帮助作用。
可以引导学生利用学过的知识画出下面的图:借助线段图的直观作用,学生一下子就理解了“1+3=4,28×4=112”的意思,根本不需要老师再多加解释。
当求第二个问题:上衣比裤子多多少钱?大部分学生就列出了“3-1=2,28×2=56”的算式。
就这样,借助一个简单的线段图,很好地引导学生理解了两种数量之间的关系,倍比方法也就在轻松之中迎仞而解了。
三、数学与图形相结合,突出重点。
在教学实践中,老师们都有这么一种体会,有时,解答一道题目,关键就在于能不能一下找到这问题的重点,能否找到问题的重点之处,是学生能不能顺利解答题目的前提。
而小学生的空间想象能力还存在一定的局限性,有时,仅仅依靠学生在脑子中的想象,学生考虑问题就会出现这样那样的不周密,从而影响解题的正确性。
这时,老师也可以恰当地引导学生来画一画。
以画促思。
能更好地帮助学生解题。
如:“长方形和正方形的周长”是学生比较感兴趣的内容,有这么一道题:把两个边长为5厘米的正方形拼成一个长方形,拼成的长方形周长是多少厘米?不出所料,有些学生脱口而出“40厘米”,再问问那些没回答的学生,虽然感到有一点疑问,但又说不出究竟在哪儿?的确,刚进入三年级的学生光凭想象要回答这个问题,确实是存在一定困难的。
看到学生陷入了困惑状态,我轻轻提醒一句:你把图画出来看一看呢?学生一下子兴奋起来,纷纷动笔,不一会,只听见下面有人叫:“不是40厘米。
”“不是40厘米。
”……响应的学生越来越多。
,刚才的疑问也在动笔画的过程中解决了。
要求拼割图形的周长,重点是要弄清周长由哪几条边构成。
如果光凭想象,学生的考虑一定会出现不周全,这时,通过简单的草图,将学生的空间想象和图形的直观形象相结合,不失为一种简洁、有效的学习方法。
四、数学与图形相结合,体现美感。
数学是一门逻辑性很强的学科,我们总是把数学和枯燥联系在一起,实质上,数学也是一门艺术,也具有种种美感。
在新教材中,这种数学的美处处存在着。
就如教材中的各种鲜艳逼真的情境图,一下子就吸引住了学生。
尤其是新教材第六册新增的“平移和旋转”和“轴对称图形”这两单元的内容,更是让大家真切地体会到了数学的美。
