课件例题与习题
正比例函数的图象与性质课件习题
在同一坐标系内画下列正比例函数的图像:
1 y 3x y x y x y 3
当k>0 时,它的图 像 经过第 一、三象 限
y 3x
3
yx
1 y x 3
1
3
1
o
x
在同一坐标系内画下列正比例函数的图像:
y 3x
y x
1 y x 3
y y 3x y x y 1 x
(1) 当k>0时,正比例函数的图像经过第一、三象 限,自变量x逐渐增大时,y的值也随着逐渐增大。 (2) 当k<0时,正比例函数的图像经过第二、四象限, 自变量x逐渐增大时,y的值则随着逐渐减小。
正 比 例 函 数
定义 图像
Y=kx(k≠0)
是经过原点和(1,k)点的一条直线 。
性 质
k>0
k<0
6.下列函数y=5x,y=-3x,y=1/2x,y=-1/3x中,y
随x的增大而减小的是———,y随x的增大而减小 且最先达到-10的是——。
能力提高:
想一想: 点燃蜡烛,蜡烛长度按照与时间成正比变短,长为21厘米 的蜡烛,已知点燃6分钟后,蜡烛变短3.6厘米,设蜡烛点 y 燃x分钟后变短y厘米,求 (1)用x表示函y数的解析式; (2)自变量x的取值范围; (3) 此蜡烛几分钟燃烧完?
能力提升!
m 2
1、已知函数 y (m 3) x , = 3 时,函数是正比例函数,图 减小 在 二、四 象限,y随x增大而
x 2、已知函数 y= 3 A(3,y1)
, 点
和点B (6,y2)在函数图象上, < 则 y1 y2(填“>”或“<”)。
x 3、已知函数 y 6
材料力学课件复习习题
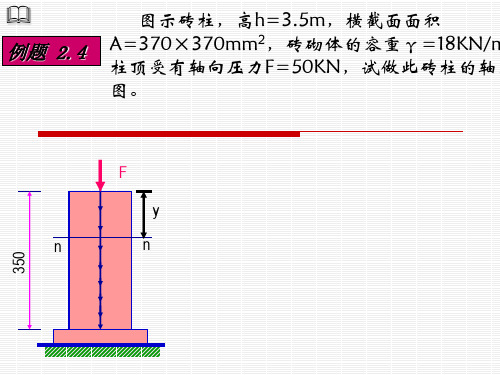
例题 5.1
F A A
A
求图所示悬臂梁A端的挠度与转角。
x
B
x
l
y
例题 5.2
求图所示悬臂梁B端的挠度与转角。
B
A
x
l
x
y
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
q
A
B
EI z
C
x
k
l 2
(4)在弯扭组合变形圆截面杆的外边界上,各点的应力状 态都处于平面应力状态。( )
(5)在弯曲与扭转组合变形圆截面杆的外边界上,各点主 应力必然是σ1> σ2 ,σ2=0,σ3<0 。 ( )
(6)在拉伸、弯曲和扭转组合变形圆截面杆的外边界上, 各点主应力必然是σ1 >0, σ2=0, σ3<0 。( )
Me
2
1
d
D
例题 4.6
20 kN
X1
图示外伸梁,,试作剪力图和弯矩图.
10kN m
X2
40 kN m
A
35kN
B
1m
4m
25kN
例题
4.9
作图示梁的内力图
3kN
D
4.5kN m
A
2kN m
B E
C
FA 10kN 1m 2m
2m
FB 2kN 1m
kN
kNm
例题
4.10
4kN m
A
B
96.4 C
l 2
l 2
200 50
z
例题 4.30
q
A
简支梁如图所示,试求梁的最底层纤维的总伸长。
核磁共振氢谱习题及例题和答案ppt课件

7.07 ppm处有一粗看为单峰的一个氢,说 明无相邻碳氢,所以苯环上有间位取代。
化学位移约为3.8 ppm 处有一积分面积为3的单峰,说明又甲氧基。
根据分子式及苯环的取代模式,分子结构式应为
15
。 例3 某化合物的分子式为C6H10O,根据氢谱推断结构
16
17
分子式为:C6H10O
Ω = C + 1–( H 2
2
7.58 (ddd, J = 8.6, 7.2, 1.7 Hz, 1H) 6.97 (ddd, J = 8.4, 6.9, 1.4 Hz, 1H)
Ω = 7 + 1- 8 = 0
H的个数比为:1 : 6 : 9 从偶合裂分规律及氢原子个 数比知分子中有三个乙基
三个氧只能是烷氧基
Ω = C + 1–( H +
2
–
1 )
2
=5
含有一个苯环或者吡啶环
δ = 7.34 ppm
3J 7-9 7.46
7.06 3J 5-6
8.50 4J 1-2
4J 0-1
在低场 7.5-9.5 ppm 有四个1:1:1:1的氢,但是 范围超出了苯环氢的化学位移,应为吡啶环
7
8
不饱和度为 5,所以还应该有一个双键或者一个脂肪环
习题 1
1
1. 所用仪器的频率是多少? 2. 表达出该峰
1. 1539.18 / 3.847 = 400 MHz 2. 3.82 (quint, J = 6.2 Hz, 1H) 2. 3.82 (sept, J = 6.2 Hz, 1H) 2. 3.82 (tt, J = 6.2 Hz, 1H)
习题 2
+
X 2
机械原理典型例题第七章轮系详解

第八页,共19页。
解法一:
差动轮系1-2-2‘-4-H
行星轮系1-2-3-H
i1H4
n1 nH n4 nH
z2 z3 = 174 z1z2 ' 33
i1H3
n1 nH n3 nH
1 n1 nH
z3 = 5
z1
i14
n1 n4
n1 n4
116
解二:
行星轮系3-2-2‘-4-H 行星轮系3-2-1-H
机械原理典型例题第七章轮系 ppt课件
第一页,共19页。
例1. 在图示轮系中,已知:蜗杆为单头且右旋,转速 n1=1440r/min,转动方向如图示,其余各轮齿数为: Z2 = 40,Z2‘ = 20,Z3 = 30,Z3’ = 18,Z4 = 54, 试: (1) 说明轮系属于何种类型; (2) 计算齿轮4的转速n4;
用箭头确定的构件的转向关系,是指转化 机构中各构件的转向关系,而非该周转轮
系中各构件绝对运动的转向关系。
第七页,共19页。
例6:已知Z1=18,Z2=36,Z2’=33,Z3=90, Z4=87,求i14
3 2 2' 4
H 1
行星轮 — Z2,Z2’ 联动关系 — n2=n2’
系杆 — H 中心轮 — 1,3,4
1800 3
600r
/
min
第六页,共19页。
2'
3 2
H
1 b
i1H3
n1 nH n3 nH
z2 z3 z1z2 '
200 nH 8 100 nH 5
nH
200 13
15.38r
/ min
注意:
转化轮系传动比的“±”号的确定错误,将导 致整个计算结果的错误。
自控原理课件及习题解答

s→0
s
1+
k sν
G0H0
r(t)=R·1(t) R(s)=R/s
ess=
1+
R lim k s→0 sν
r(t)=R·t R(s)=R/s2
ess=
R
lim s
s→0
k sν
·
r(t)=Rt2/2 R(s)=R/s3
ess=
R
lim
s→0
s2·skν
取不同的ν
R·1(t) R·t Rt2/2 R·1(t) R·t Rt2/2
用正无穷小量ε代替。
劳斯判据
系统稳定的必要条件: s6 1 3 5 7
特征方程各项系数 s5 2 44 6
均大于零!
有正有负一定不稳定!
s4 1 2 77
s3 0ε --88
缺项一定不稳定!
s2 2ε+8 7ε
-s2-5s-6=0稳定吗? s1 -8(2ε+8) -7ε2
系统稳定的充分条件: s0 7ε
引出点移动
G1
G1
H2 G2
H1
H2 G2
H1
G3
G4
H3
1 G4
G3 a G4 b
H3
综合点移动
G3 G1
向同类移动
G3
G1
G2
H1
G2 G1 H1
G4
G1
G2
H1
G4
G1
G2
H1 H1
作用分解
G3 H3
G3 H3 H3
梅逊公式介绍 R-C : △称为系统特征式
C(s) R(s)
=
∑Pk△k △
. EEˊ(rsν()=s=)C1=希-CRH实称((=ss))为RH-(C(ssⅠ))(s-型)C(系s) 统
给水处理习题及案例(学生)ppt课件

3[ Al]
32
3
P286
【习题3】某水厂采用精制硫酸铝作为混凝剂,其最 大投量为35mg/L。水厂设计水量100000m3/d。混 凝剂每日调剂3次,溶液浓度按10%计,试求溶解 池和溶液池体积各为多少?
【答案】
Q 100000m 3 / d a 35mg / L
c 10% n 3
5
注册考试
【例题】某水厂拟采用水泵混合,处理水量为 Q=24000m3/d,经2条直径均为400mm,长均为 100m的并联管道送往水厂絮凝池,若正常工作时 每条管道内总水头损失为0.45m,则管道内水流的 速度梯度G值为( )s-1。
(μ=1.14×10-3Pa·s,ρ=1000kg/m3)
【解】正常工作时每条管道内的流量应为总水量的1/2 (不应为总水量或总水量的70%),即12000m3/d。
1
u
4 225
(s
水 )2 水
g2
3
d
0.075m / s
Re
ud
33.65
1 Re 1000
说 明 应 用 过 渡 区 公 式 是 正 确 的
10
P314
【习题2】平流沉淀池设计流量为720m3/h,要求沉速 等于和大于0.4mm/s的颗粒全部去除。试按理想沉 淀池条件,求:
度为50%)投量需多少mg/L?
(已知原子量Al=27,O=16,Ca=40)
【解】投药量折合Al2O3为26×16%=4.16 mg/L Al2O3分子量为102,故投药量相当于4.16/102=
0.041mmol/L
则【CaO】=3【a】-【x】+【δ】 =3×0.041-0.1+0.2=0.223 mmol/L
赵凯华光学课件及习题答案

其物理意义:
可以通过比较两个振动的光程来考察 两个振动的步调差异。
1.5
在真空中波长为 λ 的单色光,在折射率为 n 的透明介质中从 P 沿某路径传到 Q,若 P、Q 两 点位相差为 5π,则路径 PQ 的光程为:
(1) 5λ (2) 5nλ (3) 2.5λ (4) 2.5nλ (5) 无法判断
i nsin i n sin i
2.2 全反射定律
◆ 当光线从光密媒质 射向光疏媒质时,折射 角大于入射角;当入射 角增大到某一临界值时, 折射光线消失,光线全 部反射,此现象叫全反 射。
全反射临界角:
ic s in1(n2/n1)
n 2 1 的空气对于 n1 1.5 的玻璃,临界角
ic 42
◆ 棱镜光谱仪中的色散元件色散 棱镜就是利用介质的这种性质, 将含有多种波长的复色光分散开 来。
光的可逆性原理:
当光线的方向反转时,它将逆着同一 路径传播,称为光的可逆性原理。
§3 惠更斯原理
波线
2.1 波的几何描述
波动:扰动在空间的传播 球面波波面 平面波
波面:
波面与波线
(1)在同一振源的波场中
光在均匀媒质里沿直线传播。 例:物体的影子, 针孔成像 例:海市蜃楼(mirage)
海市蜃楼(mirage)是一种折光现象,由于靠 近表面竖直方向上空气密度的剧烈变化,使 得一些远处的物体在一定区域形成图像以代 替其真实位置。这些图像是扭曲的,倒转的 或是摇摆的。
空气密度与气压、温度和水蒸气含量密切相关。
2、爱因斯坦提出了光子假说,成功地解释了 光电效应问题
3、光的某些行为象经典的“波动” 4、另一些行为却象经典的“粒子”
第1章例题与习题PPT教学课件

x xi 17.21.56364 此组数据中与均值的最大差
n 11
为:
( x x ) 2 0 .1 2 0 2 5 4 5 4 5 6
1.831.563640.26636
n
(xi x)2
i1
0.1045573
n
3 0 .3 1 3 6 7 2
0.266363
根据3σ准则,测量数据没 有坏值。
解:
R 6 1 0 .0 0 4 3 0 2 0 6 .2 4
d R 1 T 2 0 R 0 R 0 T 2 0 R 0 T
R 1 0 .0 0 4 3 0 2 0 6 1 0 0 .3 0 6 3 0 2 0 0 .0 0 4 1 0 1 0 6 0 .0 0 4 1
⑤要求垂直安装的仪表,没有能按照规定安装造成的测量误差。
解:
①随机误差;
④系统误差;
②系统误12/11
2
习题2 多次等精度测量某物质中的铁含量分别为:
1.52,1.46,1.61,1.54,1.55,1.49,1.68,1.46,1.83,1.50, 1.56, 请判断此组测量数据中是否存在坏值(粗大误差)?
解:
S S 1 S 2 S 3 3 1 0 1 0 4 1 0 9 1 0 1 2 y S x = 1 2 3 = 3 6 m m
记录笔在纸上发生多大偏移量:36mm
2020/12/11
5
习题5
某2.5级电压表量程为100V,经检验发现在50V刻度点处的示 值误差2V为最大误差,请计算该仪表在50V测点处的相对误 差,仪表相对百分误差,并判断该仪表是否合格?
解:
50V处测量相对误差: V 1 0 0 % 2 1 0 0 % 4 %
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章例题:1、某人投资一项目200,000元,期限4年,要求回报率为12%,计算4年后应得到的本利和。
2、某项投资4年后可以取得100,000元的收入,年利率为12%,计算其收入的现值。
3、C公司每年末向银行借款20000元,年利率为10%,计算其第四年末应归还的本息为多少?4、现在存入银行一笔钱,准备在以后五年中每年末得到10000元,如果利息率为10%,现在应存入多少钱?5、某人每年年初存入银行1000元,银行存款年利率为8%,问第10年末的本利和应为多少?6、某企业租用一设备,在10年中每年年初要支付租金5000元,年利息率为8%,问这些租金的现值是多少?7、某企业向银行借入一笔款项,银行贷款的年利息率为8%,银行规定从第四年起,每年年末偿还本息1000元,至第9年末还完,问这些款项的现值应为多少?8、某企业拟建立一项永久性的奖学金,每年计划颁发3万元奖学金,若利息率为6%,问企业目前应为其至少准备多少钱?练习:1、某人参加一项少儿人寿保险,保险公司给出的方案如下:从出生开始至14周岁止每年年末交存360元。
如果年收益率为8%。
(1)计算14周岁末的终值;(2)如果保费可以在参加保险时一次性交纳,问一次性应交纳多少?2、某人年初存入银行1万元,年利率4%。
要求计算:(1)每年复利一次,5年后账户余额是多少?(2)每半年复利一次,5年后账户余额是多少?(3)如果该人分5年每年末都存入相等金额,每年复利一次,则为达到本题第一问所得账户余额,每年末应存多少钱?(4)如果该人分5年每年初都存入相等金额,每年复利一次,则为达到本题第一问所得账户余额,每年初应存多少钱?3、小宋夫妇俩2000年末止已有积蓄20万元,以后每月积蓄约3500元。
现在他们准备购置房价为45万元房产,准备首付一部分,余款实行银行按揭。
已知银行按揭的月利率为0.5%,按揭从2001年1月开始。
小宋夫妇俩正在商讨购房付款的事宜。
请你帮助他们计算分析和解决下列问题:(1)如果小宋夫妇考虑现有积蓄留存5万元准备装修之用,购房时首付15万元,按揭年限想短一些,初步定在10年,采用按月等额还款方式。
请问:按小宋夫妇目前每月3500元的支付能力能否支付每月的按揭款?(2)如果小宋夫妇决定还是将按揭年限定为15年,请你为他们计算每月应付的按揭款;(3)在15年按揭的前提下,由于银行利率下调,银行规定从2003年1月起,按揭的月利率由原来的0.5%降低到0.45%,这样一来,请你计算小宋夫妇每月的按揭款可比原来少付多少?(4)如果小宋夫妇在2001年和2002年的收入大大超过了预期水平,他们想在2003年1月初将剩余13年的房款一次付清,请你按下调后的利率计算:他们在2003年1月初应一次支付多少价款?3、已知I n 复利终值复利现值年金终值年金现值系数系数系数系数0.5%,120 1.819397 0.549633 163.8793 90.073450.5%,180 2.454094 0.407482 290.8187 118.50350.5%,156 2.177237 0.459298 235.4473 108.14040.45%,156 2.014609 0.496374 225.4687 111.91680.5%,24 1.127160 0.887186 25.43196 22.562874、某企业有甲、乙两个投资项目,计划投资额均为1000万元,其收益率的概率分布如下表所示:市场状况概率甲项目乙项目好0.320%30%一般0.510%10%差0.25%-5%要求:(1)分别计算甲乙两个项目收益率的期望值。
(2)分别计算甲乙两个项目收益率的标准差。
(3)比较甲乙两个投资项目风险的大小。
(4)如果无风险收益率为6%,甲项目的风险价值系数为10%,计算甲项目投资的总收益率。
5、某公司拟进行一项投资。
目前有甲、乙两种方案可供选择。
如果投资于甲方案其原始投资额会比乙方案高60000元,但每年可获得的收益比乙方案多10000元。
假设该公司要求的最低报酬率为12%,方案的持续年限为n年,分析n处于不同取值范围时应当选择哪一种方案?6、一个男孩今年9岁,在他5岁生日时,收到一份外祖父送的礼物,这份礼物是以利率为5%的复利计息的10年到期的债券3000元。
男孩父母计划在其18、19、20、21岁生日时,各用5000元资助他的大学学习,为了实现这个计划,外祖父的礼物债券到期后,其父母将其重新投资,除了这笔投资外,其父母在孩子10至17岁生日时,每年还需进行多少投资才能完成其资助孩子的教育计划?设所有将来的投资利润率均为6%。
第三章例1:某企业从银行取得长期借款100万元,年利率为10%,期限为3年,每年付息一次,到期还本付息。
假定筹资费用率为1‰,企业所得税率为33%,则其借款成本为多少?例2:某公司在筹资前根据市场预测,拟发行一种面值为1000元、票面利率为14%、10年期、每年付息一次的债券。
预计其发行价格为1020元,发行费用占发行价格的4%,税率为33%,则该债券的筹资成本率为多少?例3:某公司拟发行某优先股,面值总额为100万元,固定股息率为15%,筹资费率预计为5%,该股票溢价发行,其筹资总额为150万元,则优先股的成本为多少?例4:某公司发行面值为1元的普通股500万股,筹资总额为1500万元,筹资费率为4%,已知第一年每股股利为0.25元,以后各年按5%的比率增长,则其成本应为多少?练习:1.某企业取得5年期长期借款1200万元,借款利率5%,银行要求企业每年付息一次,到期还本。
另外已知筹资费率为0.5%,企业所得税税率为33%。
要求:计算长期借款的资本成本。
2.某公司发行3年期公司债券,面值总额为2500万元,票面利率为8%,筹资费率为2%,企业所得税税率为33%,该债券每年付息一次,到期还本。
该公司债券售价总额有2500万元、2000万元和3000万元三种情况。
要求:分别计算以上三种情况下公司债券的资本成本。
3.某公司发行优先股,面值总额为600万元,筹资费率为4%,年股利率为12%,售价总额有600万元、550元和650万元三种情况。
要求:分别计算以上三种情况下优先股的资本成本。
4.某公司发行普通股,售价为20元/股。
已知该公司的股利逐年增长,固定增长率为6%,筹资费率为2%。
另外已知该公司当前发放的普通股股利为1.5元/股。
另外,该企业打算用留存收益筹资50万元。
要求:计算普通股及留存收益的资本成本。
5、某企业拟筹资2 500万元。
其中发行债券1000万元,筹资费率2%,债券年利率为10%,所得税率为33%;优先股500万元,年股息率7%,第三者资费率为3%;普通股1000万元,筹资费率为4%,第一年预期股利率为10%,以后各年增长4%。
偿计算该等资方案的综合资金成本。
例5:某企业生产A产品,已知固定成本为60万元,变动成本率为40%,销售额分别为400万元、200万元和100万元。
则相应的经营杠杆系数为多少?例6:某企业生产B产品,销售额为400万元,变动成本率为40%,固定成本分别为60万、30万和15万,则相应的经营杠杆系数为多少?练习6:某企业生产甲产品,固定成本为120万元,变动成本率为30%,销售额分别为1000万元、2000万元和500万元。
要求:1)计算不同销售额所对应的经营杠杆系数。
2)从中分析销售额与经营杠杆系数和经营风险的关系。
练习7.某企业生产乙产品,销售额为800万元,变动成本率为40%,固定成本分别为100万元、200万元和400万元。
要求:1)计算不同固定成本所对应的经营杠杆系数。
2)从中分析固定成本与经营杠杆系数和经营风险的关系。
例7:某企业资本总额为700万元,负债利息率为14%,销售额为1000万元,不含负债利息的变动成本率为60%,固定成本为160万元。
当其债务资本与权益资本的比例分别为3:1、6:1、9:1时,则财务杠杆系数分别为:例8:项目 A B C股本(面值1)200 100 50发行在外的股数20 10 5债务(利率8%)0 100 150资本总额200 200 200 EBIT 20 20 20I税前利润所得税(50%)税后利润EPS项目 A B CEBIT增长率20% 20% 20% 增长后的EBIT 24 24 24 债务利息税前利润所得税(50%)税后利润EPSEPS增加额普通股盈余增长率项目 A B C股本(面值1)200 100 50 发行在外的股数20 10 5 债务(利率8%)0 100 150 资本总额200 200 200 EBIT 16 16 16 I税前利润所得税(50%)税后利润EPSEBIT增长率20% 20% 20% 增长后的EBIT 19.2 19.2 19.2 债务利息税前利润所得税(50%)税后利润EPSEPS增加额普通股盈余增长率项目 A B CEBIT减低率20% 20% 20% 增长后的EBIT 12.8 12.8 12.8 债务利息税前利润所得税(50%)税后利润EPSEPS减少额普通股盈余减少率股本(面值1)200 100 50发行在外的股数20 10 5债务(利率8%)0 100 150资本总额200 200 200EBIT 10 10 10I税前利润所得税(50%)税后利润EPS练习8:某企业资本总额为2500 万元,其中权益资本与债务资本的比例为1:2,1:4和1:8,负债利息率为12%,销售额为6000万元,不含负债利息的变动成本率为60%,固定成本为500万元。
要求:1)计算不同债务规模所对应的财务杠杆系数。
2)从中分析债务规模与财务杠杆系数和财务风险的关系。
例9:某企业某月销售额为1000万元,不含负债利息的变动成本率为40%,固定成本为200万元,全部资本为5000万元,债务资本为2500万元,利息率为6%,所得税税率为33%,发行在外的普通股总股数为100万股。
则该企业的经营杠杆系数、财务杠杆系数和总杠杆系数分别为:如果该企业下月销售额增长1倍,那么该企业下月的息税前利润和普通股每股收益各增长几倍?下月的息税前利润和普通股每股收益分别是多少?例10:某企业欲筹资600万元,有两种方案供选择,两方案的筹资组合及个别资本成本见下表所示。
筹资方式甲方案乙方案筹资金额Ki 筹资金额Ki长期借款100 6%300 10%长期债券200 8%200 8%普通股300 10%100 15%合计600 600要求:确定企业初始筹资时,最佳的资本结构。
练习9:某企业原有资本1500万元,其中5年期长期债券300万元,票面利率6%,权益资本(普通股)1200万元,公司发行的普通股为16万股,每股面值75元。
