最新圆的标准方程PPT(公开课)
合集下载
圆的标准方程完整ppt课件
解决与圆有关的切线问题
圆的方程可以用来求解与圆有关的切线问题，如切线方程、切点坐 标等。
圆的方程在物理问题中的应用
描述圆形运动轨迹
在物理学中，圆的方程可以用来描述物体做圆周运动时的轨迹。
计算圆形运动的物理量
利用圆的方程，可以计算物体做圆周运动时的线速度、角速度、向 心加速度等物理量。
解决与圆有关的物理问题
切线与半径垂直
切线垂直于经过切点的 半径。
切线长定理
从圆外一点引圆的两条 切线，它们的切线长相
等。
04
圆的方程在实际问题中的应用
圆的方程在几何问题中的应用
确定圆的位置和大小
通过圆的方程，可以准确地确定圆心的坐标和半径的长度，从而 确定圆的位置和大小。
判断点与圆的位置关系
利用圆的方程，可以判断一个点是否在圆上、圆内或圆外，从而解 决相关的几何问题。
3
解决与圆有关的经济问题
圆的方程还可以用来解决一些与圆有关的经济问 题，如圆形区域的经济发展、圆形市场的竞争等 。
05
圆的方程与其他知识点的联系
圆的方程与直线方程的关系
直线与圆的位置关系
通过比较圆心到直线的距离与半径的大小关系，可以确定直线与 圆是相切、相交还是相离。
切线方程
当直线与圆相切时，切线的斜率与圆心和切点的连线垂直，由此 可以求出切线的方程。
根据两点间距离公式，有 $OP = sqrt{(x - a)^{2} + (y
- b)^{2}}$。
将 $OP = r$ 代入上式，得到 $(x - a)^{2} + (y - b)^{2} =
r^{2}$。
方程中参数的意义
$a, b$
01
圆心坐标，表示圆心的位置。
圆的方程可以用来求解与圆有关的切线问题，如切线方程、切点坐 标等。
圆的方程在物理问题中的应用
描述圆形运动轨迹
在物理学中，圆的方程可以用来描述物体做圆周运动时的轨迹。
计算圆形运动的物理量
利用圆的方程，可以计算物体做圆周运动时的线速度、角速度、向 心加速度等物理量。
解决与圆有关的物理问题
切线与半径垂直
切线垂直于经过切点的 半径。
切线长定理
从圆外一点引圆的两条 切线，它们的切线长相
等。
04
圆的方程在实际问题中的应用
圆的方程在几何问题中的应用
确定圆的位置和大小
通过圆的方程，可以准确地确定圆心的坐标和半径的长度，从而 确定圆的位置和大小。
判断点与圆的位置关系
利用圆的方程，可以判断一个点是否在圆上、圆内或圆外，从而解 决相关的几何问题。
3
解决与圆有关的经济问题
圆的方程还可以用来解决一些与圆有关的经济问 题，如圆形区域的经济发展、圆形市场的竞争等 。
05
圆的方程与其他知识点的联系
圆的方程与直线方程的关系
直线与圆的位置关系
通过比较圆心到直线的距离与半径的大小关系，可以确定直线与 圆是相切、相交还是相离。
切线方程
当直线与圆相切时，切线的斜率与圆心和切点的连线垂直，由此 可以求出切线的方程。
根据两点间距离公式，有 $OP = sqrt{(x - a)^{2} + (y
- b)^{2}}$。
将 $OP = r$ 代入上式，得到 $(x - a)^{2} + (y - b)^{2} =
r^{2}$。
方程中参数的意义
$a, b$
01
圆心坐标，表示圆心的位置。
圆的标准方程完整ppt课件
练习
1.点(2a, 1 a)在圆x2 + y2 = 4的内部,求实数 a 的 取值范围. 2.根据下列条件，求圆的方程：
（1）求过两点A(0,4)和B(4,6),且圆心在直线xy+1=0上的圆的标准方程。
（2）圆心在直线5x-3y=8上，又与两坐标轴相 切，求圆的方程。
（3）求以C(1,3)为圆心，且和直线3x-4y-7=0
程，并判断点 M1(5,7)， M2( 5,1)是否在这个圆上。
解：圆心是 A(2,3，) 半径长等于5的圆的标准方程 是：
(x2)2(y3)225
把 M1(5,7的)坐标代入方程 (x2)2(y3)225 左右两边相等，点M 1 的坐标适合圆的方程，所以点
M
在这个圆上；
1
把点 M2( 5,1的)坐标代入此方程，左右两边不 相等，点 M的2坐标不适合圆的方程，所以点 M不2在 这个圆上．
跟踪训练 已知两点M(3,8)和N(5,2)． (1)求以MN为直径的圆C的方程； (2)试判断P1(2,8)，P2(3,2)，P3(6,7)是在圆上，在 圆内，还是在圆外？
解：(1)法一：设圆心 C(a，b)，半径为 r， 则由 C 为 MN 的中点得 a＝3＋2 5＝4，b＝8＋2 2＝5， 由两点间的距离公式得
解2:设圆C的方程为 (xa)2(yb)2r2,
∵圆心在直线l:x-y+1=0上 圆经过A(1,1),B(2,-2)
待定系数法
a b1 0 (1a)2 (1b)2 r2
(2a)2 (2b)2 r2
a 3
b
2
r 5
圆 心 为 C 的 圆 的 标 准 方 程 为 ( x + 3 ) 2 ( y 2 ) 2 2 5 .
4. 圆的标准方程PPT完美课件
4. 圆的标准方程PPT完美课件
5. 这是一篇托物言志的铭文，本文言 简义丰 、讲究 修辞。 文章骈 散结合 ，以骈 句为主 ，句式 整齐， 节奏分 明，音 韵和谐 。
6.了解和名著有关的作家作品及相关 的诗句 、名言 、成语 和歇后 语等， 能按要 求向他 人推介 某部文 学名著 。
7.能够根据所提供的有关文学名著的 相关语 言信息 推断作 品的作 者、作 品的名 称和人 物形象 ，分析 人物形 象的性 格和作 品的思 想内容 并进行 简要评 价。
=1 解得b=± 2
12+(-1)2
所以切线方程为：y = x± 2
（2）在y轴上截距是 2 的切线方程。
y = ± x+ 2
4. 圆的标准方程PPT完美课件
4. 圆的标准方程PPT完美课件
思考题：
从圆x2+y2=10外一点P(4,2)向该圆引切线，求切 线方程。
x+3y=10 或 3x-y=10
4. 圆的标准方程PPT完美课件
4. 圆的标准方程PPT完美课件
练习：写出过圆x2+y2=10 上一点 M（2， )6的切线方程。
2x + 6 y =10
练习：已知圆的方程是x2+y2=1，求：
（1）斜率等于1的切线的方程；
提示：设切线方程为 y=x+b ,由圆心到切线的距离等于半
径1，得： |b|
(3) 注意圆的平面几何知识的运用以及应用圆的方 程解决实际问题。
4. 圆的标准方程PPT完美课件
4. 圆的标准方程PPT完美课件
作业：
课本P124 习题4.1 A组 1、2、3、4
4. 圆的标准方程PPT完美课件
4. 圆的标准方程PPT完美课件
圆的标准方程ppt课件完整版x-2024鲜版
2024/3/28
25
两圆相离条件（内含和外离）
内含
两圆圆心之间的距离小于两圆半径之差。
外离
两圆圆心之间的距离大于两圆半径之和。
2024/3/28
26
判断方法总结及示例
要点一
判断方法
首先根据两圆圆心距和半径和、半径差的大小关系，确定 两圆的位置关系类型（相交、相切、相离），然后根据具 体类型进一步判断是相交、内切、外切、内含还是外离。
04
2024/3/28
05
4. 从中可以看出，圆心坐标 为 $(2, -3)$，半径 $r = 1$
。
12
03
圆的图像与性质分析
2024/3/28
13
圆心位置对图像影响
圆心决定圆的位置
在平面直角坐标系中，圆心的坐标决定了圆在平面上的位置。
圆心与圆上任一点的距离等于半径
根据圆的定义，圆心到圆上任意一点的距离都等于半径，因此圆心的位置会影响圆的整体形状和大小 。
$(x - a)^{2}$ 和 $(y - b)^{2}$ 分别表示 点 $(x, y)$ 到圆心 $(a, b)$ 的水平和垂 直距离的平方。
2024/3/28
$r$ 表示圆的半径， 即从圆心到圆上任一 点的距离。
10
从一般方程到标准方程的转换
一般方程形式为
$x^{2} + y^{2} + Dx + Ey + F = 0$
当两个质点发生碰撞时，可以通过它们的运动轨迹（即两个圆的 方程）来求解碰撞点的坐标。
分析物体的受力情况
在某些物理问题中，可以通过分析物体运动轨迹的形状（如圆形 或椭圆形）来推断物体所受的力。
31
圆方程的课件ppt课件ppt
当$theta = 0$时，点为$(a, b)$ ；当$theta = frac{pi}{2}$时，点 为$(a - r, b)$；当$theta = pi$ 时，点为$(a - r, b + r)$。
03 圆的方程的求解
直接求解法
总结词
通过已知条件直接代入求解。
适用范围
适用于已知圆心和半径的情况。
工程设计
在工程设计中，圆的面积和周长公 式同样必不可少，如设计圆形机械 零件、计算圆形结构件的承载能力 等。
06 圆的对称性和极 坐标方程
圆的对称性
01
02
03
圆的对称性定义
圆关于其圆心具有对称性 ，即圆心是圆上任意两点 的中点。
圆的对称性质
圆关于其直径也具有对称 性，即直径将圆分成两个 相等的部分。
$frac{sqrt{D^2 + E^2 4F}}{2}$。
圆的参数方程
圆的参数方程：$x = a + rcostheta, y = b + rsintheta$， 其中$(a, b)$是圆心坐标，$r$是 半径，$theta$是参数。
圆的参数方程通过参数$theta$描 述了一个圆上的点的坐标。
圆的基本性质
01
圆是中心对称图形，即圆心是圆上任何一对对称点 的对称中心。
02
圆是旋转对称图形，即旋转任意角度后与原图重合 。
03
圆的直径是半径的两倍，且直径平分半径。
圆的应用
圆在日常生活中的应用非常广 泛，如车轮、钟表、餐具等。
在工程和科学领域中，圆也常 用于建筑设计、机械制造和天 文观测等方面。
在数学领域中，圆是基础几何 图形之一，可用于研究圆的性 质和定理，以及解决相关的数 学问题。
圆的标准方程公开课课件(终稿)
设点M (x,y)为圆C上任一点，则|MC|= r。
圆上所有点的集合 P = { M | |MC| = r }
y
M(x,y)
(x a)2 (y b)2 r
(x-a)2+(y-b)2=r2
C(a,b)
O
x
知识点一
(x a)2 (y b)2 r2
圆的标准方程
y
M(x,y)
圆心C(a,b),半径r
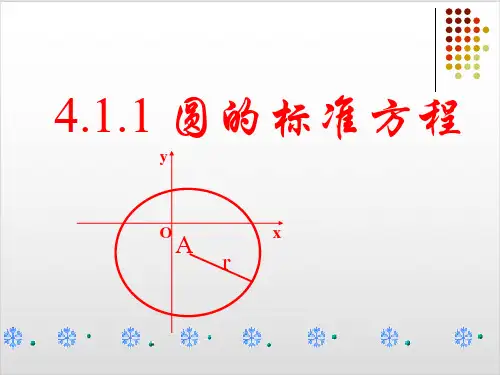
圆在直角坐标系下有什么样的方程？
y
几
何
问
题
代
数 化
O
x
探究准备
1、什么是圆？
墨 子： 圆，一中同长也。 欧几里得：平面内与定点距离等于定长的点的集合
（轨迹）是圆.
2、确定圆有需要几个要素？
圆心－－确定圆的位置(定位) 半径－－确定圆的大小(定形)
探究新知
3、圆心是C(a,b),半径是r的圆的方程是什么？
y3 2
x
x2
作业布置： 1、书面:P124 A组 2、课时训练
2,3, 4
永切隔数形数焉数
远莫离形少无能与
,
,
——
联忘分结数形分形
华 罗 庚
系 莫 分 离
几 何 代 数
家 万 事 休
合 百 般 好
时 难 入 微
时 少 直 觉
作 两 边 飞
本 是 相 倚
统
依
一
体
变式2 已知两点A(4,9), B(6, 3)，求以线段AB为直径的
R
x
D B(7,-3)
O
L1
E
C(2,-8)
圆心：两条垂直平分线的交点
解法二:∵A(5,1),B(7,-3)
圆的标准方程ppt课件
_____5______．
解析：圆 C : x2 y2 25 的圆心为C(0,0) ，半径r = 5 ， 因为 AC (8 0)2 (6 0)2 10 5 ，所以点 A 在圆外， 所以 AP 的最小值为 AC r 10 5 5 ，故答案为：5.
总结一下
圆的标准方程
6.已知 A2,2、 B2,6 ，则以 AB 为直径的圆的标准方程为_x_2____.y4 2 8
解析：线段 AB 的中点坐标为0, 4 ， AB 2 22 2 62 4 2 ，
所以，所求圆的半径为 2 2 ，故所求圆的标准方程为 x2 y 42 8 .
7.已知点 A(8, 6) 与圆C : x2 y2 25 ，P 是圆 C 上任意一点，则 AP 的最小值是
求圆的标准方程的两种方法
1.待定系数法.先设圆的标准方法 x a 2 y b 2 r2 ，再根据条件列出关于 a， b，r 的三个独立方程，通过解方程组求出 a，b，r 的值，从而得到圆的标准方程， 如例题 2 的解法.这是一种代数解法. 2.直接求解法.先根据题目条件求出圆心和半径，直接写出圆的标准方程，如例 3 的解法，这种解法往往需要圆的几何性质.
例 3 已知圆心为 C 的圆经过 A(1，1) ，B(2 ，2) 两点，且圆心 C 在直线l : x y 1 0 上， 求此圆的标准方程.
分析：设圆心 C 的坐标为 a,b .由已知条件可知， CA CB ，且a b 1 0 ， 由此可以求出圆心坐标和坐标.
解：解法1：
设圆心 C 的坐标为 (a ，b) . 因为圆心 C 在直线 l : x y 1 0 上，所以 a b 1 0 .① 因为 A，B 是圆上两点，所以| CA| | CB | . 根据两点间距离公式，有 (a 1)2 (b 1)2 (a 2)2 (b 2)2 ， 即 a 3b 3 0 .② 由①②可得 a 3，b 2 . 所以圆心 C 的坐标是 (3， 2) . 圆的半径 r | AC | (1 3)2 (1 2)2 5 .
解析：圆 C : x2 y2 25 的圆心为C(0,0) ，半径r = 5 ， 因为 AC (8 0)2 (6 0)2 10 5 ，所以点 A 在圆外， 所以 AP 的最小值为 AC r 10 5 5 ，故答案为：5.
总结一下
圆的标准方程
6.已知 A2,2、 B2,6 ，则以 AB 为直径的圆的标准方程为_x_2____.y4 2 8
解析：线段 AB 的中点坐标为0, 4 ， AB 2 22 2 62 4 2 ，
所以，所求圆的半径为 2 2 ，故所求圆的标准方程为 x2 y 42 8 .
7.已知点 A(8, 6) 与圆C : x2 y2 25 ，P 是圆 C 上任意一点，则 AP 的最小值是
求圆的标准方程的两种方法
1.待定系数法.先设圆的标准方法 x a 2 y b 2 r2 ，再根据条件列出关于 a， b，r 的三个独立方程，通过解方程组求出 a，b，r 的值，从而得到圆的标准方程， 如例题 2 的解法.这是一种代数解法. 2.直接求解法.先根据题目条件求出圆心和半径，直接写出圆的标准方程，如例 3 的解法，这种解法往往需要圆的几何性质.
例 3 已知圆心为 C 的圆经过 A(1，1) ，B(2 ，2) 两点，且圆心 C 在直线l : x y 1 0 上， 求此圆的标准方程.
分析：设圆心 C 的坐标为 a,b .由已知条件可知， CA CB ，且a b 1 0 ， 由此可以求出圆心坐标和坐标.
解：解法1：
设圆心 C 的坐标为 (a ，b) . 因为圆心 C 在直线 l : x y 1 0 上，所以 a b 1 0 .① 因为 A，B 是圆上两点，所以| CA| | CB | . 根据两点间距离公式，有 (a 1)2 (b 1)2 (a 2)2 (b 2)2 ， 即 a 3b 3 0 .② 由①②可得 a 3，b 2 . 所以圆心 C 的坐标是 (3， 2) . 圆的半径 r | AC | (1 3)2 (1 2)2 5 .
2.4.1圆的标准方程课件共23张PPT
上、圆内,还是圆外.
解:由已知得，圆心A的位置为线段P1P2的中 6) ,
P1 P2
利用两点间距离公式得 r =
=
2
4 - 6 + 9 - 3
圆的标准方程为: (x-5)2+(y-6) 2=10.
2
2
2
= 10.
2.已知P 1(4, 9) , P 2(6, 3)两点,求以线段P 1P 2为直径
-8) , 求△ABC的外接圆的标准方程.
解:线段AB的垂直平分线l1的方程是 x - 2 y - 8 = 0
同理, 线段AC的垂直平分线l2的方程是 x + 3 y + 7 = 0
x -2y-8 = 0
圆心的坐标就是方程组
的解 .
x +3y +7 = 0
x = 2,
所以, 圆心C的坐标(2 , -3) , 圆的半径
分析:设圆心C的坐标为(a, b) . 由已知条件可知 |CA|=
|CB|, 且a-b+1=0 . 由此可求出圆心坐标和半径 .
又因为线段AB是圆的一条弦 , 根据平面几何知识, AB
的中点与圆心C的连线垂直于AB , 由此可得到另一种解法.
解法1:设圆心C的坐标为(a, b) . 因为圆心C在直线 l :
分析: 不在同一条直线上的三个点可以确定一个圆 ,
三角形有唯一的外接圆 . 显然已知的三个点不在同一条直
线上 . 只要确定了a, b, r , 圆的标准方程就确定了.
例2 △ABC的三个顶点分别是A(5, 1) , B(7, -3) , C(2,
-8) , 求△ABC的外接圆的标准方程.
2
2
2
解: 设所求的方程是 x - a + y - b = r
解:由已知得，圆心A的位置为线段P1P2的中 6) ,
P1 P2
利用两点间距离公式得 r =
=
2
4 - 6 + 9 - 3
圆的标准方程为: (x-5)2+(y-6) 2=10.
2
2
2
= 10.
2.已知P 1(4, 9) , P 2(6, 3)两点,求以线段P 1P 2为直径
-8) , 求△ABC的外接圆的标准方程.
解:线段AB的垂直平分线l1的方程是 x - 2 y - 8 = 0
同理, 线段AC的垂直平分线l2的方程是 x + 3 y + 7 = 0
x -2y-8 = 0
圆心的坐标就是方程组
的解 .
x +3y +7 = 0
x = 2,
所以, 圆心C的坐标(2 , -3) , 圆的半径
分析:设圆心C的坐标为(a, b) . 由已知条件可知 |CA|=
|CB|, 且a-b+1=0 . 由此可求出圆心坐标和半径 .
又因为线段AB是圆的一条弦 , 根据平面几何知识, AB
的中点与圆心C的连线垂直于AB , 由此可得到另一种解法.
解法1:设圆心C的坐标为(a, b) . 因为圆心C在直线 l :
分析: 不在同一条直线上的三个点可以确定一个圆 ,
三角形有唯一的外接圆 . 显然已知的三个点不在同一条直
线上 . 只要确定了a, b, r , 圆的标准方程就确定了.
例2 △ABC的三个顶点分别是A(5, 1) , B(7, -3) , C(2,
-8) , 求△ABC的外接圆的标准方程.
2
2
2
解: 设所求的方程是 x - a + y - b = r
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
程，并判断点 M1(5,7)， M2( 5,1)是否在这个圆上。
解：圆心是 A(2,3，) 半径长等于5的圆的标准方程 是：
(x2)2(y3)225
怎样判断点 M0(x0在,y0圆) 圆上？还是在圆外呢？
(xa)2(y内b)呢2？r2
y
M3
M2
C
o
M1
x
知识点二：点与圆的位置关系
点与圆的位置关系:
二、探究新知，合作交流
探究一
已知圆的圆心c(a,b)及圆的
半径R,如何确定圆的方程？
y
P={M||MC|=R}
M
R
C(a,b)
O
x
基础演练
1.圆 (x－2)2+ y2=2的圆心A的坐标为__,
半径r =__.
2圆(x+1)2＋(y - 3 ) 2＝a2,(a 0)的圆心,半径是？
典型例题
例1 写出圆心为 A(2,3)，半径长等于5的圆的方
小结：
一、圆的标准方程
(xa)2(yb)2r2
y
M
C
O
x
圆心C(a,b),半径r
：则圆的标准方程为,特别地，若圆心为O(x0,20) y2 r2
二、点与圆的位置关系：
（1）点P在圆上 x0a2y0b2r2 （2）点P在圆内 x0a2y0b2r2
（3）点P在圆外 x0a2y0b2r2
三、求圆的标准方程的方法：
1 代数方法：待定系数法求
2 几何方法：数形结合
作业布置
P120 练习1、 P124 习题A组2
你对本节课哪个知识点 还有些疑惑？？？
将标准方程展开，是一个什么形式？ 它有什么特点？
结束语
谢谢大家聆听！！！
17
系
()
A在圆外 C在圆内
B在圆上 D在圆上或圆外
变式演练
圆心为A(3,1)半径长等于5的圆的方程 ( )
A (x – 3 )2+(y – 1 )2=25 B (x – 3 )2+(y + 1)2=25 C (x – 3 )2+(y + 1 )2=5 D (x + 3 )2+(y – 1 )2=5
变式一 圆心在C(8，-3),且经过点M(5,1)的 圆的方程？
(x0-a)2+(y0-b2时,点M在圆C上;
(x0-a)2+(y0-b)2>r2时,点M在圆C外.
M (x0, y0 )
M (x0, y0 )
M (x0, y0 )
O(a, b)
O(a, b)
O (a,b)
练习：
点P( 1,5)与圆x2+y2=25的位置关
圆的标准方程PPT(公开课)
创设情境 引入新课
创设情境 引入新课
师生互动探究
1、圆具有怎么样的性质？ 圆上的点到圆心的距离相等
2、确定圆有需要几个要素？
圆心－－确定圆的位置(定位) 半径－－确定圆的大小(定形)
圆在坐标系下有什么样的方程？
解
析
y
几
何
的
基
本
x
思
O
想
书少成天才功山小才就=有艰是不在苦百路分学于的勤之劳习勤一为动，的径奋+老灵正，感确学来努，的百海徒力方分无法之伤才+崖九少悲能十苦谈九成空作的话汗舟功水！！
解：圆心是 A(2,3，) 半径长等于5的圆的标准方程 是：
(x2)2(y3)225
怎样判断点 M0(x0在,y0圆) 圆上？还是在圆外呢？
(xa)2(y内b)呢2？r2
y
M3
M2
C
o
M1
x
知识点二：点与圆的位置关系
点与圆的位置关系:
二、探究新知，合作交流
探究一
已知圆的圆心c(a,b)及圆的
半径R,如何确定圆的方程？
y
P={M||MC|=R}
M
R
C(a,b)
O
x
基础演练
1.圆 (x－2)2+ y2=2的圆心A的坐标为__,
半径r =__.
2圆(x+1)2＋(y - 3 ) 2＝a2,(a 0)的圆心,半径是？
典型例题
例1 写出圆心为 A(2,3)，半径长等于5的圆的方
小结：
一、圆的标准方程
(xa)2(yb)2r2
y
M
C
O
x
圆心C(a,b),半径r
：则圆的标准方程为,特别地，若圆心为O(x0,20) y2 r2
二、点与圆的位置关系：
（1）点P在圆上 x0a2y0b2r2 （2）点P在圆内 x0a2y0b2r2
（3）点P在圆外 x0a2y0b2r2
三、求圆的标准方程的方法：
1 代数方法：待定系数法求
2 几何方法：数形结合
作业布置
P120 练习1、 P124 习题A组2
你对本节课哪个知识点 还有些疑惑？？？
将标准方程展开，是一个什么形式？ 它有什么特点？
结束语
谢谢大家聆听！！！
17
系
()
A在圆外 C在圆内
B在圆上 D在圆上或圆外
变式演练
圆心为A(3,1)半径长等于5的圆的方程 ( )
A (x – 3 )2+(y – 1 )2=25 B (x – 3 )2+(y + 1)2=25 C (x – 3 )2+(y + 1 )2=5 D (x + 3 )2+(y – 1 )2=5
变式一 圆心在C(8，-3),且经过点M(5,1)的 圆的方程？
(x0-a)2+(y0-b2时,点M在圆C上;
(x0-a)2+(y0-b)2>r2时,点M在圆C外.
M (x0, y0 )
M (x0, y0 )
M (x0, y0 )
O(a, b)
O(a, b)
O (a,b)
练习：
点P( 1,5)与圆x2+y2=25的位置关
圆的标准方程PPT(公开课)
创设情境 引入新课
创设情境 引入新课
师生互动探究
1、圆具有怎么样的性质？ 圆上的点到圆心的距离相等
2、确定圆有需要几个要素？
圆心－－确定圆的位置(定位) 半径－－确定圆的大小(定形)
圆在坐标系下有什么样的方程？
解
析
y
几
何
的
基
本
x
思
O
想
书少成天才功山小才就=有艰是不在苦百路分学于的勤之劳习勤一为动，的径奋+老灵正，感确学来努，的百海徒力方分无法之伤才+崖九少悲能十苦谈九成空作的话汗舟功水！！