算术练习题 9月26日
初一上数学真题专题练习---一元一次方程的应用(一)

一元一次方程的应用(一)【真题精选】1.《九章算术》是中国古代的数学专著,奠定了中国传统数学的基本框架.方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”译文:“假设有若干人共同出钱买羊,如果每人出5钱,那么还差45钱;如果每人出7钱,那么仍旧差3钱,求买羊的人数和羊的价钱.”设羊是x钱,可列方程为()A.=B.=C.=D.=2.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”设井深为x尺,根据题意列方程,正确的是()A.3(x+4)=4(x+1)B.3x+4=4x+1C.3(x﹣4)=4(x﹣1)D.3.某车间原计划13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,设原计划每小时生产x个零件,则所列方程为()A.13x=12(x+10)+60B.12(x+10)=13x+60C.D.4.一辆客车和一辆卡车同时从A地出发沿同一公路同向行驶,客车的行驶速度是70km/h,卡车的行驶速度是60km/h,客车比卡车早2h到达B地.若设A、B两地间的路程是xkm,可列方程()A.B.C.70x﹣60x=2D.5.用长为24cm的绳子围成一个封闭的长方形(绳子不重合),长方形的长是宽的两倍.设长方形的宽为xcm,根据题意可列方程为()A.x•2x=24B.x+2x=24C.2(x+2)=24D.2(x+2x)=24 6.如图,表中给出的是某月的月历,任意选取“U”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()A.70B.78C.161D.1057.已知下列四个应用题:①现有60个零件的加工任务,甲单独每小时可以加工4个零件,乙单独每小时可以加工6个零件.现甲乙两人合作,问两人开始工作几小时后还有20个零件没有加工?②甲乙两人从相距60km的两地同时出发,相向而行,甲的速度是4km/h,乙的速度是6km/h,问经过几小时后两人相遇后又相距20km?③甲乙两人从相距60km的两地相向而行,甲的速度是4km/h,乙的速度是6km/h,如果甲先走了20km后,乙再出发,问乙出发后几小时两人相遇?④甲乙两人从相距20km的两地同时出发,背向而行,甲的速度是4km/h,乙的速度是6km/h,问经过几小时后两人相距60km?其中可以用方程4x+6x+20=60表述题目中对应数量关系的应用题序号是()A.①②③④B.①③④C.②③④D.①②8.小王、小李和小张,同时各做120个同样的机器零件,当小王做完时,小李做了100个,小张做了80个,照这样计算,小李做完时,小张还差个没做.9.一部书稿,甲打字员打完全书要20天,乙打字员用同样的时间只能完成书稿的,两人合打这部书稿要天完成.10.甲、乙两城相距750千米,一辆大客车从甲城开往乙城共用15小时,一辆小轿车从乙城开往甲城10小时可以到达.两车同时从两城出发相向而行,小时可以相遇.11.清代文言小说集《笑笑录》记载,清代诗人徐子云曾写过一首诗:巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人共食一碗饭,四人共吃一碗羹.请问先生明算者,算来寺内几多僧?设寺内有x名僧人,则列出一元一次方程为.12.小华和小明周末到北京三山五园绿道骑行.他们按设计好的同一条线路同时出发,小华每小时骑行18km,小明每小时骑行12km,他们完成全部行程所用的时间,小明比小华多半小时.设他们这次骑行线路长为xkm,依题意,可列方程为.13.《九章算术》是我国古代数学名著,卷七“盈不足”中题目译文如下:“今有人合伙买羊,每人出5钱,还差45钱;每人出7钱,还差3钱.问合伙人数、羊价各是多少?”设合伙人数为x人,根据题意可列一元一次方程为.14.一件商品的标价是100元,进价是50元,打八折出售后这件商品的利润是元.15.《九章算术》是中国古代非常重要的一部数学典籍,被视为“算经之首”.《九章算术》大约成书于公元前200年~公元前50年,是以应用问题解法集成的体例编纂成书的,全书按题目的应用范围与解题方法划分为“方田”、“粟米”、“衰分”等九章.《九章算术》中有这样一个问题:今有共买金,人出四百,盈三千四百;人出三百,盈一百.问人数,金价各几何?其大意是:假设合伙买金,每人出400钱,还剩余3400钱;每人出300钱,还剩余100钱.问人数、金价各是多少?如果设有x个人,那么可以列方程为.16.一项工程,甲单独做10天完成,乙单独做15天完成.两人合作,天可以完成.17.在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为40?如果能,求出这三个数;如果不能,请说明理由.18.列方程解应用题十一期间,张老师从北京出发走京津高速到天津.去时在京津高速上用了1.2小时,返回时在京津高速上比去时多用18分钟,返回时平均速度降低了22千米/小时.求张老师去时在京津高速上开车的平均速度.19.列方程解应用题:某学校组织初一年级学生参加公益劳动在甲处劳动的有16人,在乙处劳动的有12人,现在另调20人去甲乙两处支援,使得在甲处劳动的人数比在乙处劳动的人数的2倍少6人,问应调往甲、乙两处各多少人?20.一项工程,甲队单独施工需要15天完成,乙队单独施工需要9天完成.现在由甲队先工作3天,剩下的由甲、乙两队合作,还需要几天才能完成任务?21.今年,小楠和哥哥的年龄之和是21岁,小楠的年龄只有哥哥的一半,小楠和哥哥各多少岁?(用方程解)22.某商场从厂家购进100个整理箱,按进价的1.5倍进行标价.当按标价卖出80个整理箱后,恰逢元旦,剩余的部分以标价的九折出售完毕,所得利润共1880元,求每个整理箱的进价.23.2020年9月的日历如图所示.(1)用1×3的长方形框出3个数,如果任意圈出一横行左右相邻的三个数,设最小的数为x,用含x的式子表示这三个数的和为;如果任意圈出一竖列上下相邻的三个数,设最小的数为y,用含y的式子表示这三个数的和为.(2)用一个2×2的正方形在此日历中框出4个数,被框住的4个数的和为84,则这四个数中最小的数为;(3)用一个3×3的正方形框在此日历中框出9个数,在框出的9个数中,记前两行共6个数的和为a1,最后一行3个数的和为a2,若|a1﹣a2|=15,请求出正方形框中位于最中心的数字m的值.24.甲班有45人,乙班有39人.现在需要从甲、乙班各抽调一些同学去参加歌咏比赛.如果从甲班抽调的人数比乙班多1人,那么甲班剩余人数恰好是乙班剩余人数的2倍.请问从甲、乙两班各抽调了多少参加歌咏比赛?25.列方程解应用题:2019年年底某高铁即将开通.以前小红回老家只能坐绿皮车,车速才60km/h,但某高铁开通之后,车速可以达到240km/h.这样就能早到4.5小时.请问提速后小红回老家需要多长时间?26.某商场进了一批豆浆机,按进价的180%标价,春节期间,为了能吸引消费者,打7折销售,此时每台豆浆机仍可获利52元,请问每台豆浆机的进价是多少元?27.列一元一次方程解应用题6月15日,新机场线一期工程正式开始试运行,轨道交通新机场线一期全长约42.75千米,全线从草桥站出发,途经磁各庄站,终到新机场北航站楼站,新机场线车辆首次采用基于城际平台的市域车型,全线行驶需20分钟(不含起始站和终点站停靠时间),若列车的平均时速为135千米,则列车在磁各庄站停靠的时间是多少分钟?28.整理一批图书,由一个人做要40h完成.现计划由一部分人先做4h,再增加2人和他们一起做8h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?一元一次方程的应用(一)参考答案与试题解析一.试题(共28小题)1.《九章算术》是中国古代的数学专著,奠定了中国传统数学的基本框架.方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”译文:“假设有若干人共同出钱买羊,如果每人出5钱,那么还差45钱;如果每人出7钱,那么仍旧差3钱,求买羊的人数和羊的价钱.”设羊是x钱,可列方程为()A.=B.=C.=D.=【分析】设羊是x钱,根据买羊的人数不变,即可得出关于x的一元一次方程,此题得解.【解答】解:设羊是x钱,根据题意得:=.故选:D.【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.2.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”设井深为x尺,根据题意列方程,正确的是()A.3(x+4)=4(x+1)B.3x+4=4x+1C.3(x﹣4)=4(x﹣1)D.【分析】用代数式表示井深即可得方程.此题中的等量关系有:①将绳三折测之,绳多四尺;②绳四折测之,绳多一尺.【解答】解:根据将绳三折测之,绳多四尺,则绳长为:3(x+4),根据绳四折测之,绳多一尺,则绳长为:4(x+1),故3(x+4)=4(x+1).故选:A.【点评】此题主要考查了由实际问题抽象出一元一次方程,不变的是井深,用代数式表示井深是此题的关键.3.某车间原计划13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,设原计划每小时生产x个零件,则所列方程为()A.13x=12(x+10)+60B.12(x+10)=13x+60C.D.【分析】首先理解题意,找出题中存在的等量关系:实际12小时生产的零件数=原计划13小时生产的零件数+60,根据此等式列方程即可.【解答】解:设原计划每小时生产x个零件,则实际每小时生产(x+10)个零件.根据等量关系列方程得:12(x+10)=13x+60.故选:B.【点评】列方程解应用题的关键是找出题目中的相等关系.4.一辆客车和一辆卡车同时从A地出发沿同一公路同向行驶,客车的行驶速度是70km/h,卡车的行驶速度是60km/h,客车比卡车早2h到达B地.若设A、B两地间的路程是xkm,可列方程()A.B.C.70x﹣60x=2D.【分析】首先根据题意,设A、B两地间的路程是xkm,然后根据:卡车行驶时间﹣客车行驶时间=2,列出方程即可.【解答】解:设A、B两地间的路程是xkm,可得:,故选:B.【点评】此题主要考查了由实际问题抽象出一元一次方程,解答此题的关键是:审题找出题中的未知量和所有的已知量,然后用含x的式子表示相关的量,找出之间的相等关系列方程.5.用长为24cm的绳子围成一个封闭的长方形(绳子不重合),长方形的长是宽的两倍.设长方形的宽为xcm,根据题意可列方程为()A.x•2x=24B.x+2x=24C.2(x+2)=24D.2(x+2x)=24【分析】根据题意用x的代数式表示出长方形的长,进而利用矩形周长公式求出即可.【解答】解:设这个长方形的宽为xcm,则长为2xcm,则可列方程:2(x+2x)=24,故选:D.【点评】此题主要考查了由实际问题抽象出一元一次方程,利用矩形周长公式得出方程是解题关键.6.如图,表中给出的是某月的月历,任意选取“U”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()A.70B.78C.161D.105【分析】设“U”型框中的正中间的数为x,则其他6个数分别为x﹣15,x﹣8,x﹣1,x+1,x﹣6,x﹣13,表示出这7个数之和,然后分别列出方程解答即可.【解答】解:设“U”型框中的正中间的数为x,则其他6个数分别为x﹣15,x﹣8,x﹣1,x+1,x﹣6,x﹣13,这7个数之和为:x﹣15+x﹣8+x﹣1+x+1+x﹣6+x﹣13=7x﹣42.由题意得:A、7x﹣42=70,解得x=16,能求出这7个数,不符合题意;B、7x﹣42=78,解得x=,不能求出这7个数,符合题意;C、7x﹣42=161,解得x=29,能求出这7个数,不符合题意;D、7x﹣42=105,解得x=21,能求出这7个数,不符合题意;故选:B.【点评】此题考查一元一次方程的实际运用,掌握“U”型框中的7个数的数字的排列规律是解决问题的关键.7.已知下列四个应用题:①现有60个零件的加工任务,甲单独每小时可以加工4个零件,乙单独每小时可以加工6个零件.现甲乙两人合作,问两人开始工作几小时后还有20个零件没有加工?②甲乙两人从相距60km的两地同时出发,相向而行,甲的速度是4km/h,乙的速度是6km/h,问经过几小时后两人相遇后又相距20km?③甲乙两人从相距60km的两地相向而行,甲的速度是4km/h,乙的速度是6km/h,如果甲先走了20km后,乙再出发,问乙出发后几小时两人相遇?④甲乙两人从相距20km的两地同时出发,背向而行,甲的速度是4km/h,乙的速度是6km/h,问经过几小时后两人相距60km?其中可以用方程4x+6x+20=60表述题目中对应数量关系的应用题序号是()A.①②③④B.①③④C.②③④D.①②【分析】①设两人开始工作x小时后还有20个零件没有加工,根据甲生产的零件数+乙生产的零件数+未加工的零件数=计划加工零件的总数,即可得出关于x的一元一次方程;②设经过x小时后两人相遇后又相距20km,根据甲的路程+乙的路程+相遇后又间隔的距离=两地间的距离,即可得出关于x的一元一次方程;③设乙出发后x小时两人相遇,根据甲的路程+乙的路程=两地间的距离,即可得出关于x的一元一次方程;④设经过x小时后两人相距60km,根据甲的路程+乙的路程+20=两人间的间距,即可得出关于x的一元一次方程.综上即可得出结论.【解答】解:①设两人开始工作x小时后还有20个零件没有加工,依题意,得:4x+6x+20=60,∴①可以用方程4x+6x+20=60来表述;②设经过x小时后两人相遇后又相距20km,依题意,得:4x+6x﹣20=60,∴②不可以用方程4x+6x+20=60来表述;③设乙出发后x小时两人相遇,依题意,得:4x+20+6x=80,∴③方程4x+6x+20=60来表述;④设经过x小时后两人相距60km,依题意,得:4x+6x+20=60,∴④可以用方程4x+6x+20=60来表述.故选:B.【点评】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.8.小王、小李和小张,同时各做120个同样的机器零件,当小王做完时,小李做了100个,小张做了80个,照这样计算,小李做完时,小张还差24个没做.【分析】设当小李做完时,小张还差x个没做,根据两人的工作效率不变且工作时间相同,即可得出关于x的一元一次方程,解之即可得出结论.【解答】解:设当小李做完时,小张还差x个没做,依题意得:=,解得:x=24.故答案为:24.【点评】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.9.一部书稿,甲打字员打完全书要20天,乙打字员用同样的时间只能完成书稿的,两人合打这部书稿要12天完成.【分析】由两打字员打字效率之间的关系可求出乙打字员打完全书所需时间,设两人合打这部书稿要x天完成,根据两人合作一天的工作量×工作时间=总工作量,即可得出关于x的一元一次方程,解之即可得出结论.【解答】解:乙打字员打完全书所需时间为20÷=30(天).设两人合打这部书稿要x天完成,依题意得:(+)x=1,解得:x=12.故答案为:12.【点评】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.10.甲、乙两城相距750千米,一辆大客车从甲城开往乙城共用15小时,一辆小轿车从乙城开往甲城10小时可以到达.两车同时从两城出发相向而行,6小时可以相遇.【分析】根据题意相遇问题中“两车路和等于750千米”列方程求解即可.【解答】解:设两车x小时可以相遇,由题意得:x+x=750,解得:x=6.答:两车同时从两城出发相向而行,6小时可以相遇.故答密为:6.【点评】本题考查了一元一次方程的应用,解题的关键是找等量关系.11.清代文言小说集《笑笑录》记载,清代诗人徐子云曾写过一首诗:巍巍古寺在山林,不知寺内几多僧.三百六十四只碗,看看用尽不差争.三人共食一碗饭,四人共吃一碗羹.请问先生明算者,算来寺内几多僧?设寺内有x名僧人,则列出一元一次方程为+=364.【分析】设寺内有x名僧人,根据题意列出方程即可求出答案.【解答】解:设寺内有x名僧人,由题意得+=364,故答案为:+=364.【点评】本题考查一元一次方程的应用,解题的关键是正确找出题中的等量关系,本题属于基础题型.12.小华和小明周末到北京三山五园绿道骑行.他们按设计好的同一条线路同时出发,小华每小时骑行18km,小明每小时骑行12km,他们完成全部行程所用的时间,小明比小华多半小时.设他们这次骑行线路长为xkm,依题意,可列方程为.【分析】根据“完成全部行程所用的时间,小明比小华多半小时”列出方程即可.【解答】解:设他们这次骑行线路长为xkm,依题意,可列方程为,故答案为:.【点评】本题考查了由实际问题抽象出一元一次方程,正确的理解题意是解题的关键.13.《九章算术》是我国古代数学名著,卷七“盈不足”中题目译文如下:“今有人合伙买羊,每人出5钱,还差45钱;每人出7钱,还差3钱.问合伙人数、羊价各是多少?”设合伙人数为x人,根据题意可列一元一次方程为5x+45=7x+3.【分析】设合伙人数为x人,根据买羊需要的钱数不变,即可得出关于x的一元一次方程,此题得解.【解答】解:设合伙人数为x人,依题意,得:5x+45=7x+3.故答案为:5x+45=7x+3.【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.14.一件商品的标价是100元,进价是50元,打八折出售后这件商品的利润是30元.【分析】设打八折出售后这件商品的利润是x元,根据题意列出方程即可求出答案.【解答】解:设打八折出售后这件商品的利润是x元,x=0.8×100﹣50=30,故答案为:30【点评】本题考查一元一次方程,解题的关键是正确找出题中的等量关系,本题属于基础题型.15.《九章算术》是中国古代非常重要的一部数学典籍,被视为“算经之首”.《九章算术》大约成书于公元前200年~公元前50年,是以应用问题解法集成的体例编纂成书的,全书按题目的应用范围与解题方法划分为“方田”、“粟米”、“衰分”等九章.《九章算术》中有这样一个问题:今有共买金,人出四百,盈三千四百;人出三百,盈一百.问人数,金价各几何?其大意是:假设合伙买金,每人出400钱,还剩余3400钱;每人出300钱,还剩余100钱.问人数、金价各是多少?如果设有x个人,那么可以列方程为400x﹣3400=300x﹣100.【分析】设有x个人,根据金的价钱不变,即可得出关于x的一元一次方程,此题得解.【解答】解:设有x个人,依题意,得:400x﹣3400=300x﹣100.故答案为:400x﹣3400=300x﹣100.【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.16.一项工程,甲单独做10天完成,乙单独做15天完成.两人合作,6天可以完成.【分析】甲、乙合作完成工程的时间=工作总量÷甲乙工效之和,没有工作总量,可设其为1.【解答】解:设工作量为1,甲乙的工作效率分别为、,故甲、乙合作完成工程的时间为1÷()=1÷=6天.故答案为:6.【点评】此题考查了一元一次方程的应用,解决问题的关键是找到所求的量的等量关系.当题中没有一些必须的量时,为了简便,可设其为1.17.在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为40?如果能,求出这三个数;如果不能,请说明理由.【分析】联系已知条件,设中间的数为x,则其它两个为x﹣7与x+7,再根据等量关系:三个日期之和能否为40,即可列出方程.【解答】解:设中间的数为x,其它两个为x﹣7与x+7,根据题意得:x﹣7+x+x+7=40,解得:x=,则不存在.【点评】此题解题关键在于表示出三个数,列出等量关系,即可得到解答.18.列方程解应用题十一期间,张老师从北京出发走京津高速到天津.去时在京津高速上用了1.2小时,返回时在京津高速上比去时多用18分钟,返回时平均速度降低了22千米/小时.求张老师去时在京津高速上开车的平均速度.【分析】设张老师去时在京津高速上开车的平均速度是x千米/小时,则返回时在京津高速上开车的平均速度是(x﹣22)千米/小时,根据路程=速度×时间结合往返路程相同,即可得出关于x的一元一次方程,解之即可得出结论.【解答】解:设张老师去时在京津高速上开车的平均速度是x千米/小时,则返回时在京津高速上开车的平均速度是(x﹣22)千米/小时,依题意,得:1.2x=(1.2+)(x﹣22),解得:x=110.答:张老师去时在京津高速上开车的平均速度是110千米/小时.【点评】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.19.列方程解应用题:某学校组织初一年级学生参加公益劳动在甲处劳动的有16人,在乙处劳动的有12人,现在另调20人去甲乙两处支援,使得在甲处劳动的人数比在乙处劳动的人数的2倍少6人,问应调往甲、乙两处各多少人?【分析】设应调往甲、乙两处的人数分别为x人和(20﹣x)人.根据甲处劳动的人数比在乙处劳动的人数的2倍少6人,构建方程即可解决问题.【解答】解:设应调往甲、乙两处的人数分别为x人和(20﹣x)人.由题意:16+x=2[12+(20﹣x)]﹣6,解得x=14,则20﹣x=6.答:调往甲、乙两处的人数分别为14人和6人.【点评】本题考查一元一次方程,解题的关键是理解题意,正确寻找等量关系构建方程解决问题,属于中考常考题型.20.一项工程,甲队单独施工需要15天完成,乙队单独施工需要9天完成.现在由甲队先工作3天,剩下的由甲、乙两队合作,还需要几天才能完成任务?【分析】设设还需x天才能完成任务,根据题意可得等量关系:甲的工作量+乙的工作量=总工作量,由等量关系可列出方程,解方程即可.【解答】解:设还需x天才能完成任务,根据题意得,解得x=4.5.答:甲、乙两队合作还需4.5天才能完成任务.【点评】此题主要考查了一元一次方程的应用,关键是表示出甲和乙的工作量,用到的公式是:工作量=工作效率×工作时间.21.今年,小楠和哥哥的年龄之和是21岁,小楠的年龄只有哥哥的一半,小楠和哥哥各多少岁?(用方程解)【分析】首先根据题意,设哥哥的年龄为x岁,则小楠的年龄为x岁,然后根据:哥哥的年龄+小楠的年龄=21,列出方程,求出x的值是多少,再用哥哥的年龄减去14,求出小楠的年龄即可.【解答】解:设哥哥的年龄为x岁,则小楠的年龄为x岁,则x+x=21,解得x=14.21﹣14=7(岁)答:今年小楠7岁,哥哥14岁.【点评】此题主要考查了一元一次方程的应用,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键.22.某商场从厂家购进100个整理箱,按进价的1.5倍进行标价.当按标价卖出80个整理箱后,恰逢元旦,剩余的部分以标价的九折出售完毕,所得利润共1880元,求每个整理箱的进价.【分析】可设每个整理箱的进价为x元,则标价为1.5x元,根据该商店获得的利润一共是1880元这个等量关系列方程求解.【解答】解:设每个整理箱的进价为x元,则标价为1.5x元,标价的九折为(1.5x×0.9)元.根据题意列方程,得:80(1.5x﹣x)+20(1.5x×0.9﹣x)=1880.解方程得:x=40.答:每个整理箱的进价为40元.【点评】考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.23.2020年9月的日历如图所示.(1)用1×3的长方形框出3个数,如果任意圈出一横行左右相邻的三个数,设最小的数为x,用含x的式子表示这三个数的和为3x+3;如果任意圈出一竖列上下相邻的三个数,设最小的数为y,用含y的式子表示这三个数的和为3y+21.(2)用一个2×2的正方形在此日历中框出4个数,被框住的4个数的和为84,则这四个数中最小的数为17;(3)用一个3×3的正方形框在此日历中框出9个数,在框出的9个数中,记前两行共6个数的和为a1,最后一行3个数的和为a2,若|a1﹣a2|=15,请求出正方形框中位于最。
【真题】宁德市中考数学试题含答案解析(Word版)

福建省宁德市中考数学试卷(解析版)一、选择题(本大题有10小题,每小题4分,共40分.每小题只有一个正确的选项,请在答题卡的相应位置填涂〕1.(4分)(•宁德)﹣3的绝对值是()A.3 B.C.D.﹣3【考点】15:绝对值.【分析】根据一个负数的绝对值是它的相反数即可求解.【解答】解:﹣3的绝对值是3.故选A.【点评】本题考查了绝对值,如果用字母a表示有理数,则数a 的绝对值要由字母a本身的取值来确定:①当a是正数时,a的绝对值是它本身a;②当a是负数时,a的绝对值是它的相反数﹣a;③当a是零时,a的绝对值是零.2.(4分)(•宁德)已知一个几何体的三种视图如图所示,则该几何体是()A.三棱柱B.三棱锥C.圆锥D.圆柱【考点】U3:由三视图判断几何体.【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解答】解:俯视图为圆的几何体为球,圆锥,圆柱,再根据其他视图,可知此几何体为圆锥.故选C.【点评】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力.3.(4分)(•宁德)如图,点M在线段AB上,则下列条件不能确定M是AB中点的是()A.BM=AB B.AM+BM=AB C.AM=BM D.AB=2AM【考点】ID:两点间的距离.【分析】直接利用两点之间的距离定义结合线段中点的性质分别分析得出答案.【解答】解:A、当BM=AB时,则M为AB的中点,故此选项错误;B、AM+BM=AB时,无法确定M为AB的中点,符合题意;C、当AM=BM时,则M为AB的中点,故此选项错误;D、当AB=2AM时,则M为AB的中点,故此选项错误;故选:B.【点评】此题主要考查了两点之间,正确把握线段中点的性质是解题关键.4.(4分)(•宁德)在△ABC中,AB=5,AC=8,则BC长不可能是()A.4 B.8 C.10 D.13【考点】K6:三角形三边关系.【专题】11 :计算题.【分析】根据三角形三边的关系得到3<BC<13,然后对各选项进行判断.【解答】解:∵AB=5,AC=8,∴3<BC<13.故选D.【点评】本题考查了三角形三边的关系:三角形任意两边之和大于第三边.5.(4分)(•宁德)下列计算正确的是()A.﹣5+2=﹣7 B.6÷(﹣2)=﹣3 C.(﹣1)=1 D.﹣20=1【考点】1G:有理数的混合运算;6E:零指数幂.【专题】11 :计算题;511:实数.【分析】各项计算得到结果,即可做出判断.【解答】解:A、原式=﹣3,不符合题意;B、原式=﹣3,符合题意;C、原式=﹣1,不符合题意;D、原式=﹣1,不符合题意,故选B【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.6.(4分)(•宁德)如图所示的分式化简,对于所列的每一步运算,依据错误的是()A.①:同分母分式的加减法法则B.②:合并同类项法则C.③:提公因式法 D.④:等式的基本性质【考点】6B:分式的加减法.【分析】根据分式的加减法法则计算即可.【解答】解:①:同分母分式的加减法法则,正确;②:合并同类项法则,正确;③:提公因式法,正确,④:分式的基本性质,故错误;故选D.【点评】此题考查了分式的加减,熟练掌握法则及运算律是解本题的关键.7.(4分)(•宁德)某创意工作室6位员工的月工资如图所示,因业务需要,现决定招聘一名新员工,若新员工的工资为4500元,则下列关于现在7位员工工资的平均数和方差的说法正确的是()A.平均数不变,方差变大B.平均数不变,方差变小C.平均数不变,方差不变D.平均数变小,方差不变【考点】W7:方差;W1:算术平均数.【分析】根据平均数、方差的定义即可解决问题.【解答】解:由题意原来6位员工的月工资平均数为4500元,因为新员工的工资为4500元,所以现在7位员工工资的平均数是4500元,由方差公式可知,7位员工工资的方差变小,故选B.【点评】本题考查方差的定义、平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题.8.(4分)(•宁德)如图,直线ι是一次函数y=kx+b的图象,若点A(3,m)在直线ι上,则m的值是()A.﹣5 B.C.D.7【考点】F8:一次函数图象上点的坐标特征.【分析】待定系数法求出直线解析式,再将点A代入求解可得.【解答】解:将(﹣2,0)、(0,1)代入,得:解得:,∴y=x+1,将点A(3,m)代入,得:+1=m,即m=,故选:C.【点评】本题主要考查直线上点的坐标特点,熟练掌握待定系数法求函数解析式是解题的关键.9.(4分)(•宁德)函数y=x3﹣3x的图象如图所示,则以下关于该函数图象及其性质的描述正确的是()A.函数最大值为2 B.函数图象最低点为(1,﹣2)C.函数图象关于原点对称D.函数图象关于y轴对称【考点】E6:函数的图象;P5:关于x轴、y轴对称的点的坐标;R6:关于原点对称的点的坐标.【专题】532:函数及其图像.【分析】观察函数图象,得出正确的表述即可.【解答】解:观察图形得:函数没有最大值,没有最低点,函数图象关于原点对称,故选C【点评】此题考查了函数的图象,关于x轴、y轴对称的点的坐标,以及关于原点对称的点的坐标,认真观察图形是解本题的关键.10.(4分)(•宁德)如图,在△ABC中,AB=AC,点D,E分别在边BC 和AC上,若AD=AE,则下列结论错误的是()A.∠ADB=∠ACB+∠CAD B.∠ADE=∠AEDC.∠CDE=∠BAD D.∠AED=2∠ECD【考点】KH:等腰三角形的性质.【分析】由三角形的外角性质、等腰三角形的性质得出选项A、B、C正确,选项D错误,即可得出答案.【解答】解:∵∠ADB是△ACD的外角,∴∠ADB=∠ACB+∠CAD,选项A正确;∵AD=AE,∴∠ADE=∠AED,选项B正确;∵AB=AC,∴∠B=∠C,∵∠ADC=∠ADE+∠CDE=∠B+∠BAD,∠AED=∠CDE+∠C,∴∠CDE+∠C+∠CDE=∠B+∠BAD,∴∠CDE=∠BAD,选项C正确;∵∠AED=∠ECD+∠CDE,∠ECD≠∠CDE,∴选项D错误;故选:D.【点评】本题考查了等腰三角形的性质、三角形的外角性质;熟练掌握等腰三角形的性质和三角形的外角性质是解决问题的关键.二、填空题(本大题有6小题,每小题4分,共24分.请将答案填入答题卡的相应位置)11.(4分)(•宁德)9月26日,我国自主设计建造的世界最大球面射电望远镜落成启用.该望远镜理论上能接收到13 700 000 000光年以外的电磁信号.数据13 700 000 000光年用科学记数法表示为 1.37×1010光年.【考点】1I:科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于1时,n是正数;当原数的绝对值小于1时,n是负数.【解答】解:13 700 000 000=1.37×1010,故答案为:1.37×1010.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.(4分)(•宁德)一元二次方程x(x+3)=0的根是x=0或﹣3.【考点】A8:解一元二次方程﹣因式分解法.【专题】11 :计算题.【分析】利用分解因式法即可求解.【解答】解:x(x+3)=0,∴x=0或x=﹣3.故答案为:x=0或x=﹣3.【点评】此题主要考查了利用因式分解的方法解一元二次方程,解题的关键是熟练进行分解因式.13.(4分)(•宁德)若矩形的面积为a2+ab,长为a+b,则宽为a.【考点】4H:整式的除法.【分析】根据多项式除以多项式的运算法则计算即可.【解答】解:矩形的宽=(a2+ab)÷(a+b)=a,故答案为:a.【点评】本题考查的是整式的除法,掌握多项式除以多项式的运算法则、因式分解是解题的关键.14.(4分)(•宁德)甲、乙两位同学参加物理实验考试,若每人只能从A、B、C、D四个实验中随机抽取一个,则甲、乙两位同学抽到同一实验的概率为.【考点】X6:列表法与树状图法.【专题】11 :计算题;543:概率及其应用.【分析】列表得出所有等可能的情况数,找出甲乙两位同学抽到同一实验的情况数,即可求出所求概率.【解答】解:列表如下:A B C DA AA BA CA DAB AB BB CB DBC AC BC CC DCD AD BD CD DD所有等可能的情况有16种,其中甲乙两位同学抽到同一实验的情况有AA,BB,CC,DD,4种情况,则P==,故答案为:【点评】此题考查了列表法与树状图法,概率=所求情况数与总情况数之比.15.(4分)(•宁德)将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合,当α最小时,点A运动的路径长为.【考点】O4:轨迹;R3:旋转对称图形.【分析】根据题意α最小值是60°,然后根据弧长公式即可求得.【解答】解:∵正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合,α最小值是60°,∴点A运动的路径长==.故答案为.【点评】本题考查了旋转对称图形,主要考查了学生的理解能力和计算能力,题目是一道比较好的题目,解此题的关键是求出α的最小值.16.(4分)(•宁德)如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,AC与OB交于点D (8,4),反比例函数y=的图象经过点D.若将菱形OABC 向左平移n个单位,使点C落在该反比例函数图象上,则n的值为2.【考点】G6:反比例函数图象上点的坐标特征;L8:菱形的性质;Q3:坐标与图形变化﹣平移.【分析】根据菱形的性质得出CD=AD,BC∥OA,根据D (8,4)和反比例函数y=的图象经过点D求出k=32,C点的纵坐标是2×4=8,求出C的坐标,即可得出答案.【解答】解:∵四边形ABCO是菱形,∴CD=AD,BC∥OA,∵D (8,4),反比例函数y=的图象经过点D,∴k=32,C点的纵坐标是2×4=8,∴y=,把y=8代入得:x=4,∴n=4﹣2=2,∴向左平移2个单位长度,反比例函数能过C点,故答案为:2.【点评】本题考查了菱形的性质,平移的性质,用待定系数法求反比例函数的解析式等知识点,能求出C的坐标是解此题的关键.三、解答题(本大题有9小题,共86分.请在答题卞的相应位置作答)17.(8分)(•宁德)化简并求值:x(x﹣2)+(x+1)2,其中x=﹣2.【考点】4J:整式的混合运算—化简求值.【专题】11 :计算题;512:整式.【分析】原式利用单项式乘以多项式,以及完全平方公式化简,去括号合并得到最简结果,把x的值代入计算即可求出值.【解答】解:原式=x2﹣2x+x2+2x+1=2x2+1,当x=﹣2时,原式=8+1=9.【点评】此题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解本题的关键.18.(8分)(•宁德)已知:不等式≤2+x(1)解该不等式,并把它的解集表示在数轴上;(2)若实数a满足a>2,说明a是否是该不等式的解.【考点】C6:解一元一次不等式;C4:在数轴上表示不等式的解集.【分析】(1)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.(2)根据不等式的解的定义求解可得.【解答】解:(1)2﹣x≤3(2+x),2﹣x≤6+3x,﹣4x≤4,x≥﹣1,解集表示在数轴上如下:(2)∵a>2,不等式的解集为x≥﹣1,而2>﹣1,∴a是不等式的解.【点评】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.19.(8分)(•宁德)如图,E,F为平行四边形ABCD的对角线BD上的两点,AE ⊥BD于点E,CF⊥BD于点F.求证:AE=CF.【考点】L5:平行四边形的性质;KD:全等三角形的判定与性质.【分析】由AE⊥BD,CF⊥BD,可得∠AEB=∠CFD=90°,又由四边形ABCD是平行四边形,可得AB∥CD,AB=CD,即可证得∠ABE=∠CDF,则可证得△ABE≌△CDF,继而证得结论.【解答】证明:∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°,在▱ABCD中,AB∥CD,AB=CD,∴∠ABE=∠CDF,在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AE=CF.【点评】此题考查了平行四边形的性质以及全等三角形的判定与性质.注意证得△ABE≌△CDF是关键.20.(8分)(•宁德)小明作业本中有一页被墨水污染了,已知他所列的方程组是正确的.写出题中被墨水污染的条件,并求解这道应用题.【考点】9A:二元一次方程组的应用.【专题】12 :应用题.【分析】被污染的条件为:同样的空调每台优惠400元,设“五一”前同样的电视每台x元,空调每台y元,根据题意列出方程组,求出方程组的解即可得到结果.【解答】解:被污染的条件为:同样的空调每台优惠400元,设“五一”前同样的电视每台x元,空调每台y元,根据题意得:,解得:,则“五一”前同样的电视每台2500元,空调每台3000元.【点评】此题考查了二元一次方程组的应用,弄清题中的等量关系是解本题的关键.21.(8分)(•宁德)某初中学校组织200位同学参加义务植树活动,每人植树的棵数在5至10之间.甲、乙两位同学分别调查了30位同学的植树情况,并将收集的数据进行了整理,绘制成统计表分别为表1和表2:表1:甲调查九年级30位同学植树情况统计表(单位:棵)每人植树情况78910人数36156频率0.10.20.50.2表2:乙调查三个年级各10位同学植树情况统计表(单位:棵)每人植树情况678910人数363116频率0.10.20.10.40.2根据以上材料回答下列问题:(1)表1中30位同学植树情况的中位数是9棵;(2)已知表2的最后两列中有一个错误的数据,这个错误的数据是11,正确的数据应该是12(3)指出哪位同学所抽取的样本能更好反映此次植树活动情况,并用该样本估计本次活动200位同学一共植树多少棵?【考点】W4:中位数;V5:用样本估计总体;V7:频数(率)分布表.【分析】(1)根据中位数定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数可得答案;(2)乙组调查了30人,根据人数和下面的频率可得错误数据为11,应为12;(3)根据样本要具有代表性可得乙同学抽取的样本比较有代表性,再利用样本估计总体的方法计算即可.【解答】解:(1)表1中30位同学植树情况的中位数是9棵,故答案为:9;(2)已知表2的最后两列中有一个错误的数据,这个错误的数据是11,正确的数据应该是12;(3)乙同学所抽取的样本能更好反映此次植树活动情况,(3×6+6×7+3×8+12×9+6×10)÷30×200=1680(棵),答:本次活动200位同学一共植树1680棵.【点评】此题主要考查了抽样调查,以及中位数,关键是掌握中位数定义,掌握抽样调查抽取的样本要具有代表性.22.(10分)(•宁德)如图,在边长为1的正方形组成的5×8方格中,△ABC 的顶点都在格点上.(1)在给定的方格中,以直线AB为对称轴,画出△ABC的轴对称图形△ABD.(2)求sin∠ABD的值.【考点】P7:作图﹣轴对称变换;T7:解直角三角形.【分析】(1)根据格点的特点作出点C关于直线AB的对称点D,连接AD,BD 即可;(2)根据格点的特点可知∠DBC=90°,再由轴对称的性质可知∠ABD=∠ABC=45°,据此可得出结论.【解答】解:(1)如图,△ABD即为所求;(2)由图可知,∠DBC=90°,∵点C与点D关于直线AB的对称,∴∠ABD=∠ABC=45°,∴sin∠ABD=sin45°=.【点评】本题考查的是作图﹣轴对称变换,熟知轴对称的性质是解答此题的关键.23.(10分)(•宁德)如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.(1)求证:直线DE是⊙O的切线;(2)若BF=10,sin∠BDE=,求DE的长.【考点】ME:切线的判定与性质;T7:解直角三角形.【分析】(1)先连接OD,根据∠ODB=∠DBE,即可得到OD∥AC,再根据DE⊥AC,可得OD⊥DE,进而得出直线DE是⊙O的切线;(2)先连接DF,根据题意得到∠F=∠BDE,在Rt△BDF中,根据=sinF=sin∠BDE=,可得BD=2,在Rt△BDE中,根据sin∠BDE==,可得BE=2,最后依据勾股定理即可得到DE的长.【解答】解:(1)如图所示,连接OD,∵OD=OB,∴∠ODB=∠OBD,∵BD平分∠OBC,∴∠OBD=∠DBE,∴∠ODB=∠DBE,∴OD∥AC,∵DE⊥AC,∴OD⊥DE,∵OD是⊙O的半径,∴直线DE是⊙O的切线;(2)如图,连接DF,∵BF是⊙O的直径,∴∠FDB=90°,∴∠F+∠OBD=90°,∵∠OBD=∠DBE,∠BDE+∠DBE=90°,∴∠F=∠BDE,在Rt△BDF中,=sinF=sin∠BDE=,∴BD=10×=2,∴在Rt△BDE中,sin∠BDE==,∴BE=2×=2,∴在Rt△BDE中,DE===4.【点评】本题主要考查了切线的判定以及解直角三角形的运用,解决问题的关键是作辅助线,构造等腰三角形以及直角三角形,解题时注意:经过半径的外端且垂直于这条半径的直线是圆的切线.24.(13分)(•宁德)在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.(1)如图1,当四边形ABCD为正方形时,求m,n的值;(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.【考点】LO:四边形综合题.【分析】(1)先判断出∠ADE=∠BAO,即可判断出△ABO≌△ADE,得出DE=OA=3,AE=OB,即可求出m;(2)先根据垂直的作法即可画出图形,判断出△ADE≌△CBF,得出CF=1,再判断出△AOB∽△DEA,即可得出OB=,即可得出结论;(3)先判断出BD⊥x轴时,求出AC的最小值,再求出DM=2,最后用勾股定理求出AE即可得出m.【解答】解:(1)如图1,过点D作DE⊥y轴于E,∴∠AED=∠AOB=90°,∴∠ADE+∠DAE=90°,∵四边形ABCD是正方形,∴AD=AB,∠BAD=90°,∴∠DAE+∠BAO=90°,∴∠ADE=∠BAO,在△ABO和△ADE中,,∴△ABO≌△ADE,∴DE=OA,AE=OB,∵A(0,3),B(m,0),D(n,4),∴OA=3,OB=m,OE=4,DE=n,∴n=3,∴OE=OA+AE=OA+OB=3+m=4,∴m=1;(2)画法:如图2,①过点A画AB的垂线l1,过点B画AB的垂线l2,②过点E(0,4),画y轴的垂线l3交l1于D,③过点D画直线l1的垂线交直线l2于点C,所以,四边形ABCD是所求作的图形,过点C作CF⊥x轴于F,∴∠CBF+∠BCF=90°,∵四边形ABCD是矩形,∴AD=BC,∠ABC=∠BAD=90°,∴∠ABO+∠CBF=90°,∴∠BCF=∠ABO,同理:∠ABO=∠DAE,∴∠BCF=∠DAE,在△ADE和△CBF中,,∴△ADE≌△CBF,∴DE=BF=n,AE=CF=1,易证△AOB∽△DEA,∴,∴,∴n=,∴OF=OB+BF=m+,∴C(m+,1);(3)如图3,由矩形的性质可知,BD=AC,∴BD最小时,AC最小,∵B(m,0),D(n,4),∴当BD⊥x轴时,BD有最小值4,此时,m=n,即:AC的最小值为4,连接BD,AC交于点M,过点A作AE⊥BD于E,由矩形的性质可知,DM=BM=BD=2,∵A(0,3),D(n,4),∴DE=1,∴EM=DM﹣DE=1,在Rt△AEM中,根据勾股定理得,AE=,∴m=,即:当m=时,矩形ABCD的对角线AC的长最短为4.【点评】此题是四边形综合题,主要考查了正方形的性质,矩形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,解(1)的关键是△ABO ≌△ADE ,解(2)的关键是△ADE ≌△CBF 和△AOB ∽△DEA ,解(3)的关键是作出辅助线,是一道中考常考题.25.(13分)(•宁德)如图,抛物线l :y=(x ﹣h )2﹣2与x 轴交于A ,B 两点(点A 在点B 的左侧),将抛物线ι在x 轴下方部分沿轴翻折,x 轴上方的图象保持不变,就组成了函数ƒ的图象. (1)若点A 的坐标为(1,0).①求抛物线l 的表达式,并直接写出当x 为何值时,函数ƒ的值y 随x 的增大而增大;②如图2,若过A 点的直线交函数ƒ的图象于另外两点P ,Q ,且S △ABQ =2S △ABP ,求点P 的坐标;(2)当2<x <3时,若函数f 的值随x 的增大而增大,直接写出h 的取值范围.【考点】HF :二次函数综合题.【分析】(1)①利用待定系数法求抛物线的解析式,由对称性求点B 的坐标,根据图象写出函数ƒ的值y 随x 的增大而增大(即呈上升趋势)的x 的取值; ②如图2,作辅助线,构建对称点F 和直角角三角形AQE ,根据S △ABQ =2S △ABP ,得QE=2PD ,证明△PAD ∽△QAE ,则,得AE=2AD ,设AD=a ,根据QE=2FD列方程可求得a 的值,并计算P 的坐标;(2)先令y=0求抛物线与x 轴的两个交点坐标,根据图象中呈上升趋势的部分,有两部分:分别讨论,并列不等式或不等式组可得h 的取值.【解答】解:(1)①把A (1,0)代入抛物线y=(x ﹣h )2﹣2中得:(x﹣h)2﹣2=0,解得:h=3或h=﹣1,∵点A在点B的左侧,∴h>0,∴h=3,∴抛物线l的表达式为:y=(x﹣3)2﹣2,∴抛物线的对称轴是:直线x=3,由对称性得:B(5,0),由图象可知:当1<x<3或x>5时,函数ƒ的值y随x的增大而增大;②如图2,作PD⊥x轴于点D,延长PD交抛物线l于点F,作QE⊥x轴于E,则PD∥QE,由对称性得:DF=PD,∵S△ABQ =2S△ABP,∴AB•QE=2×AB•PD,∴QE=2PD,∵PD∥QE,∴△PAD∽△QAE,∴,∴AE=2AD,设AD=a,则OD=1+a,OE=1+2a,P(1+a,﹣[(1+a﹣3)2﹣2]),∵点F、Q在抛物线l上,∴PD=DF=﹣[(1+a﹣3)2﹣2],QE=(1+2a﹣3)2﹣2,∴(1+2a﹣3)2﹣2=﹣2[(1+a﹣3)2﹣2],解得:a=或a=0(舍),∴P(,);(2)当y=0时,(x﹣h)2﹣2=0,解得:x=h+2或h﹣2,∵点A在点B的左侧,且h>0,∴A(h﹣2,0),B(h+2,0),如图3,作抛物线的对称轴交抛物线于点C,分两种情况:①由图象可知:图象f在AC段时,函数f的值随x的增大而增大,则,∴3≤h≤4,②由图象可知:图象f点B的右侧时,函数f的值随x的增大而增大,即:h+2≤2,h≤0,综上所述,当3≤h≤4或h≤0时,函数f的值随x的增大而增大.【点评】本题是二次函数的综合题,考查了利用待定系数法求二次函数的解析式、二次函数的增减性问题、三角形相似的性质和判定,与方程相结合,找等量关系,第二问还运用了。
最新北师大版小学数学三年级上册口算试题汇编(全册)
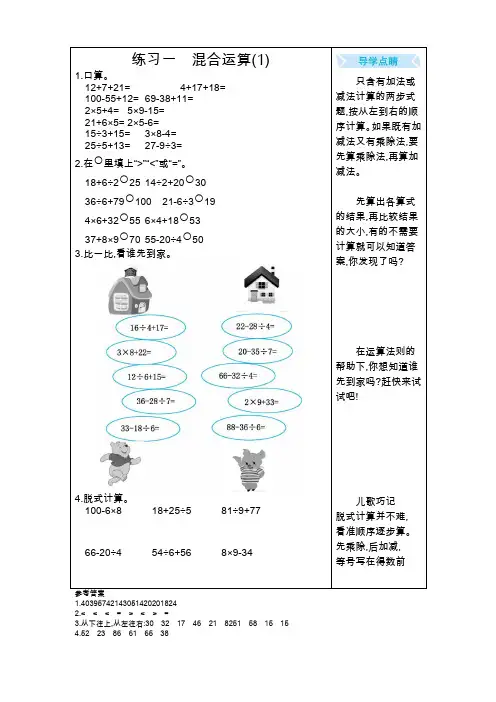
练习一混合运算(1)1.口算。
12+7+21= 4+17+18=100-55+12= 69-38+11=2×5+4= 5×9-15=21+6×5= 2×5-6=15÷3+15= 3×8-4=25÷5+13= 27-9÷3=2.在○里填上“>”“<”或“=”。
18+6÷2○25 14÷2+20○3036÷6+79○100 21-6÷3○194×6+32○55 6×4+18○5337+8×9○70 55-20÷4○503.比一比,看谁先到家。
4.脱式计算。
100-6×8 18+25÷5 81÷9+77 66-20÷4 54÷6+56 8×9-34只含有加法或减法计算的两步式题,按从左到右的顺序计算。
如果既有加减法又有乘除法,要先算乘除法,再算加减法。
先算出各算式的结果,再比较结果的大小,有的不需要计算就可以知道答案,你发现了吗?在运算法则的帮助下,你想知道谁先到家吗?赶快来试试吧!儿歌巧记脱式计算并不难, 看准顺序逐步算。
先乘除,后加减,等号写在得数前参考答案1.403957421430514202018242.< < < = > < > =3.从下往上,从左往右:30 32 17 46 21 8251 58 15 154.52 23 86 61 65 38练习二混合运算(2)1.口算。
9×(72-68)= 35÷(17-10)=(100-65)÷5= 20÷(18-13)=96-(27+18)= 10+(26-9)=(52-28)÷6= (27+54)÷9=65+(100-65)= (50+14)÷8=2.小蚂蚁搬米粒。
科途教育五年级数学每日一测9-25

科途教育五年级数学每日一测(9月25日)
姓名:得分:
1.把下面的算式转化成除数是整数的除法算式。
(1)4.96÷1.6=_______÷16 (2)1.35÷0.15=_______÷15
(3)2.7÷0.03=_______÷_______ (4)6÷0.012=_______÷_______
2.在下表中按要求填出商的近似数。
算式保留一位小数保留两位小数保留三位小数
2.89÷
3.6
50÷14
3.下面各数中哪些是有限小数?哪些是无限小数?分别填入指定的圈里。
4.把一个小数的小数点向右移动一位后,比原数多2.88,原数是()。
科途教育五年级数学每日一测(9月25日)
姓名:得分:
1.把下面的算式转化成除数是整数的除法算式。
(1)4.96÷1.6=_______÷16 (2)1.35÷0.15=_______÷15
(3)2.7÷0.03=_______÷_______ (4)6÷0.012=_______÷_______
2.在下表中按要求填出商的近似数。
算式保留一位小数保留两位小数保留三位小数
2.89÷
3.6
50÷14
3.下面各数中哪些是有限小数?哪些是无限小数?分别填入指定的圈里。
4.把一个小数的小数点向右移动一位后,比原数多2.88,原数是()。
2022年9月甘肃省甘南自治州数学必刷经典应用题测试三卷含答案解析

2022年9月甘肃省甘南自治州数学必刷经典应用题测试三卷含答案解析学校:________ 姓名:________ 考号:________ 得分:________一、应用题(精选120题,每题1分。
一、审题:在开始解答前,应仔细阅读题目,理解题目意思、数量关系、问题是什么,以及需要几步解答;二、注意格式:正确使用算式、单位和答语;三、卷面要求:书写时应使用正楷,尽量避免连笔,字迹稍大,并注意排版,确保卷面整洁;四、π一律取值3.14。
)1.六年级一共有125个学生,每个学生收集1.6千克废纸.现在已知每千克废纸可生产0.8千克再生纸,那么六年级学生收集的废纸一共可以生产多少千克再生纸?2.某车间共有60人,已知每人每天可加工甲种零件20个或乙种零件15个,并且两个甲种零件和一个乙种零件配成一套,要使得每天生产的零件配套,问加工甲、乙零件各有多少人?3.有甲乙两数,如果甲数增加1/5,它们的和是54;如果乙数减少1/5,它们的和是44.甲乙两数原来的和是多少?4.小华爸爸的年龄是爷爷的8/15,是小华的10/3.如果爷爷今年75岁,小华今年几岁?5.化肥厂要生产一批化肥,原计算每天生产3.6吨,25天可以完成,实际提前5天完成了任务,实际每天生产化肥多少吨?6.小红看一本200页的故事书已看页数和未看页数的比是3:2,已经看了多少页?7.红光饲养场养公鸡152只,母鸡624只,鸭子97只,问养鸡场养的鸡是鸭子的多少倍?8.王老师花了80元钱买了4盒钢笔作为奖品,每盒5枝,请你帮王老师算一算,每支钢笔多少钱?9.体育用品商店迎春节篮球促销:小明带了120元钱,最多能买多少个篮球?(买1~4个,每个26元;买5~9个,每个24元;买10个或10个以上,每个20元.)10.植树节那天,班主任老师带领本班学生40人去栽树,老师一人栽8棵树,男生每人栽4棵树,女生每人栽3棵树,总共栽150棵,班上有男、女生各多少人?11.小华看一本252页的故事书,已经看了12天,每天看15页,剩下的要在4天内看完,剩下的平均每天看多少页?12.一项工程,甲、乙、丙三人合作需13天完成,如果丙休息2天,乙就要多做4天,或者由甲、乙两人合作多做1天,那么这项工程由甲独做,需要多少天.13.王老师带120元钱去买课外读物,《故事会》每本3元,能买多少本《故事会》?如果《智能开发题典》每本8元,能买多少本《智能开发题典》?14.为庆祝元旦,同学们做了27朵红花和18朵黄花.每5朵扎成一束,同学们一共做了多少束花?15.小区前有一个边长是15米的正方形花坛,如果把花坛的一组对边分别增加3米,另一组对边长度不变,这个花坛的面积会增加多少?16.小华第一次月考语文成绩是90分,数学成绩是语文的0.9倍,英语成绩是数学的1.1倍,小华第一次月考英语成绩是多少?(得数保留整数)17.一辆客车和一辆货车从相距96千米的A、B两地同时出发,同向而行,货车在前,客车在后.5小时后两车相距的路程缩短为16千米.客车每小时行78千米,货车每小时行多少千米?18.老王从甲城骑自行车到乙城去办事,每小时骑15千米,回来时改骑摩托车,每小时骑33千米,骑摩托车比骑自行车少用1.8小时,求甲、乙两城间的距离.19.甲、乙两辆汽车分别从A、B两地同时相对开出,在甲车离A地30千米处与乙车相遇.相遇后两车继续前进,分别到达A、B两地后又立即返回,途中在离B地21千米处,甲车又与乙车相遇.求A、B两地的距离.20.六年级一班有男生23人,女生22人,全班学生占六年级学生总数的3/10.六年级有学生多少人?(用方程和算术方法解)21.甲、乙车间共有工人204人,若从甲车间调5人到乙车间,这时,甲车间还比乙车间多4人.问甲、乙两车间原来各有多少人?22.用彩色气球布置联欢会场.按“一个蓝球两个黄球三个红球”的顺序依次重复串成一排,请问第22个球是什么颜色?23.一块平行四边形的地,底边长120米,高约为60米,在这块地里种小麦,平均每平方米可收小麦0.56千克,这块地共收割小麦多少千克?24.六年级三班星期五的出勤率是98%,出勤人数与缺勤人数比是多少?25.有一批货物重720千克.我们打算用3辆车2次运完这批货物,平均每辆车每次运货多少千克?26.实验小学建一条长100米、宽12米的直跑道.现将60立方米的煤渣铺在跑道上,可以铺多厚?27.小亚看一本470页的书,前8天每天看25页,剩下的计划每天看30页,小亚看完这本书还要多少天?28.甲仓存粮40吨,乙仓存粮62吨,甲仓每天存入4吨,乙仓每天存入9吨,几天后乙仓存粮是甲仓的2倍?29.食堂运进一批煤,第一次用去50吨,第二次用去70吨,两次正好用去了这批煤的1/4.这批煤有多少吨?30.东方体育用品商店,第一天卖出足球148个,第一天上午卖出76个,下午卖出84个,共收人32340元.(1)平均每天卖出足球多少个?(2)平均每天营业额是多少元?(3)平均每个足球多少元?31.六年级有学生250人,其中2/5是女生,而男生的10%、女生的15%体育课考试未达标,求六年级体育达标率是多少?32.某商店7天卖出苹果840千克,梨630千克,平均每天卖出的苹果比梨多多少千克?33.同学们举行1分钟跳绳比赛,军军跳了80下,兰兰跳的是军军的58,又是欢欢的5/8,兰兰和欢欢各跳了多少下?34.某工厂男、女职工共155人,其中男职工比女职工的3/7少5人,这个厂男、女职工各多少人?35.一块长方形菜地,长是33米,宽是27米,围着这个菜地的四周跑4圈是多少米?36.王老师买了25套运动服,上衣63元,裤子47元,服装店做活动,买10套及其以上,每套便宜10元.在10套的基础上,每增加10套,每套再降价2元.算算王老师一共花了多少钱?37.一个长方体的表面积是67.92平方分米.底面的面积是19平方分米.底面周长是17.6分米,这个长方体的体积是多少立方分米.38.甲镇与乙镇相距138千米,张、王二人骑自行车分别从两镇同时出发,相向而行.张每小时骑行13千米,王每小时骑行12千米,王在途中因修车耽误1小时,然后继续行进.两人从出发到相遇经过几小时?39.一辆汽车从甲地开往乙地用了7小时,前3.5小时平均每小时行43.4千米,后3.5小时平均每小时行46.2千米.甲乙两地之间的公路长多少千米?(得数保留整数)40.一个书架,第一层放书34本,第二层放书38本,第三层放书43本,第四层放书42本,按这种做法17个这样的书架大约能放书多少本?41.大华机械厂原计划每天生产75台机床,30天可以完成任务,实际每天生产的台数比原计划多1/3.几天就完成了原计划的任务?42.15个工人7天可以完成一项任务,现要提前2天完成,如果每人工作效率一样,需要增加多少工人?43.一块梯形麦田,上底是65米,下底是87米,高是50米,如果每平方米麦田收小麦0.85千克,这块麦田可收多少千克小麦?44.师徒二人5天合做零件1320个,已知师傅每天做的个数是徒弟的1.2倍,师傅和徒弟每天各做多少个?45.童乐幼儿园共有150本书,其中90本按4:5分给小班和中班,小班分得多少本书?46.六年级进行计算比赛,共20题,规定算对一题得5分,错一题扣2分.晓华得了79分,他做对了多少题?47.某小区的停车场有电动自行车和三轮摩托车共40辆,若两种车共有95个轮子,那么电动自行车和三轮摩托车各有多少辆?48.一组学生参加电脑考试,3名女生共得分258分,5名男生平均每人得分90.8分,这组学生的平均成绩是多少分?49.客货两车从相距300千米的甲、乙两地同时相向开出,客车6小行完全程,货车8小车行完全程,两辆车出发后几小时相遇?50.甲乙两辆汽车同时从东西两站相对开出,甲车每小时行48千米,乙车每小时行46千米,5小时相遇东西两站相距多少千米?51.一个三角形的面积是40平方米,底是5米,它的高是多少米?52.商店运来37箱可乐和13箱果汁,每箱都是24瓶,一共有多少瓶?53.妈妈带小明坐长途汽车去看奶奶,早上8时出发,中午12时到达,汽车每小时行85千米.从小明家到奶奶家有多少千米?54.小明看一本故事书,第一天看了全书的1/10多10页,第二天看了全书的1/4少20页,还剩下270页,全书一共有多少页?55.商店里有气球73个,每9个扎一束,共扎多少束?还剩多少个?56.一列火车每小时行68千米,另一列火车每小时行76千米,这两列火车分别从甲乙两站同时相对开出,行了5/6小时后还相距两站之间铁路长的1/4.甲乙两站之间的铁路长多少千米?57.育才小学六年级有男生262人,女生185人.男生人数比实验小学六年级男生的1.5倍少8人,女生人数比实验小学六年级女生的1.8倍多5人.实验小学六年级男生,女生各有多少人?(用方程回答,并解设.)58.一块长方形的菜地,长是5.6米,宽是长的一半,这块菜地的周长是多少米,面积是多少平方米.59.甲车5小时行驶172千米,乙车8小时行驶263千米,哪辆车的速度快一些?60.五年级(3)班进行跳绳测验,第1组8名同学1分钟跳绳成绩如下.81 145 137 129 117 141 138 92 (1)请求出这组数据的中位数和平均数.(2)用哪个数代表这组数据的一般水平更合适?61.师徒两人一共生产了680个零件,师傅生产的零件个数比徒弟的2倍还多20个,徒弟所做的是师傅的几分之几?62.甲、乙两位老板分别以同样的价格购进一种时装,乙购进的套数比甲多1/5,然后甲、乙分别按获得80%和60%的利润定价出售.两人都全部售完后,甲仍比乙多获得一部分利润,这部分利润又恰好够他再购进这种时装9套,乙原来购进这种时装多少套?63.炯炯看一本书,前3天看了63页,按这样的速度,再看20天可以看完全书,这本书共有几页?64.一条人行道长20m,宽1.5m.如果要在这条人行道上铺上一种上底10cm,下底20cm,高5cm的梯形砖,需要多少块这样的砖?65.王老师给学生们买奖品共用去了103元,其中买了25支单价是3.4元的钢笔,剩下的钱正好买30支铅笔,每支铅笔的价格是多少?66.五年级参加植树活动.一班43人,共植树256棵;二班41人,平均每人植树4棵.(1)五年级平均每班植树多少棵?(2)你还能提出什么问题?67.甲乙两车同时同地同向而行,3小时后甲车在乙车前方15千米处;如果两车同时同地背向而行,2小时后相距150千米.甲乙两车每小时各行多少千米?68.甲、乙两车共运一批水泥,运完时,甲车运了总数的2/5多14吨,比乙车多运1/4,这批水泥共多少吨?69.某公司发行10000张对奖券,其中一等奖10名,二等奖300名,三等奖1000名.小张买了一张,问他获奖的可能性是多少,获一等奖的可能性是多少?70.实验小学要为四、五年级的同学每人购买一本价格是15元的作文辅导书,已知四年级有234人,五年级有228人,两个年级一共需要多少钱?71.一批货物,第一天运走100吨,第二天运走150吨,还剩下这批货物的40%没有运走,这批货物有多少吨(用方程解)72.有两个仓库共有粮食95吨,现运出甲仓库粮食的3/5,运出乙仓库粮食的40%,这时两仓库剩下的粮食同样多.甲、乙两个仓库原来各有粮食多少吨?73.小美买了15个黄气球,每个1.20元.小帅买了25个红气球,共花去了37.50元.(1)哪种气球便宜些,便宜多少元?(2)他们一共花去多少元?74.工厂要加工1200个零件,计划20天完成,实际3天就完成了20%,照这样计算,可提前几天完成任务?75.做一个长是8分米,宽是5分米,高是22分米的木柜,把它的外表涂上油漆,如果每平方分米用油漆0.04千克,涂这个木柜要用多少千克的油漆?76.两辆汽车同时从甲、乙两地相对开出,在离中点7.2千米处相遇.相遇时,甲车行了全程的46%.甲、乙两地相距多少千米?77.商店运进红茄克衫和黑茄克衫共85件,黑茄克衫的件数比红茄克衫的2倍还多13件.运来的这两种茄克衫各多少件?78.甲乙两辆汽车分别从相距63千米处的矿山与堆料场运料同时相向开出,时速分别为40千米和50千米,如果不计装卸时间,那么,两车往返运料自出发到第三次相遇共经过多少时间?79.甲数的1/6与乙数的1/5相等,如果甲数是108,则乙数是多少?80.筑路队铺一条公路,第一周铺了全长的1/8,第二周铺了900米,还剩4700米没有铺.这条公路全长多少米?81.甲、乙两地相距984千米,一辆汽车从甲地开往乙地,每小时行82千米,需要几小时才能到达乙地?82.王叔叔乘摩托车从甲地到乙地开会,如果每小时行35千米,要晚到1小时;如果每小时行50千米,就可以提前0.5小时到达,甲、乙两地的距离是多少千米.83.上海到南京的水路长392千米,甲、乙两船从两港同时开出,相向而行,从上海出发的船每小时行21千米,从南京开出的船每小时行28千米.求经过几小时两船在途中相遇?84.师徒两人要生产840个机器零件,开始4小时共生产了280个,照这样计算,要完成剩下的零件还需要多少小时?(用四种不同方法)85.小明早上8时30分上学,11时30分放学,中午休息3个小时,下午2时30分上学,4时30分放学,小明每天在学校的时间是多少?86.甲、乙、丙三人投资办一个商店.甲投资总数的20%,余下的由乙、丙承担,且乙比丙多投资20%,已知甲比丙少投资了9万元.乙投资多少万元?87.一块三角形菜地共收蔬菜420千克,它的底是12米,高是5米,平均每平方米收蔬菜多少千克?88.甲乙两城铁路长1098千米,一列火车于2月29日晚上10时从甲城开往乙城,在3月1日上午7时到达,这列火车每小时行多少千米?89.用铁皮做一个无盖的长方体水箱。
2022年9月山东省聊城市小升初数学内招思维应用题专项模拟三卷含答案解析

2022年9月山东省聊城市小升初数学内招思维应用题专项模拟三卷含答案解析学校:________ 姓名:________ 考号:________ 得分:________一、应用题(精选120题,每题1分。
一、审题:在开始解答前,应仔细阅读题目,理解题目意思、数量关系、问题是什么,以及需要几步解答;二、注意格式:正确使用算式、单位和答语;三、卷面要求:书写时应使用正楷,尽量避免连笔,字迹稍大,并注意排版,确保卷面整洁;四、π一律取值3.14。
)1.师、徒二人共做一批零件.师傅每天做48个,徒弟两天做68个,6天完成任务,这批零件共有多少个?2.甲乙两辆汽车分别从A、B两城同时相向而行,早上8时出发,下午1时两车相遇.已知甲车每小时行驶52千米,乙车每小时行驶78千米.这两辆汽车共行驶多远?3.在一个长50厘米,宽40厘米的长方体玻璃缸中,有一块棱长为20厘米的正方体铁块,铁块完全浸没,这时水深40厘米,若把铁块取出,缸中水深多少厘米?4.某工程由甲、乙两队合做24天完成,由乙、丙两队合做30天完成,由甲、丙两队合做40天完成,那么甲队单独做需要多少天完成.5.一个长方形的周长是24厘米,长是8厘米,宽是多少厘米.6.甲乙两港相距200千米,一艘轮船以每小时32千米的速度从甲港开往乙港,行了一段时间后,距乙港还有72千米,这艘船行了多少小时?7.甲、乙两车分别从两地相对开出,甲车每小时行86千米,乙车每小时行78千米,相遇时,相遇地点距两地的中点24千米.两地相距多少千米?8.两架模型飞机用不同长度的金属线缚住,绕同一个定点水平地旋转,方向相反,里面的一架飞机转一圈需要30秒,外边的需要60秒,从它们第一次相互错过到第二次相错,所需的时间是多少秒?9.农场有一块长200米,宽150米的长方形试验田,平均每公顷产稻谷13.8吨,这块试验田一共产稻谷多少吨?10.某校六年级一共有120名学生,每人至少参加电脑兴趣小组和科技兴趣小组中的一个,其中3/4的同学参加电脑兴趣小组,7/12的同学参加科技兴趣小组.两种兴趣小组都参加的学生一共有多少名?11.一件衣服若卖100元,可赚钱25%,若卖60元,则要亏本百分之几?12.甲乙两辆卡车同时从某地出发,运送一批货物到距离165千米的农场.甲车比乙车早到0.8小时,当甲车到达时,乙车还距离农场24千米,甲车行驶全程用了多少小时.13.王军在做一道加法计算题时,把一个加数个位上的3看成了8,十位上的9看成了5,结果得387,正确的结果应该是多少?14.爱民粮站有甲乙两个粮仓,原来乙仓存米的吨数是甲仓的2/3,从甲仓运出了40吨后,甲仓剩下的吨数与原来乙仓存米的吨数的比变为5:6.原来甲乙两仓各存米多少吨?15.仓库里有一批大米,第一天运出全部大米的一半少2吨,第二天运出余下的一半多3吨,这时仓库里还剩下12吨,仓库里原有大米多少吨?16.一辆客车和一辆货车同时从甲城开往乙城.已知客车平均每小时行驶89千米,货车平均每小时行驶71千米,4小时后两车相距多少千米?17.一个长方体汽油箱长5分米,宽2.5分米,高4分米。
初三数学计算题练习试题集
初三数学计算题练习试题答案及解析1.计算:【答案】2-.【解析】分别进行零指数幂、绝对值的化简、负整数指数幂等运算,然后合并.试题解析:原式=2+1-1+2--2=2-.【考点】1.实数的运算;2.零指数幂;3.负整数指数幂.2.计算:.【答案】﹣7.【解析】分别用平方根定义,负指数幂法则,绝对值的代数意义,零指数幂法则进行计算即可得到结果.试题解析:原式=3﹣4×4+5+1=3﹣16+5+1=﹣7.【考点】1.实数的运算2.零指数幂3.负整数指数幂.3.解不等式:并将它的解集在数轴上表示出来.【答案】x≥5,在数轴上表示解集见解析.【解析】按照解一元一次不等式的步骤解一元一次不等式,不等式的解集在数轴上表示的方法:>,≥向右画;<,≤向左画,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.试题解析:解:去分母,得解得:x≥5.它的解集在数轴上表示为:【考点】1.解一元一次不等式;2.在数轴上表示不等式的解集.4.计算:.【答案】2014【解析】原式第一项利用平方根定义化简,第二项利用绝对值的代数意义化简,第三项利用零指数幂法则计算,计算即可得到结果.试题解析:原式=5-3-1+2013=2014.【考点】实数的运算;零指数幂.5.计算:【答案】1.【解析】针对特殊角的三角函数值,负整数指数幂,绝对值,零指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果.原式=.【考点】1.实数的运算;2.特殊角的三角函数值;3.负整数指数幂;4.绝对值.6.计算:(1),(2)【答案】(1);(2).【解析】(1)分别求出值,再化简;(2)化成最简二次根式,再进行计算.试题解析:(1);(2).【考点】1.负指数次幂2.特殊角的三角函数3.绝对值4.零次幂5.二次根式混合运算.7.计算:6tan30°++(-1)2012+.【答案】2【解析】解:原式=6×-2+1+1=2.8.计算:【答案】-1.【解析】分别进行立方根、零指数幂、特殊角的三角函数值、二次根式的化简等运算,然后按照实数的运算法则计算即可.试题解析:原式==-1.考点: 1.实数的运算;2.零指数幂;3.立方根;4.特殊角的三角函数值.9.计算:【答案】.【解析】根据零指数幂,负指数幂的意义,再由算术平方根的非负性得到,再进行化简即可.试题解析:.【考点】二次根式化简.10.解方程:=0【答案】,.【解析】将方程左边分解因式,化成两个一元一次方程,求解即可.试题解析:∵∴即:x+1=0,x-9=0解得:,.考点: 解一元二次方程----分解因式法.11.计算: .【答案】1.【解析】根据锐角三角函数、二次根式的意义进行计算即可求出答案.试题解析:考点: 实数的混合运算.12.计算:.【答案】.【解析】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,首先根据特殊角的三角函数值进行化简,然后根据实数运算法则进行计算得出答案.试题解析:解:原式===.【考点】1、特殊角的三角函数值;2、实数的综合运算.13.计算:【答案】.【解析】牢记特殊角的三角函数值是解答本题的关键,然后根据实数运算法则计算出结果即可.试题解析:原式=.【考点】特殊角的三角函数值.14.计算:【答案】.【解析】此题考查了实数的运算、二次根式的运算、幂的运算及绝对值的化简.解答此类型题目要注意:一是要弄清运算顺序;二是要熟练每部分的运算法则;三是计算过程要认真.本题先同时计算幂、绝对值及二次根式的化简,最后合并同类项即可得出答案.试题解析:解:原式,.【考点】1、二次根式的化简;2、实数的运算.15.已知:,求的值.【答案】.【解析】设比值为k,用k表示出x、y、z,然后代入比例式进行计算即可得解.试题解析:设,则x=2k,y=4k,z=5k,∴.【考点】1.比例的性质;2. 待定系数法的应用.16.计算:【答案】解:原式=。
统计学计算题
统计学计算题1. 某企业生产的A、B两种产品的产量及产值资料如下:产品总产值(万元)产量的环比发展速度(%)基期报告期A B 400600580760110100★标准答案:产品名称产量单位产品成本基期报告期基期报告期甲1000 1200 10 8乙5000 5000 4 4.5丙1500 2000 8 7要求:计算三种产品的成本总指数以及由于单位产品成本变动使总成本使总成本变动的绝★标准答案:产品成本指数=由于单位产品成本变动使总成本使总成本变动的绝对额;(-)=461000-48000=-1900(万元)3. 某企业本月分三批购进某种原材料,已知每批购进的价格及总金额如下:购进批次价格(元/吨)总金额(元)一二三200190205160001900028700★标准答案:4. 某厂三个车间一季度生产情况如下:第一车间实际产量为200件,完成计划95%;第二车间实际产量280件,完成计划100%;第三车间实际产量650件,完成计划105%,请★标准答案:平均计划完成程度☆考生答案:解:三个车间总的计划产量=200/95%+280/100%+650/105%=1110(件)三个车间总的实际产量=200+280+650=1130(件)三个车间产品产量的平均计划完成程度=1130/1110*100%=101.8%商品销售额(万元)报告期价格比基期增(+)或减(-)的%基期报告期甲乙丙5070809010060+10+8-4合计200 250 —试计算价格总指数和销售量总指数。
★标准答案:企业计划产量(件)计划完成(%)实际一级品率(%)甲乙丙50034025010310198969895根据资料计算:(1)产量计划平均完成百分比;★标准答案:☆考生答案:解:(1)计划平均完成百分比=(500*1.03+340*1.01+250*0.98)/(500+340+250)*100%=101.2%(2)平均一级品率=(500*1.03*0.96+340*1.01*0.98+250*0.98*0.95)/(500*1.03+340*1.01+250*0.98)*100%=96.4%7. 某商店主要商品价格和销售额资料如下:商品计量单位价格本月销售额(万元)上月本月甲乙丙件台套100506011048631102437.8★标准答案:8. 某市场上某种蔬菜早市每斤0.25元,中午每斤0.2元,晚市每斤0.1元,现在早、中、★标准答案:.平均价格H==0.158(元)☆考生答案:解:购买的总斤数=1/0.25+1/0.2+1/0.1=19(斤)平均价格=(1+1+1)/19=0.16(元/斤)9. 某商店出售某种商品第一季度价格为6.5元,第二季度价格为6.25元,第三季度为6元,第四季度为6.2元,已知第一季度销售额3150元,第二季度销售额3000元,第三季度销★标准答案:☆考生答案:解:平均价格=(3150+3000+5400+4650)/(3150/6.5+3000/6.25+5400/6+4650/6.2)=6.20(元)10. 某厂生产某种机床配件,要经过三道工序,各加工工序的合格率分别为95.74%,★标准答案:=0.9474=94.74%企业名称2006年职工人数2005年工业总产值(万元)2006年工业总产值2006年全员劳动生产率(元/人)2006年工业总产值为2005年的(%)各企业和全公司劳动生产率为乙企业的倍数人数(人)比重(%)计划(万元)实际(万元)完成计划(%)(甲)(1)(2) (3)(4)(5)(6)(7)(8)(9)甲300 900 1500 1800乙3000 3000 130.0 260.0丙450 12.0 1200 1800 300.0合计3750 100.0试根据上表已知数据计算空格中的数字(保留一位小数并分别说明⑵、⑹、⑻、⑼栏是何★标准答案:季度2000 2001 2002 2003 20041 580 610 660 700 8502 190 200 220 230 3203 230 250 260 290 3104 620 670 710 730 780★标准答案:销售量(万斤)价格(元)2002年2003年2002年2003年甲乙丙30140100361601001.801.901.502.02.201.60试计算:(1)三种商品的销售额总指数(2)三种商品的价格综合指数和销售量综合指数★标准答案:月份 1 2 3 4 5 6产量(件)单位成本(元) 200073300072400071300073400069500068★标准答案:按农户年收入分组(元)行政村数(个)各组农户占农户总数(%)2000以下2000~4000 4000~6000 6000~8000 8000~10000 10000以上23669481015302512合计30 100 ★标准答案:☆考生答案:解:平均收入=(8%*1000+10%*3000+15%*5000+30%*7000+25%*9000+12%*11000)/100%=4910(元)16. 甲乙两企业生产同种产品,1月份各批产量和单位产品成本资料如下:甲企业乙企业单位产品成本(元)产量比重(%)单位产品成本(元)产量比重(%)第一批第二批1.0 10 1.2 301.1 20 1.1 30第三批 1.2 70 1.0 40★标准答案:☆考生答案:解:甲企业的平均单位成本=(1.0*10%+1.1*20%+1.2*70%)/100%=1.16(元)乙企业的平均单位成本=(1.2*30%+1.1*30%+1.0*40%)/100%=1.09(元)因为1.16>1.09所以甲企业的单位成本更高日期9月30日10月31日11月30日12月31日在业人口(万人)a 劳动力资源人口(万人)b280680 285685280684270686★标准答案:18. 某自行车车库4月1日有自行车320辆,4月6日调出70辆,4月18日进货120辆,4月26日调出80辆,直至月末再未发生变动,问该库4月份平均库存自行车多少辆?★标准答案:因为数据取得的资料是连续时点数列,但资料间隔不等,故采取加权平均法。
初中数学周周清检测题
2013级周周清检测题(一) 计划检测时间 9月12日 星期三一、填空题:(每小题4分,共40分) C1、当x 时,5-x 在实数范围内有意义。
当x 时,62-x 在实数范围内没有意义。
C2、在式子1x 、x (x>0)、42、-2、x y +中.是二次根式的是 。
B3、当x 时,1242-++x x 在实数范围内有意义. 当x 时,2x 有意义。
B4、若式子2)6(--x 有意义,那么x 的值是 。
C5、填空:(1x +)2(x ≥0)= 。
=-2)101(C6、在实数范围内分解下列因式: 94-x = = 。
B7、若2a =a ,则a 是 数。
2a >a ,则a 是 数。
C8.若m 12是一个正整数,则正整数m 的最小值是__ ______. C9、24= × = ; 2216y x = × × = 。
A10、化简xx 2-的结果 。
二、选择题:(每小题民2分,共10分)C1.下列式子中,是二次根式的是( ) A .x B .37 C .-7 D .xG2.下列式子中,不是二次根式的是( )A .1x B .16 C .8 D .4C3、下列各式中3a 、21b -、22a b +、220m +、144-,二次根式的个数是( ).A .4B .3C .2D .1C4、数a 没有算术平方根,则a 的取值范围是( ). A .a>0 B .a ≥0 C .a<0 D .a=0C5、下列各等式成立的是( ). A .45×25=85 B .53×42=205C .43×32=75D .53×42=206三、解答题:(1小题每题4分,2、3、4题每题10分,共50分) C1、计算:(1)9×27 (2)16×8(3)63×102 (4))16()25(-⨯-(5)a 5·ay 51C2、若1a ++1b -=0,求2a +b 的值。
2022年北京中考数学28题详解(通用6篇)
2022年北京中考数学28题详解(通用6篇)【篇一】2022年北京中考数学28题详解2022年南京市中考数学第26题详解已知函数(m为常数).(1)该函数的图像与某轴公共点的个数是()A.0B.1C.2D.1或2(2)求证:不论m为何值,该函数的图象的顶点都在函数的图象上;(3)当-2≤m≤3时,求该函数的图象的顶点纵坐标的取值范围.解:(1)△====.∵≥0,有两个实数根,∴抛物线与某轴的公共点的个数是1或2.∴选D.(2)∵顶点坐标为,把代入,得,∴不论m为何值,该函数的图象的顶点都在函数的图象上;(3)∵顶点的纵坐标为,设.画出z关于m的函数的图象如答图,结合图象可得:当m=-1时,z有最小值是0;当m=-2时,;当m=3时,.∴当-2≤m≤3时,求该函数的图象的顶点纵坐标z的取值范围是0≤z≤4..【篇二】2022年北京中考数学28题详解27.(本题10分)(原创)如图,在平面直角坐标系某Oy中,A点在某轴的正半轴上,C点在y轴的正半轴上,矩形OABC的顶点B在第一象限内,D点在AB边上,BD=3AD,连接OB,作直线CD,又知OB=10,tan∠AOB=.(1)求直线CD的解析式;(2)动点P从O点出发,沿OA以每秒2个单位长的速度向终点A匀速运动,同时,动点Q从A点出发,沿AB以每秒1个单位长的速度匀速运动到D点后,又以每秒6个单位长的速度继续向终点B匀速运动.连接PQ、OQ,设P、Q运动的时间为t(秒),△POQ的面积为S(平方单位),求S与t之间的函数关系式,并直接写出自变量t的取值范围;(3)在(2)的条件下,连接CP、CQ,问是否存在这样的t值,使得∠OPC=∠OQC?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.28.(本题10分)(原创)已知AB为⊙O的直径,CD为⊙O的一条弦,顺次连接AC、CB、BD、DA.(1)当∠ACD=30°(如图a)时,求证:CA+CB=2CD;(2)当∠ACD=45°(如图b)时,线段CA、CB、CD间的数量关系为;(3)在(2)的条件下,在⊙O上移动点C(保持AB与CD相交),过A点作AE⊥CD,交射线CB于点E,以B为顶点另作一个∠DBF,使得∠DBF=∠DBA,设直线FB与直线AE交于点G,若CD=6,AB=4,求EG的长.27.(本题10分)(原创)如图,在平面直角坐标系某Oy中,直线y=-2某+b与某轴的正半轴交于点A,与y轴的正半轴交于点B,D点在OA上,OD=2DA,C点在y轴的负半轴上,直线CD与AB交于点E().(1)求直线CD的解析式;(2)过点D作y轴的平行线,交直线AB于点F,过点F作某轴的平行线,交y轴于点G.动点P从D点出发,沿某轴的负方向以每秒1个单位长的速度匀速运动,连接GP,作PQ⊥GP,交直线CD于点Q,设动点P运动的时间为t(秒),△DPQ的面积为S(平方单位)(S≠0),求S与t之间的函数关系式,并直接写出自变量t的取值范围;(3)在(2)的条件下,将△DPQ沿某轴翻折得到△DPQ′.求t为何值时,以O、G、Q、Q′为顶点的四边形是平行四边形?请写出你的求解过程.28.(本题10分)(原创)在等腰梯形ABCD中,AD∥BC,AB=DC,AE为梯形的一条高,且AD=AE,点M在射线CD上,连接AM,作∠BAM的平分线交BC边于点N.(1)当∠B=60°,点M在CD边上(如图a)时,求证:AM-DM=BN;(2)当∠B=45°,点M在CD边的延长线上(如图b)时,线段AM、DM、BN之间的数量关系为;(3)在(2)的条件下,连接MN,过点A作AP⊥MN,垂足为点P,若点N为BC边中点,AB=24,求线段AP的长.27.(本题10分)如图,在平面直角坐标系某Oy中,直线y=-3某+6与某轴的正半轴交于点C,与y轴的正半轴交于点B,直线BA与某轴的负半轴交于点A,AB=5OC,射线BN∥某轴.(1)求直线AB的解析式;(2)动点P从B点出发,沿射线BN以每秒1个单位长的速度匀速运动,同时,动点Q从A点出发,沿线段AB以每秒1个单位长的速度匀速运动,当Q点到达终点B时,P点随之停止运动.作PM∥BC,交某轴于点M,连接PQ、QM,设点P、Q运动的时间为t(秒),△PQM的面积为S(平方单位),求S与t之间的函数关系式,并直接写出自变量t的取值范围;(3)在(2)的条件下,作△PQM的外接圆⊙R,连接RP、RQ,是否存在这样的时刻t,使得PR⊥QR?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.28.(本题10分)(原创)已知,△ABC为钝角等腰三角形,AB=AC,90°【篇三】2022年北京中考数学28题详解燕山1.2022年5月1日起,北京市全面推行生活垃圾分类.下面图标分别为厨余垃圾、可回收物、有害垃圾、其他垃圾,其中不是轴对称图形的是A.B.C.D.2.为解决延期开学期间全市初高三学生的学习需求,提升学生的实际获得,北京市教委打造了“答疑平台”,全市144000名初高三学生全部纳入在线答疑辅导范围.将144000用科学记数法表示应为A.144某8215c811412e29425321dc8966f83cfe.pngB.14.4某4378eeb5bb839cc6fae5f03c6e96a5e2.pngC.1.44某2d3b07f4be78707110251174655f1734.pngD.1.44某296ba7d1266a91ea6c8dca8791ba101c.png3.方程组f15ed60fb587748cb9fd400f08d15250.png的解为A.37e09fa13de1e24bed634f5cbfa7306e.pngB.61f0feca1cd02d244c 2561a7122764c7.pngC.fcbe841324d4c0b76394c5ac39a7e062.pngD.0e47 bc878bf3708407fea53bb1c6bc29.png4.在数轴上,点A,B分别表示实数a,b,将点A向左平移1个单位长度得到点C,若点C,B关于原点O对称,则下列结论正确的是A.a+b=1B.a+b=-1C.a-b=1D.a-b=-15.若一个多边形的内角和是720°,则该多边形的边数为A.4B.5C.6D.76.若a+b=1,则代数式77c60cc0ff1dc8adc508061f81dcebe9.png的值为A.-2B.-1C.1D.2word/media/image12_1.png7.如图,矩形ABCD中,BC=2AB,点E在边AD上,EF⊥BD于点800618943025315f869e4e1f09471012.png.若EF=1,则DE的长为word/media/image16.gif8.为了解高校学生对5G移动通信网络的消费意愿,从在校大学生中随机抽取了1000人进行调查,下面是大学生用户分类情况统计表和大学生愿意为5G套餐多支付的费用情况统计图(例如,早期体验用户中愿意为5G套餐多支付10元的人数占所有早期体验用户的50%).下列推断中,不合理的是A.早期体验用户中,愿意为5G套餐多支付10元,20元,30元的人数依次递减B.后期用户中,愿意为5G套餐多支付20元的人数最多C.愿意为5G套餐多支付10元的用户中,中期跟随用户人数最多D.愿意为5G套餐多支付20元的用户中,后期用户人数最多房山1.2022年9月25日正式通航的北京大兴国际机场,为4F级国际机场、大型国际枢纽机场.距北京大兴国际机场官方微博显示,2022年北京大兴国际机场共完成旅客吞吐量313.82万人次,保障航班约21000架次,货邮吞吐量7375.53吨,航班放行正点率达96%以上.将21000用科学记数法表示应为()A.2.1某104B.21某103C.0.21某105D.2.1某1032.一副直角三角板有不同的摆放方式,下图中满足∠α与∠β相等的摆放方式是()word/media/image17.gif3.实数word/media/image18_1.png在数轴上对应点的位置如图所示,正确的结论有()A.word/media/image19_1.pngB.word/media/image20_1.pngC.word/m edia/image21_1.pngD.word/media/image22_1.pngword/media/image23_1.png4.下列四种网络运营商的徽标中,符合轴对称图形特征的为()word/media/image24.gif5.如果2b35a3dbf01fe16271bfcc9772338edc.png,那么代数式aeb27a0ba990da2af9dc7be59c05d7bf.png的值是()A.6c8000f03d933531c86f3487fd602aea.pngB.22417f146ced89939510e 270d4201b28.pngC.8e246249212cc10c74a8511416f22695.pngD.56.若一个多边形每个内角均为120°,则该多边形是()A.五边形B.六边形C.七边形D.八边形7.某景区乘坐缆车观光游览的价目表如下:某班20名同学一起来该景区游玩,都想坐缆车观光游览,且每辆缆车必须坐满,那么他们的费用最低为()A.530元B.540元C.580元D.590元8.在关于n的函数6d1b27eab46a299b54141246a7a17cd3.png中,n 为自然数.当n=9时,S<0;当n=10时,S>0.则当S的值最小时,n的值为()A.3 B.4 C.5 D.6延庆1.最近,科学家发现了一种新型病毒,其最大直径约为0.00012mm,将0.00012用科学记数法表示为A.1.2某10-3B.1.2某10-4C.1.2某104D.12某103word/media/image24.gif2.下列各组图形中,△A"B"C"与△ABC成中心对称的是A.B.C.D.3.下列立体图形的主视图、左视图、俯视图都一样的是word/media/image32.gifA.B.C.D.4.若分式word/media/image33_1.png有意义,则某的取值范围是A.某>-2B.某<-2C.某=-2D.某≠-25.数轴上A,B,C,D四点中,有可能在以原点为圆心,以word/media/image35_1.png为半径的圆上的点是word/media/image36.gifA.点AB.点BC.点CD.点D6.如图所示,△ABC中AB边上的高线是A.线段DAB.线段CAC.线段CDD.线段BD7.下列实数中,无理数的个数是A.1个B.2个C.3个D.4个平谷(A)word/media/image41_1.png(B)word/media/image42_1.png(C)wor d/media/image43_1.png(D)word/media/image44_1.png2.剪纸是我们国家特别悠久的民间艺术形式之一,它是人们用祥和的图案企望吉祥、幸福的一种寄托.下列剪纸图形中,既是轴对称图形又是中心对称图形的是(A)(B)(C)(D)3.n边形的内角和为1800°,则该n边形的边数为(A)12(B)10(C)8(D)64.若已知实数word/media/image53_1.png满足54f3c04f73e389a5d71716b89b201d9e.png,且0e472acdb931cf142097e4ffd2094f43.png则word/media/image53_1.png 在数轴上的位置符合题意的是(A)(B)word/media/image60_1.pngword/media/image61_1.png(C)(D)5.已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作弧DE,交射线OB于点F,word/media/image62_1.png连接CF;(2)以点F为圆心,CF长为半径作弧,交弧DE于点G;(3)连接FG,CG.作射线OG.根据以上作图过程及所作图形,下列结论中错误的是(A)∠BOG=∠AOB(B)若CG=OC则∠AOB=30°(C)OF垂直平分CG(D)CG=2FG6.如果e17f4ddc54483e0b9a16a1da68db283d.png,那么代数式db13d4b4b5a09a2f7fa5e31d2fa8ca95.png的值为(A)3(B)2(C)-3(D)-2word/media/image65_1.png7.如图是6某6的正方形网格,点A,B均在格点上.如果点C也在此正方形网格的格点上,且∠ACB=90°,则满足条件的点C共有(A)3个(B)4个(C)6个(D)8个8.某校在“爱护地球,绿化祖国”的活动中,组织同学开展植树造林活动,为了了解同学的植树情况,学校抽查了初一年级所有同学的植树情况(初一年级共有两个班),并将调查数据整理绘制成如下所示的部分数据尚不完整的统计图表.下面有四个推断:word/media/image66_1.pngword/media/image67.gifa的值为20;②初一年级共有80人;③一班植树棵树的众数是3;④二班植树棵树的是中位数2.其中合理的是(A)①③(B)②word/media/image68.gif(C)②③(D)②③word/media/image68.gif密云1.下列四个角中,有可能与70°角互补的角是()word/media/image69.gifA.B.C.D.A.d8d2626a779b0ee4419bd83095f907bf.pngB.3541c7d6983e819c0d 87d0e28da0a239.pngC.de84f1e00b35586514bffba28b150aa2.pngD.a078 bf04f5307b524a3fdadd520a9db3.png3.下列各式计算正确的是()A.b0625a24ede12d5eda48c0693762b0b7.pngB.1964ffbe8459feb115 098be070c864e1.pngC.word/media/image76_1.pngD.71d83128396949f3 ce88202ab190d64f.png4.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是()word/media/image78.gifA.科克曲线B.笛卡尔心形线C.赵爽弦图D.斐波那契螺旋线5.实数a,b在数轴上的对应点的位置如图所示,下列关系式不成立的是()A.a-5>b-5B.-a>-bC.6a>6bD.a-b>06.如图,点A,B是正方体上的两个顶点,将正方体按图中所示方式展开,则在展开图中B点的位置为()A.62aaced6e784a6a5b344b43850f98398.pngB.15733ef796e744976ebf2e9dc5de8942.pngC.dfde61a1dcb68e1a930467c6b2608dd7.pngD.893113b209aa658544a5854d0437eb3f.png7.《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉;下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子;有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆打多少斗谷子?设上等稻子每捆打某斗谷子,下等稻子每捆打y斗谷子,根据题意可列方程组为()A.word/media/image85_1.pngB.word/media/image86_1.pngC.word/media/image87_1.pngD.word/media/image88_1.png8.据统计表明,2022年中国电影总票房高达642.7亿元,其中动画电影发展优势逐渐显现出来.下面的统计表反映了六年来中国上映的动画电影的相关数据:2022—2022年中国动画电影影片数量及票房统计表(以上数据摘自《中国电影产业市场前瞻与投资战略规划分析报告》)根据上表数据得出以下推断,其中结论不正确的是()A.2022年至2022年,国产动画影片数量均低于进口动画影片数量B.2022年与2022年相比,中国动画电影的数量增加了50%以上C.2022年至2022年,中国动画电影的总票房逐年增加D.2022年,中国动画电影的总票房占中国电影总票房的比例不足20%顺义1.港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一,它是世界总体跨度最长的跨海大桥,全长55000米.数字55000用科学记数法表示为(A)f433bb044d0ee577e789736a7d75425c.png(B)88880f520cd6b18b7a1cf361366b039b.png(C)912ecdd998f8ddc56a8bcf237eb31555.png(D)d4e9d2c8fa9654abf272be4a089ca8d9.png2.下列有关医疗和倡导卫生的图标中,是轴对称图形的是(A)(B)(C)(D)3.将一副三角板和一个直尺按如图所示的位置摆放,则778d5baff6f3ac33a43e3e2219499957.png的度数为word/media/image95_1.png(A)bd76c0b409f1a0fcf2abea803939c12a.png(B)b7a6631bddb55eab0d8befede9d703a9.png(C)e9034b9ae9085146a646c42feee5c6aa.png(D)6541ec7ba981890c096df172e6aac928.png4.在数轴上,点A表示数a,将点A向右平移4个单位长度得到点B,点B表示数b.若fb3cfe756580898afb3c87dadfe30259.png,则a的值为(A)1b6b3e808a3cc205dfcbe4e119f59025.png(B)02e3c1cfd03c87011d3b438dee3b08c4.png(C)768a1ed60006f190faf91d734c1c8236.png(D)c4ca4238a0b923820dcc509a6f75849b.png5.箱子内装有除颜色外均相同的28个白球及2个红球,小芬打算从箱子内摸球,以毎次摸到一球后记下颜色将球再放回的方式摸28次球.若箱子内每个球被摸到的机会相等,且前27次中摸到白球26次及红球1次,则第28次摸球时,小芬摸到红球的概率是(A)93b05c90d14a117ba52da1d743a43ab1.png(B)9ef51575e73ac02eeac7df8736c37717.png(C)56e7f66d849d2a6c1a430d38565c2e35.png(D)34ee0d866a9b16250a8dfa9301299290.png6.已知直线2db95e8e1a9267b7a1188556b2022b33.png及直线2db95e8e1a9267b7a1188556b2022b33.png外一点44c29edb103a2872f519ad0c9a0fdaaa.png.word/media/image109_1.png如图,(1)在直线l上取一点A,连接PA;(2)作PA的垂直平分线MN,分别交直线l,PA于点B,O;(3)以O为圆心,OB长为半径画弧,交直线MN于另一点Q;(4)作直线PQ.根据以上作图过程及所作图形,下列结论中错误的是(A)△OPQ≌△OAB(B)PQ∥AB(C)22912788714140982b652c0f009a4e79.png(D)若PQ=PA,则c2b0992e59a7183ac0dc59f155fc21d5.png7.用三个不等式46fa7900cc397f3a4b3fa2e72d6885e7.png,fabe23b3e4440c679ce522e2d61894b9.png,ba6cccca3c80ed7bba7e436749d8ccb2.png中的两个不等式作为题设,余下的一个不等式作为结论组成一个命题,组成真命题的个数为(A)0(B)1(C)2(D)38.小明、小聪参加了56fb78758d1a23ade50990a4cac3f3af.png跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图.图1图2根据图中信息,有下面四个推断:①这5期的集训共有56天;②小明5次测试的平均成绩是11.68秒;③从集训时间看,集训时间不是越多越好,集训时间过长,可能造成劳累,导致成绩下滑;④从测试成绩看,两人的最好成绩都是在第4期出现,建议集训时间定为14天.所有合理推断的序号是(A)①③(B)②④(C)②③(D)①④石景山1.2022年5月7日,我国自主创新研发的“东方红3号科学考察船”通过挪威DNV-GL船级社权威认证,成为全球最大静音科考船.“东方红3”是一艘a35fe7f7fe8217b4369a0af4244d1fca.png吨级深远海科考船,具有全球无限航区航行能力,可持续航行3f74a886c7f841699690962c497d4f30.png海里.将3f74a886c7f841699690962c497d4f30.png用科学记数法表示应为2.下列图形中,既是轴对称图形,又是中心对称图形的是word/media/image125.gif3.实数0cc175b9c0f1b6a831c399e269772661.png,92eb5ffee6ae2fec3ad71c777531578f.png,4a8a08f09d37b73795649038408b5f33.png在数轴上的对应点的位置如图所示,则不正确的结论是word/media/image129_1.pngword/media/image134_1.png4.如图,e182ebbc166d73366e7986813a7fc5f1.png平分002f58096ac00d40cc067e16309d1d0a.png,点3a3ea00cfc35332cedf6e5e9a32e94da.png在b86fc6b051f63d73de262d4c34e3a0a9.png上,2c9b682412689d6723e3b31653b5774c.png∥4144e097d2fa7a491cec2a7a43 22f2bc.png交e182ebbc166d73366e7986813a7fc5f1.png于点dfcf28d0734569a6a693bc8194de62bf.png,若23feaad050adb7608a4ef22734d519af.png,则87afeff17c2c7b55909953cde98281b0.png的度数为5.若一个多边形的内角和为7949f6991b8814602c3f1c3b57a58ccb.png,则该多边形的边数是word/media/image154.gif6.在下列几何体中,其三视图中没有矩形的是word/media/image155_1.png7.如图,点7fc56270e7a70fa81a5935b72eacbe29.png,9d5ed678fe57bcca610140957afab571.png,0d61f8370cad1d412f80b84d143e1257.png,f623e75af30e62bbd73d6df5b50bb7b5.png在⊙f186217753c37b9b9f958d906208506e.png上,弦e182ebbc166d73366e7986813a7fc5f1.png的延长线与弦f85b7b377112c272bc87f3e73f10508d.png的延长线相交于点3a3ea00cfc35332cedf6e5e9a32e94da.png.用①b86fc6b051f63d73de262d4c34e3a0a9.png是⊙f186217753c37b9b9f958d906208506e.png的直径,②686c1bd4d32a079e0c38401880ee31bb.png,③835227675faad41c1cac6cb6074af3a5.png中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为8.某地区经过三年的新农村建设,年经济收入实现了翻两番(即是原来的word/media/image171_1.png倍).为了更好地了解该地区的经济收入变化情况,统计了该地区新农村建设前后的年经济收入构成结构如下:建设前年经济收入结构统计图建设后年经济收入结构统计图word/media/image172.gif则下列结论中不正确的是丰台word/media/image173.gif1.2022年初,新型冠状病毒引发肺炎疫情.一方有难,八方支援,危难时刻,全国多家医院纷纷选派医护人员驰援武汉.下面是四家医院标志的图案部分,其中是轴对称图形的是齐鲁医院华西医院湘雅医院协和医院(A)(B)(C)(D)2.据报道,位于丰台区的北京排水集团槐房再生水厂,是亚洲规模最大的一座全地下再生水厂,日处理污水能力600000立方米,服务面积137平方公里.将600000用科学记数法表示为(A)0.6某105(B)0.6某106(C)6某105(D)6某106 3.正六边形的每个内角度数为4.下列几何体的主视图和俯视图完全相同的是圆锥圆柱三棱柱正方体word/media/image154.gif(A)(B)(C)(D)5.在数轴上,点A,B分别表示数a,3,点A关于原点O的对称点为点C.如果C为AB的中点,那么a的值为(A)-3(B)-1(C)1(D)3word/media/image174_1.png6.在⊙O中按如下步骤作图:.(1)作⊙O的直径AD;(2)以点D为圆心,DO长为半径画弧,交⊙O于B,C两点;(3)连接DB,DC,AB,AC,BC.根据以上作图过程及所作图形,下列四个结论中错误的是(A)∠ABD=90°(B)∠BAD=∠CBD(C)AD⊥BC(D)AC=2CDword/media/image175.gif7.某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如下表:下列三种说法:(1)厨余垃圾投放错误的有400t(2)估计可回收物投放正确的概率约为a487fed1aa3d86a23dce8cb5f4ec0cde.png(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普word/media/image179.gif其中正确的个数是(A)0(B)1(C)2(D)3(A)当a21+a51+a61=3时,选择B1这本书(B)当a22+a52+a62【篇四】2022年北京中考数学28题详解2022年数学中考热身基础训练题(28)时间:30分钟你实际使用分钟一、精心选一选1.在平面直角坐标系中,位于第三象限的点是()A.B.C.D.2.当时,的值为()A.0B.C.D.3.在中,,,则的值为()A.B.C.D.4.若方程的两个实数根为,则的值是()A.3B.C.D.5.一辆汽车由地匀速驶往相距300千米的地,汽车的速度是100千米/小时,那么汽车距离地的路程(千米)与行驶时间(小时)的函数关系用图象表示为()6.用换元法解分式方程,若设,则原方程可化为关于的整式方程是()A.B.C.D.7.李明设计了下面四种正多边形的瓷砖图案,用同一种瓷砖可以平面镶嵌的是()A.①②④B.②③④C.①③④D.①②③8.如图,点是外一点,为的一条割线,且,交于点,若,则长为()A.B.C.D.9.已知二次函数,其中满足和,则该二次函数图象的对称轴是()A.B.C.D.10.如图,已知矩形纸片,,,以为圆心,长为半径画弧交于点,将扇形剪下围成一个圆锥,则该圆锥的底面半径为()A.1B.C.D.二、细心填一填11.函数中,自变量的取值范围是.12.一组数据8,6,8,7,4,3的平均数和众数依次是.13.如图,若的半径为11cm,的半径为6cm,圆心距是13cm,则两圆的公切线长是.14.请你写出一个反比例函数的解析式,使函数值在每个象限内随自变量的增大而减小.这个解析式可以是.(写出一个符合条件的即可)15.如图,是半圆的直径,是上两点,,则的度数是.16.某城建部门计划在城市道路两旁栽1500棵树,原计划每天栽棵,考虑到季节、人员安排等因素,决定每天比原计划多栽50棵,最后提前5天完成任务,则可以列出的分式方程是.17.如图,已知的半径是10,弦长为16.现要从弦和劣弧组成的弓形上画出一个面积最大的圆,所画出的圆的半径为.18.已知一元二次方程有两个不相等的实数根,则的最大整数值为.19.如图,已知圆内接五边形中,对角线是的直径,,是的中点,则的面积是.20.如图,扇形的圆心角为,四边形是边长为1的正方形,点分别在,上,过点作交的延长线于点,那么图中阴影部分的面积为.三、开心用一用21.计算:答案:一、选择题(每小题3分,共30分)题号2345678910答案CBDABDABBC二、填空题(每小题3分,共30分)11.12.6,813.12cm14.(符合条件均给分)如15.16.17.218.019.420.三、(第21、22题各8分,第23题10分,共26分)21.解:原式【篇五】2022年北京中考数学28题详解2022年北京市高级中学学校招生考试1、选择题(本题共16分,每小题2分)1、右图是某几何体的三视图,该几何体是()A、圆柱B、圆锥C、三棱柱D、长方体2、2022年6月23日,北斗三号最后一颗全球组网卫星从西昌卫星发射中心发射升空,6月30日成功定点于距离36000公里的地球同步轨道,将36000用科学计数法表示应为()A、B、C、D、3、如图,AB和CD相交于点O,则下列结论正确的是()A、B、C、>D、2【篇六】2022年北京中考数学28题详解。
