平差习题2
测量平差所有习题
第二章思考题及习题1.精度的含义是什么?2.为什么不用真误差来衡量观测值的精度而用中误差?3.试比较中误差、平误差作为衡量精度的标准的优缺点。
4.为什么要研究极限误差,极限误差与真误差有什么关系?5.角度的精度可否用相对误差来衡量?为什么?6.平差的原则是什么?观测值的平均误差和中误差。
8.某一三角网共有三十个三角形,在相同条件下进行了观测,由于观测有误差,三角形内角之和就不等于180度,这样就得到了三十个三角形的角度闭合差W(真误差),按绝对值的大小排列如下:+0.5″,-0.6″,+0.8″,-1.0″,+1.4″,+1.7″,-1.8″,+2.1″,+2.5″,-2.7″,+2.8″,+3.0″,+3.2″,-3.6″,+4.2″,-4.8″,-5.3″,+5.9″,-6.1″+6.8″,-6.9″,+7.5″,+8.5″,-9.1″,-9.8″,+11.3″,+12.9″,-14.6″,+18.8″-21″。
①试根据该组误差分析偶然误差的特性;②求三角形内角之和的中误差;③分析最大的偶然误差与中误差的关系;④求三角网中每个角的测角中误差。
9.对三十米的一条边进行了二十次丈量,每次丈量的中误差为±0.02米,另外用同样的方法对60米的一条边进行丈量,其每次丈量的中误差为±0.03米,试问这两条边丈量结果,哪一条边的精度高?10.对30º的一个角观测了十次,每次观测的中误差为±5″。
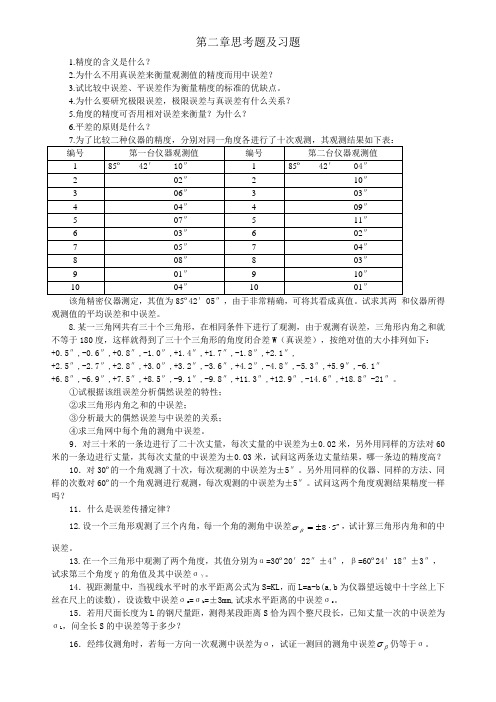
另外用同样的仪器、同样的方法、同样的次数对60º的一个角观测进行观测,每次观测的中误差为±5″。
试问这两个角度观测结果精度一样吗?11.什么是误差传播定律?12.设一个三角形观测了三个内角,每一个角的测角中误差58''⋅±=βσ,试计算三角形内角和的中误差。
13.在一个三角形中观测了两个角度,其值分别为α=30º20′22″±4″,β=60º24′18″±3″,试求第三个角度γ的角值及其中误差σγ。
平差大全---指导与习题
2.某单位购买了一台新水准仪,经过检测其精度知道,用该仪器单程测量1km 的高差中误 1. 间接平差公式汇编,设观测值的协因数阵为LL Q ,求未知参数平差值的协因数阵。
3.差是5mm 。
该单位接到一个工程任务,其中之一是需要在指定位置建立一个水准点,要求该水准点的高程中误差不大于10mm 。
经过勘查,距该水准点附近有两个高级已知水准点,一个相距约10km ,另外一个相距约20km ,现在两已知水准点之间经过新建的水准点布设一条附合路线,问用新购的水准仪进行单程测量是否满足精度要求。
(使用间接平差解答)。
3.最简单形式的单导线严密平差问题:等精度观测三个角,测角中误差"5=βσ,观测了两条边,cm cm S S 0.2,5.221==σσ,使用间接平差列观测方程并线性化。
4. 在直角多边形中(如图),测得三边之长为21L L 、及3L ,试列出该图的误差方程式。
5.在三角形ABC中,测得不等精度观测值如下:,1,3.11205111="'︒=P β2,9.21088822="'︒=P β,2,4.28314033="'︒=P β,若选取直接观测值的平差值为未知参数,试按照间接平差计算各角的平差值。
6.如图所示的直角三角形ABC 中,已知AB=100.00m (无误差),测得边长AC 和角度A ,得观测值为ml 470.1151=,,5559292"'︒=l 其中误差分别为,51mm l ±=σ,42"±=l σ试按间接平差法求三角形ABC中的平差值。
7. 图4.3中,C B A 、、是已知点, 21P P 、为待定点,网中观测了12个角度和6条边长。
已知测角中误差为5.1''±,边长测量中误差为0.2±cm ,起算数据及观测值分别列表于表4.1和表4.2。
平差试卷——精选推荐

平差试卷试卷⼀⼀、简答题(每题5分,共15分)1、何谓系统误差?测量中是如何处理的?2、误差椭圆与误差曲线是否⼀致?如何根据误差椭圆来求任意⽅向位差?3、⾃由⽹平差⽅法有哪些?秩亏⾃由⽹平差中,秩亏数如何确定的?秩亏⾃由⽹平差准则是什么?⼆、填空题(每空3分,共15分)1、常⽤衡量向量的绝对精度指标是();常⽤()作为衡量向量的相对精度指标。
2、设有同精度独⽴观测值12,L L 两个⾓值,且构成函数12sin sin ABL y S L =。
式中AB S 为已知边长,认为⽆误差。
测⾓中误差 1.2σ''=。
则该函数的中误差为()。
3、已知某待定点观测的测⾓中误差2βσ''=,测边中误差2s mm σ=。
已知点⾄待定点距离为185⽶。
则该点的点位中误差为()。
4、观测向量[]12TL L L =的权阵为4223LL P ??=,则1L P =( )。
三、下图所⽰测量控制⽹,试按要求完成如下⼯作:1、下图条件平差时,条件式个数?条件式类型?每种类型各建⽴其中⼀个,⾮线性需要线性化。
(10分)2、下图间接平差时,参数个数?误差⽅程个数?类型?每种类型各建⽴⼀个,⾮线性需要线性化。
(10分)四、已知某⼀个待定点的控制⽹中,设该点坐标为参数,采⽤间接平差得到法⽅程为:6.01 3.02 6.00xy --= ??3.02 1.58 3.40xy -++= 已计算得到单位权中误差估值0? 1.2σ''=。
求:(1)该点的误差椭圆参数;(2)该点的点位误差。
(共15分)五、下图所⽰的⽔准⽹中,已知⾼程为135.000A H m =。
⾼差观测数据列于下表中。
试任选⼀种平差法:(1)求待定点⾼程的平差值;(2)求第⼆段⾼差平差值的协因数;(3)求待定点⾼程平差值的中误差。
(共20分)名称 1 2 3 ⾼差观测值(m ) 6.885 6.890 -6.892 ⽔准路线长(km ) 428六、证明:测量平差中根据最⼩⼆乘准则可以求得参数以及观测值的平差值的唯⼀解。
测量平差试题

B测量平差基础一、 正误判断(正确“T ”,错误“F ”每题1分,共10 分)。
1.已知两段距离的长度及中误差分别为128.286m ±4.5cm 与218.268m ±4.5cm ,则其真误差与精度均相同( )。
2.如果X 与Y 的协方差0xy σ=,则其不相关( )。
3.水准测量中,按公式i icp s =(i s 为水准路线长)来定权,要求每公里高差精度相同( )。
4.可用误差椭圆来确定待定点与待定点之间的某些精度指标( )。
5.在某一平差问题中,观测数为n ,必要观测数为t ,参数个数u <t 且不独立,则该平差问题可采用附有参数的条件平差的函数模型。
( )。
6.由于同一平差问题采用不同的平差方法得到的结果不同,因此为了得到最佳平差结果,必须谨慎选择平差方法( )。
7.根据公式()222220cos sin 0360E F θσθθθ=+≤≤得到的曲线就是误差椭圆( )。
8.对于特定的平面控制网,如果按间接平差法解算,则误差方程的个数是一定的( )。
9.对于同一个观测值来说,若选定一定权常数0σ,则权愈小,其方差愈小,其精度愈高( )。
10.设观测值向量,1n L 彼此不独立,其权为()1,2,,i P i n = ,12(,,,)n Z f L L L = ,则有22211221111Z n nf f f P L P L P L P ⎛⎫⎛⎫⎛⎫∂∂∂=+++ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ ( )。
二、填空题(每空2分,共24分)。
1、设对某三角网进行同精度观测,得三角形角度闭合差分别为:3秒,-3秒,2秒,4秒,-2秒,-1秒,0秒,-4秒,3秒,-2秒,则测角中误差为 秒。
2、某平差问题函数模型)(I Q =为⎪⎪⎩⎪⎪⎨⎧=-=--=+-+=--0ˆ03060515443121x v v v v v v v v ,则该函数模型为平差方法的模型;=n ,=t ,=r ,=c ,=u 。
测量平差答案Ch2-Ch4

测量平差第二章.题目:为确定某航摄像片中一块梯形的面积,用卡规量得上底边长为1l 下底边长为2l ,高为h ,并用求积仪量得面积是S ,若设梯形面积为未知参数~X ,试按附有参数的条件平差法列出平差函数模型。
解答:带有参数的条件平差法,其方程个数的解求为:4,3,1, 1.n t r n t u ===-==方程个数为2c r u =+=~~~~12102l l h s ⎛⎫+-= ⎪⎝⎭ ~~0s x -=.题目:在如图2-7所示水准网中,A 为已知水准点,1P 、2P 、3P 为待定点,观测高差向量为12345TL h h h h h ⎡⎤=⎣⎦ ,现选取1P 、2P 、3P 点高程为未知参数123TX X X X ⎡⎤=⎣⎦ ,试列出间接平差的函数模型。
解答:~~11~~22~~33~~~423~~~5215,3,2,3A A A n t r n t u h X H h X H h X H h X X h X X ===-===-=-=-=-=-2321P.题目:在下图所示的水准网中,.A B 点为已知水准点,12.P P 点为待定水准点,观测高差为1234...h h h h 。
若三段高差为未知参数,12=X X X TX ⎡⎤⎣⎦ 3,,。
试按附有限制条件的间接平差函数模型。
解答:4,2,2,5n t r u t s r u ===>=+=112232431230A Bh X hX h X h X H X X X H ====+++-= 测量平差第三章.题目:试确定各图形按条件平差时的条件式个数及其条件方程式。
解答:()a 条件方程式个数:422r =-=条件方程式为:1430A B H h h h H +++-= 1230A H h h h H +++-=()b 条件方程式个数:844r =-=条件方程式为:424583872761650000h h h h h h h h h h h h +-=+-=+-=+-=()c 条件方程式个数为:1284r =-=条件方程式为:()d 条件方程式个数为:431r =-=条件方程式为:12343600L L L L +++-=.题目:如图3-18所示水准网,A 、B 两点的高程已知,各观测高差及路线长度如表3-6所列。
测量平差试题2

T
PL
+
Q Lˆ Lˆ
=
(BN
−1 bb
B
T
P)Q(BN
−1 bb
B
T
P)
T
=
BN
−1 bb
B
T
PQPBN
−1 bb
BT
=
BN
−1 bb
B
T
PBN
−1 bb
B
T
=
BN
−1 bb
B
T
QLˆ L = (BNb−b1BTP)Q
=
BN
B −1 T
bb
3、推导 QVXˆ (5 分)
( ) ( ) QVXˆ =
8、 平差定权时,随单位权中误差的选取不同,会导致观测量平差值的不同。(╳ )
9、 平差值的精度一定高于其观测值的精度。(√ )
10、因为 Lˆ = L +V ,故 QLˆ Lˆ = QLL − QVV 。(√ )
二、填空题(每空 1 分,共 25 分)
1、间接平差中,未知参数的选取要求满足 足数 、 函数独立 。
=
1 2
⎛1 ⎜⎝1
1 2
⎞ ⎟ ⎠
,
σ
xˆ1
=
4 ,则σˆ0
=
B
。
A、1
B、2
C、4
D、8
3、以 σˆ L
、σˆΔ
、σˆv
分别表示某一量的观测值、真误差、观测值残差的中误差,则 σ
2 L
、σ
2 Δ
、
σ
2 v
之间的关系为
B
。
A、
σ
2 L
=
σ
2 v
<
测量平差期末试题

测量平差期末试题⼀、填空。
(每空1分,共22分)1.与的⽐值称为相对中误差。
2.误差椭圆的三个参数是________、________、_________。
3.闭合导线按条件平差时条件⽅程式的个数等于___个,分别是____个____________________条件和____对_______________________条件。
4 .设某平差问题中,观测值个数为n个,必要观测数为t个,若按条件平差,条件⽅程的个数等于______个,法⽅程的个数等于_______个。
若按间接平差,误差⽅程式的个数等于______个,未知数的个数等于______个,法⽅程的个数等于____个。
5.根据误差传播定律,若某⼀站观测⾼差的中误差为2mm,在A、B两点间共观测了4站,则A、B两点间⾼差的中误差为mm。
6.导线⽹按条件平差,所列条件⽅程中的未知数,既有___________的改正数,也有___________的改正数。
7.在⽔准测量中若已知每公⾥观测⾼差的中误差均相等,且⼜知各⽔准路线的长度为Si(I=1,2,……n),则观测⾼差的权可⽤公式_________求出。
8.偶然误差的特性为:绝对值较⼩的误差出现的可能性;绝对值相等的正负误差出现的可能性;偶然误差的理论平均值。
1.__________、_________和_________合称为观测条件。
2.⽔准路线的定权⽅法有两种:根据_________定权和根据_________定权。
3.由三⾓形闭合差来计算测⾓中误差的公式为,称其为菲列罗公式。
4.由不等精度的双观测值之差计算单位权中误差的公式为σ0= ,由等精度的双观测值之差计算观测值中误差的公式为。
5 .单导线按条件平差时条件⽅程的个数永远等于个,附合导线中个坐标⽅位⾓条件和⼀对条件,闭合导线中⼀个条件和对闭合条件。
6.常⽤的衡量精度的指标有、、、1.独⽴边⾓同测⽹条件⽅程式的种类,除了具有测⾓⽹和测边⽹的条件式外,还具有反映边⾓关系的⼆种条件,它们是和。
测量平差习题集答案

测量平差习题集答案测量平差习题集答案在测量工作中,平差是一项非常重要的环节。
它通过对测量数据进行处理和分析,消除误差,得到更加准确的测量结果。
为了帮助大家更好地理解和掌握平差的方法和技巧,下面将为大家提供一些测量平差习题集的答案。
1. 题目:某测量队在进行水平控制网的测量时,测得A、B两点的水平角为α1=90°30'20",α2=269°29'40",A、B两点的距离为1000米。
已知A点的坐标为(1000, 1000),求B点的坐标。
解答:根据水平角的定义,可以得到以下关系式:α1 = α2 + 180°即90°30'20" = 269°29'40" + 180°化简得90°30'20" = 449°29'40"由于角度超过360°,需要将其转化为小于360°的形式,可以通过减去360°来实现,即:90°30'20" - 360° = 89°29'40"所以,B点的水平角为89°29'40"。
接下来,根据已知的A点坐标和AB距离,可以利用正弦定理来求解B点的坐标。
设B点的坐标为(x, y),则有:(x - 1000)^2 + (y - 1000)^2 = 1000^2根据正弦定理,可以得到以下关系式:sin(89°29'40") = (x - 1000) / 1000化简得:(x - 1000) = 1000 * sin(89°29'40")解得:x ≈ 1999.999同理,可得:y ≈ 1000.000所以,B点的坐标为(1999.999, 1000.000)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
误差理论与测量平差基础课设题目
1、有测边网如下图所示。
网中A、B、C、D为已知点,P1、P
2、P
3、P4为待定点,现
=3mm+1*10-6s,起算数据及观测边长见下,用某测距仪观测了13条边长,测距精度
s
按间接平差法求待定点坐标平差值及其中误差。
2、如图所示的测角网中,A、B、C为已知点,P1、P2为待定点,L1~L10为角度观测值,
已知点坐标与待定点近似坐标以及同精度角度观测值如下表所示,试求:(1)、误差方
程及法方程;(2)、待定点最或是坐标及点位中误差;(3)观测值改正数及平差值。
起算数据
观测数据
3、 有导线网如下图所示,A 、B 、C 、D 为已知点,P1~P6为待定点,观测了14个角度和9
条边长,已知侧较重误差βσ=10″,侧边中误差s σ=i s (mm )(i=1,2,…,9),s i 以m 为单位,已知点数据和待定点近似坐标列于下表中,设待定点坐标为参数,试按间接平差求:(1)误差方程;(2)待定点坐标平差值及点位中误差。
起算数据。
