《结构力学》第十四章结构振动与稳定1-40页精选文档
结构力学 第14章结构动力学

(1) μ<<ω时,θ/ω很小,μ接近于1。可近似地将Fsinθt 作为 静力荷载。此时振动很慢,因而FI、FR都很小。 无阻尼时,位移与荷载是同步的; 有阻尼时,位移与荷载基本上同步。
(2) μ>>ω时,μ很小,质量近似于不动或作振幅很微小的颤动。 结构的Fe、FR可以忽略,位移与荷载的相位差为180°。
§14-3 单自由度结构的自由振动
2、考虑阻尼作用时的自由振动 阻尼力的产生:外部介质的阻力,支承的摩擦等;
物体内部的作用,材料分子之间的摩擦等。
粘滞阻尼力:阻尼力与其振动的速度成正比,与速度的方向
相反。 FR y —β称为阻尼系数
考虑阻尼力时,质点m的受力图如图所示
由动力平衡得 FI FR Fe 0
图b所示的水塔,顶部水池较重, 塔身重量较轻,略去次要因素后, 可简化为图示的直立悬臂梁在顶端 支承集中质量的单自由度结构。
实际结构针对具体问题可以进行简化
§14-3 单自由度结构的自由振动
如图所示在跨中支承集中质量的简支梁,把质点m拉离原 有的弹性平衡位置,然后突然放松,则质点将在原有平衡位置 附近往复振动。在振动过程中不受外来干扰,这时的振动即是 自由振动。
t)
§14-3 单自由度结构的自由振动
y
ekt ( y0
cos t
y0
ky0
sin
t)
可写为 y bekt sin( t ) (g)
式中
b
y02
y0
ky0
2
,
tan
y0
y0 ky0
式(g)的位移-时间曲线如图所示。
—衰减的正弦曲线 k—衰减系数
§14-3 单自由度结构的自由振动
建筑结构力学稳定

y
a 4 . 32 cm 即 :189 . 3 25 . 6 12 . 74 ( 1 . 52 a / 2 ) 时合理
2
2019/2/27 建筑结构力学
求临界力:
i
L 0 . 7 6
I z 2 A 1
0 . 7 6 396 . 6 10 4 2 12 . 74 10
不 稳 定 平 衡
2019/2/27
临 界 状 建筑结构力学 态
3.压杆失稳:
4.压杆的临界压力 临界状态
对 应 的 稳 定 过 平 衡 压 力
临界压力:
Fcr
不 稳 度 定 平 衡
不 稳 定 平 衡
2019/2/27 建筑结构力学
度量梁变形的两个基本位移量
1.挠度:横截面形心沿垂直于轴线方向的线位移。用w表示。 与 y 同向为正,反之为负。 y C w C1
安全可靠地工作。
2019/2/27
建筑结构力学
一、稳定平衡与不稳定平衡 : 1. 不稳定平衡
2019/2/27
建筑结构力学
2. 稳定平衡
2019/2/27
建筑结构力学
二、压杆失稳与临界压力 : 1.理想压杆:材料绝对理想;轴线绝对直;压力绝对沿轴线作用。 2.压杆的稳定平衡与不稳定平衡:
稳 定 平 衡
M ( x) EI
即挠曲线近似微分方程。
2019/2/27
建筑结构力学
对于等截面直梁,挠曲线近似微分方程可写成如下形式:
EI f ( x ) M ( x )
2019/2/27
建筑结构力学
§2
两端铰支细长压杆的临界压力
一、两端铰支细长压杆的临界压力:
《结构力学》第十四章 结构振动与稳定剖析
D
)2
1(c 2m )
y(t ) (c1 c2t )et 不振动
cr 2m --临界阻尼系数 c c ---阻尼比 cr 2m
不振动
y(t ) et (c1 sin Dt c2 cos Dt ) (0) y 0 y 由初始条件 y(0) y0 ,大阻尼情况 0 y0 ) / D , c2 y0 c1 ( y y(t ) Aet sin( Dt D )
l
=1
11
l
=1
1 12 EI m 11 7ml 3
l
l/2
7ml 3 T 2 12 EI
2
例二.求图示体系的自振频率和周期.
解:
m/2
EI EI
m
l
EI
l
=1
2 l 11 3 EI
3
l
1 3 2l 3 m 2 3EI
EI ml 3
l
ml 3 T 2 EI
(t ) R(t ) cy
2.计阻尼自由振动 1).运动方程及其解
c-----阻尼系数
运动方程
m
y(t )
(t ) cy
(t ) m y
cy k11 y 0 m y 令 c / 2m 2y 2 y 0 y
设
k11 y(t )
A
单自由度体系不计阻尼时的自由振动是简谐振动.
振幅 初相位角
3.自振频率和周期的计算 利用计算公式
k11 1 m m 11 W mg, st W 11 g 2 st
2
算例 例一.求图示体系的自振频率和周期. 解:
结构力学第14章结构稳定

安全可靠地工作。
P
一、稳定平衡(stable equilibrium)与不稳定平衡(unstable equilibrium) 1. 不稳定平衡(unstable equilibrium)
2. 稳定平衡(stable equilibrium)
3. 稳定平衡和不稳定平衡(stable equilibrium & unstable equilibrium)
EI l B sin
nx
k
(l
x)
0 cosnl
n sin nl
(k / Pl 1) 0 0
边界条件
y(0)
0,
y(0)
Pl
, y(l
)
0
A k 0
tan nl nl 1 EI (nl)2
Bn
P (
k
1)
0
Pl
k l 解方程可得nl的最小正根 Pcr n2 EI
Structural mechanics
§14.0 压杆稳定性的概念 Conception of stability of Compress bar
构件的承载能力:
①强度(strength) ②刚度(stiffness) ③稳定性(stability)
工程中有些构
件具有足够的强度、
刚度,却不一定能
4. 随遇平衡(neutral equilibrium)
二、压杆失稳(lost stability)与临界压力(criterion compressio
1.理想压杆:材料绝对理想;轴线绝对直;压力绝对沿轴线作用。
2.压杆的稳定平衡与不稳定平衡:
稳 定 平 衡
结构力学第十四章 结构动力学

1) 集中质量法
m
将实际结构的质量看成(按一定规则)
集中在某些几何点上,除这些点之外物体是
无质量的。这样就将无限自由度系统变成一
有限自由度系统。
2) 广义坐标法
y(x) aii (x) i 1
ai ---广义坐标
i ( x) ---基函数
i (0) i (l) 0
m y(x)
广义坐标个数即 为自由度个数
1.在质量上沿位移正向加惯性力;
2.求发生位移y所需之力;
2.求外力和惯性力引起的位移;
3.令该力等于体系外力和惯性力。
3.令该位移等于体系位移。
一、柔度法
P(t) m my(t) =1 11
y(t)
l EI
11[P(t) my(t)]
P(t) my(t)
y(t) 11[P(t) my(t)]
刚度法: 柔度法:
Fs(t) FI (t) 0 k11y(t) my(t) 0
y(t) 11[my(t)]
令 2 k11 1 m m11
y(t) 2 y(t) 0
1.在质量上沿位移正向加惯性力;
m
2P.求(t)外力[和m惯y(性t)力] 引0起的位移;
P(t) my(t) 形式3上.令的该平位衡移方等程于,体实系质位上移的。运动方程
一、柔度法
P(t) m my(t) y(t)
l EI
=1 11
l
11[P(t) my(t)]
P(t) my(t)
y(t) 11[P(t) my(t)]
k11 k21
k12 k22
y1 y2
my ky P 刚度矩阵
1
k11
y1
k12
结构力学稳定理论课件2

2 0
A
6 EI l
A
0 1 ( Pl
) 2 0 (1)
Pl ( 1 2 ) 3 EI l
B
3 EI l
l
2 0
AC:
M
6 EI l
1
( Pl
) 1 ( Pl
) 2 0 ( 2 )
0 •由位移参数不全为零得稳定方程: Pl 6 EI l 3 EI 6 EI 3 EI 解得: P1 2 P2 2 , Pcr P1 2 l l l
l
例1:图示体系中AB、BC、CD各杆为刚性杆。使用两种方 法求其临界荷载。 -1C A B D P 解:1)静力法 1 k k l l l •设变形状态 λ P 求支座反力 P A D y1 M B 0 YA y2 B左 B k YA=Py1/l k C M C 0 YD YD=Py2/l C右 R1=ky1 R2=ky2 •列变形状态 的平衡方程
A点为稳定平衡, 偏离A点δΠ>0其 势能将增加,故知 稳定平衡位置的势 能为最小。
A
B C 刚性小球运动稳 定性与能量的关系 设静止点A、B、C点Π=0
对于弹性变形体系,其稳定性与能量的关系与刚性小球情 况相似。设原始平衡状态为零势能点,让体系微小偏移,荷载 在位移上做功W(外力势能UP=-W)使体系偏移,内力在变 形上产生变性能U,使体系恢复原位置。总势能Π=U+ UP即总 势能的增量δΠ。 Π=0 P P 如总势能Π=U+ UP >0(δΠ>0),体系能 恢复原位置,平衡是稳定的; B B´ λ 如总势能Π=U+ UP =0(δΠ=0),体系能 在任意位置平衡,平衡为中性的; EI=∞ 如总势能Π=U+ UP <0(δΠ<0),体系不 能恢复原位置,平衡是不稳定的。 θ 用能量法求临界荷载,依据于临界状态的 平衡条件,它等价于势能驻值原理: 弹性体系在临界状态,其总势能为驻值,即 (用于多自由度体系) δΠ=0 或:Π=0 (单自由度体系)
结构力学(完整资料).doc

【最新整理,下载后即可编辑】§13-4 连续梁的整体刚度矩阵即传统位移法:根据每个结点位移对附加约束上的约束力{F}的贡献大小进行叠加而计算所得。
一、单元集成法的力学模型和基本概念1.首先只考虑于是其中由前面的单元刚度矩阵所得,则进一步得到所以最终得到2.则这是最后总结如下的形式来作最终的计算§13-5 刚架的整体刚度矩阵思路要点:(1)设各单元已形成了整体坐标系下的单元刚度矩阵;与连续梁相比: (1)各单元考虑轴向变形;(2)每个刚结点有三个位移; (3)要采用整体坐标;(4)要处理非刚结点的特殊情况。
一、结点位移分量的统一编码——总码整体结构的结点位移向量为:相应地结点力向量为:规定:对于已知为零的结点位移分量,其总码均编为零。
其中每个单元的刚度为以下其中定位向量为:最终进行叠加求得整体刚度矩阵代入数字得定位向量:§13-6 等效结点荷载结构体系刚度方程:{F}= [K]{∆} (1)表示结点位移{∆}和结点力{F}之间的关系,反映了结构的刚度性质,而不涉及原结构上作用的实际荷载,并不是原结构的位移法基本方程。
一、位移法基本方程} ={0} (2)[K]{∆} +{FP用图来表达以上思想:二、 等效结点荷载的概念显然 {P }= –{F P }………解决了计算等效结点荷载的问题 等效原则是两种荷载在基本体系中产生相同的结点约束力 三、按单元集成法求整体结构的等效结点荷载{P } (1)局部坐标单元的等效结点荷载(2)整体坐标单元的等效结点荷载(3) 结构的等效结点荷载{P }{}[]{}P T P T=依次将每个单元等效结点荷载中的元素按照单元定位向量在结构的等效结点荷载中定位叠加。
§13-7 计算步骤和算例1 确定整体和局部坐标系、单元和结点位移编码2 形成刚度矩阵(1)形成局部坐标系下的单元刚度矩阵(2)形成整体坐标系下的单元刚度矩阵(3)“换码重排座”,形成整体结构的刚度矩阵3 形成等效结点荷载(1)形成局部坐标系下的单元固端力(2)形成整体坐标系下的单元等效结点荷载(3) “换码重排座”,形成整体结构的等效结点荷载4 解整体刚度方程,求结点位移5 求各单元的杆端内力(1)整体坐标系下的单元杆端位移(2)局部坐标系下的单元杆端位移(3)局部坐标系下的单元杆端内力§13-8 忽略轴向变形时矩形刚架的整体分析14 超静定结构总论§14-1 超静定结构解法的分类和比较超静定结构计算方法分类各种结构型式所选用的适宜解法说明:手算时,凡是多余约束多、结点位移少的结构用位移法;反之用力法。
结构力学教案 第14章 结构的稳定计算

P第十四章 结构的稳定计算14.1 两类稳定问题概述一、结构设计应满足三方面的要求1、强度2、刚度3、稳定性。
二、基本概念1、失稳:当荷载达到某一数值时,体系由稳定平衡状态转变为不稳定状态,而丧失原始平衡状态的稳定性,简称“失稳”。
工程中由于结构失稳而导致的事故时有发生,如加拿大魁北克大桥、美国华盛顿剧院的倒塌事故,1983年北京某科研楼兴建中的脚手架的整体失稳等,都是工程结构失稳的典型例子。
2、临界状态:由稳定平衡状态过度到不稳定状态的中间状态(中性平衡状态)。
3、临界荷载:临界状态时相应的荷载。
三、结构失稳的两种基本形式1、第一类失稳(分支点失稳):结构变形产生了性质上的突变,带有突然性。
2、第二类失稳(极值点失稳):虽不出现新的变形形式,但结构原来的变形将增大或材料的应力超过其许可值,结构不能正常工作。
c rc r14.2 确定临界荷载的静力法和能量法一、静力法1、临界状态的静力特征(1)体系失稳前在弹性阶段工作a 、应力、应变成线性关系。
b 、挠曲线近似微分方程成立。
(2)静力特征临界荷载具有“平衡状态的二重性”,因为它是由稳定平衡状态过渡到不稳定状态的极限状态。
2、定义:假定体系处于微弯失稳的临界状态,列出相应的平衡微分方程,进而求解临界荷载的方法。
3、步骤:(1)建立坐标系、取隔离体、绘受力图。
(2)列静力平衡方程。
(3)将挠曲线方程代入平衡方程后,利用边界条件求稳定方程。
(4)解稳定方程,求临界荷载。
4、举例 试求图示结构的临界荷载。
x解“超越方程”的两种方法: 1、逐步逼近法(试算法):2、图解法:以αl 为自变量,分别绘出z= αl 和 z=tg αl 的图形,求大于零的第一个交点, 确定αl 。
取最小根αl =4.493例14−1 图14−6(a )所示一端固定、一端自由的杆件,BC 段为刚性,A B 段弯曲刚度为EI 。
试建立临界荷载的稳定方程。
解:任一截面的弯矩为稳定方程为展开次行列式得((二、能量法1、用能量原理建立的能量准则(适用于单自由度体系)(1)三种平衡状态a 、稳定平衡: 偏离平衡位置,总势能增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 2
1 ln yn 2 yn1
利用此式,通过实验可确定 体系的阻尼比.上式也可写成
1 ln yn 2j yn j
例: 对图示体系作自由振动试验.用钢 解: 1.阻尼比
丝绳将上端拉离平衡位置2cm,用 力16.4kN,将绳突然切断,开始作 自由振动.经4周期,用时2秒,振幅
214ln1 20.0276
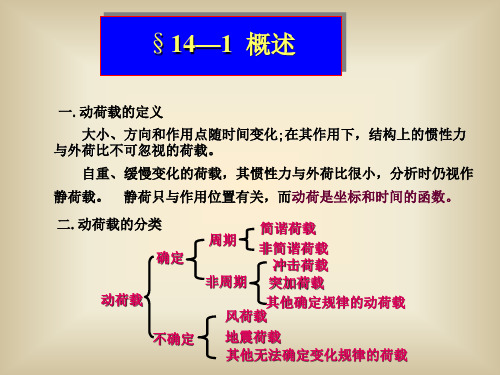
§14—2 结构振动的自由度
一. 自由度的定义 确定振动过程中结构中所有质点位置所需的独立参数的数目,称作 结构的振动自由度。
二. 自由度的确定
4)
1) 平面上的一个质点
y1
W=1
y2
y1 W=2
5)
2) W=2
W=2
弹性支座不减少振动自由度
6)
3) 计轴变时 W=2
不计轴变时 W=1 7)
为减少振动自由度,梁与刚架不 计轴向变形。
1.振动微分方程及其解
y11[m y ]
k11ym y
令
2 k11 1 m m11
y2y0
二阶线性齐次常微分方程
其通解为 y(t)A 1cot sA 2sitn 令 y0 asin
由初始条件 y(0)y0
y 0/acos
y(0) y0
y(t)asi n t ()
可得 A1 y0 A2 y0 /
解:
3EI k11 k l3
mW/g
k
3EI l3
g
3 EI l2
W
EI
k
l
k11
1
k11
3 EI
l3
k
二、阻尼对振动的影响
1.阻尼与阻尼力
阻尼:使振动衰减的作用. 阻尼产生原因: 材料的内摩擦,连接点、支承面等处的外摩擦及介质阻力等. 阻尼力: 在振动分析当中用于代替阻尼作用的阻碍振动的力。 粘滞阻尼理论假定阻尼力的大小与速度成正比,方向与速度相反。
令 2 k2临界阻尼情况
方程的通解为
tan y 0 /y (0 k0) y
k(2m )
由初y 始( t) 条B 件1e y k ( y 0 0 ( ) ,B tB 1 c 2 y 0,(o y y (t 0 0 )大B s k 阻2 y 0 s 尼) 0 y /情i 况t) n cry c(tr) 2m 2 (m C 1 kC - 2 -t临)e 界 阻k 阻尼不t尼比振系动数
FR y
-----阻尼系数
2.计阻尼自由振动
1).振动微分方程及其解
m y(t)
m y(t)
y(t)
k11y(t)
运动方程 令
m y y k1y 10
k/2m 衰减系数
y 2ky 2y0
设
y Cert
r22k r 20 特征方程
根为 rk k22
k(2m ) 小阻尼情况
b
y02
(yky0)2
l EI
yst
F
m2
F1 1
---荷载幅值作为静荷载所引起的静力位移
y(t)b k es t in t ()
k(2m ) 不振动
2).振动分析
y(t) y n
y(t)b k es t in t ()
y n1
12
tn
t n 1
t
T 2
周期延长
T
计算频率和周期可不计阻尼
振动是衰减的
yn yn1
betn be(tnT)
eT
ln yn T
yn1
对数递减量
6.若质量增加800kg,体系的周期和阻尼比
4.重量212 .57 (1/s)
m k1T1 /251(k 9)g 0
为2 多 少 8.215013 .86 (1 9/s2)
51 9 80 00
1.1 7(0 1/s)
T2 /0.53 (s)7
W m g 5.0 8(6 kN ) /2m 0.0257
§14—4 单自由度结构在简谐荷载作用下的强迫振动
一、不考虑阻尼 1.振动微分方程及其解
F(t)Fsint
F(t) m y(t)
l EI
F ---荷载幅值 ---干扰力频率
振动微分方程
m y (t) k1y 1 (t)F sitn
或
y (t)2y(t)Fsint
设
yAsin t
m
代入方程,可得
自振周期
与外界无关,体系本身固有的特性
1 2 自振园频率(自振频率)
T
a
振幅
初相位角
3.自振频率和周期的计算
利用计算公式
2km 11m 1 11mgg 11
g
st
k11 m
m1 11
mgg 11
g
st
算例 例一.求图示体系的自振频率和周期.
解:
1 1E 1(1 2 Ill3 2l1 2lll 1 2l2 ll)
y(t)y0cots y 0si nt
2.振动分析
其中
a
y02
y02
2
tan y0
y0
单自由度结构不计阻尼时的自由振动是简谐振动.
y ( t ) a st i n ) a s (t i n 2 ) ( a s( i t n 2 ) [ ] y ( t 2 )
T 2
降为1cm.求 1.阻尼比
2.刚度系数
2cm
刚度系数
3.无阻尼周期
16.4kN 4.重量
k11 1.0 4 6 .0 12 308.2150 (N/m )
5.阻尼系数
6.若质量增加800kg体系
的周期和阻尼比为多少
3.无阻尼周期
T2/40.5(s)
5.阻尼系数
2 m 36 (N 0 s1 /)m
二阶线性非齐次常微分方程
F
通解
y(t)y0 y
A m(2 2)
其中y0A 1co t sA 2si n t y(t)A 1c通解o t为 sA 2sitnm (2 F 2)sitn
2.纯强迫振动分析
yAsin t
A A
m y(st 2F---最2)大动 力m位F移2 ( 1振幅1)22
F(t) m y(t)
y2 y1
W=2
振动自由度与质点个数无关,但 不大于质点个数的2倍。
EI
W=1
8) W=1
9)
W=13 振动自由度为1的结构称作单自由度结构; 振动自由度大于1的结构称作多自由度结构; 振动自由度无限多的结构称为无限自由度结构。
§14—3 单自由度结构的自由振动
一、不计阻尼的自由振动
自由振动---由初位移、初速度引起的,在振动中无动荷载作用的振动。 分析自由振动的目的---确定体系的动力特性:频率、周期。 阻尼---耗散能量的作用。
7 l3 12 EI
1
m11
12EI 7ml3
l/2
m
EI EI
l
=1 11
l
T 2 2 7ml3
12EI
l
=1
l
例二.求图示体系的自振频率和周期. m/2 m
l
=1
解:
11
2 3
l3 EI
EI EI
l EI l
1 3m 2l3
EI ml3
l
2 3EI
T 2 ml 3
EI
例三.质点重W,求体系的频率和周期.
