结构力学

结构力学在土木工程专业中占有极为重要的地位，在它之前开设的专业基础课有《理论力学》（考试）和《材料力学》（考试），之后将开设专业基础课《弹性力学》（或《弹塑性力学》）（考查），专业课《钢筋混凝土结构》、《钢结构》（或《钢、木结构》，从课程设置上我们就可以认识到结构力学课程的重要地位。

其次，从结构的概念——建筑物和工程设施中承受、传递荷载而其骨架作用的部分成为工程结构、简称结构。

我们可以看出结构在民用和军用设施中都是无处不在的，我院作为全军工程兵的最高学府，工程兵的八大专业：桥梁、道路、渡河、地雷、爆破、筑城、伪装、机械，有四大专业：桥梁、道路、爆破、筑城是直接构筑在结构力学之上的，其他的四个专业也都与结构力学密不可分。

再者，力学是一个完整的知识体系，其基础或者说基本部分就是我们在本科阶段所需要学习的《理论力学》、《材料力学》、《结构力学》、《弹性力学》（或《弹塑性力学》）。

一般的，同志们习惯将《理论力学》、《材料力学》、《结构力学》称为“三大力学”，但是，按照笔者观点，此种分法有失精确，理由如下：《理论力学》、《材料力学》、《结构力学》、《弹性力学》虽同为基础力学，有密切的联系，但《理论力学》着重讨论物体机械运动的基本规律，而其余三门力学《材料力学》、《结构力学》、《弹性力学》着重讨论结构及其构件的强度、刚度、稳定性和动力反应等问题，其中材料力学以单个杆件为研究对象，结构力学以杆件结构（体系）为主要研究对象，弹（塑）性力学以实体合办乔结构为主要研究对象。

从教材内容上这一点也可以得到很明显的体现（内容有待扩展）通过以上的介绍，我们明确了结构力学的研究对象、研究方向，明确了结构力学在力学中所处的位置，明确了学好结构力学的重要性。

下面就要具体介绍结构力学的有关内容。

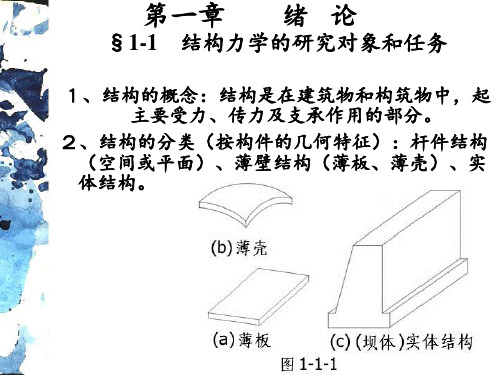
首先要从结构的分类说起，从几何角度来看，结构可分为三类：1．杆件结构——这类结构是由杆件所组成。

杆件的几何特征是横截面尺寸要比长度小得多。

梁、拱、桁架、刚架是杆件结构的典型形式。

2．板壳结构——这类结构也称为薄壁结构。

它的厚度要比长度和宽度小得多。

房屋中的楼板和壳体屋盖、水工结构中的拱坝都是板壳结构。

3．实体结构——这类结构的长、宽、厚三个尺度大小相仿。

水工结构中的重力坝属于实体结构。

狭义的结构往往指的就是杆件结构，而通常所说的结构力学就是指杆件结构力学。

结构力学的任务是根据力学原理研究在外力和其他外界因素作用下结构的内力和变形，结构的强度、刚度、稳定性和动力反应，以及结构的组成规律。

具体地说，包括以下几个方面：（1）讨论结构的组成规律和合理形式，以及结构计算简图的合理选择；（2）讨论结构内力和变形的计算方法，进行结构的强度和刚度的验算：（3）讨论结构的稳定性以及在动力荷载作用下的结构反应。

结构力学问题的研究手段包含理论分析、实验研究和数值计算三个方面。

实验研究方法的内容在实验力学和结构检验课程中讨论，理论分析和数值计算方面的内容在结构力学课程中讨论。

在结构分析中，首先把实际结构简化成计算模型，称为结构计算简图；然后再对计算简图进行计算。

结构力学中介绍的计算方法是多种多样的，但所有各种方法都要考虑下列三方面的条件：（1）力系的平衡条件或运动条件；（2）变形的几何连续条件；（3）应力与变形间的物理条件（或称为本构方程）。

结构力学的基本解法一般可以归结为：力法、位移法、和混合法。

这些解法如果用能量的形式来表达，则称为能量法。

此外，虽只计算机的出现，“电算”方法也随之应运而生，掌握与电算方法相关的知识如：能量原理、结构矩阵分析、有限元法、半解析法、结构分析软件、结构优化设计等，也已经显得越来越重要。

最后，谈一下结构力学这门课的学习方法，笔者认为，结构力学的教学和学习应该着重强调四个方面：分析能力、计算能力、自学能力、表达能力。

分述如下：1、分析能力，主要包括：选择计算简图的能力——如何对实际结构进行“删繁就简”，确定其计算简图，这是进行结构力学计算的第一步。

在结构力学课程重要初步培养这方面的能力。

2、计算能力，在结构力学课程中培养计算方面的能力包含三项：具有对各种结构惊醒计算或确定计算步骤的能力；具有对计算结果惊醒定量校核或定性判断的能力；初步具有实用结构计算程序的能力。

在这三项中，计算能力是基础——不会计算，也就不会校核。

不会手算，则点算是盲目的。

比较和判断能力可以说不计算能力要更高一层——校核并不是重复算一遍，而是要求用另一种方法来核算。

这里就要求校核者能掌握多种算法并能灵活运用。

判断则要求能用简略的方法确定计算结果的合理范围，这里要求评判这通晓结构的力学性能和各种近似算法。

适用计算程序的能力在现在也日益显得更加重要——不会电算就无法计算大型的问题，也无法提高计算效率。

作题练习，是学习结构力学的重要环节。

不作一定数量的习题，就很难对基本概念和方法又深入的理解，也很难培养好的计算能力。

但是作题也要避免各种盲目性。

举例如下：不看书，不复习，埋头作题，这是一种盲目性。

应当在理解的基础上作题，通过作题在巩固和加深理解。

贪多求快，不求甚解，这是另一种盲目性。

有的习题要精作。

一道题用三种方法作，往往比用一种方法作三道题更有收获。

只会对答数，不会自己判断，这也是一种盲目性。

要养成校核的习惯，学会自行校核的本领。

在实际工作中，计算人员要对自己教出来的计算结果负责。

这种负责精神应当及早培养。

做错了题不改正，不会从中吸取教训，这也是一种盲目性。

做错了题不改正，就是轻率地扔掉了一个良好的学习机会。

特别不要放过一个似是而非的模糊概念，因为认识真理的主要障碍不是明显的谬误，而是似是而非的“真理”。

3、自学能力。

自学九十八别人的知识变成自己的。

自学包括两个方面，一是消化已学的知识，二是摄取新的知识。

如果把知识比作一个“笔记本”，也就是说，一是要由厚变薄，二是要由薄变厚。

消化，就是要把书本上的结论用自己的话说出来，吧黑板上的论证按照自己的思路来整理，八分章分节学来的知识融成整体，把整章的丰富内容概括成简短的几句话，在自己演算的习题里穿插几行札记。

总之，要把“笔记本”由厚变薄，把收集到的珍珠用线串起来，使知识得到升华，便于存储，便于驾驭。

摄取，就是逐步扩大自己的知识领域，把“笔记本”再由薄变厚。

摄取要有选择，扩大要围绕一个中心。

首先要把中心内容扎扎实实地牢固掌握，把主要教科书精读钻研，然后有选择地阅读参考书籍和资料，这样，新知识才能在原来知识结构上生根。

4、表达能力，主要是作业要整洁，清晰，严谨。

计算书要书写整洁，因为是要给人看的。

书写整洁，与其说是一种能力，无能说是一种习惯，一种郑重和负责任的习惯。

计算书既要有形式上的整洁，更要有内容上的清晰。

作题要步骤分明，思路清晰，图形简明，数据准确。

整洁和清晰，体现了一种严谨的作风。

科学之严谨的，从事科学的人要注意培养严谨作风。

结构的几何组成分析结构的几何组成分析的目的是为了：1、检验结构是否几何可变，因为结构是建筑物的承重骨架，因此必须是几何不变体系。

2、确定为几何不变体系之后，还需要进一步确定这个几何不变体系到底是静定结构还是超静定结构，即如果没有多余约束，这结构为无多余约束的几何不变体系——静定结构，如果有多余约束，则结构唯有多余约束的几何不变体系——超静定结构。

当我们拿到了一个结构对它进行几何组成分析时，我们一般可以遵循这样的步骤来进行：首先，我们可以试着利用结构几何组成的四个规律（即三个规则或称为：“三角形规律”）来对这个结构进行分析，1、三根支杆，只看本身，四根支杆，基础算刚片；2、尽可能去掉二元体，扩大刚片，等效替换，简化结构；3、利用“两刚片规则”；4、利用“三刚片规则”（顺藤摸瓜法）；这里需要强调：三刚片体系虚铰在无穷远处的情况下几何组成分析：（1）一个无穷远虚铰若三个刚片用两个实铰与一个虚铰相联结，若形成虚铰的二平行链杆不与两实铰连线平行，则形成几何不变体；否则为几何可变体。

（2）两个虚铰在无限远处若三刚片用三铰相联结中的两虚铰为无限远虚铰，当形成两个无限远虚铰的四根链杆互相不平行时，则该体系为几何不变体系；当形成两个无限远虚铰的四根链杆互相平行时，则体系为几何瞬变体系；若形成无限远虚铰的四根链杆等长平行时，则该体系为几何可变体系。

（3）三个虚铰在无限远处三刚片分别用三对任意方向的平行链杆相联结，均为瞬变体系。

对于一般按照三角形规律组成的体系，以上的步骤就可以奏效，但我们知道，满足三角形规律只是结构几何不变的必要条件，即结构还可以按其它组成规律组成几何不变体系，上述方法如若不行；第二步，计算一下结构的计算自由度W。

引入计算自由度W，可以根据W得到一些关于自由度S和多余约束n的定性结论。

W的算法：1、把体系看作由许多刚片受铰结、刚结和链杆等约束而组成的。

体系中的复杂链杆应着合成简单约束，刚片内部如有多余约束也应计算在内。

W=3m-(3g+2h+b)m——体系中的刚片的个数；g——简单刚结的数目；h——简单铰结的数目；b——链杆根数（包括支杆）。

注：n个刚片间的复杂联结相当于个简单联结。

2、将体系中的结点看作具有自由度的对象，而将链杆（包括支杆）看作对结点施加的约束。

体系中的复杂链杆应着合成简单约束，刚片内部如有多余约束也应计算在内。

W=2i-bj——结点数目；b——简单链杆根数。

得出计算结果，如果W>0，则万事大吉，结构为几何可变；若W≤0，那么你的几何组成分析基本上是白费了，这时你应该知道W=0代表结构的约束数目和结构的自由度数目相等，如果结构在某个局部有多余约束的话，结构一定为几何可变体系，否则为无多余约束的几何不变体系；而W<0代表结构的约束数目大于结构的自由度数目，这是最不幸的一个结论，它对你的几何组成分析毫无作用。

最后一招“杀手锏”为“零载法”，该方法适用范围：W=0的桁架，但这种方法不是所有的人都掌握的，但是它的的确确是最精确、有效的方法了……力法解n次超静定结构一、概念：何谓“超静定结构”——有效约束数目大于结构数目，其力学特性：仅利用静力平衡方程无法求出全部内力！！必须引入其它辅助条件（变形协调条件），才能够求解。

二、求解：首先应该判断所需求解的超静定结构的超静定次数，这要用到我上帖所讲的内容，这里就不再重复了！在确定了待求结构的超静定次数后，我们应该明确用力法求解的基本思路，那就是：“释放、代替——平衡、协调”。

假设所求结构有n个多余约束。

在n个多余约束被解除后，代之以对应的n个多余未知力，原结构便成为静定的基本结构，考虑变形协调条件，即基本结构在比原机构多承受n个多余未知力的情况下（当然，原结构有n个多余约束），应具有与原结构相同的内力与变形。

也就是说，基本结构在原机构“解除约束处”（即为“多余未知力作用处”）沿着多余未知力的作用方向，应具有与原结构相同的位移。