同济大学数学系《高等数学》(第7版)(上册)-课后习题详解-第一章 函数与极限【圣才出品】
同济大学高等数学第七版1_1映射与函数
机动
目录
上页
下页
返回
结束
幂函数的图形和性质
yx
(是常数)
y x2
y
1
yx
(1,1)
y x
图像特点及性质：
o
1、图形都通过点（1，1）。
2、 0 时，图形过原点， 且在 (0,) 内单调增加。
1 y x
1
x
3、
0 时，图形在 (0,)
内单调减少。
机动 目录 上页 下页 返回 结束
机动 目录 上页 下页 返回 结束
M *表示 M 中排除 0 的集 ;
2. 集合之间的关系及运算 定义2 . 设有集合 A , B , 若 x A 必有 x B , 则称 A 是 B 的子集 , 或称 B 包含 A , 记作 A B .
若 例如 , 且 , 则称 A 与 B 相等, 记作 A B . ,
元素 a 属于集合 M , 记作 a M .
元素 a 不属于集合 M , 记作 a M ( 或 a M ) .
机动
目录
上页
下页
返回
结束
表示法： (1) 列举法：按某种方式列出集合中的全体元素 . 例: 有限集合 A a1 , a2 , , an
自然数集 N 0 , 1 , 2 , , n , 注 : M 为数集 (2) 描述法： M x x所具有的特征 . M 表示 M 中排除 0 与负数的集 例: 整数集合 Z x x N 或 x N p p 与 q 互质 p Z, q N , 有理数集 Q q 实数集合 R x x 为有理数或无理数
同一个函数在不同的实数集是否有界的结论可能不一样。
高等数学同济第七版上册课后习题答案
习题1-11.求下列函数的自然定义域：(1)1(3)(5)sin (7)arcsin(3);(9)ln(1);y y x y y x y x ====-=+211(2);1(4);(6)tan(1);1(8)arctan ;(10).xe y xy y x y xy e =-==+=+=解：2(1)3203x x +≥⇒≥-，即定义域为2,3⎡⎫-+∞⎪⎢⎣⎭2(2)101,x x -≠⇒≠±查看全部文档，请关注微信公众号：高校课后习题即定义域为(,1)(1,1)(1,)-∞-⋃-⋃+∞(3)0x ≠且2100x x -≥⇒≠且1x ≤即定义域为[)(]1,00,1-⋃2(4)402x x ->⇒<即定义域为(2,2)-(5)0,x ≥即定义域为[)0,+∞(6)1(),2x k k Z ππ+≠+∈即定义域为1(1,2x x R x k k Z π⎧⎫∈≠+-∈⎨⎬⎩⎭且(7)3124,x x -≤⇒≤≤即定义域为[]2,4(8)30x -≥且0x ≠，即定义域为(](,0)0,3-∞⋃(9)101x x +>⇒>-即定义域为(1,)-+∞(10)0,x ≠即定义域为(,0)(0,)-∞⋃+∞2.下列各题中，函数()f x 和()g x是否相同？为什么？222(1)()lg ,()2lg (2)(),()(3)()()(4)()1,()sec tan f x x g x x f x x g x f x g x f x g x x x========-解：（1）不同，因为定义域不同（2）不同，因为对应法则不同，,0(),0x x g x x x ≥⎧==⎨-<⎩（3）相同，因为定义域，对应法则均相同（4）不同，因为定义域不同3.设sin ,3()0,3x x x x πϕπ⎧<⎪⎪=⎨⎪≥⎪⎩求(),((),(2),644πππϕϕϕϕ--并指出函数()y x ϕ=的图形解：1()sin ,()sin 66244()sin(),(2)0,44ππππϕϕππϕϕ====-=-=-=()y x ϕ=的图形如图11-所示4.试证下列函数在指定区间内的单调性：(1);1(2)ln ,(0,)xy xy x x =-=++∞证明：1(1)()1,(,1)11x y f x x x===-+-∞--设121x x <<，因为212112()()0(1)(1)x x f x f x x x --=>--所以21()(),f x f x >即()f x 在(,1)-∞内单调增加(2)()ln ,(0,)y f x x x ==++∞设120x x <<，因为221211()()ln 0x f x f x x x x -=-+>所以21()()f x f x >即()f x 在(0,)+∞内单调增加5.设()f x 为定义在(,)l l -内的奇函数，若()f x 在(0,)l 内单调增加，证明()f x 在(,0)l -内也单调增加证明：设120l x x -<<<，则210x x l<-<-<由()f x 是奇函数，得2121()()()()f x f x f x f x -=-+-因为()f x 在(0,)l 内单调增加，所以12()()0f x f x --->即()f x 在(,0)l -内也单调增加6.设下面所考虑的函数都是定义在区间(,)l l -上的。
同济大学《高等数学》第七版上、下册答案(详解),DOC
解得 z 14
9
即所求点为 M（0，0，14 ）.
9
7. 试证：以三点 A（4，1，9），B（10，-1，6），C（2，4，3）为顶点的三角形是等腰直角三角形. 证明：因为|AB|=|AC|=7.且有 |AC|2+|AB|2=49+49=98=|BC|2. 故△ABC 为等腰直角三角形. 8. 验证： (a b) c a (b c) .
3 i 14
1 j 14
2 k.
14
14. 三个力 F1=(1,2,3), F2=(-2,3,-4), F3=(3,-4,5)同时作用于一点. 求合力 R 的大小和方向余弦.
解：R=（1-2+3，2+3-4，3-4+5）=（2，1，4）
| R | 22 12 42 21
cos 2 , cos 1 , cos 4 .
故 A 的坐标为 A(-2, 3, 0).
13. 一向量的起点是 P1（4，0，5），终点是 P2（7，1，3），试求：
（1） P1P2 在各坐标轴上的投影； （2） P1P2 的模；
（3） P1P2 的方向余弦；
（4） P1P2 方向的单位向量.
解：（1） ax Pr jx P1P2 3,
ay Pr jy P1P2 1,
练习 5-2
练习 5-3
练习 5-4
总习题五
练习 6-2
练习 6-3
(2) s 22 (3)2 (4)2 29
(3) s (1 2)2 (0 3)2 (3 4)2 67
(4) s (2 4)2 (1 2)2 (3 3)2 3 5 .
5. 求点（4，-3，5）到坐标原点和各坐标轴间的距离.
同济大学数学系《高等数学》(第7版)(上册)教材包含 笔记 课后习题 考研真题 函数与极限(圣才出品
（2）有界性
如果数列{xn}收敛，则数列{xn}一定有界。
①有界数列：存在正数 M，使得对于一切 xn 都满足不等式|xn|≤M。
②无界数列：不存在正数 M，使得对于一切 xn 都满足不等式|xn|≤M。
（3）保号性
如果
lim
n
xn
a
，且
a＞0（或
a＜0），则存在正整数
N＞0，当
n＞N
时，都有
xn＞0
（4）初等函数
5 类基本初等函数：幂函数、指数函数、对数函数、三角函数、反三角函数。
二、数列的极限
1．数列极限的定义
数列{xn}收敛于
a⇔
lim
n
xn
a
⇔∀ε＞0，∃正整数
N，当
n＞N
时，有|xn－a|＜ε。
数列{xn}是发散⇔
lim
n
xn
不存在。
2．收敛数列的性质
（1）唯一性
如果数列{xn}收敛，则它的极限唯一。
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 1 章 函数与极限
1.1 复习笔记
一、映射与函数 1．函数 （1）函数的性质（见表 1-1）
表 1-1 函数的性质
（2）反函数与复合函数 ①反函数的特点 a．函数 f 和反函数 f－1 的单调性一致。 b．f 的图像和 f－1 的图像关于直线 y＝x 对称。 ②复合函数 g 与 f 能构成复合函数 f°g 的条件是：f 的定义域与 g 的值域的交集不能为空集。 （3）函数的运算 设函数 f（x），g（x）的定义域为 Df，Dg，且定义域有交集为 D，则可定义这两个函
②如果数列{xn}有两个子数列收敛于不同的极限，则数列{xn}是发散的。
同济大学《高等数学》第七版上、下册答案(详解)
练习7-6
总习题七
练习8-1
练习8-2
>
练习8-3
练习8-4
练习8-5
练习8-6
练习8-7
练习8-8
总习题八
练习9-1
练习9-2
>>
<<>>
<<
练习9-3
练习9-4
总习题九
练习10-1
练习10-2
练习10-3
练习10-4
练习10-5
练习10-6
练习10-7
总习题十
练习111
练习112
-
0
+
无
-
-
yf(x)
1
极小值
↗
无
↗
0
拐点
↗
无
↗
-1
极大值
练习3-7
总习题三
x
(, 0)
0
f(x)
+
不存在
-
0
+
f(x)
↗
2
极大值
↘
极小值
↗
练习4-2
练习4-3
练习4-4
>>>
总习题四
练习5-1
练习5-2
练习5-3
练习5-4
总习题五
练习6-2
练习6-3
总习题六
练习7-1
练习7-2
练习7-3
练习7-4
↘
17/5
极小值
↗
6/5
拐点
↗
2
拐点
↗
x
0
(01)
1
y
+
+
同济第七版高等数学第1章习题解答
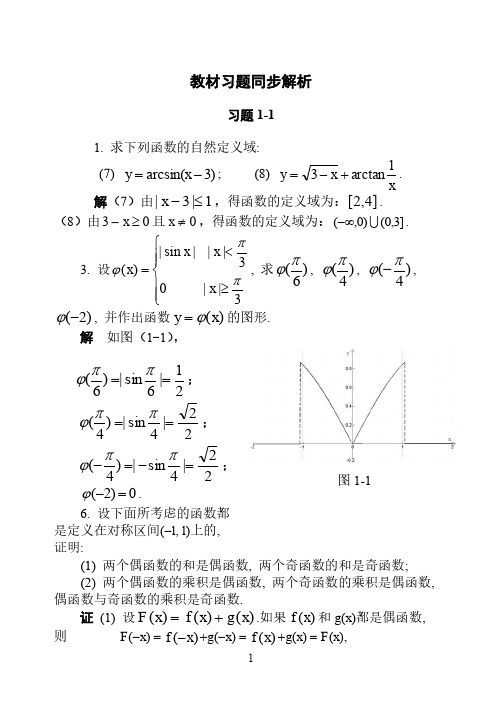
1教材习题同步解析习题1-11. 求下列函数的自然定义域:(7) )3arcsin(-=x y ; (8) xx y 1arctan 3+-=. 解（7）由1|3|≤-x ，得函数的定义域为：]4,2[.（8）由03≥-x 且0≠x ，得函数的定义域为：]3,0()0,( -∞.3. 设⎪⎪⎩⎪⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, )2(-ϕ, 并作出函数)(x y ϕ=的图形.解 如图（1-1），21|6sin |)6(==ππϕ； 22|4sin |)4(==ππϕ； 22|4sin |)4(=-=-ππϕ； 0)2(=-ϕ. 6. 设下面所考虑的函数都是定义在对称区间(-l , l )上的,证明:(1) 两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2) 两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证 (1) 设)()()(x g x f x F +=.如果)(x f 和g (x )都是偶函数, 则 F (-x ) =)(x f -+g (-x ) =)(x f +g (x ) = F (x ),图1-12所以F (x )为偶函数, 即两个偶函数的和是偶函数.如果)(x f 和g (x )都是奇函数, 则F (-x ) = f (-x ) + g (-x ) = -)(x f -g (x ) = -F (x ),所以F (x )为奇函数, 即两个奇函数的和是奇函数.(2) 设F (x ) =)(x f ⋅g (x ). 如果)(x f 和g (x )都是偶函数, 则F (-x ) = f (-x )⋅g (-x ) =)(x f ⋅g (x ) = F (x )，所以F (x )为偶函数, 即两个偶函数的积是偶函数.如果)(x f 和g (x )都是奇函数，则F (-x ) = f (-x )⋅g (-x ) = [-f (x )][-g (x )] =)(x f ⋅g (x ) = F (x ),所以F (x )为偶函数, 即两个奇函数的积是偶函数.如果)(x f 是偶函数, 而g (x )是奇函数，则F (-x ) = f (-x )⋅g (-x ) = f (x )[-g (x )] = -)(x f ⋅g (x ) = -F (x ),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.9. 求下列函数的反函数:(3)dcx b ax y ++= (ad -bc ≠0); (6)122+=x x y . 解 (3) 由dcx b ax y ++=，得a cy b dy x -+-=, 所以d cx b ax y ++=的反函数为：acx b dx y -+-=. (6)由122+=x x y ，得y y x -=1log 2, 所以122+=x x y 的反函数为：xx y -=1log 2. 10. 设函数)(x f 在数集X 上有定义, 试证: 函数)(x f 在X 上有界的充分必要条件是它在X 上既有上界又有下界.证 先证必要性.设函数)(x f 在X 上有界, 则存在正数M , 使|)(|x f ≤ M ,即 -M ≤)(x f ≤ M . 这就证明了)(x f 在X 上既有下界-M 又有上界M .再证充分性.3 设函数)(x f 在X 上有下界K 1和上界K 2, 即K 1 ≤)(x f ≤ K 2 . 取M = max{|K 1|, |K 2|}, 则-M ≤ K 1≤)(x f ≤ K 2≤M , 即|)(|x f ≤ M . 这就证明了)(x f 在X 上有界.12. 设)(x f 的定义域为]1,0[=D ，求下列函数的定义域： ⑴)(2x f ; ⑵)(sin x f ；⑶)0()(>+a a x f ;⑷)()(a x f a x f -++ )0(>a .解（1）由,11,102≤≤≤≤x x －所以)(2x f 的定义域为；]1,1[-(2) 由,1sin 0≤≤x ),()12(2Z k k x k ∈+≤≤ππ故)(sin x f 的定义域为:])12(,2[ππ+k k )(Z k ∈；(3)由,10≤+≤a x ,1a x a -≤≤－故函数)(a x f +的定义域为:]1,[a a --. (4) 由⎩⎨⎧≤-≤≤+≤1010a x a x 知,11⎩⎨⎧+≤≤-≤≤a x a a x a －从而当210≤<a 时, 定义域为:]1,[a a -；当21>a 时, 定义域为空集. 13. 设⎪⎩⎪⎨⎧>-=<=1|| 11|| 01|| 1)(x x x x f , x x g e )(=, 求)]([x g f ，)]([x f g , 并作出这两个函数的图形.解 1 |e |[()]0 |e |11 |e |1x x x f g x ⎧<⎪==⎨⎪->⎩, 即⎪⎩⎪⎨⎧>-=<=0 10 00 1)]([x x x x g f . 如图（1-2）。
1.1映射与函数 同济大学高数(第七版)上册
f ( x )
y
y f ( x)
y f ( x)
f ( x)
f ( x )
-x o x
f ( x)
x
o
x
x
2 （两边对折重合）,如 y x
偶函数图形关于y轴对称
奇函数的图形关于原点对称
3 y x （一边旋转180度得到另一边），如
函数的奇偶性质：
（1）奇函数和偶函数的定义域必定是关于原点对称的； （2）两个偶函数的和、差、积、商仍是偶函数； （3）两个奇函数的和、差仍是奇函数，两个奇函数的积、商是偶函数； （4）奇函数与偶函数的积、商是奇函数； （5）奇函数与偶函数的代数和是非奇非偶函数， （6）任一定义在区间(-a,a)(a＞0)上的函数可表示成一个奇函数与一个偶函数之和.
二、函数的概念及其几种特性
1.函数的概念
X 和Y , 若 x X , 按照某种对应法则 f , 对应 定义 设给定两个非空实数集 唯一确定的一个实数 y Y , 则称 f 是定义在X上的函数, 简记为y f ( x), 其中x为自变量, y为因变量.
X 称为函数f 的定义域, 记为D f , 数x对应的数f ( x)称为x的函数值, 函数值的集合称为函数 f 的值域, 记为R f .
x (, 1) (1, )
x [1,4) (4, )
例2 判断下列函数是否相同
(1) f ( x) x,
x (,)； (2) f ( x) lg x 2 , g ( x) 2 lg x, g ( x) x 2 , x (,)
(1)表示不同的函数，因为它们的对应法则不同 . (2)表示不同的函数，因为它们的定义域不同 .
函数的单调性
同济大学《高等数学》第七版上、下册答案(详解)
练习1-1
练习1-2
练习1-3
练习1-4
练习1-5
练习1-6
练习1-7
练习1-8
练习1-9
练习1-10
总习题一
练习2-1
练习2-2
练习2-3
练习2-4
练习2-5
总习题二
练习3-1
练习3-2
练习3-3
练习3-4
练习3-5
练习3-6
x
(2)
2
(21)
1
(11)
1
43;
+
0
+
y
+
+
+
0
0
+
yf(x)
↘
17/5
极小值
↗
6/5
拐点
↗
2
拐点
↗
x
0
(01)
练习8-4
练习8-5
练习8-6
练习8-7
练习8-8
总习题八
练习9-1
练习9-2
>>
<<>>
<<
练习9-3
练习9-4
总习题九
练习10-1
练习10-2
练习10-3
练习10-4
练习10-5
练习10-6
练习10-7
总习题十
练习111
练习112
1
高等数学(同济第七版)课后答案解析
当I V，w2时，s（!）=I - y（2-/）2=一£f2+ 2/-1 ,
当/>2HhS（f） =1.
放
/>2.
Q 16.求联系华氏温度(用F表示)和扱氏温度(用C表示)的转换公式.并求
(1)90叩的等价摄氏温度和-5 °C的等价华氏温度：
(2)是否存在一个温度值.使华氏温度汁和摄氏温度汁的读数是样的？如果存在，那么该温度值是多少？
xi
所以/（存）>/（%）,即/（W在（0, + ao）内单调增加.
公5・设/U）为定义在（-/./）内的荷函数.若/（X）在（01）内单调増加，证明/（#）在（-L0）内也单凋増加.
证设-/<X, <X2<0,则0< “2 <-A,</,由/（、）是哉函数，從/g）V（X|）=-/（-知）+f（-旳）■因为/Xx）在（OJ）内单调増加.所以y（-X!）-/（-x2）>0.从而/（旳）>/（旳），即/（X〉在《・"0）内也単调增加.
解设尸.其中叽/，均为常数.
因为〃=32。相当于。=。。/ =212。相当于C= 100°.所以
7 "*=槌
故〃=1.80+32或C=扌（F-32）.
(1)F=90°. C =刑90-32)52.2。.
C=-5。，F= 1.Xx(-5)+32= 23°.
(2)设温度値，符合题意.则有
/ = 1.8/ +32,I =-40.
尸銘EC
> =
y=•<>«< w
y=cotZ；
y=arcfiin lx I C1；
G2.卜列各题中，函数/(x)和g(x)是否相同？为什么”⑴/U) =lg/,g⑴=21gx；
同济大学数学系《高等数学》（第7版）（上册）配套题库【考研真题精选＋章节题库】
目 录第一部分 考研真题精选第1章 函数与极限第2章 导数与微分第3章 微分中值定理与导数的应用第4章 不定积分第5章 定积分第6章 定积分的应用第7章 微分方程第二部分 章节题库第1章 函数与极限第2章 导数与微分第3章 微分中值定理与导数的应用第4章 不定积分第5章 定积分第6章 定积分的应用第7章 微分方程第一部分 考研真题精选第1章 函数与极限一、选择题1若，则f（x）第二类间断点的个数为（ ）。
[数二、数三2020研] A．1B．2C．3D．4【答案】C【解析】由f（x）表达式知，间断点有x＝0，±1，2。
因为存在，故x＝0为可去间断点；因，故x＝1为第2类间断点；因，故x＝－1为第2类间断点；因，故x＝2为第2类间断点；综上，共有3个第二类间断点，故应选C项。
2当x→0时，若x－tanx与x k是同阶无穷小，则k＝（ ）。
[数一2019研]A．1B．2C．3D．4【答案】Ctanx在x＝0处的泰勒展开式为：tanx＝x＋（1/3）x3＋o（x3），因此当x→0时有x－【解析】tanx～－（1/3）x3，即x－tanx与－（1/3）x3是x→0时的等价无穷小，进一步可得x－tanx与x3是同阶无穷小，所以k＝3，故选C。
3已知方程x5－5x＋k＝0有3个不同的实根，则k的取值范围（ ）。
[数三2019研] A．（－∞，－4）B．（4，＋∞）C．{－4，4}D．（－4，4）【答案】D【解析】方程x5－5x＋k＝0有3个不同实根等价于曲线y＝x5－5x与直线y＝－k有3个不同的交点，因此研究曲线y＝x5－5x的曲线特点即可。
令f（x）＝x5－5x，则f（x）在R上连续，且f′（x）＝5x4－5，再令f′（x）＝0，得x＝±1，通过分析f′（x）在稳定点x＝±1左右两侧的符号，可知当x∈（－∞，－1）时，f′（x）＞0，f（x）单调递增；当x∈（－1，1）时，f′（x）＜0，f（x）单调递减；当x∈（1，＋∞）时，f′（x）＞0，f（x）单调递增。
同济大学高等数学(第七版)上册第一章函数
如何学好微积分 ?
1、深刻理解基本概念
2、勤于思考，敢于提问，独立完 成作业
3、快乐学习，在学习中提升自己、
华罗庚
认识自己
第一章
函数与极限
分析基础
函数 — 研究对象 极限 — 研究方法 连续 — 研究桥梁
第一节 函数
一、基本概念 二、函数及其几种基本特性 三、反函数 四、复合函数 初等函数
一、基本概念
值域 f (D) [0, )
f
(
1 2
)
2
1 2
2
f
(
1 t
)
11 , t
2, t
0t 1 t 1
y
y 1 x
y2 x
O
1
x
例：某市的出租车按如下规定收费：当行驶里程不 超过3km 时，一律收起步费 10 元；当行驶里程超 过 3km 时,除起步费外，对超过 3km 但不超过 10 km 的部分，按每千米 2 元计费，对超过 10 km 的部 分按每千米 3 元计费,试写出车费 C 与行驶里程 s 之间的函数关系。
数学中的转折点是笛卡儿的变数. 有了变数 , 运动进入了数学, 有了变数， 辩证法进入了数学 , 有了变数 , 微分和积分也就立刻成 为必要的了,而它们也就立刻产生.
高等数学的主要内容
1. 分析基础: 函数 , 极限, 连续 2. 微积分学: 一元微积分 (上册)
多元微积分 (下册) 3. 向量代数与空间解析几何 4. 无穷级数 5. 常微分方程
1.区间: 是指介于某两个实数之间的全体实数. 这两个实数叫做区间的端点.
a,b R,且a b.
{x a x b} 称为开区间, 记作 (a,b)
oa
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
即 f(x)在 X 上有界．
8 / 84
圣才电子书
十万种考研考证电子书、题库视频学习平 台
11．在下列各题中，求由所给函数构成的复合函数，并求这函数分别对应于给定自变 量值 x1 和 x2 的函数值：
8．下列各函数中哪些是周期函数？对于周期函数，指出其周期： （1）y＝cos(x－2)； （2）y＝cos4x； （3）y＝1＋sinπx； （4）y＝xcosx； （5）y＝sin2x． 解：（1）是周期函数，周期 l＝2π．
（2）是周期函数，周期 （3）是周期函数，周期 l＝2． （4）不是周期函数． （5）是周期函数，周期 l＝π．
圣才电子书
十万种考研考证电子书、题库视频学习平 台
第一章 函数与极限
1.2 课后习题详解
习题 1-1 映射与函数 1．求下列函数的自然定义域：
1 / 84
圣才电子书
十万种考研考证电子书、题库视频学习平
台
2．下列各题中，函数 f(x)和 g(x)是否相同？为什么？
故 H(x)为奇函数． 7．下列函数中哪些是偶函数，哪些是奇函数，哪些既非偶函数又非奇函数？
5 / 84
圣才电子书
十万种考研考证电子书、题库视频学习平
台
解：（1）y＝f(x)＝x2（1－x2），因为
所以 f(x)为偶函数． （2）y＝f(x)＝3x2－x3，因为
所以 f(x)既非偶函数又非奇函数．
（3）
，因为
所以 f(x)为偶函数． （4）y＝f(x)＝x（x－1）（x＋1），因为
所以 f(x)为奇函数． （5）y＝f(x)＝sinx－cosx＋1，因为
所以 f(x)既非偶函数又非奇函数．
（6）
，因为
，
所以 f(x)为偶函数．
6 / 84
圣才电子书
十万种考研考证电子书、题库视频学习平 台
（6）由
解得
，即反函数为
10．设函数 f(x)在数集 X 上有定义，试证：函数 f(x)在 X 上有界的充分必要条件是它 在 X 上既有上界又有下界．
解：设 f(x)在 X 上有界，则存在 M＞0，使得 |f(x)|≤M，x∈X
所以 －M≤f(x)≤M，x∈X
即 f(x)在 X 上有上界 M，下界－M． 反之，设 f(x)在 X 上有上界 K1，下界 K2，即 K2≤f(x)≤K1，x∈X
乘积是奇函数．
证：（1）设 f1(x)，f2(x)均为偶函数，则 f1(－x)＝f1(x)，f2(－x)＝f2(x)．
令 F(x)＝f1(x)＋f2(x)，于是
故 F(x)为偶函数．
F(－x)＝f1(－x)＋f2(－x)＝f1(x)＋f2(x)＝F(x)
设 g1(x)，g2(x)均为奇函数，则 g1(－x)＝－g1(x)，g2(－x)＝－g2(x)．令
，于是
4 / 84
圣才电子书
十万种考研考证电子书、题库视频学习平
台
G(－x)＝g1(－x)＋g2(－x)＝－g1(x)－g2(x)＝－G(x)
故 G(x)为奇函数．
（2）设 f1(x),f2(x)均为偶函数，则 f1(－x)＝f1(x)，f2(－x)＝f2(x)．令
.
（4）
时，定义域为∅．
解：（1）函数 f(x)和 g(x)不同，因其定义域不同． （2）函数 f(x)和 g(x)不同，因其对应法则不同，
． （3）函数 f(x)和 g(x)相同，因其定义域、对应法则均相同． （4）函数 f(x)和 g(x)不同，因其定义域不同．
3．设
求 图形．
解：
，并作出函数
的
ห้องสมุดไป่ตู้2 / 84
圣才电子书
内单调增加，所以
．又因为 f(x)在（0，1）
内也单调增加．
，从而 f（x2）＞f（x1），即 f(x)在（－l，0）
6．设下面所考虑的函数都是定义在区间（－l，l）上的．证明：
（1）两个偶函数的和是偶函数，两个奇函数的和是奇函数；
（2）两个偶函数的乘积是偶函数，两个奇函数的乘积是偶函数，偶函数与奇函数的
12．设 f(x)的定义域 D＝[0，1]，求下列各函数的定义域： （1）f(x2)； （2）f(sinx)；
9 / 84
圣才电子书
（3）f(x＋a)（a＞0）；
十万种考研考证电子书、题库视频学习平 台
（4）f(x＋a)＋f(x－a)（a＞0）．
解：（1） （2）
（3）
十万种考研考证电子书、题库视频学习平 台
的图形如图 1-2-1 所示．
图 1-2-1
4．试证下列函数在指定区间内的单调性：
（1）
；
（2）y＝x＋lnx，（0，＋∞）．
证：（1） 设 x1＜x2＜1．因为
所以 f（x2）＞f（x1），即 f(x)在（－∞，1）内单调增加． （2）y＝f(x)＝x＋lnx，（0，＋∞）． 设 0＜x1＜x2．因为
9．求下列函数的反函数：
解：（1）由
解得 x＝y3－1，即反函数为 y＝x3－1．
（2）由
解得
，即反函数为
7 / 84
圣才电子书
十万种考研考证电子书、题库视频学习平 台
（3）由
解得
，即反函数为
．
（4）由 数为
解得
，即反函
（5）由 y＝1＋ln（x＋2）解得
，即反函数为
，于是 F(－x)＝f1(－x)·f2(－x)＝f1(x)f2(x)＝F(x) 故 F(x)为偶函数． 设 g1(x)，g2(x)均为奇函数，则 g1(－x)＝－g1(x)，g2(－x)＝－g2(x)．令
，于是
故 G(x)为偶函数． 设 f(x)为偶函数，g(x)为奇函数，则 f(－x)＝f(x)，g(－x)＝－g(x)．令 ，于是
3 / 84
圣才电子书
十万种考研考证电子书、题库视频学习平 台
可得 f（x2）＞f（x1），所以 f(x)在（0，＋∞）内单调增加．
5．设 f(x)为定义在（－l，l）内的奇函数，若 f(x)在（0，l）内单调增加，证明 f(x)在 （－l，0）内也单调增加．
证：设－l＜x1＜x2＜0，则 0＜－x2＜－x1＜l，因为 f(x)是奇函数，所以