信息与计算科学班下学期《数学建模与数学实验》期末考查试题
《数学建模》期末考试试卷四与参考答案

《数学建模》期末考试试卷 班级 姓名 学号一、(15分)某厂利用甲、乙、丙三种原料生产A 、B 、C 、D 、E 五种产品,单位产品(万件)对原材料的消耗(吨)、原材料的限量(吨)以及单位问五种产品各生产多少才能使总利润达到最大? (1)建立线性规划问题数学模型。
(2)写出用LINGO 软件求解的程序。
二、(15分)用单纯形方法求如下线性规划问题的最优解。
123123123123max 614134248..2460,,0S x x x x x x s t x x x x x x =++++≤⎧⎪++≤⎨⎪≥⎩三、(15分)某厂生产甲、乙、丙三种产品,消耗两种主要原材料A 与B 。
每单位产品生产过程中需要消耗两种资源A 与B 的数量、可供使用的原材料数量以及单位产品利润如下表:设生产甲、乙、丙产品的数量分别为123,,x x x 单位,可以建立线性规划问题的数学模型:123123123123max 4003005006030504500..3040503000,,0S x x x x x x s t x x x x x x =++++≤⎧⎪++≤⎨⎪≥⎩利用LINGO10.0软件进行求解,得求解结果如下:Objective value: 35000.00 Total solver iterations: 2 Variable Value Reduced CostX1 50.00000 0.000000 X2 0.000000 66.66667 X3 30.00000 0.000000 Row Slack or Surplus Dual Price 1 35000.00 1.000000 2 0.000000 3.333333 3 0.000000 6.666667(1)指出问题的最优解并给出原应用问题的答案;(2)写出该线性规划问题的对偶线性规划问题,并指出对偶问题的最优解;(3)灵敏度分析结果如下:Objective Coefficient RangesCurrent Allowable Allowable Variable Coefficient Increase DecreaseX1 400.0000 200.0000 100.0000X2 300.0000 66.66667 INFINITYX3 500.0000 166.6667 66.66667Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 4500.000 1500.000 1500.0003 3000.000 1500.000 750.0000对灵敏度分析结果进行分析四、(10分)一个公司要分派4个推销员去4个地区推销某种产品,4个推销员在各个地区推销这种产品的预期利润(万元)如下表。
数学建模与数学实验试卷及答案

数学建模与数学实验试卷及答案二、本题10分(写出程序和结果) 蚌埠学院2010—2011学年第二学期2,x在 [-5 ,5] 区间内的最小值,并作图加以验证。
求函数yxe,,,3《数学建模与数学实验》补考试卷答案f1=inline('x.^2 +exp(-x)-3') 注意事项:1、适用班级:09数学与应用数学本科1,2班2、本试卷共1页,附答题纸1页。
满分100分。
x=fmin(f1,-5,5)3、考查时间100分钟。
y=f1(x)4、考查方式:开卷 fplot(f1,[-5,5]) 一、填空:(每空4分,共60分)x = 0.3517,y== -2.1728 123111,,,,,,,,,三、本题15分(写出程序和结果) 1. 已知,,则A的秩为 3 ,A的特征值为 A,612B,234,,,,,,,,,215531,,,,,360000xx,,,12,max2.5fxx,,求解:,stxx..250000,,,1212-1.9766 4.4883 + 0.7734i 4.4883 - 0.7734i ,若令A([1,3],:)= B([2,3],:),则,x,150001,A(2,:)= 6 1 2 ;解: xxx,,,22,123,model: 2. 的解为 1.25 ,0.25 0.5 ;xxx,,,521,123max=2.5*x1+x2; ,242xxx,,,123,3*x1+x2<=60000;装订线内不要答题 2*x1+x2<=50000; 3. 将1234521 分解成质因数乘积的命令为_factor(sym(‘1234521’)),x1<=15000;结果为_ (3)^4*(15241)__ ; endax4. 求,其命令格式为 syms x a; limit((1+a/x)^x,x,inf) ,结果为lim(1),max=55000 x1=10000 x2=30000 ,,xxexp(a) ; 四、本题15分(写出程序及结果)xx,31已知: x=1: 0.5 : 5, y=[ 3. 2, 6. 1, 7, 7. 3, 7. 6, 8,7.9,9, 10 ] dx5. 求积分的命令格式为syms x; int((x^3+x)/(x+1),x,0,1); ,x,10求4阶拟合多项式,并画图比较. ( vpa(ans,6)), 积分结果为 11/6-2*log(2) (化简为0.44704) ;clear all 5326. 求多项式的根,其命令格式为p=[5, 0,-8,12,0,-1]fxxxx()58121,,,,x=1: 0.5 : 5; y=[ 3.2,6.1,7,7.3,7.6,8,7.9,9,10];x=roots(p),结果为-1.7194 0.8317 + 0.8110i 0.8317 - 0.8110i 0.3230 -0.2669; p=polyfit(x,y,4);x1=1:0.1:5;y1=polyval(p,x1);7. 求解方程lnx+2x-1= 0的命令为 solve('log(x) +2*x - 1 = 0');vpa(ans) ,结果为 0.6874_; plot(x,y,'.b',x1,y1,'-r') ,n8. =(2*a+2)*(1/2/a^2/(a+1)-1/2/(a+1)) 。
数学建模与数学实验期末

5、对于泛函极值问题,可以利用欧拉方程给出极值必要条件。 正确答案: 错误 解析:
二、 单选题(共 12 题,60 分)
1、层次分析法模型中,我们介绍了一致矩阵的概念,四阶一致矩阵的模最大特 征值为
A、 3 B、 4 C、 5 D、 6 正确答案: B 解析:
期末备用
一、 判断题(共 5 题,15 分) 1、
通过数学建模的方法处理实际问题,通常可以取得理想的结果, 但数学建模本身的缺陷与局限性也是非常明显的。
正确答案: 正确 解析:
2、三次样条插值法的精度一般高于多项式拟合。 正确答案: 错误 解析:
3、在层次分析法中,如果比较矩阵的标度不是完全取 1 至 9 的整数或其倒数, 也可以利用 Saaty 推荐的随机一致性指标判断矩阵的一致性。 正确答案: 错误 解析:
正确答案: 解析:
2、
正确答案: 解析: 四、 其它(共 1 题,8 分) 1、
正确答案: 解析:
A、 10 B、 11 C、 12 D、 13 正确答案: B 解析:
4、
A、 150
B、 200 C、 250 D、 300 正确答案: B 解析:
5、
A、 1% B、 1.5% C、 2% D、 3% 正确答案: C 解析:
6、
A、 0 B、 1 C、 2 D、 3 正确答案: D 解析:
7、
A、 不含常数项的二次函数 B、 幂函数
C、 指数函数 D、 以上都不合理 正确答案: B 解析:
8、
A、 0<a<1 B、 1<a<2 C、 2<a<3 D、 a>3 正确答案: B 解析:
《数学建模》期末试卷A

《数学建模》期末试卷A一、填空题(每题2分,共20分)1、在数学建模中,我们将所要研究的问题________化。
2、在解决实际问题时,我们常常需要收集大量的数据,这些数据通常是不________的。
3、在建立数学模型时,我们通常需要对变量进行假设,这些假设通常是对________的描述。
4、在解决实际问题时,我们通常需要对多个因素进行________,以确定哪些因素对所要研究的问题有显著影响。
5、在建立数学模型时,我们通常需要对数据进行________,以发现数据之间的规律和关系。
6、在解决实际问题时,我们通常需要将复杂的问题________化,以方便我们更好地理解和解决它们。
7、在建立数学模型时,我们通常需要将实际问题________化,以将其转化为数学问题。
8、在解决实际问题时,我们通常需要考虑实际情况的________性,以避免我们的解决方案过于理想化。
9、在建立数学模型时,我们通常需要使用数学语言来________模型,以方便我们更好地描述和解决它。
10、在解决实际问题时,我们通常需要使用计算机来帮助我们进行________和计算。
二、选择题(每题3分,共30分)11、在下列选项中,不属于数学建模步骤的是()。
A.确定变量和参数B.建立模型C.进行实验D.验证模型12、在下列选项中,不属于数学建模方法的是()。
A.归纳法B.演绎法C.类比法D.反证法13、在下列选项中,不属于数学建模应用领域的是()。
A.物理学B.工程学C.经济学D.政治学14、在下列选项中,不属于数学建模语言的是()。
A.文字语言B.符号语言C.图形语言D.自然语言15、在下列选项中,不属于数学建模原则的是()。
A.简洁性原则B.一致性原则C.可行性原则D.可重复性原则16、在下列选项中,不属于数学建模步骤的是()。
A.对数据进行分析和处理B.对模型进行假设和定义C.对模型进行检验和修正D.对结果进行解释和应用17、在下列选项中,不属于数学建模应用领域的是()。
《数学建模与数学实验》期末考查试卷
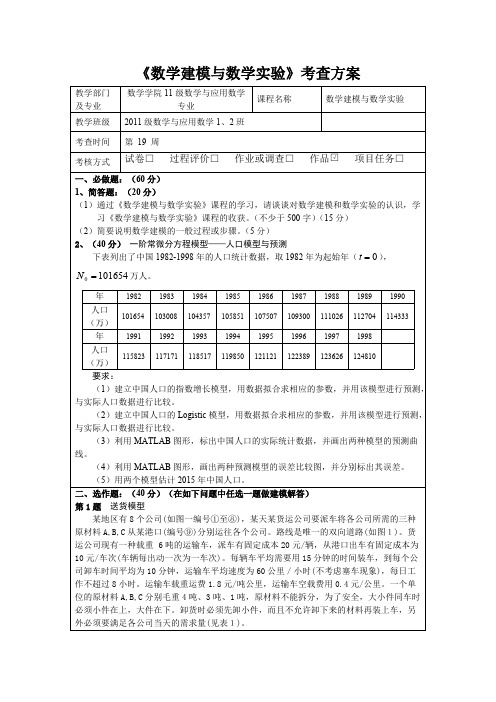
《数学建模与数学实验》考查方案教学部门及专业数学学院11级数学与应用数学专业课程名称数学建模与数学实验教学班级2011级数学与应用数学1、2班考查时间第 19 周考核方式试卷□ 过程评价□ 作业或调查□ 作品 项目任务□ □√一、必做题:(60分)1、简答题:(20分)(1)通过《数学建模与数学实验》课程的学习,请谈谈对数学建模和数学实验的认识,学习《数学建模与数学实验》课程的收获。
(不少于500字)(15分)(2)简要说明数学建模的一般过程或步骤。
(5分)2、(40分) 一阶常微分方程模型——人口模型与预测下表列出了中国1982-1998年的人口统计数据,取1982年为起始年(),0=t 万人。
1016540=N 年198219831984198519861987198819891990人口(万)101654103008104357105851107507109300111026112704114333年19911992199319941995199619971998人口(万)115823117171118517119850121121122389123626124810要求:(1)建立中国人口的指数增长模型,用数据拟合求相应的参数,并用该模型进行预测,与实际人口数据进行比较。
(2)建立中国人口的Logistic 模型,用数据拟合求相应的参数,并用该模型进行预测,与实际人口数据进行比较。
(3)利用MATLAB 图形,标出中国人口的实际统计数据,并画出两种模型的预测曲线。
(4)利用MATLAB 图形,画出两种预测模型的误差比较图,并分别标出其误差。
(5)用两个模型估计2015年中国人口。
二、选作题:(40分)(在如下问题中任选一题做建模解答)第1题 送货模型某地区有8个公司(如图一编号①至⑧),某天某货运公司要派车将各公司所需的三种原材料A,B,C 从某港口(编号⑨)分别运往各个公司。
路线是唯一的双向道路(如图1)。
数学建模期末试题及答案

数学建模期末试题及答案1. 题目描述这是一份数学建模期末试题,包含多个问题,旨在考察学生对数学建模的理解和应用能力。
以下是试题的具体描述及答案解析。
2. 问题一某城市的交通流量与时间呈周期性变化,根据历史数据,可以得到一个交通流量函数,如下所示:\[f(t) = 100 + 50\sin(\frac{2\pi}{24}t)\]其中,t表示时间(小时),f(t)表示交通流量。
请回答以下问题:a) 请解释一下该函数的含义。
b) 根据该函数,该城市的最大交通流量是多少?c) 在哪个时间段,该城市的交通流量较低?【解析】a) 该函数表示交通流量f(t)随时间t的变化规律。
通过观察函数,可以发现交通流量与时间的关系是周期性变化,每24小时一个周期。
函数中的sin函数表示交通流量在周期内的变化,振幅为50,即交通流量的最大值与最小值之差为50。
基准流量为100,表示在交通最不繁忙的时刻,流量为100辆。
b) 最大交通流量为基准流量100辆与振幅50辆之和,即150辆。
c) 交通流量较低的时间段为振幅为负值的时刻,即最小值出现的时间段。
3. 问题二某学校的图书馆借书规则如下:- 学生每次最多可以借5本书,每本书的借阅期限为30天。
- 学生可以在借阅期限结束后进行续借,每次续借可以延长借阅期限30天。
请回答以下问题:a) 一个学生在10天内连续借了3次书,分别是2本、3本和4本,请写出该学生在每次借书后的总借书数。
b) 如果一个学生借了5本书,每本都是在借阅期限后进行续借,借了10年,最后一次续借后,该学生一共续借了几次书?【解析】a) 总的借书数为每次借书的累加和。
学生第一次借2本,总共借书数为2本;第二次借3本,总共借书数为2 + 3 = 5本;第三次借4本,总共借书数为5 + 4 = 9本。
b) 学生每本书借阅期限为30天,10年为3650天,每次借书续借可以延长借阅期限30天。
因此,学生续借次数为10年÷30天= 121次。
2013 – 2014 学年第二学期《数学建模与数学实验》期末考察

2013 – 2014 学年第二学期《数学建模与数学实验》期末考察问题A 题某厂向用户提供发动机,合同规定,第一、二、三季度末分别交货40台、60台、80台.每季度的生产费用为2f+=x)(bxax(单位:元), 其中x是该季度生产的台数.若交货后有剩余,可用于下季度交货,但需支付存储费,每台每季度c元.已知工厂每季度最大生产能力为100台,第一季度开始时无存货,设a=50、b=0.2、c=4,问:工厂应如何安排生产计划,才能既满足合同又使总费用最低.讨论a、b、c变化对计划的影响,并作出合理的解释.B 题讨论资金积累、国民收入与人口增长的关系.(1)若国民平均收入x与人口平均资金积累y成正比,说明仅当总资金积累的相对增长率k大于人口的相对增长率r时,国民平均收入才是增长的.(2)作出k(x)和r(x)的示意图,分析人口激增会导致什么后果.C题交巡警服务平台的设置与调度“有困难找警察”,是家喻户晓的一句流行语。
警察肩负着刑事执法、治安管理、交通管理、服务群众四大职能。
为了更有效地贯彻实施这些职能,需要在市区的一些交通要道和重要部位设置交巡警服务平台。
每个交巡警服务平台的职能和警力配备基本相同。
由于警务资源是有限的,如何根据城市的实际情况与需求合理地设置交巡警服务平台、分配各平台的管辖范围、调度警务资源是警务部门面临的一个实际课题。
试就某市设置交巡警服务平台的相关情况,建立数学模型分析研究下面的问题:(1) 附图1给出了该市中心城区A的交通网络和现有的20个交巡警服务平台的设置情况示意图,相关的数据信息见附件2。
请为各交巡警服务平台分配管辖范围,使其在所管辖的范围内出现突发事件时,尽量能在3分钟内有交巡警(警车的时速为60km/h)到达事发地。
(2) 对于重大突发事件,需要调度全区20个交巡警服务平台的警力资源,对进出该区的13条交通要道实现快速全封锁。
实际中一个平台的警力最多封锁一个路口,请给出该区交巡警服务平台警力合理的调度方案。
数学建模期末练习题

数学建模期末练习题射线扫描成像在医学领域有着广泛的应用。
对于一台射线扫描成像设备,我们将设扫描区域的平面模型为D,该模型区域内有若干个感兴趣的物体O。
设扫描仪的扫描平面为P,我们需要确定物体O的边界曲线在扫描平面P上的投影。
为了简化问题,我们假设扫描区域的边界曲线可以近似为N条不相交的曲线段的集合。
请你通过使用数学建模的方法,给出一种算法来求解物体O在扫描平面P上的投影。
一、问题描述在一台射线扫描成像设备中,我们需要求解物体O在扫描平面P上的投影。
设物体O的边界曲线为C,P的方程为f(x, y) = 0。
我们需要求解物体O的边界曲线在扫描平面P上的参数方程。
二、问题分析1. 对于物体O的边界曲线C,可以通过采集扫描数据得到。
我们可以将C计算为一系列离散的点集。
2. 我们可以通过计算点集C中的每个点在扫描平面P上的投影点,来确定物体O在扫描平面P上的投影。
三、算法设计1. 输入:物体O的边界曲线C,扫描平面P的方程f(x, y) = 0。
2. 遍历曲线C中的每个点(x, y),计算其在平面P上的投影点(x', y'):- 将点(x, y)代入平面P的方程,解得点(x', y'),即为该点在平面P上的投影点。
3. 输出:物体O在扫描平面P上的投影的参数方程。
四、实现步骤1. 遍历物体O的边界曲线C,对于每个点(x, y),计算其在扫描平面P上的投影点(x', y')。
2. 将计算得到的投影点集合按照顺序连接,得到物体O的投影曲线。
3. 输出物体O的投影曲线的参数方程。
五、实例演示假设物体O的边界曲线C为抛物线 y = x^2,扫描平面P的方程为 y = 0。
1. 对于曲线C上的点(1, 1),其在平面P上的投影点为(1, 0)。
2. 对于曲线C上的点(2, 4),其在平面P上的投影点为(2, 0)。
3. 连接投影点(1, 0)和(2, 0),得到物体O在扫描平面P上的投影曲线为线段(x, 0),x ∈ [1, 2]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5题课程安排优化问题
某年级学生共分四个班,现需要为其安排下学期课程表(课程开设及任课教师情况见表1),具体要求如下:
1、每星期一至星期五上午可以安排四节课,下午可以安排两节课,课程安排均为两节连上;
备注:
建模题要求严格按照数学建模的步骤来写论文;建模题最少写5页,正文统一用小四号宋体,1.5倍行距,一级标题用四号加粗宋体,题目用三号加粗宋体。
交卷形式:纸质文档和电子文档;
交卷时间:第20周最后一堂课前上交,过时没交答卷的同学做缺考处理;.
注:如有答卷雷同,则同时计0分,如查实为抄袭网上已有论文计0分。
C4
A4
C4
B4
2
A1
C5
A2
C6
A3
C5
A4
C6
B5
4
A1
C5
A2
C6
A3
C5
A4
C6
(1)请给出你认为比较合理的班级课程安排表;
(2)如果教师上课节数不做限制,请修改你的模型并重新求解;
(3)如果可用排课教室多于4个,请修改你的模型并重新求解。
第6题房地产销售问题
我市某房地产公司通过对历史资料进行回归分析(即数据拟合),并结合2008年上半年可能出现的影响楼盘销售的因素,预测该公司2008年上半年的销售情况如下表所示:
(2)公司销售部门预测:在计划期内的某个月进行降价促销,当产品价格下降为220元/件时,则接下来的两个月中6%的需求会提前到促销月发生。试就一月份(淡季)促销和四月份(旺季)促销两种方案以及不促销最优方案(1)进行对比分析,进而选取最优的产销规划方案。
第8题自命题
要求是自己感兴趣的问题,有一定的难度和一定的现实意义。注:严禁网上直接拷贝。
1993
1994
1995
1996
1997
1998
人口
(万)
115823
117171
118517
119850
121121
122389
123626
124810
要求:
(1)建立中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
(2)建立中国人口的Logistic模型,并用该模型进行预测,与实际人口数据进行比较。
下表列出了中国1982-1998年的人口统计数据,取1982年为起始年( ), 万人, 万人。
年
1982
1983
1984
1985
1986
1987
1988
1989
1990
人口
(万)
101654
103008
104357
105851
107507
109300
111026
112704
114333
年
1991
1992
《数学建模与数学实验》考查方案
教学部门
数学学院
课程名称
数学建模与数学实验
教学班级
2013级信息与计算科学班
考查时间
第20周
一、简答题:(30分)
通过《数学建模与数学实验》课程的学习,请谈谈对数学建模的认识,学习《数学建模与数学实验》课程的收获。(500字左右)
二、建模题:(70分)(任选一题)
第1题一阶常微分方程模型——人口模型与预测
要求:
1、货运公司派出运输车6辆,每辆车从港口出发(不定方向)后运输途中不允许掉头,应如何调度(每辆车的运载方案,运输成本)使得运费最小。
2、每辆车在运输途中可随时掉头,若要使得成本最小,货运公司怎么安排车辆数?应如何调度?
3、(1)如果有载重量为4吨、6吨、8吨三种运输车,载重运费都是1.8元/吨公里,空载费用分别为0.2,0.4,0.7元/公里,其他费用一样,又如何安排车辆数和调度方案?(2)当各个公司间都有或者部分有道路直接相通时,分析运输调度的难度所在,给出你的解决问题的想法(可结合实际情况深入分析)。
该公司希望在上半年就把建造好的房屋全部销售完,为使利润最大化,需要制定出从2008年1月到6月每月的建造计划(即每月完成多少套,以平均每套120平方米计算)。
(1)如果公司的月建造能力没有限制,并允许期房(即尚未建好的房屋)销售,但在6月底前要全部完成交房,如何制定月建造计划?
(2)如果公司的月建造能力限于33套(以平均每套120平方米计算),并且允许期房(即尚未建好的房屋)销售,但在6月底前要全部完成交房,又该如何制定月建造计划?
第7题产销问题
某企业主要生产一种手工产品,在现有的营销策略下,年初对上半年6个月的产品需求预测如表1所示。
表1.产品需求预测估计值(件)
月份
1月
2月
3月
4月
5月
6月
预计需求量
1000
1100
1150
1300
1400
1300
1月初工人数为10人,工人每月工作21天,每天工作8小时,按规定,工人每个月加班时间不得超过10个小时。1月初的库存量为200台。产品的销售价格为240元/件。该产品的销售特点是,如果当月的需求不能得到满足,顾客愿意等待该需求在后续的某个月内得到满足,但公司需要对产品的价格进行打折,可以用缺货损失来表示。6月末的库存为0(不允许缺货)。各种成本费用如表2所示。
要求:
(1)建立狼的运动轨迹微分模型。
(2)画出兔子与狼的运动轨迹图形。
(3)用解析方法求解,问兔子能否安全回到巢穴?
(4)用数值方法求解,问兔子能否安全回到巢穴?
第4题多元回归模型
设某公司生产的商品在市场一的销售价格为 (元/件)、用于商品的广告费用为 (万元)、销售量为 (万件)的连续12个月的统计数据如下表所示。
月份
1 2 3 4 5 6
销售量(套)
42 32 41 67 25 29
该公司的楼盘2007年12月的销售均价为4800元/平方米,平均每套120平方米,2008年上半年的售价保持不变。2007年12月末尚有49套现房未售出。商品房从规划到售出会发生下列费用:(1)建造成本,包括固定成本(主要是指购地、机器设备的折旧)和可变成本(钢材、水泥、装饰材料和人工成本等,其中人工成本在可变成本中占到大约40%),按照2007年12月份的建材价格计算,可变成本(万元)与商品房建造套数(以平均每套120平方米计算)的平方成正比,比例系数为0.5。且可变成本与建材价格上涨幅度有关,例如建材价格上涨10%,则可变成本是按前面方法计算结果的1.1倍。(2)销售费用,与当月销售金额成正比。(3)折旧,建造好的商品房未售出的必须计提折旧,折旧分40年平均摊销,即该公司生产的商品房平均每套每月的折旧为48万元/(40*12)=0.1万元。
近年以来,央行和国家发改委等部门出台了一系列措施平抑建材价格,但由于对建材需求结构而言,总体上求大于供的市场状况没有得到根本改善,预计今年建材的价格仍会有一定的增长。预计的增长速度(以2007年12月的价格为基准)见下表:
月份
1 2 3 4 5 6
增长速度
10% 10% 15% 15% 20% 20%
表2.产品各项成本费用
原材料成本
库存成本
缺货损失
外包成本
培训费用
100元/件
10元/件/月
20元/件/月
200元/件
50元/人
解聘费用
产品加工时间
工人正常工资
工人加班工资
100元/人
1.6小时/件
12元/小时/人
18元/小时/人
(1)若你是公司决策人员,请建立数学模型并制定出一个成本最低、利润最大的最优产销方案;
图1 唯一的运输路线图和里程数
公司
材料
①Байду номын сангаас
②
③
④
⑤
⑥
⑦
⑧
4
1
2
3
1
0
2
5
B
1
5
0
1
2
4
2
3
C
5
2
4
2
4
3
5
1
表1 各公司所需要的货物量
第3题高阶常微分方程模型——饿狼追兔问题
现有一只兔子、一匹狼,兔子位于狼的正西100米处,假设兔子与狼同时发现对方并一起起跑,兔子往正北60米处的巢穴跑,而狼在追兔子。已知兔子、狼是匀速跑且狼的速度是兔子的两倍。
1.问题分析
2.模型假设即补充一些假设条件,使问题简化,但需合理(是此次比赛论文好坏的关键)
3.符号说明
4.模型建立与求解(必要时包括计算方法设计及计算机实现(MATLAB))
5.结果分析与检验(简述)
6.讨论模型的优缺点,改进方向,推广新思想(简述)
7.参考文献(参考文献要在论文中引用)
参考文献在正文引用处用方括号标示参考文献的编号,如[1][3]等,引用书籍还必须指出页码。参考文献按正文中的引用次序列出,其中书籍的表述方式为:
月份
销售价格
广告费用
销售量
1
100
5.50
55
2
90
6.30
70
3
80
7.20
90
4
70
7.00
100
5
70
6.30
90
6
70
7.35
105
7
70
5.60
80
8
65
7.15
110
9
60
7.50
125
10
60
6.90
115
11
55
7.15
130
