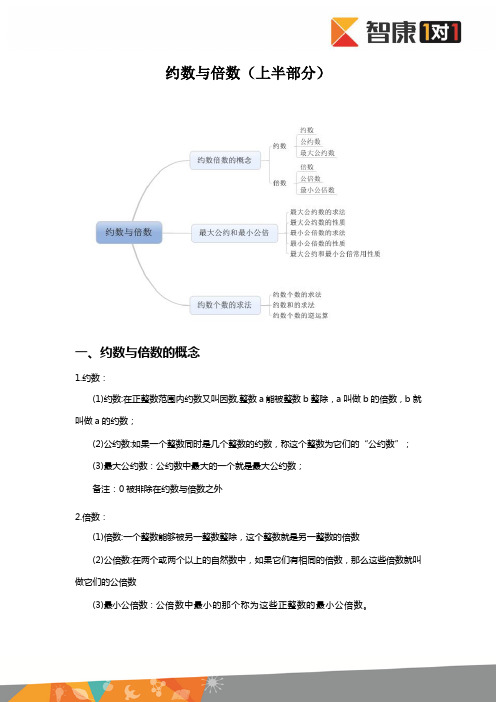
约数与倍数
约数与倍 约数与倍 数
0 ;所以 1515 和 600 的最大公约数是
15. (适用于数比较大,不容易直接找到约数的时候) 分数求公约: 先把带分数化成假分数,其他分数不变;求出各个分数的分母的最小公倍数 a;求出各 个分数的分子的最大公约数 b; 2.最大公约数的性质: ①几个数都除以它们的最大公约数,所得的几个商是互质数; ②几个数的公约数,都是这几个数的最大公约数的约数;
例题 2:一个自然数,它的最大的约数和次大的约数的和是 111,这个自然数是________. 【考点】约数 【难度】3 星 【题型】填空
【关键词】2007 年,第十二届,华杯赛,六年级,决赛,第 7 题 【答案】因为 111 是奇数,而奇数=奇数+偶数,所以所求数的最大约数与次大约数必为 一奇一偶。而一个数的最大约数是其自身,而一个数如有偶约数此数必为偶数,而一个偶数 1 的次大约数应为这个偶数的 ,设这个次大约数为 a,则最大约数为 2a,a+2a=111,求 2 得 a=37,2a=74,即所求数为 74。
b 即为所求. a
③几个数都乘以一个自然数 n , 所得的积的最大公约数等于这几个数的最大公约数乘以
n.
例题 1:2004 的约数中,比 100 大且比 200 小的约数是 【考点】约数 【难度】1 星 【题型】填空
。
【关键词】2004 年,希望杯,第二届,五年级,初赛,第 4 题,5 分 【答案】2004=3×4×167,所以结果为 167
例题 5: N 为自然数,且 N 1 , N 2 、……、 N 9 与 690 都有大于 Biblioteka 的公约数. N 的最 小值为多少?
约数与倍数

约数与倍数基础知识:1. 如果一个自然数a能被自然数b整除,那么称a为b的倍数,b为a的约数.如果一个自然数同时是若干个自然数的约数,那么称这个自然数是这若干个自然数的公约数。
在所有公约数中最大的一个公约数,称为这若干个自然数的最大公约数. 自然数a、b、c的最大公约数通常用符号(a,b,c)表示.例如:(8,12)=4,(6,9,15)=3.2. 互质定义:如果两个或几个数的最大公约数为1,则称这两个或几个数互质.3.如果一个自然数同时是若干个自然数的倍数,那么称这个自然数是这若干个自然数的公倍数.在所有公倍数中最小的一个公倍数,称为这若干个自然数的最小公倍数. 自然数a、b、c的最小公倍数通常用符号[a,b,c]表示.例如:[8,12]=24,[6,9,15]=90.4.约数个数公式、约数和公式.例1.360有多少个约数?[答疑编号5721260101]1【答案】24【解答】,所以360共有24个约数.例2. 一个数是6的倍数,但它的约数之和与6互质,这个数最小是.[答疑编号5721260102]【答案】36【解答】这个数可以表示成,与6互质,所以x≥2,y≥2,故最小数为.基础知识5.求最大公约数和最小公倍数的基本方法:(1)分解质因数法:将每个数分解质因数,观察这些数中包含哪些质因数,①找公共部分,并将这些数的公共部分相乘,所得乘积即为这组数的最大公约数;②观察这些质因数的最高次方,并相乘,所得乘积即为这组数的最小公倍数.(2)辗转相除法: 两数为a、b的最大公约数(a,b)的步骤如下:用b除a,得a=bm......x(0≤x). 若x=0,则(a,b)=b;若x≠0,则再用x除b,得b=xn......y (0≤y).若y=0,则(a,b)=x,若y≠0,则继续用y除x,则继如此下去,直到能整除为止.其最后一个非零除数即为(a,b).2(3)两个数的最大公约数与它们的最小公倍数的乘积等于这两个数的乘积:(a,b)×[a,b] =a×b.例3.甲、乙两个自然数的乘积比甲数的平方小1988,那么满足上述条件的自然数有几组?[答疑编号5721260103]【答案】6组【解答】,由此得a和a-b的值为1988的互补因子.1988有(1+1)×(1+1)×(2+1)=12个约数,所以答案为6组.例4.已知将自然数84的全部约数的乘积分解质因数为,那么△+◇+□等于.[答疑编号5721260104]【答案】24【解答】,它有3×2×2=12个约数.这些约数可以分成两两一组,使得同一组的两个数的乘积就是84,因此所有这些约数的乘积就是 .所以△+◇+□=12+6+6=24.3例5.两数乘积为2800,而且已知其中一数的约数个数比另一数的约数个数多1.那么这两个数分别是 .[答疑编号5721260105]【答案】175和16【解答】,两数的约数个数相差1,则两数约数的个数必为一奇一偶.而一个数的约数个数为奇数,它必为完全平方数,它可能是1、、、、、,经试验只有这个平方数取,另一个数为时,分别有5、6个约数.所以这两个数分别为175和16.例6.三位数A的所有奇约数之和是403,那么A最大可能是多少?[答疑编号5721260106]【答案】900【解答】先考虑A的奇数部分B,利用奇偶分析可知B有奇数个约数,所以B是完全平方数,又403<21×21,所以B只可能是、……可得B=225. 那么A最大是225×4=900.例7.一个正整数是2004的倍数,且恰有24个约数是偶数,那么这个数最多有个约数是奇数.[答疑编号5721260107]4【答案】12【解答】2004是4的倍数,所以偶约数至少是奇约数的2倍,所以为12个.例8.小文买红蓝两种笔各1支用了17元,两种笔的单价都是整元,并且红笔比蓝笔贵.小张打算用35元来买这两种笔(允许全部买其中一种),可是他无论怎样买都不能恰好把35元用完,问红笔、蓝笔每支各多少元?[答疑编号5721260108]【答案】红笔每支13元,蓝笔每支4元【解答】35=5×7,两种笔的单价不能是5元和7元(否则35元可全部用完);由于不是5元和7元,那么也不是17-5=12(元)和17-7=10(元);17元可用完,而35元不能用完,那么笔价不会是35-17=18(元)的约数:1、2、3、6、9、18,当然也不会是17-1=16、17-2=15、17-3=14、17-6=11、17-9=8,故笔价又排除了:1、2、3、6、8、9、11、14、15、16.综上所述,只有4和13未被排除,而4+13=17,所以红笔每支13元,蓝笔每支4元.引例1.求15708和6468的最大公约数、最小公倍数.[答疑编号5721260201]5【解析】方法一:方法二:15708=6468×2+2772 6468=2772×2+9242772=924×3引例2.1007、10017、100117、1001117和10011117的最大公约数是 .[答疑编号5721260202]【答案】53【解析】因为1007×10-10017=53,所以最大公约数肯定是53或1.因为1007=53×19,而且数列中每个数都是前一个数的10倍减去53,所以只要前一个数是53的倍数那么后一个数就也是53的倍数,因此数列中每个数都是53的倍数.例1.已知两数的最大公约数是21,最小公倍数是126,求这两个数的和是多少?[答疑编号5721260203]6【解析】要求这两个数的和,我们可先求出这两个数各是多少.设这两个数为a、b,a<b.因为这两个数的最大公约数是21,故设a=21m,b=21n,且(m,n)=1.因为这两个数的最小公倍数是126,所以126=21×m×n,于是m×n =6,因此,这两个数的和为21+126=147,或42+63=105.所以这两个数的和为147或105.例2.已知自然数A、B满足以下两个性质:(1)A、B不互素;(2)A、B的最大公约数与最小公倍数之和为35.那么A+B的最小值是多少?[答疑编号5721260204]【答案】25【解析】A、B的最大公约数一定是它们最小公倍数的约数.因为A、B的最大公约数与最小公倍数的和是35,所以35是两数最大公约数的倍数.它们的最大公约数可能是5或7.如果A、B的最大公约数是5,则A、B的最小公倍数是30,此时有A=5、B=30或A=10、B=15;如果A、B的最大公约数是7,则A、B的最小公倍数是28,此时有A=7,B =28.所以A+B的最小值为10+15=25.7例3.两个数的最小公倍数比它们的最大公约数的3倍多15,请写出这两个数的所有可能值.[答疑编号5721260205]【答案】1和18, 2和9, 3和24, 5和30,10和15, 15和60 【解析】设两个数a、b,则[a,b]=3×(a,b)+15,且15是(a,b)的倍数,故a和b可以为1和18, 2和9, 3和24, 5和30,10和15, 15和60.例4. 三位数☆◇☆与四位数☆☆◇◇的最大公约数是22,那么☆+◇=.[答疑编号5721260206]【答案】6【解析】两个数的最大公约数是22,☆☆◇◇是11的倍数,所以◇是偶数,22是☆◇☆的约数,☆是偶数,◇=2☆,所以◇=4,☆=2,所以◇+☆=6.例5.试用2,3,4,5,6,7六个数字组成两个三位数,使这两个三位数与540的最大公约数尽可能大?[答疑编号5721260207]8【答案】324、756【解析】因为,而2,3,4,5,6,7中只有一个5,因此这六个数字组成的两个三位数中不会有公约数5,所以这两个三位数与540的最大公约数只可能为,再进行试验,108×2=216,216中1不是已知数字,108×3=324,还剩5,6,7三个数字,而108×7=756,于是问题得到解决.例6.已知甲数的12倍与乙数的15倍的最大公约数是1440,那么甲数和乙数的最大公约数最小可以是多少?[答疑编号5721260208]【答案】24【解析】1440整除12×甲数和15×乙数,所以1440÷12=120和1440÷15=96分别要整除甲数和乙数,所以甲数和乙数的最大公约数至少为(120,96)=24.当甲数和乙数分别为120和96时,它们的最大公约数为24,所以它们的最大公约数最小可以是24.例7.定义表示a和b的最大公约数,那么使得和同时成立的三位数a= .[答疑编号5721260209]【答案】237【解析】根据题意:是21的倍数,所以a是3的倍数,a除以7余6,9a+63是60的倍数,a除以4余1,a除以5余2,所以a=60×4-3=237.例8.已知a与b,a与c,b与c的最小公倍数分别是60,90和36。
倍数与约数的认识与运用

倍数与约数的认识与运用倍数和约数是数学中常见的概念,对于数的性质及其运算具有重要意义。
本文将探讨倍数和约数的概念、性质以及如何运用于实际问题中。
一、倍数的概念和性质倍数是指一个数可以被另一个数整除,某个数的倍数是指可以由该数与任意整数相乘得到的数。
举例来说,6的倍数可以是6、12、18等,因为它们都可以被6整除。
倍数的性质如下:1. 一个数的倍数无穷多。
因为可以通过乘以任意整数,得到该数的任意倍数。
2. 任意一个数都是它自身的倍数。
比如,5是5的倍数,12是12的倍数。
3. 任意一个数的倍数都是它本身的约数。
因为倍数可以整除原数。
二、约数的概念和性质约数是指一个数可以整除另一个数,某个数的约数是指可以整除该数的所有正整数。
例如,12的约数可以是1、2、3、4、6、12。
约数的性质如下:1. 任意一个数的约数都是正整数。
因为约数必须整除原数,而负数和小数无法整除正整数。
2. 一个数的约数个数有限,且不超过它本身的平方根。
例如,12的约数个数为6,而不会大于12的平方根4。
3. 一个数的约数之间具有对称性。
比如,如果a是b的约数,则b 也是a的约数。
三、倍数和约数的运用1. 最大公约数和最小公倍数最大公约数是指两个或多个数共有的约数中最大的一个数。
最小公倍数是指两个或多个数公有的倍数中最小的一个数。
寻找最大公约数和最小公倍数的方法可以借助到倍数和约数的相关性质。
2. 素数的判断素数是指只能被1和自身整除的数,没有其他约数的数。
如果能够通过判断是否有除了1和本身以外的约数,可以确定一个数是否为素数。
3. 分解质因数分解质因数是将一个数分解成若干个素数相乘的形式。
通过对一个数进行质因数分解,可以更好地理解倍数和约数的概念。
4. 问题解决中的运用在实际问题解决中,倍数和约数的概念经常被运用。
例如,在分配任务时,需要考虑人数的约数,以确保任务平均分配;在制定时间表时,需要考虑时间的倍数,以充分利用时间资源。
小学数学中的倍数与约数

小学数学中的倍数与约数在小学数学的学习中,倍数与约数是一个非常基础且重要的概念。
理解了倍数与约数的概念,对于后续数学知识的学习和应用具有很大的帮助。
本文将详细介绍倍数与约数的含义以及相关的性质和应用。
1. 倍数的定义与性质倍数指的是一个数能够被另一个数整除,即后者是前者的倍数。
具体地说,如果存在整数m和n,使得m ×n = a,那么b就是a的倍数。
其中,m为倍数关系的倍数,a为被乘数,n为乘数。
在学习倍数的过程中,我们需要了解和掌握一些倍数的性质:1) 任何数的倍数包括它本身和0。
例如,整数a的倍数包括:a,2a,3a,-a,0等。
2) 一个数的倍数可以无穷多个,也可以没有。
例如,2的倍数有:2,4,6,8,10......而3的倍数有:3,6,9,12,15......3) 两个数的公倍数是它们的倍数的公共部分。
例如,8的倍数有:8,16,24,32......12的倍数有:12,24,36,48......那么8和12的公倍数就是24。
2. 约数的定义与性质约数是指能够整除被除数的数,也可以叫做因数。
具体地说,如果存在整数m和n,使得m × n = a,那么m就是a的约数。
与倍数相似,约数也有一些性质需要我们了解和掌握:1) 除数一定是被除数的约数。
例如,4除以2等于2,说明2是4的约数。
2) 一个数的约数数量是有限的。
例如,数7的约数有1和7,而没有其他的约数。
3) 两个数的公约数是它们的约数的公共部分。
例如,12的约数有:1,2,3,4,6,12,而15的约数有:1,3,5,15,那么12和15的公约数就是1和3。
3. 倍数与约数的关系与应用在小学数学的学习中,倍数与约数的关系是密切相关的。
更准确地说,一个数的倍数同时也是它的约数。
通过对倍数与约数的学习,我们可以应用于以下几个方面:1) 最大公约数:最大公约数即为两个或多个数中最大的公约数。
通过列举数的约数并找到其公共部分即可求出最大公约数。
约数和倍数的意义

contents
目录
• 约数的定义和性质 • 倍数的定义和性质 • 约数和倍数的关系 • 约数和倍数的运算规则
01
CATALOGUE
约数的定义和性质
约数的定义
约数
如果整数a除以整数b(b≠0)所得的商是整数,并且余数是 零,那么我们就说a能被b整除,或b能整除a。此时,我们就 称a是b的一个约数。
约数的定义也可以表述为
如果整数a能被整数b(b≠0)除尽,那么我们说a是b的倍数 ,或b是a的约数。
约数的性质
01
02
03
约数性质1
一个数的约数的个数是有 限的,最小的约数是1, 最大的约数是它本身。
约数性质2
一个数的约数中,最小的 是这个数的质因数分解中 的质因数的幂次的最小值 次幂的乘积。
约数性质3
约数和倍数的除法规则
总结词
约数和倍数的除法规则与普通数的除法规则 相同,即相除时遵循相同的数学运算规则。
详细描述
约数和倍数在进行除法运算时,同样需要遵 循数学中的除法交换律、结合律等基本运算 规则。例如,如果a是b的约数,c是d的约 数,那么a/c的结果仍为b的约数或d的约数 ,同理可证b/c、a/d等结果也满足约数的 性质。
完全倍数
一个数是另一个数的整数倍,这个倍数就是完全倍数。例如,6是2的3倍,3是 3的1倍。
不完全倍数
一个数是另一个数的非整数倍,这个倍数就是不完全倍数。例如,9是3的 2.999...倍。
03
CATALOGUE
约数和倍数的关系
约数和倍数的关系
约数和倍数是两个相互依存的 概念,一个数是另一个数的约 数,另一个数就是它的倍数。
04
CATALOGUE
倍数约数和倍数的应用

倍数约数和倍数的应用倍数、约数和倍数的应用在数学中,倍数和约数是一对重要的概念,它们在实际生活中的应用十分广泛。
本文将详细介绍倍数、约数的概念及其应用,并分析在不同场景下如何使用倍数和约数进行问题求解。
一、倍数的概念及应用倍数是指一个数能够被另一个数整除,也就是说,如果a能够被b整除,那么a就是b的倍数。
例如,24是12的倍数,因为24能够被12整除。
倍数的应用非常广泛,下面我们来看几个实际场景。
1. 班级年级排座位问题在学校的班级里,学生们通常按照某种规则排座位。
假设一个班级有48个学生,老师希望将他们均匀地分成若干组,请问多少人为一组是最合适的?我们可以通过寻找48的所有因数来解决这个问题。
48能被1、2、3、4、6、8、12、16、24、48整除,这些数分别是48的因数。
我们可以发现,48除以2、3、4、6、8、12、16、24、48所得的商分别是24、16、12、8、6、4、3、2、1。
根据排座位的要求,我们可以认为每组最合适的人数就是48的因数中间的那个数,也就是8。
因此,班级里每组最合适的人数是8人。
2. 数列问题在数学中,数列是指按照一定规律排列成的数的集合。
假设有一个数列,其中的数满足每个数都是2的倍数,则这个数列中的数是如何排列的呢?我们可以根据倍数的概念,将数列中的所有数进行递增排列。
例如,2、4、6、8、10……就是一个按照2的倍数排列的数列。
这种排列方式可以帮助我们更好地理解数列中的规律,从而解决数学题目或是应用到实际生活中。
二、约数的概念及应用约数是指一个数能够整除另一个数,也就是说,如果a能够整除b,那么a就是b的约数。
约数的应用同样十分广泛,下面我们来看几个实际场景。
1. 整除问题在实际生活中,经常会涉及到一些整除问题。
例如,某公司要将100个苹果平均分给10个员工,每个员工应该分到多少个苹果?我们可以通过寻找100的所有约数来解决这个问题。
100能被1、2、4、5、10、20、25、50和100整除,这些数分别是100的约数。
四年级数学数的倍数和约数

四年级数学数的倍数和约数数学是一门充满魅力的学科,在学习数学的过程中,我们会遇到许多有趣的概念和知识点。
其中,数的倍数和约数是我们学习数学的基础,它们对理解数学的发展和应用具有重要的意义。
本文将介绍四年级数学中的数的倍数和约数,帮助大家更好地理解和应用这些概念。
一、数的倍数数的倍数是指一个数能够被另一个数整除,也就是说,一个数是另一个数的倍数,通常用乘法来表示。
举个例子,如果我们说4是8的倍数,那么就意味着8能够被4整除。
具体而言,一个数的倍数是由这个数与任意整数相乘得到的。
例如,4的倍数可以是4、8、12、16等。
在计算数的倍数时,有一些基本规律需要注意。
首先,每个数都是其自身的倍数,即任何数乘以1都等于这个数本身。
其次,每个数都是0的倍数,因为任何数乘以0都等于0。
此外,一个正整数的倍数可以是正整数、负整数或零。
例如,4的倍数可以是4、-4、8、-8、12、-12等。
了解数的倍数对解决一些实际问题非常有帮助。
例如,在购物时,如果我们知道某个商品的价格是6元,而我们有12元可以购买多个这个商品,我们可以通过计算12除以6的商,得出我们可以购买2个这个商品。
这个计算过程中,我们就在使用数的倍数的概念。
二、数的约数数的约数是指能够整除一个数的数,也就是说,能够整除一个数的数就是这个数的约数。
例如,6的约数包括1、2、3、6。
一个数的约数有两个特殊的约数,即1和它本身,这是因为任何数除以1和它自己都能得到整数的结果。
在计算数的约数时,我们需要注意以下几点。
首先,一个数的约数的个数是有限的,不会无穷无尽。
其次,对于一个正整数n,它的最小正因数是2,即大于1且小于n的最小整数。
最后,一个数的约数具有一定的规律性,即如果一个数是另一个数的约数,那么这个数的倍数也是这个数的约数。
了解数的约数对于解决一些实际问题也非常有帮助。
例如,我们在分发物品时,如果我们知道有24个物品需要平均分给12个人,我们可以通过计算24除以12的商,得出每个人可以得到2个物品。
了解倍数与约数的定义与判定

了解倍数与约数的定义与判定倍数与约数是数学中常见的概念,对于理解和运用数字关系具有重要意义。
本文将详细介绍倍数与约数的定义以及判定方法,并通过实例来帮助读者更好地理解。
一、倍数的定义与判定倍数是指一个数能够被另一个数整除,即能够用另一个数乘以某个整数获得的数。
具体来说,如果说a能被b整除,那么a就是b的倍数。
例如,6能被2整除,因此6是2的倍数。
判定一个数是否是另一个数的倍数,我们可以使用取余运算来实现。
如果一个数能够被另一个数整除,即余数为0,那么该数就是另一个数的倍数。
例如,我们来判定48是否是8的倍数。
我们可以进行48除以8的运算,结果为6,余数为0。
因此,48是8的倍数。
二、约数的定义与判定约数是指能够整除一个数的数。
换句话说,如果一个数能够被另一个数整除,那么这个数就是另一个数的约数。
例如,2是4的约数,因为2能够整除4。
判定一个数是否是另一个数的约数,我们同样可以使用取余运算。
如果一个数能够整除另一个数,即余数为0,那么该数就是另一个数的约数。
例如,我们来判定12的约数。
我们可以将12除以不同的数,如3、4、6等等。
如果结果的余数均为0,那么这些数就是12的约数。
三、倍数与约数的关系倍数和约数之间存在着密切的关系。
如果一个数x是另一个数y的倍数,那么y一定是x的约数。
相反地,如果一个数x是另一个数y的约数,那么y一定是x的倍数。
这是因为倍数与约数本质上是数的整除关系的两种表达方式。
如果一个数x能够整除另一个数y,那么x就是y的约数,y就是x的倍数。
因此,倍数与约数是相互对应的。
举个例子来说明,我们考虑数字12。
12是3的倍数,同时12的约数有1、2、3、4、6和12。
其中3是12的约数,而12又是3的倍数。
这充分展示了倍数与约数之间的对应关系。
四、实例分析为了更好地理解倍数与约数的定义与判定,我们来分析一个实际问题。
假设我们需要判断一个数x是否是另一个数y的倍数。
我们可以通过以下步骤来进行:1. 用x去除以y,如果余数为0,说明x是y的倍数;2. 如果余数不为0,说明x不是y的倍数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
约数和倍数,最大公约数和最小公倍数
约数和倍数是不同的。
约数又叫因数 factor ,倍数 multiple 。
两者相互依存。
如果 (即 能被 整除), 那么 就是 的倍数, 就是 的约数。
注意:每个数(1除外)至少有两个约数,1和它本身。
1也是这个数最小的约数,它本身是这个数最大的约数。
知识要点
1. 一个数的约数的个数是有限个(finite),但是它的倍数的个数有无限个(infinite)。
2. 约数不大于原数,倍数不小于原数
3. 约数是除法得到的,倍数是乘以一个正整数得到的
4. 约数和倍数都是一系列的数组成的
5. 公因数和最大公因数
6. 公倍数和最小公倍数
7. 分解素因数
8. 辗转相除法
9. 约数个数定理
10. 只在自然数(零除外)范围内研究倍数和因数
约数的个数及个数定理
为了得到一个数的约数个数,首先需要将这个数进行素因数分解,并将结果写成 指数形式,即将相同素因数的乘积写成指数形式,如 。
指数形式:一个合数的约数个数,等于它的素因数分解式中每个素因数的个数(即指数)加1的连乘。
对于一个大于 1 正整数 可以分解质因数:
则 的正约数的个数就是 。
其中 是 的指数
分解素因数是关键
Python 语言中有一个模块 sympy, 其中有一个函数 factorint(n) 就可以分解素因数。
>>> import sympy
>>> sympy.factorint(32)
{2: 5}
>>> sympy.factorint(132)
{2: 2, 3: 1, 11: 1}
>>> sympy.factorint(35)
{5: 1, 7: 1}
>>> sympy.factorint(360)
{2: 3, 3: 2, 5: 1}
>>> sympy.factorint(240)
{2: 4, 3: 1, 5: 1}
p ∣n n p n p p n p 表示k 个p 相乘k n 个a 相乘,记成a ,它是乘法的简写形式。
n N N =p =∏i =1k
i a i p ⋅1a 1p ⋯p 2a 2k a k N f (N )=(a +∏i =1k
i 1)=(a +11)(a +21)⋯(a +k 1)a 、a 、a 、⋯、a 123k p 、p 、p 、⋯、p 123k
>>> import math, sympy
>>> math.gcd(1547,1573)
13
>>> sympy.gcd(1547,1573)
13
>>> from sympy.abc import x
>>> sympy.gcd(x**2 - 1, x**2 - 3*x + 2)
x - 1
例题
例题1 求32的约数个数和各个约数
解:
个约数。
它们分别是 例题2 求35的约数个数和各个约数
解:
个约数。
它们分别是 例题3 求360的约数个数,其中奇数有多少个?
解:
个约数。
奇数约数不能是2的倍数,故只能是3和5的倍数,共有个奇数约数。
例题4 求240的约数个数,它所有约数的乘积有多少个约数?
解:
个约数
20个约数正好可以配成10对,故所有约数乘积为 ,共有 个约数。
例题5 两数乘积为2800,已知其中一个数的约数个数比另一个数的约数个数多1,这两个数分别是多少?
解:一个数的约数个数比另一个数的约数个数多1,则必定有一个数的约数个数是奇数。
, 约数个数为 , 可以拆成 所以这两个数分别是 。
例题6 计算题
∵32=25
∴32有(5+1)=61×32,2×16,4×8
∵35=5×7∴35有(1+1)×(1+1)=41×35,5×7
∵360=2×33×25
∴360有(3+1)×(2+1)×(1+1)=24(2+1)×(1+1)=6∵240=2×43×5,
∴240有(4+1)×(1+1)×(1+1)=20240=10
(2×43×5)=102×403×10510(40+1)×(10+1)×(10+1)=4961∵2800=2×45×27(4+1)×(2+1)×(1+1)=30=5×62×4(5×27)
16和175(1)(391,357),[391,357];(2)(18,24,36),[18,24,36]
解:例题7 求 1547、1573、1859 这三个数的最大公约数和最小公倍数。
解析:表面看,这三个数不容易分解素因数,我们采用辗转相除法。
现在可以分解素因数了。
练习题
1. 72共有多少个约数?其中有多少个约数是3的倍数?
2. 5400共有多少个约数?求出所有约数乘积的素因数分解。
3. 两数乘积为2100,已知其中一个数的约数个数比另一个数的约数个数的2倍还多1,这两个数分别是多少?
4. 计算 (25,105), [25,105], (24,28,42), [24,28,42]
5. (1)求1085和1178的最大公约数和最小公倍数;(2)求3553、3910和1411的最大公约数。
(1)∵391=17×23,357=3×7×17
∴(391,357)=17,[391,357]=3×7×17×23=8211
(2)∵18=2×3,24=22×33,36=2×232
∴(18,24,26)=2×3=6,[18,24,36]=2×33=272
∵1573mod 1547=26,1547mod 26=13,∴13是它们的公约数
∵1573=11×213,1547=7×13×17,1859=11×13,
2∴13是它们的最大公约数,7×11×213=21001×11×13=143143是它们的最小公倍数
6. 自然数是 1,2,3,...,10的倍数,且它恰好有72个约数,那么的最小值是多少?
n n
作业
1. 1350的约数有多少个?其中有多少个是奇数?
2. 在1~600中,恰好有3个约数的数有几个?
3. 将1080分解成两个数的乘积,其中一个数的约数比另一个多1,那么这两个数分别是多少?
4. 计算:(1)gcd(28,72), [28,72]; (2) gcd(28,44,260), [28,44,260]
5. 利用辗转相除法计算: (1) gcd(7191,38211), (2) [693,546,378]。
