高考数学刍甍、羡除、刍童楔形四棱台的体积公式

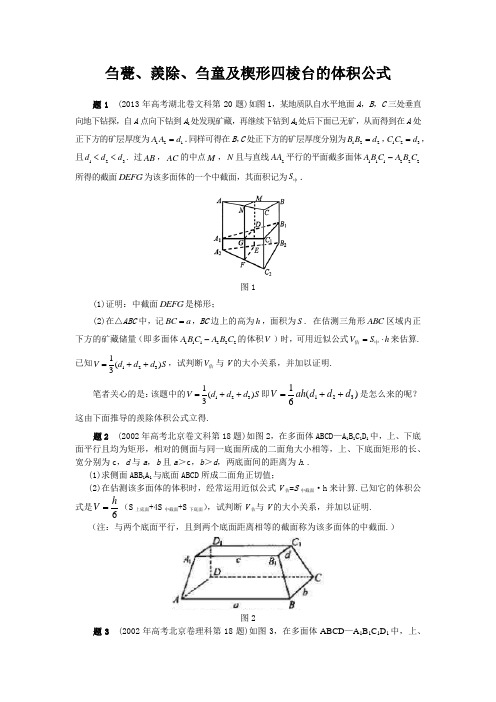
刍甍、羨除、刍童及楔形四棱台的体积公式题1 (2013年高考湖北卷文科第20题)如图1，某地质队自水平地面A ，B ，C 三处垂直向地下钻探，自A 点向下钻到A 1处发现矿藏，再继续下钻到A 2处后下面已无矿，从而得到在A 处正下方的矿层厚度为121A A d =．同样可得在B ，C 处正下方的矿层厚度分别为122B B d =，123C C d =，且123d d d <<. 过AB ，AC 的中点M ，N 且与直线2AA 平行的平面截多面体111222A B C A B C -所得的截面DEFG 为该多面体的一个中截面，其面积记为S 中．图1(1)证明：中截面DEFG 是梯形；(2)在△ABC 中，记BC a =，BC 边上的高为h ，面积为S . 在估测三角形ABC 区域内正下方的矿藏储量（即多面体111222A B C A B C -的体积V ）时，可用近似公式V S h =⋅估中来估算. 已知1231()3V d d d S =++，试判断V 估与V 的大小关系，并加以证明.笔者关心的是：该题中的1231()3V d d d S =++即)(61321d d d ah V ++=是怎么来的呢？这由下面推导的羨除体积公式立得.题2 (2002年高考北京卷文科第18题)如图2，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，上、下底面矩形的长、宽分别为c ，d 与a ，b 且a ＞c ，b ＞d ，两底面间的距离为h .. (1)求侧面ABB 1A 1与底面ABCD 所成二面角正切值；(2)在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是6hV =（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明. （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面.）图2题3 (2002年高考北京卷理科第18题)如图3，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E ，F 两点，上、下底面矩形的长、宽分别为c ，d 与a ，b 且a ＞c ，b ＞d ，两底面间的距离为h ..(1)求侧面ABB 1A 1与底面ABCD 所成二面角的大小； (2)证明：EF//面ABCD(3)在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是6hV =（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明. （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面.）图3笔者关心的是：高考题2,3中的6hV =（S 上底面+4S中截面+S下底面）即[(2)(2)]6hV a c b c a d =+++是怎么来的呢？这由下面推导的刍童体积公式立得.《九章算术·商功》篇有部分题目涉及到刍甍、羨除、刍童及楔形四棱台的体积公式，这些公式秦汉时人都已掌握，下面来推导它们.1.刍甍刍甍是图4所示中的五面体ABCDEF，其中EF DC AB ////，底面ABCD 是平行四边形.设a AB =，直线CD AB 、之间的距离是h ，直线EF 与平面ABCD 之间的距离是H ，则其体积)2(6c a HhV +=.图4证明 如图5所示.设点F E ,在面ABCD 上的射影分别是点F E '',.图5我们把平面ABCD 分成三块区域：区域I 指该平面位于直线AD 左侧的部分(不包括直线AD )，区域II 指该平面夹在直线BC AD 、之间的部分(包括直线这两条直线)，区域III 指该平面位于直线BC 右侧的部分(不包括直线BC ).应分六种情形来证明： (1)点F E '',均位于区域I ；(2)点E '位于区域I ，点F '位于区域II ； (3)点E '位于区域I ，点F '位于区域III ； (4)点F E '',均位于区域II ； (5)点E '位于区域II ，点F '位于区域III ； (6)点F E '',均位于区域III .下面只对情形(5)予以证明：过点E '作CD GH ⊥于H '，交AB 于G ；过点F '作CD IJ ⊥于I ，交AB 于J ，得H E E h GH ='=,，所以=-+=-)(BJIC AGHD FJI EGH V V V V 四棱锥四棱锥直三棱柱 =-+=-+)(32)(32GJIH ABCD BJIC AGHD S S Hc Hh S S H c Hh )2(6)(32c a Hh ch ah H c Hh +=-+=证毕！ 2.羨除羨除是图6所示中的五面体ABCDEF，其中EF DC AB ////，底面ABCD 是梯形.设)(,b a b DC a AB >==，直线CD AB 、之间的距离是h ，直线EF 与平面ABCD 之间的距离是H ，则其体积)(6c b a HhV ++=.图6证明 用补形法可证.图7如图7所示，延长CD 至R ，使RC AB =，得刍甍ABCREF ，由刍甍的体积公式，得)(62)(3)2(6c b a Hh h b a H c a Hh V V V ADR E ABCREF ++=-⋅-+=-=-三棱锥刍甍 注 羨除的体积公式是由刍甍的体积公式推得的；当羨除的下底面梯形变成平行四边形时(即图4所示中的b a =时的情形)，羨除就变成了刍甍，也得刍甍的体积公式是羨除的体积公式的极限情形.3.刍童刍童是图8所示中的六面体D C B A ABCD ''''-，其中面//ABCD 面D C B A ''''，底面ABCD 、底面D C B A ''''均是平行四边形.设b B A a AB =''=,，直线CD AB 、之间的距离是h ，D C B A ''''、之间的距离是h '，面D C B A ABCD ''''、之间的距离是H，则其体积])2()2[(6h a a h a a HV '+'+'+=.图8证明 如图9所示，可得面A B AB ''与平行平面D C B A ABCD ''''、的交线B A AB ''、平行,所以CD B A //''.连结C BD A '',.图9由刍甍的体积公式，得])2()2[(6h a a h a a HV V V D C B A CD ABCD A B '+'+'+=+=''''''刍甍刍甍注 刍童的体积公式是由刍甍的体积公式推得的；当刍童的上底面平行四边形变成线段时(即图4所示中的0='h 时的情形)，刍童就变成了刍甍，也得刍甍的体积公式是刍童的体积公式的极限情形. 4.楔形四棱台楔形四棱台是图10所示中的六面体D C B A ABCD ''''-，其中面//ABCD 面D C B A ''''，底面ABCD、底面D C B A ''''均是梯形.设b D C b B A b CD a AB '=''=''==,,,，面CD AB 、之间的距离是h ，D C B A ''''、之间的距离是h '，面D C B A ABCD ''''、之间的距离是H ，则其体积])()[(6h b b a h a b a HV '+'+'+'++=.图10 图11证明 如图11所示，可得CD B A //''.连结C B D A '',.由羨除的体积公式，得])()[(6h b b a h a b a HV V V D C B A CD ABCD A B '+'+'+'++=+=''''''羡除羡除 注 楔形四棱台的体积公式是由羨除的体积公式推得的；当楔形四棱台的上底面的梯形变成线段时(即图4中的0='h 时的情形)，楔形四棱台就变成了羨除，也得刍甍的体积公式是楔形四棱台的体积公式的极限情形.由刍甍的体积公式可推得羨除、刍童、楔形四棱台的体积公式，由楔形四棱台的体积公式也可推得刍甍的体积公式.题4 (1999年高考全国卷文科、理科第10题)如图12所示，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，23,//=EF AB EF ，EF 与面ABCD 的距离为2，则该多面体的体积为( )A.29 B.5 C.6 D.215图12解 D.由刍甍的体积公式可得.题5 (2007年全国高中数学联赛江苏赛区复赛第一试第9题)如图13，在多面体ABCDEF 中，已知四边形ABCD 是边长为3的正方形，3//,2EF AB EF =.若该多面体的体积为152，则EF 与AC 的距离为 .图13解 2.设直线EF 与平面AC 的距离为H ，由刍甍的体积公式可得153323262H ⋅⎛⎫=⋅+ ⎪⎝⎭2H =进而可得：异面直线,EF AC 的距离为2H =.题6 (2005年高考全国卷I 理科第4题即文科第5题)如图14，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且△ADE 、△BCF 均为正三角形，EF //AB ，EF =2，则该多面体的体积为( )A.32 B.33C.34D.23图14解 A.设棱,AD BC 的中点分别是,S T ，在等腰梯形EFTS 中可得1,2,ST EF ES FT ====，可求得该等腰梯形的高即直线EF 与平面ABCD 的距离22=H . 所以由刍甍的体积公式可得多面体ABCDEF的体积为12(212)63⋅+=. 题7 (1983年美国邀请赛题)图15中的多面体的底面是边长为s 的正方形，上面的棱平行于底面，其长为s 2，其余棱长也都为s ，若26=s ，求这个多面体的体积.图15解 288.由刍甍的体积公式可得(先算得s H 22=).在该题中，当1=s 时就是高考题2.。