高中物理竞赛-原子物理:X光衍射-小角X光散射周期体系等(共40张PPT) 课件
合集下载
高中物理竞赛-原子物理:X光衍射-晶体对X射线的衍射方向(共38张PPT) 课件

dl 1 2 sin q
sinq的最大值为1,可知最小测定d尺寸为l/2, 理论上最大可测尺寸为无穷大,实际上为几个
1 2 sin q dl
q
O 2q
入射线和衍射线之间的夹角为2q ,为实际工作中所 测的角度,习惯上称2q角为衍射角,称q为Bragg角。
关于Bragg方程的讨论
(1) X射线衍射与可见光反射的差异
S0/l
S/l
导出Bragg方程
S/l
q
s
q
S0 /l
| s | 2sin q 1 ld
即l = 2dsinq
导出Laue方程
s
S
S0
l
hb1
kb2
lb3
a1
•
S
S0
l
a1
•
(hb1
kb2
lb3
)
h
a1 • (S S0 ) hl
同理
a2 • (S S0 ) kl a3 • (S S0 ) ll
有些情况下晶体虽然满足布拉格方程,但不一定 出现衍射线,即所谓系统消光
3.1.2 Polyanyi方程
S
S0
a
S0
S
X
光程差
a sin nl
a
X
tg X
D
a l sin
3.1.3 Laue方程
一维点阵的单位矢量为a(即周期为|a|),入射X 光单位矢量为S0,散射单位矢量为S
S
a
C D
(a)可见光在任意入射角方向 均能产生反射,而X射线则 只能在有限的布拉格角方向 1 才产生反射。
(b)虽然Bragg借用了反射几 2 何,但衍射并非反射,而是 一定厚度内许多间距相同晶 面共同作用的结果。
sinq的最大值为1,可知最小测定d尺寸为l/2, 理论上最大可测尺寸为无穷大,实际上为几个
1 2 sin q dl
q
O 2q
入射线和衍射线之间的夹角为2q ,为实际工作中所 测的角度,习惯上称2q角为衍射角,称q为Bragg角。
关于Bragg方程的讨论
(1) X射线衍射与可见光反射的差异
S0/l
S/l
导出Bragg方程
S/l
q
s
q
S0 /l
| s | 2sin q 1 ld
即l = 2dsinq
导出Laue方程
s
S
S0
l
hb1
kb2
lb3
a1
•
S
S0
l
a1
•
(hb1
kb2
lb3
)
h
a1 • (S S0 ) hl
同理
a2 • (S S0 ) kl a3 • (S S0 ) ll
有些情况下晶体虽然满足布拉格方程,但不一定 出现衍射线,即所谓系统消光
3.1.2 Polyanyi方程
S
S0
a
S0
S
X
光程差
a sin nl
a
X
tg X
D
a l sin
3.1.3 Laue方程
一维点阵的单位矢量为a(即周期为|a|),入射X 光单位矢量为S0,散射单位矢量为S
S
a
C D
(a)可见光在任意入射角方向 均能产生反射,而X射线则 只能在有限的布拉格角方向 1 才产生反射。
(b)虽然Bragg借用了反射几 2 何,但衍射并非反射,而是 一定厚度内许多间距相同晶 面共同作用的结果。
2022-2023学年高二物理竞赛课件:晶体的X射线衍射

的几何和与一个电子的散射波的振幅之比, 称为原子散射因子
一个原子内的各个电子散射的电磁波的相互干涉,其结果常用原子散射
因子表示
i 2 sr
f (s) e (r )d
s S S0
描述原子对X射线的散射能力, (r ) 为电子云密度。
第一章要点
Page 4
(3)几何结构因子:
几何结构因子的定义: 原胞内所有t个原子在某一方向上引起的散射波的总振幅与某一电子
元素的非金属性 元素的金属性
Page 7
2、晶体结合的基本类型
晶体结构的物理原因: 结合,结合能, 能量最低原理. 1) 晶体取哪种结构取决于组成这种结构晶体的结合能的大小及热运动 状态, 它与组成物质的原子的电子组态密切相关, 也与晶体的能带结构 及其填充情况相关.
【? 是结构决定电子运动状态还是电子的运动状态决定晶体的结 构? 答: 相互依赖. 】
晶体的X射线衍射第一章要点来自Page 2晶体的X射线衍射
(1)劳厄方程:入射波矢k和散射波矢k0 满足
Rl (k k0 ) 2
k k0 nK h
时,出现晶体对该光的衍射加强--劳厄斑。
建立劳厄衍射方程的基本出发点是:考虑为每一结构基元(相应于点阵点) 的衍射叠加。 建立布拉格衍射方程的基本出发点是:考虑为每组晶面族的反射。
第二章要点
Page 9
共价键的饱和性 共价键只能由未配对的电子形成,同一原子中兩个自旋相反的价电
子也不能与其它原子的电子配对 共价键的方向性
方向性即指只在某一特定方向上形成共价键。由于非満壳层电子分 布的非对称性,因而总是在电子云密度最大的方向成键。这就是共价键 具有方向性的物理本质。电子云交迭得越厉害,共价键越稳固。
2020年高中物理竞赛-原子物理:X光衍射-晶体对X射线的衍射强度(共21张PPT) 课件

面心晶胞:四个原子坐标分别是(0 0 0),(½ ½ 0), (½ 0 ½),(0 ½ ½)
| F | fei2 0 fei2 h/ 2k / 2 fe fe i2 k / 2l / 2 i2 l / 2h/ 2
f 1 ei hk ei kl ei lh
当h, k, l为全奇或全偶,(h+k),(k+l) 和
不同原子的振幅:
A1 A0 exp(i2 s r1)
A2 A0 exp(i2 s r2 )
……
Aj A0 exp(i2 s rj )
A1 A1 A3 AN
A0 exp(i2 s r1) A0 exp(i2 s r2 ) A0 exp(i2 s rN )
N
A0 exp(i2 s rj ) j 1
A(x) A0ei2 sr
S0/l
r为实空间中原子的位置矢量
r u ja1 v ja2 wja3
s为倒易空间中倒易点的矢量
A
S0/l r
s S/l
s
O
S0/l
s hb1 kb2 lb3
s r u ja1 v ja2 wja3 hb1 kb2 lb3
hu j kvj lw j
(h+k)一定是整数,分两种情况:
(1)如果h和k均为偶数或均为奇数,则和为偶数 |F| = 2f |F|2 = 4f 2
(2)如果h和k一奇一偶,则和为奇数 |F| = 0 |F|2 = 0
不论哪种情况,l值对|F|均无影响。111,112,113或021,022,023的|F| 值均为2f。011,012,013或101,102,103的|F|值均为0。
系统消光:由于原子在晶胞中位置不 同而导致某些衍射方向的强度为零
高二物理竞赛X 射线衍射课件
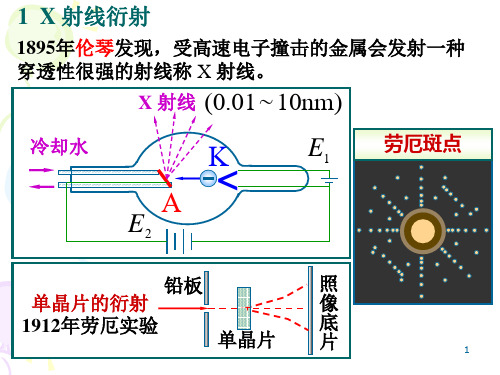
DNA 分子的X衍射照片
DNA 分子的双螺旋结构 3
介绍
大口径全息光栅及其沟槽的部分 显微照片。
用原子力显微镜获得的正
弦相位光栅的浮雕轮廓
4
孔雀羽毛的黄、褐、绿、蓝四色形成“眼”。右下图 为绿色区域的羽支横截面上的纳米尺度周期结构的显 微照片,图中左上白色三角形为羽支中心部分。
(复旦大学资剑教授提供)
暗纹条件: b sin 3 6
2
明纹条件: b sin 3 (2k 1) k 1
2
2
2
8
2. 将一束波长 589nm 的平行光垂直入射在 1cm
内有500条刻痕的平面衍射光栅上,光栅的透光缝宽 度 a 与其间距 b 相等,求:
(1) 光线垂直入射时,能看到几条谱线?哪几级?
d
2 10 6 5.89 107
3.39
kmax 3
故在屏上能看到零级明纹,1, 3 共5条谱线。
10
(2) 倾斜入射 正的级次: d (sin sin ) k1
d
+
0 _
负的级次: d (sin sin ) k211
令
2
正的级次: d(sin sin ) k1
k1
d (sin
1)
2106 (0.5 1) 0.589 106
5.09
k1max 5
负的级次: d (sin sin ) k2
k2
d (sin
1)
2106 (0.5 1) 0.589 106
1.69
k2max 1
12
k1max 5
k2max 1
k 2, 4, 缺级
故在屏上能看到零级明纹,1, 3, 5 共5条谱线。
最新2019-小角X射线散射原理与应用ppt课件-PPT课件

Characterisation of the LDL-MOT drug complexes with SAXS
L D L n a tiv e L D L c o n tro l L D L -M O T (5 0 M O T m o le c u le s p e r L D L )
L D L n a tiv e L D L re c o n s titu te d L D L -M O T (5 0 M O T m o le c u le s p e r L D L )
400 600 800 1000
d
0 200
# d e te c to r c h a n n e l
q : q : q 1 : 2 : 3 1 2 3
Sketch model of lyotropic lamellar liquid crystal
lyotropic Hexagonal liquid crystal
Solution SAX-Scattering of Ag nanoparticles
X-ray power: 2kW (CuKα), exposure-time: 1000 s
Background-subtracted raw-data
1400 1200
Guinier-Plot
3
Intensity (counts)
E 2
比表面
• Porod定理主要提示了散射强度随散射角度变化的渐 近行为。 • 它可用于判断散射体系的理想与否,以及计算不变量 Q和比表面SP等结构参数。
Fractal Systems
Characterization of Fractal System
ln[I(h)h-1]
年高二物理竞赛康普顿散射课件
EK即为K 壳层电子结合能的数值, 从K 壳层发射出来的最大动能Emax为 :
Emax E EK 41.33KeV
例:钨的K吸收限为0.0178nm,K线系的平均波长为 λKα=0.0211nm,λKβ=0.0184nm,λKγ=0.0179nm。
(1)试画出钨的X射线能级图; (2)若用高压为80keV的X射线管产生的辐射照在钨上,
Wn 80 0 80keV
例:钨的K吸收限为0.0178nm,K线系的平均波长为 λKα=0.0211nm,λKβ=0.0184nm,λKγ=0.0179nm。
EK
1240nm eV 0.0178nm
69.7keV
E=0 EN=-0.4keV
n∞ N, n=4
EK
1240nm eV 0.0211nm
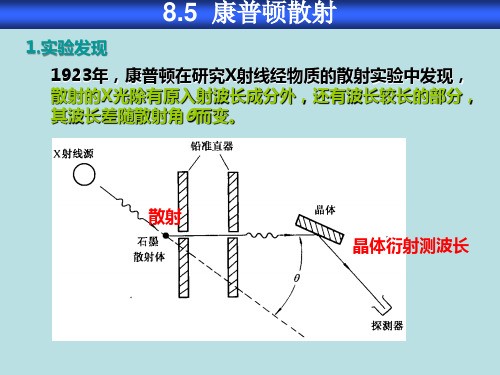
8.5 康普顿散射
1.实验发现
1923年,康普顿在研究X射线经物质的散射实验中发现, 散射的X光除有原入射波长成分外,还有波长较长的部分,
其波长差随散射角θ而变。
散射
晶体衍射测波长
X射线发射谱线波数同X射线吸收限波数的关系: 如:Kα1线是K能级和LIII能级之间 的跃迁产生的,所以Kα1线的波 数等于K吸收限和LIII吸收限波数 只差。
EK
1240nm eV 0.0178nm
69.7keV
EK
1240nm eV 0.0211nm
58.8keV
EK
1240nm eV 0.0184nm
67.4keV
1240nm
EK
eV 0.0179nm
69.3keV
EL EK EK 10.9keV EM EK EK 2.3keV EN EK EK 0.4keV
讨论:
高二物理竞赛课件:X 射线的衍射( diffraction of X-rays )

电子 :0.1A 1A(10 -2 10 -1 nm)
所以电子显微镜分辨本领很高,可观察物质 的结构。
▲ 在正常照明下,人眼瞳孔直径约为3mm,
对 = 0.55 m(5500A )的黄光, 1,
可分辨约 9m 远处的相距 2mm 的两个点 (见书P177例4.2)。 ▲ 夜间观看汽车灯,远看是一个亮点,逐渐 移近才看出是两个灯。
四、实际观察X 射线衍射的作法
1、劳厄法:
使用 连续的X射线照射晶体,得到所有晶
面族反射的主极大。每个主极大对应一个亮斑 (劳厄斑)。这样得到的衍射图叫劳厄 (Laue)相。
此法可定晶轴方向。
准直缝 晶体 X射线
劳厄斑
····
• d•
• •
• • • ••• ••• •••
• • • •
• • • •
••••••
2、粉末法:
SiO2 的劳厄相
用确定 的X射线入射到多晶
粉末。大量无规晶面取向,总
可使布拉格条件满足。这样得
到的衍射图叫德拜 (Dedye)相。
此法可定晶格常数。
粉末铝 的德拜相
五次对称准晶体的 电子衍射图
1984年中国科学院郭可信和叶恒强院士在研究 二十面晶体时,在Ti--Ni--V急冷合金中发现的 五次对称现象,与国外在同年发现的AI--Mn准 晶体有异曲同工之妙。五晶体对称性的发现是 对传统晶体学的突破。
的散射光加强
3 、面间散射光的干涉: AC CB 2d sinΦ
散射光干涉加强条件:
应用
——布拉格公式
已知、 可测d — X 射线晶体结构分析。 已知、d可测 — X 射线光谱分析。
布拉格父子(W.H.Bragg, W.L.Bragg ) 由于利用X射线分析晶体结构的杰出工作, 共同获得了1915年的诺贝尔物理学奖。
所以电子显微镜分辨本领很高,可观察物质 的结构。
▲ 在正常照明下,人眼瞳孔直径约为3mm,
对 = 0.55 m(5500A )的黄光, 1,
可分辨约 9m 远处的相距 2mm 的两个点 (见书P177例4.2)。 ▲ 夜间观看汽车灯,远看是一个亮点,逐渐 移近才看出是两个灯。
四、实际观察X 射线衍射的作法
1、劳厄法:
使用 连续的X射线照射晶体,得到所有晶
面族反射的主极大。每个主极大对应一个亮斑 (劳厄斑)。这样得到的衍射图叫劳厄 (Laue)相。
此法可定晶轴方向。
准直缝 晶体 X射线
劳厄斑
····
• d•
• •
• • • ••• ••• •••
• • • •
• • • •
••••••
2、粉末法:
SiO2 的劳厄相
用确定 的X射线入射到多晶
粉末。大量无规晶面取向,总
可使布拉格条件满足。这样得
到的衍射图叫德拜 (Dedye)相。
此法可定晶格常数。
粉末铝 的德拜相
五次对称准晶体的 电子衍射图
1984年中国科学院郭可信和叶恒强院士在研究 二十面晶体时,在Ti--Ni--V急冷合金中发现的 五次对称现象,与国外在同年发现的AI--Mn准 晶体有异曲同工之妙。五晶体对称性的发现是 对传统晶体学的突破。
的散射光加强
3 、面间散射光的干涉: AC CB 2d sinΦ
散射光干涉加强条件:
应用
——布拉格公式
已知、 可测d — X 射线晶体结构分析。 已知、d可测 — X 射线光谱分析。
布拉格父子(W.H.Bragg, W.L.Bragg ) 由于利用X射线分析晶体结构的杰出工作, 共同获得了1915年的诺贝尔物理学奖。
小角X射线散射简介(课堂PPT)

新型光学附件的 产生可得到平行度较高且通量较 大的X射线。
9
准直系统
小角X射线散射
Gobel Mirror 线平行汇聚光镜
单色性 高强度 准直光束
抛物线型多层膜,利用不同层面材料的晶面间距值不同, 使所有层面的衍射线变为发散度为0.04°的单色平行光。
Lens 点平行汇聚光镜
电光源的发散光经过Lens的数万条异形光导毛细管后, 将:
a. 研究溶液中的微粒;
b. 动态过程研究;
c. 研究高分子材料;
d. 电子显微镜方法不能确定颗粒内部密闭的微孔,SAXS可以;
e. 小角X射线散射可以得到样品的统计平均信息;
f. 小角X射线散射可以准确地确定两相间比内表面和颗粒体积百分数等
参数,而TEM方法往往很难得到这些参量的准确结果,因为不是全部颗
衍射角度:4-170°
由晶格点阵产生的相干散射
样品
小角X射线散射(SAXS) 散射角: 0-4° 由电子密度变化引起的散射
5
小角X射线散射
小角 X射线散射(Small-Angle X-ray Scattering)是一种用 于纳米结构材料的可靠而且经济的无损分析方法。SAXS能 够给出1-100纳米范围内的颗粒尺度和尺度分布以及液体、 粉末和块材的形貌和取向分布等方面的信息。
•在样品颗粒不对称或 表现有择优取向的情 况下分析样品
•HI-STAR探测器是一 种真正意义上的具有 光子计数能力的无噪 实时二维探测器
15
Nanography
新型小角X射线散射技术简介
Nanography 可以得到样品 具有µm量级 SAXS分辨率 的实空间图像。
16
分析软件
新型小角X射线散射技术简介
9
准直系统
小角X射线散射
Gobel Mirror 线平行汇聚光镜
单色性 高强度 准直光束
抛物线型多层膜,利用不同层面材料的晶面间距值不同, 使所有层面的衍射线变为发散度为0.04°的单色平行光。
Lens 点平行汇聚光镜
电光源的发散光经过Lens的数万条异形光导毛细管后, 将:
a. 研究溶液中的微粒;
b. 动态过程研究;
c. 研究高分子材料;
d. 电子显微镜方法不能确定颗粒内部密闭的微孔,SAXS可以;
e. 小角X射线散射可以得到样品的统计平均信息;
f. 小角X射线散射可以准确地确定两相间比内表面和颗粒体积百分数等
参数,而TEM方法往往很难得到这些参量的准确结果,因为不是全部颗
衍射角度:4-170°
由晶格点阵产生的相干散射
样品
小角X射线散射(SAXS) 散射角: 0-4° 由电子密度变化引起的散射
5
小角X射线散射
小角 X射线散射(Small-Angle X-ray Scattering)是一种用 于纳米结构材料的可靠而且经济的无损分析方法。SAXS能 够给出1-100纳米范围内的颗粒尺度和尺度分布以及液体、 粉末和块材的形貌和取向分布等方面的信息。
•在样品颗粒不对称或 表现有择优取向的情 况下分析样品
•HI-STAR探测器是一 种真正意义上的具有 光子计数能力的无噪 实时二维探测器
15
Nanography
新型小角X射线散射技术简介
Nanography 可以得到样品 具有µm量级 SAXS分辨率 的实空间图像。
16
分析软件
新型小角X射线散射技术简介
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WAXS分析
如果发生共晶
(a)
(010) (011)
PET
(100)
(1)晶格参数应按摩尔分数线性加
a=fPEIaPEI+ fPETaPET
110
含5mol%IPT的共聚物100衍射 100
应向低角区移动0.2
90
5IPT 10IPT
பைடு நூலகம்18
21
24
27
2 (deg)
(011) (010) (100)
Lc(Å)
dac
da or dc
z
(102 nm-6)
3
PE at 31C
c=0.85
2
S/V=0.065nm-1
1
0
-1
0 10 20 30 40 50
z (nm)
inter-layer correlation peak
PET共聚物的结晶行为
Time-resolved X-ray scattering and calorimetric studies on the crystallization behaviors of poly(ethylene terephthalate) (PET) and its copolymers containing isophthalate units
dc基本不受共聚组成的 影响,表明IPT不在晶 格之中
共聚单元含量越高, da越大,表明IPT处于 无定形区
dc(Å)
da (Å)
130 120 110 100 90 80 70 60
55
50
45
40
35 165
PET 5IPT 10IPT
180 195 210 225
Tc(C)
Intensity (a.u.)
(2)衍射峰应有加宽 实验没有发现
80
70 (b)
60
0
5
10
IPT Content(mol.-%)
Heat flow (mW)
DSC熔点观察
0
-1000
-2000
10IPT(208)
5IPT(208) PET(230)
210 220 230 240 250 260
括号中为结晶温度
T (C)
均可发现两个熔点,低温熔点为二次结晶,高温熔点为主结晶
根据熔融热求得结晶度 (完全结晶均聚物H=117.6J/g)
结晶度与积分不变量的关系:
Q xc (1 xc )(c a )2
回想
Q V ( )212
(z)-z曲线的最初下降斜率外推至z=0,即求得Q
100
50
95
40
85
75
30
60
20
31°C
10
0 0 0.2
0.4 0.6 q (nm-1)
0.8 1.0
利用相关函数计算体积分数
(z) I (q)q2 cos(qz)dq
0
4
c
1 4
S V
dc
a
1 4
S V
da
S 4 V (da dc )
Q ( )212
d / dz ()2 / dac
γ(z)/γ(0)
1
L
0
-1 l1
10
30
z(nm)
PET crystallized at 210C
发现
➢l1总是小于l2 ➢同样过冷度结晶的PET的l1总是大于共聚物, l2 总是小于共聚物 ➢PET的熔点总是高于共聚物,表明晶片厚
推断
l1代表晶片厚度dc, l2代表无定形区厚度da
L(Å)
da (Å)
(a) 3200
(b)
3200
2800
2800
2400
2400
Intensity (a.u.)
t(s)
Intensity (a.u.)
t(s)
2000
2000
时间分
解的小
1600
1600
角X光
1200
1200
衍射
800
800
400
400
0
0
0.3 0.6 0.9 1.2 1.5
q (nm-1)
0.3 0.6 0..9 1.2 1.5
160 150 140 130 120 110 100 90 80 70 60 50 40
0
230C 220C 210C 205C 200C 195C 190C 170C
(a)PET
700
1400 2100
t(s)
dc(Å)
da (Å)
L(Å)
160 150 140 130 120 110 100 90 80 70 60 50 40
2020高中物理竞赛
原子物理——X光衍射
6.5 周期体系
dc
da dac
dac
dac
dc
da
利用Fourier逆变换构造一维相关函数
(z) 1 I (q)q2eiqzdq 1 I (q)q2 cos(qz)dq
2
0
采用相对强度时一般使用归一化的相关函数(z)
I (q)q2 cos(qz)dq I (q)q2 cos(qz)dq
Polymer 44 (2003) 2509–2518
研究主题:IPT是否参与结晶?
共聚物的制备路线
PET:Mw=36000 Tm0=275.4C
5IPT: Mw=37000 Tm0=266.5C
10IPT: Mw=36000 Tm0=261.9C
5IPT:IPT4.9mol%, 10IPT:IPT9.8mol%
q (nm-1)
(a) PET isothermal crystallization at 230C
(b) 5IPT at 216C 随结晶的进行峰出现、变大,峰位向高q值移动,即长周期变小
从强度分布I(q)经Fourier逆变换得到一维相关函数 (z)/(0) ,从中得到长周期 L和一个厚度 l1, l2 =L- l1
0
220C 210C 200C 195C 190C 185C 180 C
(b)5IPT
500 1000 1500 2000 2500
t(s)
dc(Å)
等温结晶过程中,L、da随时间下降,dc基本不变 不同结晶温度的dc不同
dc 尺 寸 在 38-58Å, 相 当 于4-6个ET单元,而共聚 物中IPT单元的间隔平均 为26-38个ET单元,足以 将IPT排除在晶格之外
1(z) 0
0
I (q)q2dq
Q
0
理想周期体系的相关函数如下:称为自相关三角形
A
1 (z)
OC B
D
d E
z
2d
OA (0) 1
BD da ad
BO (da ) a / b
BA 1/ b
OC abd AD 的斜率 1/ abd
由于各种非理想因素,实际得到的相关函数如下
1.0
0.5
1(z)
0.0
-0.5 0
1
2
x/d
OA (0) 1
BD da ad
A
BO (da ) a / b
BA 1/ b
OC abd AD 的斜率 1/ abd
1(z)
O
C
B
D
d
PE在125C完成主结晶后冷却
q2 /e2(103 nm-6)
80
125°C
70
110
60
105
