二次函数与几何综合——面积问题
九年级数学上册:动态几何中面积问题与二次函数结合

在九年级数学上册中,动态几何和二次函数是两个重要的内容,它们在数学中都占据着重要的地位。
而将动态几何中的面积问题与二次函数结合起来,则能够更深入地理解这两个内容,并发现它们之间的联系和应用。
接下来,我将以从简到繁、由浅入深的方式,探讨九年级数学上册中动态几何中面积问题与二次函数的结合。
1. 动态几何中的面积问题动态几何是指随着图形形状的变化而变化的几何学问题。
在九年级数学上册中,我们学习了一些常见的动态几何问题,比如图形的变化规律、面积的变化等。
在动态几何中,面积问题是一个重要的内容,我们常常需要根据图形的形状变化来求解图形的面积。
2. 二次函数的基本概念二次函数是数学中的重要内容之一,它的图像是一个抛物线。
在九年级数学上册中,我们学习了二次函数的基本概念,包括二次函数的一般式和顶点式等。
了解二次函数的基本概念,可以帮助我们更好地理解和应用二次函数。
3. 面积问题与二次函数的结合将动态几何中的面积问题与二次函数结合起来,可以帮助我们更深入地理解这两个内容,并发现它们之间的联系和应用。
在实际问题中,常常会遇到需要求解动态几何图形的面积,而这时候可以借助二次函数的知识来求解。
4. 个人观点和理解我认为,动态几何中的面积问题与二次函数的结合,不仅能够帮助我们更深入地理解这两个内容,而且还能够拓展我们的数学思维,提高我们的数学应用能力。
通过综合运用动态几何和二次函数的知识,可以更好地解决实际生活中的问题,并培养我们的创新意识和解决问题的能力。
总结在九年级数学上册中,动态几何中的面积问题与二次函数的结合,是一个重要而有价值的内容。
通过学习和掌握这个内容,可以帮助我们更好地理解动态几何和二次函数,并且提高我们的数学应用能力和创新意识。
期待通过文章的阐述,你能更全面、深刻和灵活地理解这个主题。
通过这篇文章,我希望你能够更深入地理解九年级数学上册中动态几何中面积问题与二次函数的结合,并且能够在实际问题中灵活运用这些知识。
5二次函数与几何综合(2013-2014)

2014年中考解决方案和二次函数相关的面积学生姓名:上课时间:本讲属于二次函数几何综合的一个模块。
和二次函数相关的面积类问题经常会在压轴题出现,尤其是代数几何综合题,而九年级上的期末试卷中也会常常出现。
通过此讲,学生应该掌握基本的面积计算方法并体会方程思想在此讲的应用☞考点说明:求三角形面积有方法3 方法一:补形法图①ABC OBC OAC OAB S S S S =+-△△△△,图②ABC BCD AOB ACDO S S S S =--△△△梯形 图③+ABC ACD AOB BODE S S S S =-△△△梯形,图④ABC ADEO ACD BCE AOB S S S S S =---△△△△矩形④③②①E DD D xy OABCxy OABCx y OABCC BAOy x方法二:分割法图⑤+ABC ACD BCD S S S =△△△,图⑥+ABC BCD ABD S S S =△△△12ABC A B S CD x x =⋅△-,12ABC A C S BD y y =⋅△-⑤Dxy OABC⑥xy OABC D方法三:平行线转化法图⑦ABC BDA S S =△△(过C 点作AB 的平行线CD ,则两三角形同底等高)中考说明 和二次函数相关的面积例题精讲⑦CBA Oy xD一、 坐标系中的面积【例1】 在平面直角坐标系中,已知抛物线经过A (-4,0),B (0,-4),C (2,0)三点.(1)求抛物线的解析式.(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)探究当S 取最大值时,点M 的横坐标m 与A 、B 两点横坐标的关系.xyO BC MA【巩固】已知:抛物线c x ax y ++=22,对称轴为直线1-=x ,抛物线与y 轴交于点C ,与x 轴交于()0,3-A 、B 两点.(1)求直线AC 的解析式;(2)若点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值;yxO DCB A【例2】 已知抛物线c bx x y ++=2的顶点为P ,与y 轴交于点A ,与直线OP 交于点B .(1)如图1,若点P 的横坐标为1,点B 的坐标为(3,6),试确定抛物线的解析式; (2)在(1)的条件下,若点M 是直线AB 下方抛物线上的一点,且B 3A M S ∆=,求点M 的坐标;AAP PBOOxxyy图1 图2【巩固】如图,抛物线y =ax2+3x +a +5与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C (0,4),D 为OC 的中点. (1)求a 的值;(2)在抛物线的对称轴上是否存在点G ,使△GBC 中BC 边上的高为522?若存在,求出点G 的坐标;若不存在,请说明理由.AB C O yxED【例3】 如图, 已知抛物线经过坐标原点O 及)0,32( A ,其顶点为B (m ,3),C 是AB 中点,点E 是直线OC 上的一个动点 (点E 与点O 不重合),点D 在y 轴上, 且EO =ED .(1)求此抛物线及直线OC 的解析式;(2)连接AD , 当点E 运动到何处时,△AED 的面积为433,请直接写出此时E 点的坐标. y xOC B A【巩固】在平面直角坐标系xOy 中,抛物线222y x mx m m =-++的顶点为C .(1)求点C 的坐标(用含m 的代数式表示);(2)直线2y x =+与抛物线交于A 、B 两点,点A 在抛物线的对称轴左侧,若P 为直线OC 上一动点,求△APB 的面积;【例4】 已知:如图,抛物线22(0)y ax ax c a =-+≠与y 轴交于点(0,3)C ,与x 轴交于A 、B 两点,点A 的坐标为(1,0)-.(1)求抛物线的解析式及顶点D 的坐标;(2)设点P 是在第一象限内抛物线上的一个动点,求使与四边形ACDB 面积相等的四边形ACPB 的点P 的坐标;y xODCB A【巩固】如图,已知点A(23,2),点B(4,0),将△OAB绕点O顺时针旋转α角(0°<α<90°)得到△OCD(O、A、B的对应点分别为O、C、D),将△OAB沿x轴负方向平移m个单位得到△EFG(m>0,O、A、B的对应点分别为E、F、G),α,m的值恰好使点C、D、F落在同一反比例函数y=kx(k≠0)的图象上.(1)∠AOB=________°, =________°;(2)求经过点A、B、F三点的抛物线的解析式;(3)若(2)中抛物线的顶点为M,抛物线与直线EF的另一个交点为H,抛物线上的点P满足以P、M、F、A为顶点的四边形的面积与四边形MFAH的面积相等(点P不与点H重合),请直接写出满足条件的点P的个数,并求位于直线EF上方的点P的坐标.O AB xyO AB xy备用图二、 二次函数与动点图形面积☞考点说明:因为动点产生的面积问题,需要考虑动点的运动情况,及分类讨论【例5】 如图,在直角坐标系中,梯形ABCD 的底边AB 在x 轴上,底边CD 的端点D 在y 轴上,直线CB的表达式为y =-4 3x +163,点A ,D 的坐标分别为(-4,0),(0,4).动点P 自A 点出发,在AB 上匀速运行,动点Q 自点B 出发,在折线BCD 上匀速运行,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动.设点P 运动t (秒)时,△OPQ 的面积为S (不能构成△OPQ 的动点除外).(1)求出点B ,C 的坐标;(2)求S 随t 变化的函数关系式(注明t 的取值范围); (3)当t 为何值时S 有最大值?并求出最大值.BCOAxyDP QB CO Ax yD(备用图1)B CO A xyD(备用图2)【巩固】如图,梯形ABCD 中,AD ∥BC ,∠BAD =90°,CE ⊥AD 于点E ,AD =8cm ,BC =4cm ,AB =5cm .从初始时刻开始,动点P 、Q 分别从点A 、B 同时出发,运动速度均为1cm/s ,动点P 沿A →B →C →E 的方向运动,到点E 停止;动点Q 沿B →C →E →D 的方向运动,到点D 停止,设运动时间为x s ,△PAQ 的面积为y cm 2.(这里规定:线段是面积为0的三角形)解答下列问题: (1)当x =2s 时,y =_________cm 2;当x = 92 s 时,y =_________cm 2;(2)当5≤x ≤14时,求y 与x 之间的函数关系式;(3)当动点P 在线段BC 上运动时,求出使y = 415 S 梯形ABCD 的x 的值;【选作】直接写出在整个运动过程中,使PQ 与四边形ABCE 的对角线平行的所有x 的值.CD A BE PQ CDA BE备用图【例6】 (11年中考)如图,在直角梯形ABCD 中,∠D =∠BCD =90°,∠B =60°,AB =6,AD =9,点E 是CD 上的一个动点(E 不与D 重合),过点E 作EF ∥AC ,交AD 于点F (当E 运动到C 时,EF 与AC 重合),把△DEF 沿着EF 对折,点D 的对应点是点G .设DE =x ,△GEF 与梯形ABCD 重叠部分的面积为y .(1)求CD 的长及∠1的度数;(2)若点G 恰好在BC 上,求此时x 的值;(3)求y 与x 之间的函数关系式,并求x 为何值时,y 的值最大?最大值是多少?ABCEDFG1【巩固】如图,矩形ABCD 中,AB =6,BC =23,点O 是AB 的中点,点P 在AB 的延长线上,且BP =3.一动点E 从O 点出发,以每秒1个单位长度的速度沿OA 匀速运动,到达A 点后,立即以原速度沿AO 返回;另一动点F 从P 点出发,以每秒1个单位长度的速度沿射线PA 匀速运动,点E 、F 同时出发,当两点相遇时停止运动,在点E 、F 的运动过程中,以EF 为边作等边△EFG ,使△EFG 和矩形ABCD 在射线PA 的同侧.设运动的时间为t 秒(t ≥0). (1)当等边△EFG 的边FG 恰好经过点C 时,求运动时间t 的值;(2)在整个运动过程中,设等边△EFG 和矩形ABCD 重叠部分的面积为S ,请直接写出S 与t 之间的函数关系式和相应的自变量t 的取值范围;A B CDO F PE三、抛物线内特殊三角形的面积☞考点说明: 我们经常会碰到特殊ABC △,其中点A 、B 分别为二次函数与x 轴的两个交点,C 为抛物线的顶点,则三角形的面积公式是328ABC S a =△△ ① 若ABC △为直角三角形时,21ABC S a=△② 若ABC △为等边三角形时,233ABC S a=△ 记住这些公式,会有助于我们提高做题速度CyxOB A【例1】 已知二次函数图2+y x bx c =+像的对称轴在y 轴的右侧,且图像与y 轴交于点(03)D ,,与x 轴交于A 、B 两点,顶点为C ,ABC △的面积为8,则二次函数的解析式为________【巩固】k 为何值时,抛物线23+4y x kx k =+与x 轴的两交点A 、B 及顶点C 满足90ACB ∠=°【题1】已知:如图,抛物线22y ax ax c =-+ (0a ≠)与y 轴交于点C ( 0 ,4) ,与x 轴交于点A ,B ,点A 的坐标为( 4 ,0). (1) 求该抛物线的解析式;(2)点Q 是线段AB 上的动点,过点Q 作QE ∥AC ,交BC 于点E ,连接CQ . 当CQE ∆的面积最大时,求点Q 的坐标;课后作业【题2】如图1,在平面直角坐标系xOy 中,直线l :34y x m =+与x 轴、y 轴分别交于点A 和点B (0,-1),抛物线212y x bx c =++经过点B ,且与直线l 的另一个交点为C (4,n ). (1) 求n 的值和抛物线的解析式;(2) 点D 在抛物线上,且点D 的横坐标为t (0< t <4).DE ∥y 轴交直线l 于点E ,点F 在直线l 上,且四边形DFEG 为矩形(如图2).若矩形DFEG 的周长为p ,求p 与t 的函数关系式以及p 的最大值;图1图2【题3】已知二次函数23332-+-=mx mx y 的图象与x 轴交于点A (23,0)、点B ,与y 轴交于点C . (1)求点B 坐标;(2)点P 从点C 出发以每秒1个单位的速度沿线段CO 向O 点运动,到达点O 后停止运动,过点P 作AC PQ //交OA 于点Q ,将四边形PQAC 沿PQ 翻折,得到四边形''C PQA ,设点P 的运动时间为t .①当t 为何值时,点'A 恰好落在二次函数23332-+-=mx mx y 图象的对称轴上; ②设四边形''C PQA 落在第一象限内的图形面积为S ,求S 关于t 的函数关系式,并求出S 的最大值.。
二次函数的应用(面积最值问题)

二次函数的应用(面积最值问题)[例1]:在矩形ABCD 中,AB=6cm ,BC=12cm ,点P 从点A 出发,沿AB 边向点B 以1cm /s 的速度移动,同时点Q 从点B 出发沿BC 边向点C 以2cm /s 的速度移动,如果P 、Q 两点同时出发,分别到达B 、C 两点后就停止移动.(1)运动第t 秒时,△PBQ 的面积y(cm²)是多少? (2)此时五边形APQCD 的面积是S(cm²),写出S 与t 的函数关系式,并指出自变量的取值X 围.(3)t 为何值时s 最小,最小值时多少? 答案:6336333607266126262621)1(2222有最小值等于时;当)()()()()()(S t t S t t t t t S tt t t y =∴+-=<<+-=+--⨯=+-=⋅-=[例2]:小明的家门前有一块空地,空地外有一面长10米的围墙,为了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的方便,准备在花圃的中间再围出一条宽为一米的通道与在左右花圃各放一个1米宽的门(木质).花圃的长与宽如何设计才能使花圃的面积最大?解:设花圃的宽为x 米,面积为S 平方米则长为:x x 4342432-=+-(米)则:)434(x x S -=x x 3442+-=4289)417(42+--=x ∵104340≤-<x∴2176<≤x∵6417<,∴S 与x 的二次函数的顶点不在自变量x 的X 围内, 而当2176<≤x 内,S 随x 的增大而减小,∴当6=x 时,604289)4176(42max =+--=S (平方米) 答:可设计成宽6米,长10米的矩形花圃,这样的花圃面积最大.[例3]:已知边长为4的正方形截去一个角后成为五边形ABCDE (如图),其中AF=2,BF=1.试在AB 上求一点P ,使矩形PNDM 有最大面积. 解:设矩形PNDM 的边DN=x ,NP=y , 则矩形PNDM 的面积S=xy (2≤x≤4) 易知CN=4-x ,EM=4-y . 过点B 作BH ⊥PN 于点H 则有△AFB ∽△BHP ∴PHBHBF AF =,即3412--=y x , ∴521+-=x y , x x xy S 5212+-==)42(≤≤x ,此二次函数的图象开口向下,对称轴为x=5, ∴当x≤5时,函数值y 随x 的增大而增大, 对于42≤≤x 来说,当x=4时,12454212=⨯+⨯-=最大S . 【评析】本题是一道代数几何综合题,把相似三角形与二次函数的知识有机的结合在一起,能很好考查学生的综合应用能力.同时,也给学生探索解题思路留下了思维空间.[例4]:某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.4米的正方形ABCD ,点E 、F 分别在边BC 和CD 上,△CFE 、△ABE 和四边形AEFD 均由单一材料制成,制成△CFE 、△ABE 和四边形AEFD 的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按图(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH .(1)判断图(2)中四边形EFGH 是何形状,并说明理由;(2)E 、F 在什么位置时,定制这批地砖所需的材料费用最省? 解:(1) 四边形EFGH 是正方形.图(2)可以看作是由四块图(1)所示地砖绕C 点 按顺(逆)时针方向旋转90°后得到的, 故CE =CF =CG .∴△CEF 是等腰直角三角形因此四边形EFGH 是正方形.(2)设CE =x , 则BE =0.4-x ,每块地砖的费用为y 元那么:y =x ×30+×0.4×(0.4-x )×20+[0.16-x -×0.4×(0.4-x )×10])24.02.0(102+-=x x3.2)1.0(102+-=x )4.00(<<x当x =0.1时,y 有最小值,即费用为最省,此时CE =CF =0.1.答:当CE =CF =0.1米时,总费用最省.作业布置:1.(2008XXXX)某人从地面垂直向上抛出一小球,小球的高度h (单位:米)与小球运动时间t (单位:秒)的函数关系式是,那么小球运动中的最大高度=最大h 4.9米.2.(2008庆阳市)XX 市“安居工程”新建成的一批楼房都是8层高,房子的价格y (元/平方米)随楼层数x (楼)的变化而变化(x =1,2,3,4,5,6,7,8);已知点(x ,y )都在一个二次函数的图像上,(如图所示),则6楼房子的价格为元/平方米.5 m 12m ABCD提示:利用对称性,答案:2080.3.如图所示,在一个直角△MBN 的内部作一个长方形ABCD ,其中AB 和BC 分别在两直角边上,设AB =x m ,长方形的面积为y m 2,要使长方形的面积最大,其边长x 应为( D )A .424m B .6 m C .15 m D .25m 解:AB =x m ,AD=b ,长方形的面积为y m 2∵AD ∥BC ∴△MAD ∽△MBN ∴MB MA BN AD =,即5512x b -=,)5(512x b -= )5(512)5(5122x x x x xb y --=-⋅==, 当5.2=x 时,y 有最大值.4.(2008XXXX)将一X 边长为30㎝的正方形纸片的四角分别剪去一个边长为x㎝的小正方形,然后折叠成一个无盖的长方体.当x取下面哪个数值时,长方体的体积最大( C ) A .7 B .6 C .5 D .45.如图,铅球运动员掷铅球的高度y (m)与水平距离x (m)之间的函数关系式是:35321212++-=x x y ,则该运动员此次掷铅球的成绩是( D ) A .6 mB .12 mC .8 mD .10m解:令0=y ,则:02082=--x x 0)10)(2(=-+x xxyOAM (图5) (图7) 6.某幢建筑物,从10 m 高的窗口A ,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图6,如果抛物线的最高点M 离墙1 m ,离地面340m ,则水流落地点B 离墙的距离OB 是( B )A .2 mB .3 mC .4 mD .5 m解:顶点为)340,1(,设340)1(2+-=x a y ,将点)10,0(代入,310-=a 令0340)1(3102=+--=x y ,得:4)1(2=-x ,所以OB=37.(2007乌兰察布)小明在某次投篮中,球的运动路线是抛物线21 3.55y x =-+的一部分,如图7所示,若命中篮圈中心,则他与篮底的距离L 是( B ) A .4.6m B .4.5m C .4m D .3.5m8.某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD ,花园的一边靠墙,另三边用总长为40m 的栅栏围成.若设花园的宽为x(m) ,花园的面积为y(m²).(1)求y 与x 之间的函数关系,并写出自变量的取值X 围;(2)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当x 取何值时,花园的面积最大,最大面积是多少? 解:)240(x x y -=)20(22x x --=200)10(22+--=x∵152400≤-<x ∴205.12<≤x∵二次函数的顶点不在自变量x 的X 围内, 而当205.12<≤x 内,y 随x 的增大而减小, ∴当5.12=x 时,5.187200)105.12(22max =+--=y (平方米)答:当5.12=x 米时花园的面积最大,最大面积是187.5平方米.9.如图,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50 m 长的篱笆围成中间有一道篱笆隔墙的养鸡场,设它的长度为x 米.(1)要使鸡场面积最大,鸡场的长度应为多少m ? (2)如果中间有n (n 是大于1的整数)道篱笆隔墙,要使鸡场面积最大,鸡场的长应为多少米?比较(1)(2)的结果,你能得到什么结论?解:(1)∵长为x 米,则宽为350x-米,设面积为S 平方米. )50(313502x x x x S --=-⋅= 3625)25(312+--=x ∴当25=x 时,3625max =S (平方米)即:鸡场的长度为25米时,面积最大. (2)中间有n 道篱笆,则宽为250+-n x米,设面积为S 平方米. 则:)50(212502x x n n x x S -+-=+-⋅= 2625)25(212++-+-=n x n ∴当25=x 时,2625max +=n S (平方米)由(1)(2)可知,无论中间有几道篱笆墙,要使面积最大,长都是25米. 即:使面积最大的x 值与中间有多少道隔墙无关.10.如图,矩形ABCD 的边AB=6 cm ,BC=8cm ,在BC 上取一点P ,在CD 边上取一点Q ,使∠APQ 成直角,设BP=x cm ,CQ=y cm ,试以x 为自变量,写出y 与x 的函数关系式.ACD P Q解:∵∠APQ=90°,∴∠APB+∠QPC=90°. ∵∠APB+∠BAP=90°,∴∠QPC=∠BAP ,∠B=∠C=90° .∴△ABP ∽△PCQ.,86,yxx CQ BP PC AB =-= ∴x x y 34612+-=.11.(2006年XX 市)如图,在矩形ABCD 中,AB=2AD ,线段EF=10.在EF 上取一点M ,分别以EM 、MF 为一边作矩形EMNH 、矩形MFGN ,使矩形MFGN ∽矩形ABCD .令MN=x ,当x 为何值时,矩形EMNH 的面积S 有最大值?最大值是多少? 解:∵矩形MFGN ∽矩形ABCD ∴MF=2MN =2x ∴ EM=10-2x∴S=x (10-2x )=-2x 2+10x=-2(x-2.5)2+12.5 ∵1020<<x ,∴50<<x当x=2.5时,S 有最大值12.512.(2008XX 内江)如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为0.5 米. 答案:如图所示建立直角坐标系则:设c ax y +=2将点)1,5.0(-,)5.2,1(代入,⎩⎨⎧+=+-⨯=ca c a 5.2)5.0(12,解得⎩⎨⎧==5.02c a 5.022+=x y 顶点)5.0,0(,最低点距地面0.5米.13.(2008XXXX)小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.(1)求S 与x 之间的函数关系式,并写出自变量x 的取值X 围; (2)当x 是多少时,矩形场地面积S 最大?最大面积是多少? 解:(1)根据题意,得x x x xS 3022602+-=⋅-=自变量的取值X 围是(2)∵01<-=a ,∴S 有最大值当时,答:当为15米时,才能使矩形场地面积最大,最大面积是225平方米.14.(2008年XX 市)随着绿城XX 近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉与树木,根据市场调查与预测,种植树木的利润与投资量成正比例关系,如图12-①所示;种植花卉的利润与投资量成二次函数关系,如图12-②所示(注:利润与投资量的单位:万元)(1)分别求出利润与关于投资量的函数关系式;(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少? 解:(1)设=,由图12-①所示,函数=的图像过(1,2),所以2=,故利润关于投资量的函数关系式是=;因为该抛物线的顶点是原点,所以设2y =,由图12-②所示,函数2y =的图像过(2,2),所以,故利润2y 关于投资量的函数关系式是2221x y =; (2)设这位专业户投入种植花卉万元(),则投入种植树木(x -8)万元,他获得的利润是万元,根据题意,得 ==+21y y +==∵021>=a ∴当时,的最小值是14;∴他至少获得14万元的利润.因为,所以在对称轴2=x 的右侧, z 随x 的增大而增大所以,当8=x 时,z 的最大值为32.15.(08XX 聊城)如图,把一X 长10cm ,宽8cm 的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).(1)要使长方体盒子的底面积为48cm 2,那么剪去的正方形的边长为多少?(2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由;(3)如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形,然后折合成一个有盖的长方体盒子,是否有侧面积最大的情况;如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由.解:(1)设正方形的边长为cm ,则.即.解得(不合题意,舍去),.剪去的正方形的边长为1cm . (2)有侧面积最大的情况.设正方形的边长为cm ,盒子的侧面积为cm 2,则与的函数关系式为:.即.改写为.当时,.即当剪去的正方形的边长为2.25cm 时, 长方体盒子的侧面积最大为40.5cm 2.(3)有侧面积最大的情况.设正方形的边长为cm ,盒子的侧面积为cm 2.若按图1所示的方法剪折, 则与的函数关系式为:x xx x y ⋅-⋅+-=22102)28(2 即.当时,.若按图2所示的方法剪折, 则与的函数关系式为:x xx x y ⋅-⋅+-=2282)210(2. 即.当时,.比较以上两种剪折方法可以看出,按图2所示的方法剪折得到的盒子侧面积最大,即当剪去的正方形的边长为cm 时,折成的有盖长方体盒子的侧面积最大,最大面积为cm 2.16.(08XX)一座拱桥的轮廓是抛物线型(如图16所示),拱高6m ,跨度20m ,相邻两支柱间的距离均为5m .(1)将抛物线放在所给的直角坐标系中(如图17所示),求抛物线的解析式; (2)求支柱的长度;(3)拱桥下地平面是双向行车道(正中间是一条宽2m 的隔离带),其中的一条行车道能否并排行驶宽2m 、高3m 的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.解:(1)根据题目条件,的坐标分别是.设抛物线的解析式为,将的坐标代入,得解得.所以抛物线的表达式是.(2)可设,于是从而支柱的长度是米.(3)设是隔离带的宽,是三辆车的宽度和,则点坐标是.过点作垂直交抛物线于,则.根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.。
专题:二次函数与几何图形综合——图形面积问题(后附答案)【精品】
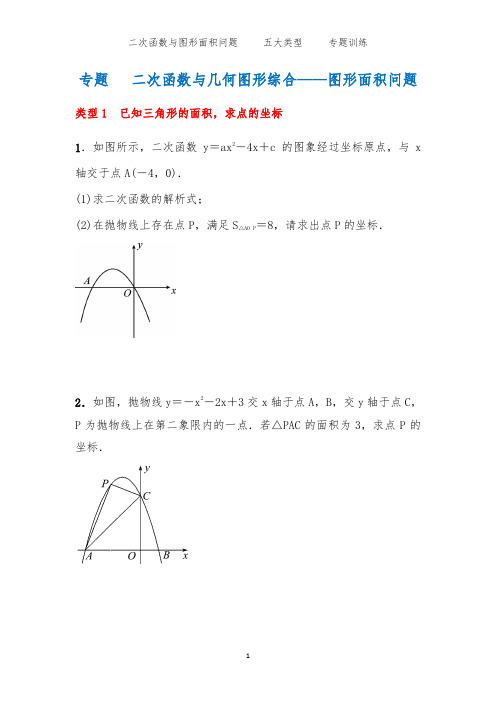
专题二次函数与几何图形综合——图形面积问题类型1 已知三角形的面积,求点的坐标
1.如图所示,二次函数y=ax2-4x+c的图象经过坐标原点,与x 轴交于点A(-4,0).
(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AO P=8,请求出点P的坐标.
2.如图,抛物线y=-x2-2x+3交x轴于点A,B,交y轴于点C,P为抛物线上在第二象限内的一点.若△PAC的面积为3,求点P的坐标.
类型2 已知三角形面积之间的数量关系,求点的坐标
3.如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).(1)求出图象与x轴的交点A,B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=5
4
S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
类型3 求三角形面积的最值
4.如图,直线l:y=-3x+3与x轴、y轴分别相交于A,B两点,抛物线y=ax2-2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数解析式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM,BM.设点M的横坐标为m,△ABM的面积为S,求S关于m的函数解析式,并求出S的最大值.。
二次函数应用几何图形的最大面积问题教学课件

求解极值点
通过求导数并令其为0,找到函 数的极值点。
确定最大面积
根据极值点和单调性,确定几 何图形的最大面积对应的点。
05
练习题与答案解析
练习题
01
02
03
题目1
一个矩形ABCD的面积为 12,其中AB=2,求BC的 最大值。
题目2
一个直角三角形ABC的面 积为6,其中∠C=90°, AC=3,求BC的最大值。
详细描述
首先设定三角形的底和高为二次函数 的变量,然后根据二次函数的性质, 找到使面积最大的底和高的值。
利用二次函数求圆形面积的最大值
总结词
通过设定圆的半径为二次函数的变量 ,利用二次函数的性质求圆的最大面 积。
详细描述
首先设定圆的半径为二次函数的变量 ,然后根据二次函数的性质,找到使 面积最大的半径的值。
02
几何图形可以由二次函数图像与x 轴、y轴的交点确定,进而形成三 角形、矩形、平行四边形等。
二次函数的最值与几何图形面积的关系
二次函数的最值出现在顶点处,此时 对应的x值为函数的零点或对称轴。
几何图形面积的最大值或最小值出现 在二次函数最值处,可以通过求导数 或配方法找到最值点。Βιβλιοθήκη 02常见几何图形面积公式
题目3
一个等腰三角形ABC的面 积为10,其中AB=AC, ∠B=45°,求BC的最大值 。
答案解析
解析1
设BC=x,则矩形的面积可以表 示为2x=12,解得x=6。由于AB 已经给定为2,所以BC的最大值
为6。
解析2
设BC=x,则直角三角形的面积 可以表示为1/2×3x=6,解得 x=4。由于AC已经给定为3,所
《二次函数与图形面积问题》PPT课件 人教版九年级数学

即当AC、BD的长均为5时,四边形ABCD的面积最大.
2.用一段长为30m的篱笆围成一个一边靠墙的矩形菜园(如 图所示),墙长为18m,这个矩形的长,宽各为多少时, 菜园的面积最大,最大面积是多少?
解:设矩形的长为x m,面积为y m2,则矩形的宽为15- 2xm.
y
x
15
x
2
=
1 2
x2
15x.
二次函数与图 形面积问题
R·九年级上册
复习导入
用你认为最简单的方法求出顶点坐标,说
出开口方向,对称轴及最值.
(1)y=x2-4x-5
开口方向 对称轴 顶点坐标 最小值
向上 x=2 (2,-9) -9
(2)y=-x2+x+ 1 4
向上
x=1 4
(1 ,1) 22 1
2
探究新知
知识点 利用二次函数解决最大(小)面积问题
2
2
x2
5x
A
B
所以当
x= -
2
5 (-
1
=5 )
时,S取最大值,S最大值
1 52 2
5 5=
25 2
2
当AC,BD的长均为5时,四边形ABCD的面积最大.
6. 一块三角形材料如图所示,∠A=30°,∠C=90°,
AB=12. 用这块材料剪出一个矩形CDEF,其中,点D,
E,F分别在BC,AB,AC上,要使剪出的矩形CDEF的
D
GC
则AH=a-x,HE = a - x2 + x2 ,
H
S正方形EFGH [ (a - x)2 x2 ]2 =2 x2 2ax + a2
当x=
a 2
二次函数应用-几何图形的最大面积问题精品PPT课件

Q1cm/秒B
∴ 当P、Q同时运动2秒后ΔPBQ的面积y最大 最大面积是C,AD⊥BC, BC=160cm ,AD=120cm,
(1)设矩形EFGH的长HG=y,宽HE=x,确定y与x的函 数关系式;
(2)当x为何值时,矩形EFGH的面积S最大?
最 值。
2。有取值范围的在端点或顶点处取最值。
自学教材20页 “动脑筋”
例1:如图,在一面靠墙的空地上用长为24米 的篱笆,围成中间隔有两道篱笆的长方形花 圃,设花圃的宽AB为x米,面积为S平方米。 (1)求S与x的函数关系式及自变量的取值范围。
(2)当x取何值时所围成的花圃面积最大,
最大值是多少?
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
演讲人:XXXXXX 时 间:XX年XX月XX日
(四)课堂小结
1. 对于面积最值问题应该设图形一边长为自 变量,所求面积为函数建立二次函数的模型, 利用二次函数有关知识求得最值,要注意函数 的自变量的取值范围。
2. 用函数知识求解实际问题,需要把实际问 题转化为数学问题再建立函数模型求解,解要 符合实际题意,要注意数与形结合。
1.在一幅长60 cm,宽40 cm的矩形风景画的四周 镶一条金色纸边,制成一幅矩形挂图,如图所示, 如果要使整个挂图的面积是y cm2,设金色纸边 的宽度为x cm,那么y关于x的函数是( ) A.y=(60+2x)(40+2x)
(一)思前想后
1.二次函数y=ax2+bx+c(a≠0)的顶点坐标、 对称轴和最值
2.(1)求函数y=x2+2x-3的最值。 (2)求函数y=x2+2x-3 (0≤x ≤ 3)
“二次函数”面积最值问题的几种解法

“二次函数”面积最值问题的几种解法以微课堂公益课堂,奥数国家级教练与四位特级教师联手执教。
二次函数是初中数学的一个重点、难点,也是中考数学必考的一个知识点。
特别是在压轴题中,二次函数和几何综合出现的题型,才是最大的区分度。
而求三角形面积的最值问题,更是常见。
今天介绍二次函数考试题型种,面积最值问题的4种常用解法。
同学们只要熟练运用一两种解法,炉火纯青,在考试答题的时候,能够轻松答题,就好。
原题:在(1)中的抛物线上的第二象限是否存在一点P,使△PBC的面积最大?若存在,求出P点的坐标及△PBC的面积最大值,若没有,请说明理由。
考试题型,大多类似于此。
求面积最大值的动点坐标,并求出面积最大值。
一般解题思路和步骤是,设动点P的坐标,然后用代数式表达各线段的长。
通过公式计算,得出二次函数顶点式,则坐标和最值,即出。
解法一:补形,割形法。
方法要点是,把所求图像的面积适当的割补,转化成有利于面积表达的常规几何图形。
请看解题步骤。
解法二:铅锤定理,面积=铅锤高度×水平宽度÷2。
这是三角形面积表达方法的一种非常重要的定理。
铅锤定理,在教材上没有,但是大多数数学老师都会作为重点,在课堂上讲解。
因为,铅锤定理,在很多地方都用的到。
这里,也有铅锤定理的简单推导,建议大家认真体会。
解法二:铅锤定理,在求二次函数三角形面积最值问题,运用非常多。
设动点P的坐标,然后用代数式分别表达出铅锤高度和水平宽度,然后利用铅锤定理的计算公式,得出二次函数,必有最大值。
解法三:切线法。
这其实属于高中内容。
但是,基础好的同学也很容易理解,可以看看,提前了解一下。
解法四:三角函数法。
请大家认真看上面的解题步骤。
总之,从以上的四种解法可以得出一个规律。
过点P做辅助线,然后利用相关性质,找出各元素之间的关系。
设动点P的坐标,然后找出各线段的代数式,再通过面积计算公式,得出二次函数顶点式,求出三角形面积的最大值。
对于同学们中考数学来说,只要你熟练掌握解法一和解法二,那么二次函数几何综合题中,求三角形面积最大值问题,就非常简单了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“P+S自能发展教育”数学教学课案
学科:数学年级:九年级备课人:李龙
课题:二次函数与几何综合——面积问题课型:专题课课时数:1课时
教学目标1、掌握常见的面积问题模型及处理方法
2、灵活运用数形结合思想解决相关问题
教学重难点重点:面积问题的转化方法难点:数形结合思想的运用
教学辅工具多媒体、小白板
教学流程师生活动设计意图
课前预
习
一、课前预习,自能感知
1:已知A(-1,0),B(3,0),P(4,2),求PAB
S
∆
.
2:已知C(1,-3),D(1,1),P(4,2),求PCD
S
∆
.
3:已知抛物线223
y x x
=--与x轴交于A、B两点(A左B右),
P为x轴上方抛物线上一点,若6
PAB
S
∆
=,求P点坐标.
变式1:若P为抛物线上一点,6
PAB
S
∆
=,求P点坐标.
变式2:C(m,1),D(n,1)(m<n)在抛物线上,若P为抛物线上
一点,45
PCD
S
∆
=,求P点坐标.
设计意图:
本节作为二次函数
与几何综合中的一
个重要专题,是九年
级调考与中考的常
考考点,课前预习部
分通过几个简单的
预习题让学生熟悉
常见的面积问题的
解法,以及让学生自
己总结出数学模型,
掌握通性通法。
思考:以上题目中的三角形的边有什么共同特征?
你能否总结出具有这类特征的三角形的面积的通用求法?
师生活动:学生分小组展示预习成果,提炼出面积问题的基本模
型,老师引导各小组互相补充完善,最终得出正确的模型及解决
办法。
课
中
展
示
交
流
二、课中探究,自能发现
【探究】如图,已知直线
1
3
2
y x
=+与抛物线2
1
2
y x
=交于A、B两
点,P为直线AB下方的抛物线上一点,且
PAB
S
∆
=5,求P点坐标.
解题思路:线转坐标,改“斜”归“正”
具体方法:
1、K形法(补形):从三角形的各顶点作坐标轴的平行线,得K字
形,用面积和差计算;
2、铅垂法:过所求点作轴的平行线,用面积和差计算;
3、牵引法:过所求点作其对边的平行线与坐标轴相交,得一与所求
三角形面积相同的三角形.
师生活动:各小组展示自己的解题方法,其他小组点评该方法的优
劣处,老师引导学生对常见的解题方法进行总结。
设计意图:
探究部分给出了一
道非常经典的题目,
本题解法众多,但是
核心方法依然是之
前总结的通性通法,
需要学生根据题目
条件把较复杂的情
况转化为自己熟悉
的模型。
此题老师要求各小
组尽可能多的想出
不同的解法,以此让
学生熟悉面积问题
常见的转换方法,并
且总结出各种方法
的优劣之处,达到灵
活选取解法的目的。
三、巩固提高,自能建构
1、如图,已知直线132
y x =
+与抛物线21
2y x =交于A 、B 两点,在
直线AB 下方的抛物线上一点是否存在点P ,使PAB S ∆的值最大?若存在,求P 点坐标;若不存在,请说明理由. (请尝试多种解法)
师生活动:学生分小组讨论,学生结合前面的方法来解决这道问题,老师引导学生找到这两题的联系,以加深学生对方法的理解。
四、 知识延伸,自能拓展
1、(2018武汉中考)已知抛物线L :y =-x 2+2x +1,如图1,过定
点的直线y =kx -k +4(k <0)与抛物线L 交于点M 、N .若△BMN 的面积等于1,求k 的值.
师生活动:学生独立思考3分钟,然后小组讨论交换意见,老师巡堂为学生解惑。
设计意图:
这一部分是上一部分题目的一个变式,此题是求面积的最值,学生可通过探究部分总结的解法,类比的解决本题。
需要注意的是求最值可以采取代数方法也可以通过几何作图来说明。
设计意图:
本题为2018年武汉中考题,让学生提前感受中考题,了解中考的考法。
本题在前面的基础上加大了计算的难度,但学生依然可以通过前面的方法来入手解决本题,以此让学生体会化繁为简的思想。
五、 课堂检测,自能参与
1、(2017武汉元调)已知抛物线y =2
1x 2
+mx -2m -2(m >0)与x 轴交于A 、B 两点,点A 在点B 的左边,与y 轴交于点C ,抛物线上
有一点D (-1,n ),若△ACD 的面积为5,求m 的值
设计意图:
这一部分选取了
2017年的元调题,可
以让学生对本节课
所学内容进一步的
加深理解,并灵活运
用总结出的方法。
课
后
作业
勤学早P 45
板书设计
二次函数与几何综合——面积问题 1、常见模型:
当AB //x 轴时, 当CD //y 轴时,
12PAB A B P A S x x y y ∆=
-⋅- 1
2
PCD C D P C S y y x x ∆=-⋅- 2、解题思路:线转坐标,改“斜”归“正” 3、具体方法:
①K 形法(补形); ②铅垂法; ③牵引法:
教学 反思。
