3.5《三角形的内切圆》同步练习
3.5_用15三角形的内切圆

E
B
┓
C
2,已知Rt△ABC的两直角边分别为a,b,你会求它的 内切圆半径吗? A
┐
●
B
C 10
小
结
1.掌握三角形内切圆的概念; 2.会画三角形的内切圆;
3.
三角形的内心的性质有哪些
11
练习:
在Rt△ABC中,∠C=90°,AC=3,AB=5, 则它的内切圆与外接圆半径分别为( )
C
A.1.5,2.5 C.1,2.5
老师提示:若点I是外心呢?
7
跟踪训练
1.如图1,⊙O内切于△ABC,切点为D,E,F.已知 ∠B=50°∠C=60°,• 连接OE,OF,DE,DF,那么∠EDF 等于( ) B A.40° B.55° C.65° D.70°
2.如图2,⊙O是△A BC的内切圆,D,E,F是切点,
B 点,∠A=50°,∠C=60°,• 则∠DOE=( ) A.70° B.110° C.120° D. 140°
o
C B
内心: 三角形 内切圆 的圆心
三角形三条 角平分线的 交点
A
O
B
1.到三边的距离 相等; 2.OA、OB、OC 分别平分∠BAC、 ∠ABC、∠ACB C 3.内心在三角形内 部.
16
例1. 如图,△ABC中,O是内心,∠A的平分线和 △ABC的外接圆相交于点D. 求证:DO=DB
证明:连接BO, ∵ AD是∠BAC的平分线 ∴ ∠1=∠2, 同理 ∠3=∠4, 而 ∠BOD=∠1+∠3, ∠ OBD=∠4+∠5, 又 ∵∠2=∠5, ∴∠BOD=∠OBD. ∴DO=DB.
A
12
B
3 4 5
O C D
人教版九年级上册数学专题训练《三角形的内切圆》
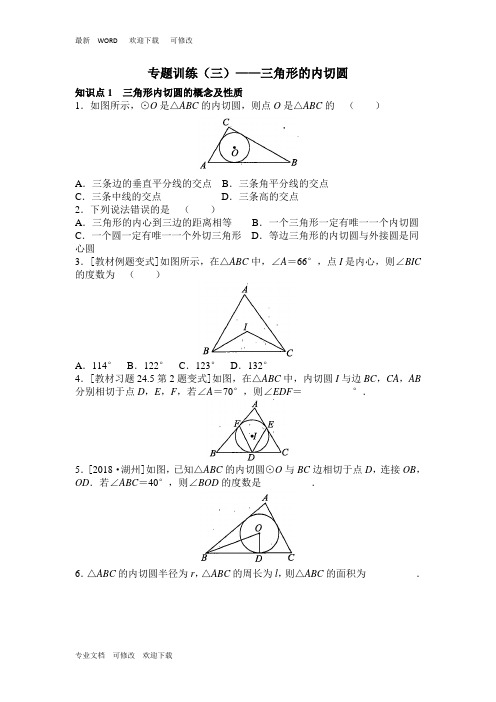
专题训练(三)——三角形的内切圆知识点1 三角形内切圆的概念及性质1.如图所示,⊙O是△ABC的内切圆,则点O是△ABC的()A.三条边的垂直平分线的交点B.三条角平分线的交点C.三条中线的交点D.三条高的交点2.下列说法错误的是()A.三角形的内心到三边的距离相等B.一个三角形一定有唯一一个内切圆C.一个圆一定有唯一一个外切三角形D.等边三角形的内切圆与外接圆是同心圆3.[教材例题变式]如图所示,在△ABC中,∠A=66°,点I是内心,则∠BIC 的度数为()A.114°B.122°C.123°D.132°4.[教材习题24.5第2题变式]如图,在△ABC中,内切圆I与边BC,CA,AB 分别相切于点D,E,F,若∠A=70°,则∠EDF=__________°.5.[2018·湖州]如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,OD.若∠ABC=40°,则∠BOD的度数是__________.6.△ABC的内切圆半径为r,△ABC的周长为l,则△ABC的面积为__________.知识点2 作三角形的内切圆7.为美化校园,学校准备在如图所示的三角形空地上修建一个面积最大的圆形花坛,请在图中画出这个圆形花坛(保留作图痕迹,不要求写作法).练习8.如图所示,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则()A.EF>AE+BF B.EF<AE+BF C.EF=AE+BF D.EF≤AE+BF9.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,如图,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”()A.3步B.5步C.6步D.8步10.如图,△ABC是一张三角形纸片,⊙O是它的内切圆,D,E是⊙O的两个切点,已知AD=6 cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是()A.9 cm B.12 cm C.15 cm D.18 cm11.如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为()A .∠AIB =∠AOB B .∠AIB ≠∠AOBC .121802AIB AOB ∠-∠=°D .121802AOB AIB ∠-∠=°12.如图,Rt △ABC 的内切圆⊙O 切斜边AB 于点D ,切BC 于点E ,BO 的延长线交AC 于点M .求证:BO ·BC =BD ·BM .13.[教材习题24.5第5题变式]如图,E 为△ABC 内一点,AE 的延长线交△ABC 的外接圆⊙O 于点D ,且DB =DC =DE .求证:E 为△ABC 的内心.14.数学活动:求重叠部分的面积(1)问题情境:如图①,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点P 与等边三角形ABC 的内心O 重合,已知OA =2,则图中重叠部分△PAB 的面积是__________.(2)探究:在(1)的条件下,将纸片绕点P 旋转至如图②所示的位置,纸片两边分别与AC ,AB 交于点E ,F ,则图②中重叠部分的面积与图①中重叠部分的面积是否相等?若相等,请给予证明;若不相等,请说明理由.15.已知△ABC 的内切圆⊙O 与AB ,BC ,AC 分别相切于点D ,E ,F ,若EF DE ,如图①.(1)判断△ABC 的形状,并证明你的结论;(2)设AE 与DF 相交于点M ,如图②,AF =2FC =4,求AM 的长.1、最困难的事就是认识自己。
三角形的内切圆和外接圆综合练习题

三角形的内切圆和外接圆综合练习题三角形是几何学中的基本图形之一,而三角形的内切圆和外接圆是与三角形密切相关的重要概念。
本文将针对内切圆和外接圆,提供一些综合练习题,帮助读者更好地理解和掌握这些概念。
练习题一:内切圆的性质1. 证明:对于任意三角形ABC,其内切圆的圆心O与三角形的内心I和重心G共线。
2. 若三角形ABC的内切圆的半径为r,三角形的半周长为s,证明:AI+BI+CI=2s。
3. 若三角形ABC的内切圆的半径为r,三角形的面积为S,证明:S=r*s,其中s为三角形的半周长。
练习题二:内接圆与外接圆关系1. 如果一个三角形的内切圆和外接圆的半径分别为r和R,证明:r<=R/2。
2. 若一个三角形的内切圆和外接圆的半径分别为r和R,证明:r^2=2Rr,其中r和R分别为内切圆和外接圆的半径。
3. 若一个三角形的内切圆和外接圆的半径分别为r和R,证明:r(R+r)=s,其中s为三角形的半周长。
练习题三:内切圆和外接圆的半径关系1. 三角形ABC的内切圆半径为r,外接圆半径为R,外接圆的圆心为O。
若角A=60°,角B=90°,求R:r。
2. 已知三角形ABC的内切圆半径为r,三角形BCD的外接圆半径为R,求证:(R-r)^2=(a-b)(a-c),其中a、b、c分别为三角形BCD的三边长。
这些练习题旨在帮助读者巩固对于三角形内切圆和外接圆的理解,掌握相关的性质和公式,并能够运用这些知识解决具体的问题。
通过练习,读者将能更加深入地理解三角形的性质与相关的几何概念。
总结:本文围绕三角形的内切圆和外接圆的知识点,给出了一些综合练习题。
这些练习题覆盖了内切圆和外接圆的性质、关系和半径之间的关系。
通过解答这些练习题,读者能够提高对于三角形相关概念的理解和应用能力,为进一步的几何学知识的学习打下坚实的基础。
继续努力学习和练习,相信读者能够在几何学领域取得更大的成就!。
三角形的内切圆练习题

三角形的内切圆练习题三角形的内切圆练习题在数学中,三角形是一个基础而重要的概念。
而在三角形的内部,有一个特殊的圆形,称为内切圆。
内切圆是可以与三角形的三条边都相切的圆形,它有着许多有趣的性质和应用。
在本文中,我们将通过一些练习题来探索三角形的内切圆。
练习题1:设三角形ABC的三个内角分别为∠A、∠B和∠C,内切圆的半径为r。
证明:三角形ABC的面积S等于内切圆的半径r与三角形ABC三边长之和的乘积的一半,即S = r × (AB + BC + AC) / 2。
解答:我们可以通过两种方法来证明这个结论。
方法一:利用三角形的高度我们知道,三角形的面积可以通过底边与高度的乘积来计算。
考虑三角形ABC,假设内切圆的圆心为O,与三边AB、BC和AC分别相切于点D、E和F。
连接AO、BO和CO,分别延长到与内切圆相交于点P、Q和R。
由于AO与DO垂直且相等,所以DO是三角形ABC的高度。
同样地,EO和FO也是三角形ABC 的高度。
因此,我们可以得到三角形ABC的面积S = DO × AB / 2 + EO × BC /2 + FO × AC / 2。
另一方面,根据内切圆的性质,我们知道DO = EO = FO = r。
将这个结果代入到上面的等式中,我们可以得到S = r × (AB + BC + AC) / 2,证明完成。
方法二:利用三角形的面积公式我们知道,三角形ABC的面积可以通过海伦公式来计算,即S = √[s(s - AB)(s- BC)(s - AC)],其中s是三角形的半周长,即s = (AB + BC + AC) / 2。
我们将这个面积公式代入到S = r × (AB + BC + AC) / 2中,可以得到S = √[s(s - AB)(s - BC)(s - AC)] = r × (AB + BC + AC) / 2。
通过对等式两边进行平方操作,我们可以得到等式两边的平方相等,从而证明了这个结论。
三角形的内切圆-练习题 含答案

三角形的内切圆副标题题号一二总分得分一、选择题(本大题共2小题,共6.0分)1.下列语句正确的个数是过平面上三点可以作一个圆;平分弦的直径垂直于弦;在同圆或等圆中,相等的弦所对的圆周角相等;三角形的内心到三角形各边的距离相等.A. 1个B. 2个C. 3个D. 4个【答案】A【解析】解:过平面上不在同一直线上的三点可以作一个圆,错误;平分弦不是直径的直径垂直于弦,故错误;在同圆或等圆中,相等的弦所对的圆周角相等,错误;三角形的内心到三角形各边的距离相等,正确,正确的有1个,故选A.利用确定圆的条件、垂径定理、圆周角定理及三角形的内心的性质分别判断后即可确定正确的选项;本题考查了确定圆的条件、垂径定理、圆周角定理及三角形的内心的性质等知识,解题的关键是能够了解有关的定义及定理,难度不大.2.如图,在中,,点I是内心,则的大小为A.B.C.D.【答案】C【解析】解:,,点I是内心,,,,,故选:C.根据三角形内角和定理求出,根据内心的概念得到,,根据三角形内角和定理计算即可.本题考查的是三角形的内切圆和内心,掌握三角形的内心的概念、三角形内角和定理是解题的关键.二、填空题(本大题共1小题,共3.0分)3.如图,O是内一点,且O到三边AB、BC、CA的距离相等,若,则______度【答案】125【解析】解:点O到三边AB、BC、CA的距离相等,点O是三角形的内心,.根据点O到三边AB、BC、CA的距离相等,知三角形是内心,从而结合角平分线的定义和三角形的内角和定理,即可得到.熟悉三角形的内心的性质:三角形的内心是三角形的三条角平分线的交点,它到三角形的三边的距离相等;当O是内心时,则.。
中考数学复习----《三角形的内切圆与内心》知识点总结与专项练习题(含答案解析)

中考数学复习----《三角形的内切圆与内心》知识点总结与专项练习题(含答案解析)知识点总结1. 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
几何语言:若弦CD AB ,交于点P ,则PD PC PB PA ⋅=⋅。
推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
几何语言:若AB 是直径,CD 垂直AB 于点P ,则PB PA PD PC ⋅==22。
2. 弦切角定理:(1)弦切角的定义:如图像∠ACP 这样,顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
(2)弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半。
等于这条弧所对的圆周角。
即∠PCA=∠PBC 。
3. 切线长定理:(1)切线长定义:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。
(2)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角。
4. 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT2=PA•PB(切割线定理)。
推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
几何语言:∵PBA,PDC是⊙O的割线∴PD•PC=PA•PB由上可知:PT2=PA•PB=PC•PD。
5. 三角形的内切圆与内心:内切圆与内心的概念:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
三角形的内心就是三角形三个内角角平分线的交点。
练习题1、(2022•恩施州)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π).【分析】根据题意,先作出相应的辅助线,然后求出内切圆的半径,再根据图形可知:阴影部分的面积=△ABC的面积﹣正方形CEOD的面积﹣⊙O面积的,代入数据计算即可.【解答】解:作OD⊥AC于点D,作OE⊥CB于点E,作OF⊥AB于点F,连接OA、OC、OB,如图,∵∠C=90°,OD=OE=OF,∴四边形CEOD是正方形,∵AC=4,BC=3,∠C=90°,∴AB===5,∵S△ABC=S△AOC+S△COB+S△BOA,∴=,解得OD=OE=OF=1,∴图中阴影部分的面积为:﹣1×1﹣π×12×=5﹣π,故答案为:5﹣π.2、(2022•泰州)如图,△ABC中,∠C=90°,AC=8,BC=6,O为内心,过点O的直线分别与AC、AB边相交于点D、E.若DE=CD+BE,则线段CD的长为.【分析】连接BO,CO,结合内心的概念及平行线的判定分析可得当DE=CD+BE时,DE∥BC,从而利用相似三角形的判定和性质分析计算.【解答】解:如图,过点O的直线分别与AC、AB边相交于点D、E,连接BO,CO,∵O为△ABC的内心,∴CO平分∠ACB,BO平分∠ABC,∴∠BCO=∠ACO,∠CBO=∠ABO,当CD=OD时,则∠OCD=∠COD,∴∠BCO=∠COD,∴BC∥DE,∴∠CBO=∠BOE,∴BE=OE,则DE=CD+BE,设CD=OD=x,BE=OE=y,在Rt△ABC中,AB==10,∴,即,解得,∴CD=2,过点O作D′E′⊥AB,作DE∥BC,∵点O为△ABC的内心,∴OD=OE′,在Rt△ODD′和Rt△OE′E中,,∴△ODD′≌△OE′E(ASA),∴OE=OD′,∴D′E′=DE=CD+BE=CD′+BE′=2+=,在△AD′E′和△ABC中,,∴△AD′E′∽△ABC,∴,∴,解得:AD′=,∴CD′=AC﹣AD′=,故答案为:2或.3、(2022•黔东南州)如图,在△ABC中,∠A=80°,半径为3cm的⊙O是△ABC的内切圆,连接OB、OC,则图中阴影部分的面积是cm2.(结果用含π的式子表示)【分析】根据角A的度数和内切圆的性质,得出圆心角DOE的度数即可得出阴影部分的面积.【解答】解:∵∠A=80°,⊙O是△ABC的内切圆,∴∠DOE=180°﹣()=180°﹣(180°﹣∠A)=130°,∴S扇形DOE==(cm2),故答案为:.4、(2022•宜宾)我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为.【分析】如图,设内切圆的圆心为O,连接OE、OD,则四边形EODC为正方形,然后利用内切圆和直角三角形的性质得到AC+BC=AB+6,(BC﹣AC)2=49,接着利用完全平方公式进行代数变形,最后解关于AB的一元二次方程解决问题.【解答】解:如图,设内切圆的圆心为O,连接OE、OD,则四边形EODC为正方形,∴OE=OD=3=,∴AC+BC﹣AB=6,∴AC+BC=AB+6,∴(AC+BC)2=(AB+6)2,∴BC2+AC2+2BC×AC=AB2+12AB+36,而BC2+AC2=AB2,∴2BC×AC=12AB+36①,∵小正方形的面积为49,∴(BC﹣AC)2=49,∴BC2+AC2﹣2BC×AC=49②,把①代入②中得AB2﹣12AB﹣85=0,∴(AB﹣17)(AB+5)=0,∴AB=17(负值舍去),∴大正方形的面积为289.故答案为:289.。
初中数学《三角形的内切圆、外切圆》专题练习试卷及答案

6《三角形的内切圆、外接圆》专题练习试卷1. 如图,⊙O 为△ABC 的内切圆,AC =10,AB =8,BC =9,点D ,E 分别为BC ,AC 上的点,且DE 为⊙O 的切线,则△CDE 的周长为( )A .9B .7C .11D .81题图 2题图 3题图2. 如图,AB 、AC 、BD 是⊙O 的切线,切点分别是P 、C 、D .若AB =5,AC =3,则BD 的长是( )A .4B .3C .2D .13. 如图,△ABC 内接于圆,D 是BC 上一点,将∠B 沿AD 翻折,B 点正好落在圆点E 处,若∠C =50°,则∠BAE 的度数是( )A .40°B .50°C .80°D .90°4.已知:如图,∠C =90°,内切圆O 分别与BC 、AC 相切于点D 、E ,判断四边形ODCE 的形状,并说明理由.4题图65.如图,在△ABC 中,∠A =60°,∠C =70°,点O 是△ABC 的内心,BO 的延长线交AC 于点D ,求∠BDC 的度数.5题图弧长和扇形面积题型:1. 已知正六边形的边长为8,则较短的对角线长为 .2. 如图,正六边形ABCDEF 内接于⊙O 其边长为2,则⊙O 的内接正三角形ACE 的边长为 .2题图 5题图 3.一圆锥的侧面积是底面积的2倍,这个圆锥的侧面展开图所对应的扇形的圆心角是( ).A .120° B.180° C.240° D.300°4.底面圆半径为3cm ,高为4cm 的圆锥侧面积是( ).A .7.5π cm 2B .12π cm 2C .15πcm 2D .24π cm 25.如图是两个半圆,点O 为大半圆的圆心, AB 是大半圆的弦关与小半圆相切,且AB =24.问:能求出阴影部分的面积吗?若能,求出此面积;若不能,试说明理由.6.如图,若⊙O的周长为20πcm,⊙A、⊙B的周长都是4πcm,⊙A在⊙O内沿⊙O滚动,⊙B在⊙O外沿⊙O滚动,⊙B转动6周回到原来的位置,而⊙A只需转动4周即可,你能说出其中的道理吗?6题图参考答案1. C. 解析:设AB,AC,BC和圆的切点分别是P,N,M,CM=x,根据切线长定理,得CN=CM=x,BM=BP=9﹣x,AN=AP=10﹣x.则有9﹣x+10﹣x=8,解得:x=5.5.所以△CDE的周长=CD+CE+QF+DQ=2x=11.故选:C.1题图2. C. 解析:∵AC、AP为⊙O的切线,∴AC=AP=3,∵BP、BD为⊙O的切线,∴BP=BD,∴BD=PB=AB﹣AP=5﹣3=2.故选:C.63. C. 解析:连接BE,如图所示:,由折叠的性质可得:AB=AE,∴AB AE∴∠ABE=∠AEB=∠C=50°,∴∠BAE=180°﹣50°﹣50°=80°.故选:C.Array3题图4. 解:四边形ODCE为正方形,理由如下:∵内切圆O分别与BC、AC相切于点D、E,∴OE⊥AC,OD⊥BC.∵∠C=90°,∴四边形ODCE为矩形.又∵OD=OE,∴四边形ODCE为正方形.5. 解:∵∠A=60°,∠C=70°,∴∠ABC=50°,∵点O为△ABC的内心,∴∠DBC=∠ABC=25°,∵∠ACB=78°,∠DBC+∠C+∠BDC=180°,∴∠BDC=180°﹣78°﹣25°=77°.66弧长和扇形面积题型:1. 8. 解析:如图,六边形ABCDEF 是正六边形,连接BF ,作AH ⊥BF 于点H ,1题图根据题意可知:BF 为较短对角线,∵六边形ABCDEF 是正六边形,∴AB =AF =8,∠BAF =120°,∵AH ⊥BF ,∴∠BAH=12∠BAF =60°, ∴∠ABH =30°,∴AH=12AB =4, 根据勾股定理,得4,∴BF =2BH =8. 故答案为:8.2. 2. 解析:连接OB 交AC 于H .2题图在正六边形ABCDEF 中,∵AB =BC ,∠ABC =120°,6∴AB BC =,∴OB ⊥AC ,∴∠ABH =∠CBH =60°,AH =CH ,∴AH,∴AC =,故答案为.3. B. 解析:由得,∴.∴n =180°. 4. C. 解析:可求圆锥母线长是5cm .∴圆锥的侧面积为:π×3×5=15π.5. 解:将小圆向右平移,使两圆变成同心圆,如图,连OB ,过O 作OC ⊥AB 于C 点,则AC=BC =12,∵AB 是大半圆的弦且与小半圆相切,∴OC 为小圆的半径,∴S 阴影部分=S 大半圆-S 小半圆=12π•OB 2-12π•OC 2=12π(OB 2-OC 2)=12πAC 2=72π. 故答案为72π.5题图6. 解:∵圆O 的周长为20πcm ,∴圆O 的半径=10cm ,∵圆A 圆B 周长都是4πcm ,∴圆A 圆B 周长半径都是2,∴圆A 在圆O 内沿圆O 滚动半径是10﹣2=8,圆B 在圆O 外沿圆O 滚动半径是10+2=12∴要回到原来的位置,圆B 转动的周数=12÷2=6,圆A 转动的周数=8÷2=4.22rl r ππ=2l r =22180n r r ππ=。
(整理版)《三角形的内切圆》练习题

《三角形的内切圆》练习题
一、复习回忆
判断直线是圆的切线有哪些方法?
二、探索活动
活动一:如图1,点P在⊙O上,过点P作⊙O的切线.
活动二:如图2,点D、E、F在⊙O上,分别过点D、E、F作⊙O的切线,3条切线两两相交于点A、B、C.
活动三:△ABC,如何作⊙O,使它与△ABC的3边都相切呢?
与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.
问题1:分别作出以下三角形的内切圆,并观察内心的位置,你有什么发现?
问题2:比拟三角形的外心和内心,完成以下表格.
名称确定方法“心〞的性质“心〞的位置
外心〔三角形外接圆
的圆心〕
内心〔三角形内切圆
的圆心〕
三、达标训练
1.如图,I 是△ABC 的内心.根据以下条件,求∠BIC 的度数. 〔1〕∠B=50°,∠C=60°; 〔2〕∠A=50°.
2.如图,在△ABC 中,内切圆O 与边BC 、CA 、AB 分别相切于点D 、E 、F.
〔1〕当∠B=60°,∠C=70°,求∠EDF 的度数.
〔2〕假设连结EF ,那么△DEF 是什么三角形〔从角的方面考虑〕?并说明理由.
3.如图,等边△ABC 的边长为a .求它的内切圆与外接圆的半径.
四、延伸拓展
1.如图,Rt △A BC 中,∠C=90°,内切圆⊙I 分别切A C ,BC 于D ,E. 〔1〕四边形CDIE 是什么特殊四边形?为什么? 〔2〕如果AC=8,BC=6,求⊙I 的半径.
A
B
C I
D
E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.5 三角形的内切圆同步练习
◆基础训练
1.如图1,⊙O内切于△ABC,切点为D,E,F.已知∠B=50°,∠C=60°,?连结OE,OF,DE,DF,那么∠EDF等于()
A.40°B.55°C.65°D.70°
图1 图2 图3
2.如图2,⊙O是△ABC的内切圆,D,E,F是切点,∠A=50°,∠C=60°,?则∠DOE=()
A.70°B.110°C.120°D.130°
3.如图3,△ABC中,∠A=45°,I是内心,则∠BIC=()
A.112.5°B.112°C.125°D.55°
4.下列命题正确的是()
A.三角形的内心到三角形三个顶点的距离相等
B.三角形的内心不一定在三角形的内部
C.等边三角形的内心,外心重合
D.一个圆一定有唯一一个外切三角形
5.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分
别为()
A.1.5,2.5 B.2,5 C.1, 2.5 D.2,2.5
6.如图,在△ABC中,AB=AC,内切圆O与边BC,AC,AB分别切于D,E,F.
(1)求证:BF=CE;
(2)若∠C=30°,CE=23,求AC的长.
7.如图,⊙I切△ABC的边分别为D,E,F,∠B=70°,∠C=60°,M是DEF 上的动点(与D,E不重合),∠DMF的大小一定吗?若一定,求出∠DMF的大小;若不一定,请说明理由.
8.如图,△ABC中,∠A=m°.
(1)如图(1),当O是△ABC的内心时,求∠BOC的度数;
(2)如图(2),当O是△ABC的外心时,求∠BOC的度数;
(3)如图(3),当O是高线BD与CE的交点时,求∠BOC的度数.
◆提高训练
9.如图,在半径为R的圆内作一个内接正方形,?然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是()
A.(
2
2
)n R B.(1
2
)n R C.(1
2
)n-1R D.(2
2
)n-1R。
